Optimized Adversarial Tactics for Disrupting Cooperative Multi-Agent Reinforcement Learning

Abstract

Multi-agent reinforcement learning has demonstrated excellent performance in complex decision-making tasks such as electronic games, power grid management, and autonomous driving. However, its vulnerability to adversarial attacks may impede its widespread application. Currently, research on adversarial attacks in reinforcement learning primarily focuses on single-agent scenarios, while studies in multi-agent settings are relatively limited, especially regarding how to achieve optimized attacks with fewer steps. This paper aims to bridge the gap by proposing a heuristic exploration-based attack method named the Search for Key steps and Key agents Attack (SKKA). Unlike previous studies that train a reinforcement learning model to explore attack strategies, our approach relies on a constructed predictive model and a T-value function to search for the optimal attack strategy. The predictive model predicts the environment and agent states after executing the current attack for a certain period, based on simulated environment feedback. The T-value function is then used to evaluate the effectiveness of the current attack. We select the strategy with the highest attack effectiveness from all possible attacks and execute it in the real environment. Experimental results demonstrate that our attack method ensures maximum attack effectiveness while greatly reducing the number of attack steps, thereby improving attack efficiency. In the StarCraft Multi-Agent Challenge (SMAC) scenario, by attacking 5–15% of the time steps, we can reduce the win rate from 99% to nearly 0%. By attacking approximately 20% of the agents and 24% of the time steps, we can reduce the win rate to around 3%.

1. Introduction

Technological advancements have ushered in a new era of artificial intelligence, accompanied by significant progress in reinforcement learning (RL) in recent years. RL has been applied in various fields, including autonomous driving [1], power grid management [2], digital gaming [3,4,5], network defense systems [6,7,8,9], and vehicle control systems (e.g., distributed drive electric vehicles [10]). In such safety-critical cyber-physical systems, adversarial vulnerabilities could propagate through cooperative agents, leading to catastrophic failures. RL functions by learning policies that maximize long-term rewards, enabling agents to navigate through sequences of decisions in complex environments. RL can be broadly classified into single-agent reinforcement learning and multi-agent reinforcement learning (MARL) based on the number of agents involved.

Given the widespread application of RL, research on its robustness has gained particular significance. Numerous studies have underscored the susceptibility of current RL algorithms to adversarial attacks [11,12], which can lead to erroneous actions by the agents and subsequent undesirable consequences. Unlike adversarial attacks in traditional deep learning, those in deep reinforcement learning not only target immediate impacts but also aim for enduring effects on tasks, ultimately diminishing the model’s long-term rewards or inducing task failure [13]. In the current research landscape of reinforcement learning, most studies have focused on attacking single-agent reinforcement learning, with few investigations of adversarial attacks in MARL. Hence, researching how to efficiently and covertly execute adversarial attacks on MARL holds substantial importance. In current research, certain studies have overlooked the concealment aspect of attacks, resulting in attacks spanning entire task rounds [14]. Such wide-reaching attacks are susceptible to detection. Furthermore, certain methods for generating attack strategies based on RL essentially entail training a model using RL algorithms, albeit with different training objectives. Consequently, these methods are characterized by lengthy training durations, high computational costs, and a dearth of lightweight solutions. Additionally, while some rule-based adversarial attack methods have been proposed, most research has centered on single-agent RL [11,13,15], and there has been limited exploration in the MARL domain. Moreover, certain rule-based adversarial attack methods are only effective for discrete-action-space RL algorithms and cannot be applied in continuous action spaces. Furthermore, many of these methods encounter challenges with threshold determination [11,16]. Determining the appropriate threshold requires repetitive testing across various scenarios.

The notion of being more covert here encompasses two dimensions: fewer attack steps and fewer attack targets. To achieve this goal, we propose two strategies: Search for Key Steps and Search for Key Agent. In the first stage, we sequentially execute m-step attacks at each moment in a task round and predict the final state using a constructed prediction model. The attack effectiveness is evaluated by combining the predicted state with the value function T, and then the optimal attack timing t can be selected based on the best-performing test during this process. In the second stage, within the time interval $t\to t+m$, we test the effectiveness of individually attacking M agents one by one. This helps determine the weight of each agent, thereby establishing the priority of attack targets. Through these steps the attack timing and targets are determined, and we execute the attack using the worst-action selection strategy. We validated the effectiveness of this method in MPE and SMAC environments.

The main contributions of this paper are the following:

• We propose to search for critical attack steps, determining the optimal timing for attacks and thus enhancing the stealthiness of attacks along the temporal dimension.
• We prioritize agents during attacks, enabling more efficient attacks with fewer targeted agents.
• The effectiveness of the method has been validated in MPE and SMAC environments.

The remainder of this paper is organized as follows. Section 2 summarizes the current state of research on adversarial attacks in the field of RL. Section 3 introduces relevant prior knowledge and problem formulation. Section 4 provides a detailed description of the proposed adversarial attack method. Section 5 presents experimental details and an analysis of the experimental results. Section 6 provides concluding remarks and discusses potential future research directions.

2. Related Work

Attack targets in RL. In the current literature, adversarial attacks in RL are categorized as observation-based attacks [11,13,17,18,19], action-based attacks [20,21,22,23,24], environment-based attacks [25,26], reward-based attacks [27,28,29], and communication-based attacks [30,31]. Observation-, environment-, and communication-based attacks perturb agents’ input information, leading them to make erroneous decisions based on the perturbed input data. Some environment-based attacks, similar to reward-based attacks, are conducted during the training phase. These involve subtle modifications to the environment or reward values during training to prevent agents from obtaining an optimal strategy. Action-based attacks directly modify the output actions of agents. The ultimate goal of any of these attacks is to disrupt the execution of correct decision actions by agents, thereby reducing long-term rewards. Contingent on whether RL is used to acquire attack strategies, existing attack methods can be divided into two categories: learning-based or rule-based.

Learning-based adversarial attack in RL. In the context of MARL, Wang et al. [32] considered the selection of agents and actions as a mixed-space problem, leveraging HyAR [33] for its solution. In adversarial training, the capabilities of attackers are continually enhanced. Lin et al. [14] treated non-victim agents as part of the environment, thus transforming the problem of solving adversarial strategies into the task of finding the solution for single-agent RL with minimal reward. However, this approach overlooks the mutual influence between agents. In a study [20], sparse attacks were first applied in MARL scenarios. RL algorithms were deployed to learn adversarial attack strategies, seeking to maximize the reduction in reward by attacking fewer agents in fewer steps. Li et al. [15] argue that treating the model as a white box for attack purposes is unrealistic. They advocate for treating the model as a black box, training an adversarial agent and integrating it into the entire system to deviate from the original optimal strategy. Li et al. [34] employed a unilateral influence filter to decompose mutual information, quantifying the unilateral impact of adversarial agents on victim agents. This optimization framework enhances attack efficacy by leveraging a target adversarial oracle that generates worst-case target actions for each victim, thereby coercing the adversarial policy to steer victims toward collective failure. The crux of obtaining attack strategies through RL is still a process of training models using RL algorithms, albeit with different training objectives. Thus, while such methods may yield optimal attack strategies, they often incur significant time and computational costs. Additionally, their generalization performance is poor, requiring the training of different models for various algorithms and scenarios.

Rule-based adversarial attack in RL. To enhance the stealthiness of attacks, Lin et al. [11] proposed a timing attack method that determines whether to initiate an attack at a given moment by calculating the difference between the maximum and minimum probabilities in the current action space. A greater difference in action probabilities indicates a higher tendency towards certain actions, thus warranting an attack. However, this method overlooks the long-term impact of attacks. Similar approaches were proposed by Li et al. [15], incorporating weighted parameters to account for the long-term impact of attacks. Sun et al. [13] constructed a predictive model to forecast the system’s next state and employed a step-wise search process to identify adversarial strategies. Zan et al. [35] proposed a clustering-based approach that partitions agents into distinct groups according to their observational data. At each time step, the method selects the group with the maximum cumulative reward value as the attack target. Adversarial examples crafted against the agents’ policy networks are subsequently injected into their observations. However, rule-based methods like these encounter a significant challenge in threshold determination. Adjusting these thresholds may require continuous experimentation to suit different situations and scenarios. Furthermore, attack timings determined by rule-based approaches are not necessarily optimal, and may fail in effectively regulating attack frequencies.

In efforts to address these challenges, we developed a method that integrates predictive modeling to determine the optimal attack steps and target agents. Our approach is essentially a rule-based adversarial attack method, but unlike previous methods, the focus is on MARL and ours does not require manually setting attack thresholds. The effectiveness of our method was validated through experimentation, as discussed in detail below.

3. Preliminaries

Attacker objective. The goal of adversarial attacks in MARL is to diminish long-term rewards. Here, we aim to devise even more covert attacks, implying a necessity to target fewer time steps and fewer agents within a team. Therefore, identifying critical attack steps and critical agents becomes our primary objective.

Attacker capability. Some recent research focused on adversarial attacks executed on the states or observations of agents. In contrast, we focus on adversarial perturbations executed on the action space of agents. Specifically, we assume that the attacker can directly manipulate the actions of agents [20]. This assumption is plausible in real-world scenarios. For instance, if a device malfunctions, an agent may be unable to execute correct actions based on its observations and could resort instead to unpredictable random actions. Alternatively, if an attacker infiltrates an agent’s system, they may gain temporary control over its actions. The potentiality of these scenarios is a foundational premise for the present study.

Problem formulation. The essence of MARL is examining the decision-making process of multiple agents acting as entities interacting with an external environment. This decision-making process is typically formalized in mathematical terms as a Multi-Agent Markov Decision Process (MMDP). The MMDP is represented by a tuple $({\left\{S_i\right\}}_{i=1}^n,{\left\{A_i\right\}}_{i=1}^n,R,P,\gamma )$, where $\left\{S_i\right\}$ represents the state space, and $\left\{A_i\right\}$ denotes the action space of the set of agents. Each agent i has its own state space $S_i$ and action space $A_i$. At each time step t, $s_{i,t}$ and $a_{i,t}$ denote the state and action of agent i, respectively. P represents the state transition function. ${\mathit{s}}_{\mathit{t}+\mathbf{1}}\sim P({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$, where t denotes the time step, ${\mathit{s}}_{\mathit{t}}={\left\{s_{i,t}\right\}}_{i=1}^n$ represents the current state, ${\mathit{s}}_{\mathit{t}+\mathbf{1}}$ represents the next state, and ${\mathit{a}}_{\mathit{t}}={\left\{a_{i,t}\right\}}_{i=1}^n=\{a_{1,t},a_{2,t},\dots ,a_{n,t}\}$ represents the action space of n agents at time step t. The variable $a_{i,t}$ denotes the action of the ith agent at time step t. R represents the reward function, and the reward value of a team is $r_t=R({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}},{\mathit{s}}_{\mathit{t}+\mathbf{1}})$. $\gamma$ is the discount factor, $\gamma \in [0,1]$. The total reward of an episode is ${\sum }_{t\in TS}{\gamma }^t\left(r_t\right)$. The goal of MARL is to maximize return, which can be formulated as an optimization problem to identify the maximum value.

$$max{E}_{s_0\sim p_0,a_t\sim \pi ,s_{t+1}\sim P}[\sum _{t\in TS}{\gamma }^{t}R({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}},{\mathit{s}}_{\mathit{t}+\mathbf{1}})]$$

(1)

where $p_0$ is the initial state, and $\pi$ represents the algorithmic policy, which is a set of action sequences. The optimal policy is the $\pi$ that maximizes the return. $TS$ represents the set of total time steps in an episode.

MARL adversarial attacks target the opposite goal: A set of policies that minimize the long-term reward value are found, subject to constraints on the number of time steps and the number of agents involved in the attack. The optimization problem, originally aiming to maximize the value, is now transformed into a minimization problem under certain constraints.

$$\begin{array}{c}min{E}_{s_0\sim p_0,a_t\sim \pi ,s_{t+1}\sim P}\left[\sum _{t\in TS}{\gamma }^{t}R({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}},{\mathit{s}}_{\mathit{t}+\mathbf{1}})\right]\end{array}$$

(2)

The attacked time sequence of m steps is defined as $T{S}^{\prime }=\{t_{i+1},\dots ,t_{i+m}\}$. The time sequence that is not attacked is defined as $T{S}^{*}=\{t_1,\dots ,t_i,t_{i+m+1},\dots ,t_{\left|TS\right|}\}$. $T{S}^{\prime }\cup T{S}^{*}=TS$. The set of action sequences executed according to the optimal policy is defined as a*, and the set of action sequences executing adversarial attacks is defined as a′.

$$\begin{array}{c}min{E}_{s_0\sim p_0,a_t\sim \pi ,s_{t+1}\sim P}\\ [{\displaystyle \sum _{t\in T{S}^{*}}}{\gamma }^{t}R({\mathit{s}}_{\mathit{t}}\mathbf{,}{\mathit{a}}_{\mathit{t}}^{\mathbf{*}}\mathbf{,}{\mathit{s}}_{\mathit{t}+\mathbf{1}})+\sum _{t\in TS\prime }{\gamma }^{t}R({\mathit{s}}_{\mathit{t}}\mathbf{,}{\mathit{a}}_{\mathit{t}}^{\mathbf{\prime }}\mathbf{,}{\mathit{s}}_{\mathit{t}+\mathbf{1}})]\\ s.t.m\le \left|TS\right|\end{array}$$

(3)

The set of actions executed by k agents performing adversarial actions at time t is defined as ${\mathit{a}}_{\mathit{k},\mathit{t}}^{\mathbf{\prime }}=\{a_{i_1,t},a_{i_2,t},\dots ,a_{i_k,t}\}$, while the set of action sequences executed by the remaining $n-k$ agents following the optimal policy is defined as ${\mathit{a}}_{\mathbf{-}\mathit{k}\mathbf{,}\mathit{t}}^{\mathbf{*}}$, $k\in [0,n]$.

$$\begin{array}{c}min{E}_{s_0\sim p_0,a_t\sim \pi ,s_{t+1}\sim P}\\ [{\displaystyle \sum _{t\in T{S}^{*}}}{\gamma }^{t}R({\mathit{s}}_{\mathit{t}}\mathbf{,}{\mathit{a}}_{\mathit{t}}^{\mathbf{*}}\mathbf{,}{\mathit{s}}_{\mathit{t}+\mathbf{1}})+{\displaystyle \sum _{t\in TS\prime }}{\gamma }^{t}R({\mathit{s}}_{\mathit{t}}\mathbf{,}{\mathit{a}}_{\mathbf{-}\mathit{k},\mathit{t}}^{\mathbf{*}}\mathbf{,}{\mathit{a}}_{\mathit{k}\mathbf{,}\mathit{t}}^{\mathbf{\prime }}\mathbf{,}{\mathit{s}}_{\mathit{t}+\mathbf{1}})]\\ s.t.k\le nandm\le \left|TS\right|\end{array}$$

(4)

In this minimization problem, the objective is to find the time step range $TS\prime$ and the set of k agents targeted for attack that will minimize the return. Parameters k and m control the extent of the attack. Specifically, Equation (3) addresses the determination of the attack time step range $\{s_t,s_{t+1},\dots ,s_{t+m}\}$, while Equation (4) determines the set of attack targets $\{a_{i_1},a_{i_2},\dots ,a_{i_k}\}$.

4. Algorithm

To achieve the attack objective proposed in Section 3, this paper introduces the Search for Key steps and Key agents Attack algorithm. The attack is ultimately executed using the worst-case action attack strategy, i.e., selecting the action with the lowest Q-value in the action space or the action opposite to the optimal action. As shown in Figure 1, attacks are executed on the phase of action execution. Our methodological process consists of three main parts: constructing a predictive model, exploring optimal attack steps, and prioritizing the agents to be attacked before executing the attack based on the critical steps of key agents. Specific details are provided below.

4.1. Attack Methodology

As shown in Figure 2, the specific attack process consists of three stages. The first stage involves searching for the optimal attack timing through the predictive model and T-value function, which determine the key attack sequence $\{S_{t+1},S_{t+2},\dots ,S_{t+m}\}$. The attack priority of agents is determined in the second stage. This involves conducting m attack tests sequentially for n agents. By comparing the differences in T-values with the baseline and the length of the episode, the corresponding weight for each agent is determined, establishing the order in which they are subsequently attacked. Once the attack sequence $\{S_{t+1},S_{t+2},\dots ,S_{t+m}\}$ and agent priorities $\{A_1,A_2,\dots ,A_n\}$ are determined, the third stage begins by executing the attack strategy in a real-world scenario. This ultimately leads to task failure or a significant decrease in long-term reward values.

4.2. Predictive Model Construction

In the construction phase of the predictive model, we built a DNN architecture with two hidden layers. We employed mean squared error (MSE) as the loss function and Adam as the optimization algorithm. The role of the predictive model $PM$ is such that $PM({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})\to {\mathit{s}}_{\mathit{t}+\mathbf{1}}$. Here, ${\mathit{s}}_{\mathit{t}}$ represents the state at time t, which is also the observation of the entire environment; ${\mathit{a}}_{\mathit{t}}$ represents the actions taken by agents at time t. The pair $({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$ forms an input $<{\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}}>$, and after passing through the predictive model $PM$, the next time step’s state ${\mathit{s}}_{\mathit{t}+\mathbf{1}}$ can be predicted as shown in Figure 3. By amalgamating the agents’ policies, the predictive model $PM$ can predict a series of state–action sequences $\{({\mathit{s}}_{\mathit{t}}\mathbf{,}{\mathit{a}}_{\mathit{t}})\mathbf{,}({\mathit{s}}_{\mathit{t}+\mathbf{1}},{\mathit{a}}_{\mathit{t}+\mathbf{1}}),\dots \}$. Distinct predictive models are required for different scenarios. Taking the StarCraft Multi-Agent Challenge (SMAC) as an example, its network architecture satisfies

$${\Phi }_{\mathrm{NN}}=\left({\mathbb{R}}^{d_s+d_a}\stackrel{{\mathrm{FC}}_{256}}{⟶}{\mathbb{R}}^{256}\stackrel{\mathrm{ReLU}}{⟶}{\mathbb{R}}^{128}\stackrel{{\mathrm{FC}}_{d_s}}{⟶}{\mathbb{R}}^{d_s}\right)$$

(5)

where $d_s$ and $d_a$, respectively, denote the dimensions of the state space and joint action space. The optimization objective of the model is to minimize the multi-step prediction error:

$${\mathcal{L}}_{\mathrm{MSE}}={\mathbb{E}}_{{\mathbf{a}}_{\mathbf{t}}\sim \pi }\left[\parallel PM(s_t,{\mathbf{a}}_t)-s_{t+1}{\parallel }_2^2\right]$$

(6)

We anticipate that this predictive model will adeptly capture feedback from the real environment and infer the final state. Based on this final state, a state value is obtained that can be used to describe the task completion status, which is determined by the T-value function. The T-value function serves as a state evaluation metric that quantifies task completion progress in the current state. Its definition varies across different scenarios: it may represent either direct reward values or their additive inverse, constituting the attacker’s estimation and approximation of the reward function. Specifically, in the SMAC, this function is formulated as the numerical difference in surviving units. Conversely, in the MPE, it is defined as the sum of distances between agents and their designated landmarks.

4.3. Search for Key Steps

The optimal attack timing is determined by traversing all time steps and sequentially executing m-step attacks. The attack strategy is defined by the worst-case action. The number of attack steps m is determined and the T-value function and predictive model P are established. Initially, P is fed with the initial state $S_0$. In conjunction with the action set obtained through the policy of agents, the final state set $S_{\left|TS\right|}$ is determined. This $S_{\left|TS\right|}$ serves as the baseline result of the predictive model’s predictions, denoted as $S_{baseline}$. The value of $T\left(S_{\left|TS\right|}\right)$ forms the baseline for the T-value, denoted as $T_{baseline}$. This process iterates $\left|TS\right|$ times, with each iteration executing adversarial attack actions $\{A_{t+1}^{\prime },\dots ,A_{t+m}^{\prime }\}$ from time t to $t+m(t:0,1,\dots ,|TS\left|\right)$. The final state $S_i$ is obtained, and then the corresponding T-value $T\left(S_i\right)$ is calculated. The absolute difference $|T\left(S_i\right)-T_{baseline}|$ is saved to DT. This value reflects the difference between the attack’s effectiveness after executing the m-step attack strategy starting from time t and the baseline, where a greater difference indicates better effectiveness. Once the traversal is complete, a list of DT values for all final states after executing the m-step attack is generated. The step sequence $\{S_{t+1},S_{t+2},\dots ,S_{t+m}\}$ with the optimal attack effectiveness, i.e., the maximum difference, is defined as the key step sequence. It is worth noting that during this search for key steps, the attack strategy is applied to all agents. The algorithm flow is described in Algorithm 1.

Algorithm 1 Search for Key Steps

Input: P, T, m, $p_0$, $Actor$, $Acto{r}_{ad}$

Output: t, $s_{baseline}$

1:  $s_0=p_0$

2:  for i in $TS$ do

3:        $a_i=Actor\left(s_i\right)$

4:        $s_{i+1}=P(s_i,a_i)$

5:        $s_i=s_{i+1}$

6:        $s_{baseline}=s_i$

7:  end for

8:  $baseline=T\left(s_{baseline}\right)$ // Computing the baseline in the normal.

9:  $s_0^{\prime }=p_0$

10:  for i in $TS$ do

11:       for j in $TS$ do

12:             if $i<=j<i+m$ then

13:                   $a_j^{\prime }=Acto{r}_{ad}\left(s_j^{\prime }\right)$

14:             else

15:                   $a_j^{\prime }=Actor\left(s_j^{\prime }\right)$

16:             end if

17:             $s_{j+1}^{\prime }=PM(s_j^{\prime },a_j^{\prime })$

18:             $s_j^{\prime }=s_{j+1}^{\prime }$

19:             $s_{baseline}^{\prime }=s_{j+1}^{\prime }$

20:       end for

21:       $DT.append\left(\right|T\left(s_{baseline}^{\prime }\right)-T\left(s_{baseline}\right)\left|\right)$

22:  end for

23:  $t=DT.index\left(max\right(DT\left)\right)$ //The index corresponding to the maximum DT value indicates the moment of the attack.

24:  return t,$s_{baseline}$

4.4. Search for Key Agents

While assuming there are n agents, after obtaining the key attack steps $\{S_{t+1},\dots ,S_{t+m}\}$, each individual agent is attacked in turn. This involves the targeted agent executing the worst-case action, while the remaining agents follow their normal strategy. The final state, denoted as $S_j$ after the attack, is obtained, and the corresponding T-value $T\left(S_j\right)$ is calculated. The difference $|T\left(S_j\right)-T_{baseline}|$ and the length of episodes serve as the weight indicators for agent i. A larger disparity and more time steps, indicating better attack effectiveness, correspond to a higher weight assigned to the agent, thereby elevating its priority during attack execution. Conducting sequential attacks on n agents yields a list of attack priorities for the agents. This list dictates the sequence in which agents are selected for adversarial attacks. The algorithm is outlined as Algorithm 2.

Algorithm 2 Search for Key Agents

Input: P, T, m, $p_0$, $Actor$, $Acto{r}_{ad}$, t, $S_{baseline}$

Output: $weights$

1: $s_0=p_0$

2: for i in range(n) do

3:       for j in $TS$ do

4:             if $t<=j<t+m$then

5:                   $a_{i,j}=Acto{r}_{ad}\left(s_j\right)$

6:                   $a_{-i,j}=Actor\left(s_j\right)$

7:             else

8:                   $a_j=Actor\left(s_j\right)$

9:             end if

10:             $s_{j+1}=PM(s_j,a_j)$

11:             $s_j=s_{j+1}$

12:             $s_i=s_j$

13:       end for

14:       $DT.append\left(\right|T\left(s_i\right)-T\left(s_{baseline}\right)\left|\right)$

15: end for

16: Determine the weights of agents in descending order based on the numerical DT values from large to small.

17: return weights

4.5. Complexity Analysis

This section analyzes the differences in the solution spaces between the proposed method and learning-based adversarial attack strategy generation methods from a computational complexity perspective, thereby revealing the underlying efficiency of the proposed approach. Consider a multi-agent environment with N agents. The attack horizon spans m steps within a total episode length of M steps.

RL-based methods require the global optimization of the attack policy within a Markov Decision Process (MDP) framework. Assuming the state dimension in the multi-agent environment is d, the state space scales as $\mathcal{O}\left(d^M\right)$. Assuming the action space dimension per agent is a, the joint action space for N agents scales as $\mathcal{O}\left(a^N\right)$. Consequently, for M time steps, the action search space scales as $\mathcal{O}\left({\left(a^N\right)}^M\right)=\mathcal{O}\left(a^{N\times M}\right)$. Since an adversarial attack policy represents a mapping function from states to actions, the size of the policy space is determined by the Cartesian product of the state space and the action space:

$$\mathcal{O}\left(d^M\times a^{N\times M}\right)$$

This analysis demonstrates that RL-based methods exhibit double exponential complexity. Their computational burden grows explosively (exponentially) with the number of agents N and the total episode length M.

The proposed method employs a phased heuristic search to identify adversarial attack strategies, selecting adversarial actions via a worst-action selection policy. Its solution space consists of two sequential stages: Search for key steps: The objective of this first stage is to identify the optimal continuous m-step attack window within the total M steps. The state space explored during this stage scales as $\mathcal{O}(M\times d^m)$. Search for key agents: The second stage involves traversing all N agents, where the state transition space scales as $\mathcal{O}(N\times d^m)$.

Therefore, the overall complexity of the proposed method is the linear combination of these two stages:

$$\mathcal{O}(M\times d^m+N\times d^m)=\mathcal{O}(M\times d^m)$$

Compared to RL-based methods, the proposed approach significantly reduces the solution space and substantially enhances computational efficiency by leveraging phased pruning and a novel two-stage heuristic search strategy.

5. Experiments

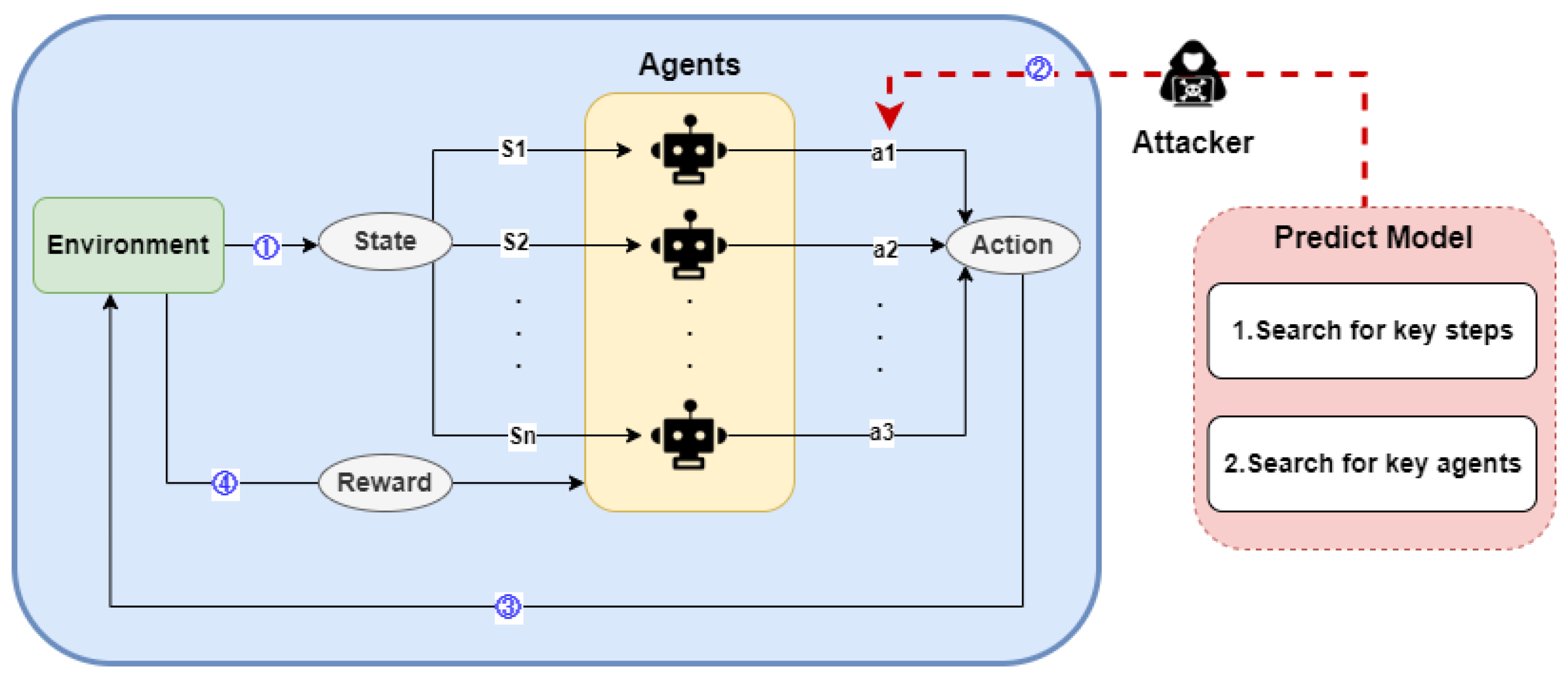
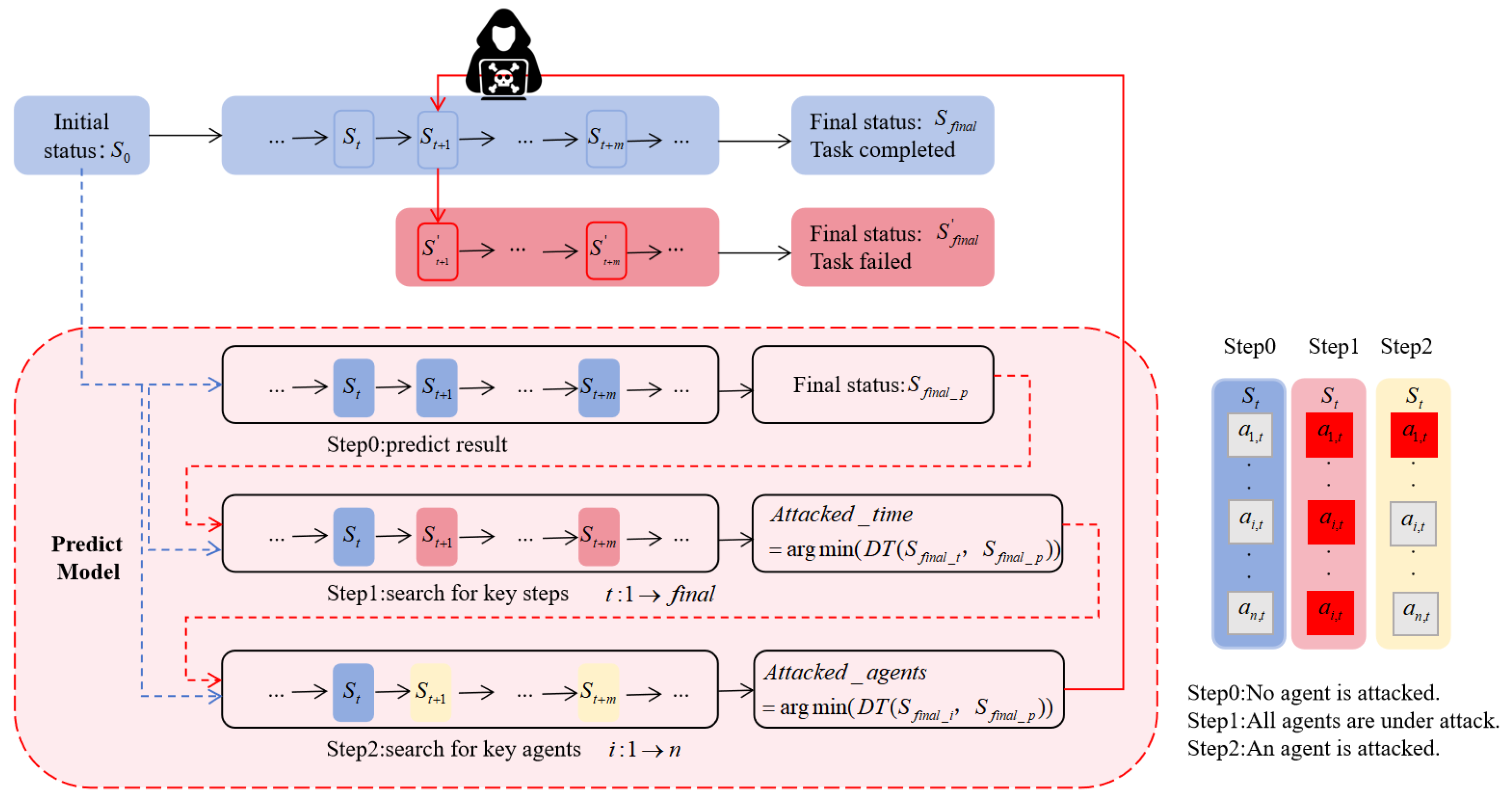
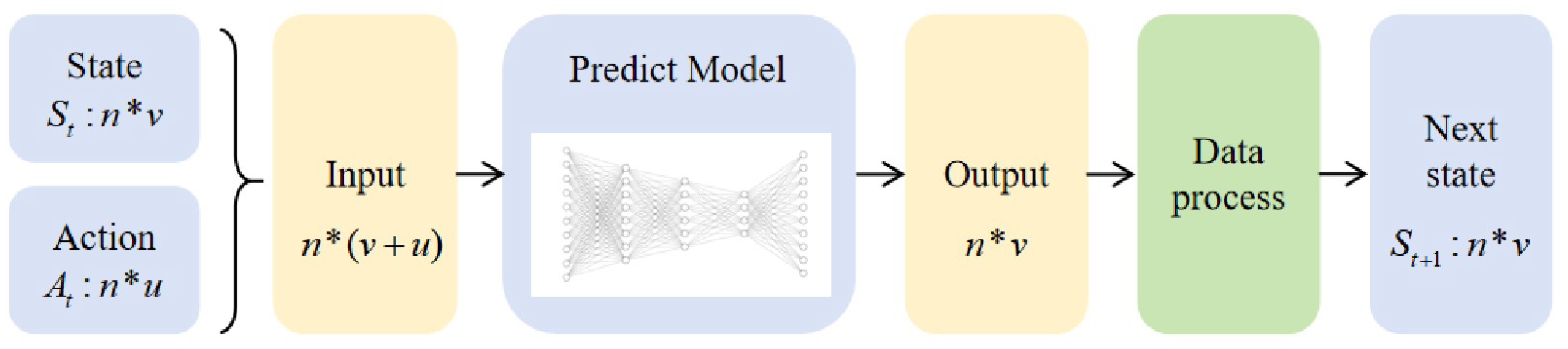
This section primarily outlines the process of evaluating the effectiveness of our attacks through experiments, including the experimental setup and implementation process. The tested algorithms include MADDPG [36] and Qmix [37]. The experiments were conducted in scenarios such as ‘simple spread’ in the Multi-Agent Particle Environment (MPE) and several map scenarios in the StarCraft Multi-Agent Challenge (SMAC). The MPE and SMAC were selected as our experimental environments because they represent two distinct types of experimental scenarios. In the MPE, the action space is continuous, whereas in the SMAC, it is discrete. Additionally, the SMAC is a well-established environment for MARL, characterized by a more complex experimental setup. The experimental scenarios are illustrated in Figure 4 and Figure 5.

5.1. Environment

Example 1: MPE. The MPE [36], developed by OpenAI, is a set of time-discrete, spatially continuous, two-dimensional multi-agent environments. It is widely used for the simulation and validation of various MARL algorithms. The experimental environment includes multiple task scenarios, among which we focused on the “simple spread” scenario. This involves cooperative multi-agent tasks where agents strive to prevent collisions while covering all landmarks through cooperation. Notably, the action space of agents is continuous. To ensure reproducibility and fairness, we generated 1000 sets of random coordinates for both agents and landmarks. During the testing process, these 1000 sets of random coordinates were used sequentially, ensuring complete consistency in the experimental scenarios between the baseline and the attack tests.

Example 2: SMAC. We also evaluated our attack methods in an SMAC environment [37]. StarCraft2 is a real-time strategy game in which players attempt to defeat opponents by consistently producing resources and expanding their army. This environment is widely used in the realm of MARL. There are many built-in maps in the SMAC corresponding to different scenarios, among which we selected several representative maps: 2s3z, 3 m, and 25 m.

5.2. Evaluation Metrics

We evaluate the effectiveness of the attack from two dimensions, the effectiveness of the attack and its concealment:

• Effectiveness: Due to the differences in experimental scenarios, we use different evaluation metrics for each scenario. In the MPE scenario, we assess task completion using the T value or reward. A higher T value or a lower reward indicates a more effective attack. In the SMAC scenario, we evaluate attack effectiveness based on the win rate; a lower win rate signifies a more effective attack.
• Concealment: The concealment metric is defined as $F=(k\ast m)/(n\ast TS)=(k/n)\ast (m/TS),F\in [0,1]$, where k is the number of attacked agents, n is the total number of agents, m is the number of steps taken to attack, and $TS$ is the total number of time steps. A smaller F value indicates that fewer agents are attacked and fewer time steps are involved, meaning the attack is more concealed.

5.3. Implementation

Example 1: MPE. We used MADDPG to obtain the optimal policy to be attacked, with training episodes set to 100,000 and episode length set to 25. Ultimately, the average reward converged to approximately −1.5. In this scenario, the T-function was set as the sum of the distances between agents and the nearest landmarks. Conducting 1000 tests on this model yielded an average reward of −1.514 and an average T-value of 0.660. We utilized these data as the baseline for the attack experiments.

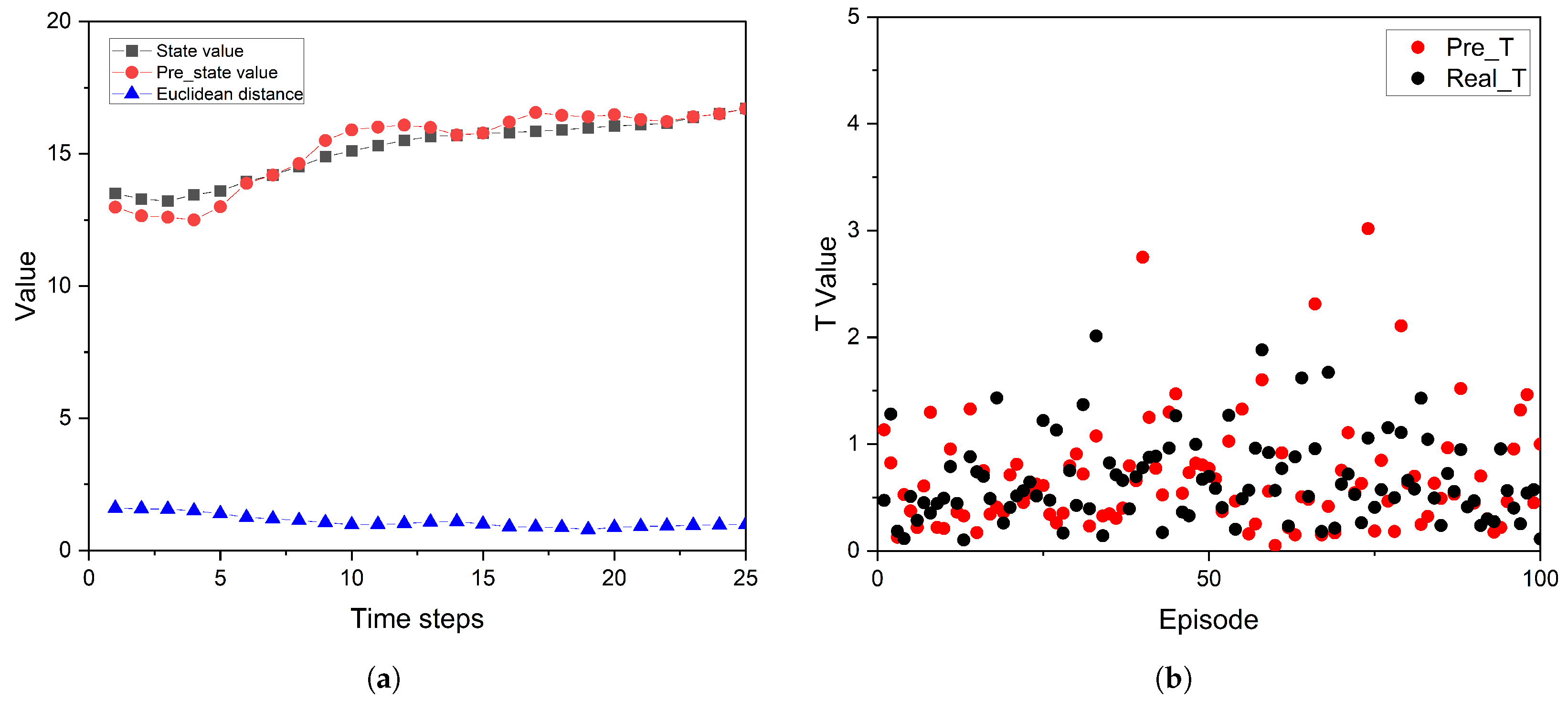
To construct a predictive model, we utilized the trained model described above for 10,000 tests. The data generated in each round of testing were collected into a training set for the predictive model. We used observations and actions in each round as inputs and the subsequent observation as an output. We assessed the performance of the predictive model using two metrics. Firstly, we replaced the normal environmental update function with the predictive model to obtain the next state values for 100 episodes. Compared to the baseline average T-value of 0.660, the results show an average T-value of 0.687. Apart from a few outliers, the overall trend of the predictive T-value closely resembles the baseline, indicating that the predictive model can effectively simulate real environments. Secondly, for individual tasks, we measured the accuracy of the predictive results by calculating the Euclidean distance between real and predicted state values, as shown in the Figure 6. With these two metrics, we trained a predictive model that fits the environment iteration well and can serve as a basis for searching key attack steps and key agents.

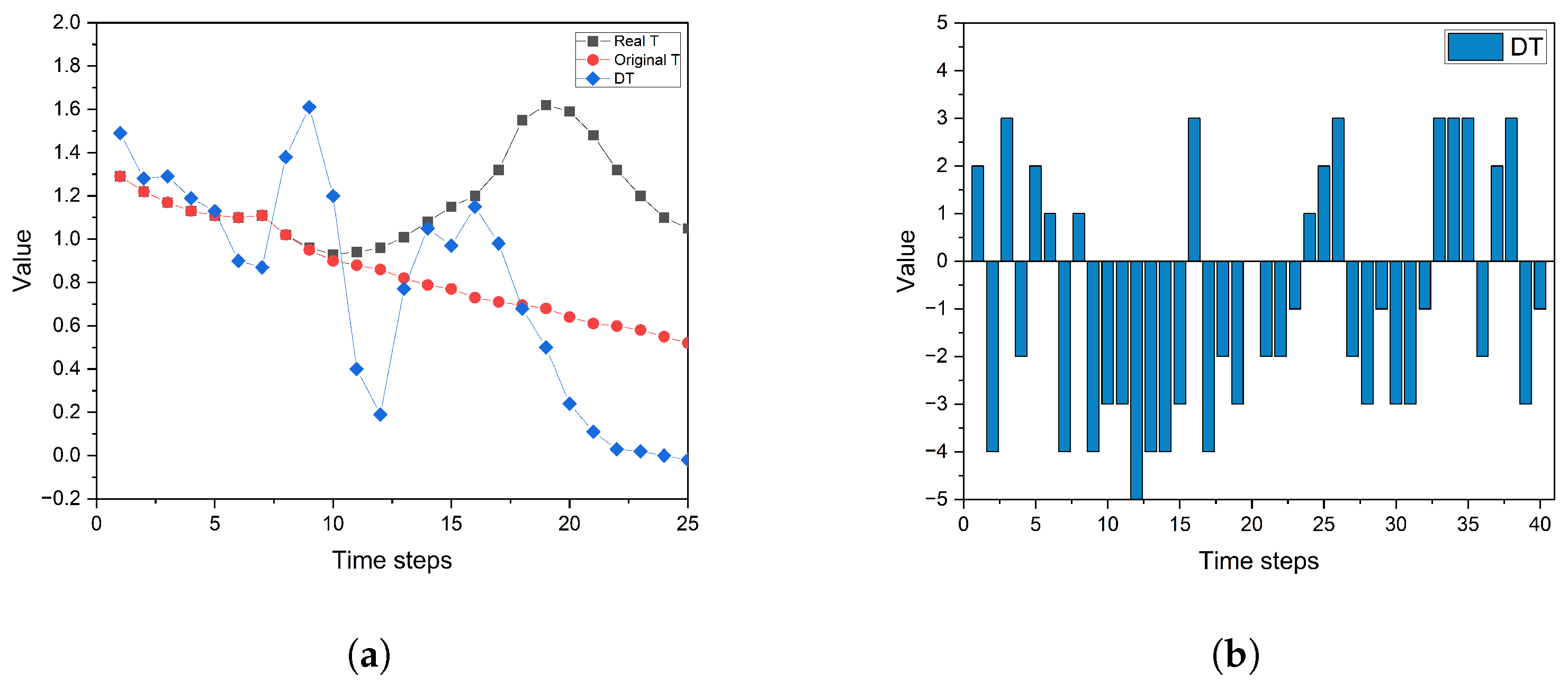
In the current scenario, the attack strategy involves negating the real action values. Figure 7a illustrates the changes in actual T-values, T-values after the attack, and ensuing differences (DT values) in a specific round. With m set to 10, the search results indicate that starting from the 9th step, executing an attack maximized the DT value. Therefore, the ninth step can be defined as the key step. Steps 9 to 18 were designated as the attack steps in which the attack strategy is executed. The T-value curve shows an immediate increase in T-values after the attack, reaching the maximum deviation in the final attack step. The agent moves closer to the landmark under the control of the original model, but by the end of the round, it fails to reach the T-value level of the baseline. This indicates an inability to cover or approach the landmark within the fixed number of rounds.

Example 2: SMAC. We selected three maps, including 2s3z, 3 m, and 25 m, as experimental scenarios. Taking the 2s3z map as an example, we conducted 2,050,000 rounds of gameplay training using the QMIX algorithm, resulting in an average win rate of 97.8% and a mean return of around 20. To construct the predictive model (PM), we collected observations and action sets from each round during a 10,000-round testing process. The combination of observations and actions was input to the PM, while the subsequent observations served as the output. To evaluate the PM’s performance, we replaced the environment’s state update values with the PM’s output during 100 rounds of testing gameplay. The results show a win rate of up to 92% out of 100 rounds. Compared to the normal gameplay win rate of 97.8%, this indicates that the PM effectively fulfills its predictive role. Additionally, in a single round of gameplay, we measured the deviation in the prediction results by calculating the Euclidean distance between the observations updated normally at each step and the predicted observations.

In this scenario, the attack strategy entails directing agents to take actions with the lowest Q-value. The T-value function is defined by the disparity between the number of friendly surviving agents and the number of enemy-surviving agents. A positive T-value denotes victory in the game, while a negative T-value signifies defeat. Additionally, a smaller T-value indicates better performance of the attack. We set m to 5 and conducted one key-step search. The results indicate that attacking from the 12th step yielded the minimum T-value, so we defined the 12th step as the key step. Under the conditions of m = 5 attack steps and the lowest Q-value attack strategy, the win rate in 100 game rounds is 13%. Compared to the normal win rate of 97% in 100 game rounds, this indicates a significant improvement in performance for this attack pattern.

After determining the key step, we proceeded to adjust the value of m and conducted attack tests with step lengths of 3, 5, and 7. In

Table 1. Testing attack effectiveness with different m in 2s3z.

m	Win Rate (%)	TS
1	91	51.38
2	74	54.68
3	56	53.37
5	13	52.43
7	0	50.93

, the results show that with a step length of 3, the win rate in 100 game rounds drops to around 50% from the original 98%. With a step length of 5, the win rate decreases to around 10%. Increasing the attack step length to 7 almost guarantees a 100% failure rate in all game rounds. It is worth noting that in these attack tests, the attack step length of 3 accounted for only about 5% of the total episode steps. Even with a step length of 7, it did not exceed 15% of the total episode steps. After identifying the key step, we proceeded to search for the key agents while keeping the key step fixed. We determined the key agents by individually testing the weight of each agent in the attack. Agents were prioritized by sorting tuples $(t,s)$, where t represents the T-values and s denotes episode steps, in ascending order of t and descending order of s. The experimental results are shown in

Table 2. Determining agent priority based on key steps.

Agent ID	T-Value	TS	Priority
0	2	52	3
1	−1	56	1
2	2	49	4
3	1	50	2
4	4	49	5

.

5.4. Results and Evaluation

Example 1: MPE. In this scenario, we validate the effectiveness of our method by setting the same stealth indicators, i.e., attacking the same number of time steps and agents. The results show that the method proposed in this paper performs better. We initialized 1000 sets of random points, where three points corresponded to agent positions, and the remaining three corresponded to landmark positions in each set. Using three attack methods and the constructed set of random points, we conducted 1000 experiments. We evaluated the attack effectiveness using two metrics: T-value and reward. A larger T-value and a smaller reward indicate a more effective attack compared to the baseline. The average T-value and reward are calculated as the final experimental results. The two attack methods compared in this context were the following:

• RSRA: Executing m-step attacks at random steps and with a random agent.
• LMS: Executing opposite actions in the final m steps.

The results are shown in

Table 3. Contrast experiment in MPE.

Mode	All Agents (F = 0.40)		Single Agent (F = 0.13)
	T-Value	Reward	T-Value	Reward
baseline	0.660	−1.514	0.660	−1.514
SKKA	1.217	−1.964	0.932	−1.682
RSRA	0.968	−1.776	0.691	−1.557
LMS	1.054	−1.903	0.835	−1.712

. When m = 10, the attack effectiveness of SKKA is significant for both individual agents and all agents. In the case of attacking all agents, F = 0.4, the T-value increased by 84.4%, and the reward decreased by 29.7%, indicating an improvement in attack performance. In the case of attacking a single agent, F = 0.13, the T-value increased by 41.2%, and the reward decreased by 11.1%. Compared to similar methods, the effectiveness of the attack is still maintained even when the number of attacked agents is reduced.

Example 2: SMAC. To further validate the stealth and advantages of the proposed method, we conducted comparative experiments in the SMAC. The experimental results show that SKKA has higher stealth under the same attack effectiveness. In certain scenarios, SKKA outperforms similar methods in terms of both effectiveness and stealth. We compared win rates against benchmark opponents using three attack methods. The win rate of the model trained by the RL algorithm over 1000 games was used as the baseline. The proposed attack algorithm SKKA, along with three other attack algorithms, were employed to attack the model using 1000 games for each test. A lower win rate, accompanied by a lower F value, indicates a better performance for the attack method. The three attack methods include the following:

• STA: An attack method proposed by Lin [11] based on rules. In the present experiment, the attack timing determination was based on computing the average action probability divergence among agents, subject to a predefined maximum-step constraint for adversarial interventions.
• RSRARA: Random selection of attack steps, agents, and actions during the attack.
• RSRALA: Execution of the action with the lowest Q-value for random agents at random steps.

First, we used the “search for key steps” method to determine the attack time steps. At the target attack time step, we attacked all agents, and the experimental results are shown in

Table 4. Search for Key Steps results (F value).

Map	2s3z		3 m		25 m
Attack Mode	Win Rate	$\mathit{F}$	Win Rate	$\mathit{F}$	Win Rate	$\mathit{F}$
SKKA	0	0.137	0	0.174	0	0.110
STA	0	0.217	0	0.389	0	0.098
RSRALA	1	0.396	4.5	0.415	3	0.190
RSRARA	8	0.574	4.7	0.755	2	0.280

. The results indicate that when the win rates are very low, SKKA demonstrates the best stealth, i.e., the lowest F-value. For instance, in the 2s3z scenario, with win rates all at 0, SKKA’s stealth is 0.137, while STA’s stealth is 0.217. In contrast, RSRALA and RSRARA, which have worse attack effectiveness, also exhibit worse stealth. The specific experimental data can be found in

Table 5. Search for Key Steps results.

Map	2s3z		3 m		25 m
Attack Mode	Win Rate (%)	m/TS	Win Rate (%)	m/TS	Win Rate (%)	m/TS
baseline	97.9	0/44.833	99.3	0/21.826	99.5	0/31.731
SKKA	56	3/53.37	23.5	2/22.589	15	1/38.55
	13	5/52.43	12	3/20.242	3	2/32.163
	0	7/50.93	0	4/23.009	0	3/27.147
STA	19	7/56.51	72.6	4/27.827	58	1/38.17
	5	10/58.54	25	8/32.298	8	2/35.15
	0	13/59.78	0.1	12/30.88	0	3/30.56
RSRALA	35	7/58.36	42.7	4/26.071	23	3/36.03
	15	15/64.08	34.4	10/31.218	14	5/35.86
	1	30/75.65	4.5	20/48.159	3	7/36.86
RSRARA	62	7/51.969	12.1	10/25.312	24	5/33.11
	20	15/53.38	4.7	20/26.495	9	7/38.99
	8	30/52.24	0	25/26.521	2	10/35.73

.

Next, we further used the “search for key agents” method to determine the range of agents being attacked, aiming to enhance the stealth of the attack. The experimental results are shown in

Table 6. Search for Key Agents results (F value).

Map	2s3z		3 m		25 m
Attack Mode	Win Rate	F	Win Rate	F	Win Rate	F
SKKA	10	0.078	2	0.128	0	0.051
STA	20	0.112	2	0.192	0	0.060
RSRALA	11	0.291	6.3	0.399	18	0.127
RSRARA	32	0.348	6.1	0.503	39	0.099

. The results demonstrate that, while keeping the attack time steps unchanged, reducing the number of attacked agents decreases the attack’s effectiveness but further improves the stealth. The detailed experimental data are illustrated in

Table 7. Search for Key Agents results.

Map	2s3z			3 m			25 m
Attack Mode	Win Rate (%)	$\mathit{k}$	m/TS	Win Rate (%)	$\mathit{k}$	m/TS	Win Rate (%)	$\mathit{k}$	m/TS
SKKA	61	1	7/56.76	27	1	4/22.93	64	1	20/39.08
	24	2	7/55.52	2	2	4/20.88	3	5	10/42.81
	10	3	7/53.50	0	3	4/23.00	0	10	4/31.12
STA	78	1	13/52.24	8	1	12/24.56	85	1	30/38.91
	32	2	13/70.79	2	2	12/21.56	5	5	10/48.91
	20	3	13/69.59	1	3	12/36.73	0	10	5/33.13
RSRALA	72	1	30/54.53	27	1	20/25.571	92	1	20/37.04
	30	2	30/63.15	6.3	2	20/33.367	29	5	15/36.64
	11	3	30/61.77	4.5	3	20/48.159	18	10	10/31.53
RSRARA	84	1	30/50.08	26.5	1	20/24.19	93	1	30/33.52
	59	2	30/52.53	6.1	2	20/22.526	40	5	20/39.08
	32	3	30/51.66	4.7	3	20/26.495	39	10	10/40.22

. Compared to similar methods, our method not only further enhances stealth but also achieves superior attack effectiveness.

6. Conclusions

In this study, our primary focus revolves around investigating adversarial attacks in MARL. Our aim is to deploy more covert attack methods to target RL algorithms, achieving effective attacks in fewer steps and with fewer agents involved. To validate the efficacy of our attack approach, we conducted experiments in both MPE and SMAC environments. These environments utilize the MADDPG and QMIX algorithms, representing actor–critic and value-based approaches, respectively. We successfully validated the effectiveness of the proposed method in both environments. We conducted comparative experiments with several different attack methods. The results demonstrate that our approach achieves lower win rates in games with fewer attack steps and fewer agents compared to the other methods. Our method is simpler than using RL for identifying attack strategies, and incurs lower computational and time costs. The experiments conducted in this study highlight the vulnerability of current RL algorithms, where even a relatively low attack cost can render models ineffective. Enhancing the robustness of RL algorithms remains a key focus for future research.

While SKKA demonstrates high efficiency in adversarial attacks within MPE and SMAC environments, its applicability to real-world physical systems requires further validation. The experiments focused on simulated environments with discrete/continuous action spaces; scenarios involving complex dynamics (e.g., sensor noise, communication delays, or hardware constraints) remain unexplored. Additionally, SKKA assumes attackers possess full knowledge of victim agents’ policies—a white-box setting that may not hold in all practical cases. Future work will explore black-box extensions and robustness testing in industrial control systems.