Methodology for Designing Broadband DC Link Filters for Voltage Source Converters
Abstract
1. Introduction
- Aluminum electrolytic capacitors:Electrolyte capacitors are mostly used in industrial applications. Their dielectric strength is limited to approx. 450V (although there are also special versions with a maximum applicable voltage of 600 V), which is why typical applications in the range 600–900 V usually use two capacitors connected in series. To increase the total capacity and/or current-carrying capability, several capacitors are usually connected in parallel. Compared to other types of capacitors, they achieve the highest energy density and the lowest cost per joule. However, the large space requirement due to the low current-carrying capability, wear and tear caused by the evaporation of the electrolyte solution, is disadvantageous. Furthermore, compared to the film capacitor, it has a much higher, strongly frequency-dependent ESR and thus a significantly lower efficiency and a lower current-carrying capability. Electrolyte capacitors are polarised and can only be used for DC voltage applications. The main areas of application are industrial applications.
- Multilayer ceramic capacitors:Multilayer ceramic capacitors (MLCCs) have smaller construction volumes in comparison to electrolyte capacitors, larger frequency ranges, and higher operating temperatures of up to 200 °C. Disadvantages, however, are higher costs and mechanical sensitivity. Parasitic effects like DC and AC bias dependence have to be taken into account [30,31,32,33,34,35,36]. They are often manufactured in surface mounted device (SMD) designs and are used for complex applications on printed circuit boards.
- Metallised film capacitors:Metallised Polypropylene film capacitors (MPPFCs) offer a balanced design for higher-voltage applications (e.g., over 500 V) in terms of cost and ESR, capacitance, ripple, current, and reliability. However, they have the disadvantages of a large volume and a moderate upper operating temperature. Parasitic effects like eddy currents and skin and proximity effects influence their filtering effect, especially for higher frequencies, and have to be taken into account [37,38,39,40,41,42,43]. Related to the current-carrying capability, the costs of MPPFCs are about one third of the costs for electrolyte capacitors. Because of this, they are preferred for applications with high distortion currents, such as in the drive train of electric vehicles [44].
2. Basic Filter Design
- Low -frequency (LF) filter: Reduce the DC voltage ripple generated from the modulation scheme.
- High-frequency (HF) filter: Limit the switching overvoltage to a fixed level.
- Course of action:
- 1.
- First estimations based on analytic calculations.
- 2.
- Component selection for LF filter.
- 3.
- Time-based simulation model of VSC and filter.
- 4.
- Component selection for HF filter.
- 5.
- Determine impedance of mechanical components.
- 6.
- Integration in time-based simulation model.
- 7.
- Validation on experimental setup.
3. Exemplary Filter Design
3.1. First Estimations Based on Analytic Calculations
- This results in
- Current-carrying capability: ;
- Necessary capacity: .
3.2. Component Selection for LF Filter
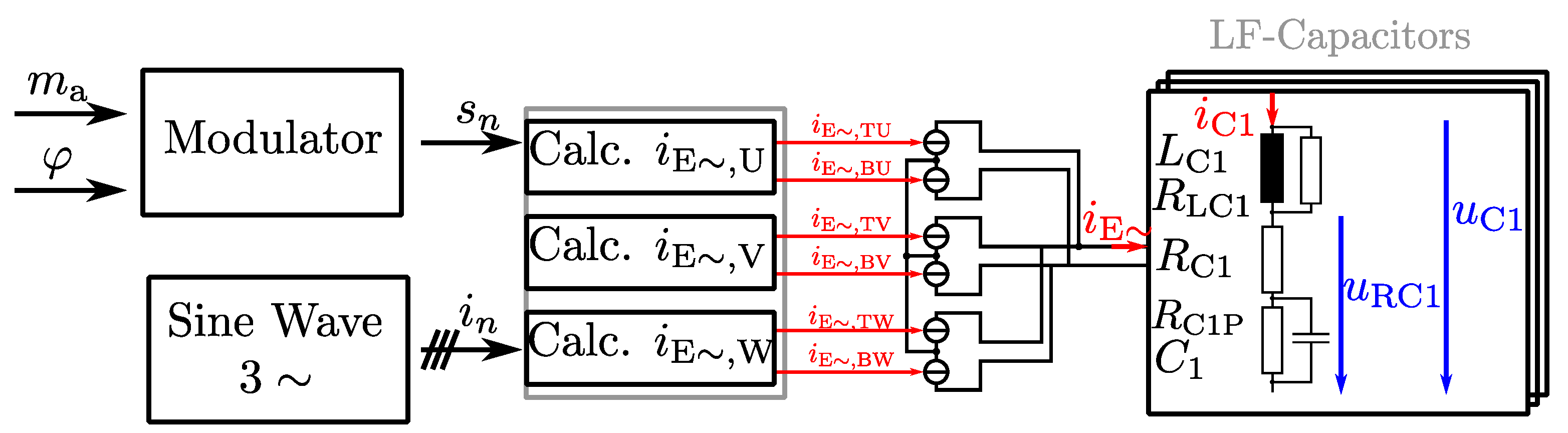
3.3. Time-Based Simulation Model Step I
- : Top switch of phase leg n on, corresponding bottom switch off.
- : Commutation between top and bottom switches.
- : Top switch of phase leg n off, corresponding bottom switch on.
3.4. Component Selection for HF Filter
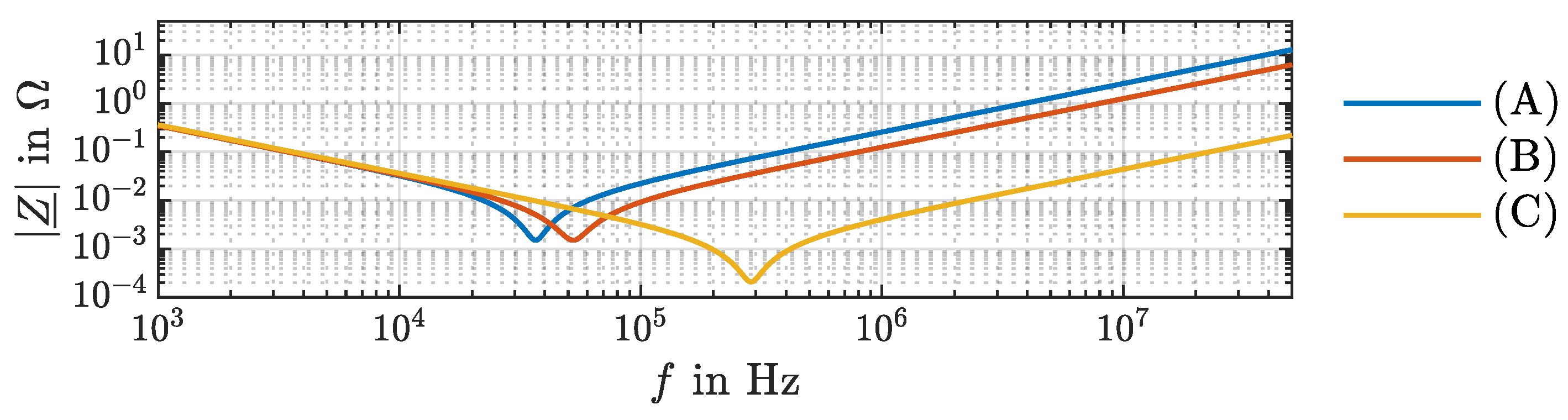
3.5. Determine Impedance of Mechanical Components
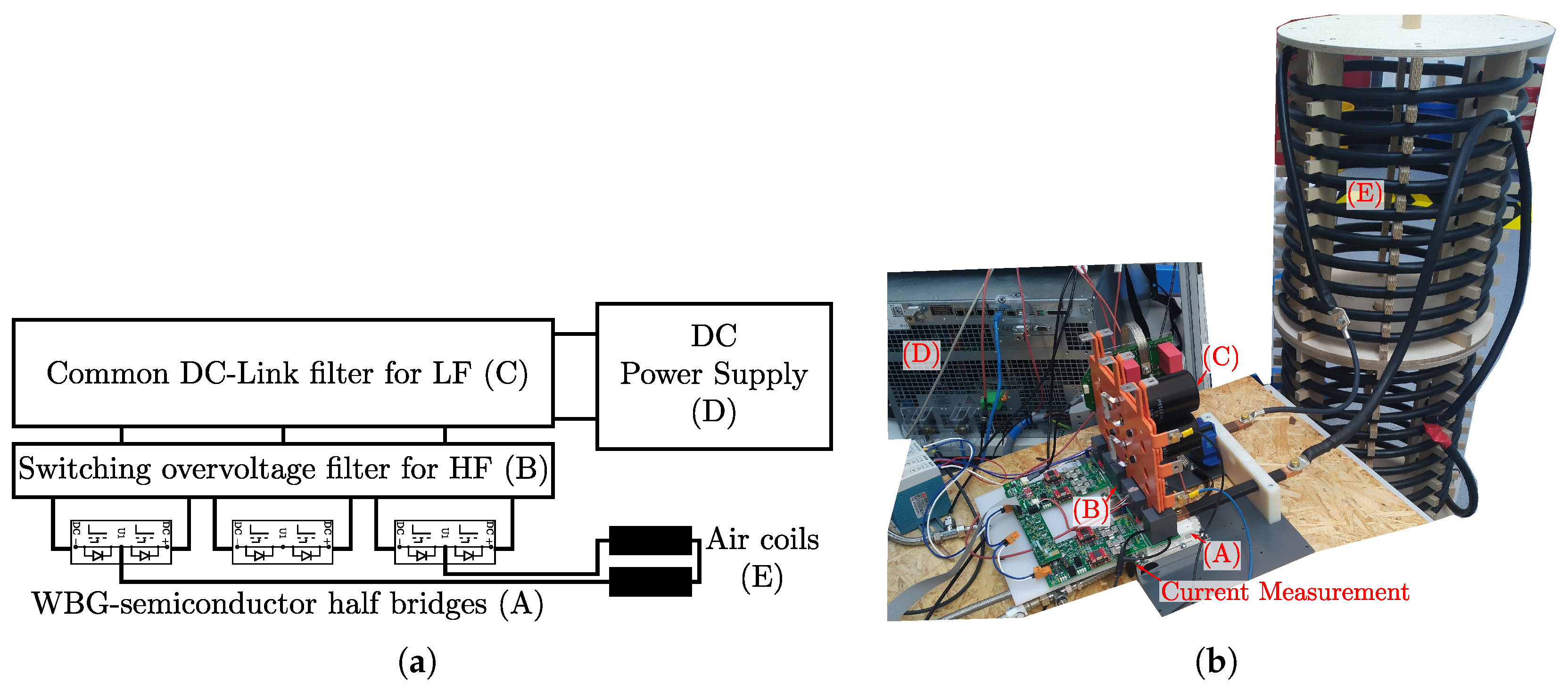
3.6. Integration in Time-Based Simulation Model
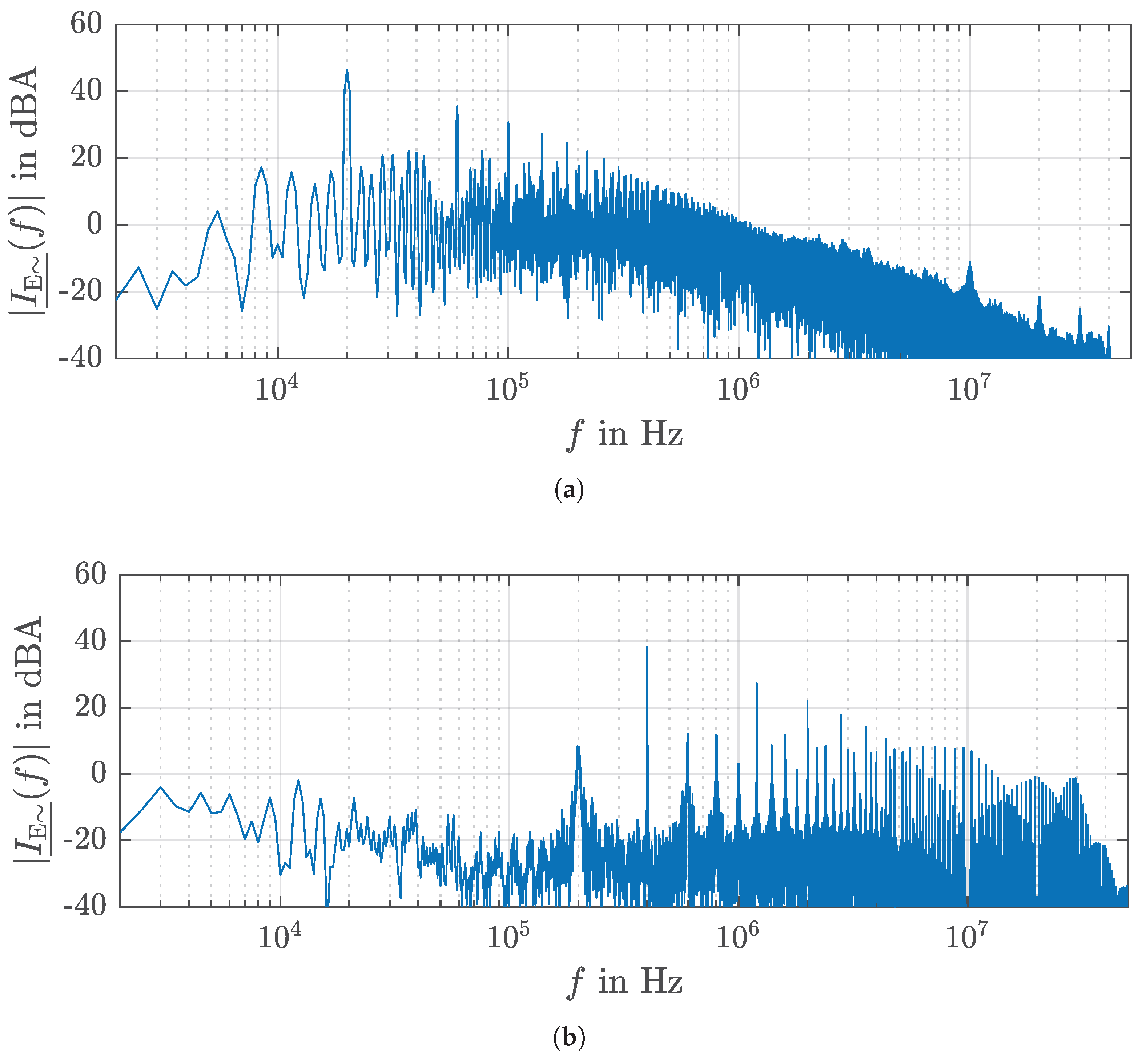
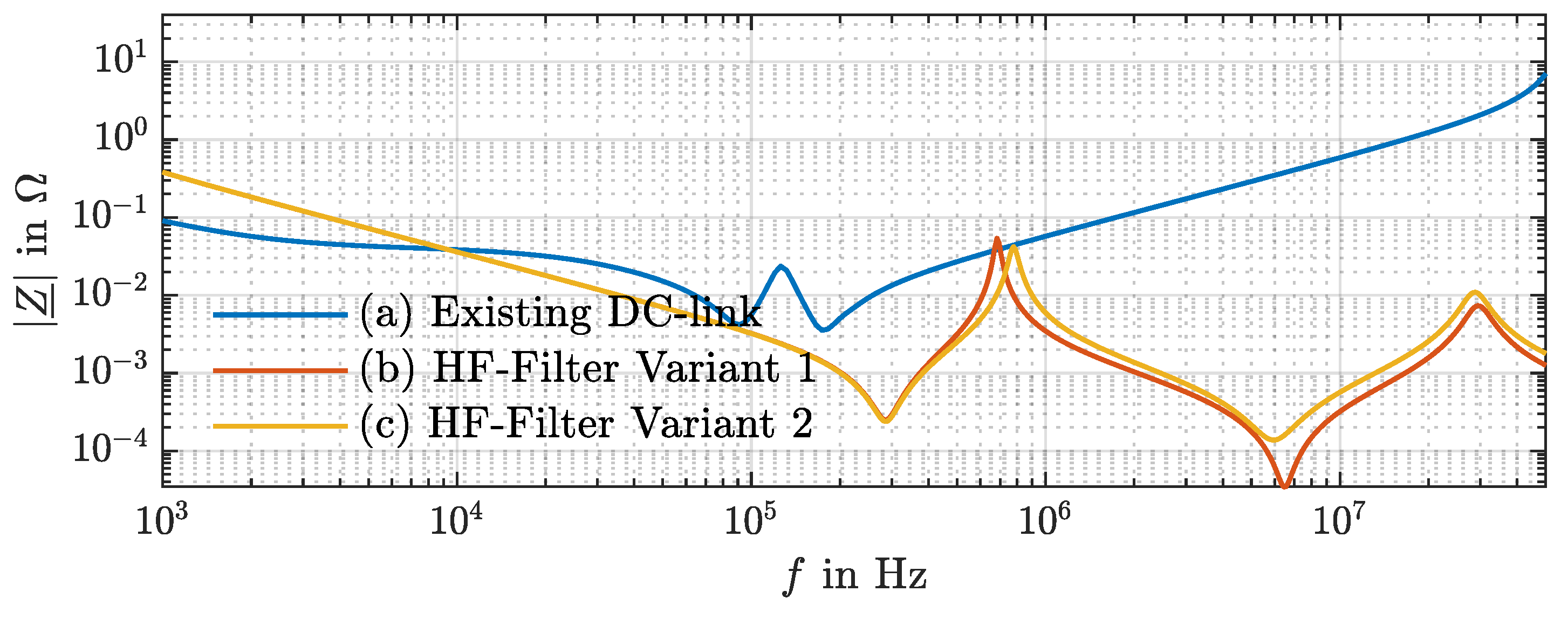
- Results for different HF filter configurations:
- (a)
- Existing DC link: HF filter consists of six film capacitors close to the half-bridge power modules. LF filter is built from electrolyte capacitors.
- (b)
- HF Filter Variant 1: 78 ceramic capacitors are close to the half-bridge power modules.
- (c)
- HF Filter Variant 2: 60 ceramic capacitors are set in series with low-inductance resistors for damping resonances.
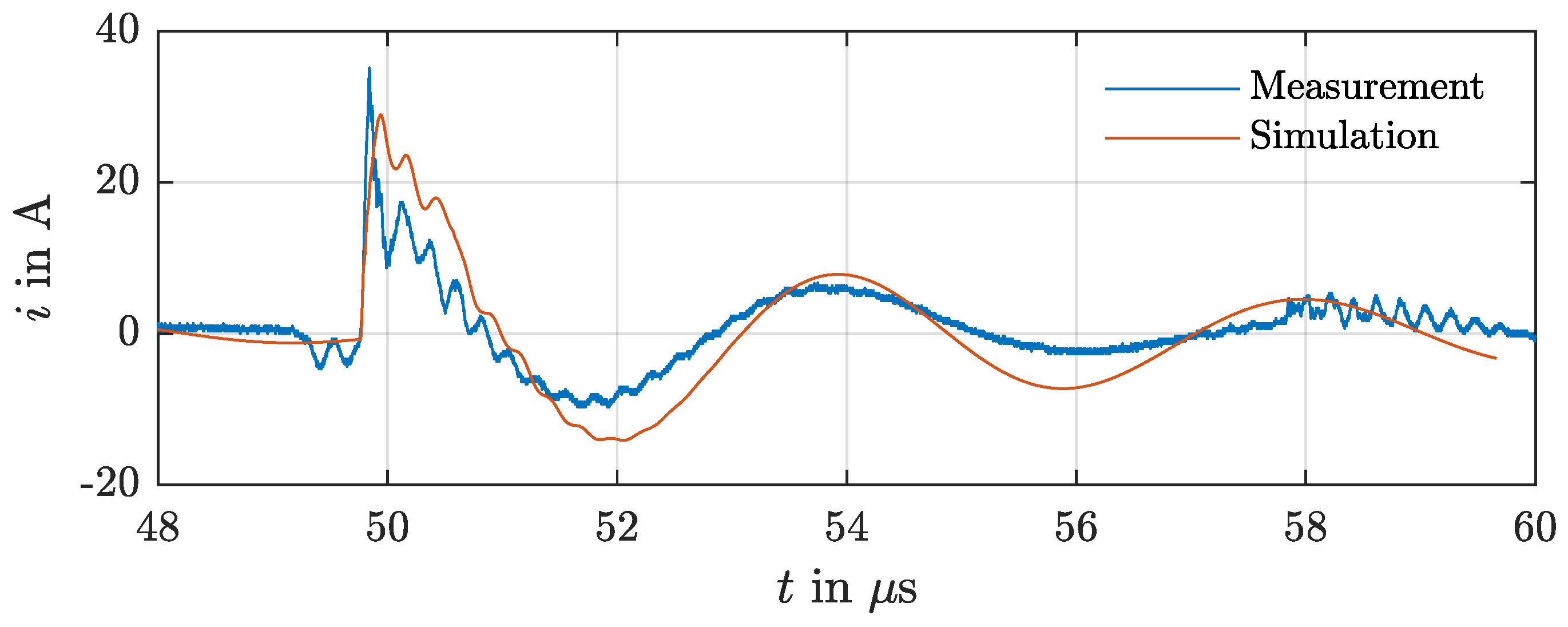
4. Validation of Simulation Model
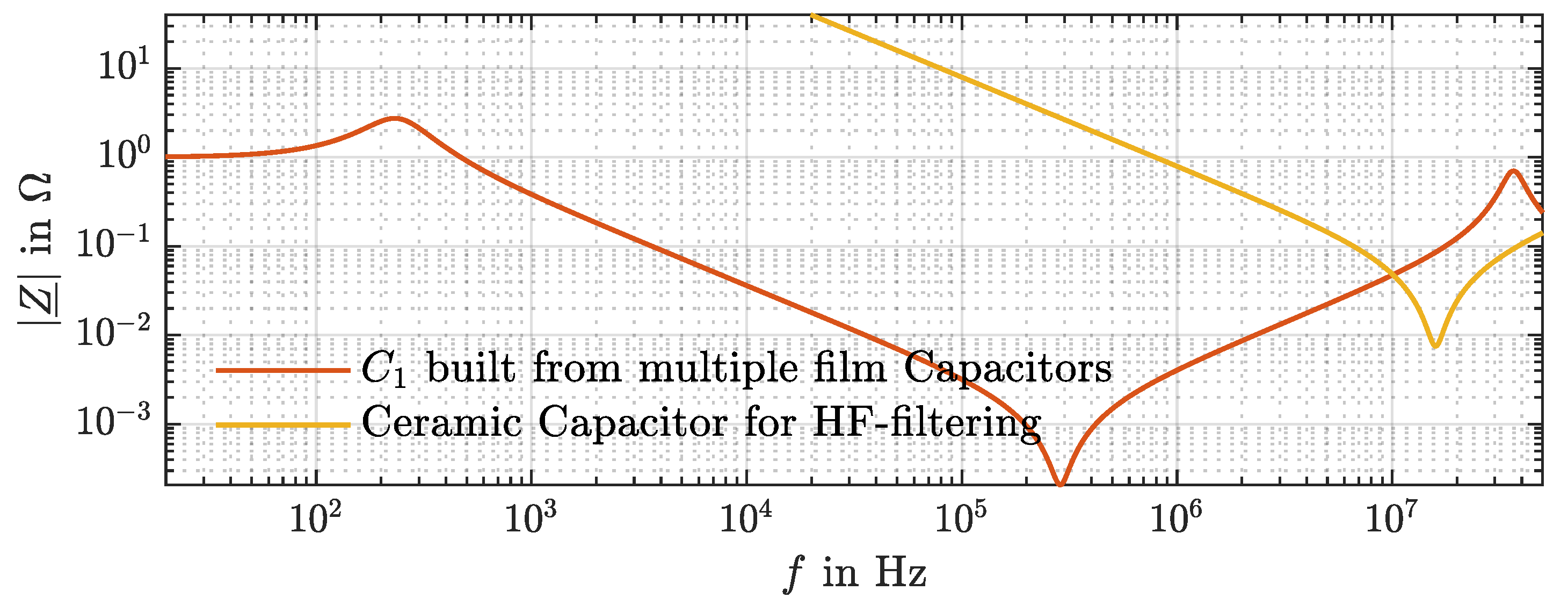
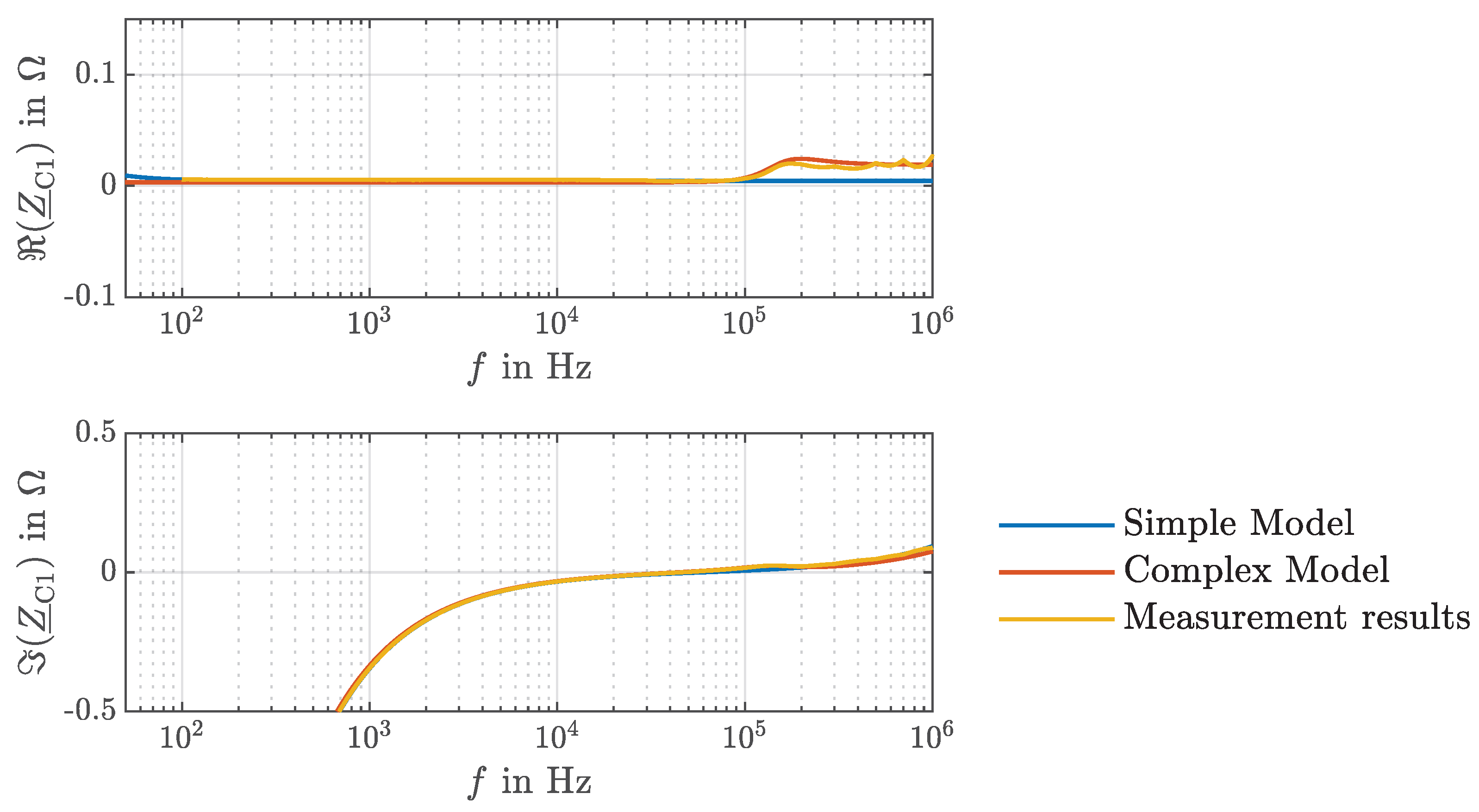
5. Non-Linear Loss Effects in Film Capacitors
- Skin effect;
- Proximity effect;
- Eddy currents.
- 1.
- To map skin and proximity losses within the capacitor, the inductance at mapping the ESL is substituted. The skin losses are represented by a first-order high-pass filter consisting of the resistor and the inductance . To account for the proximity losses, the inductance is also implemented in the capacitor model.
- 2.
- To represent the eddy currents and the additional losses caused by them, a second-order high-pass filter (parallel dipole) consisting of the inductance , the resistance , and the capacitance is implemented in the capacitor model.
6. Discussion
- Temperature and current dependent behaviour;
- Production-related component tolerances;
- Resonances occurring in the composite system.
- Model restrictions:
- Higher switching frequencies
7. Future Development
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DC | Direct current |
| VSC | Voltage source converter |
| DM | Differential mode |
| HF | High frequency |
| WBG | Wide bandgap |
| SVM | Space vector modulation |
| MPPFC | Metallised polypropylene film capacitor |
| ESL | Equivalent Series Inductance |
| ESR | Equivalent Series Resistance |
References
- Kolar, J.W.; Round, S.D. Analytical calculation of the RMS current stress on the DC-link capacitor of voltage-PWM converter systems. IEEE Proc.—Electr. Power Appl. 2006, 153, 535. [Google Scholar] [CrossRef]
- Dahono, P.A.; Sato, Y.; Kataoka, T. Analysis and minimization of ripple components of input current and voltage of PWM inverters. IEEE Trans. Ind. Appl. 1996, 32, 945–950. [Google Scholar] [CrossRef]
- Holmes, D.G. A general analytical method for determining the theoretical harmonic components of carrier based PWM strategies. In Proceedings of the Conference Record of 1998 IEEE Industry Applications Conference. Thirty-Third IAS Annual Meeting, St. Louis, MO, USA, 12–15 October 1998; pp. 1207–1214. [Google Scholar] [CrossRef]
- Huang, X.; Lai, J.-S.; Pepa, E. Analytical evaluation of modulation effect on three-phase inverter differential mode noise prediction. In Proceedings of the Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition, 2004. APEC ’04, Anaheim, CA, USA, 22–26 February 2004; pp. 681–687. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical tools for carrier based PWM methods. In Proceedings of the PESC97. Record 28th Annual IEEE Power Electronics Specialists Conference. Formerly Power Conditioning Specialists Conference 1970–1971. Power Processing and Electronic Specialists Conference 1972, St. Louis, MO, USA, 22–27 June 1997; pp. 1462–1471. [Google Scholar] [CrossRef]
- Un, E.; Hava, A.M. Performance Analysis and Comparison of Reduced Common Mode Voltage PWM and Standard PWM Techniques for Three-Phase Voltage Source Inverters. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, 2006. APEC ’06, Dallas, TX, USA, 19–23 March 2006; pp. 303–309. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Simple analytical and graphical methods for carrier-based PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 49–61. [Google Scholar] [CrossRef]
- Gu, B.G.; Nam, K. A DC-link capacitor minimization method through direct capacitor current control. IEEE Trans. Ind. Appl. 2006, 42, 573–581. [Google Scholar] [CrossRef]
- Welchko, B.A. Analytical calculation of the RMS current stress on the DC link capacitor for a VSI employing reduced common mode voltage PWM. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Un, E.; Hava, A.M. A Near-State PWM Method with Reduced Switching Losses and Reduced Common-Mode Voltage for Three-Phase Voltage Source Inverters. IEEE Trans. Ind. Appl. 2009, 45, 782–793. [Google Scholar] [CrossRef]
- Hava, A.M.; Ün, E. A High-Performance PWM Algorithm for Common-Mode Voltage Reduction in Three-Phase Voltage Source Inverters. IEEE Trans. Power Electron. 2011, 26, 1998–2008. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Patin, N.; Friedrich, G. PWM strategy dedicated to the reduction of DC bus capacitor stress in embedded three phase inverter. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011. [Google Scholar] [CrossRef]
- Cetin, N.O.; Hava, A.M. Topology and PWM method dependency of high frequency leakage current characteristics of voltage source inverter driven AC motor drives. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3430–3437. [Google Scholar] [CrossRef]
- Cao, W.; Wang, F.; Jiang, D. Variable switching frequency PWM strategy for inverter switching loss and system noise reduction in electric/hybrid vehicle motor drives. In Proceedings of the 2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 17–21 March 2013. [Google Scholar] [CrossRef]
- Sommer, C.; Merkert, A.; Mertens, A. A new control method for minimizing the DC-link capacitor current of HEV inverter systems. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014. [Google Scholar] [CrossRef]
- Basler, B.; Greiner, T.; Heidrich, P. Reduction of DC link capacitor stress for double three-phase drive unit through shifted control and phase displacement. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, NSW, Australia, 9–12 June 2015; pp. 887–889. [Google Scholar] [CrossRef]
- Berlinecke, J.; Henke, M.; Plikat, R. Ansteuerverfahren multiphasiger E-Antriebe–Simulation und Bewertung von Raumzeigermodulationen. In Proceedings of the 10. Tagung Elektrische Antriebstechnologie für Hybrid- und Elektrofahrzeuge, Würzburg, Deutschland, 27 September 2017. [Google Scholar]
- Lamp, J. IGBT Peak Voltage Measurement and Snubber Capacitor Specification; Semikron: Singapore, 2008. [Google Scholar]
- Zhao, S.; Zhang, M.; Zhang, Z.; Zhu, N.; Zhao, Y.; Li, H.; Ding, L. Analytic Model of the Voltage Oscillation in a High-Power Converter with Silicon Carbide Devices. IEEE Trans. Ind. Appl. 2024, 60, 3345–3358. [Google Scholar] [CrossRef]
- Babaki, A.; Golsorkhi, M.S.; Christensen, N.; Baharizadeh, M.; Behrendt, S.; Beyer, J.; Ebel, T. Parasitic-Based Model for Characterizing False Turn-On and Switching-Based Voltage Oscillation in Hybrid T-Type Converter. Electronics 2024, 13, 1808. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, S.; Baisden, A.; Wang, F.; Boroyevich, D. EMI Suppression in Voltage Source Converters by Utilizing dc-link Decoupling Capacitors. IEEE Trans. Power Electron. 2007, 22, 1417–1428. [Google Scholar] [CrossRef]
- Schulting, P.; Kubon, D.; De Doncker, R.W. Electrical design considerations for a 4 kW buck converter with normally-off GaN devices at a Dc-link voltage of 400 V. In Proceedings of the 2016 IEEE 2nd Annual Southern Power Electronics Conference (SPEC), Auckland, New Zealand, 5–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Stewart, J.; Neely, J.; Delhotal, J.; Flicker, J. DC link bus design for high frequency, high temperature converters. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 809–815. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, Z.; Ericsen, T.; Raju, R.; Burgos, R.; Boroyevich, D. Advances in Power Conversion and Drives for Shipboard Systems. Proc. IEEE 2015, 103, 2285–2311. [Google Scholar] [CrossRef]
- Laird, I.; Yuan, X.; Scoltock, J.; Forsyth, A.J. A Design Optimization Tool for Maximizing the Power Density of 3-Phase DC–AC Converters Using Silicon Carbide (SiC) Devices. IEEE Trans. Power Electron. 2018, 33, 2913–2932. [Google Scholar] [CrossRef]
- Parvez, M.; Pereira, A.T.; Ertugrul, N.; Weste, N.H.E.; Abbott, D.; Al-Sarawi, S.F. Wide Bandgap DC–DC Converter Topologies for Power Applications. Proc. IEEE 2021, 109, 1253–1275. [Google Scholar] [CrossRef]
- Forte, G.; Spampinato, A. High Power-Density Design Based on WBG GaN Devices for Three-Phase Motor Drives. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Napoli, Italy, 19–21 June 2024; pp. 65–70. [Google Scholar] [CrossRef]
- Nasrin, M.S.; Khan, F.H.; Alam, M.K. Quantifying Device Degradation in Live Power Converters Using SSTDR Assisted Impedance Matrix. IEEE Trans. Power Electron. 2014, 29, 3116–3131. [Google Scholar] [CrossRef]
- Wang, H.; Blaabjerg, F. Reliability of Capacitors for DC-Link Applications in Power Electronic Converters - An Overview. IEEE Trans. Ind. Appl. 2014, 50, 3569–3578. [Google Scholar] [CrossRef]
- Novák, I. DC and AC Bias Dependence of Capacitors. In Proceedings of the DesignCon, Santa Clara, CA, USA, 27 September 2011. [Google Scholar]
- Sullivan, C.; Sun, Y.; Kern, A. Improved distributed model for capacitors in high-performance packages. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002. [Google Scholar] [CrossRef]
- Tyshko, A.; Balevicius, S. Specifics of the X7R capacitors application in the high frequency inverters. In Proceedings of the 2016 IEEE 36th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 19–21 April 2016. [Google Scholar] [CrossRef]
- Coday, S.; Barth, C.B.; Pilawa-Podgurski, R.C. Characterization and Modeling of Ceramic Capacitor Losses under Large Signal Operating Conditions. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018. [Google Scholar] [CrossRef]
- Haag, H.; Haemmerle, F.; Ben-Yaakov, S. Voltage Bias Effect on the ESR of Ferroelectric Ceramic Capacitors. In Proceedings of the PCIM Europe digial days 2020 International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management Proceedings, Berlin, Germany, 7–8 July 2020. [Google Scholar]
- Haag, H.; Mitterbacher, A.; Haemmerle, F. Losses in Ferroelectric Dielectric Ceramic Capacitors due to Electromechanical Resonances. In Proceedings of the PCIM Europe digial days 2020 International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management Proceedings, Berlin, Germany, 7–8 July 2020. [Google Scholar]
- Wöhrle, D.; Armbruster, C.; Schöner, C. Design of a Fast Switching 200 kVA SiC Drive Inverter for Aviation Application. In Proceedings of the PCIM Europe 2023; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 9–11 May 2023. [Google Scholar] [CrossRef]
- Joubert, C.; Béroual, A.; Rojat, G. Magnetic field and current distribution in metallized capacitors. J. Appl. Phys. 1994, 76, 5288–5293. [Google Scholar] [CrossRef]
- Iorga, C. Compartmental analysis of dielectric absorption in capacitors. IEEE Trans. Dielectr. Electr. Insul. 2000, 7, 187–192. [Google Scholar] [CrossRef]
- Joubert, C.; Béroual, A.; Rojat, G. Asymmetrical current distribution in metallized film capacitors. J. Appl. Phys. 2004, 95, 6420–6425. [Google Scholar] [CrossRef]
- Kundert, K. Modeling Dielectric Absorption in Capacitors; Technical report; Designers Guide Consulting Inc.: Boulder, CO, USA, 2008. [Google Scholar]
- Hosking, T. Eddy Current Effects in Film Capacitors and Their Impact on Interconnect Systems in High Power Applications; Technical report, Power Ring Division; SBE Inc.: San Francisco, CA, USA, 2009. [Google Scholar]
- Makdessi, M.; Sari, A.; Venet, P. Improved model of metalized film capacitors. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 582–593. [Google Scholar] [CrossRef]
- Li, H.; Huang, X.; Li, Z.; Li, H.; Wang, W.; Wang, B.; Zhang, Q.; Lin, F. Modeling of ESR in metallized film capacitors and its implication on pulse handling capability. Microelectron. Reliab. 2015, 55, 1046–1053. [Google Scholar] [CrossRef]
- Wen, H.; Xiao, W.; Wen, X.; Armstrong, P. Analysis and Evaluation of DC-Link Capacitors for High-Power-Density Electric Vehicle Drive Systems. IEEE Trans. Veh. Technol. 2012, 61, 2950–2964. [Google Scholar] [CrossRef]
- Zhang, H.; Wheeler, N.; Grant, D. Switching harmonics in the DC link current in a PWM AC-DC-AC converter. In Proceedings of the IAS ’95. Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995. [Google Scholar] [CrossRef]
- Mariscotti, A. Analysis of the DC-link current spectrum in voltage source inverters. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 484–491. [Google Scholar] [CrossRef]
- Holmes, D.G. Pulse Width Modulation for Power Converters; Wiley-Blackwell: Oxford, UK, 2003. [Google Scholar]
- Zhang, D.; Wang, F.; Burgos, R.; Lai, R.; Boroyevich, D. DC-Link Ripple Current Reduction for Paralleled Three-Phase Voltage-Source Converters with Interleaving. IEEE Trans. Power Electron. 2011, 26, 1741–1753. [Google Scholar] [CrossRef]
- McGrath, B.; Holmes, D. A General Analytical Method for Calculating Inverter DC-Link Current Harmonics. IEEE Trans. Ind. Appl. 2009, 45, 1851–1859. [Google Scholar] [CrossRef]
- Schoerle, S.; Hoene, E.; Lang, K.D. Automotive high voltage grid simulation modelling and simulation high voltage car grids from system prospective. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Gothenburg, Sweden, 1–4 September 2014. [Google Scholar] [CrossRef]
- Siami, S.; Joubert, C.; Glaize, C. High frequency model for power electronics capacitors. IEEE Trans. Power Electron. 2001, 16, 157–166. [Google Scholar] [CrossRef]
- Yang, X.; Li, J.; Ding, Y.; Xu, M.; Zhu, X.F.; Zhu, J. Observation of Transient Parity-Time Symmetry in Electronic Systems. Phys. Rev. Lett. 2022, 128, 065701. [Google Scholar] [CrossRef]
- Yan, D.; Hang, L.; He, Y.; He, Z.; Zeng, P. An Accurate Switching Transient Analytical Model for GaN HEMT under the Influence of Nonlinear Parameters. Energies 2022, 15, 2966. [Google Scholar] [CrossRef]
- Duraij, M.; Xiao, Y.; Zsurzsan, G.; Zhang, Z. Switching Performance in a GaN Power Stage at Extreme Temperature Conditions. In Proceedings of the 2021 IEEE 8th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Redondo Beach, CA, USA, 7–11 November 2021; pp. 135–139. [Google Scholar] [CrossRef]
- Li, B.; Wang, G.; Liu, S.; Zhao, N.; Zhang, G.; Zhang, X.; Xu, D. Modeling and Analysis of Bridge-Leg Crosstalk of GaN HEMT Considering Nonlinear Junction Capacitances. IEEE Trans. Power Electron. 2021, 36, 4429–4439. [Google Scholar] [CrossRef]
- Zulauf, G.; Park, S.; Liang, W.; Surakitbovorn, K.N.; Rivas-Davila, J. COSS Losses in 600 V GaN Power Semiconductors in Soft-Switched, High- and Very-High-Frequency Power Converters. IEEE Trans. Power Electron. 2018, 33, 10748–10763. [Google Scholar] [CrossRef]
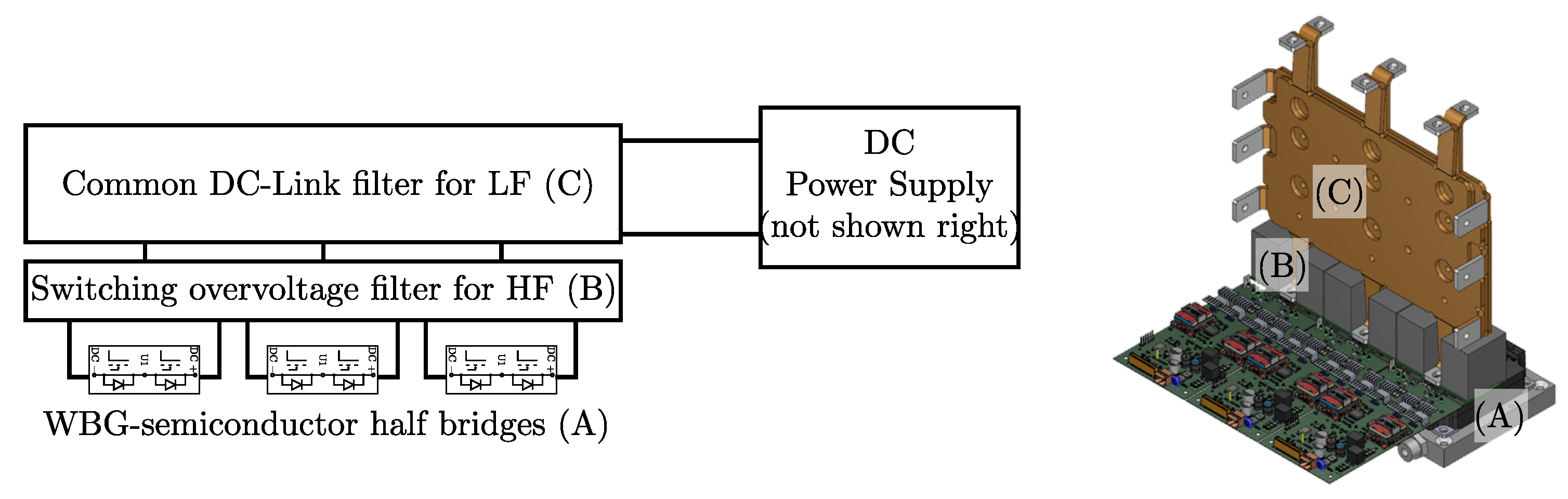
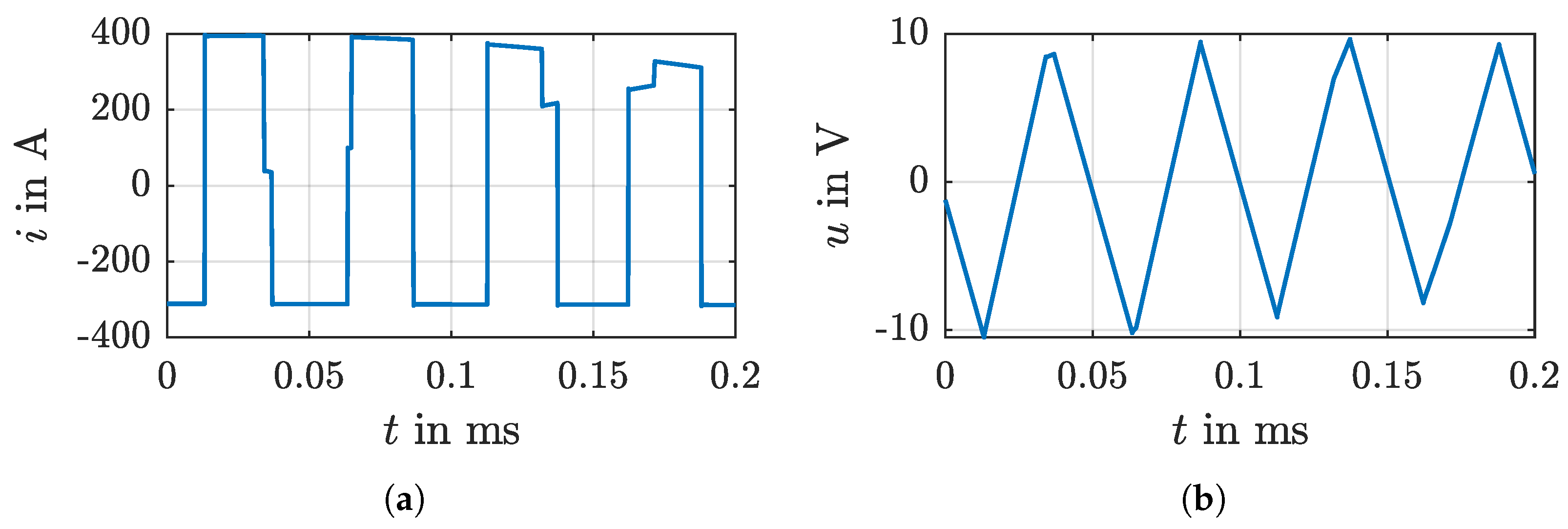




| Parameter | Value |
|---|---|
| Switching frequency range | 10 kHz … 200 kHz |
| Current-carrying capability (RMS) | 500 A |
| Maximum DC-terminal voltage | 1.2 kV |
| Modulation scheme | Space vector modulation (SVM) |
| (a) | (b) | (c) | |
|---|---|---|---|
| LF filter: Single capacitor peak current | - | 5.5 A | 5.1 A |
| HF filter: Single ceramic capacitor RMS current | - | 0.7 A | 0.6 A |
| HF filter: Single ceramic capacitor peak current | - | 5.1 A | 6.4 A |
| Voltage overshoot at power module | 29 V | 18 V | 20 V |
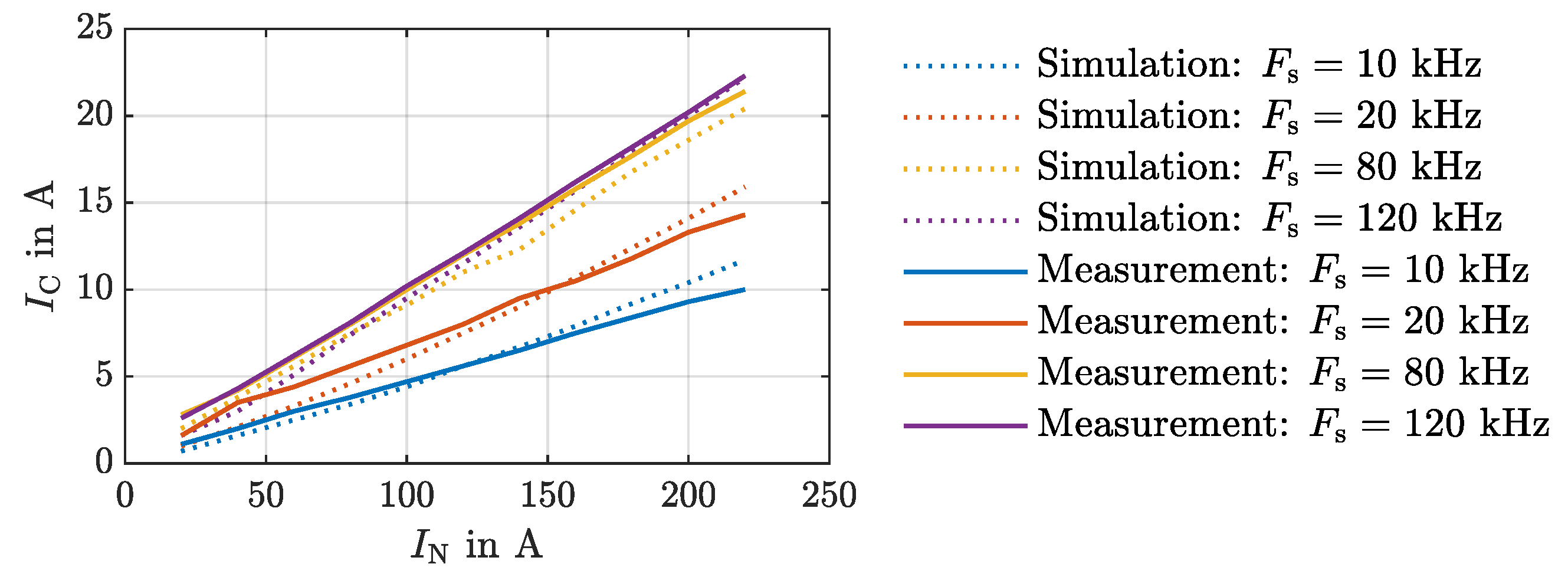
| AC-Side RMS Current | Modulation Level | HF Capacitor Current Stress | Relative | |
|---|---|---|---|---|
| Measurement | Simulation | Error | ||
| 0.0176 | 1.1 | 0.7 | +36% | |
| 0.0250 | 2.0 | 1.6 | +20% | |
| 0.0308 | 3.0 | 2.5 | +17% | |
| 0.0358 | 3.8 | 3.4 | +11% | |
| 0.0400 | 4.7 | 4.4 | +6% | |
| 0.0442 | 5.6 | 5.6 | +0% | |
| 0.0475 | 6.5 | 6.7 | −3% | |
| 0.0508 | 7.5 | 7.9 | −5% | |
| 0.0542 | 8.4 | 9.2 | −10% | |
| 0.0567 | 9.3 | 10.4 | −12% | |
| 0.0600 | 10.0 | 11.7 | −17% | |
| AC-Side RMS Current | Modulation Level | Relative Error | ||
|---|---|---|---|---|
| kHz | kHz | kHz | ||
| 0.0176 | +36% | +29% | +38% | |
| 0.0250 | +40% | +10% | +30% | |
| 0.0308 | +25% | +8% | +18% | |
| 0.0358 | +18% | +6% | +9% | |
| 0.0400 | +12% | +9% | +7% | |
| 0.0442 | +6% | +8% | +5% | |
| 0.0475 | +5% | +11% | −4% | |
| 0.0508 | −2% | +8% | −3% | |
| 0.0542 | −5% | +5% | +2% | |
| 0.0567 | −6% | +6% | +1% | |
| 0.0600 | −11% | +5% | 0% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raab, S.; Weickert, S.; Kasten, H. Methodology for Designing Broadband DC Link Filters for Voltage Source Converters. Electronics 2025, 14, 2743. https://doi.org/10.3390/electronics14142743
Raab S, Weickert S, Kasten H. Methodology for Designing Broadband DC Link Filters for Voltage Source Converters. Electronics. 2025; 14(14):2743. https://doi.org/10.3390/electronics14142743
Chicago/Turabian StyleRaab, Sebastian, Sebastian Weickert, and Henning Kasten. 2025. "Methodology for Designing Broadband DC Link Filters for Voltage Source Converters" Electronics 14, no. 14: 2743. https://doi.org/10.3390/electronics14142743
APA StyleRaab, S., Weickert, S., & Kasten, H. (2025). Methodology for Designing Broadband DC Link Filters for Voltage Source Converters. Electronics, 14(14), 2743. https://doi.org/10.3390/electronics14142743






