Abstract
In this study, a terahertz microfluidic multi-band sensor was designed. Unlike previous microfluidic absorption sensors that rely on dipole resonance, the proposed sensor uses a physical mechanism for absorption by exciting higher-order lattice resonances in microfluidic structures. With a Fabry–Perot cavity, the sensor can form an absorption peak with a high quality factor (Q) and narrow full width at half maximum (FWHM). A high Q value and a narrow FWHM are valuable in the field of sensing and provide strong support for high-precision sensing. On this basis, the sensing performance of the device was investigated. The simulation results clearly show that the absorption sensor has ultra-high sensitivity, which reaches 400 GHz/Refractive Index Unit (RIU). In addition, the sensor generates three absorption peaks, overcoming the limitations of a single frequency band in a composite resonance mode and multidimensional frequency response, which has potential application value in the field of volatile organic compound (VOC) sensing.
1. Introduction
A terahertz wave refers to an electromagnetic wave between microwave and infrared waves, with a frequency range of 0.1–10 THz [1]. It is characterized by low photon energy, strong penetration ability, and water absorption [2]. A metamaterial is an artificially designed synthetic material with electromagnetic properties that materials in nature do not have [3,4,5]. By adjusting its unit structure, the local electric field can be enhanced to strengthen the interaction between electromagnetic waves and matter [6]. A change in the refractive index of the surrounding environment can translate into a significant change in electromagnetic properties, so metamaterials can be used in the field of sensing [7].
In recent years, terahertz sensing and metamaterials have been combined as an efficient, non-destructive, and label-free detection technology that is widely used in optical devices and detectors, such as terahertz modulators, terahertz switches, terahertz lenses, and terahertz sensors [8,9,10,11,12,13,14]. Landy et al. [15] first proposed a single-band metamaterial absorber with high absorption in the microwave band. Saadeldin et al. [16] provided a nearly perfect metamaterial absorber design, which achieved an absorption rate of 0.99 at 2.249 THz and a high sensitivity of 300 GHz/RIU in the refractive index range of 1.0 to 1.39. Guo et al. [17] designed a terahertz metamaterial biosensor based on an open-square-ring resonant structure, which generated an extremely narrow absorption peak with a sensitivity of 91.5 GHz/RIU when the refractive index of the analyte increased from 1.0 to 1.8. Xiao et al. [18] proposed a compact graphene metamaterial sensor and analyzed the mechanism of its electromagnetically induced transparency (EIT) effect. The EIT effect was excited by the strong coupling of light and dark modes, resulting in a refractive index sensitivity of 2.828 THz/RIU. Recently, Qu et al. [19] created a high-performance terahertz microfluidic sensor based on Fabry–Perot resonance, which achieved dual-band absorption in the frequency range of 0.2–1.2 THz, with sensitivities of 159 GHz/RIU and 226 GHz/RIU, respectively, and realized the detection of edible oil. Since metamaterial absorbers were introduced into the field of terahertz sensing and detection, researchers have continuously explored methods to improve their sensing performance. On the one hand, adjusting the structure of the metal resonance unit on the surfaces of metamaterials can provide a sharper resonance peak and then optimize the Q value of the sensor to achieve a leap in sensitivity. On the other hand, carefully planning the structure of the resonance unit and constructing a metamaterial absorber with multiple resonance peaks can achieve accurate multi-point docking between the sensor and the characteristic frequency of the substance to be measured, which can enrich the information dimension reflecting the difference between substances [20].
In recent years, the combination of microfluidic technology [21] and metamaterials has provided a new method for the detection of liquid samples [22]. The height of the microfluidic channel, that is, the volume of the measured analyte, is on the order of micrometers, which greatly reduces the influence of water on terahertz waves. When the electromagnetic wave is incident, the Fabry–Perot structure of the metamaterial absorber binds the energy of the incident wave to the cavity of the absorber; the analyte in the channel acts as the dielectric layer of the absorber, which coincides with the reflecting cavity, thus enhancing the local electric field and effectively improving the sensitivity of the sensor [23]. Metamaterial absorbers integrated with microfluidic technology have made great progress in improving selectivity for VOC detection. Enric perarnau et al. [24] assumed that the thickness and properties of the polymer layer played a key role in affecting the selectivity of microchannels and proved the potential of using microfluidic gas detectors in environmental monitoring. Ghazi et al. [25] developed a sensor for the selective detection of VOCs and proved that the radius and number of microfeatures of the microfluidic channels played a significant role in improving the selectivity of the sensor. Guo et al. [26] designed a novel microfluidic chip based on the 4-aminohydrazine-5-mercapto-1,2,4-triazole (AHMT) method for the detection of formaldehyde. The sensor was almost unaffected by acetaldehyde, other VOCs, and acid–base conditions, demonstrating high selectivity.
Although many sensing structures for multi-band absorption have emerged based on metamaterial absorbers integrated with microfluidics, many shortcomings remain. For example, in pursuit of higher sensing sensitivity, metamaterial structures have advanced from two-dimensional to three-dimensional [27,28,29]. Although the three-dimensional structure can expand the electromagnetic field to three-dimensional space and strengthen the interaction between the analyte and electromagnetic wave, it also directly increases the manufacturing difficulty. In addition, most of the terahertz microfluidic sensors reported above are based on the dipole resonance mechanism. Terahertz microfluidic sensors designed based on this mechanism have a low Q value and a wide FWHM during resonance. As is well known, the Q value reflects the sensor’s ability to store electromagnetic wave energy. A large Q value is often closely related to the high sensitivity and stability of the sensor and is the key index that must be considered in the sensor design. Meanwhile, a narrow FWHM reflects the strong anti-interference and detail resolution abilities of the sensor. A high Q value and a narrow FWHM can be regarded as the two core elements affecting the sensing performance. However, few reported terahertz microfluidic sensors can simultaneously meet both requirements.
A multi-band terahertz sensor combining a high-order response and microfluidics is proposed in this paper. Its resonant unit structure is simple and is composed of two ring-shaped structures and a rectangular-shaped structure. It can produce three resonance peaks in the frequency range of 0.7–1.6 THz, with absorption rates of 0.976, 0.864, and 0.977, and the corresponding Q values are 21, 19, and 123, respectively. Compared with previous microfluidic multi-band sensors, this absorption sensor can achieve a higher Q value and narrower FWHM and has a simple structure that is easy to manufacture. The simulation results show that this design can achieve high-order resonance at specific frequencies through this simple structure, and the sensor sensitivity can reach 400 GHz/RIU, which has great application advantages in the field of VOC sensing.
2. Structure Design and Model
The structure of the designed multi-band metamaterial absorption sensor is shown in Figure 1. Figure 1a,b show a schematic diagram of the three-dimensional structure and a sectional view of the microfluidic sensor. The whole structure is composed of five parts: from top to bottom are the cover layer, the metal resonant structure, the microfluidic channel, the metal reflective layer, and the substrate. Figure 1c shows a top view of a single unit in the metal resonant structure. This unit structure is composed of two metal ring structures and a rectangular-type structure. The selected metal is gold, with a conductivity of 4.09 × 107 s/m. The specific structural parameters are as follows: w = 5 µm, I = 90 µm, r = 28 µm, y = 45 µm, Px = 138 µm, and Py = 155 µm. The thickness of the cover layer above the resonant structure can vary. Silicon dioxide with a thickness of t1 = 50 µm was chosen for the cover layer because silicon-based materials have better transmission and transmission properties in the terahertz band. The microfluidic channel height h is set at 9 µm, the thickness of the silicon substrate t3 is 400 µm, and the metal resonance structure and metal layer thickness t2 are both 200 nm. The electromagnetic wave is incident from the top and travels downward until it reaches the metal layer. It is reflected by the metal layer and reacts with the analyte—the dielectric in the channel—so that there is enough field strength in the analyte to improve the sensing performance.
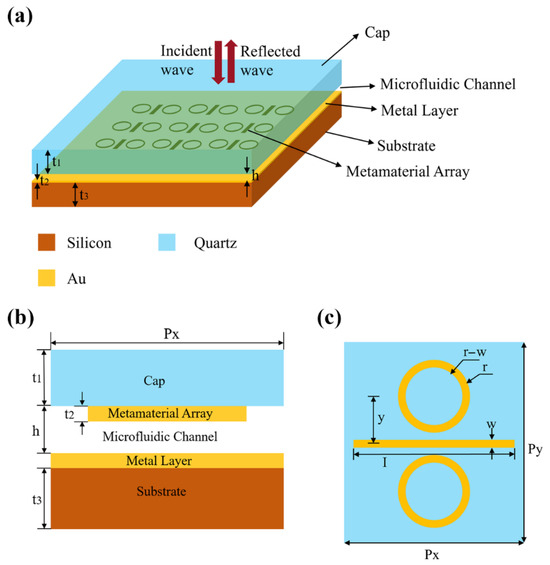
Figure 1.
A schematic of the microfluidic sensor. (a) A schematic diagram of the three-dimensional structure of the sensor; (b) a sectional schematic diagram of the sensor; (c) a structural diagram of a resonant unit of the sensor.
The multi-physics simulation software COMSOL (Version Multiphysics® 6.2) was used for this solution, which is based on the finite element method and uses a numerical method to solve physical problems. This work focused on electromagnetic resonance problems in the field of wave optics and did not involve multi-physics field coupling. In the solving process, the ewfd module under wave optics was used. Floquet periodic boundary conditions were used for the four edges of the element to simulate the infinite two-dimensional array. The perfectly matched layer (PML) on top of the cell can absorb the excitation modes of the source port and any higher-order modes generated by the periodic structure. The port was set above the silicon dioxide cover layer. Because the skin depth of terahertz waves in gold is insufficient to allow them to enter the interior of the gold layer, total reflection occurs when terahertz waves reach the bottom gold layer. Therefore, only one port was set up to balance the emission of electromagnetic waves and the detection of absorption and reflection. In addition, a plane wave was used as the excitation source to vertically irradiate the absorption sensor structure along the z-axis direction so as to complete the whole simulation process and provide accurate data support and a theoretical basis for subsequent analysis and research. The hardware foundation used in this simulation is a 12th Gen Intel (R) Core (TM) i5-12500 processor with 16 GB of memory (Dell Computer, Xiamen, China). Based on these hardware conditions, the physical field mesh selection is finer, with frequency domain scanning ranging from 0.7 to 1.6 THz and a step size of 0.0001 THz. A single simulation cycle takes about eight hours.
3. Results and Discussion
The absorption of electromagnetic waves by the sensor can be expressed as follows:
where is the absorption rate, is the reflectivity, and is the transmissivity. The microfluidic channel acts as the dielectric layer of the Fabry–Perot cavity. When a terahertz wave is incident, the Fabry–Perot structure of the metamaterial absorber binds the energy of the incident wave to the cavity of the absorber; a schematic diagram of its optical path is shown in Figure 2. From top to bottom are the metal array, the absorption dielectric layer in the channel, and the metal reflection layer. When a terahertz wave is incident to this structure from the upper cover layer, one part of the terahertz wave at the interface between the cover layer and the dielectric (including metal arrays and analytes in channels) is reflected into the cover layer, and the other part enters the channel dielectric layer and continues to propagate. Because the thickness of the metal reflection layer is much greater than the skin depth of the terahertz wave in the metal, the terahertz wave cannot pass through the metal layer, so when it reaches the metal reflection layer, total reflection occurs. At this time, . The electromagnetic wave reflected by the bottom metal layer will reach the cover dielectric interface again to reflect and transmit. The transmitted part will enter the cover layer, and the reflected part will continue to propagate in the channel dielectric layer and continue to reflect and transmit. The theory of destructive interference in a Fabry–Perot structure can be expressed as
where k0 represents the free-space wavenumber, d represents the thickness of the dielectric layer (the channel height h), represents its reflection phase, and N represents the resonance order. Here, n is the effective refractive index that includes the localized field effect of metasurfaces, reflecting the macroscopic optical response of the analyte in non-uniform electromagnetic fields. When the electromagnetic wave is reflected from the bottom metal reflector to the interface between the cover layer and the dielectric, the phase difference between the two reflected or transmitted waves can be an integral multiple of 2 π by designing the appropriate channel height. At this time, the electromagnetic wave meets the cancellation interference condition and can be obtained. At this point, the Fabry–Perot cavity satisfies the resonance condition, 2nh = Nλ, where λ is the wavelength of the incident electromagnetic wave, and the sensor achieves perfect absorption.
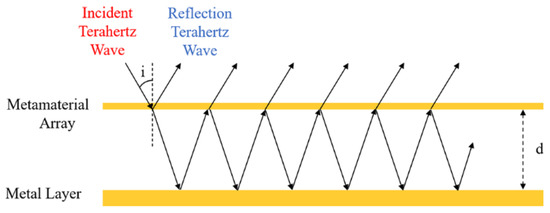
Figure 2.
A schematic diagram of a typical Fabry–Perot cavity; “i” represents the incident angle of terahertz wave.
In the structural composition of metamaterials, the metal structure under the cover occupies a key position and constitutes the main part of a metamaterial. When the electromagnetic wave penetrates the cover and enters the channel, it will interact with the metasurface and then cause the resonance phenomenon. It is worth noting that there is a close and significant correlation between the absorption frequency of the sensor and the resonance frequency induced by the metasurface. When the resonant structure is carefully designed, the sensor successfully shows three absorption peaks with a high absorption rate. Figure 3 shows the absorption spectrum of the sensor in the 0.7 THz to 1.6 THz band when the refractive index n of the analyte in the channel is 1.3. The black curve represents absorptivity, and the red curve represents reflectivity. At the three frequency points of 0.912 THz, 1.161 THz, and 1.414 THz, the absorptivity of the sensor rises to the maximum, and the specific values are 0.976, 0.864, and 0.977, respectively. These are named modes A, B, and C, respectively. According to the relevant definitions of Q value and FWHM [30], mode A has a Q value of 21 and an FWHM of 42.9 GHz; mode B has a Q value of 19 and an FWHM of 61.2 GHz; and mode C has a Q value as high as 123 and an FWHM of 11.5 GHz. Obviously, the Q value and FWHM of the third resonance peak are significantly higher and lower, respectively, than those of the first two. Thus, the formation mechanism of the third absorption peak is much different from that of the first two peaks. The following results also show that the higher-order response absorption peak of mode C is generated by the combination of dipole resonance and lattice surface resonance.
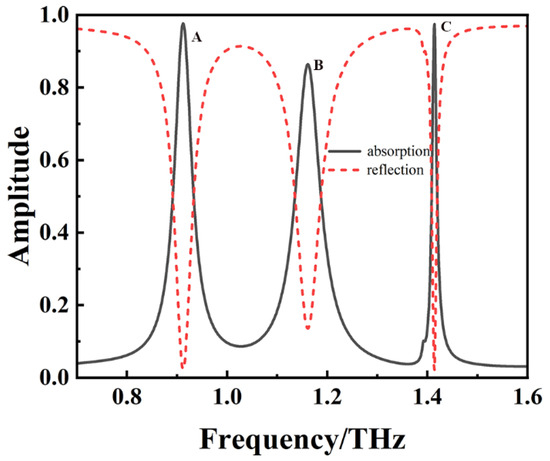
Figure 3.
The absorption spectrum of the sensor.
In order to further explain the physical mechanism of the resonant absorption of the sensor, the near-field distribution of the metal resonant unit structure at the resonant frequency is shown in Figure 4. In the case of sensor mode A shown in Figure 4a,d, the electric field and its z-component show obvious distribution characteristics; that is, they are mainly concentrated at both ends of the rectangular structure, while in the area outside the rectangular structure, the electric field accumulation phenomenon is almost zero. The distribution law of the z-component of the electric field is consistent with this, and the electric field distribution is typical of the dipole resonance mode. This phenomenon strongly indicates that the incident terahertz wave reacts with the sensor to produce dipole resonance. Similarly, for mode B, as shown in Figure 4b,e, the electric field and its z-component for the sensor are mainly distributed on the metal arms on both sides of the two metal ring structures. In the rest of the metal ring, the concentration of the electric field is extremely weak. It can be seen that the electric field component of the incident terahertz wave and the resonant ring in the sensor also cause dipole resonance. In this process, the incident electromagnetic wave energy is largely absorbed due to the resonance characteristics of the metal structure and manifests as two absorption peaks with high absorptivity, modes A and B, in the spectrum. In summary, the dipole resonance generated by two metal structures with different shapes can form two resonance peaks with different frequencies and different absorptivities, which proves that building a multi-resonance sensing system by combining different metal structures is an effective method. However, the resonance mode of mode C is significantly different from that of modes A and B. In Figure 4c,f, the distribution of the resonant electric field and the z-component of the electric field can be clearly observed. The electric field is distributed not only at both ends of the ring and rectangular structures but also in the non-metallic area inside the unit, and the coverage of the electric field in the non-metallic area far exceeds that on the metal arm. Therefore, mode C does not rely solely on the dipole resonance generated by the metal structure but on the high-order response caused by the synergistic effect of dipole resonance and lattice surface resonance. Compared with modes A and B, mode C has a greater electromagnetic field overlap with analytes in microfluidics; that is, its Q value is quite large, and the FWHM is abnormally narrow. These two characteristics are exactly the key conditions for the preparation of high-sensitivity sensors.
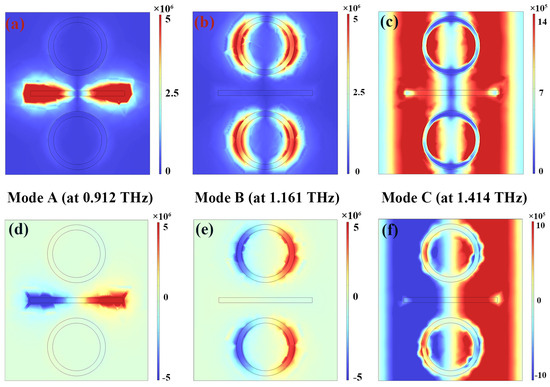
Figure 4.
The distribution of the near field (the amplitude of the electric field in (a) and the z-component of the electric field in (d)) at the resonance peak A at 0.912 THz; the distribution of the near field (the amplitude of the electric field in (b) and the z-component of the electric field in (e)) at the resonance peak B at 1.161 THz; the distribution of the near field (the amplitude of the electric field in (c) and the z-component of the electric field in (f)) at the resonance peak C at 1.414 THz. The simulation results show that in mode C, the overlap between the electric field and the analyte in the microfluidic channel is higher.
Figure 5 clearly shows the magnetic field distribution in the x–z plane of the cap and channel of the microfluidic sensor in the resonant state, where Figure 5a–c correspond to modes A, B, and C, respectively. Through observation, it can be found that the incident electromagnetic wave energy shows a clear aggregation trend, mainly concentrated in the microfluidic channel and caprock area. In particular, mode C shows a wider magnetic field distribution area in the microfluidic channel, which more effectively limits the electromagnetic wave energy in the microfluidic channel cavity, resulting in its Q value being significantly higher than that of mode A or B. When electromagnetic waves are irradiated on the metal resonant unit, opposite polarity charges will accumulate at both ends of the bimetallic ring and rectangular metal. Electric dipole resonance occurs on the metal, which will have a strong coupling effect with the metal plate structure at the bottom, resulting in a reverse charge distribution in the metal layer structure at the bottom. Its presence will cause reverse currents to form on the upper and lower surfaces of the metal resonant structure, thereby forming a strong magnetic field resonance. At this time, a concentrated magnetic field will accumulate directly below the metal. This feature can be clearly observed in the magnetic field distribution in Figure 5a,b, which shows the marked accumulation of a strong magnetic field under the metal ring structure and rectangular structure. In contrast to the previous two magnetic field distribution modes, the magnetic field distribution of mode C in the channel is not limited to right below the metal structure but also exists under other regions of the non-metal structure, which further proves that the absorption peak at 1.414 THz is a high-order response mechanism caused by the combination of dipole resonance and lattice surface resonance from the metal array.
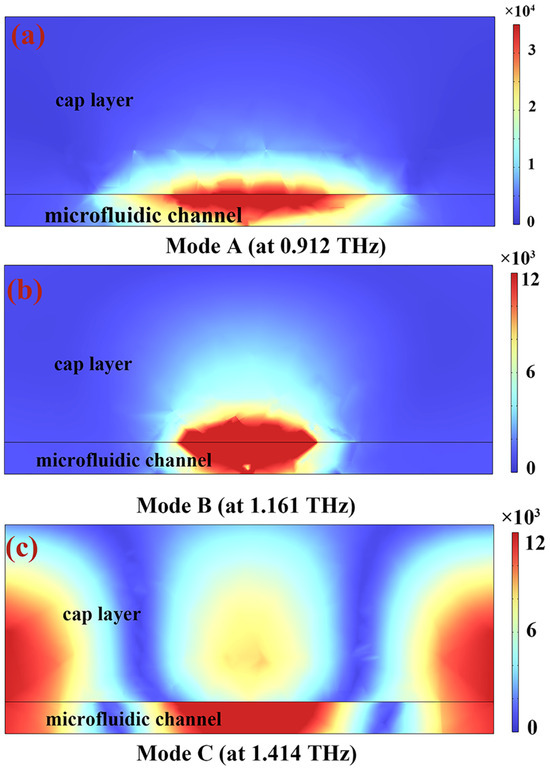
Figure 5.
The magnetic field distribution in a microfluidic channel. (a–c) represent modes A, B, and C, respectively. The simulation results show that, in mode C, the overlap between the magnetic field and the analyte in the microfluidic channel is higher.
It is not difficult to imagine that this high-order response mechanism will be affected by the metal structure dipole parameters and lattice period parameters. However, through in-depth analysis of the absorption spectra corresponding to changes in the metal structure and lattice period parameters, as shown in Figure 6a–d, it can be found that changing the metal structure hardly affects the absorption peak, while changing the lattice period Py causes a significant shift in the resonant frequency. This phenomenon can be reasonably explained by the electric field distribution in metal and non-metal regions in mode C. Figure 4a–c show that, at 1.414 THz, compared with the electric field on the bimetallic ring and rectangular-type metal structures, most of the electric field is concentrated in the non-metallic region, so the influence of changing the metal structure on the resonance peak is relatively small and not enough to cause an obvious frequency shift.
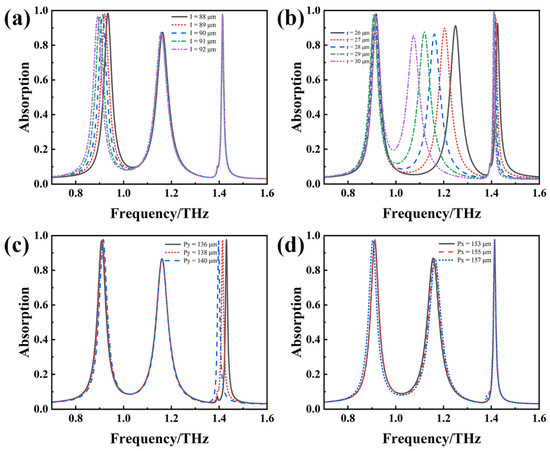
Figure 6.
Absorption spectra with changes in length (I) in (a); radius (r) in (b); lattice period (Py) in (c); and lattice period (Px) in (d).
In order to further verify the resonance absorption phenomenon and theory mentioned above, this study further explored the influence of the microfluidic channel height and related parameters on the absorption spectrum. Under the premise of maintaining the constant size of the structure above the channel, the mechanism of the effect of channel height h on the absorption performance was comprehensively studied for a channel analyte refractive index n = 1.3. The absorption curves at different channel heights are shown in Figure 7.
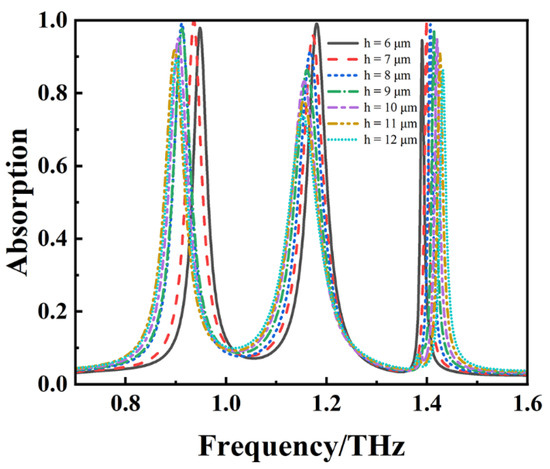
Figure 7.
Absorption spectra for various microfluidic channel heights.
It can be observed that with the continuous increase in microfluidic thickness h, modes A and B exhibit a frequency redshift phenomenon; that is, the resonant frequency decreases. This is because as the height h of the cavity increases, in order to maintain phase matching (the phase difference between light traveling back and forth once inside the cavity is an integer multiple of 2π), the wavelength λ needs to increase accordingly. Due to the inverse proportionality between frequency f and wavelength λ (f = c/λ, where c is the speed of light), an increase in wavelength leads to a redshift. Unlike modes A and B, as the thickness of the microfluidic channel increases, the resonant frequency of mode C undergoes a blue shift; that is, the resonant frequency increases. This is because when mode C occurs, the distribution of the electromagnetic field greatly overlaps with the analyte dielectric in the channel, as shown in Figure 4c,f. At this time, the effective refractive index will increase due to the metasurface effect. As h increases, the overlap area between the electromagnetic fields of the microfluidic analyte and the metal structure decreases, and the metasurface effect decreases, resulting in a decrease in the effective refractive index. In order to meet the phase matching condition, λ needs to be reduced; that is, mode C undergoes a blue shift. Figure 8a clearly shows that as the channel height h gradually decreases, the absorption rates of the three resonance peaks show a gradual increase. It is particularly noteworthy that when the channel height h reaches 7 μm, the absorbance of modes A and C reaches the peak state. However, as the channel height h continues to decrease, the absorptivity of modes A and C gradually decreases. This phenomenon shows that the optimal height of the microfluidic channel is 7 μm in modes A and C. This is because once the channel height deviates from this optimal value, the sensor will not be able to meet the previously mentioned phase conditions of electromagnetic waves on both sides of the cover dielectric interface in modes A and C, which means that only part of the electromagnetic waves superimposed by multiple reflections on the caprock dielectric interface can undergo destructive interference, or they can even experience interference enhancement, and finally, the absorption frequency will change. The Q value is closely related to the channel height h. As shown in Figure 8b, the Q values corresponding to the resonant frequencies of the three absorption peaks show a downward trend with the gradual increase in channel height. The reason for this phenomenon is that the increase in channel height decreases the efficiency of energy storage in the resonator. Further observation shows that the Q value of mode C is about four times higher than those of other absorption peaks, regardless of how the channel height h changes, and its advantage is very significant. From the perspective of the electric field distribution, the electric field in mode C accumulates over a wide range, covering almost the entire lattice unit, while the electric field energy of the other two resonance peaks is mainly stored in the metal structure; this means that mode C has a stronger ability to store electromagnetic fields, and thus, its Q value is much higher than those of the other absorption peaks. In addition, changing the channel height directly affects the degree of overlap between electromagnetic waves and analytes, leading to changes in the Q value and fluctuations in the FWHM of the absorber. After considering the comprehensive impact of various parameters, it was determined that h = 9 μm is optimal. At this point, the parameters of modes A, B, and C reach a relatively balanced state, which can achieve a near-ideal overall performance.
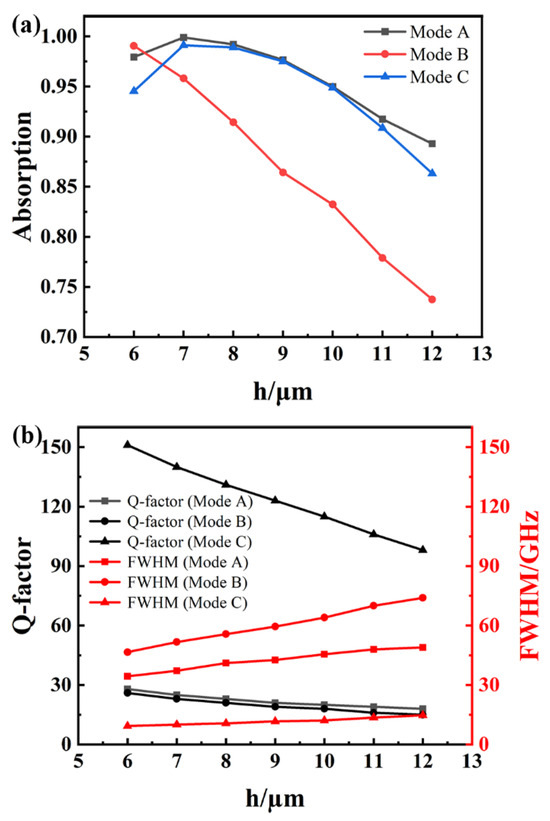
Figure 8.
(a) Effect of microfluidic channel height on absorption rate and FWHM; (b) effect of microfluidic channel height on Q-factor.
To further investigate the formation mechanism of higher-order lattice resonances in mode C, a multipole decomposition method was used for a more in-depth analysis. Multipole decomposition, as a mathematical tool for decomposing electromagnetic fields, can decompose complex electromagnetic fields into a series of modes that characterize different near-field distributions. The scattering characteristics of these modes are the electromagnetic response characteristics of the device. Therefore, the calculation results of multipole decomposition can be used to describe the interaction between electromagnetic fields and devices [31,32]. When the device is in an electromagnetic field, specific near-field distributions are generated inside, and the scattering characteristics of these near-field distributions are reflected in the electromagnetic response of the optical structure. By calculating the current density in the material to obtain the intensity of each multipole mode, the electromagnetic response of the device can be determined and its scattering characteristics can be analyzed. In this study, the electric dipole moment (ED), magnetic dipole moment (MD), toroidal dipole moment (TD), electric quadrupole moment (EQ), and magnetic quadrupole moment (MQ) were obtained by integrating the current density in the Cartesian coordinate system, achieving an effective description of the interaction process between electromagnetic fields and matter. The specific calculation formula is as follows [33,34]:
Among them, J is the current density; r is the coordinate vector; c is the speed of light; and ω is the angular frequency of the incident electromagnetic wave; δαβ is the δ function. The scattering power corresponding to different multipole moments (scattering power IED of electric dipole, scattering power IMD of magnetic dipole, scattering power ITD of toroidal dipole, scattering power IEQ of relectric quadrupole, scattering power IMQ of magnetic quadrupole) can be expressed as follows:
The multipole decomposition calculation was carried out for mode C excited by the resonant structure, and the scattering power calculation results are shown in Figure 9. The results clearly demonstrate the contribution of different multipole moments to mode C, with MD and EQ confirmed as the main contributors to mode C. From Figure 4f, it can be seen that there are charge accumulations of opposite polarity in the non-metallic regions at both ends along the central axis. These pairs of charges, which are separated by a certain distance and have equal charges but opposite polarities, form a set of EDs. Similarly, the metal rings at both ends of the central axis accumulate charges of opposite polarity to the non-metallic region, forming another set of EDs with opposite directions. Eventually, two sets of EDs with opposite directions are formed in the lattice resonance unit, together forming a set of EQs. In addition, due to the induction of charges of opposite polarity on the upper and lower surfaces of the metal resonant structure, the charges move in a directional manner under the action of the electric potential field, ultimately forming a circular current on the upper and lower surfaces. The center of this circular current generates a set of MDs perpendicular to the current plane. Figure 5c intuitively shows the magnetic field distribution excited by the MDs in mode C within the channel. The above phenomenon is completely consistent with the conclusion drawn from the multipole decomposition calculation that EQ and MD are the main contributors to mode C. As shown in Figure 6a–d, when changing the length I of the rectangular structure and the r of the bimetallic ring structure, both modes A and B will have corresponding frequency point shifts, which are not constrained by the lattice period parameters Px and Py, indicating that modes A and B are local dipole resonance responses. However, whether changing the length I of the rectangular structure or the r value of the double-ring metal structure, the resonant frequency of mode C is almost unchanged compared with those of modes A and B. When the lattice period parameters Px and Py are changed, it is found that the resonant frequency of mode C changes greatly when Py is changed. It is confirmed that the absorption peak C mainly comes from the surface lattice resonance of the whole metamaterial because the surface lattice resonance is very sensitive to a change in the lattice period, while the parameter change in the metal array itself has little effect on the surface lattice resonance [35,36]. More precisely, the coupling of EQ and MD produces high-order lattice resonance.
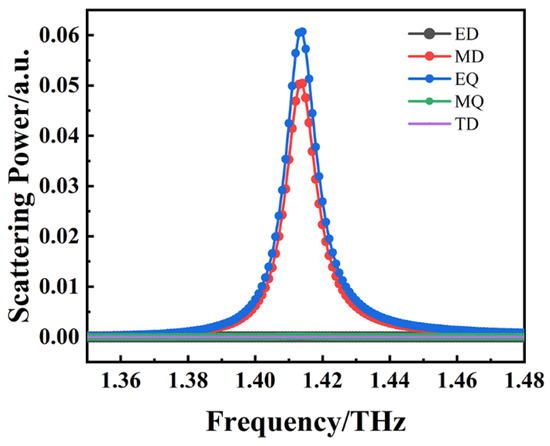
Figure 9.
The multipole decomposition calculation results of mode C.
Figure 10a shows the absorption spectra corresponding to the three absorption peaks when the refractive index of the analyte in the microfluidic channel changes. It shows that as the refractive index n of the analyte increases from 1.3 to 1.4 in steps of 0.02, the three absorption peaks all show significant shifts toward lower frequencies. The reason for this phenomenon is that the change in the refractive index of the analyte changes the dielectric environment around the metamaterial and then affects the phase difference between the electromagnetic waves on both sides of the dielectric cap interface, which is finally reflected in a shift in the resonant frequency point on the spectrum. Further observation shows that the frequency shift resolution of the third peak is significantly higher than that of the other two resonance peaks. The reason is that mode C has a much higher Q value and a narrower FWHM. The electric field diagrams in Figure 4a–c also show that mode C has the strongest ability to store electric field and thus shows a higher value in the sensing field. In addition, the refractive index detection range (1.3–1.4) of the multi-band terahertz sensor just covers the refractive indices of many common VOCs [37], which demonstrates its high application potential in gas sensing and other fields.
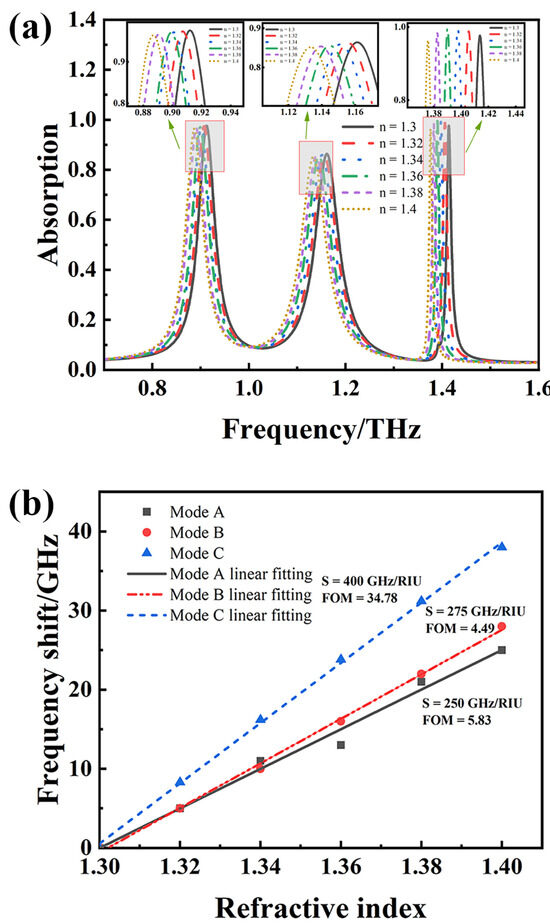
Figure 10.
(a) Absorption spectra corresponding to different refractive indices; (b) frequency shifts corresponding to different refractive indices.
In terms of sensor performance evaluation, the refractive index sensitivity (S) is a key indicator. The larger its value, the greater the sensor’s sensitivity to subtle changes in the surrounding dielectric [38]. Its calculation formula is , where represents the change in resonance frequency, is the change in the refractive index, and its unit is RIU. In addition, the figure of merit (FOM) can be used to comprehensively characterize the performance of the sensor for a more scientific comparison of the advantages and disadvantages of sensors in different frequency bands; its calculation formula is [39]. The data in Figure 10b show that when the refractive index n of the analyte changes from 1.3 to 1.4 (in steps of 0.02), the resonant frequency shift of the sensor gradually increases, and it generally shows a good linear relationship with the refractive index.
After linear fitting, the sensitivity of the sensor in modes A, B, and C reached 250 GHz/RIU, 275 GHz/RIU, and 400 GHz/RIU, respectively, and the corresponding FOM values were 5.83, 4.49, and 34.78, respectively. Obviously, the sensitivity and FOM value of mode C are significantly better than those of the other two modes. In Table 1, the resonance mechanism for references [40,41,42,43,44,45] is surface plasmon resonance (SPR), which achieves sensing via resonance absorption when the wave vector of incident light matches the collective oscillation of free electrons on the metal surface. The resonance mechanism for references [44,45] is localized surface plasmon resonance (LSPR), which achieves absorption sensing via the collective oscillation of the free electrons of metal nanoparticles when illuminated at a specific wavelength. Comparing the FOM values of references [42,45] reveals that the comprehensive performance of SPR-based sensors is better than that of LSPR-based sensors. The higher Q value and narrower FWHM for reference [42] further demonstrate the importance of these two parameters in improving sensor performance. Table 1 shows the performance comparison results between the sensors in this work and those in references from the literature. It can be observed that this design has a higher sensitivity and Q value, as well as a narrower FWHM. The FOM value shows that this design has better sensing performance.

Table 1.
A comparison of the overall performance of the proposed terahertz refractive index sensor in this work with that of sensors from previously reported simulations.
4. Conclusions
A multi-band terahertz metamaterial absorber integrated with microfluidics is proposed. Its resonant unit is composed of a unique double-ring metal structure and a rectangular-type metal structure. Three resonant absorption peaks with high absorption rates are successfully obtained. In particular, the third resonance peak exhibits a large Q value and a very narrow FWHM. The resonance mechanisms of the three absorption peaks were explored in depth through near-field analysis. The results show that the first two absorption peaks are derived from the dipole response caused by the interaction of the rectangular and double-ring metal structures with electromagnetic waves, respectively, while the third resonance peak is a high-order response generated by the synergistic effect of dipole resonance and metamaterial surface lattice resonance. Among them, mode C, with a high Q value and narrow FWHM, has high application value in the sensing field. The sensing performance of the three resonant absorption peaks was further analyzed. The results show that mode C is the most sensitive to a change in the refractive index of the analyte in the channel. Its sensing sensitivity is as high as 400 GHz/RIU, and the FOM value is 34.78. Compared with other sensors, it shows superior sensing performance, providing a new idea and direction for the application of VOC sensing.
Author Contributions
Conceptualization, B.Z., H.S. (Hao Shen) and L.W.; methodology, L.W., X.D. and Y.L.; software, Y.L. and L.W.; validation, B.Z., H.S. (Haitao Song) and Q.L.; formal analysis, L.W. and Q.L.; investigation, B.Z., H.S. (Hao Shen) and Y.N.; resources, Y.N. and H.S. (Hao Shen); data curation, Y.N., H.S. (Haitao Song) and X.D.; writing—original draft preparation, L.W. and B.Z.; writing—review and editing, B.Z., Q.L. and Y.L.; visualization, B.Z., X.D. and L.W.; supervision, Y.N. and H.S. (Haitao Song); project administration, B.Z. and H.S. (Hao Shen); funding acquisition, B.Z., H.S. (Hao Shen) and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Yangtze River Delta Innovation and Entrepreneurship Joint Carrier Demonstration Project (23002430100), the Wuxi Science and Technology Development Fund Project (K20241036), the National Natural Science Foundation of China (61903159), and the Natural Science Foundation of Jiangsu Province (BK20190617).
Data Availability Statement
The data that support the findings of this study are available from the first author or corresponding authors upon reasonable request.
Conflicts of Interest
Authors Hao Shen and Haitao Song were employed by the company Shanghai Artificial Intelligence Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhang, X.C. Terahertz wave imaging: Horizons and hurdles. Phys. Med. Biol. 2002, 47, 3667–3677. [Google Scholar] [CrossRef] [PubMed]
- Romain, X.; Baida, F.; Boyer, P. Extended Malus law with terahertz metallic metamaterials for sensitive detection with giant tunable quality factor. Phys. Rev. B 2016, 94, 045407. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite dielectric with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef]
- Zhao, X.G.; Fan, K.B.; Zhang, J.D.; Keiser, G.R.; Duan, G.W.; Averitt, R.D.; Zhang, X. Voltage-tunable dual-layer terahertz metamaterials. Microsyst. Nanoeng. 2016, 2, 16025. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.L.; Zhao, Q.; Kang, L.; Zhou, J.; Lippens, D. Experimental verification of isotropic and polarization properties of high permittivity-based metamaterial. Phys. Rev. B 2009, 80, 195119. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, X.F.; Liang, L.J.; Yao, J.Q. Research progress in the application of biosensors by using metamaterial in terahertz wave. Spectrosc. Spectr. Anal. 2014, 34, 2365–2371. [Google Scholar]
- Nakata, Y.; Fukawa, K.; Nakanishi, T.; Urade, Y.; Okimura, K.; Miyamaru, F. Reconfigurable terahertz quarter-wave plate for helicity switching based on babinet inversion of an anisotropic checkerboard metasurface. Phys. Rev. Appl. 2019, 11, 044008. [Google Scholar] [CrossRef]
- Choi, W.J.; Cheng, G.; Huang, Z.Y.; Zhang, S.; Norris, T.B.; Kotov, N.A. Terahertz circular dichroism spectroscopy of biomaterials enabled by kirigami polarization modulators. Nat. Mater. 2019, 18, 820–826. [Google Scholar] [CrossRef]
- Zhao, X.G.; Wang, Y.; Schalch, J.; Duan, G.W.; Crernin, K.; Zhang, J.D.; Chen, C.X.; Averitt, R.D.; Zhang, X. Optically modulated ultra-broadband all-silicon metamaterial terahertz absorbers. ACS Photonics 2019, 6, 830–837. [Google Scholar] [CrossRef]
- Zakir, S.; Bilal, R.M.H.; Naveed, M.A.; Baqir, M.A.; Khan, M.U.A.; Ali, M.M.; Saeed, M.A.; Mehmood, M.Q.; Massoud, Y. Polarization-insensitive, broadband, and tunable terahertz absorber using slotted-square graphene meta-rings. IEEE Photonics J. 2022, 15, 1–8. [Google Scholar] [CrossRef]
- Vafapour, Z.; Troy, W.; Rashidi, A. Colon cancer detection by designing and analytical evaluation of a water-based THz metamaterial perfect absorber. IEEE Sens. J. 2021, 21, 19307–19313. [Google Scholar] [CrossRef]
- Wang, B.X.; He, Y.H.; Lou, P.C.; Xing, W.H. Design of a dual-band terahertz metamaterial absorber using two identical square patches for sensing application. Nanoscale Adv. 2020, 2, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.Y.; Cai, W.J.; Xiao, L.H.; Xiao, B.G.; Qin, J.Y. Design and simulation of tunable metal-graphene hybrid metamaterial terahertz modulator based on electromagnetically induced transparency. Opt. Quantum Electron. 2024, 56, 1058. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Saadeldin, A.S.; Hameed, M.F.O.; Elkaramany, E.M.A.; Obayya, S.S.A. Highly sensitive terahertz metamaterial sensor. IEEE Sens. J. 2019, 19, 7993–7999. [Google Scholar] [CrossRef]
- Guo, W.J.; Zhai, L.H.; El-Bahy, Z.M.; Lu, Z.M.; Li, L.; Elnaggar, A.Y.; Ibrahim, M.M.; Cao, H.L.; Lin, J.; Wang, B. Terahertz metamaterial biosensor based on open square ring. Adv. Compos. Hybrid Mater. 2023, 6, 92. [Google Scholar] [CrossRef]
- Xiao, B.G.; Ma, Z.Y.; Cai, W.J.; Xiao, L.H.; Mi, H.M. Design and simulation of a compact graphene metamaterial sensor with high sensitivity based on electromagnetically induced transparency. Opt. Eng. 2023, 62, 087107. [Google Scholar] [CrossRef]
- Qu, W.W.; Li, Z.R.; Li, G.L.; Deng, H.; Xiong, Z.G. High-performance terahertz microfluidic sensors based on Fabry-Perot resonance. Opt. Mater. 2024, 155, 115862. [Google Scholar] [CrossRef]
- Fu, Y.J.; Li, S.H.; Chen, Y.; Zhang, X.F.; Chen, K.J. A multi-band absorber based on a dual-trident structure for sensing application. Opt. Quantum Electron. 2021, 53, 124. [Google Scholar] [CrossRef]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Weisenstein, C.; Richter, M.; Wigger, A.K.; Bosserhoff, A.; Bolivar, P.H. Substrate-integrated microfluidics for sensitive biosensing with complementary THz metamaterials in water. Appl. Phys. Lett. 2022, 120, 053702. [Google Scholar] [CrossRef]
- Lan, F.; Luo, F.; Mazumder, P.; Yang, Z.Q.; Meng, L.; Bao, Z.Q.; Zhou, J.; Zhang, Y.X.; Liang, S.X.; Shi, Z.J.; et al. Dual-band refractometric terahertz biosensing with intense wave-matter-overlap microfluidic channel. Biomed. Opt. Express 2019, 10, 3789–3799. [Google Scholar] [CrossRef] [PubMed]
- Ollé, E.P.; Farré-Lladós, J.; Casals-Terré, J.; Martínez, J.A.L. Enhanced selectivity of a 3D-printed microfluidic gas detector towards different volatile organic compounds (VOCs) for the effective monitoring of indoor air quality in vehicles. Environ. Technol. Innov. 2024, 33, 103481. [Google Scholar] [CrossRef]
- Ghazi, M.; Janfaza, S.; Tahmooressi, H.; Tasnim, N.; Hoorfar, M. Selective detection of VOCs using microfluidic gas sensor with embedded cylindrical microfeatures coated with graphene oxide. J. Hazard. Mater. 2022, 424, 127566. [Google Scholar] [CrossRef]
- Guo, X.L.; Chen, Y.; Jiang, H.L.; Qiu, X.B.; Yu, D.L. Smartphone-based microfluidic colorimetric sensor for gaseous formaldehyde determination with high sensitivity and selectivity. Sensors 2018, 18, 3141. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.P.; Deng, H.; Xiong, Z.G.; Shang, L.P. Terahertz sensor based on a three-dimensional double I-type metamaterial integrated microfluidic channel. Appl. Opt. 2021, 60, 3816–3822. [Google Scholar] [CrossRef]
- Yin, W.; Shen, Z.L.; Li, S.N.; Zhang, L.Y.; Chen, X.F. A three-dimensional dual-band terahertz perfect absorber as a highly sensitive sensor. Front. Phys. 2021, 9, 665280. [Google Scholar] [CrossRef]
- Zhu, M.; Zhang, L.; Ma, S.Q.; Wang, J.; Su, J.S.; Liu, A.C. Terahertz metamaterial designs for capturing and detecting circulating tumor cells. Mater. Res. Express 2019, 6, 045805. [Google Scholar] [CrossRef]
- Banerjee, S.; Dutta, P.; Jha, A.; Tripathi, P.R.; Srinivasulu, A.; Appasani, B.; Ravariu, C. A triple band highly sensitive refractive index sensor using terahertz metamaterial perfect absorber. Prog. Electromagn. Res. M 2022, 107, 13–23. [Google Scholar] [CrossRef]
- Koshelev, K.; Favraud, G.; Bogdanov, A.; Kivshar, Y.; Fratalocchi, A. Nonradiating photonics with resonant dielectric nanostructures. Nanophotonics 2019, 8, 725–745. [Google Scholar] [CrossRef]
- Sadrieva, Z.F.; Sinev, I.S.; Koshelev, K.L.; Samusev, A.; Iorsh, I.V.; Takayama, O.; Malureanu, R.; Bogdanov, A.A.; Lavrinenko, A.V. Transition from Optical Bound States in the Continuum to Leaky Resonances: Role of substrate and roughness. ACS Photonics 2017, 4, 723–727. [Google Scholar] [CrossRef]
- Huang, Y.W.; Chen, W.T.; Wu, P.C.; Fedotov, V.; Savinov, V.; Ho, Y.Z.; Chau, Y.F.; Zheludev, N.I.; Tsai, D.P. Design of plasmonic toroidal metamaterials at optical frequencies. Opt. Express 2012, 20, 1760–1768. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.C.; Gao, Y.C. High-Q resonances induced by toroidal dipole bound states in the continuum in terahertz metasurfaces. Crystals 2025, 15, 96. [Google Scholar] [CrossRef]
- Dey, D.; Schatz, G.C. Plasmonic surface lattice resonances in nanoparticle arrays. MRS Bull. 2024, 49, 421–430. [Google Scholar] [CrossRef]
- Karimi, V.; Babicheva, V.E. Dipole-lattice nanoparticle resonances in finite arrays. Opt. Express 2023, 31, 16857–16871. [Google Scholar] [CrossRef] [PubMed]
- Sohi, P.A.; Singh, P.; Kahrizi, M. Localized surface plasmon resonance biosensor designed for high refractive index volatile organic compound (VOC) biomarkers detection in visible spectrum. Optik 2022, 257, 168748. [Google Scholar] [CrossRef]
- Xiao, B.G.; Wang, Y.C.; Tong, S.J.; Qin, J.Y.; Zhang, D.P.; Xiao, L.H. Graphene electromagnetically induced transparent polarization-insensitive sensors in the mid-infrared frequency band. Appl. Opt. 2023, 62, 8178–8183. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Z.Q.; Qi, J.W.; Jiang, M.L.; Chen, J.; Li, Y.D.; Sun, Q. Ultra-high figure of merit refractive index sensor based on concentric ring and disk resonator. J. Opt. 2023, 52, 120–127. [Google Scholar] [CrossRef]
- Veeraselvam, A.; Mohammed, G.N.A.; Savarimuthu, K.; Anguera, J.; Paul, J.C.; Krishnan, R.K. Refractive index-based terahertz sensor using graphene for material characterization. Sensors 2021, 21, 8151. [Google Scholar] [CrossRef]
- Zhan, Y.; Yin, H.Y.; Wang, J.H.; Yao, H.W.; Fan, C.Z. Tunable multiple band THz perfect absorber with InSb metamaterial for enhanced sensing application. Results Opt. 2022, 8, 100255. [Google Scholar] [CrossRef]
- Jadeja, R.; Surve, J.; Parmar, T.; Patel, S.K.; Al-Zahrani, F.A. Detection of peptides employing a THz metasurface based sensor. Diam. Relat. Mater. 2023, 132, 109675. [Google Scholar] [CrossRef]
- Patel, S.K.; Surve, J.; Parmar, J. Detection of cancer with graphene metasurface-based highly efficient sensors. Diam. Relat. Mater. 2022, 129, 109367. [Google Scholar] [CrossRef]
- Wang, G.Q.; Lang, T.T.; Hong, Z. Metallic metamaterial terahertz sensors for simultaneous measurement of temperature and refractive index. Appl. Opt. 2020, 59, 5385–5390. [Google Scholar] [CrossRef]
- Alkorbi, A.S.; Wekalao, J.; Patel, S.K.; Na, N.; Jalalah, M.; Harraz, F.A.; Almawgani, A.H.M. Design and analysis of a graphene/gold nanostructure metasurface surface plasmon resonance sensor for biomedical applications. Plasmonics 2024, 20, 3573–3582. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).