Resilient Event-Triggered H_∞ Control for a Class of LFC Systems Subject to Deception Attacks

Abstract

This paper explores an event-triggered load frequency control (LFC) strategy for smart grids incorporating electric vehicles (EVs) under the influence of random deception attacks. The aggressive attack signals are launched over the channels between the sensor and controller, compromising the integrity of transmitted data and disrupting LFC commands. For the purpose of addressing bandwidth constraints, an event-triggered transmission scheme (ETTS) is developed to minimize communication frequency. Additionally, to mitigate the impact of random deception attacks in public environment, an integrated networked power grid model is proposed, where the joint impact of ETTS and deceptive interference is captured within a unified analytical structure. Based on this framework, a sufficient condition for stabilization is established, enabling the concurrent design of the ${\mathcal{H}}_{\infty }$ controller gain and the triggering condition. Finally, two case studies are offered to illustrate the effectiveness of the employed scheme.

1. Introduction

Modern electric power grids are a typical example of networked control architectures, where generation facilities, sensing equipment, and control units are interconnected via large-scale communication infrastructures [1,2,3,4]. Within these systems, load frequency control (LFC) is vital for suppressing frequency deviations induced by variations in power demand [5,6,7,8]. In recent developments, electrical vehicles (EVs) [9,10] have emerged as promising technologies due to their potential to curb emissions of greenhouse gases and lessen the dependence on fossil-based energy. EVs can both draw power from and supply power to the grid, presenting new opportunities for integration with power systems. This bidirectional interaction enables EVs to provide auxiliary services, such as frequency and voltage regulation, thereby enhancing grid stability and efficiency.

LFC is a critical component of smart grids, responsible for maintaining optimal system frequency and managing power exchanges between areas [11]. In modern smart grids, the LFC system heavily relies on advanced communication technologies, which also introduce various security vulnerabilities. Typically, data acquisition systems forego high-level encryption for authentication due to the stringent real-time demands of LFC data, rendering them highly susceptible to cyberthreats such as deception attacks [12,13] and denial-of-service (DoS) attacks [14,15]. DoS attacks interfere with the communication between the phasor measurement unit (PMU) and the LFC system, while deception attacks undermine data integrity, thereby impairing the control center’s ability to make informed decisions. In some extreme cases, such attacks may cause significant frequency deviations, potentially resulting in power system failure [16]. Consequently, it is imperative to explore robust control techniques that can withstand deceptions in power systems, which ensure both system stability and smart grid network security.

The integration of Smart Microgrids (SMGs) into LFC has been extensively studied in the literature [17,18,19,20]. For instance, by designing an appropriate feedback controller and leveraging SMGs participation, LFC can effectively regulate frequency deviations and enhance overall power system stability. However, power systems operating within wired/wireless communication networks face unavoidable issues including communication delays, packet dropouts, and cyberattacks. In recent years, these issues have attracted significant attention from researchers [21,22,23]. For example, in [17], an adaptive multi-objective fuzzy proportional-integral-derivative controller is proposed for the LFC of islanded SMGs. Hu et al. [21] have proposed multi-power systems subject to unknown load disturbances and intermittent denial-of-service (DoS) attacks, and a resilient load frequency controller has been devised. Peng et al. have discussed an adaptive event-triggering ${\mathcal{H}}_{\infty }$ LFC scheme, where the event-triggering threshold can be dynamically adjusted to save more resources, while maintaining the expected control performance. In [24], a robust cooperative LFC strategy for multi-area power systems via a hierarchical control approach has been devised. Despite these advancements, the influence of EVs on frequency domains for power systems warrants a deeper exploration.

Notably, most existing investigations adopt a time-triggered scheme, where sensors sample system outputs at fixed intervals and immediately transmit the data to the controller. In this building, the sampling period is chosen conservatively to ensure the system performance even under worst-case conditions, To maintain system effectiveness under adverse conditions, such as severe disturbances, prolonged delays, or undesired noises, the sampling period is deliberately set with a conservative margin. Nevertheless, since such scenarios occur infrequently, this conservative strategy results in redundant sampling, yielding unnecessary bandwidth consumption and increased computational burden on the controller. As a result, developing an efficient yet resource-conscious scheduling algorithm named event-triggered communication scheme has been recognized as reliable control approach [25,26,27,28,29]. Under this scheme, sampled measurements are transmitted only when specific conditions are met, effectively reducing communication overhead in the network. However, combining event-triggered schemes with LFC to construct a unified model poses significant challenges, which encourages us to study deeply.

It should be highlighted that in a networked power system, both control and communication signals are often delivered via open-access networks, which exposes them to significant cyberattack risks [30,31]. For instance, as reported in [32], cyberattacks can lead to severe consequences, including information leakage, destruction of critical infrastructure, and other devastating impacts. Consequently, ensuring the security of power systems is an issue of paramount importance. A wealth of research has been conducted in this area (see [12,33,34]). Among various cyberthreats, deception attacks stand out as one of the most critical, as they compromise data integrity by altering its content. There has been an increasing focus on investigating deception attacks (see [30,34,35]). For example, the optimal linear deception attacks targeting remote state estimation has been explored in [32], and the metric of K-L divergence has been adopted for measuring the statistical distribution of transmission sequence. As a typical deception attacks, a class of zero trace stealthy attacks has been researched for distributed secondary control in DC microgrids (DCmGs) [36], which can degrade the control objective while keep stealthy to implemented detectors. Furthermore, a recursive filter design problem was considered in [35] for a type of time-varying discrete sequential systems under deception attacks. As typical networked systems, power systems for LFC are particularly vulnerable to malicious adversaries [23]. However, despite the critical nature of this issue, cyberattack resilience in the LFC of power systems remains less examined. Addressing this gap serves as the second key motivation of this research.

In this work, an event-triggered ${\mathcal{H}}_{\infty }$ controller has been developed within the context of power systems. It is evident that the research into LFC controller design is still in its infancy and the challenges underlying this study stem from the following aspects: (1) How can we formulate a comprehensive model that incorporates the LFC dynamics, random deception attacks, and the event-triggered mechanism? (2) How can we design the suitable communication protocol for reducing computational overhead? (3) How can we deploy a resilient ${\mathcal{H}}_{\infty }$ controller to effectively mitigate the adverse impacts of cyberattacks?

Based on the previous analysis, this study investigates ${\mathcal{H}}_{\infty }$ load frequency control in power systems subject to limited bandwidth and exposed communication channels. For optimizing communication resources while enhancing control performance, an event-triggered transmission scheme (ETTS) is put forward, which enables more efficient data transmission and reduces unnecessary communication. In order to capture real-world complexities, the concerned system model also accounts for randomly occurring deception attacks; an event-triggered feedback controller is designed to ensure the asymptotically mean-square stability (AMSS) of power systems, with rigorously derived sufficient conditions. Furthermore, the controller gain and event-triggered parameter are jointly optimized by solving linear matrix inequalities, thereby achieving both security and efficiency. The main contributions of this work are outlined below:

• An integrated model of a networked power system is established, which simultaneously accounts for communication delays, stochastic deception attacks, and ETTS.
• An ETTS is proposed to minimize redundant transmission while enhancing control performance. Different from the traditional time-triggered scheme, ETTS effectively utilizes sampled data selectively, reducing the computation burden fairly.
• An event-triggered ${\mathcal{H}}_{\infty }$ LFC design method is carefully developed to jointly optimize the output-feedback controller gain along with the communication parameters. Unlike conventional time-triggered controllers, the proposed ${\mathcal{H}}_{\infty }$ LFC controller enhances control performance by effectively utilizing available information, even in the presence of deception attacks, achieving superior resilience compared to standard approaches.

Organizations: The remainder of this paper is organized as follows. Section 1 introduces the system description and fundamental concepts, covering the system model and the relevant ETTS used in the following analysis. Section 3 presents the stability criterion for the power systems under investigation. In Section 4, two cases are given to validate the usefulness of the developed method. Lastly, Section 5 summarizes this work.

Notations: The notation used in this paper follows standard conventions unless otherwise specified. The set of natural numbers is denoted by $\mathbb{N}$. The symbols $\mathbb{R}$, ${\mathbb{R}}^n$, and ${\mathbb{R}}^{n\times m}$ represent the set of real numbers, the space of n-dimensional real numbers, and the space of $n\times m$ real matrices, respectively. The transpose of a matrix A is denoted by $A^T$. The notation ${\left[A_{ij}\right]}_{n\times n}$ indicates an $n\times n$ block matrix, where the block at the ith row and jth column is $A_{ij}$. The identity matrix of appropriate dimensions is represented by I. The function $\mathrm{diag}\left\{·\right\}$ constructs a diagonal matrix. The notation $\left|\right|·\left|\right|$ denotes the Euclidean norm for vectors and the induced 2-norm for matrices. Lastly, $\mathbb{E}\left\{·\right\}$ represents the expectation of a given stochastic variable.

2. Problem Setup

This part presents the dynamic modeling of load frequency control (LFC) systems integrated into electric vehicles (EVs), taking into account load disturbances to better reflect the actual behavior of power systems, as discussed in [37]. The proposed system architecture is depicted in Figure 1; based on the information flow and transfer functions illustrated, the entire control loop involves the following modules, including EVs, governors, turbines, and generators. The controller generates output signals that regulate the power frequency deviation of the generator through two control subloops. In the first path, the controller output is distributed to the governor via a regulation gain. The signal then passes through the governor dynamics and the governor droop characteristics to produce a speed control signal, which is further processed by the turbine dynamics to generate the turbine output power. In another subloop, the controller output is allocated to the EVs module, leading to the incremental change in the EVs’ output power. Taking external disturbance into account, the total generation power can be calculated from the turbine and the EVs unit. The relevant physical variables are summarized in

Table 1. Notations.

Parameters	Meaning
f	frequency deviation
$X_g$	governor valve position
$P_g$	turbine output power
$P_e$	incremental changes in EVs
$P_l$	load disturbance
$P_c$	control input
${\alpha }_g$	thermal turbine
${\alpha }_e$	participation factor
D	load damping coefficient
M	inertia constant
$R_g$	governor
${\rho }_e$	droop characteristic
$T_g$	speed governor
$T_t$	turbine time constant
$K_e$	gain constant
$T_e$	time constant
b	frequency bias constant

. Moreover, two definitions are added.  

Definition 1

(State-space method). The state-space method is a modeling method describing system dynamics with a set of differential or difference equations, which are especially suitable for analyzing multi-input multi-output (MIMO) systems.

Definition 2

(Asymptotically mean-square stability (AMSS)). Mathematically, a stochastic system is said to be AMSS if

$$\underset{k\to \infty }{lim}\mathbb{E}\left\{\left|\right|x_k{\left|\right|}^2\right\}=0,$$

where $x_k$ denotes the system state at instant k.

On the basis of the flow chart included in Figure 1, one has

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill f\left(s\right)& ={\displaystyle \frac{1}{D+sM}}(P_g\left(s\right)+P_e\left(s\right)-P_l\left(s\right)),\hfill \\ \hfill X_g\left(s\right)& ={\displaystyle \frac{1}{1+s{T}_g}}({\alpha }_g{P}_c\left(s\right)-{\displaystyle \frac{1}{R_g}}f\left(s\right)),\hfill \\ \hfill P_g\left(s\right)& ={\displaystyle \frac{1}{1+s{T}_t}}{X}_g\left(s\right),\hfill \\ \hfill P_e\left(s\right)& ={\displaystyle \frac{K_e}{1+s{T}_e}}({\alpha }_e{P}_c\left(s\right)-{\rho }_{e}f\left(s\right)),\hfill \\ \hfill \mathsf{\Delta }\left(s\right)& ={\displaystyle \frac{1}{s}}ACE\left(s\right)={\displaystyle \frac{1}{s}}bf\left(s\right).\hfill \end{array}\right.\end{array}$$

(1)

By applying the inverse Laplace Transform for (1), one has

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \dot{f}\left(t\right)& ={\displaystyle \frac{1}{M}}(P_g\left(t\right)+P_e\left(t\right)-P_l\left(t\right)-Df\left(t\right)),\hfill \\ \hfill {\dot{X}}_g\left(t\right)& ={\displaystyle \frac{1}{T_g}}({\alpha }_g{P}_c\left(t\right)-{\displaystyle \frac{1}{R_g}}f\left(t\right)-X_g\left(t\right)),\hfill \\ \hfill {\dot{P}}_g\left(t\right)& ={\displaystyle \frac{1}{T_t}}(X_g\left(t\right)-P_g\left(t\right)),\hfill \\ \hfill {\dot{P}}_e\left(t\right)& ={\displaystyle \frac{K_e}{T_e}}({\alpha }_e{P}_c\left(t\right)-{\rho }_{e}f\left(t\right))-{\displaystyle \frac{1}{T_e}}{P}_e\left(t\right),\hfill \\ \hfill \dot{\mathsf{\Delta }}\left(t\right)& =bf\left(t\right).\hfill \end{array}\right.\end{array}$$

(2)

Define

$$\begin{array}{cc}\hfill x\left(t\right)& ={[f\left(t\right),X_g\left(t\right),P_g\left(t\right),P_e\left(t\right),\mathsf{\Delta }\left(t\right)]}^T,\hfill \\ \hfill y\left(t\right)& ={[f\left(t\right),\mathsf{\Delta }\left(t\right)]}^T,\hfill \\ \hfill u\left(t\right)& =P_c\left(t\right),\hfill \\ \hfill \varpi \left(t\right)& =P_l\left(t\right).\hfill \end{array}$$

According to the state-space method in Definition 1, the LFC system has the following expression.

$$\left\{\begin{array}{cc}\hfill \dot{x}\left(t\right)& =Ax\left(t\right)+Bu\left(t\right)+D\varpi \left(t\right),\hfill \\ \hfill y\left(t\right)& =Cx\left(t\right),\hfill \end{array}\right.$$

(3)

where A, B, C, and D indicate system matrices, $x\left(t\right)$, $u\left(t\right)$, and $\varpi \left(t\right)$ represent the state vector, the control input, and external disturbance, respectively, and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill A& =\left[\begin{array}{ccccc}-{\displaystyle \frac{D}{M}}& 0& {\displaystyle \frac{1}{M}}& {\displaystyle \frac{1}{M}}& 0\\ -{\displaystyle \frac{1}{R_g{T}_g}}& -{\displaystyle \frac{1}{T_g}}& 0& 0& 0\\ 0& {\displaystyle \frac{1}{T_t}}& -{\displaystyle \frac{1}{T_t}}& 0& 0\\ -{\displaystyle \frac{{\rho }_e{K}_e}{T_e}}& 0& 0& -{\displaystyle \frac{1}{T_e}}& 0\\ b& 0& 0& 0& 0\end{array}\right],\hfill \\ \hfill B& ={\left[\begin{array}{ccccc}0& {\displaystyle \frac{{\alpha }_g}{T_g}}& 0& {\displaystyle \frac{{\alpha }_e{K}_e}{T_e}}& 0\end{array}\right]}^T,\hfill \\ \hfill C& =\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1\end{array}\right],\hfill \\ \hfill D& ={\left[\begin{array}{ccccc}-{\displaystyle \frac{1}{M}}& 0& 0& 0& 0\end{array}\right]}^T.\hfill \end{array}\end{array}$$

2.1. ETTS

This subsection introduces an event-based communication protocol to optimize the utilization of communication bandwidth while maintaining optimal system performance. Defining h as the sampling period of the concerned LFC systems. The most recent triggering instant and the next triggering instant are indicated by $t_{k}h$ and $t_{k+1}h$, respectively, and the next triggering instant can be determined by:

$$\begin{array}{cc}\hfill t_{k+1}h& \triangleq t_{k}h+\underset{i\in \mathbb{N}}{min}\left\{ih|e^T\left(t\right)\mathsf{\Psi }e\left(t\right)>\sigma x^T\left(t_{k}h\right)\mathsf{\Psi }x\left(t_{k}h\right)\right\},\hfill \\ \hfill e\left(t\right)& \triangleq x(t_{k}h+ih)-x\left(t_{k}h\right),\hfill \end{array}$$

(4)

where $\mathsf{\Psi }$ denotes the triggering threshold matrix and $0<\sigma \le 1$ represents the threshold value.

Remark 1.

In practical systems, transmitted signals are susceptible to various anomalies, including malicious attacks, network-induced delays, data packet losses, and so forth. Though irregularities may occur with low probability from a statistical standpoint, they can still pose significant threats to the system performance. It is worth noting that the employed ETTS plays a crucial role in mitigating the impact of abnormal signals and relieving computation burden. As expressed in (3), the adopted ETTS reduces to the general time-triggered manner when $\sigma =0$.

It is well-known that time delay is a common yet unavoidable network-induced phenomenon in LFC systems, which must be carefully considered in network communication. In this article, as shown in Figure 2, the interval between $t_{1}h$ and $t_{2}h$ can be divided into five subintervals according to the designed principle. Consequently, by means of the virtual partition method proposed in [25], for any given time period between two consecutive triggering instants $t_{k}h$ and $t_{k+1}h$, after considering the respective time delays at the triggering instant from the sensor to the controller, it can be expressed by the following subperiods:

$$\begin{array}{cc}\hfill & [t_{k}h+{\mu }_{t_k},t_{k+1}h+{\mu }_{t_{k+1}})=\bigcup _{i=0}^{f_M}{\mathcal{I}}_i,\hfill \\ \hfill & \left\{\begin{array}{c}{\mathcal{I}}_0=[t_{k}h+{\mu }_{t_k},(t_k+1)h+\overline{\mu }),\hfill \\ {\mathcal{I}}_i=[(t_k+i)h+\overline{\mu },(t_k+i+1)h+\overline{\mu }),i=1,\dots ,f_M-1,\hfill \\ {\mathcal{I}}_{f_M}=[(t_k+f_M)h+\overline{\mu },t_{k+1}h+{\mu }_{t_{k+1}}),\hfill \end{array}\right.\hfill \end{array}$$

(5)

where $\overline{\mu }$ indicates the upper bound of ${\mu }_{t_k}$.

We now consider the following two cases:

Case 1: If $t_{k+1}h+{\mu }_{t_{k+1}}\le t_{k}h+h+\overline{\mu }$, define a function $\mu \left(t\right)$ as

$$\mu \left(t\right)=t-t_{k}h,t\in [t_{k}h+{\mu }_{t_k},t_{k+1}h+{\mu }_{t_{k+1}}).$$

(6)

Obviously, ${\mu }_{t_k}\le \mu \left(t\right)\le (t_{k+1}-t_k)h+{\mu }_{t_{k+1}}\le h+\overline{\mu }$.

Case 2: If $t_{k}h+h+\overline{\mu }<t_{k+1}h+{\mu }_{t_{k+1}}$, one has

$$\begin{array}{c}\hfill \mu \left(t\right)=\left\{\begin{array}{c}t-t_{k}h,t\in {\mathcal{I}}_0,\hfill \\ t-t_{k}h-ih,t\in {\mathcal{I}}_i,i=1,\dots ,f_M-1,\hfill \\ t-t_{k}h-f_{M}h,t\in {\mathcal{I}}_{f_M}.\hfill \end{array}\right.\end{array}$$

(7)

Therefore, we have

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mu }_{t_k}\le \mu \left(t\right)\le h+\overline{\mu },t\in {\mathcal{I}}_0,\hfill \\ {\mu }_{t_k}\le \overline{\mu }\le \mu \left(t\right)\le h+\overline{\mu },t\in {\mathcal{I}}_i,i=1,\dots ,f_M-1,\hfill \\ {\mu }_{t_k}\le \overline{\mu }\le \mu \left(t\right)\le h+\overline{\mu },t\in {\mathcal{I}}_{f_M},\hfill \end{array}\right.\end{array}$$

(8)

and $0\le {\mu }_{t_k}\le \mu \left(t\right)\le h+\overline{\mu }\triangleq {\mu }_M$. From (4), one has

$$\begin{array}{c}\hfill e\left(t\right)=\left\{\begin{array}{c}0,t\in {\mathcal{I}}_0,\hfill \\ x(t_k+ih)-x\left(t_{k}h\right),t\in {\mathcal{I}}_i,i=1,\dots ,f_M-1,\hfill \\ x(t_k+f_{M}h)-x\left(t_{k}h\right),t\in {\mathcal{I}}_{f_M}.\hfill \end{array}\right.\end{array}$$

(9)

Therefore

$$\begin{array}{cc}\hfill e\left(t\right)& =x(t-\mu \left(t\right))-x\left(t_{k}h\right),t\in {\mathcal{I}}_i.\hfill \end{array}$$

(10)

2.2. Random Deception Attacks

In this article, it is assumed that the measurement signals are subject to random deception attacks governed by malicious adversaries. On the basis of the above analysis, an indicator variable $\lambda \left(t\right)$ is introduced to formulate this scene, and the actual measurement signal is as follows:

$$\overline{y}\left(t\right)=(1-\lambda \left(t\right))y\left(t\right)+\lambda \left(t\right)\psi \left(y\left(t\right)\right),$$

(11)

where $\psi \left(y\right(t\left)\right)$ denotes the injected data during the process of deception attack, and satisfies the following:

$${\left|\right|\psi \left(y\left(t\right)\right)\left|\right|}_2\le {\left|\right|Gy\left(t\right)\left|\right|}_2,$$

(12)

with G being a known matrix of appropriate dimensions. Specifically, the random variable $\lambda \left(t\right)$ follows a Bernoulli distribution with the following expression:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left\{\lambda \left(t\right)=1\right\}& =\overline{\lambda },\hfill \\ \hfill \mathrm{Pr}\left\{\lambda \left(t\right)=0\right\}& =1-\overline{\lambda },\hfill \end{array}$$

(13)

where $\overline{\lambda }\in [0,1]$.

Remark 2.

According to (7), (8) and (9), it can be observed that the matrix G represents the upper bound of the nonlinearity of $\psi \left(y\right(t\left)\right)$. On the other hand, $\lambda \left(t\right)$ regulates the randomness of the deception attacks. Particularly, when $\lambda \left(t\right)=1$, this indicates that the system is under attack. Conversely, when $\lambda \left(t\right)=0$, the system runs normally. From the stand of defender, the randomness of the attacks stems from the fact that their success heavily depends on the fluctuating detection capabilities of protective equipment or software. Moreover, the modified measurement signal $\psi \left(y\right(t\left)\right)$ is supposed to be bounded, as deception attacks with large amplitudes are more likely to be detected by attackers, making subtle attacks preferable.

To mitigate the adverse impacts caused by randomly occurring deception attacks, the output feedback controller can be designed as follows:

$$\begin{array}{cc}\hfill u\left(t\right)=& -Ky\left(t_{k}h\right)\hfill \\ \hfill =& -(1-\lambda \left(t\right))KC(x(t-\mu \left(t\right))-e\left(t\right))-\lambda \left(t\right)K\psi \left(y\left(t_{k}h\right)\right),\hfill \end{array}$$

(14)

thereby, one has

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& Ax\left(t\right)-(1-\lambda \left(t\right))BKC(x(t-\mu \left(t\right))-e\left(t\right))-\lambda \left(t\right)BK\psi \left(y\left(t_{k}h\right)\right)+D\varpi \left(t\right).\hfill \end{array}$$

(15)

This paper aims to develop the event-based controller (10) to ensure that the system (3), running under the ETTS (4) and subject to randomly occurring deception attacks (7), achieves AMSS while meeting the ${\mathcal{H}}_{\infty }$ performance index. Correspondingly, the following requirements should be satisfied:

• The LFC system (3), in the absence of external disturbances $\varpi \left(t\right)$, should be AMSS;
• Under zero initial conditions, the system satisfies the performance requirement $\mathbb{E}\left\{{\left|\right|y\left(t\right)\left|\right|}^2\right\}\le \mathbb{E}\left\{{\gamma }^2{\left|\right|\varpi \left(t\right)\left|\right|}^2\right\}$ for any nonnegative noises $\varpi \left(t\right)\in L_2[0,\infty )$, where $\gamma >0$ represents a prescribed performance bound.

3. Main Results

For paving the way of subsequent analysis, the following lemma is employed in the proof of the main results.

Lemma 1

([38]). Give the symmetric matrix S with the following expression:

$$\begin{array}{c}\hfill S=\left[\begin{array}{cc}{S}_{11}& S_{12}\\ S_{12}^T& S_{22}\end{array}\right],\end{array}$$

then the following statements are equivalent:

• $S<0$;
• $S_{11}<0,S_{22}-S_{12}^T{S}_{11}^{-1}{S}_{12}<0$;
• $S_{22}<0,S_{11}-S_{12}{S}_{22}^{-1}{S}_{12}^T<0$.

This section formulates two theorems to tackle key challenges concerning the AMSS of the closed-loop LFC system, its disturbance suppression capability, and the gain computation for the event-based ${\mathcal{H}}_{\infty }$ controller.

Theorem 1.

Given fixed values of σ, κ, ${\mu }_M$, and γ and a specified feedback gain K, the LFC system (3) is AMSS with an ${\mathcal{H}}_{\infty }$ performance bound γ, provided that there exist positive definite matrices $P>0$, $Q>0$, $\mathsf{\Psi }>0$, and $R>0$, Z meeting

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\mathsf{\Gamma }}_{11}& \ast \\ {\mathsf{\Gamma }}_{21}& {\mathsf{\Gamma }}_{22}\end{array}\right]& <0,\end{array}$$

(16)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}R& Z^T\\ Z& R\end{array}\right]& >0,\end{array}$$

(17)

where ${\mathsf{\Gamma }}_{11}={\left[\mathsf{\Theta }\right]}_{ 2\times 2}$ and $\kappa =\sqrt{\lambda (1-\lambda )}$, and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathsf{\Theta }}_{11}^{11}& =A^{T}P+PA+Q-R,\hfill \\ \hfill {\mathsf{\Theta }}_{11}^{21}& =(1-\overline{\lambda })C^T{K}^T{B}^{T}P+R-Z,\hfill \\ \hfill {\mathsf{\Theta }}_{11}^{22}& =\sigma \mathsf{\Psi }-2R+Z+Z^T,\hfill \\ \hfill {\mathsf{\Theta }}_{21}^{11}& =Z,{\mathsf{\Theta }}_{21}^{12}=R-Z,\hfill \\ \hfill {\mathsf{\Theta }}_{21}^{21}& =-(1-\overline{\lambda })C^T{K}^T{B}^{T}P,\hfill \\ \hfill {\mathsf{\Theta }}_{21}^{22}& =-\sigma \mathsf{\Psi },{\mathsf{\Theta }}_{21}^{31}=\overline{\lambda }{C}^T{K}^T{B}^{T}P,{\mathsf{\Theta }}_{21}^{41}=D^{T}P,\hfill \\ \hfill {\mathsf{\Theta }}_{22}& =diag\left\{-Q-R,\sigma \mathsf{\Psi }-\mathsf{\Psi },-\overline{\lambda }P,-{\gamma }^{2}I\right\},\hfill \\ \hfill {\mathsf{\Gamma }}_{21}& =col\left\{{\mu }_{M}R{\mathsf{\Lambda }}_1,{\mu }_{M}R{\mathsf{\Lambda }}_2,{\mathsf{{\rm Y}}}_1,{\mathsf{{\rm Y}}}_2\right\},\hfill \\ \hfill {\mathsf{\Gamma }}_{22}& =diag\left\{-R,-R,-P,-I\right\},\hfill \\ \hfill {\mathsf{\Lambda }}_1& =[A,-(1-\overline{\lambda })BKC,0,(1-\overline{\lambda })BKC,-\overline{\lambda }BKC,D],\hfill \\ \hfill {\mathsf{\Lambda }}_2& =[0,\kappa BKC,0,-\kappa BKC,-\kappa BKC,0],\hfill \\ \hfill {\mathsf{{\rm Y}}}_1& =[0,\sqrt{\overline{\lambda }}PGC,0,-\sqrt{\overline{\lambda }}PGC,0,0],\hfill \\ \hfill {\mathsf{{\rm Y}}}_2& =[C,0,0,0,0,0].\hfill \end{array}\end{array}$$

Proof. 

Construct the Lyapunov functional as follows:

$$\begin{array}{cc}\hfill V\left(t\right)=& x^T\left(t\right)Px\left(t\right)+{\int }_{t-{\mu }_M}^t{x}^T\left(\zeta \right)Qx\left(\zeta \right)d\zeta +{\mu }_M{\int }_{t-{\mu }_M}^t{\int }_{\zeta }^t{\dot{x}}^T\left(s\right)R\dot{x}\left(s\right)dsd\zeta .\hfill \end{array}$$

(18)

For $t\in {\mathcal{I}}_i$, applying the infinitesimal operator [39] on $V\left(t\right)$, one has

$$\begin{array}{cc}\hfill \mathbb{E}\left\{\mathcal{L}\left(V\right(t\left)\right)\right\}=& x^T\left(t\right)Qx\left(t\right)+2{\dot{x}}^T\left(t\right)Px\left(t\right)-x^T(t-{\mu }_M)Qx(t-{\mu }_M)\hfill \\ & +{\mu }_M^2{\dot{x}}^T\left(t\right)R\dot{x}\left(t\right)-{\mu }_M{\int }_{t-{\mu }_M}^t{\dot{x}}^T\left(\zeta \right)R\dot{x}\left(\zeta \right)d\zeta -e^T\left(t\right)\mathsf{\Psi }e\left(t\right)\hfill \\ & +e^T\left(t\right)\mathsf{\Psi }e\left(t\right)-y^T\left(t\right)y\left(t\right)+{\gamma }^2{\varpi }^T\left(t\right)\varpi \left(t\right)+y^T\left(t\right)y\left(t\right)\hfill \\ & -\overline{\lambda }{\psi }^T\left(y\left(t_{k}h\right)\right)P\psi \left(y\left(t_{k}h\right)\right)+\overline{\lambda }{\psi }^T\left(y\left(t_{k}h\right)\right)P\psi \left(y\left(t_{k}h\right)\right)\hfill \\ & -{\gamma }^2{\varpi }^T\left(t\right)\varpi \left(t\right).\hfill \end{array}$$

(19)

Furthermore, from (4), one has

$$e^T\left(t\right)\mathsf{\Psi }e\left(t\right)\le \sigma (x^T(t-\mu \left(t\right))-e^T\left(t\right))\mathsf{\Psi }(x(t-\mu \left(t\right))-e\left(t\right)).$$

(20)

In addition, it can be seen from (8) that there exists a symmetric matrix P satisfying

$${\psi }^T\left(y\left(t_{k}h\right)\right)P\psi \left(y\left(t_{k}h\right)\right)\le (x^T(t-\mu \left(t\right))-e^T\left(t\right))C^T{G}^{T}PGC(x(t-\mu \left(t\right))-e\left(t\right)).$$

(21)

On the other hand, the reciprocally convex method in [40] is used to tackle the cross item in (19). Hence, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill -{\mu }_M{\int }_{t-{\mu }_M}^t{\dot{x}}^T\left(\zeta \right)R\dot{x}\left(\zeta \right)d\zeta \le & \left[\begin{array}{cc}{\varsigma }_1^T& {\varsigma }_2^T\end{array}\right]\left[\begin{array}{cc}R& Z^T\\ Z& R\end{array}\right]\left[\begin{array}{c}{\varsigma }_1\\ {\varsigma }_2\end{array}\right],\hfill \end{array}\end{array}$$

(22)

where ${\varsigma }_1=x\left(t\right)-x(t-\mu \left(t\right))$, ${\varsigma }_2=x(t-\mu \left(t\right))-x(t-{\mu }_M)$.

Therefore, one can attain from (18)–(22) that

$$\begin{array}{cc}\hfill \mathbb{E}\left\{\mathcal{L}\left(V\right(t\left)\right)\right\}\le & {\vartheta }^T\left(t\right)({\mathsf{\Gamma }}_{11}-{\mathsf{\Gamma }}_{21}^T{\mathsf{\Gamma }}_{22}^{-1}{\mathsf{\Gamma }}_{21})\vartheta \left(t\right)-y^T\left(t\right)y\left(t\right)+{\gamma }^2{\varpi }^T\left(t\right)\varpi \left(t\right),\hfill \end{array}$$

(23)

where $\vartheta \left(t\right)={[x^T\left(t\right),x^T(t-\mu \left(t\right)),x^T(t-{\mu }_M),e^T\left(t\right),{\psi }^T\left(x\left(t\right)\right),{\omega }^T\left(t\right)]}^T.$

By utilizing Schur complement Lemma 1 from (16), one has

$${\mathsf{\Gamma }}_{11}-{\mathsf{\Gamma }}_{21}^T{\mathsf{\Gamma }}_{22}^{-1}{\mathsf{\Gamma }}_{21}\le 0.$$

In addition, one has

$$\mathbb{E}\left\{\mathcal{L}\left(V\right(t\left)\right)\right\}\le -y^T\left(t\right)y\left(t\right)+{\gamma }^2{\varpi }^T\left(t\right)\varpi \left(t\right).$$

(24)

Integrating both sides of (24) from 0 to ∞, and under zero initial conditions, it is easy to derive that

$${\int }_0^{\infty }{y}^T\left(\zeta \right)y\left(\zeta \right)d\zeta \le {\int }_0^{\infty }{\gamma }^2{\varpi }^{\zeta }\varpi \left(\zeta \right)d\zeta ,$$

(25)

i.e., $\mathbb{E}\left\{{\left|\right|y\left(t\right)\left|\right|}^2\right\}\le \mathbb{E}\left\{{\gamma }^2{\left|\right|\varpi \left(t\right)\left|\right|}^2\right\}$. Hence, the disturbance suppression index is ensured. When $\varpi \left(t\right)=0$, it can be summarized that the system (3) is AMSS. This ends the proof.    □

The addressed event-triggered ${\mathcal{H}}_{\infty }$ controller has successfully considered both AMSS and ${\mathcal{H}}_{\infty }$ performance. Meanwhile, the matrix constraints established in Theorem 1 provide a set of sufficient conditions for the relevant performance indices. However, determining the event-triggered controller gain remains a significant challenge, which serves as the drive for the listed theorem.

Theorem 2.

Given preset parameters σ, κ, ${\mu }_M$, γ, ϱ, and ε, the LFC system (3) is AMSS with an ${\mathcal{H}}_{\infty }$ norm threshold γ, when there exist matrices $H>0$, $\check{Q}>0$, $\check{\mathsf{\Psi }}>0$, $\check{R}>0$, $\check{Z}$, M, and Y meeting

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\mathsf{\Gamma }}_{11}& \ast \\ {\mathsf{\Gamma }}_{21}& {\mathsf{\Gamma }}_{22}\end{array}\right]& <0,\end{array}$$

(26)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}\check{R}& {\check{Z}}^T\\ \check{Z}& \check{R}\end{array}\right]& >0,\end{array}$$

(27)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}-\epsilon I& \ast \\ MC-CH& -I\end{array}\right]& <0,\end{array}$$

(28)

where ${\check{\mathsf{\Gamma }}}_{11}={\left[\check{\mathsf{\Theta }}\right]}_{2\times 2}$, $\kappa =\sqrt{\lambda (1-\lambda )}$, and

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\check{\mathsf{\Theta }}}_{11}^{11}& =AH+H{A}^T+\check{Q}-\check{R},\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{11}^{21}& =(1-\overline{\lambda })C^T{Y}^T{B}^T+\check{R}-\check{Z},\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{11}^{22}& =\sigma \check{\mathsf{\Psi }}-2\check{R}+\check{Z}+{\check{Z}}^T,\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{21}^{11}& =\check{Z},{\check{\mathsf{\Theta }}}_{21}^{12}=\check{R}-\check{Z},\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{21}^{21}& =-(1-\overline{\lambda })C^T{Y}^T{B}^T,\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{21}^{22}& =-\sigma \check{\mathsf{\Psi }},{\check{\mathsf{\Theta }}}_{21}^{31}=\overline{\lambda }{C}^T{Y}^T{B}^T,{\check{\mathsf{\Theta }}}_{21}^{41}=D^T,\hfill \\ \hfill {\check{\mathsf{\Theta }}}_{22}& =diag\left\{-\check{Q}-\check{R},\sigma \check{\mathsf{\Psi }}-\check{\mathsf{\Psi }},-\overline{\lambda }H,-{\gamma }^{2}I\right\},\hfill \\ \hfill {\check{\mathsf{\Gamma }}}_{21}& =col\left\{{\mu }_M{\check{\mathsf{\Lambda }}}_1,{\mu }_M{\check{\mathsf{\Lambda }}}_2,{\check{\mathsf{{\rm Y}}}}_1,{\check{\mathsf{{\rm Y}}}}_2\right\},\hfill \\ \hfill {\check{\mathsf{\Gamma }}}_{22}& =diag\left\{{\varrho }^2\check{R}-2\varrho H,{\varrho }^2\check{R}-2\varrho H,-H,-I\right\},\hfill \\ \hfill {\check{\mathsf{\Lambda }}}_1& =[AH,-(1-\overline{\lambda })BYC,0,(1-\overline{\lambda })BYC,-\overline{\lambda }BYC,D],\hfill \\ \hfill {\check{\mathsf{\Lambda }}}_2& =[0,\kappa BYC,0,-\kappa BYC,-\kappa BYC,0],\hfill \\ \hfill {\check{\mathsf{{\rm Y}}}}_1& =[0,\sqrt{\overline{\lambda }}GCH,0,-\sqrt{\overline{\lambda }}GCH,0,0],\hfill \\ \hfill {\check{\mathsf{{\rm Y}}}}_2& =[CH,0,0,0,0,0].\hfill \end{array}\end{array}$$

Then, the event-triggered ${\mathcal{H}}_{\infty }$ controller gain can be derived as $K=Y{M}^{-1}$.

Proof. 

For brevity, define

$$\begin{array}{cc}\hfill H& =P^{-1},\check{Q}=HQH,\check{R}=HRH,\hfill \\ \hfill \check{Z}& =HZH,\check{\mathsf{\Psi }}=H\mathsf{\Psi }H,\hfill \\ \hfill {\mathsf{\Omega }}_1& \triangleq \mathrm{diag}\left\{H,H,H,H,H,I\right\},\hfill \\ \hfill {\mathsf{\Omega }}_2& \triangleq \mathrm{diag}\left\{R^{-1},R^{-1},H,I\right\}.\hfill \end{array}$$

With the aid of the following inequality:

$$-H{\check{R}}^{-1}H\le {\varrho }^2{\check{R}}^{-1}-2\varrho H,$$

and pre- and postmultiplying both sides of (16) and (17) by $\mathrm{diag}\left\{{\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2\right\}$ and $\mathrm{diag}\left\{H,H\right\}$, respectively. Naturally, (26) and (27) can be obtained. Then, $KCH$ and $CH$ are substituted with $YC$ and $MC$, respectively. Following a similar control design technique as in [41], we establish that

$${(MC-CH)}^T(MC-CH)=0.$$

According to Lemma 1, the above equation can be reformulated into an optimization problem with the format of (28). This completes the proof.    □

Remark 3.

A key assumption in simulation-based methods, such as those proposed in [21,22], is that the controller gains must be known a priori. If these gains are not prefixed, the aforementioned methods become inapplicable. Nevertheless, as illustrated in this study, the controller gains can be designed using Theorem 2, which highlights a key advantage of the proposed scheme.

According to Theorems 1 and 2, the state stability, ${\mathcal{H}}_{\infty }$ performance, and synthesis of the expected event-triggered controller are designed through the application of matrix techniques, stochastic methods, Lyapunov stability theory, and other advanced approaches. Since this article considers complex factors such as the event-based communication scheme and stochastic deception attacks, the derived sufficient criteria inherently incorporate these elements. Moreover, the matrix constraints included in two theorems have been gained using Matlab R2018b simulation technology.

To illustrate the implementation of Theorem 2 and derive the gain for the designed event-triggered ${\mathcal{H}}_{\infty }$ controller, the following Algorithm 1 is given in this section.

Algorithm 1 Event-based ${\mathcal{H}}_{\infty }$ controller design algorithm.
Step 1.	Initialize values of $x\left(0\right)$, $\gamma$, $\delta$, $\kappa$, ${\mu }_M$, G, $\psi \left(y\right(t\left)\right)$, $\varpi \left(t\right)$;
Step 2.	Formulate kinetic model (3) of the LFC system;
Step 3.	Design the employed event-based ${\mathcal{H}}_{\infty }$ controller (10) that satisfies AMSS and the ${\mathcal{H}}_{\infty }$ performance index;
Step 4.	Solve the LMIs in Theorem 2 and derive the controller gain K.

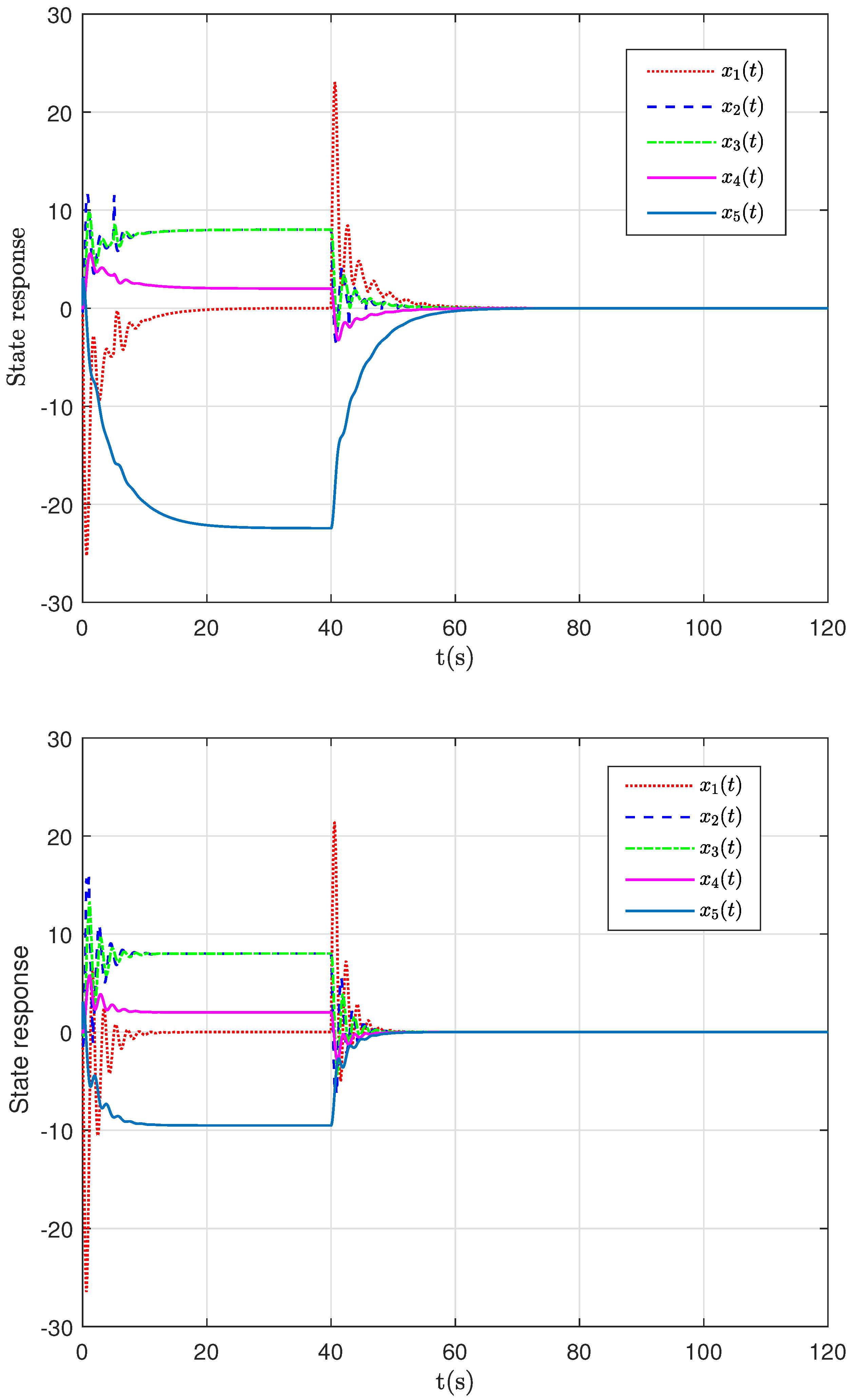
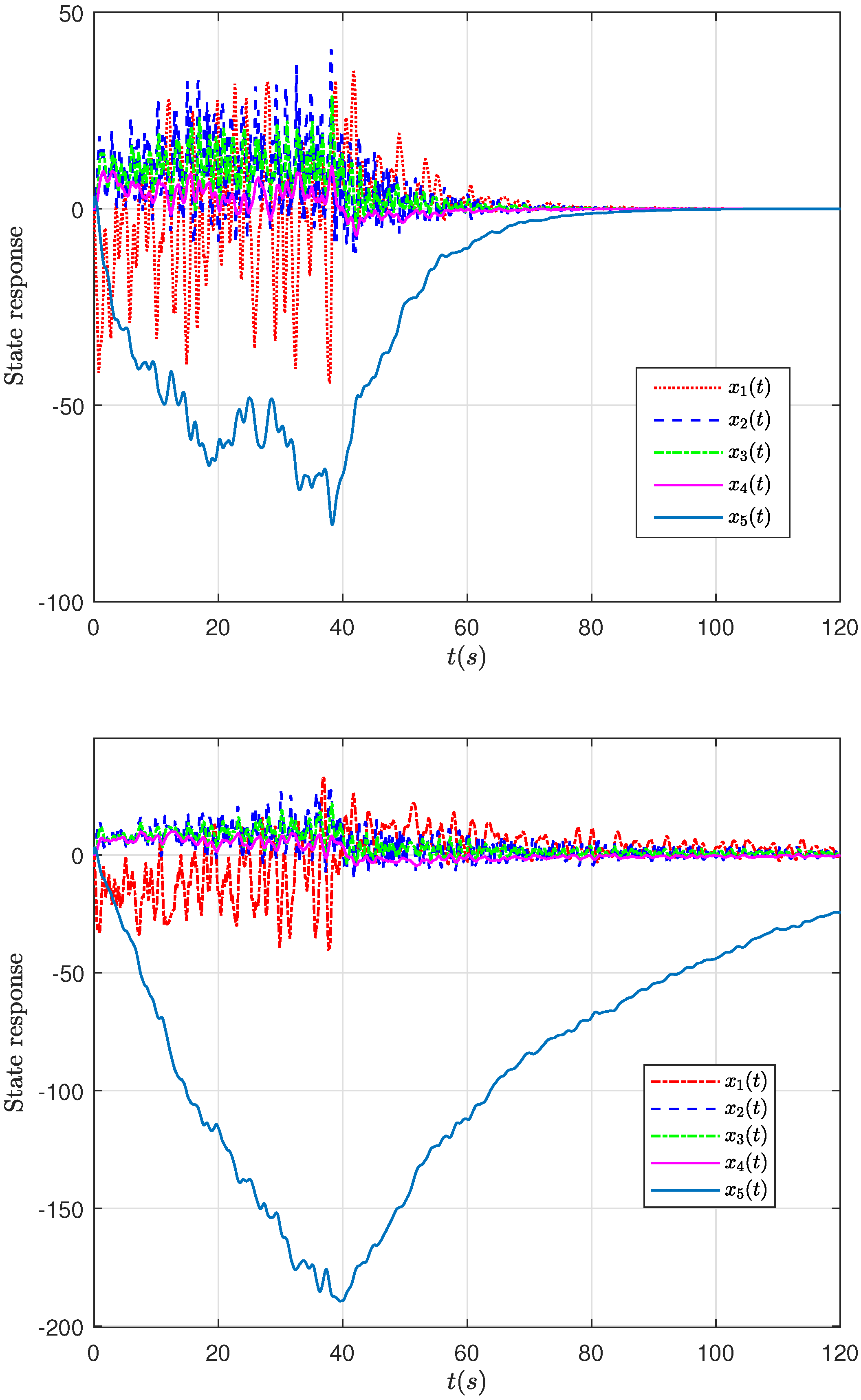
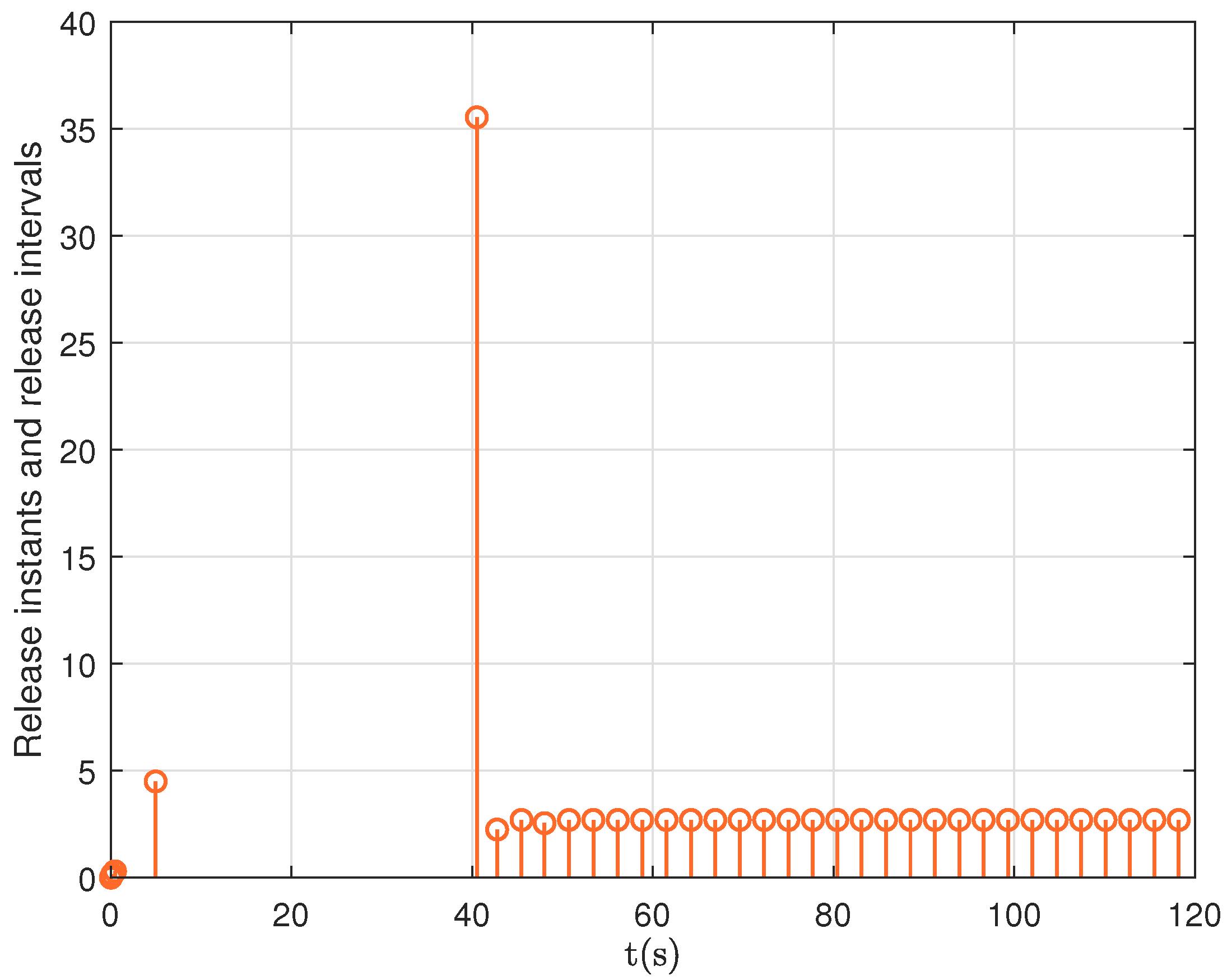
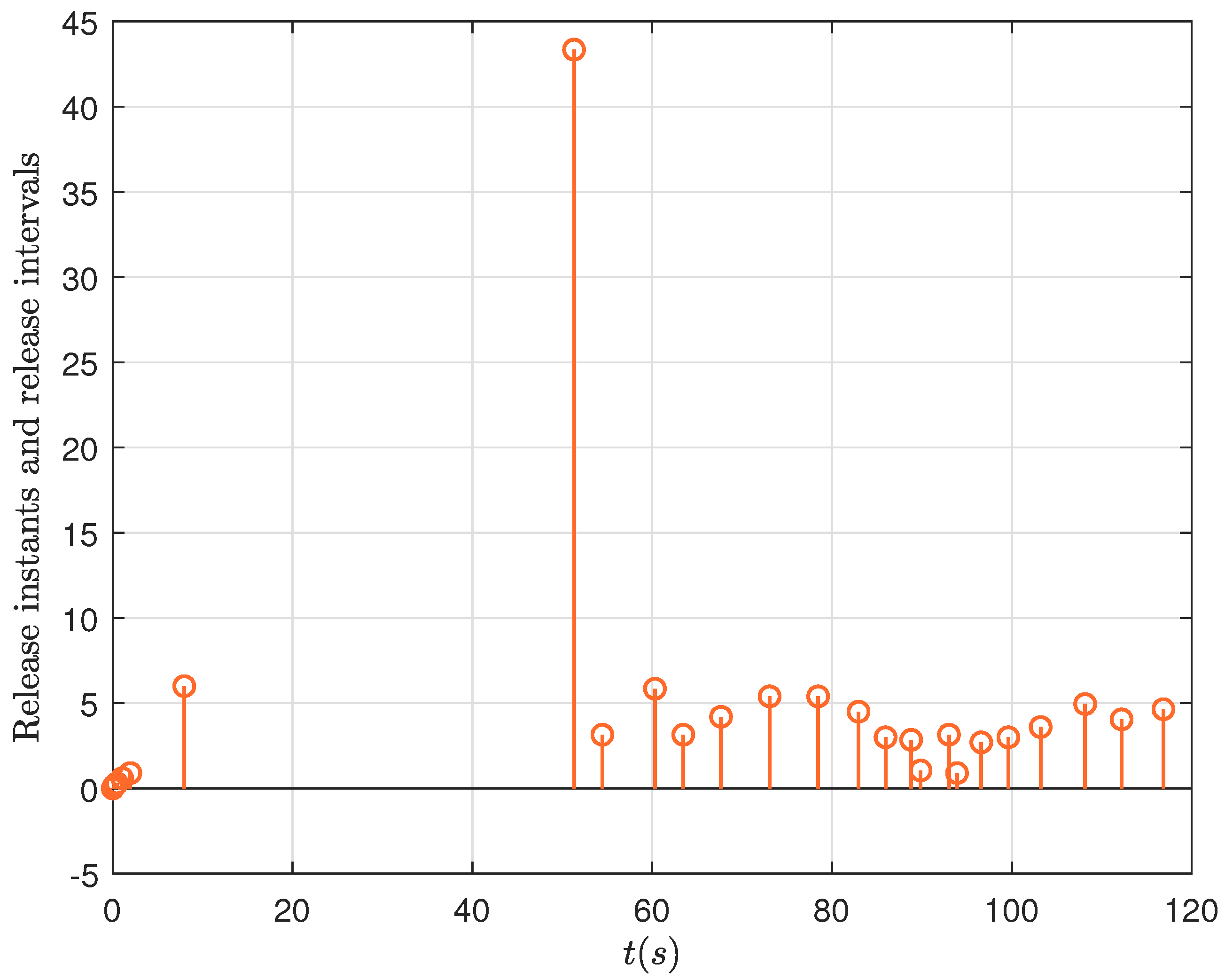
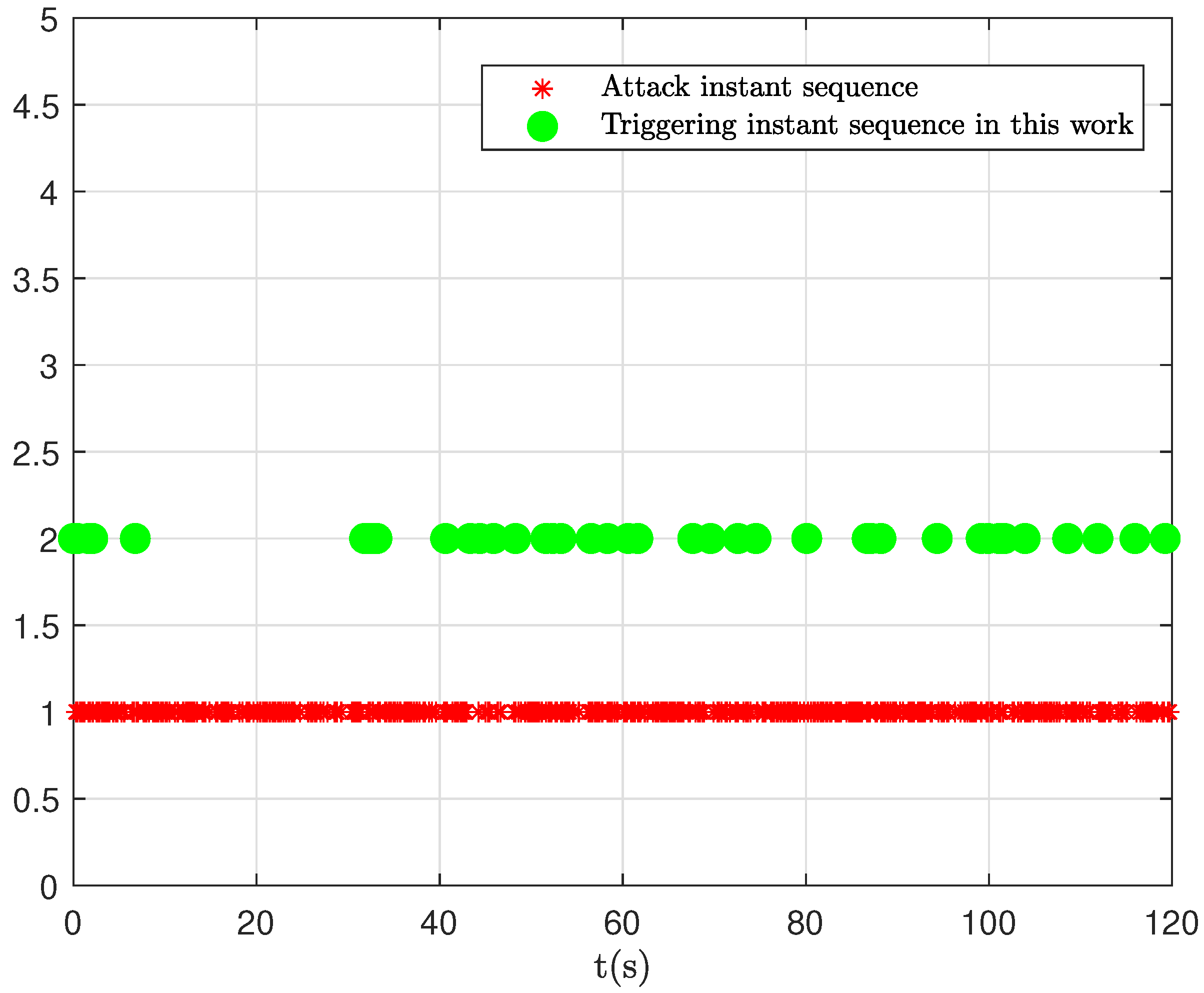
4. Case Studies

This section focuses on evaluating the effectiveness of the proposed control strategy by analyzing a power system with LFC subject to stochastic deception attacks. Certain electrical parameters are expressed in

Table 2. System parameters of the LFC scheme.

D	M	${\mathit{R}}_{\mathit{g}}$	${\mathit{T}}_{\mathit{g}}$	${\mathit{T}}_{\mathit{t}}$	${\mathit{\rho }}_{\mathit{e}}$	${\mathit{K}}_{\mathit{e}}$	${\mathit{T}}_{\mathit{e}}$	b	${\mathit{\alpha }}_{\mathit{g}}$	${\mathit{\alpha }}_{\mathit{e}}$
0.0083	0.1667	2.4	0.08	0.3	0.42	1	1	0.425	0.8	0.2

.

Set $x\left(0\right)=[0.2;0.5;0.5;0.2;0.3]$, with other parameters given as $\gamma =10$, $\delta =0.5$, $\overline{\lambda }=0.5$, ${\mu }_M=0.1s$, $G=\mathrm{diag}\left\{0.2,0.1\right\}$ and $\psi \left(y\left(t\right)\right)=[-tanh\left(0.2y_1\left(t\right)\right),tanh\left(0.1y_2\left(t\right)\right)]$. $\varpi \left(t\right)$ follows:

$$\varpi \left(t\right)=\left\{\begin{array}{c}0.01,0<t\le 40,\hfill \\ 0,t>40.\hfill \end{array}\right.$$

An event-triggered ${\mathcal{H}}_{\infty }$ controller is employed to regulate the nominal frequency of the power system (e.g., near-zero frequency difference). Define the controller without considering network attacks as Controller 1, and the controller with considering network attacks as Controller 2. To verify the effectiveness of the proposed control method against deception attacks, two cases are examined.

• Case 1: This case demonstrates that, in the absence of deception attacks, both Controller 1 and Controller 2 successfully stabilize the power system;
• Case 2: In this case, random deception attacks are introduced. Simulation results show that, compared to Controller 1, Controller 2 provides a significantly smoother and improved system response.

Figure 3 illustrates that the system (3) achieves the AMSS by Controller 1 and 2 in the absence of deception attacks; Figure 4 reflects that when deception attacks occur, Controller 2 still preserves good system performance more effectively while Controller 1 fails. The negative impacts brought from deception attacks are counteracted to a great extent. Therefore, it is apparent to see that the designed ${\mathcal{H}}_{\infty }$ controller (Controller 2) in this study can realize stronger control performance under cyberattacks.

On the other side, Figure 5 and Figure 6 show the triggering instants and the triggering intervals in this article, respectively. Compared to the conventional time-triggered scheme, the proposed ETTS demonstrates significantly greater ability to optimize network bandwidth utilization. In Figure 7, the red asterisk and the green dot represent the attack instant and trigger sequences, respectively, where the developed event-triggered mechanism regulates the number of triggered data packets according to the frequency of deception attacks.

Specially, as depicted in Figure 5 and Figure 6, the number of triggering events decreases in the presence of attacks. The reason behind this is that the proposed triggered fashion strategically reduces data packet transmissions when cyberattacks or other anomalies happen, hence minimizing the risk of packet corruption. In other words, under such communication protocols, the system demonstrates strong resilience to deception attacks and effectively mitigates false triggers caused by cyberattacks.

5. Conclusions

This study presents an event-triggered ${\mathcal{H}}_{\infty }$ load frequency control (LFC) strategy for power systems, particularly incorporating electric vehicles (EVs). By employing an event-based communication scheme, the data transmission and the network burden can be reduced and alleviated, while maintaining satisfactory control performance in contrast to conventional time-triggered approaches. Specially, it compensates for the detrimental effects of random deception attacks through the resilient controller. Sufficient conditions for the AMSS of the closed-loop system has been obtained by utilizing the Lyapunov theory in terms of LMIs. The simulation results illustrate the feasibility and availability of the proposed method for power systems under limited bandwidth and cyberthreats. Future work involves exploring distributed and full decentralized event-triggered LFC schemes, as well as data-driven and model-free control methods for resilient controller design in large-scale power networks [42].