High- and Low-Rank Optimization of SNOVA on ARMv8: From High-Security Applications to IoT Efficiency

Abstract

The increasing threat of quantum computing to traditional cryptographic systems has prompted intense research into post-quantum schemes. Despite SNOVA’s potential for lightweight and secure digital signatures, its performance on embedded devices (e.g., ARMv8 platforms) remains underexplored. This research addresses this gap by presenting the optimal SNOVA implementations on embedded devices. This paper presents a performance-optimized implementation of the SNOVA post-quantum digital signature scheme on ARMv8 processors. SNOVA is a multivariate cryptographic algorithm under consideration in the NIST’s additional signature standardization. Our work targets the performance bottlenecks in the SNOVA scheme. Specifically, we employ matrix arithmetic over ${\mathbb{GF}}_{16}$ and AES-CTR-based pseudorandom number generation by exploiting the NEON SIMD extension and tailoring the computations to the matrix rank. At a low level, we develop rank-specific SIMD kernels for addition and multiplication. Rank 4 matrices (i.e., 16 bytes) are handled using fully vectorized instructions that align with 128-bit-wise registers, while rank 2 matrices (i.e., 4 bytes) are processed in batches of four to ensure full SIMD occupancy. At the high level, core routines such as key generation and signature evaluation are structurally refactored to provide aligned memory layouts for batched execution. This joint optimization across algorithmic layers reduces the overhead and enables seamless hardware acceleration. The resulting implementation supports 12 SNOVA parameter sets and demonstrates substantial efficiency improvements compared to the reference baseline. These results highlight that fine-grained SIMD adaptation is essential for the efficient deployment of multivariate cryptography on modern embedded platforms.

1. Introduction

The rapid advancement of quantum computing poses a significant threat to classical public key cryptographic systems, including RSA (i.e., Digital Signature Algorithm) and Elliptic Curve Cryptography (ECC), all of which rely on the presumed intractability of number-theoretic problems. Quantum algorithms, such as Shor’s algorithm for integer factorization and discrete logarithms [1] and Grover’s algorithm for unstructured search [2], can break the fundamental security assumptions underlying these schemes. These theoretical breakthroughs have sparked extensive research examining the implications of quantum computing for modern cryptographic infrastructures [3]. In response, the National Institute of Standards and Technology (NIST) launched the Post-Quantum Cryptography (PQC) Standardization Project to evaluate and standardize cryptographic algorithms that are secure against quantum adversaries [4,5]. Multivariate public key cryptography (MPKC) is recognized for its low computational complexity and fast signature generation [6].

SNOVA (Simple Noncommutative Unbalanced Oil and Vinegar scheme with randomness Alignment) was submitted to the NIST’s call for additional signature schemes. SNOVA extends the classical Unbalanced Oil and Vinegar (UOV) framework [7] by introducing structured randomness alignment and tunable security parameters. This scheme offers multiple parameter configurations designed to optimize the trade-off between the key size, signature size, and computational cost [8].

Among the various parameter configurations supported by SNOVA, this work focuses on two representative settings: $l=2$ and $l=4$. These choices reflect contrasting deployment goals. The $l=2$ (rank 2) configuration targets resource-constrained environments, such as Internet of Things (IoT) devices, where computational and memory efficiency is critical. On the other hand, the $l=4$ (rank 4) configuration aligns with high-assurance applications and satisfies the security objectives outlined in standards like CNSA 2.0, https://media.defense.gov/2022/Sep/07/2003071836/-1/-1/0/CSI_CNSA_2.0_FAQ_.PDF, accessed on 2 July 2025. Although the $l=3$ setting (rank 3) was initially examined, it was excluded from optimization due to inefficiencies in SIMD alignment on ARMv8 platforms. By selecting these two ranks, we aim to evaluate SNOVA’s performance across both ends of the efficiency security spectrum.

Although a portable reference implementation of SNOVA in C has been provided, its performance on embedded systems, particularly those based on the ARM architecture, remains underexplored. The ARMv8 architecture, which powers many mobile, embedded, and low-power platforms, supports 64-bit execution via AArch64 and features NEON, a Single Instruction, Multiple Data (SIMD) extension for efficient 128-bit vector operations [9]. These features collectively make ARMv8 a compelling platform for implementing lightweight post-quantum signature schemes such as SNOVA. In this paper, we present a performance-optimized implementation of SNOVA targeting ARMv8-based processors, demonstrating significant improvements in efficiency and scalability.

The remainder of this paper is organized as follows: Section 2 discusses related work on SNOVA and PQC implementations on ARM platforms. Section 3 describes our optimization strategies and implementation methodology. Section 4 presents performance measurements and comparisons. Section 5 provides a discussion of the implementation challenges and architectural limitations, particularly for non-aligned matrix dimensions. Finally, Section 6 concludes this paper.

The key contributions of this work are summarized as follows:

• Optimization of Matrix Operations over ${\mathrm{GF}}_{16}$: In this work, we present an optimized implementation of the SNOVA signature algorithm targeting the Apple M2 processor, based on the ARMv8 architecture. Our implementation leverages 128-bit vector registers and AES-accelerated instructions to optimize three core components: finite field arithmetic over ${\mathrm{GF}}_{16}$, matrix operations in the signature generation process, and pseudorandom generation based on AES-CTR mode. In particular, we apply distinct strategies depending on the matrix ring dimension l. For the $l=4$ setting (rank 4), additive operations are implemented using low-level EOR assembly instructions to exploit SIMD-style XOR reductions. For $l=2$ (rank 2), we batch four $2\times 2$ additions together using vectorized routines. These optimizations are integrated into key procedures such as gen_F and gen_P22, resulting in measurable performance gains. Although the $l=3$ setting (rank 3) was also considered, SIMD misalignment issues made it unsuitable for optimization on ARMv8. Hence, our implementation focuses on $l=2$ and $l=4$.
• Cycle-Level Benchmarking Across Selected SNOVA Parameter Sets: We evaluate our implementation on the Apple M2 processor using cycle-accurate measurements. The results demonstrate an up to 68.7% improvement in the rank 4 configurations compared to the reference implementation, confirming the benefits of rank-specific vectorization. The evaluation includes six parameter sets, selected from two distinct ranks, to represent the range of SNOVA configurations. All tests are conducted on real hardware without emulation, ensuring an accurate assessment of the algorithm’s scalability and platform level.
• Public Release of the Optimized Implementation and the Validation Approach: To facilitate reproducibility and further research, we publicly release the optimized SNOVA implementation targeting ARMv8 platforms. The source code is available at https://github.com/minunejip/PQC-ARMv8/tree/main/SNOVA, accessed on 2 July 2025. To ensure correctness, we included compile-time switches that allow assembly-optimized modules to selectively be enabled or disabled. Using the test_sign() routine, we validated that both pure C and assembly-enhanced paths produce consistent and correct results in the same environment.

2. Related Work

2.1. Post-Quantum Cryptography and Additional Signature Competition

To address the threat posed by quantum computing, the NIST launched the PQC Standardization Project in 2016 [5]. Unlike traditional public key algorithms based on integer factorization or discrete logarithms, PQC schemes rely on quantum-resistant hardness assumptions such as lattice problems, multivariate polynomials, and error-correcting codes [6].

The standardization effort officially began in 2017 with 69 initial submissions. After several rounds of evaluation, the NIST announced in July 2022 the selection of CRYSTALS-Kyber (FIPS 203) for public key encryption and CRYSTALS-Dilithium (FIPS 204) and SPHINCS+ (FIPS 205) for digital signatures [5]. Each algorithm was published as a separate Federal Information Processing Standard, and the final versions were formally approved in August 2024. In March 2025, the NIST announced the selection of Hamming Quasi-Cyclic (HQC), a code-based key encapsulation mechanism, as the fifth post-quantum cryptographic standard [5]. HQC was introduced to increase the cryptographic diversity by complementing lattice-based schemes such as Kyber. Unlike lattice-based constructions, HQC is built on the hardness of decoding random linear codes.

However, as all selected digital signature algorithms were based on structured lattice assumptions, concerns were raised about the lack of mathematical diversity. In response, the NIST initiated a call for additional signatures in 2022, aiming to evaluate multivariate, code-based, and hash-based digital signature schemes that offer strong security, practical performance, and suitability for constrained environments [4].

In the first round of the additional signature process, 40 submissions were received. Following the initial evaluation, 14 candidates advanced to round 2 in early 2024. Among these, SNOVA, a multivariate-based signature scheme, drew attention due to its compact structure and potential for efficient vectorized implementation [8]. The NIST continues to evaluate these candidates, and future rounds are expected to determine which schemes will proceed toward standardization.

2.2. The SNOVA Signature Scheme

SNOVA is a multivariate public key signature scheme that extends the classical UOV framework with structural enhancements designed to reduce the key size and improve the performance [8]. Its core innovation lies in the use of noncommutative matrix operations over ${\mathbb{GF}}_{{16}^m}$, which enhance the resistance against algebraic and structural attacks. To reduce the public key size further, SNOVA employs a compressed central map representation and a structured randomness alignment mechanism [10].

At the heart of the scheme are multivariate quadratic polynomials of the form

$$P_i\left(X\right)=\sum _{j=1}^n\sum _{k=1}^n{a}_{ijk}{x}_j{x}_k+\sum _{j=1}^n{b}_{ij}{x}_j+c_i,$$

(1)

where the coefficients $a_{ijk},b_{ij},c_i\in G{F}_{16}$, and $x_j$ denotes the input variables.

The private key consists of multiple affine and linear transformation matrices, which define the central map and support the signing process:

$$SK=(A_a,B_a,Q_{a1},Q_{a2},T_{12}),$$

(2)

where $A_a$ and $B_a$ handle input mixing, $Q_{a1}$ and $Q_{a2}$ define the nonlinear central map, and $T_{12}$ manages randomness alignment.

The public key is formed by compressing the central map after applying the private transformations. It is represented as

$$PK=(P_{11},P_{12},P_{21},P_{22}),$$

(3)

where each $P_{ij}$ denotes a submatrix encoding a portion of the transformed polynomial map.

These structured key representations enable efficient matrix-based signing and verification procedures. SNOVA uses matrix multiplications and affine transformations to accelerate the computations and reduce the memory footprint—features particularly advantageous on constrained platforms.

SNOVA supports parameter sets grouped into three NIST-defined security levels: Levels I, III, and V. Each level specifies the values for the number of vinegar variables (v) and oil variables (o), the field size ($q=16$), and the central map degree (l). These are summarized in

Table 1. SNOVA parameters categorized by NIST security level.

Security Level	Security Strength Indicator (Bits)	Vinegar Variables (v)	Oil Variables (o)	Field Size (q)	Degree (l)
I	128	24	5	16	4
III	192	43	25	16	2
V	256	60	10	16	4

.

To support both flexibility and performance, SNOVA defines two types of secret keys: the esk (extended secret key), which includes auxiliary data for faster signing, and the ssk (seed-type secret key), which is optimized for low-resource platforms.

To offer a clearer perspective on SNOVA’s resource characteristics, we provide a comparison in

Table 2. Key and signature sizes for NIST PQC schemes and SNOVA variants (in bytes).

Scheme	Public Key	Secret Key (esk/ssk)	Signature
Dilithium-II	1312	2528	2420
Dilithium-III	1952	4000	3293
Dilithium-V	2592	4864	4595
Falcon-512	897	1281	666
Falcon-1024	1793	2305	1280
SPHINCS+-128s	32	64	7856
SPHINCS+-128f	32	64	17,088
SPHINCS+-192s	48	96	16,224
SPHINCS+-192f	48	96	36,584
SPHINCS+-256s	64	128	29,792
SPHINCS+-256f	64	128	49,856
SNOVA (37-17-16-2)	9842	91,440/48	124
SNOVA (25-8-16-3)	2320	39,576/48	164.5
SNOVA (24-5-16-4)	1016	36,848/48	248
SNOVA (56-25-16-2)	31,266	300,848/48	178
SNOVA (49-11-16-3)	6005.5	177,060/48	286
SNOVA (37-8-16-4)	4112	133,040/48	376
SNOVA (24-5-16-5)	1578.5	60,048/48	378.5
SNOVA (75-33-16-2)	71,890	704,532/48	232
SNOVA (66-15-16-3)	15,203.5	435,423/48	380.5
SNOVA (60-10-16-4)	8016	395,248/48	576
SNOVA (29-6-16-5)	2716	100,398/48	453.5
HQC-128	2249	2289	4497
HQC-192	4522	4562	9042
HQC-256	7245	7285	14,485
McEliece-348864	261,120	6492	96
McEliece-460896	524,160	13,608	156
McEliece-6688128	1,044,992	13,932	194
McEliece-6960119	1,047,319	13,948	208
McEliece-8192128	1,357,824	14,120	208

summarizing the public key, secret key, and signature sizes of the major NIST post-quantum digital signature schemes, along with representative SNOVA configurations. This comparison helps highlight the memory footprint differences across lattice-based, hash-based, code-based, and multivariate-based schemes.

SNOVA’s multivariate structure naturally leads to relatively large secret keys [11], due to the inclusion of trapdoor matrices and auxiliary mappings. However, its public key size remains moderate in many parameter sets [12,13,14,15], and the signature size is notably small—typically ranging from 90 to 560 bytes—even at higher security levels. This is in stark contrast to hash-based schemes like SPHINCS+ [16], which exhibit much larger signature sizes (up to 50 KB). Each SNOVA signature also includes a 16-byte initialization vector (IV), which we report explicitly in the table.

Given its compact design and algebraic robustness, SNOVA is well suited to efficient implementation on ARMv8 processors that support NEON SIMD acceleration. At the time of writing, SNOVA is under active evaluation in round 2 of the additional signature process [5].

2.3. AES-CTR and Pseudorandom Generation

AES (Advanced Encryption Standard) is a widely adopted symmetric key block cipher that operates on 128-bit data blocks and supports key sizes of 128, 192, or 256 bits [17]. For AES-128, encryption consists of 10 rounds, each composed of the SubBytes, ShiftRows, MixColumns, and AddRoundKey transformations. These layered operations ensure strong diffusion and confusion, essential for resisting known cryptanalytic attacks.

In AES-CTR, a nonce concatenated with a counter is encrypted using AES to produce a pseudorandom keystream [18]. This keystream is then XORed with the plaintext to produce ciphertext—or used directly in cryptographic applications requiring pseudorandom data. Because each counter block is independent, the mode allows for efficient parallelization and streaming.

In the context of post-quantum digital signature schemes such as SNOVA, AES-CTR is employed as an internal pseudorandom number generator. It is used to sample secret vectors and ephemeral randomness during key generation and signing. This makes AES-CTR a practical alternative to hash-based constructions or external PRNGs, especially when reproducibility and efficiency are required [19].

Although the traditional implementations of AES are often software-based, modern processors such as those based on the ARMv8 architecture include dedicated instructions (e.g., AESE and AESMC) for hardware-accelerated encryption [9]. These instructions significantly reduce the latency of each round and are particularly advantageous for embedded platforms, where AES-CTR is frequently used as a lightweight randomness generator.

2.4. The ARMv8 Architecture and NEON SIMD Support

The ARMv8 architecture is a 64-bit instruction set architecture that powers a wide range of mobile and embedded devices, including smartphones, tablets, and energy-efficient microcontrollers [9]. It introduces the AArch64 execution mode, which extends the general-purpose register file to 31 64-bit registers and adopts uniform 32-bit instruction encoding. This design enables efficient instruction decoding and facilitates high-performance in-order and out-of-order pipelines.

A distinctive feature of ARMv8 is its support for NEON, a Single Instruction, Multiple Data (SIMD) extension designed for parallel data processing. NEON includes 32 vector registers, each 128 bits wide, capable of operating on multiple 8-, 16-, 32-, or 64-bit lanes in parallel. These vector registers enable high-throughput execution of operations on packed data, making them highly suitable for applications in cryptography, signal processing, and machine learning.

NEON supports a wide range of operations, including arithmetic, bitwise logic, shift, and memory access instructions. For instance, the EOR instruction performs element-wise bitwise XOR across all vector lanes, while LD1 and ST1 enable efficient aligned memory loads and stores. These vectorized operations are particularly advantageous in cryptographic primitives where parallelism is abundant—such as in matrix addition, polynomial multiplication, and S-box layers.

Additionally, the ARMv8 architecture provides specialized cryptographic instructions like AESE and AESMC, which accelerate block cipher operations such as AES. When used alongside NEON, these instructions enable lightweight and low-latency implementations of symmetric cryptographic components such as AES-CTR generators, authenticated encryption, or message authentication codes.

Due to this rich instruction set and hardware-level parallelism, ARMv8 has become a popular research platform for optimizing post-quantum cryptographic schemes [20,21,22]. Its energy-efficient yet powerful execution model offers an ideal balance between performance and deployability on real-world embedded systems.

2.5. Programming with ARM NEON Intrinsics

ARM NEON intrinsics offer a high-level programming interface for utilizing SIMD capabilities on ARMv8 architectures through C or C++ code. Each intrinsic maps directly to a low-level vector instruction, enabling developers to write portable and readable parallel code without relying on assembly.

These intrinsics operate on 128-bit NEON vector registers and support parallel operations across multiple data elements. For instance, a single register can hold sixteen 8-bit integers, eight 16-bit integers, four 32-bit integers, or two 64-bit integers [9]. This structure enables efficient vectorized execution of operations such as addition, multiplication, and bitwise logic within a single instruction cycle.

For example, vdupq_n_u8 replicates a single 8-bit constant across all 16 lanes of a vector register. The veorq_u8 intrinsic computes the bitwise XOR of two such registers in parallel, and vgetq_lane_u8 extracts a specific byte from a vector register for scalar use. These operations correspond to ARMv8 assembly instructions such as DUP, VEOR, and UMOV, respectively.

NEON intrinsics are particularly advantageous for implementing cryptographic routines that benefit from data-level parallelism. Applications such as finite field arithmetic, matrix multiplication, and bytewise permutations can be significantly accelerated using this interface. Moreover, compilers can optimize the memory access and instruction scheduling when intrinsics are used instead of raw assembly [21].

By abstracting low-level instructions while retaining precise control over vector operations, NEON intrinsics enable efficient, maintainable, and scalable SIMD implementations—making them an indispensable tool for optimizing post-quantum cryptographic algorithms on ARMv8 processors.

3. The Proposed Method

3.1. Optimization of Addition Operations

The SNOVA algorithm operates over the finite field ${\mathbb{GF}}_{16}$, defined by the irreducible polynomial $f\left(x\right)=x^4+x+1$ over ${\mathbb{GF}}_2$ [23,24]. Each field element is represented as a 4-bit binary value corresponding to a polynomial of degree at most 3.

Addition in ${\mathbb{GF}}_{16}$ is implemented using bitwise XOR:

$$a+b=a\oplus b$$

(4)

This operation corresponds to binary addition without carry. For example, let $a=0101$ and $b=1011$ in binary. Then,

$$a\oplus b=1110$$

(5)

To optimize this operation on ARMv8, we leverage both scalar and SIMD instructions.

Table 3. The instructions and intrinsics used in the optimized SNOVA matrix-addition kernel. Xt, Wt, Vt, Vd—destination registers; Xn—address register (used as ptr in intrinsics); Vn, Vm—source vector registers; T—arrangement specifier (e.g., .16B).

Instruction	Operands	Description	Operation
LD1	Vt.T,[Xn]	Load one to four single-element structures (typically 16 bytes) from memory into vector register(s).	Vt ← [Xn]
EOR	Vd.T, Vn.T, Vm.T	Bitwise XOR of two vector registers. All corresponding lanes are XORed element-wise.	Vd ← Vn ⊕ Vm
ST1	Vt.T,[Xn]	Store one to four single element structures from vector register(s) to memory.	[Xn] ← Vt
vld1q_u8	Xn	Load 16 consecutive 8-bit values from memory at address register Xn into a NEON vector (uint8x16_t).	Vd ← [Xn]
veorq_u8	Vn, Vm	Compute bitwise XOR between two 128-bit NEON vectors. Equivalent to EOR Vd.16B, Vn.16B, Vm.16B.	Vd ← Vn ⊕ Vm
vst1q_u8	Xn, Vd	Store contents of NEON vector Vd (16 lanes) to memory at address register Xn.	[Xn] ← Vd

summarizes the instruction set utilized in SNOVA’s matrix addition routines. This table is adapted from [25], which presents a practical reference for vector-based bitwise operations.

Figure 1 shows the SIMD-optimized data flow for rank 4 matrix addition, illustrating how two 16-byte inputs are loaded into NEON registers, combined using EOR, and stored back into memory.

To maximize the SIMD efficiency, we design rank-specific addition strategies. SNOVA’s parameter configurations involve matrices of varying dimensions depending on the central map degree l. We present two optimized implementations tailored to rank 2 and rank 4, both of which benefit from the regularity of the matrix shapes and fixed byte sizes.

To illustrate the memory layout and vectorization strategies employed in our implementation better, Figure 2 provides a visual overview of matrix addition in SNOVA for rank 2 and rank 4. In the rank 2 case, multiple $2\times 2$ matrices are grouped and processed in a batched SIMD manner. In contrast, the rank 4 matrices exactly match the SIMD register width, allowing for the direct application of vector operations without additional restructuring.

• Rank 4 ($4\times 4$):

Each matrix consists of 16 one-byte field elements (16 bytes total), perfectly aligned with NEON’s 128-bit vector register. This alignment allows us to process the entire matrix addition using a minimal instruction sequence, two loads, one XOR, and one store without requiring any iteration or branching. Such a structure is ideally suited to SIMD execution, enabling highly parallel and cache-friendly computation.

The instruction-level details of our rank-4 implementation are summarized in Algorithm 1:

Algorithm 1 Rank 4 matrix addition in ${\mathbb{GF}}_{16}$

Require:  $x0$: address of matrix A (16 bytes)  1:        $x1$: address of matrix B (16 bytes)  2:        $x2$: address of output matrix C Ensure:  $C=A\oplus B$  3: LD1 {v0.16b}, [x0]        ▹ load A into v0  4: LD1 {v1.16b}, [x1]        ▹ load B into v1  5: EOR v1.16b, v0.16b, v1.16b     ▹$v1\leftarrow v0\oplus v1$  6: ST1 {v1.16b}, [x2]       ▹ store result to C

Compared to the scalar baseline which iterates over all 16 field elements and applies separate load, XOR, and store operations per byte, this SIMD-based strategy executes a single instruction per operation type. By reducing the total instruction count by more than an order of magnitude and eliminating the loop overhead, our approach improves the instruction throughput and data locality, delivering highly efficient matrix addition on ARMv8 processors.

• Rank 2 ($2\times 2$):

Each rank 2 matrix in SNOVA contains only four field elements (4 bytes), offering insufficient granularity for effective SIMD execution. A naive scalar implementation iterates over each field element using nested loops, issuing independent memory accesses and XOR operations for all 16 bits. While functionally correct, this results in a significant control overhead and inefficient use of the processor resources.

Unlike the rank 4 matrices, which occupy an entire 128-bit SIMD register, rank 2 matrices are too small to justify direct vectorization. Mapping a $2\times 2$ matrix to either a 64-bit general-purpose register or a SIMD register results in severe underutilization—only 25% of the register width is effectively used. Furthermore, the overhead introduced by the explicit register management and load/store instructions in assembly can degrade the performance even below that of the scalar C baseline.

To overcome this limitation, we adopt a batch-based vectorization strategy. By aggregating four $2\times 2$ matrices—totalling exactly 16 bytes—into a single 128-bit SIMD register, we fully utilize the vector width and perform all four additions in parallel with a single XOR instruction. This design amortizes the cost of memory operations and unlocks parallelism even for small matrix operations.

The low-level implementation of this routine is encapsulated in gf16m_rank2_add_batch4, which takes pointers to two contiguous blocks of four matrices and performs element-wise XOR using NEON intrinsics. Its behavior is summarized in the following Algorithm 2:

Algorithm 2 Rank 2 matrix addition in ${\mathbb{GF}}_{16}$ (4 matrices batched)

Require:  $x0$: address of 4 matrices $A_0,\dots ,A_3$ (16 bytes)  1:        $x1$: address of 4 matrices $B_0,\dots ,B_3$ (16 bytes)  2:        $x2$: address of 4 outputs $C_0,\dots ,C_3$ Ensure:  $C_i=A_i\oplus B_i\mathrm{for}i=0,1,2,3$  3: v0 = vld1q_u8(x0)           ▹ load $A_0$–$A_3$  4: v1 = vld1q_u8(x1)           ▹ load $B_0$–$B_3$  5: v2 = veorq_u8(v0, v1)        ▹$v2\leftarrow v0\oplus v1$  6: vst1q_u8(x2, v2)           ▹ store $C_0$–$C_3$

However, to use this batched kernel efficiently, the calling function must prepare four matrices in a contiguous memory layout. This requirement differs from the rank 4 case, where each matrix naturally fits a SIMD register and can be processed independently.

To enable batching, we introduce loop tiling and data restructuring into upper-level modules such as gen_F, gen_P22, and sign_digest_core. These routines are adapted to accumulate temporary results from multiple multiplications into aligned buffers, enabling the use of gf16m_rank2_add_batch4 instead of performing four separate scalar additions.

The following pseudocode captures the structure of this integration, as used in gen_F:

Algorithm 3 Vectorized rank 2 accumulation in gen_F

1: for $k=0$ to K step 4 do          ▹ process four columns per iteration   2:     $blk\leftarrow min(4,K-k)$             ▹ limit to remaining columns   3:     for $kk=0$ to $blk-1$ do              ▹ initialize accumulators   4:         $C[k+kk]\leftarrow P[k+kk]$                ▹ copy base matrix   5:     end for   6:     for $idx=0$ to $V-1$ do            ▹ loop over vinegar variables   7:         for $kk=0$ to $blk-1$ do   8:            $T\left[kk\right]\leftarrow A\left[idx\right]·B\left[idx\right][k+kk]$         ▹ rank 2 matrix multiply   9:         end for 10:         if $blk==4$ then 11:            gf16m_rank2_add_batch4(T, C)  ▹ vectorized addition of four matrices 12:         else 13:            for $kk=0$ to $blk-1$ do 14:                gf16m_add(C[k+kk], T[kk], C[k+kk])      ▹ scalar fallback 15:            end for 16:         end if 17:     end for 18: end for

Algorithm 3 reflects the structure used in modules like gen_F to facilitate rank 2 vectorized addition. It works by tiling the k loop into blocks of four matrices, the exact size that fits into a 128-bit NEON register. The outer loop slices the k dimension into groups of four matrices, storing the results of matrix multiplications into a temporary buffer. If the current block contains exactly four matrices, the batched addition is applied using gf16m_rank2_add_batch4. For remaining tail cases (1–3 matrices), scalar addition is used instead to maintain correctness without vector underutilization.

This approach ensures that the memory alignment and batch size requirements of SIMD instructions are respected while preserving the functional logic of the original scalar loop. Compared to per-element scalar accumulation, this batched structure reduces the instruction count and improves the data locality, especially in inner loops where the same accumulation pattern is repeated.

3.2. Multiplication Optimization

Matrix multiplication over ${\mathbb{GF}}_{16}$ is one of the most performance-critical operations in SNOVA, appearing frequently during public key generation, signature creation, and verification. As its computational cost dominates the total execution time, effective optimization of this operation is essential.

To address this, we employ the NEON SIMD extension on ARMv8 processors. NEON provides 128-bit vector registers capable of performing parallel operations on up to sixteen 8-bit elements, which is particularly suitable for matrix arithmetic over ${\mathbb{GF}}_{16}$.

Matrix multiplication in ${\mathbb{GF}}_{16}$ is defined as

$$C\left[i\right]\left[j\right]=\sum _{k}A\left[i\right]\left[k\right]·B\left[k\right]\left[j\right]$$

(6)

where both multiplication and addition are field operations. While addition is a simple XOR, multiplication requires polynomial arithmetic modulo, the irreducible polynomial $f\left(x\right)=x^4+x+1$ [23]. 

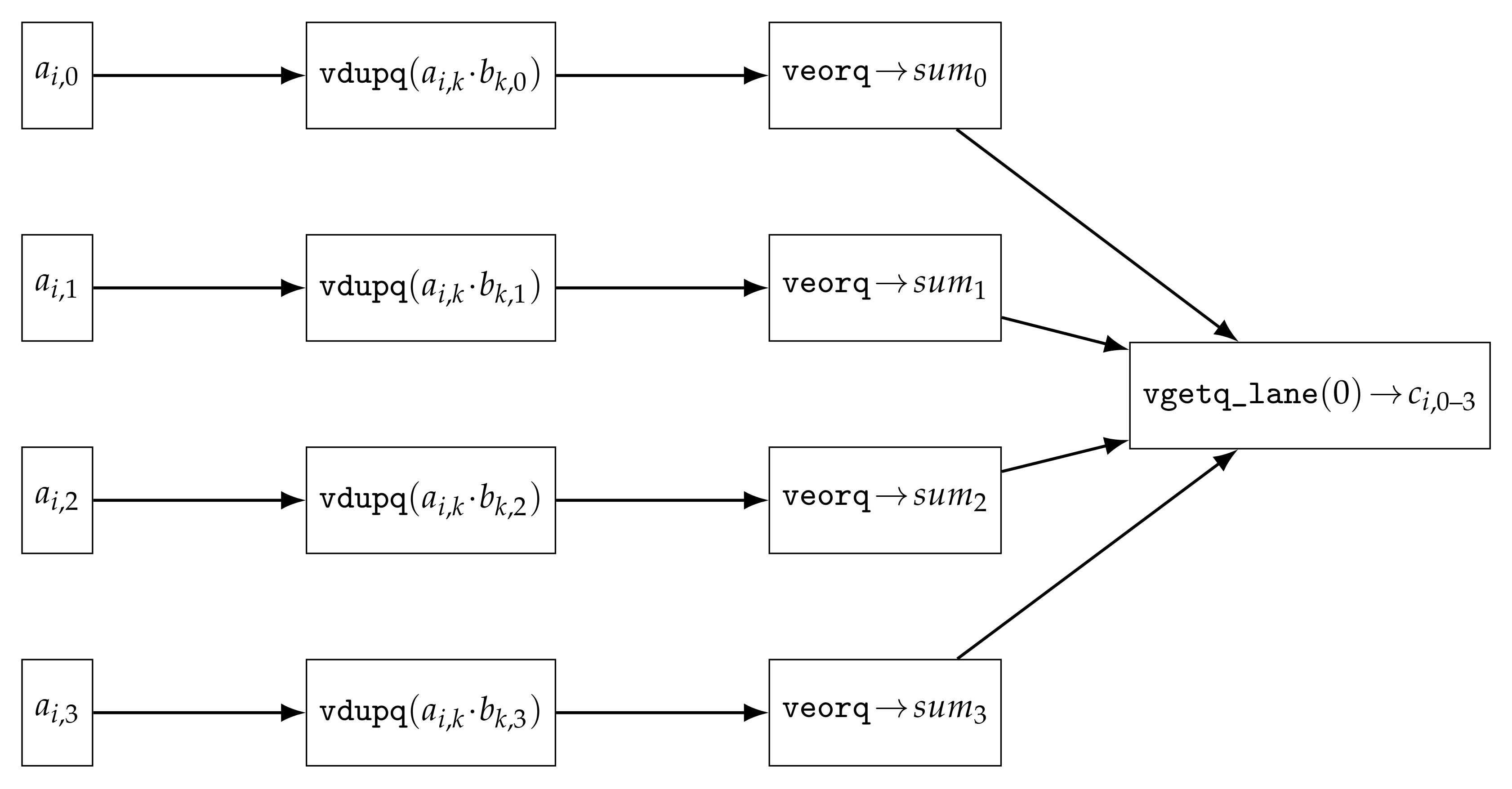
Figure 3 depicts the SIMD-based flow of rank 4 GF(16) matrix multiplication, where each element of the row vector is broadcast, XOR-accumulated, and extracted to produce the output.

To accelerate these operations, we implement all inner loops using NEON intrinsics.

Table 4. NEON intrinsics used in the optimized SNOVA matrix multiplication kernel; V: vector register; imm: 8-bit immediate constant; n: lane index; Xn: address pointer.

Intrinsic	Operands	Description	Operation
vdupq_n_u8	imm	Broadcasts an 8-bit constant across all 16 lanes of a 128-bit vector register	Vd $\leftarrow \{imm,\dots ,imm\}$
veorq_u8	Vn, Vm	Performs element-wise XOR of two 128-bit vectors	Vd ← Vn ⊕ Vm
vgetq_lane_u8	V, n	Extracts the n-th byte of a 128-bit vector to a scalar register	Wd ← V[n]

contains the following instructions that form the core of our multiplication kernel:

The NEON-based implementation avoids scalar instructions entirely. Scalar field elements are broadcast using vdupq_n_u8, and vectorized XOR accumulation is performed using veorq_u8. Once all products are computed and summed, the results are extracted using vgetq_lane_u8. Figure 4 provides a visual overview of how SIMD lanes are utilized in rank 2 and rank 4 matrix multiplications.

The following, Algorithm 4, presents the high-level logic behind SNOVA’s multiplication kernel. Each loop iterates over the matrix indices, performs broadcast and parallel accumulated multiplications, and writes the result to memory.

Algorithm 4 SNOVA ${\mathbb{GF}}_{16}$ Multiplication Optimization

Require:  Matrix A and B of size $r\times r$ Ensure:  Matrix $C=A\times B$ over ${\mathbb{GF}}_{16}$   1: for $i=0$ to $r-1$ do                  ▹ iterate rows of A   2:     for $j=0$ to $r-1$ do                 ▹ iterate cols of B   3:         $C\left[i\right]\left[j\right]\leftarrow 0$                  ▹ clear accumulator   4:         for $k=0$ to $r-1$ do               ▹ dot-product index   5:            $C\left[i\right]\left[j\right]\leftarrow C\left[i\right]\left[j\right]\oplus \left(A\right[i\left]\right[k]·B[k\left]\right[j\left]\right)$  ▹ fused multiply–add over ${\mathbb{GF}}_{16}$   6:         end for   7:     end for   8: end for

We implement a fully unrolled version of this algorithm for rank 4 matrices to exploit register-level parallelism like that in Algorithm 5:

Algorithm 5 NEON-based ${\mathbb{GF}}_{16}$ matrix multiplication for rank 4.

Require:  Row vector $a\left[4\right]$, column vectors $b\left[4\right]$ Ensure:  Output vector $c\left[4\right]$   1: for$i=0$ to 3 do      ▹ iterate rows   2:     $su{m}_0\leftarrow$vdupq_n_u8($a\left[i\right]\left[0\right]·b\left[0\right]\left[0\right]$)       ▹ initial product, col 0   3:     $su{m}_1\leftarrow$vdupq_n_u8($a\left[i\right]\left[0\right]·b\left[1\right]\left[0\right]$)       ▹ initial product, col 1   4:     $su{m}_2\leftarrow$vdupq_n_u8($a\left[i\right]\left[0\right]·b\left[2\right]\left[0\right]$)       ▹ initial product, col 2   5:     $su{m}_3\leftarrow$vdupq_n_u8($a\left[i\right]\left[0\right]·b\left[3\right]\left[0\right]$)       ▹ initial product, col 3   6:     for $k=1$ to 3 do      ▹ accumulate remaining terms   7:         $pro{d}_0\leftarrow$vdupq_n_u8($a\left[i\right]\left[k\right]·b\left[0\right]\left[k\right]$)   8:         $pro{d}_1\leftarrow$vdupq_n_u8($a\left[i\right]\left[k\right]·b\left[1\right]\left[k\right]$)   9:         $pro{d}_2\leftarrow$vdupq_n_u8($a\left[i\right]\left[k\right]·b\left[2\right]\left[k\right]$) 10:         $pro{d}_3\leftarrow$vdupq_n_u8($a\left[i\right]\left[k\right]·b\left[3\right]\left[k\right]$) 11:         $su{m}_0\leftarrow$veorq_u8($su{m}_0$, $pro{d}_0$)          ▹ XOR accumulate 12:         $su{m}_1\leftarrow$veorq_u8($su{m}_1$, $pro{d}_1$) 13:         $su{m}_2\leftarrow$veorq_u8($su{m}_2$, $pro{d}_2$) 14:         $su{m}_3\leftarrow$veorq_u8($su{m}_3$, $pro{d}_3$) 15:     end for 16:     $c\left[i\right]\left[0\right]\leftarrow$vgetq_lane_u8($su{m}_0$, 0)           ▹ extract result 17:     $c\left[i\right]\left[1\right]\leftarrow$vgetq_lane_u8($su{m}_1$, 0) 18:     $c\left[i\right]\left[2\right]\leftarrow$vgetq_lane_u8($su{m}_2$, 0) 19:     $c\left[i\right]\left[3\right]\leftarrow$vgetq_lane_u8($su{m}_3$, 0) 20: end for

This SIMD-centric approach minimizes the control flow and the instruction count. The multiplication logic is embedded into a unified dispatch macro gf16m_neon_mul, which ensures a consistent performance across all kernel variants. A comprehensive summary of the techniques is presented in the following,

Table 5. ${\mathbb{GF}}_{16}$ matrix multiplication characteristics by rank.

Rank	Matrix Size	Mults	Adds (XORs)	SIMD Strategy	Optimization Notes
2	$2\times 2$	8	4	Two lanes	Two field multiplications per output; accumulation performed via XOR across two SIMD lanes.
4	$4\times 4$	64	48	Four lanes	All computations mapped to NEON vector operations; no scalar fallback or alignment penalties.

:

3.3. The AES Accelerator for CTR Mode

The SNOVA signature scheme employs AES-128 CTR mode to generate the pseudorandom values required during key generation and signature sampling [26]. In the original mupq framework, this was implemented using BearSSL’s [27] bit-sliced AES core, which prioritizes portability and side-channel resistance. However, due to its nonstandard key schedule and data layout, it is incompatible with ARMv8’s dedicated AES instructions, such as AESE and AESMC.

To address this, we replaced the BearSSL core with a custom AES-128 CTR implementation written in the ARMv8 assembly. This version uses the standard AES key schedule and adopts the CTR mode structure proposed by Gauravaram et al. [28], originally developed for GCM on ARM platforms. The implementation leverages hardware-supported AES instructions and NEON vector registers to achieve high-throughput encryption.

The instructions used for the operation are as shown in

Table 6. Instruction set used in the AES-CTR accelerator for SNOVA; Xt, Xs, Vt, Vd: destination register; Xn: address register; Vn, Vm: source vector registers; imm: immediate constant.

asm	Operands	Description	Operation
STP	Xt, Xs, [Xn,#imm]!	Store a pair of 64-bit general registers to memory (pre-indexed write-back)	[Xn,#imm] ← {Xt, Xs}
MOV	Xt, imm/Vd, Vn	Move immediately into a general-purpose register or copy an entire 128-bit vector register	Xt ← imm/Vd ← Vn
LDP	Vt, Vn, [Xn]	Load a pair of 128-bit SIMD registers from memory	{Vt, Vn} ← [Xn]
AESE	Vd, Vn	AES round: SubBytes + ShiftRows + AddRoundKey (no MixColumns) (state in Vd, round key in Vn)	Vd $\leftarrow AESRound(Vd\oplus Vn)$
AESMC	Vd, Vn	Apply AES MixColumns transformation to each column of the 128-bit state	Vd $\leftarrow MixColumns\left(Vn\right)$
ADD	Vd, Vn, Vm	Add two 128-bit vectors element-wise (unsigned)	Vd ← Vn + Vm

. All operations are performed using ARMv8 vector instructions, including LD1, AESE, AESMC, and ST1, minimizing memory latency while maximizing the throughput [9]. These instructions form the backbone of SNOVA’s CTR mode pseudorandom generator, fully contained within the NEON register file.

The description of Algorithm  6 is as follows. The entire AES CTR routine is written in assembly to maximize the instruction-level control and eliminate runtime branching. Registers x0–x3 are assigned to the output buffer, input length, nonce pointer, and round key pointer, respectively. The function prologue saves the frame pointer and the link register using STP.

Algorithm 6 AES-128 CTR mode accelerator.

Require:  Output buffer C, input length n (bytes), 16-byte nonce N, 176-byte round-key array $R[0\dots 10]$ Ensure:  Encrypted ciphertext C of n bytes   1: Initialization:                 ▹ set up constants   2: $B\leftarrow n/16$               ▹ number of 16-byte blocks   3: Load $R\left[0\right],\dots ,R\left[10\right]$ into NEON registers     ▹ preload round keys   4: $\mathtt{Ctr}\leftarrow N\parallel 0x01$              ▹ nonce  + initial counter   5: $\mathtt{Inc}\leftarrow 0x01$                 ▹ vector for counter++   6: for$i=0$ to $B-1$do              ▹ encrypt each block   7:     $T\leftarrow \mathtt{Ctr}$                     ▹ copy counter   8:     for $j=0$ to 9 do              ▹ 10 standard rounds   9:         $T\leftarrow \mathtt{AESE}(T,R[j\left]\right)$ 10:         $T\leftarrow \mathtt{AESMC}\left(T\right)$ 11:     end for 12:     $T\leftarrow \mathtt{AESE}(T,R[10\left]\right)$         ▹ final round (no MixColumns) 13:     Store T to $C\left[i\right]$                ▹ write ciphertext 14:     $\mathtt{Ctr}\leftarrow \mathtt{Ctr}+\mathtt{Inc}$                ▹ increment counter 15: end for

All 11 round keys (176 bytes) are preloaded into vector registers q6–q16. The counter block is initialized using v5 for the nonce and v1 for the increment, forming a 128-bit counter beginning with nonce ∥ 0x01. The increment is handled with ADD v5.16b, v5.16b, v1.16b for each 16-byte block.

For every block, the encryption process follows the standard AES-128 structure: ten rounds of AESE/AESMC, followed by a final round of AESE only [29]. The output is stored using a calculated offset in x4, via STR q0, [x0, x4, LSL #4]. The block loop progresses with ADD x4, x4, #1 and is controlled by CMP and B.GE.

All computations—including the counter increment, round transformations, and memory access—are performed within NEON registers. This allows for efficient pipelining, minimal latency, and high energy efficiency on ARMv8 cores.

According to the benchmarks by Gouvea et al. [28], AES-128 CTR on ARMv8 achieved 1.84 cycles per byte (cpb) on the Cortex-A57 and 1.19 cpb on the Apple A8X. This outperformed previous ARMv7 implementations using bit-sliced techniques, which required up to 9.8 cpb, showing an 8.1× performance gain when adopting native AES instructions.

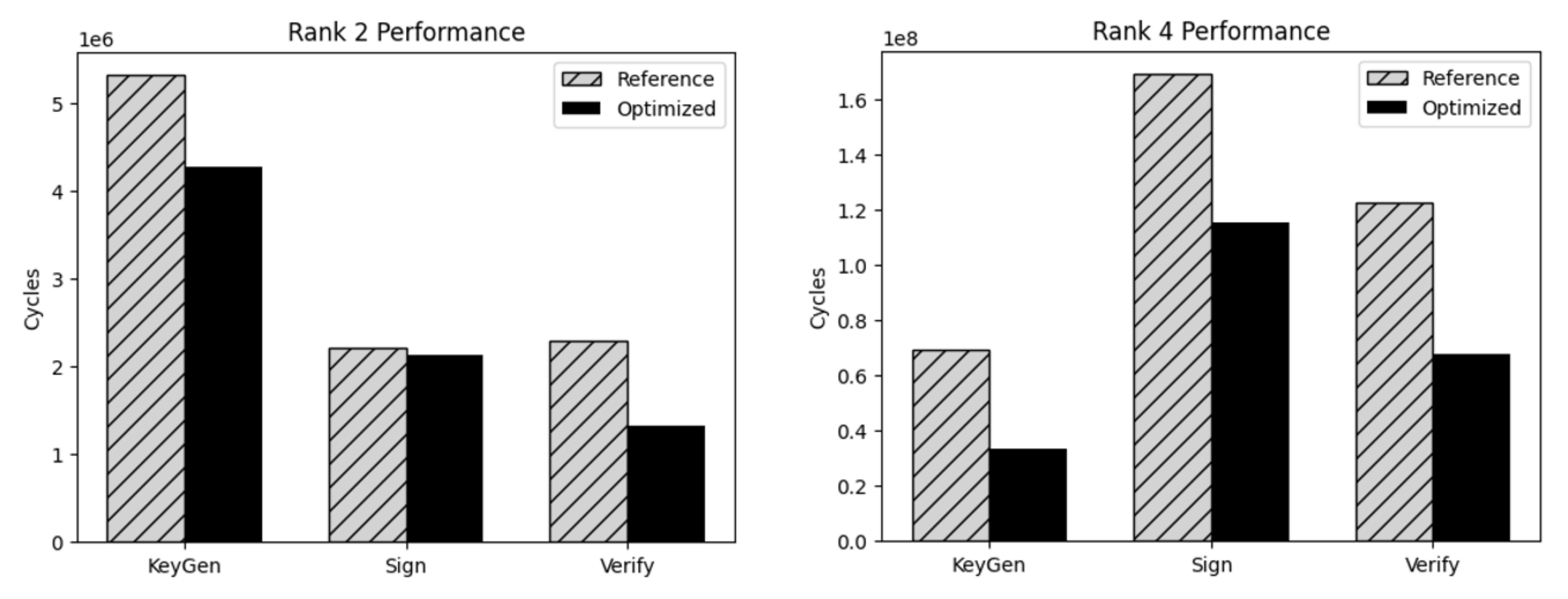
3.4. Overall Time Complexity and Performance Gains

This section analyzes the asymptotic and practical performance of SNOVA, comparing the baseline scalar implementation with our ARMv8/NEON-optimized variant. While the overall asymptotic complexity remains unchanged, our optimizations significantly reduce the constant factors in key routines.

• Baseline Cost of SNOVA

According to the round 2 specification [30], evaluating the central map involves

$$NP=m{n}^2{l}^3(l^2+l)\left(2{log}_2^{2}q+{log}_{2}q\right)$$

(7)

G${\mathrm{F}}_{16}$ operations, where $n=v+o$, $m=o$, and $q=2^4=16$. The dominant term is asymptotically $\Theta \left(n^2{l}^3\right)$, driven by cubic matrix multiplications over small field elements.

The key contributors to the runtime are

• Matrix addition: $O\left(l^2\right)$ byte-wise XORs;
• Matrix multiplication: $O\left(l^3\right)$ G${\mathrm{F}}_{16}$ multiply-and-add operations;
• Pseudorandom generation (PRNG): AES-CTR rounds with the cost proportional to the byte length.

• Constant-Factor Savings from NEON Kernels

While the asymptotic complexity remains unaffected, our ARMv8-optimized kernels offer significant constant-factor improvements in the performance. For rank 4 matrix additions, the SIMD implementation uses a single load, XOR, and store instructions to process 16 bytes at once—replacing 16 independent scalar operations. Similarly, rank 2 matrices are batched into groups of four, allowing a single NEON operation to handle what would otherwise require four separate scalar loops.

In the case of field multiplication, scalar multiply–add loops are replaced with vectorized broadcast and XOR operations using NEON lanes, enabling up to 16 field multiplications to be processed in parallel.

For AES-based pseudorandom generation, we replace the bit-sliced software implementation with native ‘AESE’ and ‘AESMC’ instructions. This reduces the cycle cost per byte from roughly 9.8 to 1.2, effectively removing PRNG from the critical path of key generation and signing.

• Interpretation

The asymptotic order remains unchanged. Despite aggressive SIMD optimization, SNOVA retains its theoretical complexity of $\Theta \left(n^2{l}^3\right)$. The improvements are entirely in the leading constant, making the algorithm faster but not asymptotically different.

SIMD efficiency depends on the matrix rank. Rank 4 matrices (16 bytes) map exactly to NEON’s 128-bit registers, enabling minimal instruction sequences and substantial speed-up. In contrast, rank 2 matrices require batching strategies, which still offer measurable improvements but with reduced parallelism efficiency.

The PRNG overhead is eliminated. The switch from bit-sliced AES to native AESE/AESMC instructions reduced the cost of AES-CTR significantly. As a result, the pseudorandom generator is no longer a bottleneck in key generation and signing routines.

In summary, the NEON-optimized implementation maintains the asymptotic computational profile of SNOVA while significantly improving the constant-factor performance across key routines. Quantitative performance data is discussed in the next section.

4. Evaluation

4.1. The Benchmarking Environment

To evaluate the performance of our optimized SNOVA implementation on the ARMv8 architecture, we conducted benchmarking using the mupq codebase, https://github.com/mupq (accessed on 2 July 2025), an extended framework derived from pqm4. Although originally developed for Cortex-M microcontrollers, mupq provides a consistent interface for benchmarking PQC schemes [31]. In this work, we integrated SNOVA into mupq to enable architecture-aware optimization and a fair performance comparison within a clean and dependency-free environment. In particular, the use of mupq allowed us to remove the OpenSSL [32] dependency present in the original SNOVA reference implementation, ensuring that the benchmarking results were not influenced by external library behavior or platform-specific optimizations [33].

We measured the cycle counts for three core digital signature operations: key generation (crypto_sign_keypair), signing (crypto_sign), and verification (crypto_sign_verify). These operations represent the entire cryptographic workload of SNOVA and are sufficient for evaluating overall efficiency.

All benchmarks were executed natively on an Apple M2 processor with 8 GB of RAM running macOS 13.3 under the default power management settings (Apple Inc., Cupertino, CA, USA). The implementation was compiled using GCC 14.0.3 with the following compiler flags: -O3 -Wall -Wextra -march=native -fomit-frame-pointer -Wno-sign-compare -Wno-unused-but-set-variable -Wno-unused-parameter -Wno-unused-result. Development was conducted in a Visual Studio Code ver. 1.101.2 environment.

To obtain cycle-accurate measurements, we employed a custom rdtsc() function based on Apple Silicon’s Performance Monitoring Unit (PMU). This routine dynamically loads the internal kperf framework and retrieves the CPMU_CORE_CYCLE value using kpc_get_thread_counters(). The code was adapted from an open-source implementation designed for Apple M1 systems, https://gist.github.com/dougallj/5bafb113492047c865c0c8cfbc930155 (accessed on 2 July 2025), and allows for precise low-level cycle counting without relying on external timers or OS-level profilers [9].

Figure 5 illustrates the cycle counts for key generation, signing, and verification under the ssk configuration. Each group compares the reference and optimized implementations. The results are presented for two representative parameter sets: snova-28-17-16-2-ssk for rank 2 and snova-60-10-16-4-ssk for rank 4.

4.2. The Performance Results

We evaluated the performance of our optimized SNOVA implementation using two types of parameter sets: the extended secret key (esk) and the seed-type secret key (ssk). A total of 18 parameter sets are defined in SNOVA, evenly divided between these two configurations.

The esk configuration includes precomputed data that accelerates the signing process. Although it introduces a slight overhead into key generation and verification, its design targets high-speed signature generation. In contrast, the ssk configuration is minimal and lightweight, designed for compact key representation and constrained environments.

The results for the esk configuration are summarized in

Table 7. The SNOVA esk parameter set on ARMv8: reference vs. optimized implementations.

Parameter	Work	Reference (Cycles)	Optimized (Cycles)
snova-24-5-16-4-esk	KeyGen	3,472,334	1,397,397
	Sign	15,763,938	10,701,647
	Verify	10,625,667	5,896,232
snova-28-17-16-2-esk	KeyGen	5,307,318	4,279,677
	Sign	2,206,219	2,122,220
	Verify	2,259,092	1,333,874
snova-37-8-16-4-esk	KeyGen	18,109,917	8,638,768
	Sign	59,246,538	41,764,038
	Verify	40,621,178	22,474,363
snova-43-25-16-2-esk	KeyGen	24,770,581	21,958,300
	Sign	7,277,210	7,020,197
	Verify	7,608,390	4,453,395
snova-60-10-16-4-esk	KeyGen	69,140,879	33,366,952
	Sign	168,716,148	115,326,826
	Verify	122,552,988	67,557,083
snova-61-33-16-2-esk	KeyGen	81,817,579	75,028,244
	Sign	17,997,496	17,381,776
	Verify	19,194,847	11,202,642

. The reference column refers to the SNOVA implementation included in mupq, which serves as the baseline for the performance comparison.

The largest performance gains were observed in the rank 4 configurations, which were perfectly aligned with the 128-bit NEON SIMD width. For instance, snova-24-5-16-4-esk achieved a 59.8% reduction in the key generation time, 32.1% in signing, and 44.5% in verification. Similar improvements were recorded for snova-37-8-16-4-esk and snova-60-10-16-4-esk, with the verification speed-ups reaching up to 44.9%.

These gains stem from the full SIMD coverage provided by the 16-element matrices in rank 4. Matrix operations are executed without padding, branching, or scalar fallback, resulting in the optimal pipeline and cache utilization.

The rank 2 configurations, while limited in matrix size, still benefit from our batch-based vectorization technique. For example, snova-28-17-16-2-esk showed an up to 41.0% improvement in verification and a 19.4% improvement in key generation. snova-61-33-16-2-esk and snova-43-25-16-2-esk similarly exhibited verification reductions of 41.6% and 41.5%, respectively. Although the signing gains remain modest (around 3–4%), this is expected given the reduced SIMD parallelism available for small matrix ranks.

Figure 6 presents the performance comparison of the ssk configuration for rank 2 and rank 4, based on the representative parameter sets snova-28-17-16-2-ssk and snova-60-10-16-4-ssk. Similar to the esk configuration, the most significant performance improvements are observed in the rank 4 instances, where the matrix dimensions align exactly with the 128-bit SIMD width of NEON.

The results for the esk configuration are summarized in

Table 8. SNOVA ssk parameter set on ARMv8: reference vs. optimized implementations.

Parameter	Operation	Reference (Cycles)	Optimized (Cycles)
snova-24-5-16-4-ssk	KeyGen	3,161,211	1,398,051
	Sign	15,533,328	10,813,110
	Verify	10,666,814	5,911,300
snova-28-17-16-2-ssk	KeyGen	5,315,622	4,266,349
	Sign	2,215,086	2,125,769
	Verify	2,296,711	1,332,643
snova-37-8-16-4-ssk	KeyGen	20,798,540	8,641,155
	Sign	59,903,820	41,767,317
	Verify	40,681,072	22,403,073
snova-43-25-16-2-ssk	KeyGen	25,068,870	21,989,730
	Sign	7,227,857	6,994,077
	Verify	7,591,994	4,449,776
snova-60-10-16-4-ssk	KeyGen	69,064,527	33,406,482
	Sign	168,849,241	115,361,855
	Verify	122,586,412	67,590,321
snova-61-33-16-2-ssk	KeyGen	82,114,717	75,171,728
	Sign	17,823,375	17,292,521
	Verify	19,263,216	11,203,544

. The largest gains were achieved in the rank 4 configurations. Key generation was accelerated by up to 58.5% (snova-24-5-16-4-ssk), signing by 32.6% (snova-24-5-16-4-ssk), and verification by as much as 45.5% (snova-24-5-16-4-ssk).

These improvements stem from the fact that $4\times 4$ matrices fully populate NEON vector registers, enabling the optimal instruction throughput and minimal overhead during XOR and multiplication operations.

The rank 2 parameters also showed meaningful improvements, especially in verification and key generation. For example, snova-28-17-16-2-ssk and snova-43-25-16-2-ssk demonstrated up to 42.0% and 41.4% gains in verification, respectively. Although rgw gains in signing were relatively minor, ranging from 3 to 5%, they remained consistent across parameter sets.

Overall, the results confirm that both Rank 2 and Rank 4 configurations benefit from our SIMD-aware optimization strategies, with the most substantial improvements naturally arising in higher-rank instances where SIMD lanes are fully utilized.

4.3. A Comparison with the NIST PQC Signature Schemes and Other State-of-the-Art Post-Quantum Signature Schemes on ARMv8

To provide a comprehensive perspective on the performance of our optimized SNOVA implementation, we compare it with major NIST post-quantum signature schemes, including CRYSTALS-Dilithium, Falcon, and SPHINCS+ (SHAKE variants only).

Table 9. Cycle-level performance comparison with NIST PQC signature schemes (measured on ARMv8 platform).

Scheme (Parameter Set)	KeyGen (Cycles)	Sign (Cycles)	Verify (Cycles)
Dilithium2	278,954	450,483	281,907
Dilithium3	482,104	2,465,069	440,805
Dilithium5	734,609	1,463,427	737,849
Falcon-512	37,959,474	10,617,704	132,067
Falcon-1024	108,091,196	23,159,283	281,777
SPHINCS+-shake-128f-simple	5,676,001	131,239,147	7,812,153
SPHINCS+-shake-128s-simple	359,032,336	2,725,259,275	2,763,529
SPHINCS+-shake-192f-simple	8,233,255	212,061,614	11,374,784
SPHINCS+-shake-192s-simple	524,022,262	4,710,044,154	3,872,933
SPHINCS+-shake-256f-simple	21,778,482	440,803,080	11,778,032
SPHINCS+-shake-256s-simple	346,536,078	4,124,025,081	5,538,012
SNOVA-24-5-16-4-esk	1,397,397	10,701,647	5,896,232
SNOVA-28-17-16-2-esk	4,279,677	2,122,220	1,333,874
SNOVA-37-8-16-4-esk	8,638,768	41,764,038	22,474,363
SNOVA-43-25-16-2-esk	21,958,300	7,020,197	4,453,395
SNOVA-60-10-16-4-esk	33,366,952	115,326,826	67,557,083
SNOVA-61-33-16-2-esk	75,028,244	17,381,776	11,202,642
SNOVA-24-5-16-4-ssk	1,398,051	10,813,110	5,911,300
SNOVA-28-17-16-2-ssk	4,266,349	2,125,769	1,332,643
SNOVA-37-8-16-4-ssk	8,641,155	41,767,317	22,403,073
SNOVA-43-25-16-2-ssk	21,989,730	6,994,077	4,449,776
SNOVA-60-10-16-4-ssk	33,406,482	115,361,855	67,590,321
SNOVA-61-33-16-2-ssk	75,171,728	17,292,521	11,203,544

presents the average cycle counts for key generation, signing, and verification operations across representative parameter sets. Both our esk and ssk variants are included for completeness.

Compared to lattice-based schemes such as Dilithium, SNOVA exhibits a significantly lower key generation cost and a comparable or better signing speed under mid-level security settings (e.g., SNOVA-28-17-16-2 vs. Dilithium2). While Falcon achieves extremely fast verification times, it does so at the cost of a much higher key generation overhead—two orders of magnitude larger than that for SNOVA variants. When compared to SPHINCS+ (a hash-based scheme), SNOVA shows a distinct advantage in its signing speed and memory efficiency. SPHINCS+ variants typically incur multi-hundred-million cycle costs for signing, especially in s-simple configurations.

These results demonstrate that SNOVA offers a competitive trade-off among speed, parameter flexibility, and hardware efficiency, making it particularly suited to constrained ARMv8-class devices. Our SIMD-based matrix optimization enables a wide spectrum of configurations, covering both high-security and low-latency requirements across different application scenarios.

Beyond the above cycle-level benchmarks, we also summarize recent state-of-the-art implementations of prominent post-quantum signature schemes on ARMv8 platforms.

Table 10. Cycle-level speed-ups of ARM-optimized PQC signature schemes.

Scheme	Keygen	Sign	Verify
Dilithium [20]	+43.8%	+113.2%	+41.9%
HAETAE [22]	+16–27%	+16–27%	+16–27%
Falcon [21]	—	+42%	+200–290%
SNOVA (this work)	+68.7%	+31.7%	+44.8%

highlights the cycle-level speed-ups achieved by Dilithium, HAETAE, Falcon, and our SNOVA implementation.

Specifically, CRYSTALS–Dilithium implementations on ARMv8 have focused on mitigating the bottlenecks in NTT and pointwise multiplication, leveraging NEON SIMD vectorization and register holding to minimize the memory access overhead. The benchmarks demonstrated up to a 2.6× speed-up in NTT computations, a 43.8% speed-up in key generation, a 113.2% speed-up in signing, and a 41.9% speed-up in verification, albeit with a slightly increased code size.

HAETAE utilized advanced NEON instructions (SQDMULH, SHSUB, SMULL) and data reordering strategies to achieve notable gains: an NTT speed-up of 3.07×, an INTT speed-up of 3.63×, and Montgomery multiplication improvements of up to 9.15×. These enhancements translated into approximately 16–27% improvements across the key generation, signing, and verification phases.

Falcon optimized the twiddle-factor tables to reduce the memory footprint and restructured the NTT stages using the Cooley–Tukey and Gentleman–Sande algorithms. Incorporating Barrett reduction and Montgomery multiplication reduced the modular reduction overhead further. The benchmarks show that Falcon achieved an up to 1.42× speed-up in signing and verification 3–3.9× faster than that with Dilithium.

In comparison, our SNOVA implementation employs rank-specific SIMD kernels for matrix operations over ${\mathrm{GF}}_{16}$, demonstrating an up to 68.7% reduction in the key generation time, a 31.7% reduction in the signing time, and a 44.8% reduction in the verification time relative to those at the baseline on Apple M2 processors. While the computational nature of SNOVA differs from that of polynomial-based schemes, our results match or exceed the improvements observed in other state-of-the-art ARMv8-optimized post-quantum signature schemes.

These findings reinforce SNOVA’s suitability for ARMv8-class platforms and its potential as a competitive, efficient option among post-quantum signature algorithms targeting constrained environments.

5. Discussion

While our vectorized implementation of SNOVA achieved substantial performance gains for rank 2 and rank 4 matrices, attempts to accelerate the rank 3 computations proved largely ineffective. The root cause lies in the intrinsic mismatch between the matrix size and the SIMD register width on ARMv8. Specifically, rank 3 matrices consist of nine field elements, requiring nine bytes of storage—just beyond the 64-bit (eight-byte) capacity of a general-purpose register and significantly underutilizing the 128-bit SIMD register. This dimensional irregularity results in inefficient SIMD packing and wasted register bandwidth regardless of whether NEON or scalar registers are used.

To partially address this, we designed a hybrid strategy that combined SIMD and scalar instructions. In this approach, the first eight bytes of each matrix are processed using NEON instructions, while the remaining one byte is handled separately using scalar instructions. This hybrid approach is illustrated in Figure 7 and formally described in Algorithm 7. The matrix operands are loaded into the lower 64 bits of the SIMD register via LDR, XORed using EOR, and stored back using STR. The ninth byte is then processed using scalar LDRB, EOR, and STRB instructions.

Despite the architectural soundness of this hybrid implementation, our benchmarks revealed no measurable speed-up compared to the baseline scalar version. The benefits of partial vectorization are effectively nullified by the overhead of separately handling the ninth byte. Furthermore, rank 3’s matrix size prevents the batching approach successfully employed in rank 2, where four matrices fit neatly into one SIMD register. In rank 3, batching would require nontrivial reorganization of the memory and loop structures, which would likely introduce more overhead than benefit.

Algorithm 7 Rank 3 matrix addition in ${\mathbb{GF}}_{16}$ on ARMv8.

Require:  $x0$: address of matrix A (nine bytes)   1:        $x1$: address of matrix B (nine bytes)   2:        $x2$: address of output matrix C Ensure:  $C=A\oplus B$   3: LDR d0, [x0]            ▹ load first eight bytes of A   4: LDR d1, [x1]            ▹ load first eight bytes of B   5: EOR v0.8b, v0.8b, v1.8b   ▹ XOR A and B (lower eight bytes)   6: STR d0, [x2]                ▹ store result to C   7: LDRB w3, [x0, #8]             ▹ load last byte of A   8: LDRB w4, [x1, #8]             ▹ load last byte of B   9: EOR w3, w3, w4               ▹ XOR final bytes 10: STRB w3, [x2, #8]                ▹ store to C

Consequently, we opted not to include rank 3 in our final performance evaluations. This result highlights a broader insight: SIMD acceleration is highly sensitive to the data shape and alignment. Efficient vectorization requires not only hardware capability but also a matching computational granularity. In the case of SNOVA, rank 2 and rank 4 matrices meet these criteria, while rank 3 falls into an unfortunate middle ground where neither scalar nor vector approaches dominate.

In addition, the limitation observed with the rank 3 matrices stems from the mismatch between the 9-byte data block and the 16-byte NEON SIMD register width. This results in underutilization of the register lanes, requiring either padding (which increases the memory footprint and can lead to unnecessary load/store cycles) or hybrid scalar handling (which adds a branching and instruction overhead). Both approaches introduce additional memory and execution complexity, negating the potential benefits from parallelism.

As a potential direction for future work, we plan to investigate advanced data packing strategies, including grouping multiple rank 3 matrices into larger blocks to amortize the scalar tail overhead. Another possibility involves exploring padding schemes where additional dummy bytes are inserted to align the data with the SIMD register boundaries, potentially combined with runtime masking techniques. Finally, emerging ARM architectures with wider SIMD registers or support for variable-length vectors (e.g., ARM SVE) could offer new avenues for vectorization of irregular data structures such as rank 3 matrices.

Beyond the Apple M2 platform, our optimization strategies—particularly those leveraging NEON SIMD instructions for matrix operations—are generally applicable to other ARMv8-based processors such as the Cortex-A series. Since NEON is a standard feature of the ARMv8-A architecture, we expect that the fundamental vectorization techniques (e.g., batched matrix addition, SIMD-driven finite field arithmetic) will translate directly, though specific cycle-level improvements may vary depending on processor features such as the cache size, memory bandwidth, and pipeline depth. Investigating the performance portability across multiple ARMv8 cores remains an important direction for future work.

Finally, we acknowledge that while our low-level SIMD optimizations yield significant performance gains, they may also introduce potential side-channel vulnerabilities such as timing or power analysis risks. Fully assessing and mitigating such risks lie beyond the scope of this work but represent an important avenue for future research to ensure cryptographic robustness against physical and microarchitectural attacks.

6. Conclusions

This paper presented an optimized implementation of the SNOVA digital signature scheme on ARMv8 architectures. By exploiting the platform’s SIMD capabilities—particularly through NEON vector instructions—we accelerated performance-critical operations including key generation, signing, and verification without compromising the compatibility with existing parameter sets.

Our approach targeted both the high-level and low-level components of the SNOVA implementation. At the low level, we designed rank-aware SIMD kernels for matrix addition and multiplication over ${\mathbb{GF}}_{16}$, maximizing the lane utilization for rank 4 matrices and applying batch-based strategies to rank 2. At the high level, we restructured core routines such as gen_F, gen_P22, and sign_digest_core to accommodate contiguous memory layouts, enabling effective invocation of these SIMD kernels. This two-layered design ensures that the hardware-level optimizations are fully exposed at the software level, bridging the architectural features with algorithmic needs.

The optimized implementation supports 12 SNOVA parameter sets (after excluding rank 3 instances) across both the esk and ssk configurations. Empirical benchmarks on the Apple M2 (ARMv8) show that for the rank 4 parameters, key generation was accelerated by up to 68.7%, signing by 31.7%, and verification by 44.8%. Even in rank 2 settings, the performance improved by up to 19.7% in key generation and 41.9% in verification, confirming the effectiveness of fine-grained batching.

Our findings affirm that SIMD-centric optimization is a viable and impactful strategy for post-quantum schemes in constrained environments. The demonstrated gains make SNOVA more practical for real-world deployment on mobile, IoT, and edge platforms scenarios where both cryptographic strength and performance are imperative. Future work may investigate rank-generalized vectorization and the broader applicability to similar multivariate schemes.