Hybrid Stochastic–Information Gap Decision Theory Method for Robust Operation of Water–Energy Nexus Considering Leakage
Abstract
1. Introduction
- A cooperative optimization model is proposed to jointly optimize the operation of the WEN considering the uncertainties from renewable generation, electrical demand, water demand, and potential leakage in the WDN. To the best of the authors’ knowledge, this is the first optimal operation model of WEN taking the impacts of water leakage into account, which enhances the reliability and robustness of the proposed model.
- Combining the advantages of both stochastic optimization and IGDT, a hybrid stochastic–IGDT approach is proposed to handle both the probabilistic uncertainties and potential leakage in the cooperative operation model of the WEN.
- A risk-averse strategy of the proposed hybrid stochastic–IGDT model of the WEN is applied to solve the joint operational decision problem of the WEN to provide necessary robustness to the operator, and a linearization method is presented to solve the proposed model efficiently.
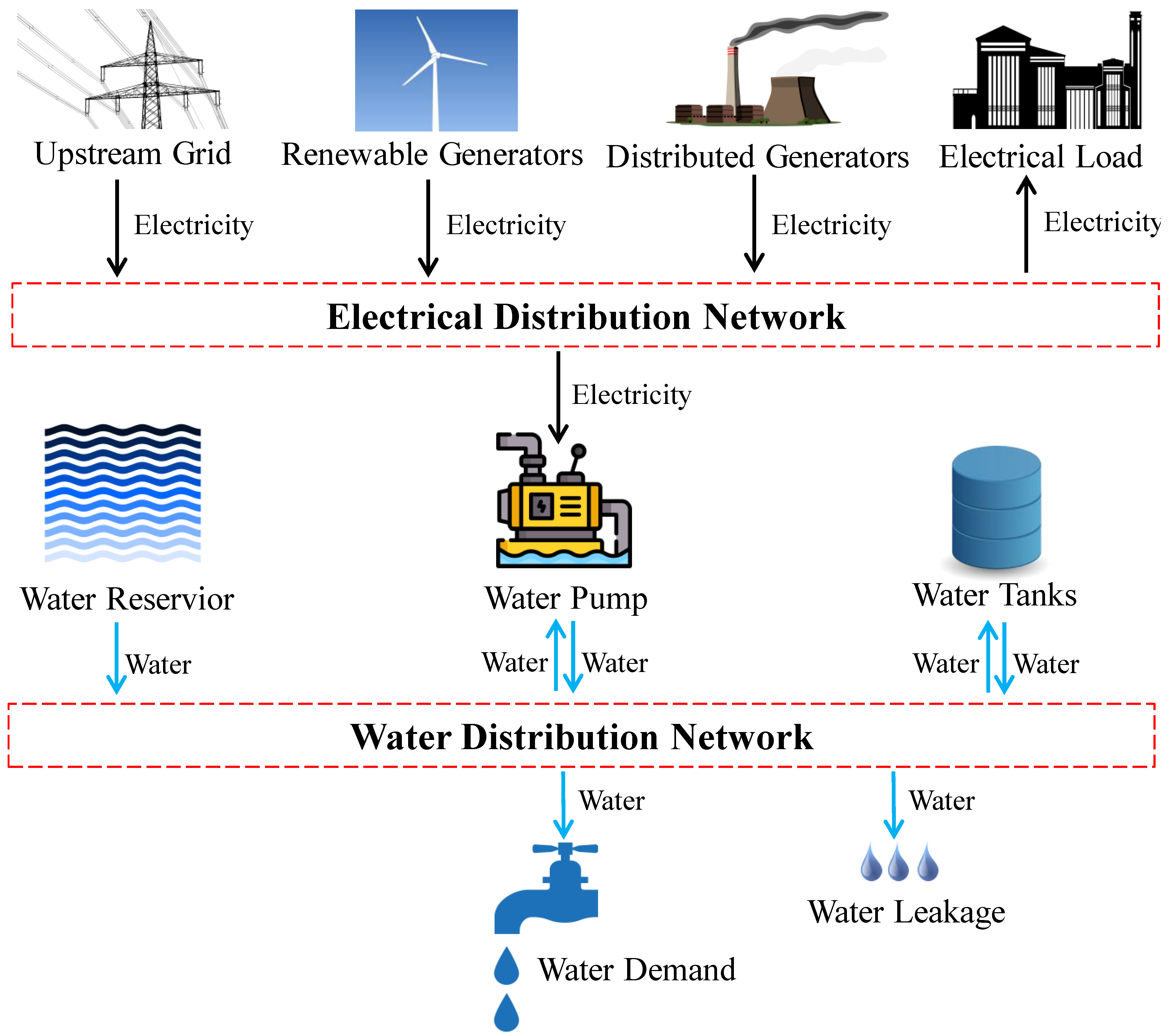
2. Cooperative Optimization Model of Water–Energy Nexus
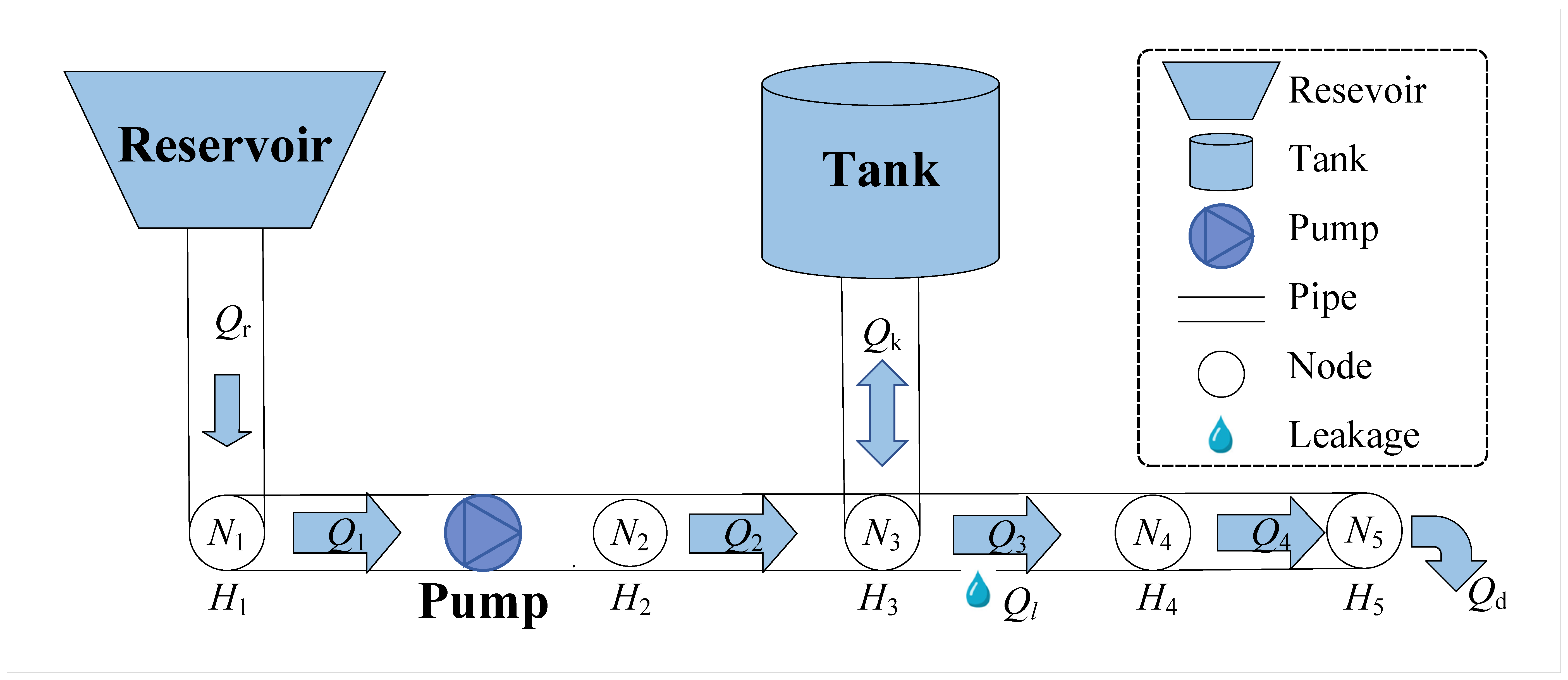
2.1. Configuration of Water Distribution System
2.1.1. Reservoir Constraints
2.1.2. Water Tank Constraints
2.1.3. Pumps Constraints
2.1.4. Node and Pipeline Constraints
2.1.5. Water Leakage Constraints
2.2. Power Distribution Network Constraints
2.2.1. Power Flow Constraints
2.2.2. Distributed Generator Constraints
2.3. Optimal Operation Model of WEN
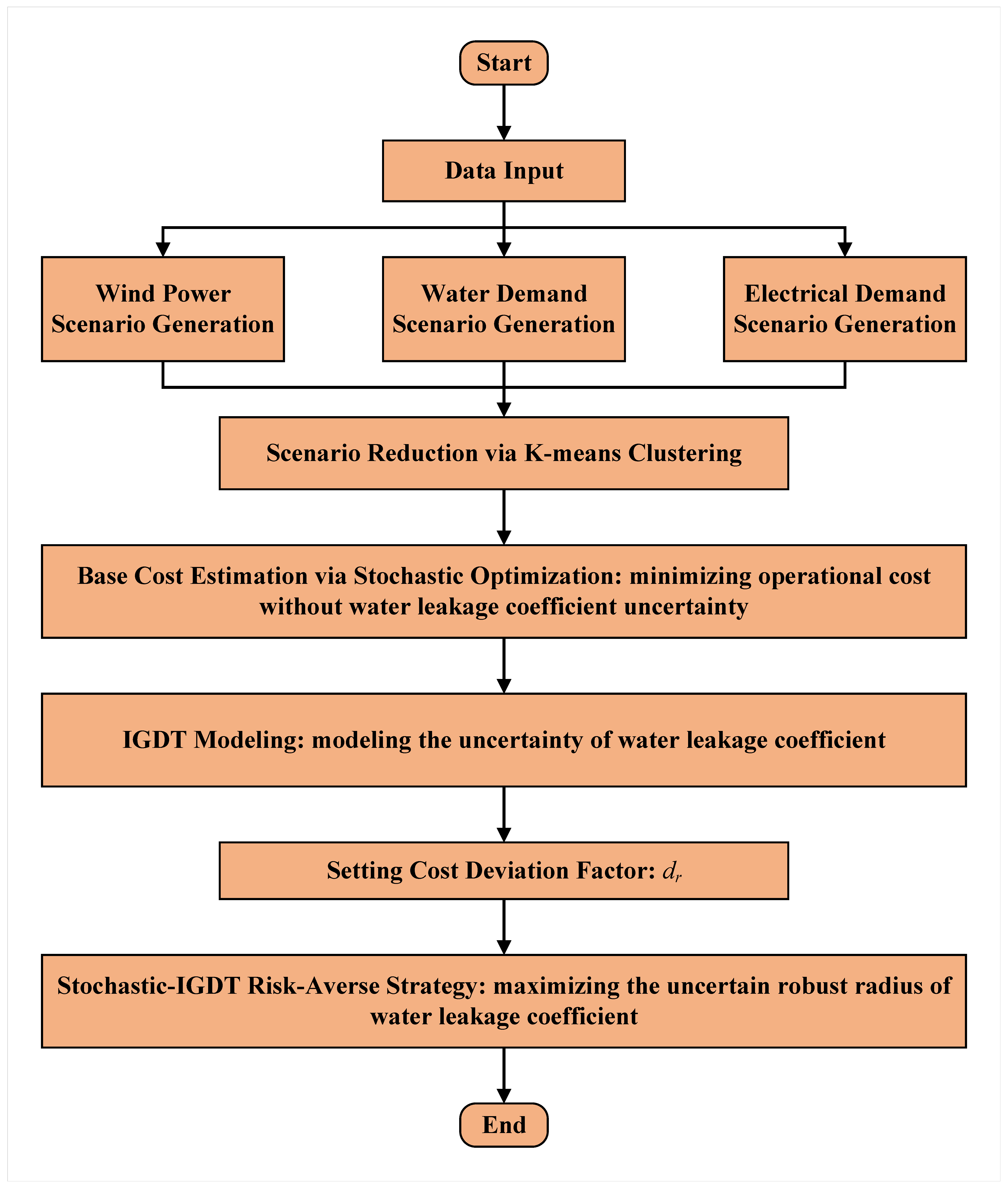
3. Hybrid Stochastic–IGDT Model of WEN Considering Leakage
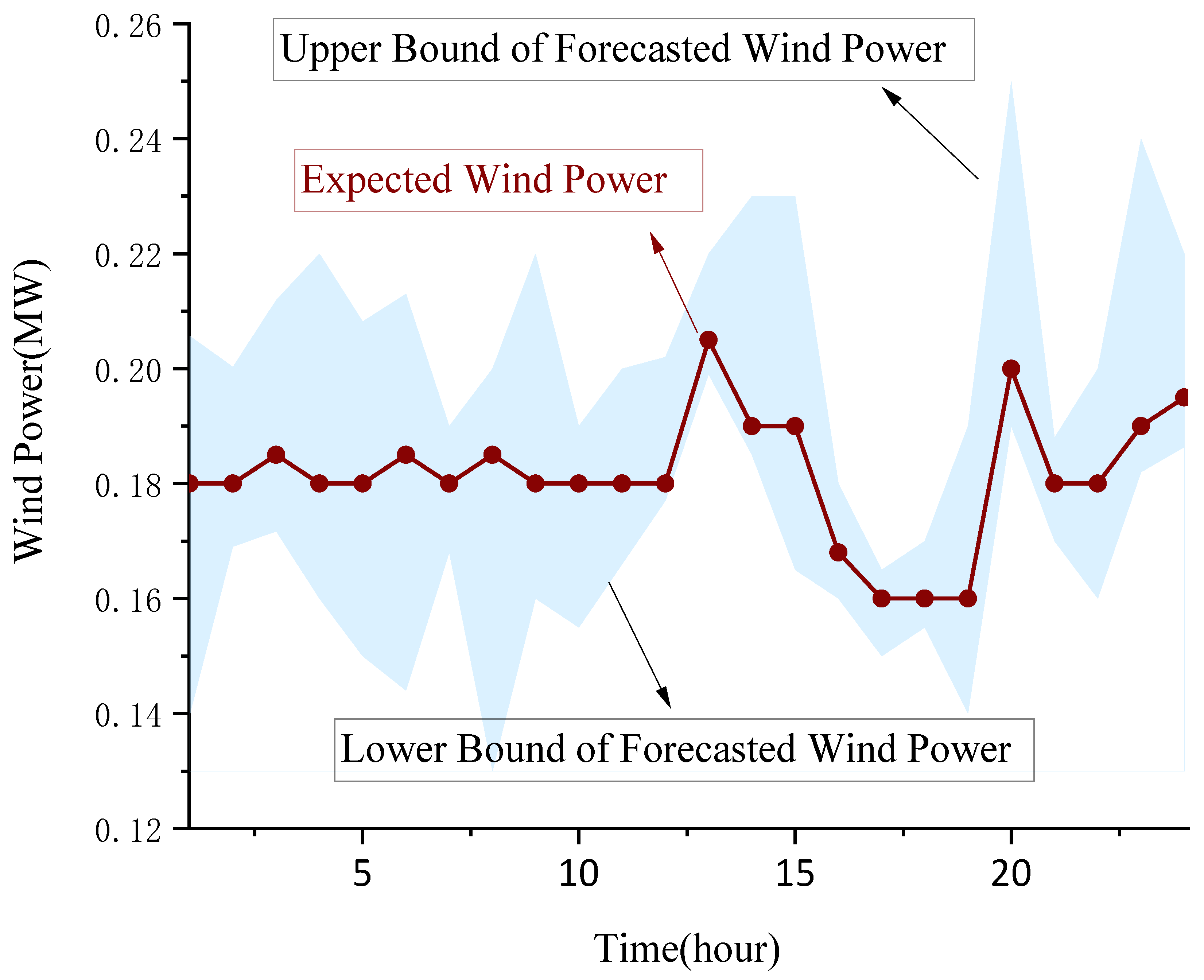
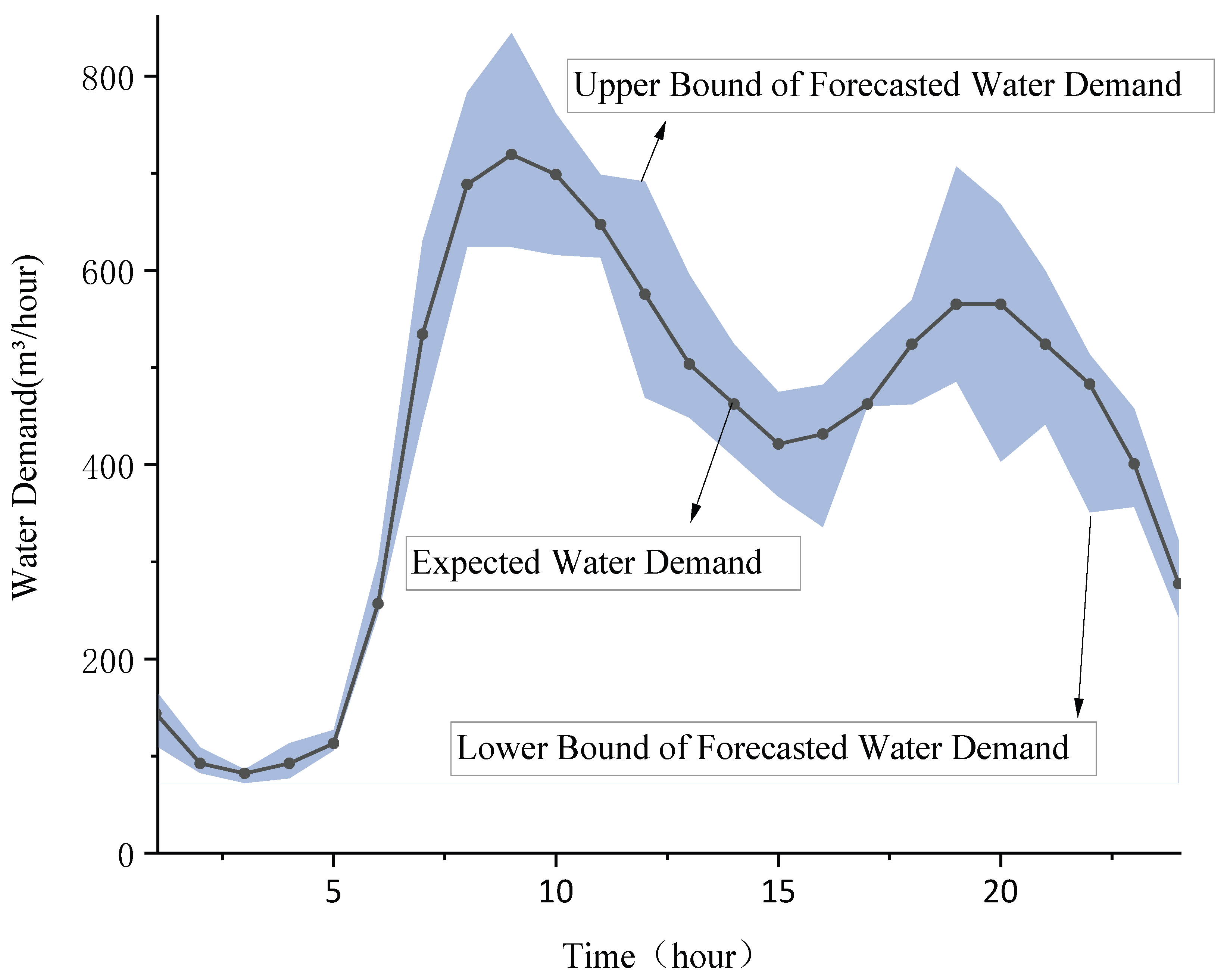
3.1. Probabilistic Uncertainty Modeling and Scenario Generation
3.2. Stochastic Optimization Model
3.3. Hybrid Stochastic–IGDT Optimization
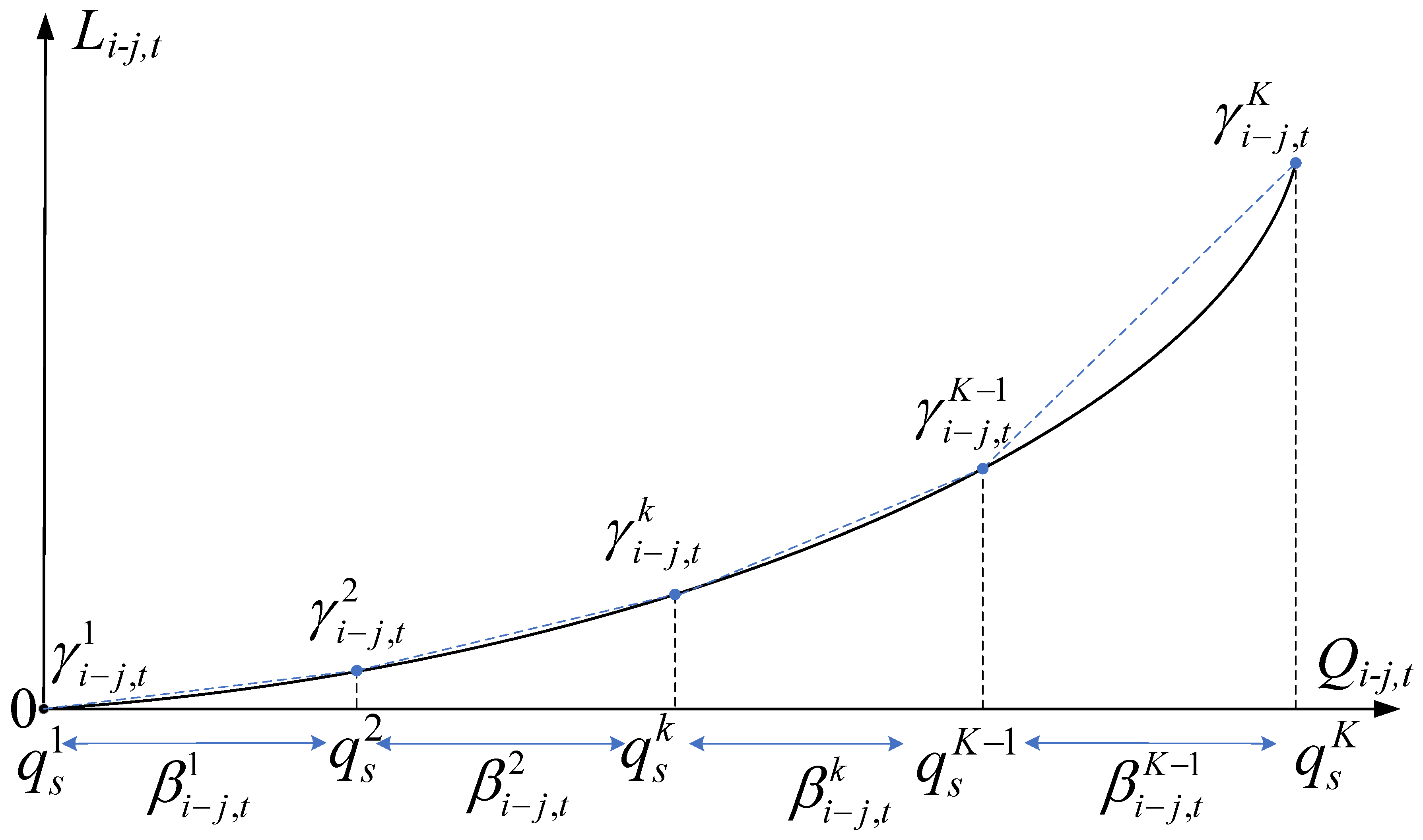
4. Linearization and Solution Method of Hybrid Stochastic–IGDT Model
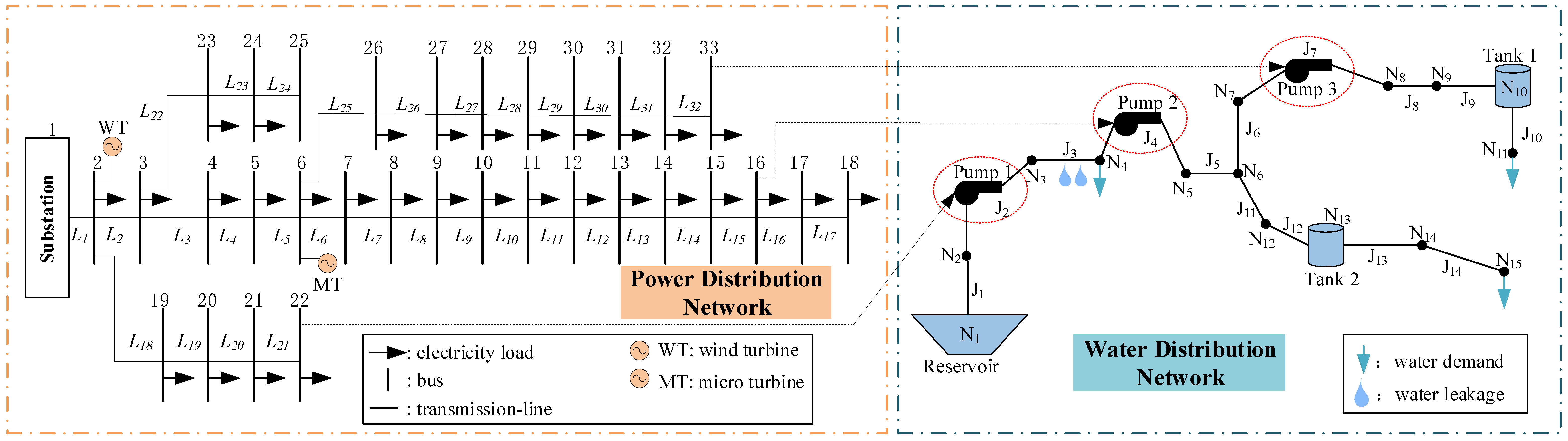
5. Simulation and Discussions
5.1. Key Parameters in Case Studies
5.2. Case Study Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Set of scheduling time intervals | |
| Set of nodes in the water distribution network | |
| Set of reservoir nodes in the water distribution network | |
| Set of water tank nodes in the water distribution network | |
| Set of pipes in the water distribution network | |
| Set of pipes without pumps in the water distribution network | |
| Set of pipes with pumps in the water distribution network (equivalent to the set of pumps) | |
| Set of nodes in the electrical distribution network | |
| Set of branches in the electrical distribution network | |
| Set of distributed generators | |
| Set of distributed generators connected to node i in the electrical distribution network | |
| Set of renewable generation units (e.g., wind turbines) | |
| Set of renewable generation units installed at node i in the electrical distribution network | |
| Set of pumps | |
| Set of pumps connected to node i in the electrical distribution network | |
| Water head at node i in the water distribution network at time t | |
| Elevation head at node i in the water distribution network at time t | |
| Lower bound of water head at node i in the water distribution network | |
| Upper bound of water head at node i in the water distribution network | |
| Water flow from node k to node i at time t | |
| Water flow from the reservoir to node i at time t | |
| Water demand at node i in the water distribution network at time t | |
| Water flow between the water tank and node i (inflow or outflow) at time t | |
| Flow rate of water tank k at time t | |
| Maximum flow rate of water tank k | |
| Stored water volume in water tank k at time t | |
| Lower bound of stored water volume in water tank k | |
| Upper bound of stored water volume in water tank k | |
| Duration of each time interval | |
| Head added by pump u at time t | |
| Speed of pump u at time t | |
| Pump - specific parameters of pump u (used in the head - flow model) | |
| Pump-specific parameters of pump u (used in the power-flow model) | |
| Electrical power consumption of pump u at time t | |
| Active power output of distributed generator d at time t | |
| Reactive power output of distributed generator d at time t | |
| Active power output of wind turbine w at time t | |
| Active power demand of electrical loads (excluding pumps) at node i in the electrical distribution network at time t | |
| Reactive power demand of electrical loads (excluding pumps) at node i in the electrical distribution network at time t | |
| Active power flow from node i to node j in the electrical distribution network at time t |
| Reactive power flow from node i to node j in the electrical distribution network at time t | |
| Upper limit of active power flow in branch of the electrical distribution network | |
| Upper limit of reactive power flow in branch of the electrical distribution network | |
| Resistance of branch in the electrical distribution network | |
| Reactance of branch in the electrical distribution network | |
| Voltage at node i in the electrical distribution network at time t | |
| Rated voltage at the root bus of the electrical distribution network | |
| Lower limit of voltage in the electrical distribution network | |
| Upper limit of voltage in the electrical distribution network | |
| Price of electricity procurement from the upstream grid at time t | |
| Generation cost coefficients of distributed generator d | |
| Purchase price per cubic meter of water from the reservoir | |
| Actual output power of wind turbine w at time t | |
| Predicted or expected output power of wind turbine w at time t | |
| Forecast error of wind generation of wind turbine w at time t | |
| Actual electrical load power at node i in the electrical distribution network at time t | |
| Predicted or expected electrical load power at node i in the electrical distribution network at time t | |
| Forecast error of electrical load power at node i in the electrical distribution network at time t | |
| Actual water demand at node i in the water distribution network at time t | |
| Predicted or expected water demand at node i in the water distribution network at time t | |
| Forecast error of water demand at node i in the water distribution network at time t | |
| Leakage coefficient of pipes in the water distribution network | |
| Uncertainty set of the leakage coefficient | |
| Estimated leakage coefficient | |
| Uncertainty horizon parameter (uncertainty radius in IGDT) | |
| Robustness factor set by the WEN operator | |
| Expected operational cost of the WEN in the stochastic optimization model | |
| Optimal solution of the stochastic optimization model (when minimizing the expected operational cost) | |
| Actual operational cost of the WEN considering leakage uncertainty | |
| Probability of scenario s | |
| Water head loss in pipe in the water distribution network at time t | |
| Resistance coefficient of pipe in the water distribution network | |
| Friction coefficient of pipe in the water distribution network | |
| Length of pipe in the water distribution network | |
| Diameter of pipe in the water distribution network | |
| Cross - sectional area of pipe in the water distribution network | |
| g | Acceleration due to gravity |
| Leakage rate of pipe in the water distribution network at time t | |
| Leakage exponent (exponent used to describe the relationship between leakage rate and water head) | |
| Active power exchange between the upstream grid and the electrical distribution network at time t | |
| Reactive power exchange between the upstream grid and the electrical distribution network at time t | |
| Upper limit of active power output of distributed generator d | |
| Upper limit of reactive power output of distributed generator d | |
| Lower limit of reactive power output of distributed generator d | |
| Binary variable used for the linearization of the water head loss constraint in the water distribution network (related to pipe , time t, and segment k) | |
| Continuous variable used for the linearization of the water head loss constraint in the water distribution network (related to pipe , time t, and segment k) | |
| Sampling value of water flow for the linearization of the water head loss function of pipe in the water distribution network | |
| Linear approximation of water head loss in pipe at time t in the water distribution network | |
| Continuous variable related to pump u, time t, and coordinates for the linearization of pump-related constraints | |
| Binary variable related to pump u, time t, and coordinates for the linearization of pump-related constraints (representing the upper-left triangle vertex) | |
| Binary variable related to pump u, time t, and coordinates for the linearization of pump-related constraints (representing the lower - right triangle vertex) | |
| Sampling value of pump u’s water flow for the linearization of pump - related constraints | |
| Sampling value of pump u’s speed for the linearization of pump - related constraints | |
| Linear approximation of the head gain of pump u at time t | |
| Linear approximation of the power consumption of pump u at time t | |
| CVaR | Conditional Value-at-Risk |
| DG | Distributed generator |
| DRO | Distributionally robust optimization |
| EDN | Electrical distribution network |
| IGDT | Information gap decision theory |
| IES | Integrated energy system |
| LP | Linear programming |
| MINLP | Mixed - integer nonlinear programming |
| NLP | Nonlinear programming |
| RO | Robust optimization |
| SO | Stochastic optimization |
| WDN | Water distribution network |
| WEN | Water - Energy Nexus |
References
- Birol, F. World Energy Outlook 2016; IEA: Paris, France, 2016. [Google Scholar]
- Denig-Chakroff, D. Reducing Electricity Used for Water Production: Questions State Commissions Should Ask Regulated Utilities; National Regulatory Research Institute: Columbus, OH, USA, 2008. [Google Scholar]
- Tan, X.; Abedi, M.; Klausner, J.F.; Bénard, A. Modeling and experimental validation of light-splitting semi-transparent solar water heater using NIR cut-off film as the rooftop of a greenhouse for arid regions. Appl. Energy 2024, 368, 123489. [Google Scholar] [CrossRef]
- Busby, J.W.; Baker, K.; Bazilian, M.D.; Gilbert, A.Q.; Grubert, E.; Rai, V.; Rhodes, J.D.; Shidore, S.; Smith, C.A.; Webber, M.E. Cascading risks: Understanding the 2021 winter blackout in Texas. Energy Res. Soc. Sci. 2021, 77, 102106. [Google Scholar] [CrossRef]
- Gao, L.; Han, X.; Chen, X.; Liu, B.; Li, Y. The Spring Drought in Yunnan Province of China: Variation Characteristics, Leading Impact Factors, and Physical Mechanisms. Atmosphere 2023, 14, 294. [Google Scholar] [CrossRef]
- Oikonomou, K.; Parvania, M. Optimal coordinated operation of interdependent power and water distribution systems. IEEE Trans. Smart Grid 2020, 11, 4784–4794. [Google Scholar] [CrossRef]
- Zamzam, A.S.; Dall’Anese, E.; Zhao, C.; Taylor, J.A.; Sidiropoulos, N.D. Optimal Water–Power Flow-Problem: Formulation and Distributed Optimal Solution. IEEE Trans. Control Netw. Syst. 2019, 6, 37–47. [Google Scholar] [CrossRef]
- Kernan, R.; Liu, X.; McLoone, S.; Fox, B. Demand side management of an urban water supply using wholesale electricity price. Appl. Energy 2017, 189, 395–402. [Google Scholar] [CrossRef]
- Alnahhal, Z.; Shaaban, M.F.; Hamouda, M.A.; Majozi, T.; Bardan, M.A. A Water-Energy Nexus Approach for the Co-Optimization of Electric and Water Systems. IEEE Access 2023, 11, 28762–28770. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.; Turitsyn, K. Micro Water-Energy Nexus: Optimal Demand-Side Management and Quasi-Convex Hull Relaxation. IEEE Trans. Control Netw. Syst. 2019, 6, 1313–1322. [Google Scholar] [CrossRef]
- Li, Q.; Yu, S.; Al-Sumaiti, A.; Turitsyn, K. Modeling and Co-Optimization of a Micro Water-Energy Nexus for Smart Communities. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Sarajevo, Bosnia and Herzegovina, 21–25 October 2018; pp. 1–5. [Google Scholar]
- Fang, S.; Wang, C.; Lin, Y.; Zhao, C. Optimal Energy Scheduling and Sensitivity Analysis for Integrated Power–Water–Heat Systems. IEEE Syst. J. 2021, 16, 5176–5187. [Google Scholar] [CrossRef]
- Yu, D.; Li, Z.; Fan, S.; Sun, T. Optimal management of an energy-water-carbon nexus employing carbon capturing and storing technology via downside risk constraint approach. J. Clean. Prod. 2023, 418, 138168. [Google Scholar] [CrossRef]
- Zhao, P.; Gu, C.; Cao, Z.; Ai, Q.; Xiang, Y.; Ding, T.; Lu, X.; Chen, X.; Li, S. Water-energy nexus management for power systems. IEEE Trans. Power Syst. 2020, 36, 2542–2554. [Google Scholar] [CrossRef]
- Zhao, P.; Li, S.; Hu, P.J.H.; Gu, C.; Lu, S.; Ding, S.; Cao, Z.; Xie, D.; Xiang, Y. Blockchain-Based Water-Energy Transactive Management With Spatial-Temporal Uncertainties. IEEE Trans. Smart Grid 2023, 14, 2903–2920. [Google Scholar] [CrossRef]
- Wang, C.; Gao, N.; Wang, J.; Jia, N.; Bi, T.; Martin, K. Robust Operation of a Water-Energy Nexus: A Multi-Energy Perspective. IEEE Trans. Sustain. Energy 2020, 11, 2698–2712. [Google Scholar] [CrossRef]
- Audits, E.W. Water Loss Control for Public Water Systems; US EPA: Washington, DC, USA, 2013. [Google Scholar]
- Rogers, D. Leaking water networks: An economic and environmental disaster. Procedia Eng. 2014, 70, 1421–1429. [Google Scholar] [CrossRef]
- Valek, A.M.; Sušnik, J.; Grafakos, S. Quantification of the urban water-energy nexus in México City, México, with an assessment of water-system related carbon emissions. Sci. Total Environ. 2017, 590, 258–268. [Google Scholar] [CrossRef]
- Liemberger, R.; Wyatt, A. Quantifying the global non-revenue water problem. Water Supply 2019, 19, 831–837. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, Z. Co-Optimization of Water-Energy Nexus Systems and Challenges. Eng. Proc. 2024, 69, 54. [Google Scholar]
- Powell, W.B. A unified framework for stochastic optimization. Eur. J. Oper. Res. 2019, 275, 795–821. [Google Scholar] [CrossRef]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 283. [Google Scholar]
- Chow, Y.; Tamar, A.; Mannor, S.; Pavone, M. Risk-sensitive and robust decision-making: A cvar optimization approach. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Jordehi, A.R.; Javadi, M.S.; Shafie-khah, M.; Catalão, J.P. Information gap decision theory (IGDT)-based robust scheduling of combined cooling, heat and power energy hubs. Energy 2021, 231, 120918. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, S.; Taha, A.F.; Summers, T.H. Optimal pump control for water distribution networks via data-based distributional robustness. IEEE Trans. Control Syst. Technol. 2022, 31, 114–129. [Google Scholar] [CrossRef]
- Alhazmi, M.; Dehghanian, P.; Nazemi, M.; Oikonomou, K. Uncertainty-informed operation coordination in a water-energy nexus. IEEE Trans. Ind. Inform. 2022, 19, 6439–6449. [Google Scholar] [CrossRef]
- Rodriguez-Garcia, L.; Hosseini, M.M.; Mosier, T.M.; Parvania, M. Resilience Analytics for Interdependent Power and Water Distribution Systems. IEEE Trans. Power Syst. 2022, 37, 4244–4257. [Google Scholar] [CrossRef]
- Liou, C.P. Limitations and proper use of the Hazen-Williams equation. J. Hydraul. Eng. 1998, 124, 951–954. [Google Scholar] [CrossRef]
- Schwaller, J.; van Zyl, J.V. Modeling the pressure-leakage response of water distribution systems based on individual leak behavior. J. Hydraul. Eng. 2015, 141, 04014089. [Google Scholar] [CrossRef]
- Sousa, J.; Martinho, N.; Muranho, J.; Marques, A.S. Leakage Calibration in Water Distribution Networks with Pressure-Driven Analysis: A Real Case Study. Environ. Sci. Proc. 2020, 2, 59. [Google Scholar]
- McQueen, D.H.; Hyland, P.R.; Watson, S.J. Monte Carlo simulation of residential electricity demand for forecasting maximum demand on distribution networks. IEEE Trans. Power Syst. 2004, 19, 1685–1689. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Ghatak, S.R.; Acharjee, P. Multi-Scenario Based Bi-Level Coordinated Planning of Active Distribution System Under Uncertain Environment. IEEE Trans. Ind. Appl. 2020, 56, 850–863. [Google Scholar] [CrossRef]
- Ekmekcioğlu, Ö.; Başakın, E.E.; Özger, M. Discharge coefficient equation to calculate the leakage from pipe networks. J. Inst. Sci. Technol. 2020, 10, 1737–1746. [Google Scholar] [CrossRef]
- Mohammadi-Ivatloo, B.; Zareipour, H.; Amjady, N.; Ehsan, M. Application of information-gap decision theory to risk-constrained self-scheduling of GenCos. IEEE Trans. Power Syst. 2013, 28, 1093–1102. [Google Scholar] [CrossRef]
- Lin, M.H.; Carlsson, J.G.; Ge, D.; Shi, J.; Tsai, J.F. A review of piecewise linearization methods. Math. Probl. Eng. 2013, 2013, 101376. [Google Scholar] [CrossRef]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Deliv. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Oikonomou, K.; Parvania, M. Optimal Coordination of Water Distribution Energy Flexibility with Power Systems Operation. IEEE Trans. Smart Grid 2019, 10, 1101–1110. [Google Scholar] [CrossRef]
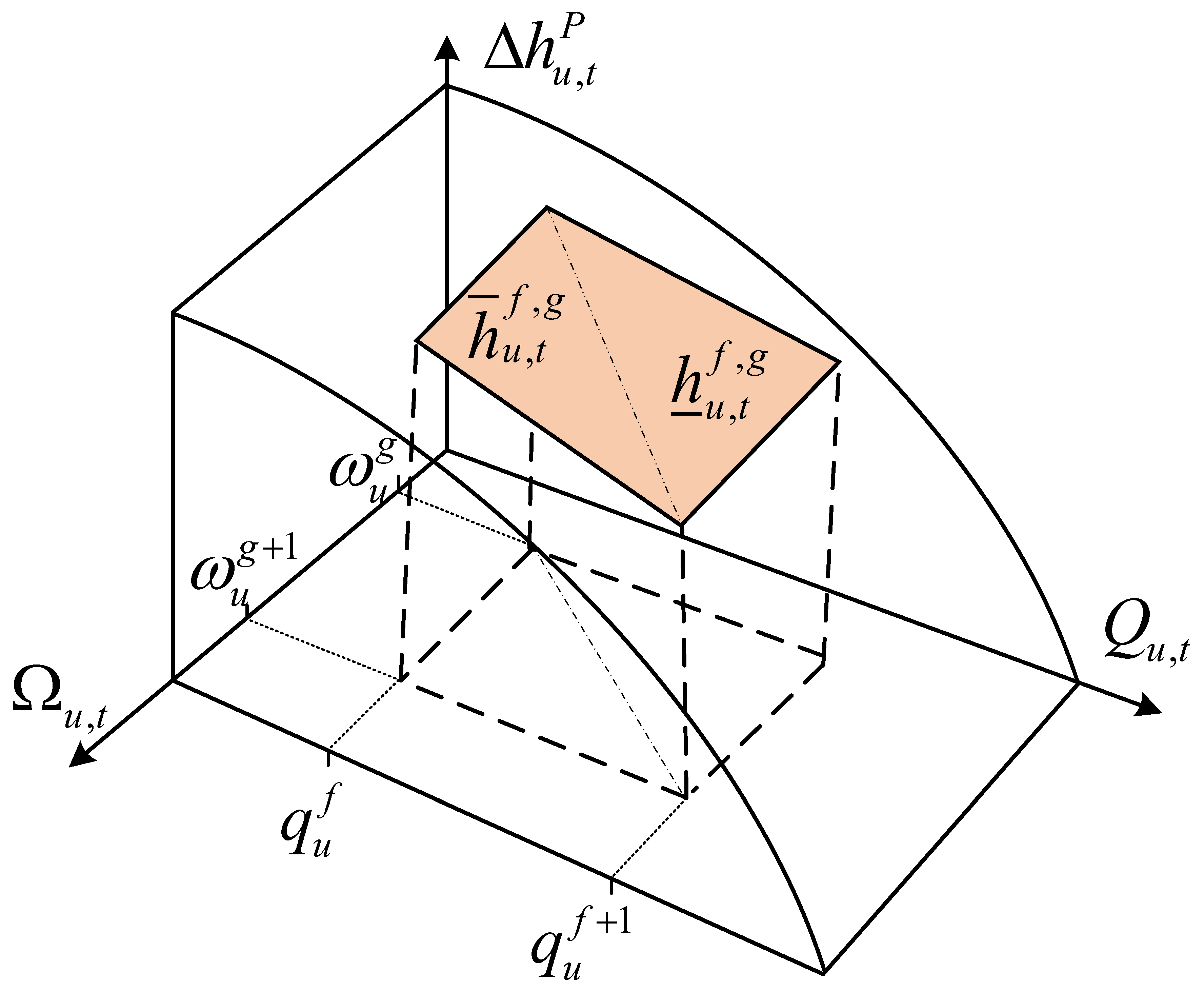
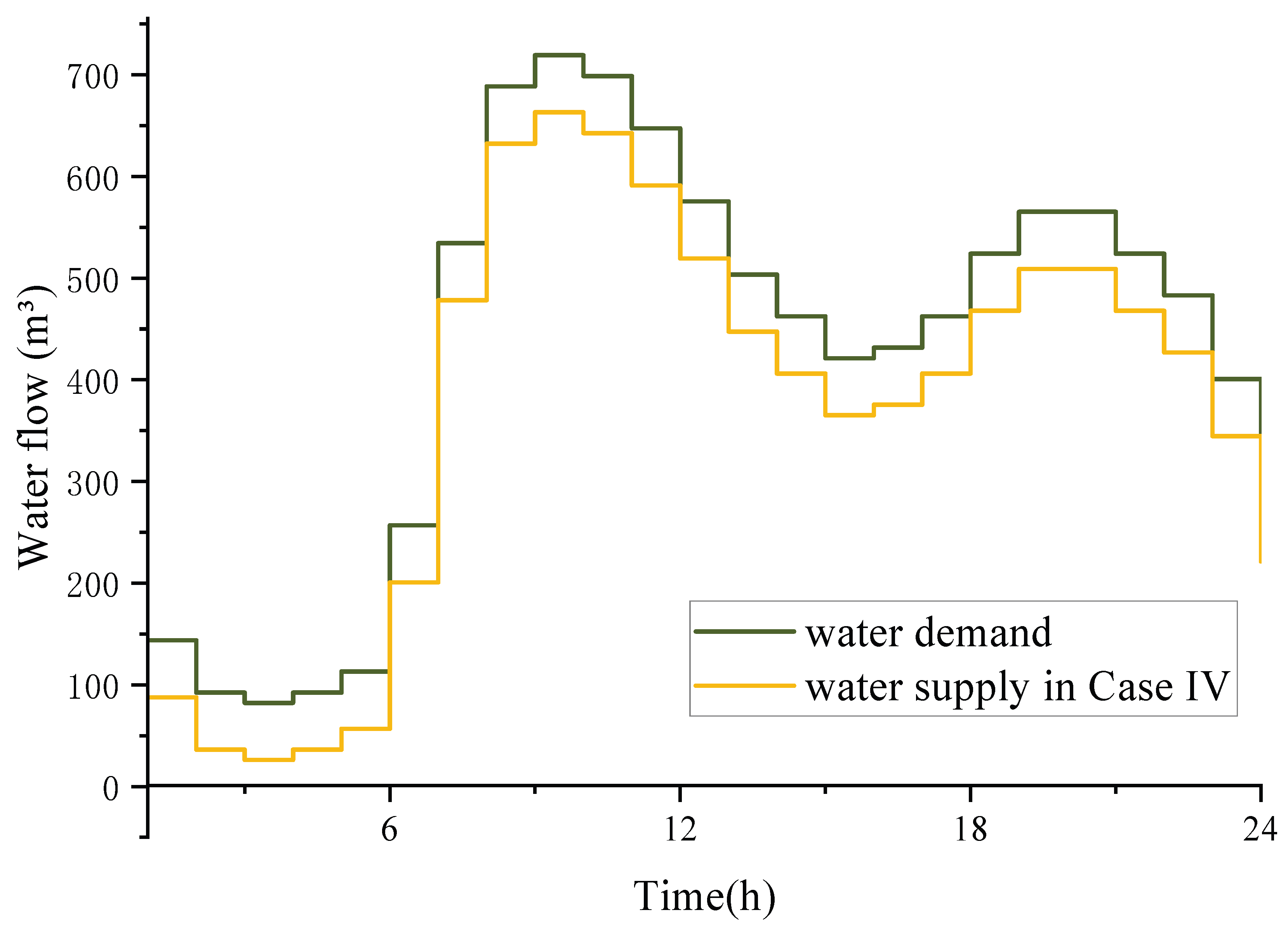
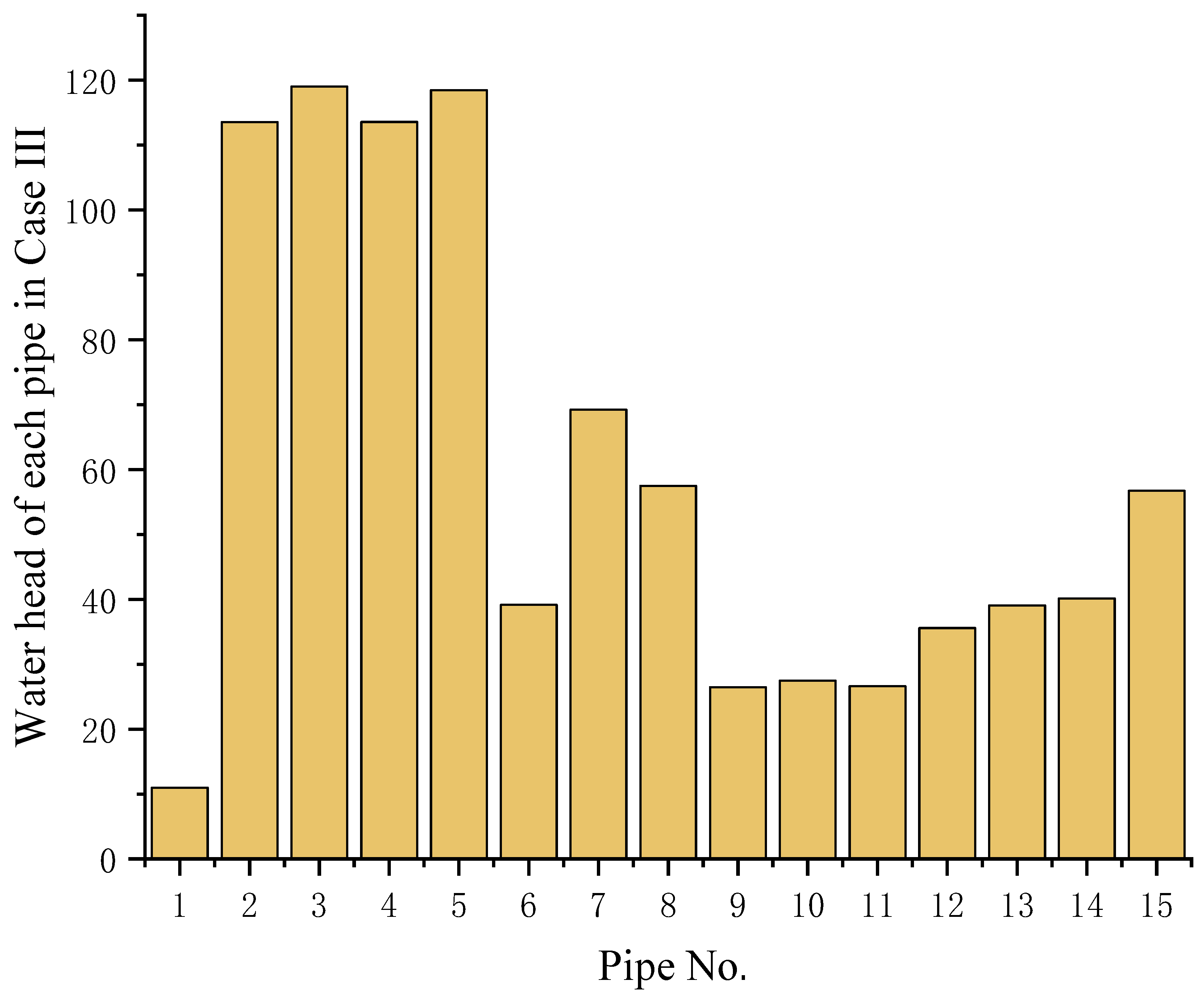
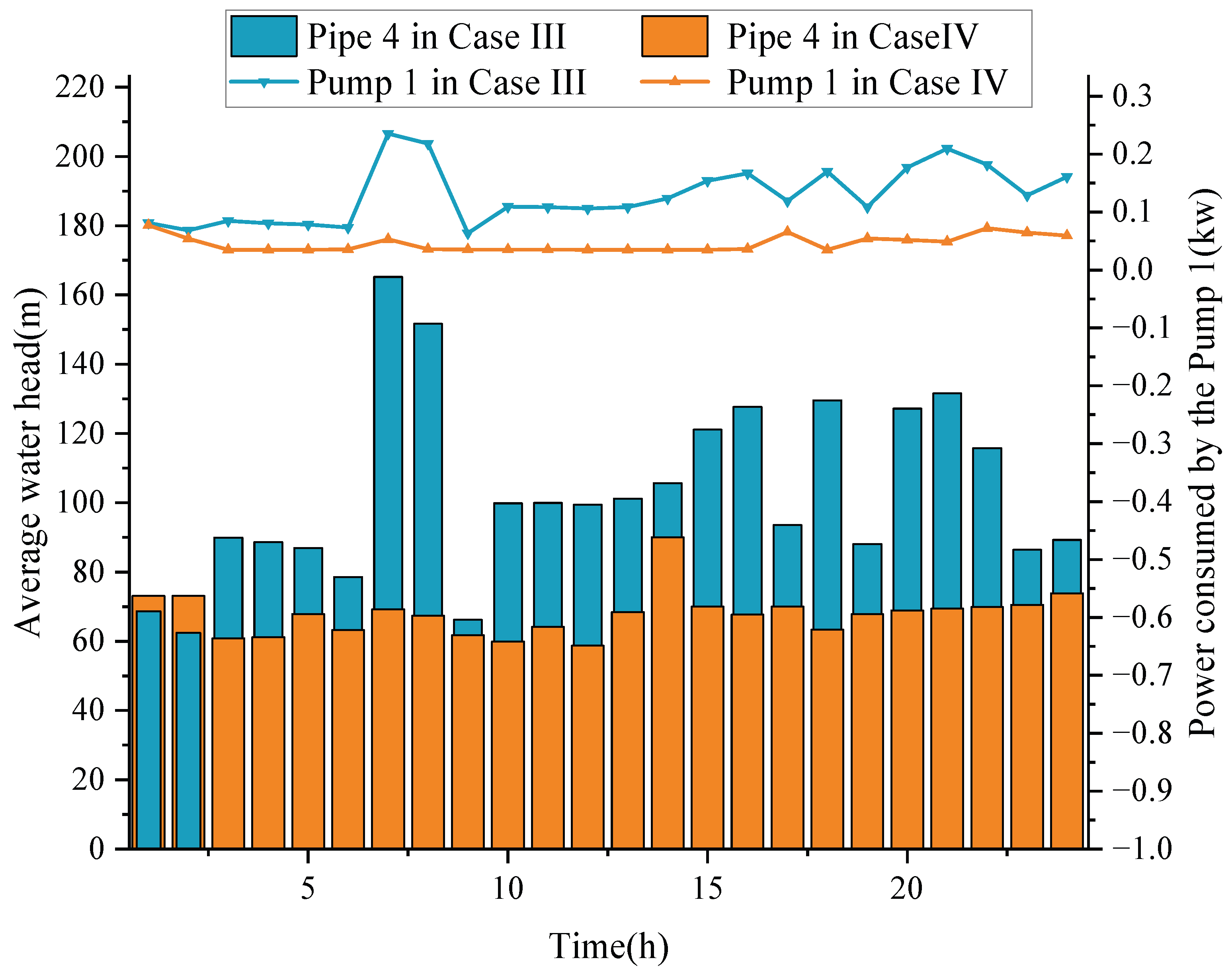
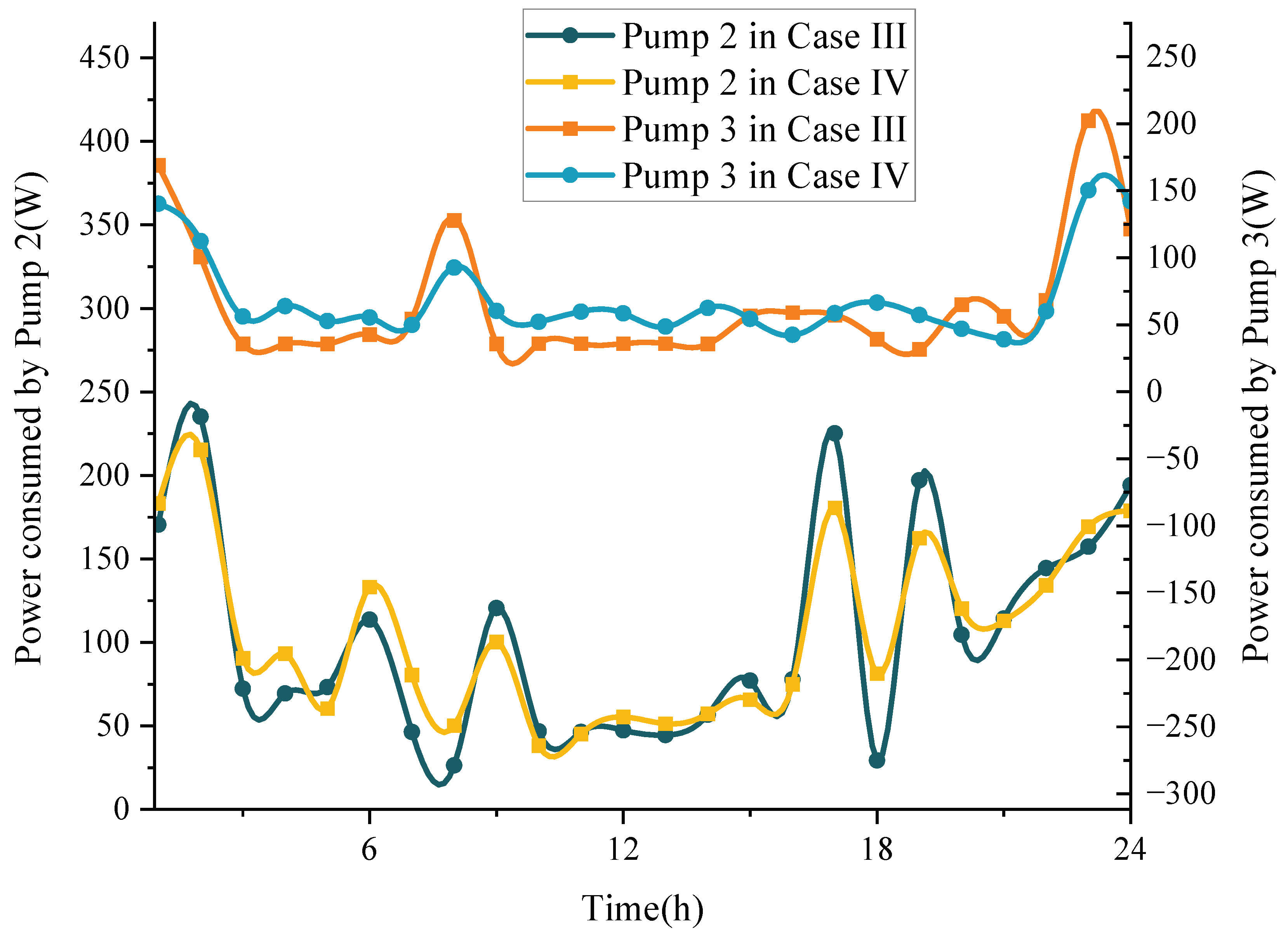
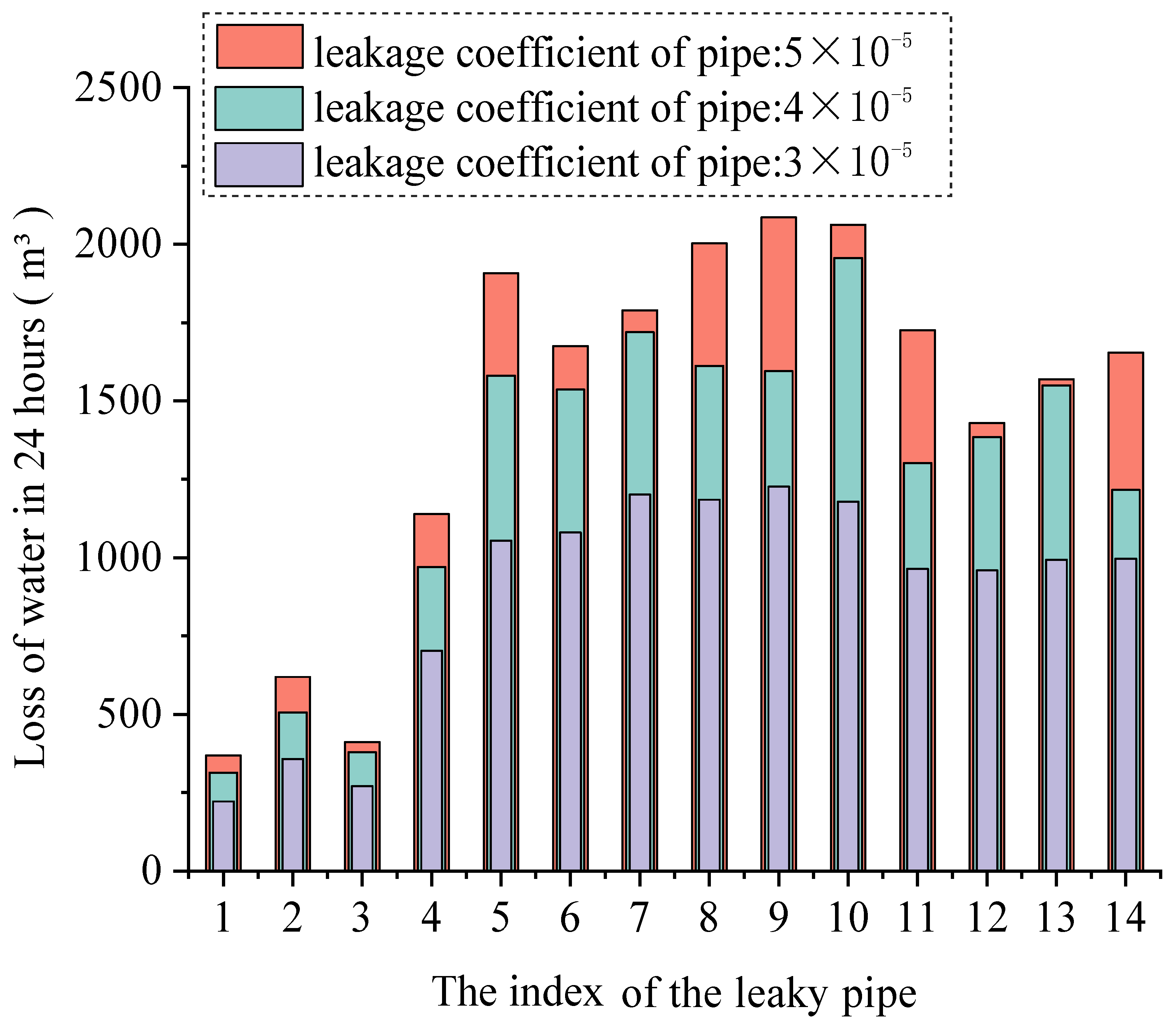
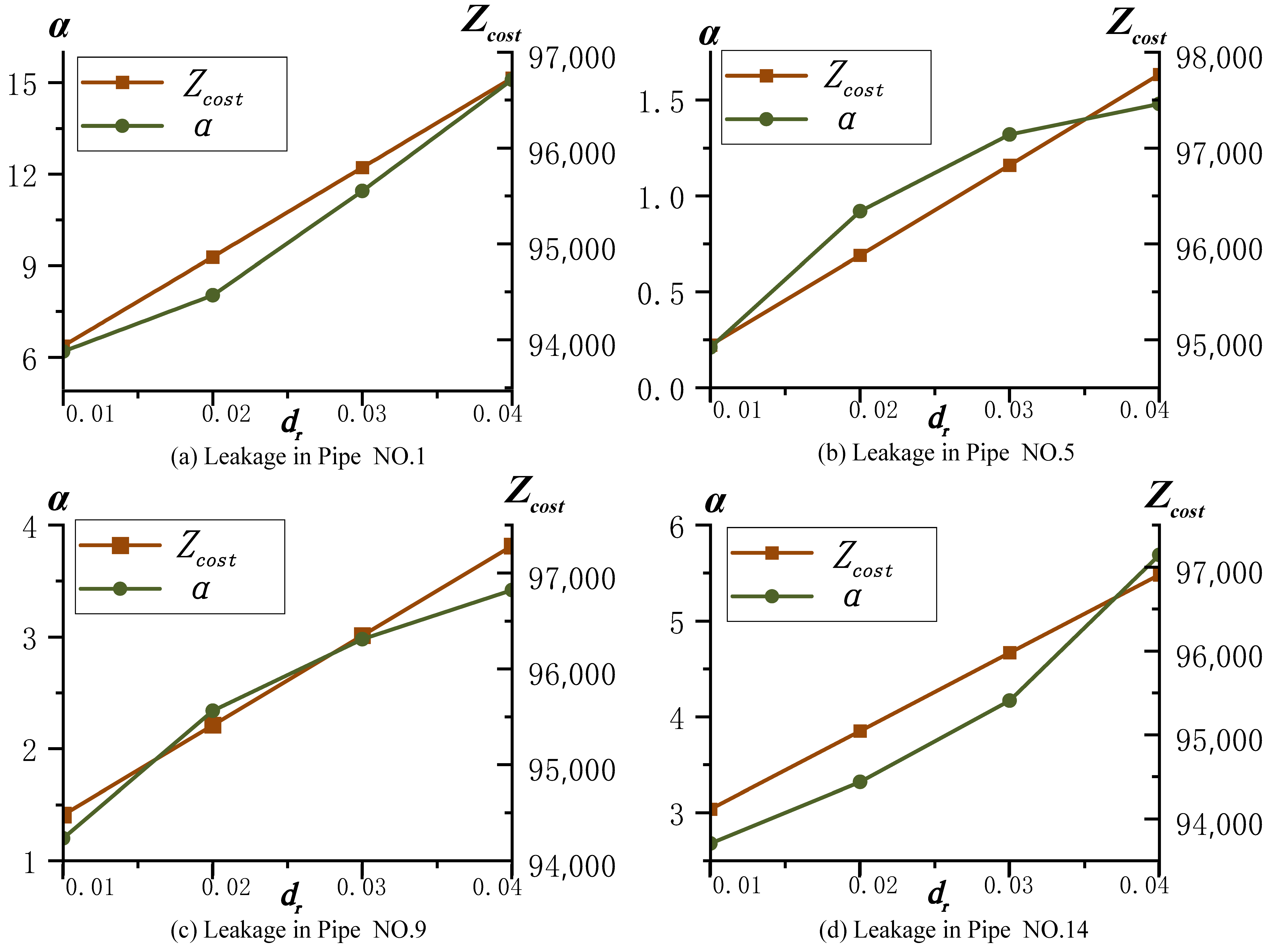
| Method | Probability Dependency | Key Advantages | Main Limiltation |
|---|---|---|---|
| SO | Strong (requires distribution) | Statistically modeled uncertainty | Sensitive to distribution errors and high computational cost |
| RO | None (bounds only) | Worst-case feasibility | Overly conservative solutions |
| CVaR | Strong (requires distribution) | Tail risk control | Distribution sensitivity |
| IGDT | None (bounds only) | Handle distribution-free uncertainties | Parameter sensitivity and cannot utilize the probability |
| Hybrid Stochastic -IGDT | Partial | Handles mixed uncertainties | Complex model structure |
| Scenario No. Probability | 1 0.200 | 2 0.073 | 3 0.034 | 4 0.027 | 5 0.006 |
| Scenario No. Probability | 6 0.066 | 7 0.100 | 8 0.134 | 9 0.260 | 10 0.100 |
| Case | Co-Optimized | Leakage Considered | Power Expense (CNY) | Purchased Water (m3) | Total Operational Cost (CNY) |
|---|---|---|---|---|---|
| Case I | × | × | 70,861.45 | 30,795.54 | 117,054.76 |
| Case II | × | ✓ | 73,348.22 | 32,274.93 | 121,760.62 |
| Case III | ✓ | × | 43,842.31 | 30,795.54 | 90,035.62 |
| Case IV | ✓ | ✓ | 45,288.59 | 32,180.49 | 93,559.33 |
| Approach | Power Expense (CNY) | Purchased Water (m3) | Total Cost (CNY) | Solving Time (s) |
|---|---|---|---|---|
| Piecewise Linearization | 43,842.31 | 30,795.54 | 90,035.62 | 120.52 |
| Non-Linearized | 43,839.78 | 30,802.32 | 90,042.37 | 935.43 |
| Comparison Indicator | SO | Hybrid Stochastic–IGDT |
|---|---|---|
| Leakage Coefficient | Parameter () | Variable |
| System Total Cost (Normal Conditions) | CNY 93,559.33 | CNY 96,366.11 |
| System Total Cost( Extreme Leakage Conditions ) | CNY 110,496.83 | CNY 96,366.79 |
| Water Supply Satisfaction Rate ( Extreme Leakage Conditions ) | 20% | 99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Liu, Z.; Wu, Q.-H. Hybrid Stochastic–Information Gap Decision Theory Method for Robust Operation of Water–Energy Nexus Considering Leakage. Electronics 2025, 14, 2644. https://doi.org/10.3390/electronics14132644
Zeng J, Liu Z, Wu Q-H. Hybrid Stochastic–Information Gap Decision Theory Method for Robust Operation of Water–Energy Nexus Considering Leakage. Electronics. 2025; 14(13):2644. https://doi.org/10.3390/electronics14132644
Chicago/Turabian StyleZeng, Jiawei, Zhaoxi Liu, and Qing-Hua Wu. 2025. "Hybrid Stochastic–Information Gap Decision Theory Method for Robust Operation of Water–Energy Nexus Considering Leakage" Electronics 14, no. 13: 2644. https://doi.org/10.3390/electronics14132644
APA StyleZeng, J., Liu, Z., & Wu, Q.-H. (2025). Hybrid Stochastic–Information Gap Decision Theory Method for Robust Operation of Water–Energy Nexus Considering Leakage. Electronics, 14(13), 2644. https://doi.org/10.3390/electronics14132644






