Abstract
Predicting human motion is a fundamental part of many applications such as animation and human–robot interaction. We propose a novel recurrent neural network (RNN) model, which can predict the trajectory of human movement using a single frame of the pose information and the initial velocity. This contrasts with previous works that required multiple frames of a person’s past motion history to predict future sequences. Our method leverages the trajectory and pose information to predict the most likely motion sequences, overcoming the challenge of ambiguity due to the high variation in poses. In this work, we demonstrate that our method is capable of learning the human’s movement and predicting the human’s trajectory. The human body is divided into five parts to study the relationships among the internal motions. This enables a better model to predict future trajectories according to the current human pose. Our approach surpasses several baseline methods on the Human 3.6M dataset and achieves state-of-the-art performance.
1. Introduction
Comprehending and predicting human trajectory is widely applied to augmented reality [1,2], animation [3,4], and person re-identification [5,6]. However, understanding and perceiving human behavior is still challenging, since it involves human intentions, which are difficult for machines to learn.
Traditional approaches capture the spatial characteristics of human motion by imposing physical-based constraints such as the inverted pendulum model [7], passive dynamics [8], or the zero moment point model [9]. Although human motion follows physical laws, statistical models often fail to accurately represent pose dynamics, leading to unrealistic motion synthesis.
With the proliferation of deep learning methods, recurrent neural network-based models have been used in the prediction of human motion [10,11,12]. These models perceive human pose features as temporal sequences and forecast future 3D poses. Unlike other sequential prediction problems, such as speech recognition, machine translation, and text summarization, the prediction of human motion involves the human kinematic system, which is subject to strict temporal and spatial constraints. Therefore, methods have been proposed to improve the performance of regular recurrent neural networks (RNNs). Although using an RNN for a sequential prediction problem is an intuitive choice, convolutional networks (CNs) could be another promising approach for this task. Works based on graph convolutional networks (GCNs) treat the human skeleton as a graph and perform well at extracting spatial dependencies [13,14,15]. However, setting the adjacency matrix needs prior knowledge of skeletal connections. When the skeletal structure changes, these methods usually require manual efforts to update the adjacency matrix. More recently, transformer-based methods exhibit superior performance on long-range prediction tasks [16,17,18] by mitigating error accumulation and better capturing complex joint interactions over extended sequences. Other efforts leverage generative adversarial networks (GANs) to predict probabilistic human motion [19,20] or extract discriminative topological features to learn patterns [21]. However, they do not include the prediction of a 2D trajectory. The absence of a prediction of global position leads to synthesized characters staying in the center of the window without moving. The problems of human pose prediction and trajectory prediction are strongly correlated and should not be considered as two independent tasks.
While GCNs and transformers are alternatives, Gated Recurrent Units (GRUs) better match our problem constraints. GCNs over-specialize to skeletal graphs when velocity suffices for intent, and transformers require a large amount of training data to learn attention weights effectively. GRUs provide lightweight sequential modeling ideal for deterministic trajectory rollout from sparse inputs. For this purpose, we propose a motion prediction model incorporating GRUs [22], which adaptively learn an embedding of the 3D pose from different skeleton scales without human intervention. The predicted pose and the current velocity will be fed to another RNN that projects the curvature of the future trajectory. Because the pose network is trained independently, it can be replaced with other pose estimation methods if desired. Unlike prior works [11,14,23] that require a motion sequence as input, our approach adopts a one-to-many structure for RNN. Thus we only need a single frame of the motion to predict during the inference stage. Using a single image instead of a video not only simplifies the data collection process as images are more readily available than videos, but also avoids potential motion blur or video compression artifacts. Most works output the positions of joints to demonstrate the predicted pose; however, we represent the predicted skeleton by the quaternion form, which can be converted into the BVH format that is easily loaded by professional animation software. We also show that this pipeline can target the predicted motion onto virtual characters.
To summarize, the main contributions of the paper are as follows:
- We design a novel Dual-GRU architecture. The hierarchical design decouples coarse trajectory shaping from fine-grained refinement, which is distinct from prior single-step predictors.
- We propose two novel loss functions. The pose loss function models human motion continuity in the quaternion space for joint angles. The trajectory loss function preserves realistic motion regardless of global coordinates.
- We introduce a method to automatically decide the coefficients of the losses by dynamically adjusting the scale of the skeleton.
2. Related Work
In this section, we review the most relevant literature on motion prediction, pose forecasting, and animation synthesis, noting how these methods utilize the trajectory and so delineate the novelty of our approach.
2.1. Pose Prediction
Owing to the success of the sequence-to-sequence model [22,24], RNN models have become a common approach for human pose prediction. Examples are an Encoder–Recurrent–Decoder (ERD) model that adds a nonlinear encoder and decoder to the recurrent layers [10] and a sequence learning model that adds a residual architecture to predict the velocity of human motion [11]. To improve the robustness of the model and avoid motion drift and degradation, a dropout autoencoder before a three-layer RNN was used to reduce the accumulated error [12]. Quaternions were shown to perform better than widely used exponential maps to parameterize rotation [25] within a simple but effective network that encodes average speed and a ground trajectory to synthesize long-term locomotion.
GAN- and CN-based methods are also used to predict human pose sequences. For example, a GAN model predicted probabilistic human motions [19] and was improved by an enhanced discriminator with a bidirectional framework [20]. A convolutional sequence-to-sequence model captured information on spatial–temporal dynamics [13] and a graph convolutional network was incorporated with the surrounding situation into the prediction model [26]. Correlations among the trajectories of joints were used to represent skeletal structure [23] and a state-of-the-art decomposition of the trajectory features of each joint into speed, orientations, and the last frame position was achieved [27].
Recent methods have also used transformer architectures for sequential pose modeling. PoseFormer [16] applies temporal transformers for efficient global attention over pose sequences. MotionBERT [17] extends this to motion data with masked reconstruction objectives, while MotionAGFormer [18] introduces a dual-stream Transformer–GCNFormer block, mixing global attention and local graph-based filtering to efficiently model spatio-temporal structure.
Despite these advancements, many methods, including several transformer-based approaches, still primarily predict 3D poses relative to the root joint. Predicting poses directly in the world coordinate system remains a significant challenge addressed by fewer works [25,28], though it is crucial for applications requiring global trajectory and interaction with the environment.
2.2. Social Motion Forecasting
Social human motion forecasting models predict the path of movement by learning the social interactions among humans and scenarios. Social-LSTM [29] introduces a social pooling layer to foresee the human movement by avoiding nearby pedestrians. Similarly, Trajectron++ [30] introduces a graph-structured recurrent model: it encodes each scene as a sequence of spatio-temporal graphs with nodes as agents, then applies a graph neural network (GNN) coupled with an RNN-based generative encoder–decoder (CVAE) to produce probabilistic, interaction-aware trajectory forecasts. Meanwhile, JointLearning [31] examines pose prediction and trajectory forecasting jointly with a GRU to extract temporal information and a social pooling layer to learn the social clues. Another influential model, PECNet [32], conditions on high-level goals by first inferring likely endpoints via a CVAE and then using a non-local social pooling mechanism to incorporate all agents’ histories.
These methods assume a substantial observed trajectory history and explicit modeling of nearby scene contexts and social agents, making their models hard to generalize. In contrast, our approach forgoes both multi-step observation sequences and explicit social modeling. The proposed method relies only on a single pose frame and its instantaneous motion—a lightweight representation comprising the agent’s initial speed and local orientation—to drive the forecast. By not requiring past trajectory data, we eliminate the need for recurrent history encoders, and by not modeling neighbors, we avoid complex social pooling or GNN modules. This minimalist formulation leverages immediate kinematic cues as sufficient predictive features, drastically simplifying the architecture. Despite its simplicity, our method can effectively forecast future paths, distinguishing itself from the above paradigms, which hinge on lengthy histories and elaborate social interaction mechanisms. The result is a streamlined predictor that operates on one-frame initialization, highlighting a fundamentally different design philosophy compared to prevailing socially aware, multi-frame trajectory predictors.
2.3. Motion Synthesis
Motion synthesis methods are widely studied in computer graphics and they can produce human motions by learning the motion manifold. Factored conditional restricted Boltzmann machines were developed to represent different styles of motion [33]. Over the past decade, deep learning has dominated the field in preference to probabilistic approaches. A deep learning framework with a convolutional autoencoder was proposed to generate realistic human sequences [3]. The long short-term memory network-based architecture was improved to better fit the task of synthesizing motions by adding a temporal embedding and a scheduled target-noise vector [4]. Unlike motion prediction approaches, motion synthesis needs additional high-level parameters such as gait, phase, and foot contact to animate the character.
3. Pose and Trajectory Prediction
In this section, the detailed RNN structures for trajectory and pose prediction are introduced. We begin by adopting a new method to automatically determine the scaling factor for the skeleton. This enables us to generalize our approach to different datasets, even when the scaling coefficient is not provided. The pose network takes the current pose and velocity as input and predicts the pose for the next frame. The trajectory network extracts the motion feature from the pose using the pose encoder, which includes five two-layer GRU blocks that extract pose features from five parts: two arms, two legs, and the torso. Each two-layer GRU block aims to learn the temporal features of one part of the human. The decoder then learns the spatial relationship of those pose features given the current velocity. To capture the trajectory’s characteristics adequately, we carefully designed a new loss that considers both rotation and velocity for the trajectory network.
3.1. Trajectory and Skeleton Model
Several motion capture datasets are available; however, these datasets often use different formats and scaling factors to represent poses, requiring data conversion into a unified format suitable for training the network. To address this issue, we propose a novel method to compute the scaling coefficient, enabling alignment across all datasets. By dynamically scaling the skeleton, the network becomes adaptable to skeletons of varying proportions (e.g., different humanoid sizes or shapes), ensuring that loss terms are appropriately weighted and invariant to the skeleton scale. This adaptability enhances the model’s ability to generalize across datasets or scenarios involving varying body proportions. Additionally, automatically determining the coefficients eliminates the need for manual tuning of loss weights for each application. This approach saves time, reduces trial-and-error experimentation, and ensures consistent results across different configurations.
We treat the root joint as the origin of the skeleton’s local coordinate system and compute the 3D coordinates for each joint. A quaternion representation is adopted to describe the relationships among joints, instead of the commonly used Euler angles and exponential maps, as all representations in suffer from gimbal lock problems [34].
As part of training the trajectory network, the global velocity in the XZ-plane would normally be used. However, this has a drawback as an input feature, as if the human model rotates at the initial point, all the values for the global velocity will change, yet the shape of the predicted path should stay the same. Thus a facing direction f is defined to overcome this limitation. We form the facing plane by connecting the joints (left hip, right hip, and upper torso (Figure 1)) and determine the vector perpendicular to the facing plane. The cross product of this vector with the vertical Y-axis yields the facing direction on the XZ-plane. A low pass filter is applied to smooth the turbulent facing direction due to the motion capture error. Then the angle between the moving direction m and the face direction f is the feature fed to the network, where .

Figure 1.
The image on the left shows the representation of 25 joints for the skeleton in the Human 3.6M dataset. The image on the right shows the physiological definition of the anatomical landmarks [35].
When humans move, certain joints are interdependent. Thus, the joints are manually split into five groups, allowing the individual two-layer GRU unit to be focused on capturing the local movement features. For instance, when a person steps out with their right leg, there is a significant change in the position of the right foot, knee, and hip joint compared to the other joints. The motion of the right leg in this situation serves as an indicator for future motion and should be highlighted by the network. The joints are formed into five groups: torso (joints 0, 1, 2, 3, and 4), left leg (joints 15, 16, 17, 18, and 19), right leg (joints 20, 21, 22, 23, and 24), left arm (joints 5, 6, 7, 8, and 9), and right arm (joints 10, 11, 12, 13, and 14) (Figure 1).
Each dataset stores bone lengths differently, but some datasets do not provide detailed instructions for users to convert the bone length into commonly used units such as meters. To overcome this problem, bone length estimation is necessary when the unit of bone length is not known. The upper torso in the left image of Figure 1 has a similar position as T4 in the right image and the bottom torso in the left image has a similar position as the PSIS-Level in the right image. Since the length between T4 and the PSIS-level is consistent for adults [35], we assume that the sum of the bone length l with the unknown unit between the upper torso and center torso and the bone length between the center torso and bottom torso stay the same. The summation result s is 0.424 m for men, 0.387 m for women, and 0.402 m for unknown identity [35]. By doing so, different types of skeletons can be matched to each other. It is also beneficial to determine the loss coefficients by using the skeleton scalar .
3.2. Network Structure
An RNN is a class of neural network that consists of internal states to process input of variable sizes. Given an input sequence X with length i, update the hidden state by using the input at timestamp t and the previous hidden state , which contains the information from timestamp 1 to timestamp . The hidden state can be computed using the following equation:
where f is a nonlinear operation that connects the previous hidden state and the input to the current hidden state. Plain RNNs may not retain long-term dependencies in sequences due to the hidden state being updated at each time step, causing the earlier trends to vanish from the hidden state. They are susceptible to the gradient vanishing problem, where the gradients to update the weights can become very small, leading to slow convergence or even complete stagnation [36]. To overcome the gradient vanishing problem, GRUs and Long Short-Term Memory Networks (LSTMs) utilize a gating mechanism to update or forget data, allowing them to capture significant information from long sequence data. In our work, we adopt the GRU as the main hidden module of the neural network model as GRUs have been shown to be more efficient in terms of training time and inference time without sacrificing accuracy than LSTM [37,38,39].
For human trajectory prediction, assume the recurrent network is provided with a sequence of the pose, denoted as , and the velocity, denoted as . Our goal is to predict the sequence of the future trajectory . At the time step the pose is described using joint angles in quaternion form, so that , where is the quaternion of the j-th joint of the t-th frame.
Figure 2 illustrates the high-level architecture of a dual-network system designed for humanoid motion prediction, comprising a pose network and a trajectory network. Each component works collaboratively to generate smooth and realistic predictions of position, pose, and orientation over time. The I/O specification for the dual-network system can be found in Table 1.
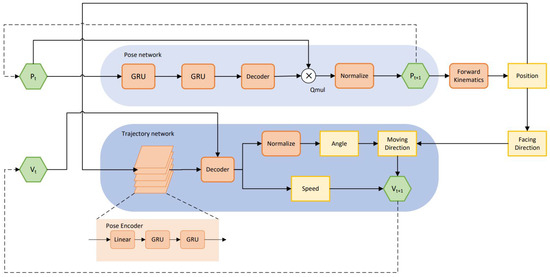
Figure 2.
The architectures of our network. The operator “QMul” is the multiplication of two quaternions. P gives the joint angles of the pose and V is the velocity of the trajectory. Green hexagons represent the inputs and outputs of the system. Red blocks represent the submodules of the model. Yellow blocks represent the parameters.

Table 1.
Input and output specifications for the pose network and trajectory network.
The pose network, located at the top, takes the quaternion of the pose as input and predicts the quaternion of the next frame pose as output. The predicted pose is processed through forward kinematics to obtain the 3D key joints in the Cartesian coordinate system, enabling the facing direction to be inferred by the method introduced in Section 3.1.
The trajectory network, located at the bottom, comprises two components: the pose encoder on the left and the trajectory decoder on the right. The pose encoder takes the Cartesian coordinates of all joints as input and feeds them to five two-layer GRU modules, which learn the comprehensive encoded motion features for each part of the body. The trajectory decoder uses the motion features provided by the pose encoder and the previous trajectory prediction to generate future movement . The output of the decoder includes two parts: the rotation angles and that describe how the target rotates, and the speed s that describes how fast the person moves. The speed s is expressed in units of centimeters per frame. Since our model operates in discrete time steps (frames), this reflects the displacement per frame rather than per second.
3.3. Training Loss
In this section, we explain the design of the loss functions used for both the pose and trajectory networks. Our goal is to ensure that the model can accurately predict future motion in a way that is robust to orientation and coordinate system alignment.
3.3.1. Pose Loss
For pose prediction, we use the quaternion representation to describe joint orientations, which avoids the singularities and discontinuities found in Euler angles. However, quaternions have a known ambiguity: q and represent the same rotation.
To address this, we calculate the geodesic distance loss between the ground truth quaternion of the pose and the predicted quaternion of the pose using the following equations:
where is the modulus function.
This loss captures the smallest rotation needed to align the two quaternions and respects the geometry of the rotation space.
3.3.2. Trajectory Loss
Rather than predicting the global 2D root joint position directly, we model the trajectory as a combination of two interpretable components. One is the scalar speed value s indicating how fast the person is moving. Another is the local orientation angle , representing the direction of movement relative to the person’s facing direction in the XZ-plane. The facing direction can be computed using the vector orthogonal to the plane defined by left hip, right hip, and upper torso joints.
To avoid discontinuities around the angle wrap-around (Figure 3), we predict and instead of . This ensures a continuous and differentiable output space. The prediction result is normalized and always satisfies the condition . Thus, the rotation matrix can then be formed as shown below:
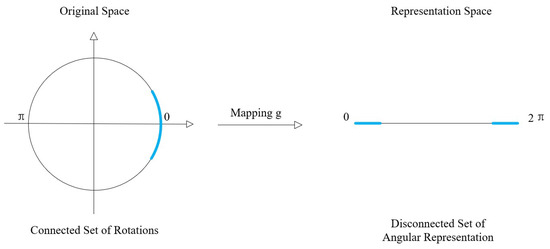
Figure 3.
An example to illustrate the discontinuity problem caused by angular representation. The blue line, which is continuous in the original space, becomes disconnected in the representation space.
The predicted movement direction is then , where is the unit vector of the facing direction f. Combined with the scalar value speed s, the final displacement is calculated as .
To account for different skeleton scales across datasets, we apply a scale factor and define the trajectory loss as follows:
This formulation ensures that the model learns to model velocity more robustly and interpretably than conventional MSE-based trajectory losses. Unlike previous works that directly regress Cartesian displacements, our formulation aligns predictions with the human’s local orientation.
Together, these two losses guide the model to produce physically plausible motion trajectories and realistic joint orientations while maintaining invariance to global positioning.
4. Experimental Settings
In this section, we assess the network’s performance on a widely used benchmark dataset, Human 3.6M. We also introduce the settings to evaluate the impact of our contribution.
4.1. Dataset and Data Pre-Processing
The Human 3.6M dataset [40] comprises 3.6 million 3D poses performed by seven actors, with a skeleton consisting of 32 joints sampled at 50 Hz. For this experiment, we removed seven duplicated joints from the skeleton. Given the large variation in poses in this dataset, we only evaluated our method on the walking category and downsampled the sequence to 25 Hz. To ensure consistency with other approaches [10,11], we followed the same split into training and testing sets and reserved group 5 for testing, while using the remaining groups for training.
To demonstrate the robustness and consistency of our network, we also utilize the Edinburgh Locomotion dataset [3] for visualizing pose and trajectory predictions. The Edinburgh Locomotion dataset is extensive and comprises a collection of freely available large online databases [41,42,43,44], along with additional data from internal captures [3]. This dataset encompasses various types of locomotion, including walking, jogging, and running, and consists of roughly six million frames of motion capture data, recorded at a rate of 120 frames per second, ensuring high-quality recordings.
Because both datasets do not provide quaternion labels, we first transformed the given Euler angle labels into quaternion labels. Assuming the Tate–Bryant convention with a rotation sequence of yaw to pitch to roll, we can derive the corresponding quaternion q for the roll, pitch, and yaw angles in Euler angle representation in the following way:
4.2. Network Implementation
We implemented all of our proposed methods on the Pytorch 1.7.0 [45] framework. Each GRU module has 1024 hidden units. The decoder in the pose network comprises two dense layers. The first hidden layer has a dimension of 512, and the second hidden layer has a dimension of 100 to match the number of quaternion parameters of joints. The trajectory network’s decoder shares the same architecture but with fewer hidden units: 256 for the first dense layer and 3 for the second dense layer. The trajectory network’s pose encoder projects the coordinates of the joints in the corresponding group to 32-dimensional features.
We adopted the Adam optimizer [46] and clipped the gradient norm to 1. The initial training rate was set to be 0.0001 with a constant decay rate . The Exponential Linear Unit (ELU) [47] served as the activation function in both the encoder and decoder. We utilized batch training with a mini-batch size of 8.
We proposed two types of models for the testing stage. During training as well as testing, the first model reads 50 frames (two seconds) of the motion sequence and predicts the next 25 frames (one second) of the pose and trajectory. The second model only requires a single frame of motion to predict the next 25 frames. To encourage the model to use less information to make a prediction, we feed either the predicted result or the ground truth during the training process, except for the first frame where we always provide the ground truth. It involves a dynamic adjustment mechanism defined by the formula , where t is a time step and k is a hyperparameter that controls the feeding ratio of the ground truth and the predicted value. When , the ground truth values are used. Otherwise, the predicted values are used. By introducing this mechanism, the frequency of switching between ground truth and predicted values can be controlled, thereby influencing the training dynamics and the model’s performance.
5. Results
We performed two types of evaluations: first, we conducted a study to qualitatively evaluate the prediction of human locomotion given only a single-frame pose and root velocity information, since forecasting the higher dynamics of motion using limited features is very challenging; second, we evaluated our human trajectory prediction using both qualitative and quantitative analysis.
5.1. Human Pose Prediction
For our human motion evaluation, we predicted human motion sequences from an initial pose and velocity. Figure 4 shows examples of predicted poses in the BVH format loaded by Blender 4.0 (https://www.blender.org, Blender is a software suite designed to facilitate the creation of high-quality 3D graphics, models, and animations for use in production environments).

Figure 4.
Examples of pose and trajectory prediction. Given the first frame of the initial pose (the leftmost one), our network is able to predict the sequence of following motions for the next second.
Figure 4 presents a detailed visualization of the prediction of humanoid locomotion, captured from different perspectives and arrangements. The left images depict the side view of the motion, while the right images show the corresponding top view. Each panel illustrates a sequence of a humanoid model walking, depicted in six phases of its gait cycle, with accompanying trajectories for foot motion (red and green lines) and the center of mass (CoM) (blue lines).
It can be observed that the network predicts smooth and consistent poses and trajectories throughout the gait cycle. Additionally, the network demonstrates the ability to adapt naturally to changes in initial velocity, producing realistic turning motions and maintaining dynamic stability.
Figure 5 illustrates that using quaternion-based loss functions (L2 angle loss or geodesic loss) significantly improves angle predictions. Additionally, it facilitates faster convergence of the network for the position prediction compared to the position loss only method. Among the two quaternion-based losses, the geodesic loss (pink line) slightly outperforms the L2 angle loss (green line) in the angle loss subplot, highlighting its effectiveness in training for accurate motion prediction. As mentioned earlier, the antipodal representation causes discontinuity, making it challenging for the system to learn the pattern. In contrast to the position-based loss, which does not utilize the parameterized skeleton constraints and requires additional effort for reprojection onto the skeleton [3], the geodesic loss is based on quaternions that always satisfy the skeletal constraints.
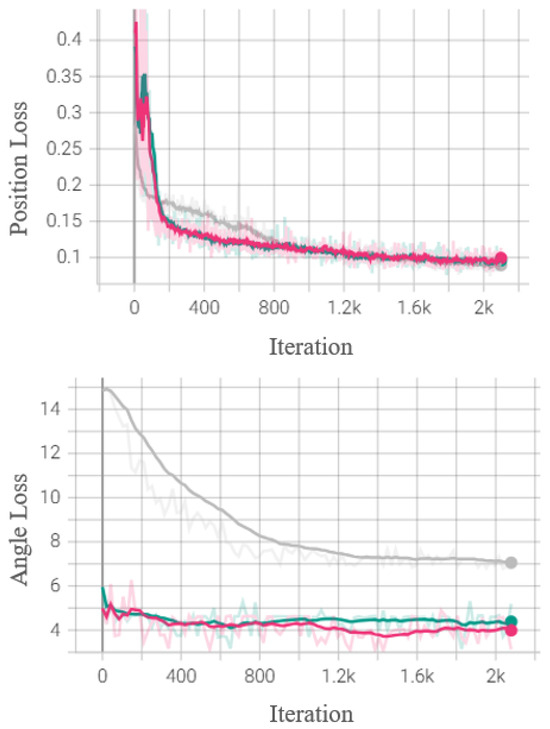
Figure 5.
The graph shows the position loss and the angle loss of positions in the validation set. The grey line represents the training without quaternion loss, the green line represents the training with quaternion L2 angle loss, and the pink line represents the training with quaternion geodesic loss.
We conduct a number of controlled experiments to analyze the performance of each component on the Edinburgh Locomotion dataset [3]. Table 2 summarizes the comparison results between different configurations, marked as 1 to 5. The models were tested on Euler angle error (yaw, pitch, and roll) and quaternion error (, , , ), with the final performance metrics including Euler Mean Absolute Error (EMAE) and Quaternion Mean Absolute Error (QMAE). For all the experiments, we use the same architecture shown in Figure 2. We then apply various methods to this basic architecture and examine their respective effects.

Table 2.
Comparison results of methods on Edinburgh Locomotion dataset [3]. (Best result in bold).
- Method I: Use dynamic adjustment mechanism? If yes, we gradually reduce the feeding ratio of the ground truth. If no, we always feed the ground truth for the first 50 frames.
- Method II: Use the quaternion loss? If yes, we use both the position loss and the quaternion loss. If no, we use the position loss only.
- Method III: Use the geodesic distance loss? If yes, we calculate the geodesic distance between the ground truth and the predicted values. If no, we calculate the L2 loss instead.
The ablation results emphasize the importance of combining the dynamic adjustment mechanism (Method I), quaternion loss (Method II), and the geodesic distance loss (Method III) for achieving the best overall performance. The model that uses all three methods outperforms all other configurations by a significant margin. The results show that omitting any of these critical components leads to considerable performance degradation. Specifically, the dynamic adjustment mechanism and quaternion loss are crucial for achieving accurate angle and rotation predictions, while the geodesic distance loss offers a moderate improvement over traditional L2 loss.
5.2. Human Trajectory Prediction
We trained two separate trajectory networks for human trajectory prediction, but they share the pose network discussed above. One trajectory network followed the experimental setup conducted by [10], while the other read the initial frame coordinate of the joints and the velocity of the root joint. We adopted two widely used metrics to evaluate trajectory prediction: average displacement error (ADE) and final displacement error (FDE) [29,48,49]. ADE computes the mean L2 distance between all trajectory points, while FDE computes the mean L2 distance between final trajectory points.
To the best of our knowledge, there is currently no method that predicts the trajectory based solely on the pose. Therefore, we proposed three baseline methods for comparison. To ensure fairness in the evaluation, we did not train the pose network separately for each method. Instead, we provided the same joint coordinates as input to all networks. During training and testing, every baseline was fed 50 frames of motion to predict the next 25 frames.
Baseline 1: A plain two-layer GRU network was constructed that reads both pose and trajectory features and predicts the Cartesian coordinates of the root joints. The mean squared error (MSE) loss was used for training the network.
Baseline 2: The network was built based on the publicly available code [11], and the input dimension was modified to match the feature dimension. The sampling-based loss proposed by Martinez [11] was used for the root joint coordinates.
Baseline 3: A strong RNN baseline designed for human pose prediction, similar to that in [50], was adopted. The Quaternion Transform Layer, which transforms the predicted pose from exponential maps to quaternion, was turned off. During the experiment, we observed that training with pose features lowered the accuracy of trajectory prediction. Thus, only the trajectory feature was used as input, and the same loss as in Baseline 1 was used for training.
Table 3 demonstrates that our method outperforms all baseline methods. A slightly lower performance was observed for the single-frame-based network compared to our regular (multi-frame-based) network. However, the single-frame approach was consistently better than all the baseline methods. This result highlights the effectiveness of a loss function that depends on the decomposition of the velocity compared to an MSE loss function based on position. Additionally, the pose encoder proved useful in extracting relevant features from the pose, as demonstrated by its improvement over the performance of the Baseline 3 method, which does not take advantage of the extra pose information.

Table 3.
Trajectory prediction on the Human 3.6M Dataset [40]. (Best result in bold).
We also present qualitative results for our methods and baseline comparisons. Figure 6 displays the predicted trajectories for each method by following the guideline from [10]. Each triangle node represents the exact predicted position of the root joints in the XZ-plane. The X-axis and Y-axis represent the distance (units of meters) from the origin of the world coordinate system. One advantage of our network is its accurate prediction of the direction faced. For example, in plot 1, Baseline 1 has the smallest final displacement error, while Baseline 3 is close to our result. However, our direction faced is more similar to the ground truth along the trajectory. If we extend the prediction time, we can expect the gap between our method and the baseline methods to become larger. Plot 3 provides further evidence to support this argument, as our method is the only one that turns right at the end, as in the ground truth, while all other methods turn left. Another advantage of our method is that it preserves the motion pattern. In the plot, the ground truth makes a sharp turn. Although our method does not turn as sharply, due to the high dynamic of the motion, the network learns that the person is about to turn from the previous pose features, while all other baselines fail to do so.
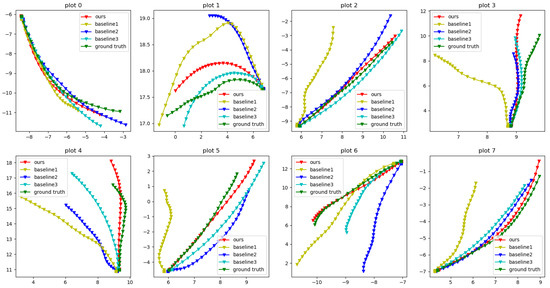
Figure 6.
The prediction of the trajectory path for the next 1000 ms.
6. Limitations
Although our method demonstrates robust performance under minimal input, it also operates under specific assumptions that may limit generalization in certain scenarios:
- Pose Quality: The framework assumes high-quality input poses (e.g., from motion capture systems). Noisy or heavily occluded poses can degrade prediction quality.
- No Scene or Interaction Modeling: Our model does not account for environmental constraints (e.g., obstacles) or social interactions with other agents. It may therefore struggle in dense or interactive environments.
- Failure Cases: Abrupt changes in motion intent (e.g., sudden turns or stops) and pattern transitions (e.g., walking to running) are common failure modes due to the lack of temporal or contextual cues.
These limitations provide a foundation for future research, such as incorporating uncertainty-aware velocity estimators or leveraging lightweight scene priors.
7. Conclusions
In this paper, we present a novel trajectory loss function that leverages velocity decomposition to focus on accurately predicting the directions faced. Our recurrent neural network is trained to predict trajectories without incorporating information on social interactions. To address pose feature challenges, we introduced a pose encoder that establishes the relationship between pose and trajectory. We also conduct an in-depth analysis of velocity representations and suggest training our model with angle and speed. Our extensive experiments demonstrate the effectiveness of our proposed network and show its state-of-the-art performance on the Human 3.6M dataset.
Author Contributions
Conceptualization, Y.H. and H.Y.; methodology, Y.H.; software, Y.H.; validation, Y.H.; formal analysis, Y.H.; investigation, Y.H. and H.Y.; resources, H.Y.; data curation, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, H.Y.; visualization, Y.H.; supervision, H.Y.; project administration, H.Y.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Hong Kong Innovation and Technology Commission (InnoHK Project CIMDA), and City University of Hong Kong (Projects 9610034 and 9610460).
Data Availability Statement
The datasets presented in this article are not readily available because the data are part of an ongoing study. Requests to access the datasets should be directed to the following work Learning pose prior via Large Language Model.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Villegas, R.; Yang, J.; Ceylan, D.; Lee, H. Neural kinematic networks for unsupervised motion retargetting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8639–8648. [Google Scholar]
- Maskeliūnas, R.; Damaševičius, R.; Blažauskas, T.; Canbulut, C.; Adomavičienė, A.; Griškevičius, J. BiomacVR: A virtual reality-based system for precise human posture and motion analysis in rehabilitation exercises using depth sensors. Electronics 2023, 12, 339. [Google Scholar] [CrossRef]
- Holden, D.; Saito, J.; Komura, T. A deep learning framework for character motion synthesis and editing. ACM Trans. Graph. (TOG) 2016, 35, 1–11. [Google Scholar] [CrossRef]
- Harvey, F.G.; Yurick, M.; Nowrouzezahrai, D.; Pal, C. Robust motion in-betweening. ACM Trans. Graph. (TOG) 2020, 39, 60:1–60:12. [Google Scholar] [CrossRef]
- Wang, C.; He, S.; Wu, M.; Lam, S.K.; Tiwari, P.; Gao, X. Looking Clearer with Text: A Hierarchical Context Blending Network for Occluded Person Re-Identification. IEEE Trans. Inf. Forensics Secur. 2025, 20, 4296–4307. [Google Scholar] [CrossRef]
- Gao, X.; Chen, Z.; Wei, J.; Wang, R.; Zhao, Z. Deep Mutual Distillation for Unsupervised Domain Adaptation Person Re-identification. IEEE Trans. Multimed. 2025, 27, 1059–1071. [Google Scholar] [CrossRef]
- Ha, T.; Choi, C.H. An effective trajectory generation method for bipedal walking. Robot. Auton. Syst. 2007, 55, 795–810. [Google Scholar] [CrossRef]
- Collins, S.H.; Adamczyk, P.G.; Kuo, A.D. Dynamic arm swinging in human walking. Proc. R. Soc. B Biol. Sci. 2009, 276, 3679–3688. [Google Scholar] [CrossRef]
- Hirukawa, H.; Hattori, S.; Kajita, S.; Harada, K.; Kaneko, K.; Kanehiro, F.; Morisawa, M.; Nakaoka, S. A pattern generator of humanoid robots walking on a rough terrain. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 2181–2187. [Google Scholar]
- Fragkiadaki, K.; Levine, S.; Felsen, P.; Malik, J. Recurrent network models for human dynamics. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4346–4354. [Google Scholar]
- Martinez, J.; Black, M.J.; Romero, J. On human motion prediction using recurrent neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2891–2900. [Google Scholar]
- Ghosh, P.; Song, J.; Aksan, E.; Hilliges, O. Learning human motion models for long-term predictions. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 458–466. [Google Scholar]
- Li, C.; Zhang, Z.; Lee, W.S.; Lee, G.H. Convolutional sequence to sequence model for human dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5226–5234. [Google Scholar]
- Li, M.; Chen, S.; Zhao, Y.; Zhang, Y.; Wang, Y.; Tian, Q. Multiscale Spatio-Temporal Graph Neural Networks for 3D Skeleton-Based Motion Prediction. IEEE Trans. Image Process. 2021, 30, 7760–7775. [Google Scholar] [CrossRef]
- Pang, C.; Gao, X.; Chen, Z.; Lyu, L. Self-adaptive graph with nonlocal attention network for skeleton-based action recognition. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 17057–17069. [Google Scholar] [CrossRef]
- Zheng, C.; Zhu, S.; Mendieta, M.; Yang, T.; Chen, C.; Ding, Z. 3D Human Pose Estimation with Spatial and Temporal Transformers. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021. [Google Scholar]
- Zhu, W.; Ma, X.; Liu, Z.; Liu, L.; Wu, W.; Wang, Y. MotionBERT: A Unified Perspective on Learning Human Motion Representations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Mehraban, S.; Adeli, V.; Taati, B. Motionagformer: Enhancing 3d human pose estimation with a transformer-gcnformer network. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 6920–6930. [Google Scholar]
- Barsoum, E.; Kender, J.; Liu, Z. Hp-gan: Probabilistic 3d human motion prediction via gan. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1418–1427. [Google Scholar]
- Kundu, J.N.; Gor, M.; Babu, R.V. Bihmp-gan: Bidirectional 3d human motion prediction gan. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 8553–8560. [Google Scholar]
- Wang, C.; Cao, R.; Wang, R. Learning discriminative topological structure information representation for 2D shape and social network classification via persistent homology. Knowl.-Based Syst. 2025, 311, 113125. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the International conference on Machine Learning, PMLR, Lile, France, 6–11 July 2015; pp. 2067–2075. [Google Scholar]
- Liu, X.; Yin, J.; Liu, J.; Ding, P.; Liu, J.; Liu, H. Trajectorycnn: A new spatio-temporal feature learning network for human motion prediction. IEEE Trans. Circuits Syst. Video Technol. 2020, 31, 2133–2146. [Google Scholar] [CrossRef]
- Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory recurrent neural network architectures for large scale acoustic modeling. Proc. Interspeech 2014, 2014, 338–342. [Google Scholar]
- Pavllo, D.; Grangier, D.; Auli, M. Quaternet: A quaternion-based recurrent model for human motion. arXiv 2018, arXiv:1805.06485. [Google Scholar]
- Fujita, T.; Kawanishi, Y. Future pose prediction from 3d human skeleton sequence with surrounding situation. Sensors 2023, 23, 876. [Google Scholar] [CrossRef]
- Liu, Z.; Su, P.; Wu, S.; Shen, X.; Chen, H.; Hao, Y.; Wang, M. Motion prediction using trajectory cues. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 13299–13308. [Google Scholar]
- Zaier, M.; Wannous, H.; Drira, H.; Boonaert, J. A dual perspective of human motion analysis-3d pose estimation and 2d trajectory prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 2189–2199. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NA, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-feasible trajectory forecasting with heterogeneous data. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 683–700. [Google Scholar]
- Adeli, V.; Adeli, E.; Reid, I.; Niebles, J.C.; Rezatofighi, H. Socially and contextually aware human motion and pose forecasting. IEEE Robot. Autom. Lett. 2020, 5, 6033–6040. [Google Scholar] [CrossRef]
- Daniel, N.; Larey, A.; Aknin, E.; Osswald, G.A.; Caldwell, J.M.; Rochman, M.; Collins, M.H.; Yang, G.Y.; Arva, N.C.; Capocelli, K.E.; et al. PECNet: A deep multi-label segmentation network for eosinophilic esophagitis biopsy diagnostics. arXiv 2021, arXiv:2103.02015. [Google Scholar]
- Taylor, G.W.; Hinton, G.E. Factored conditional restricted Boltzmann machines for modeling motion style. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 1025–1032. [Google Scholar]
- Grassia, F.S. Practical parameterization of rotations using the exponential map. J. Graph. Tools 1998, 3, 29–48. [Google Scholar] [CrossRef]
- Ernst, M.J.; Rast, F.M.; Bauer, C.M.; Marcar, V.L.; Kool, J. Determination of thoracic and lumbar spinal processes by their percentage position between C7 and the PSIS level. BMC Res. Notes 2013, 6, 58. [Google Scholar] [CrossRef]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Jiang, X.; Sun, J.; Li, C.; Ding, H. Video image defogging recognition based on recurrent neural network. IEEE Trans. Ind. Informatics 2018, 14, 3281–3288. [Google Scholar] [CrossRef]
- Lin, C.B.; Dong, Z.; Kuan, W.K.; Huang, Y.F. A framework for fall detection based on OpenPose skeleton and LSTM/GRU models. Appl. Sci. 2020, 11, 329. [Google Scholar] [CrossRef]
- Ma, H.; Cao, J.; Mi, B.; Huang, D.; Liu, Y.; Li, S. A gru-based lightweight system for can intrusion detection in real time. Secur. Commun. Netw. 2022, 2022, 5827056. [Google Scholar] [CrossRef]
- Ionescu, C.; Papava, D.; Olaru, V.; Sminchisescu, C. Human3.6M: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
- Lab, C.G. CMU Graphics Lab Motion Capture Database Converted to FBX. Available online: https://mocap.cs.cmu.edu/ (accessed on 25 June 2025).
- Müller, M.; Röder, T.; Clausen, M.; Eberhardt, B.; Krüger, B.; Weber, A. Mocap database hdm05. Institut Inform. II Univ. Bonn 2007, 2. Available online: https://resources.mpi-inf.mpg.de/HDM05/ (accessed on 25 June 2025).
- Ofli, F.; Chaudhry, R.; Kurillo, G.; Vidal, R.; Bajcsy, R. Berkeley mhad: A comprehensive multimodal human action database. In Proceedings of the 2013 IEEE Workshop on Applications of Computer Vision (WACV), Clearwater Beach, FL, USA, 15–17 January 2013; pp. 53–60. [Google Scholar]
- Xia, S.; Wang, C.; Chai, J.; Hodgins, J. Realtime style transfer for unlabeled heterogeneous human motion. ACM Trans. Graph. (TOG) 2015, 34, 1–10. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., Alché-Buc, F.d., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-stgcnn: A social spatio-temporal graph convolutional neural network for human trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 14424–14432. [Google Scholar]
- Wang, H.; Dong, J.; Cheng, B.; Feng, J. PVRED: A Position-Velocity Recurrent Encoder-Decoder for Human Motion Prediction. IEEE Trans. Image Process. 2021, 30, 6096–6106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
