CaDCR: An Efficient Cascaded Dynamic Collaborative Reasoning Framework for Intelligent Recognition Systems

Abstract

To address the challenges of high computational cost and energy consumption posed by deep neural networks in embedded systems, this paper presents CaDCR, a lightweight dynamic collaborative reasoning framework. By integrating a feature discrepancy-guided skipping mechanism with a depth-sensitive early exit mechanism, the framework establishes hierarchical decision logic: dynamically selects execution paths of network blocks based on the complexity of input samples and enables early exit for simple samples through shallow confidence assessment, thereby forming an adaptive computational resource allocation strategy. CaDCR can both constantly suppress unnecessary computational cost for simple samples and satisfy hard resource constraints by forcibly terminating the inference process for all samples. Based on this framework, we design a cascaded inference system tailored for embedded system deployment to tackle practical deployment challenges. Experiments on the CIFAR-10/100, SpeechCommands datasets demonstrate that CaDCR maintains accuracy comparable to or higher than baseline models while significantly reducing computational cost by approximately 40–70% within a controllable accuracy loss margin. In deployment tests on the STM32 embedded platform, the framework’s performance matches theoretical expectations, further verifying its effectiveness in reducing energy consumption and accelerating inference speed.

1. Introduction

In recent years, with the advancement of deep learning technology, deep neural networks have demonstrated exceptional performance in fields such as autonomous driving [1], speech recognition [2], and image recognition [3,4,5]. However, these models involve millions or even billions of computational operations. Their high computational complexity and lengthy inference time severely restrict deployment in resource-constrained environments [6] (e.g., mobile devices, embedded systems, and edge devices). To address the above challenges, researchers have conducted extensive studies on model design. Lightweight model design involves using more simplified and less computationally intensive operations, such as group convolution, depthwise separable convolution, dilated convolution, and other methods. Based on these approaches, models such as MobileNet [7], ShuffleNet [8], and Inception [9] have been developed. However, the inference process of such models still involves high computational cost and parameter counts, often resulting in lengthy inference time in the absence of dedicated hardware acceleration.

Studies have shown that deep neural networks universally suffer from parameter redundancy and over-parameterization issues [10]. A large number of neuron connections not only increases computational cost but may also degrade model accuracy due to information noise. Therefore, model compression can be achieved by reducing the number of network parameters, neurons, and pruning unnecessary neurons. Common methods include model quantization [10,11,12], model pruning [13,14], low-rank matrix factorization [15], knowledge distillation [16], etc. Although these methods compress the model’s computational cost and parameters, they do not significantly address the complexity issue of models; simple classification tasks still require passing through the entire network.

Han et al. systematically reviewed Dynamic Neural Networks (DNNs) [17]. DNNs’ core advantage lies in their ability to adaptively adjust network structures or computational paths during inference based on input sample characteristics (such as image complexity or dynamic features of time-series data). DNNs offer the following key advantages: First, by activating specific network components (e.g., layers, channels, or subnetworks) on-demand, dynamic networks reduce computations for simple samples or low-information regions. Second, through data-driven architectural or parameter adjustments, dynamic networks can significantly expand the parameter space, thereby enhancing feature representation capabilities. Third, dynamic networks can adapt computational budgets according to hardware devices and task requirements. It is noteworthy that such dynamism also introduces new security considerations: studies show adversarial examples can surgically target specific computational stages, e.g., altering critical features through localized perturbations [18].

Numerous research directions have emerged based on DNNs. For example, some studies investigate early exit mechanisms by adding side branches and setting early exit points at different layers of deep neural networks [19,20,21,22]. When a sample can be classified with high confidence at an early layer, it exits directly through the early exit classifier, reducing computations for remaining layers. Studies [23,24,25,26,27,28] on dynamic skipping mechanisms demonstrate that these approaches can significantly reduce computational cost while maintaining prediction accuracy, achieved by dynamically skipping redundant network blocks. However, in strictly resource-constrained scenarios (such as a maximum FLOPs budget of x), merely relying on simple dynamic networks fails to meet hard constraints. Although Wang et al. [29] proposed the DDI framework, making the first attempt to fuse the two mechanisms, but it did not explicitly discuss the synergy between the two mechanisms, and its complex inference mechanisms are often difficult to reproduce.

Based on the above discussions, the contributions of this paper are as follows:

(1)

We propose a learning method based on local feature discrepancy to improve the complex training mechanism of dynamic skipping mechanisms, which is detailed in Section 3.1.

(2)

Aiming to achieve a simpler and more convenient fusion of dynamic skipping mechanisms and early exit mechanisms, we introduce the CaDCR framework, as elaborated in Section 3.3. This framework enables dynamic decision-making on which network blocks to execute, and allows simple samples to exit the network early for classification, thereby reducing energy consumption and inference time, and enables anytime classification under computational budget constraints. Additionally, a pruning strategy is designed to minimize unnecessary computational and storage overheads.

(3)

For networks designed under the CaDCR framework, we propose a cascaded system deployment scheme and implement it on embedded devices, providing them with inference capabilities for skipping and early exiting. The deployment details and experimental results are presented in Section 4.5.

The implementation of this framework consists of two main stages. In the first stage, the dynamic skipping mechanism is trained by inserting a skip gating network after each network block (e.g., residual block), which uses binary masks to determine whether to skip or execute subsequent blocks. During the training of the skipping mechanism, we employ Softmax for training and gradient propagation, combined with a feature discrepancy-driven auxiliary loss, to automatically learn the allocation strategy of computational resources and balance model accuracy with computational efficiency. In the second stage, we insert early exit classifiers (also via skip gating networks) into the optimal network obtained from the first stage, enabling both mechanisms simultaneously during training. To ensure that the original skipping decisions remain unaffected, no loss from the skip gating networks is added during training, and forward propagation is performed using “hard” decisions. During inference, early exit judgments are made before skipping mechanism judgments to avoid conflicts. Furthermore, to encourage the model to exit as early as possible, we design a depth-sensitive weight joint loss to promote earlier exits. It is important to emphasize that this paper does not focus on the optimization of branch networks.

The remaining sections of this paper are structured as follows: Section 2 reviews related research on dynamic skipping mechanisms, early exit mechanisms, and their fusion strategies, analyzing the technical characteristics and limitations of existing approaches. Section 3 elaborates on the design of the CaDCR framework, including the proposed LFDS (Local Feature Discrepancy-guided Dynamic Skipping), DSWE (Depth-Sensitive Weight Early Exit), and their hierarchical collaborative strategy. Section 4 validates the framework’s performance in computational efficiency and accuracy retention through multiple experiments, while analyzing the collaborative relationships and model behavior. Finally, Section 5 summarizes the research achievements and outlines potential future research directions.

2. Related Works

In the research of deep learning models in resource-constrained scenarios, dynamic neural networks have emerged as a critical direction due to their ability to adaptively adjust computational paths based on input characteristics. This section reviews the current research from three aspects: dynamic skipping mechanisms, early exit mechanisms, and their fusion mechanism, analyzes the technical characteristics and limitations of each approach, and provides a theoretical basis for the design of the CaDCR framework.

2.1. Dynamic Skipping Mechanism

Early forms of dynamic skipping mechanisms were proposed by Highway networks [30], which introduced gating mechanisms to control information flow, enabling automatic path adjustment in deeper networks and providing foundational ideas for subsequent research. Due to the residual blocks and balanced dimensionality of ResNet [31], it has gradually become the mainstream platform for dynamic skipping mechanism research. Most studies on skipping mechanisms are based on ResNet variants.

Blockdrop [23] uses reinforcement learning to dynamically select residual block execution paths, significantly reducing computational cost while maintaining prediction accuracy. SkipNet [24] designs multiple types of gating networks, achieving dynamic skipping of redundant residual blocks in residual networks through a hybrid learning algorithm (combining supervised learning and reinforcement learning). EnergyNet [25] introduces an energy-aware dynamic routing strategy, integrating gating networks with an energy loss function to significantly reduce energy consumption during inference in convolutional neural networks while maintaining or improving prediction accuracy. ConvNet-AIG [26] learns category-related inference graphs to discover hierarchical structures of categories without explicit supervision. E2-Train [27] proposes an input-dependent selective layer update (SLU) strategy, dynamically selecting different subsets of CNN layers for update in each mini-batch during the training phase. DFS [32] views different bitwidths as intermediate states of layer skipping. For each input, it dynamically determines the bitwidths for both weights and activations of each layer through a dynamic gating network, enabling “fractional” execution. While the above methods have achieved remarkable performance, most of them are difficult to implement and not suitable for deployment in edge systems.

2.2. Early Exit Mechanism

Classic research on early exit mechanisms can be traced back to BranchyNet [19], which proposed constructing branch networks as early exit classifiers to enable early termination via side branches for samples meeting confidence thresholds. This foundational paradigm has provided critical references for subsequent research, with diverse research directions emerging based on different focuses.

In terms of confidence measurement methods, existing studies primarily employ the following techniques: FlexDNN [20] measures prediction confidence via the entropy value of samples, terminating inference early if the entropy falls below a predefined threshold. Reference [33] uses the highest probability value in the output vector of the Softmax layer to assess prediction confidence. Reference [34] uses a stopping function as the confidence criterion. E2CM [35] proposes a class-mean-based exit strategy, making exit decisions without classifiers by comparing layer output features with global sample class mean features. Regarding model training strategies, research teams have demonstrated distinct technical characteristics: BranchyNet [19] trains by integrating loss functions of each side branch as a unified optimization problem. MSDNet [36] introduces a progressive training strategy, alternately freezing trained branch parameters and updating subsequent networks during iterations. EPNet [37] adopts a two-stage training approach: first, fully training the backbone network, then freezing backbone parameters and independently training each side branch classifier.

Additionally, addressing issues such as exit network diversity, threshold uncertainty, and insertion position selection in early exit mechanisms, related research is shifting toward automated search directions. The DyCE [38] framework proposes a search algorithm that generates optimal configurations based on user-defined performance-complexity preferences. EDANAS [21] leverages neural architecture search (NAS) technology to simultaneously complete architectural design and parameter optimization of early exit networks.

2.3. Fusion Mechanism

Systematic research on the collaborative optimization of dynamic skipping and early exit mechanisms is currently in an exploratory phase. E2-Train [27] reduces energy consumption during training through three complementary optimization strategies at data, model, and algorithm levels: stochastic mini-batch dropping at the data level, input-dependent selective layer update at the model level, and predictive sign gradient descent at the algorithm level. The DDI [29] framework has made efforts to fuse these mechanisms by providing channel skipping capabilities for dynamic skipping and inserting early exit classifiers at fixed positions. However, their content primarily focuses on the skipping mechanism, with a relatively simplistic fusion process and complex training, while failing to adequately explain the synergy between the two methods.

3. Design of the CaDCR Framework

In application scenarios of edge and embedded devices, computational resources and energy supply are often subject to hard constraints [29], while traditional methods struggle to effectively address the dynamic complexity of models. The framework aims to simply and effectively tackle the dynamic complexity of models, enabling on-demand activation of computations. Its core lies in the principle that—at any time and for any input sample—when one meets the preset hard resource constraints, one must immediately cease computation and output a prediction result. This section first elaborates on the principle of the dynamic skipping mechanism, constructing a local feature discrepancy-guided dynamic skipping mechanism that reduces training complexity via a feature discrepancy-driven auxiliary loss. Subsequently, we design a depth-sensitive weight early exit mechanism, embedding lightweight classification branches based on depthwise separable convolutions and hierarchical loss constraints. Finally, the framework proposes a phased training strategy to achieve the fusion of the two mechanisms.

Figure 1 illustrates the overall architecture of the CaDCR framework, comprising three key functional modules: skip gating networks, early exit classifiers, and pruning. Skip gating networks dynamically adjust computational cost based on input difficulty. Early exit classifiers enable classification accuracy maintenance under preset resource constraints. The pruning module prunes unnecessary connections to save storage resources. Each module will be elaborated on in the subsequent sections.

3.1. CaDCR Framework Components 1: Local Feature Discrepancy-Guided Dynamic Skipping Mechanism (LFDS)

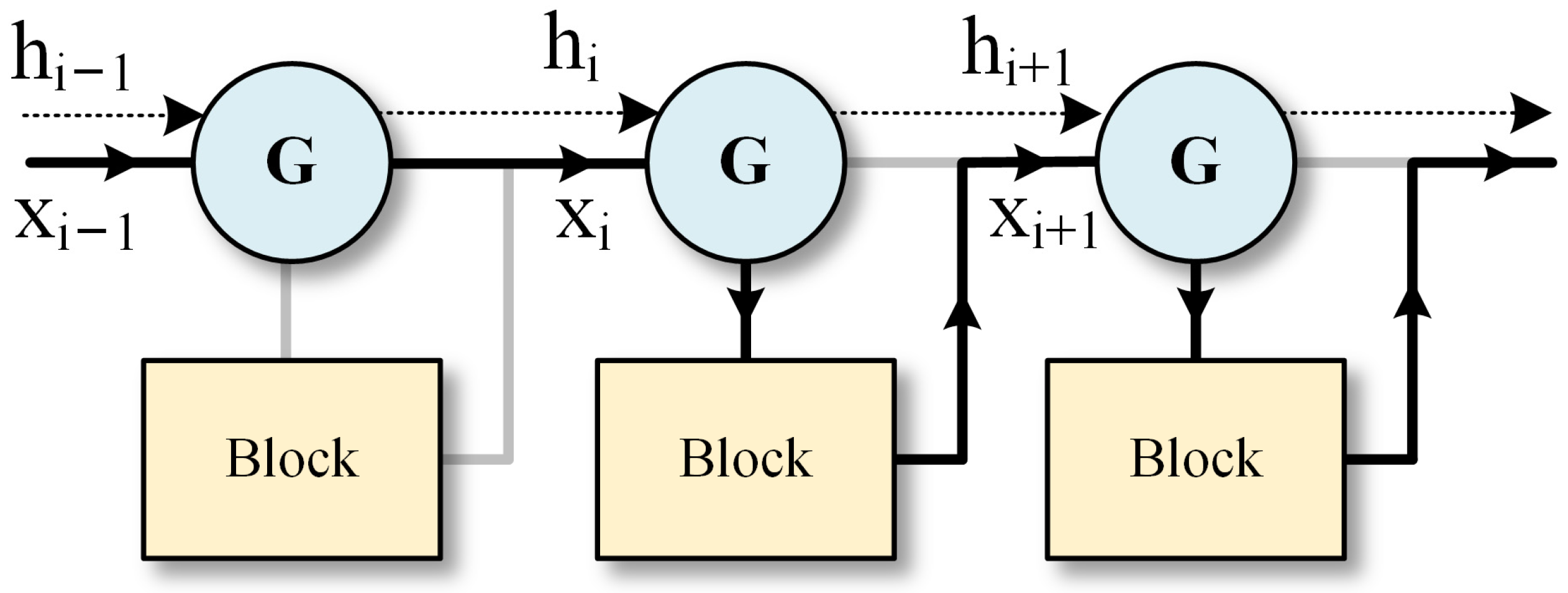
Deep neural networks exhibit excellent performance in various tasks, yet the increase in network depth significantly elevates computational cost and inference time. In reality, not all input data requires processing through a fully deep network—some simple samples can be predicted using a small number of network layers. The CaDCR framework reduces inference computation by dynamically skipping partial convolutional layers (residual blocks) in the network. The operational logic of this mechanism is illustrated in Figure 2.

First, the sample enters the skip gating network for judgment. If the gating network is confident in skipping the current network block for the sample, it will jump to the next network block; otherwise, it will execute the current block. Regarding the structural design of gating networks, SkipNet [24] proposed two types: the Feed-forward Gate (FFGate) and the Recurrent Gate (RNNGate). RNNGate outperforms FFGate due to its shared parameters in the RNN layer, demonstrating advantages not only in computational efficiency (lower cost) but also in prediction accuracy, with almost negligible computational cost. Based on these advantages, this framework takes the design of RNNGate as a benchmark and employs an LSTM layer as the hidden layer to construct the gating network, as shown in the Skip Gating Network of Figure 1. To ensure compatibility between residual blocks of different output dimensions and the same gating network, adaptive average pooling and 1 × 1 convolutional layers are used to unify the number of channels.

Taking ResNet as the backbone network, we demonstrate the inference process of the dynamic skipping mechanism [24]. Assuming the input sample to the i-th layer is $x_i$ the gating network is denoted as $G(·)$, and the i-th residual block is denoted as $B_i(·)$, the formula during inference is expressed as follows:

$$x_{i+1}=\underset{G\left(x_i\right)}{\underbrace{\sigma \left(W_i·LSTM\left(B_i\left(x_i\right)\right)\right)}}·B_i\left(x_i\right)+\left(1-G\left(x_i\right)\right)·x_i$$

(1)

It is worth noting that the binary decisions {0, 1} output by the gating network are discrete and non-differentiable, posing challenges for model training. The solution proposed by SkipNet involves first using pre-supervised training to learn the discrete mechanism, followed by leveraging reinforcement learning to optimize the parameters in the decision-making process.

To streamline the training process, we propose a guidance approach based on local feature discrepancy (called LFDS), replacing the indirect optimization of reinforcement learning with direct supervisory signals to reduce training complexity. We introduce this discrepancy as an auxiliary loss term, encouraging the gating mechanism to skip when the output information of the current layer significantly differs from that of the previous layer. During the model’s forward propagation, the L2 norm is used to compute the discrepancy between the output features of each layer and those of the previous layer, serving as the input signal for gating decisions:

$$D_i={‖F_i\left(x_i\right)-F_{i-1}\left(x_{i-1}\right)‖}_2^2$$

(2)

where $F(·)$ denotes the output features of the gating network. The resulting discrepancy $D_i$ cannot be directly used as a probability and must be mapped to the (0, 1) interval to guide the target probability for skipping:

$$p_i=sigmoid\left(-\kappa ·D_i\right)={\displaystyle \frac{1}{1+\mathrm{e}\mathrm{x}\mathrm{p}(\kappa ·D_i)}}$$

(3)

where $\kappa$ serves as a temperature coefficient to guide the skipping tendency, thereby enhancing the sensitivity of discrepancies to skipping propensity. When the discrepancy is large, the Sigmoid output approaches 0, corresponding to a low skipping probability (retaining the layer). Conversely, when the discrepancy is small, the Sigmoid output approaches 1, enabling the gating network to output a high skipping probability (skipping the layer). The binary cross-entropy (BCE) loss is employed as the auxiliary loss function, formulated as:

$${\mathcal{L}}_{BCE}={\displaystyle \frac{1}{N}}\sum _{i=1}^{N}BCE(p_i,G(x_i\left)\right)$$

(4)

The total loss function is composed of the classification loss and the auxiliary loss:

$${\mathcal{L}}_{TOTAL}={\mathcal{L}}_{CE}+\lambda {\mathcal{L}}_{BCE}$$

(5)

Following the aforementioned improvements, the network gains the capability to autonomously select skipping strategies based on diverse inputs. The extent of network skipping can be regulated by adjusting the weight $\lambda$ of the auxiliary loss. Figure 3 illustrates the process through which the skip gating network learns the skipping mechanism by leveraging Equation (2). When the feature discrepancy is substantial, the skip gating network tends to make execution decisions; conversely, when the feature discrepancy is minimal, it inclines toward making skipping decisions.

3.2. CaDCR Framework Components 2: Depth-Sensitive Weight Early Exit Mechanism (DSWE)

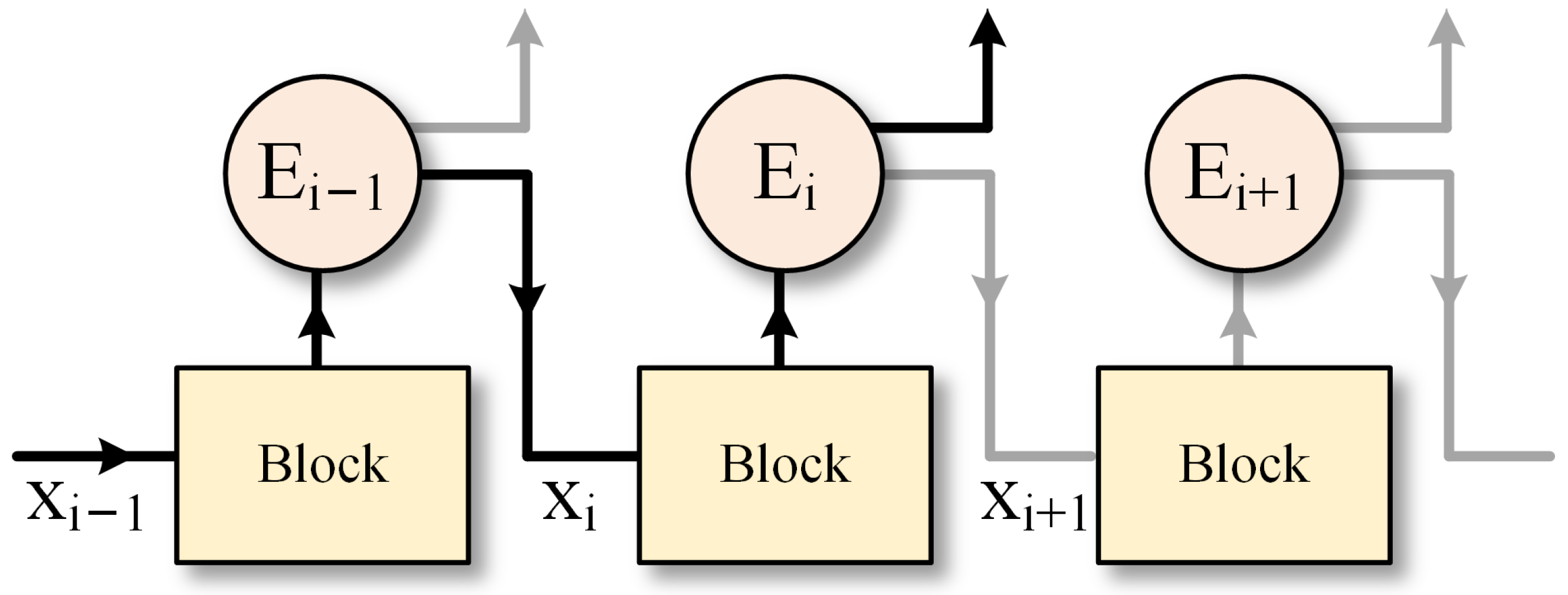
Deep neural networks commonly exhibit computational redundancy when processing simple samples [39]—shallow network architectures often possess sufficient predictive capability, yet completing the full network computation flow incurs unnecessary consumption of computational resources. To address this, the CaDCR framework embeds early exit classifiers at critical network layers. When sample features processed by shallow layers achieve a classification confidence score exceeding a predefined threshold, the inference process can terminate early via the branch classifier. The operational logic of this mechanism is illustrated in Figure 4.

Early exit classifiers are typically integrated into the backbone network in the form of branch networks, requiring a balance between computational efficiency and classification accuracy. For example, Chen et al. employed a single fully connected layer as the architecture for exit branches, though this approach is often limited by dimensionality issues and lacks flexibility in practical applications [40]. Other designs include multiple fully connected layers [41], a convolutional block [42], and so on. Considering that depthwise separable convolutions offer the advantages of fewer parameters and stronger learning capability, this paper designs lightweight exit branches based on depthwise separable convolutions. The network architecture is shown in the Early Exit Classifier of Figure 1.

Assuming the input sample to the i-th layer is $x_i$ and the early exit classifier is denoted as $E_i(·)$, the formula during inference is expressed as:

$$x_{i+1}=\left\{\begin{array}{c}Exit\\ B_i\left(x_i\right)\end{array}\right.\begin{array}{c}if H\left(E_i\left(x_i\right)\right)<\tau \\ else\end{array}$$

(6)

The early exit classifier employs entropy as the confidence threshold. When the entropy of the classified data is less than a predefined threshold, the data is considered to meet the classification requirement, and the inference process can terminate early to avoid deep-layer computations. During the training phase, a joint training approach is adopted for the early exit classifiers, treating the backbone network and all branch classifiers as a unified optimization problem.

To encourage the model to prioritize classification through shallow branches, depth-sensitive weights ${\omega }_i$ are employed for loss regularization. This approach is referred to as DSWE. The training loss is expressed as:

$${\mathcal{L}}_{EXIT}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\omega }_i·{\mathcal{L}}_{CE}\left(p_i,E_i\left(x_i\right)\right), {\omega }_i=1+{\displaystyle \frac{i}{N}}\alpha$$

(7)

The weight design of ${\omega }_i$ encourages the model to exit early within its capability, rather than forcing all samples to exit at shallow layers. If shallow features are insufficient, the classifier automatically continues computation because its confidence is lower than $\tau$; in this case, the penalty of ${\omega }_i$ does not take effect because the exit decision is not triggered.

3.3. Hierarchical Integration of Collaborative Mechanisms

To achieve collaborative optimization of the two mechanisms, training the CaDCR framework involves two phases. Taking ResNet as the backbone network, this section elaborates on the design principles and implementation details of each phase:

Phase 1: Select the backbone network for pretraining (pretraining is optional), and insert skip gating networks after each residual block. Note that the last residual block is excluded from this insertion as it directly feeds into the classifier. To guide the model in learning skipping strategies, the average skipping rate is constrained via a regularization term coefficient to meet our predefined expectations.

Phase 2: Embed early exit classifiers at the same positions in the network trained in Phase 1. During training, a hierarchical loss function is adopted without altering the backbone network parameters, so as to avoid disrupting the key paths learned by LFDS. Notably, to address the priority conflict issue when both mechanisms coexist, this framework proposes a hierarchical decision logic: during inference, the confidence judgment of early exit is prioritized. If the exit criteria are met, the classification result is directly output; otherwise, skipping decisions are made.

Based on the above-described decision mechanism, the inference logic can be expressed as:

$$x_i=\left\{\begin{array}{c}Exit\\ G\left(x_i\right)·B_i\left(x_i\right)+\left(1-G\left(x_i\right)\right)·x_i\end{array}\right.\begin{array}{c}if H\left(E_i\left(x_i\right)\right)<\tau \\ else\end{array}$$

(8)

where $H(·)$ denotes entropy, and $\tau$ represents the confidence threshold. This strategy ensures that simple samples terminate computation early via the early exit mechanism, while complex samples leverage the dynamic skipping mechanism to bypass redundant residual blocks, thereby forming a hierarchical computational control strategy that achieves efficient allocation of computational resources during the processing of samples with varying complexity. This also ensures that the feature extraction paths of the backbone network have been screened according to sample complexity. Blocks with high skipping rates typically correspond to redundant computations involving minimal feature changes, while early exit points are inserted at positions with strong feature discriminability to guarantee the feature quality required by early exit classifiers.

3.4. After Training

Training through two stages can result in a complex and bulky network with multiple branches, which is contrary to our original intent and necessitates further network processing. Each passage through an early exit classifier involves computations in branch networks, introducing non-trivial computational overhead. Empirical observations from training and debugging reveal that blocks with a skipping rate approaching 1 emerge when the auxiliary loss weight $\lambda$ is high, and blocks with high skipping rates exhibit very low exit rates. These phenomena are linked to the inference-time design, and we leverage these insights to prune the network:

(1)

Set a high threshold for the skipping rate, and prune residual blocks whose skipping rates exceed this threshold. Such blocks, having been consistently skipped, contribute negligibly to feature representation and can be directly removed to reduce network depth.

(2)

Prune gating networks with a skipping rate of 0 to eliminate redundant computations.

(3)

Prune underperforming branches to avoid unnecessary computations and memory usage. As noted by FlexDNN [20], early exits do not always lead to computational reduction in all scenarios; a trade-off is required between the overhead of early exits and their resulting gains.

Following the above optimization steps, we constructed the overall network architecture of the CaDCR framework as illustrated in Figure 1. Leveraging the characteristics of its forward propagation, the network is treated as a cascade system where each module dynamically determines whether to activate the next computational unit based on input samples. This design enables stage-wise activation in embedded systems, achieving low-power consumption and high inference speed.

4. Experiments, Analysis, and Discussion

To validate the practical performance of the CaDCR framework in computational efficiency, classification accuracy, and embedded deployment scenarios, this chapter presents the experimental design and discussion. Experiments establish a benchmark comparison system using ResNet38/74 as backbone networks, based on CIFAR-10/100 and SpeechCommands datasets. We evaluate the optimization efficacy of LFDS through comparative analysis and test the CaDCR framework’s adaptability under hard resource constraints. Through analyzing the stage-wise training strategy and verifying mechanism synergy, we elaborate the design principles of the framework. By integrating feature discrepancy distribution and category-level computational path visualization, we decode the model’s decision-making logic. Finally, we implement cascaded system deployment on the STM32 platform.

4.1. Experimental Design and Baseline Models

Datasets and Backbone Networks: This paper employs the CIFAR-10/100 and SpeechCommands datasets as benchmark sets, using common data augmentation schemes. ResNet38 and ResNet74 are adopted as backbone networks. The residual blocks of each network are divided into three groups with an equal number of blocks per group.

Skip Gating Networks: The output of each residual block is flattened and fed into an LSTM layer with a hidden unit size of 10. Its output undergoes further compression and non-linear mapping to generate a probability value, which guides whether to skip the current residual block.

Early Exit Classifiers: Since they do not share parameters, they are designed to be resource-efficient. Average pooling is used to adapt to residual blocks with different output channel numbers, followed by depthwise separable convolutions with both input and output channels set to 64. The depthwise convolution employs a 3 × 3 kernel size.

Insertion Positions: Both networks use the same insertion positions to ensure meaningful placement: corresponding modules are inserted after each residual block, except for the last one. This design ensures that the first residual block focuses on feature extraction, while the last residual block connects directly to the final classification layer.

The selected baseline models and their classification accuracies are presented in

Table 1. Baseline models and classification accuracy.

Baseline Model	Layers	CIFAR-10	CIFAR-100	SpeechCommands v0.02
ResNet38	[6, 6, 6]	92.57%	68.52%	92.76%
ResNet74	[12, 12, 12]	93.09%	70.45%	93.5%

:

4.2. Performance of the Proposed LFDS Method and CaDCR Framework

4.2.1. Performance of the LFDS Method

To verify and demonstrate the overall performance of the LFDS method in this paper, we use CIFAR10 as the dataset for comparison with other state-of-the-art (SOTA) methods. The comparison of FLOPs/accuracy is shown in the figure below. Since the FLOPs of the skipping gating network account for only 0.1% of the backbone network, they are not included in the calculation. In Figure 5, We compare LFDS with other cutting-edge skipping methods. When compare FLOPs, LFDS achieves a Top-1 accuracy similar to EnergyNet, ResNet38-DFS [32] and ResNet-IADI, outperforming SkipNet and BlockDrop. At 90% accuracy, its computational cost is only 38.46% of SkipNet. As IADI and DFS employ finer-grained strategies, ResNet-LFDS slightly lags behind these methods in performance; however, LFDS is simpler and more straightforward to implement, making it better suited for deployment in edge systems with limited computational capabilities—a merit unmatched by other approaches.

When compared with the baseline models ResNet38 and ResNet74 in Figure 6, the proposed method achieves 1.01% and 0.76% higher accuracy while consuming 76.10% and 74.85% of their FLOPs, respectively. When the accuracy is comparable to the baselines, the FLOPs occupied are only 61.95% and 47.37%. At 90% accuracy, the FLOPs account for 23.59% and 12.29% of the baselines, respectively. Overall, when the FLOPs are equivalent, the classification accuracy gaps between the two types of networks are minimal, with nearly identical FLOPs/Accuracy curves.

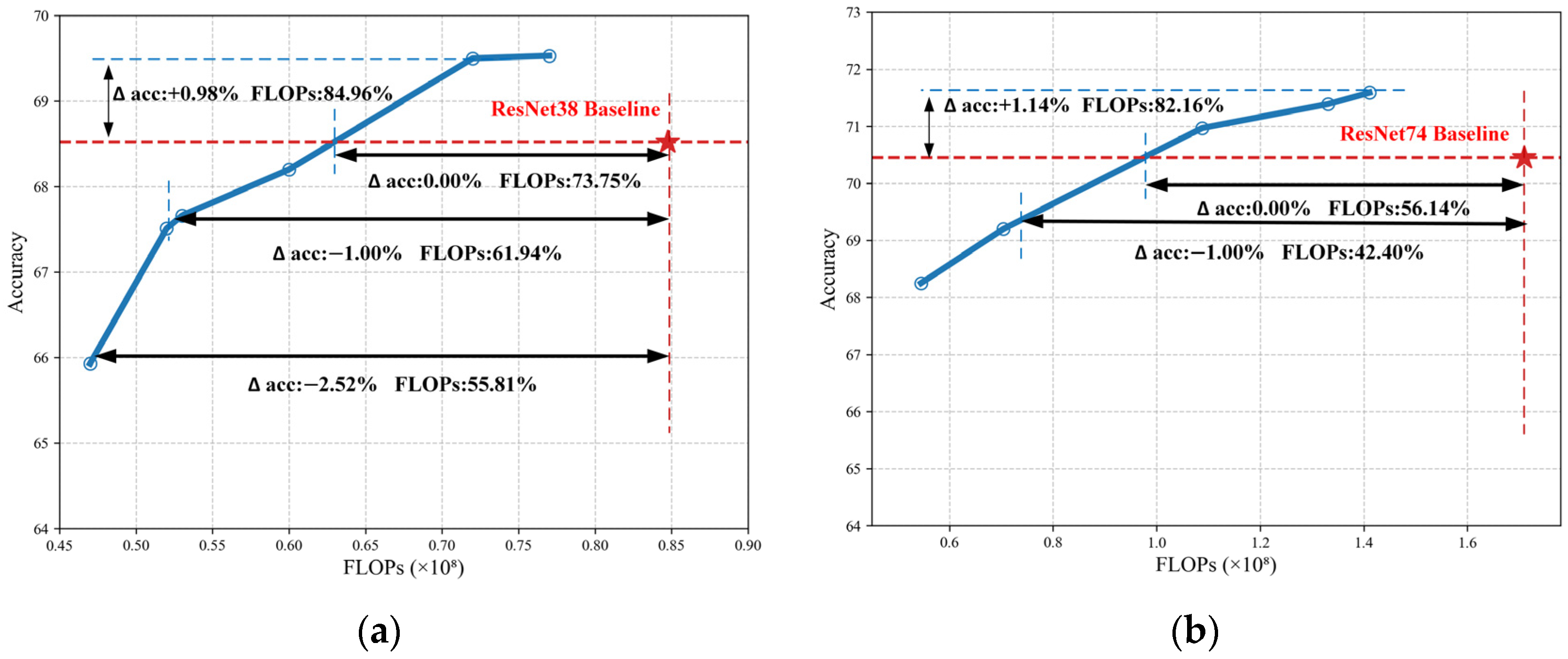
The performance on the CIFAR-100 dataset follows a similar pattern. In Figure 7, the proposed method achieves 0.98% and 1.14% higher accuracy while consuming 84.96% and 82.16% of the FLOPs of the baseline ResNet38 and ResNet74 models, respectively. When achieving the same Top-1 accuracy as the baselines, the FLOPs occupied are 73.75% and 56.14% of the baseline values.

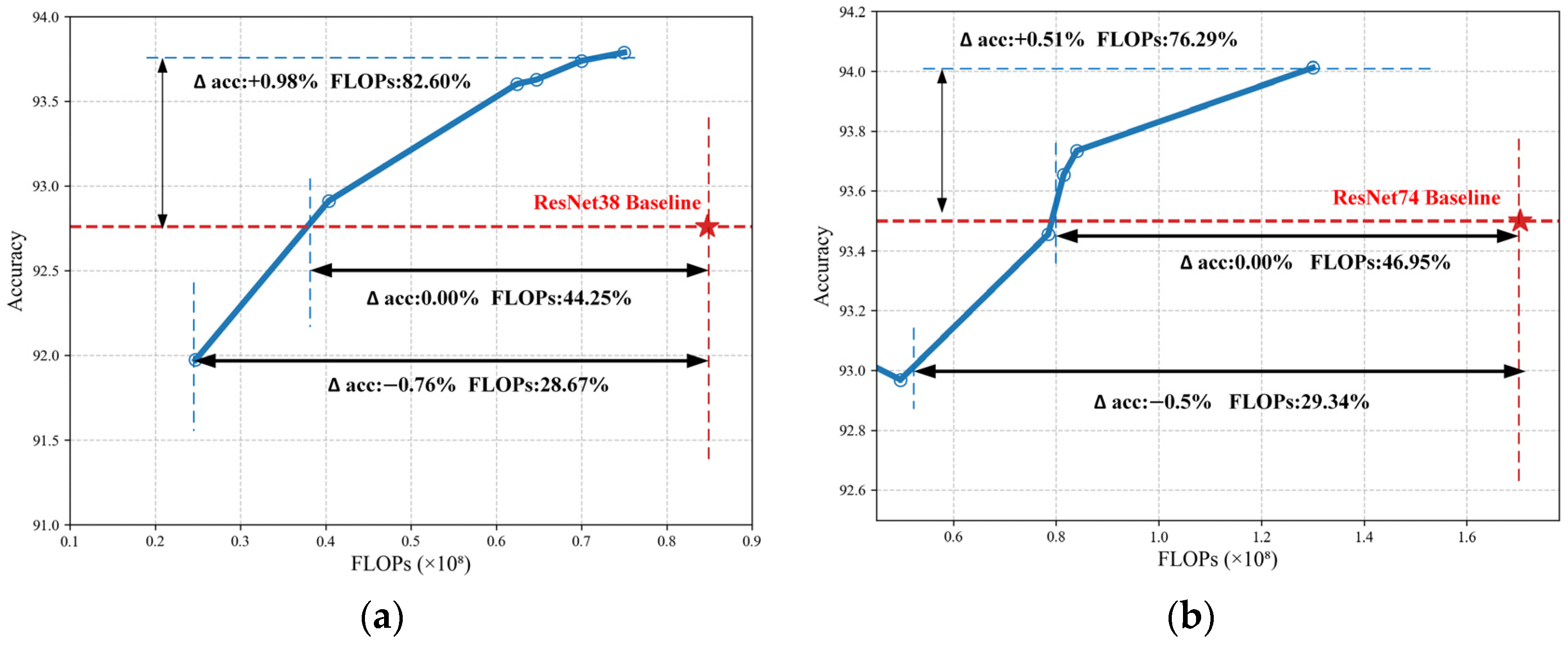
LFDS also demonstrates similar performance on the SpeechCommands dataset, which features time-series characteristics, as observed in the previously discussed scenarios. Experimental results in Figure 8 demonstrate that when using ResNet38 as the backbone network, LFDS reduces the computational cost to 82.60% of the baseline model while maintaining a Top-1 accuracy of 93.74%. When achieving accuracy comparable to the baseline model, the FLOPs are only 44.25% of the original computational cost. For the deeper ResNet74 architecture, LFDS achieves an accuracy of 94.01% (a 0.51% improvement over the baseline), while reducing FLOPs to 76.29%. Under equivalent accuracy conditions, the computational cost can be further reduced to 46.95%.

4.2.2. Performance of the CaDCR Under Hard Resource Constraints

To evaluate the ability of the DSWE method alone and the CaDCR framework to adapt to the hard resource constraints typical in embedded systems, we conducted experiments under predefined computational budgets. Specifically, we enforced a preassigned computational limit (measured in FLOPs) during inference. For each test sample, the framework halts processing and immediately outputs a prediction upon reaching the accumulated computational budget, leveraging the nearest available early exit classifier. The selected base networks include ResNet20 (42 M), ResNet26 (56 M), ResNet32 (70 M), and ResNet38 (85 M).

Table 2. Comparison between CaDCR and base model under resource constraints on CIFAR-10.

FLOPs	Base Acc	DSWE Acc	CaDCR Acc	Δ Acc
42 M	91.12%	88.35%	91.55%	+0.43%
58 M	91.60%	89.77%	92.42%	+0.82%
74 M	92.33%	90.34%	92.48%	+0.15%
84 M	92.50%	91.02%	93.26%	+0.76%

presents the accuracy results under different hard constraints using ResNet74 as the base network. ResNet-CaDCR achieves comparable or even higher accuracy than the baseline models across various FLOPs constraints, while DSWE alone not only performs worse than CaDCR but also fails to match the accuracy of baseline models, demonstrating the effectiveness of CaDCR.

4.3. Optimization of Training Strategies and Synergy Analysis

This section explores the training strategies and synergy of LFDS and DSWE in the CaDCR framework, aiming to achieve efficient computational resource allocation through hierarchical optimization and mechanism collaboration. To avoid parameter conflicts during dynamic mechanism integration, CaDCR adopts a stage-wise training strategy: first, training LFDS to determine efficient backbone paths, then embedding and training DSWE’s early exit classifiers based on stable features. This decouples their optimization goals to prevent interference. In synergy, LFDS dynamically selects execution paths by sample complexity to reduce average computation, while DSWE enforces early termination via lightweight classifiers and confidence thresholds under hard resource constraints. Their collaboration addresses computational efficiency at different levels, enabling the framework to operate under hard resource limits.

4.3.1. Advantages of Stage-Wise Training Methods

As mentioned earlier, during training, the skipping mechanism is trained first, followed by the branches, while during inference, the early exit judgment is performed before the skipping mechanism judgment. Overall, the purpose of this design is to enable stage-wise decoupling optimization of the network and achieve progressive complexity control. The skipping mechanism first determines the efficient computational path of the backbone network, after which branch classifiers are added based on stable features. The objectives of the two components are optimized in stages to avoid mutual interference.

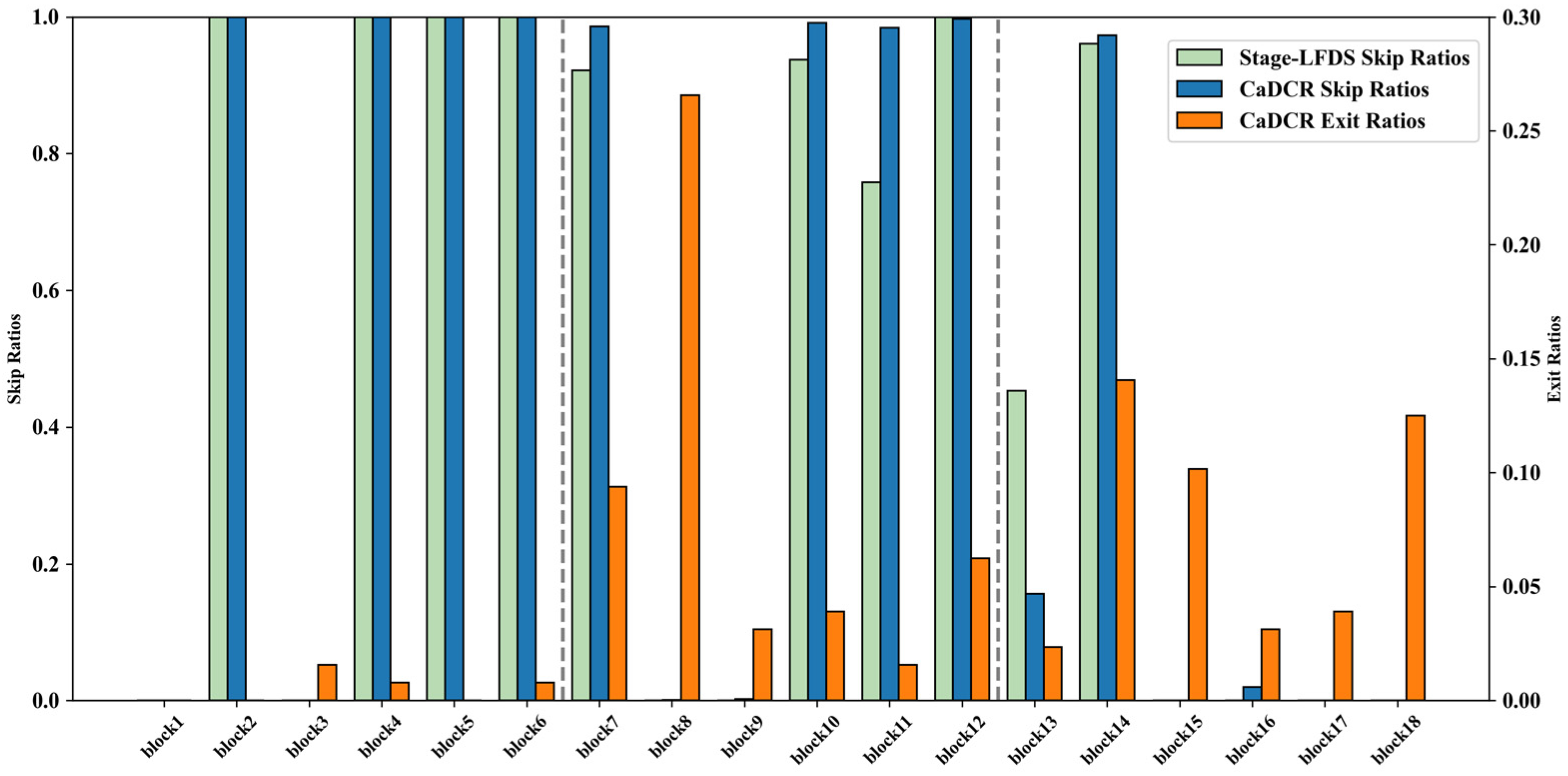
During the second-stage training, although joint loss optimization was not performed, the skipping strategy inevitably undergoes slight adjustments. As shown in Figure 9, the skipping rates and exit rates under the ResNet38-CaDCR framework with medium skipping weights are presented. In Figure 9, it can be observed that the skipping rates in the second phase are more concentrated and stable compared to the first phase, indicating that the introduction of the early exit mechanism optimizes the skipping distribution. Notably, high skipping rates correspond to low exit rates, while low skipping rates correlate with high exit rates—clear evidence of the collaborative operation of the two mechanisms and a demonstration that they can indeed complement each other.

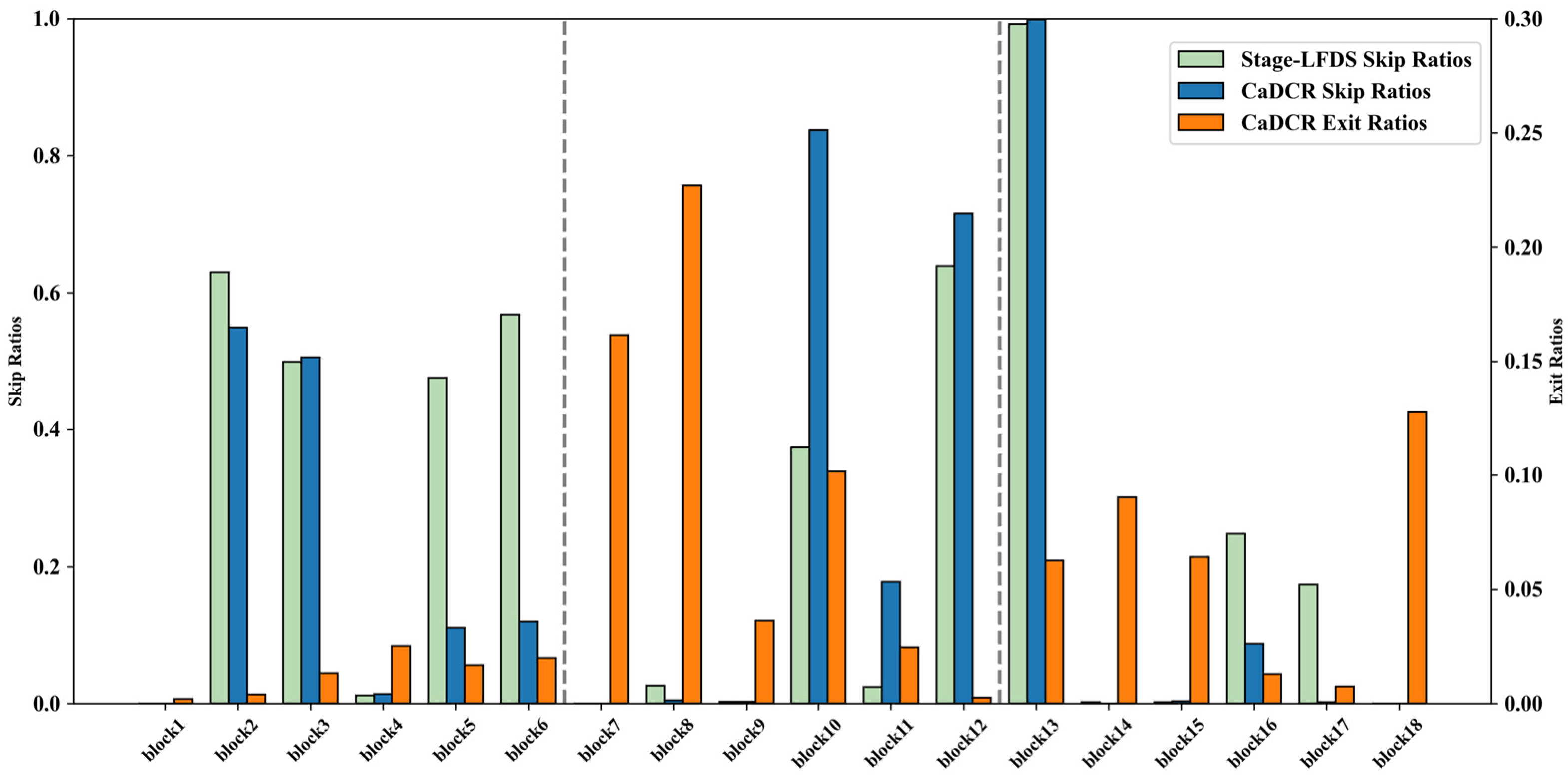
As shown in Figure 10, the comparison of skipping rates and exit rates under low skipping weights is presented. The model tends to encourage more early exits in sections with fewer skips, which is consistent with the earlier conclusion.

The goal of branch training is to enable samples to exit as early as possible to terminate computations under resource constraints, which requires a stable feature distribution. Introducing skipping mechanisms afterward may disrupt the features on which branch classifiers depend, leading to performance degradation. Therefore, it is essential to stabilize the skipping strategy before integrating early exit classifiers.

4.3.2. Synergy Between LFDS and DSWE

To demonstrate the independent contribution of LFDS and its synergistic effect with DSWE, this experiment conducts comparisons using three control models: the original ResNet (without dynamic mechanisms), ResNet-LFDS with only LFDS enabled, and ResNet-CaDCR under the full CaDCR framework. It is important to note that the total FLOPs of CaDCR include the computational overhead of early exit classifiers, while baseline models retain standard FLOPs to ensure fair comparison.

As shown in Figure 11, on the CIFAR-10 dataset, taking ResNet38-LFDS with a medium skip ratio as an example, FLOPs are reduced to 51.50% of the baseline model while maintaining a Top-1 accuracy loss of less than 1% (92.57% to 91.72%). This result indicates that the LFDS mechanism effectively identifies and skips redundant residual blocks, significantly enhancing computational efficiency. Further introducing DSWE reduces the FLOPs of ResNet38-CaDCR to 37.10% of the baseline model, with an accuracy decrease of only 0.82% (90.90%), validating the collaborative optimization capability of LFDS and DSWE.

Additionally, the complementarity between LFDS and DSWE varies significantly across different skipping rate scenarios. At high skipping rates, DSWE has limited FLOPs optimization space (about 8% reduction) because dynamic skipping has already drastically reduced the computational path, leaving fewer layers available for early termination and diminishing DSWE’s effectiveness. Conversely, at low skipping rates, DSWE contributes more significantly, achieving an additional approximately 30% reduction in FLOPs. This suggests that when more computational layers are retained, DSWE can effectively avoid deep-layer redundant computations by terminating inference for low-confidence samples early.

The core of the synergy between LFDS and DSWE lies in their joint resolution of computational efficiency issues at different levels, endowing the framework with the capability to operate under hard resource constraints. LFDS dynamically selects the execution paths of residual blocks in the backbone network based on input sample complexity, significantly reducing the average computational cost per sample. However, relying solely on LFDS has a critical limitation: for complex samples, even after skipping redundant blocks, the final execution path may still exceed the predefined resource budget. The introduction of the DSWE mechanism addresses this issue. By embedding lightweight classifiers at key layers and setting confidence thresholds, DSWE enforces early termination of inference for all samples when the predefined computational budget is reached.

4.4. Model Behavior Analysis

Taking the performance of ResNet38-CaDCR with medium skipping rates on the CIFAR-10 dataset as an example, we conduct a model behavior analysis. To verify the effectiveness of the adaptive skipping mechanism in making decisions based on feature discrepancy, we analyzed the distribution of inter-layer feature discrepancies when the network executes or skips layers. As shown in Figure 12, the blue histogram represents skipped samples, whose distribution is concentrated in regions with extremely low feature discrepancies; the orange histogram represents executed samples, with a significantly concentrated distribution in regions with higher feature discrepancies. These two clearly separated distributions indicate that the network’s skipping decision mechanism can effectively distinguish when to execute or skip layers based on the magnitude of feature discrepancies.

Furthermore, to demonstrate whether small feature discrepancies indicate redundancy, we fully trained the network and forced the layers with “small feature discrepancies and skipped” to execute. As shown in Figure 12, where “1” denotes samples with unchanged predictions and “0” denotes those with altered predictions, the prediction invariance rate remained consistently high after forcing these minimal-discrepancy layers to execute, with most model predictions unchanged. This indicates that under the LFDS mechanism, low feature discrepancies indeed correspond to strong layer redundancy. In other words, when the feature difference of a layer is small, its impact on the final classification result is limited, and its function tends to be redundant.

Figure 13 illustrates the preferences of different image categories for residual block skipping, revealing through analysis the underlying computational characteristics of the network: the network adopts distinct computational paths for images of different categories. For simple samples (e.g., automobiles, ships), the network tends to skip more residual blocks; when faced with complex samples (e.g., cats, birds), it reduces skipping and executes more computational layers to extract deeper features.

Figure 14 illustrates the classification difficulty of different image categories and corresponding confusion matrices, with the network divided into three equal parts. Samples are categorized into three groups based on early exit positions: EASY (exiting at the first part), MEDIUM (exiting at the second part), and HARD (exiting at the third part). Each part lists the top three labels with the highest exit counts. The analysis reveals distinct behavioral patterns of the model when processing samples of varying difficulty: For EASY samples, the model typically completes accurate classification at shallower network layers. These samples exhibit obvious features, clear boundaries, or distinct colors, leading to minimal feature discrepancies that require no excessive complex computations. Contrary to intuition, frog-class samples show a high frequency of early exits, indicating their features can be effectively recognized at initial stages. For MEDIUM samples, although the features are relatively clear, the model still requires intermediate-layer feature extraction and analysis. During this process, the model dynamically selects to skip residual blocks with insignificant feature discrepancies while performing classification based on the sample’s specific characteristics. For HARD samples, the features are often complex and ambiguous, sometimes even indistinguishable by humans. In such cases, the model must leverage the full depth and complexity of the network to extract and classify features accurately. The confusion matrix confirms that simple categories like car and ship, with unique features, show minimal confusion when exiting at shallow layers. In contrast, categories such as dog vs. cat, plagued by overlapping visual features, still exhibit misclassifications even with deep-layer processing, underscoring the model’s reliance on deep-network fine-grained feature extraction for high-similarity feature discrimination.

We observe similar behavioral patterns in the SpeechCommands dataset, where we categorize samples and reveal distinct characteristics across different difficulty levels. Analysis shows that EASY samples are predominantly composed of high-frequency digits and basic commands (e.g., yes, stop, two); MEDIUM samples largely comprise numerical terms and action-oriented vocabulary (e.g., go, six, on); and HARD samples predominantly feature homophonic words and abstract concepts (e.g., bed, bird, learn).

4.5. Embedded System Deployment and Performance Testing

To achieve a streamlined deployment process, we utilize STMicroelectronics’ STM32 series microcontrollers and their X-CUBE-AI package. This framework provides a complete suite of tools and libraries for evaluating resource usage, computational performance, model accuracy, and supports multiple popular frameworks (e.g., PyTorch 2.5.1).

Notably, the network designed under the CaDCR framework incorporates conditional judgments, entropy calculation, and early exit decision logic during forward inference. However, the X-CUBE-AI import module does not support such dynamic control flow, presenting compatibility issues that preclude direct deployment on embedded platforms. Our solution involves deploying pruned network blocks and classifiers as independent sub-modules: the feature extraction layers preceding residual blocks form one sub-module, each residual block is isolated as a separate sub-module, the classification network following residual blocks constitutes another sub-module, each early exit classifier operates as an independent sub-module, and the skip gating network—due to its shared parameter mechanism—is partitioned into a dedicated sub-module. With this modular decomposition, the entire network is structured as a cascaded architecture. During inference, these blocks are activated stage by stage based on the input sample features and the network’s dynamic decisions.

We transform the network’s dynamic decision logic into a hardware-friendly static cascaded architecture, enabling low-power inference through sequential execution and conditional judgment between modules. As shown in Figure 15, the schematic of the cascaded system design treats collections of residual blocks, early exit classifiers, and skip gating networks as individual stages. Upon data input, the high-speed clock is activated, with the first block functioning as a feature extractor to initiate Stage 1. Within Stage 1, the early exit branch network $E_1$ determines whether to terminate inference; if not, the skip gating network $G$ evaluates whether to bypass the next block. A skip command triggers progression to Stage 2 for discrimination by$E_1$, with this process repeating until an exit condition is satisfied or the final classification layer is reached. Samples that exit at any stage leave subsequent stages inactive, while skipped blocks remain deactivated when skipping conditions are met, thereby minimizing power consumption and computational operations by dynamically activating only necessary modules.

The pruned network is saved and converted into the ONNX format supported by X-CUBE-AI, then imported into STM32CubeMX. The testing platform is STM32F746G-DISCO, with all parameters stored in external FLASH and SRAM. Operate at a frequency of 216 MHz. Following the cascaded system design methodology described earlier, low (L) and medium (M) skipping rates are employed as the testing basis for performing classification inference on a set of image samples from the CIFAR-10 dataset. Real-time power consumption is measured using a power detector, and the average test results are presented in

Table 3. Comparison of average test results across models.

Model.		Accuracy	FLOPs	Inference Time	Power Consumption
ResNet38	Base	92.50%	83.82 M	2.19 s	3.52 W
	CaDCR-L	92.22%	40.56 M	1.08 s	1.67 W
	CaDCR-M	90.85%	34.12 M	0.97 s	1.45 W
ResNet74	Base	93.10%	169.27 M	4.66 s	5.77 W
	CaDCR-L	92.14%	70.79 M	1.97 s	2.40 W
	CaDCR-M	91.50%	60.37 M	1.70 s	2.19 W

.

As shown in Table 3, the model’s accuracy and FLOPs are generally consistent with those observed during design and testing. In embedded device deployment tests, the CaDCR framework significantly enhances inference efficiency while reducing power consumption and computational resource usage through modular design and dynamic inference mechanisms. However, it is worth noting that this study does not focus on the research of early exit mechanisms; the accuracy can still be improved by using appropriate training methods.

For ResNet38-CaDCR-L, while maintaining accuracy comparable to the baseline model, FLOPs are reduced from 83.82 M to 40.56 M; inference time shortens from 2.19 s to 1.08 s, and power consumption decreases from 3.52 W to 1.67 W. At medium skipping rates, it still retains high accuracy (90.85%), with FLOPs dropping from the baseline’s 83.82 M to 34.12 M; inference time decreases from 2.19 s to 0.97 s, and power consumption falls from 3.52 W to 1.45 W. ResNet74-CaDCR-L achieves baseline-comparable classification accuracy (−1%), with FLOPs reduced from 169.27 M to 70.79 M; inference time shortens from 4.66 s to 1.97 s, and power consumption decreases from 5.77 W to 2.40 W. At medium skipping rates, accuracy decreases by 1.6%, FLOPs are reduced to 60.37 M, inference time shortens to 1.70 s, and power consumption drops to 2.19 W. In practical applications, model configurations can be selected according to hard constraints. For instance, CaDCR-L emerges as a suitable choice when higher accuracy is required. If accuracy is not a priority but computational constraints are, then CaDCR-M becomes the preferable option.

5. Conclusions

Addressing the challenges of computational efficiency and energy consumption optimization for deep neural networks in embedded systems, this paper presents the CaDCR framework, which achieves adaptive regulation of computational paths through the integration of dynamic skipping and early exit mechanisms. Specifically, a local feature discrepancy-guided skip gating network dynamically skips redundant residual blocks, while lightweight early exit branches—guided by depth-sensitive weight loss constraints—facilitate early classification of simple samples. The two mechanisms achieve collaborative optimization through a stage-wise training strategy.

Experimental results indicate that LFDS achieves accuracy comparable to SOTA methods with a simpler implementation. Under hard resource constraints, the CaDCR framework outperforms baseline models in accuracy. It significantly reduces computational resource consumption and inference time by approximately 40–70% on CIFAR-10/100 benchmark datasets while maintaining classification accuracy comparable to baseline models. On the STM32 embedded platform, the cascaded system design translates dynamic decision logic into a hardware-friendly modular execution architecture, enabling simultaneous optimization of inference time and power consumption.

Future work will focus on dynamic inference optimization for cross-modal tasks, exploring ways to further enhance the generalization capability of gating mechanisms, and integrating neural architecture search to develop more refined computational resource allocation strategies. Furthermore, while the adaptive mechanisms of dynamic neural networks can enhance computational efficiency, their input-dependent dynamic routing characteristics may instead become vulnerable points against perturbations. How to explicitly incorporate perturbation resistance mechanisms into network architecture design is also a potential future research direction.