Multi-Layer Cryptosystem Using Reversible Cellular Automata

Abstract

The growing need for adaptable and efficient hardware-based encryption methods has led to increased interest in unconventional models such as cellular automata (CA). This study presents the hardware design and the field programmable gate array (FPGA)-based implementation of a multi-layer symmetric block encryption algorithm built on the principles of reversible cellular automata (RCA). The algorithm operates on 128-bit plaintext blocks processed over iterative rounds and integrates five RCA components, each assigned with specific transformation roles to ensure high data diffusion. A 256-bit secret key that governs the rule configuration yields a vast keyspace, significantly enhancing resistance to brute-force attacks. Key elements such as rule-based evolution, neighborhood radius, and hybrid cellular automata for random state generation are also integrated into the hardware logic. All cryptographic components, including initialization, encryption logic, and control, are built exclusively using CA, ensuring design consistency and low complexity. The cryptosystem takes advantage of the localized interactions and naturally parallel CA structure, which align with the architecture of FPGA devices, making them a suitable platform for implementing such encryption schemes. The results demonstrate the feasibility of deploying multi-layer RCA encryption schemes on reconfigurable devices and provide a viable path toward efficient and secure hardware-level encryption systems.

1. Introduction

In the current digital era, the exponential growth of interconnected devices and the expanding scope of sensitive data transmitted across networks have significantly increased the demand for robust and adaptable encryption systems. Traditional cryptographic methods such as Data Encryption Standard (DES) or Advanced Encryption Standard (AES) have proven effective in many applications, but their centralized and sequential architectures present limitations in environments requiring high parallelism, scalability, or hardware-level optimization [1]. This has prompted a growing body of research into alternative encryption models that leverage unconventional computing paradigms, particularly those inspired by naturally distributed systems.

In response to evolving security demands and emerging computational threats [2], particularly those posed by quantum computing [3], researchers have increasingly turned to alternative encryption methodologies rooted in complex systems and non-linear dynamics. Chaos-based encryption schemes have gained attention due to their sensitivity to initial conditions and pseudorandom behavior, which offer potential advantages in secure communication and image encryption [4]; however, their cryptographic strength remains a topic of ongoing research, with certain schemes found to be vulnerable under rigorous cryptanalysis. Similarly, bio-inspired models, including neural networks [5] and memristive neuron architectures [6], have been used to generate dynamic and adaptive encryption, often with improved resistance to cryptanalysis. Other approaches have drawn from swarm intelligence [7] and hyperchaotic maps [8] to introduce higher levels of complexity and unpredictability into cryptographic processes.

Within this growing field of unconventional techniques, cellular automata offer a structurally simple yet computationally rich framework. Their local rule-based evolution and scalability align well with hardware implementation, distinguishing them as a practical candidate among alternative cryptographic methods. Several studies have explored the application of one-dimensional cellular automata (CA) in encryption [9], including hybrid cellular automata using rule combinations (such as 90/150) for pseudorandom number generation [10], and reversible cellular automata (RCA) for bidirectional state evolution [11]. Recent advancements in reconfigurable hardware, particularly field-programmable gate array (FPGA), offer a compelling opportunity to implement CA-based cryptosystems efficiently by exploiting their structural compatibility with parallel processing models [12].

In recent years, complex dynamic systems, such as those modeled by chaos theory, neural structures, and cellular automata, have emerged as valuable foundations for cryptographic systems due to their inherent unpredictability and sensitivity to initial conditions [13,14,15]. The shift from software- to hardware-based encryption systems has also become increasingly relevant, especially with the growing demand for real-time data processing in constrained environments. FPGA platforms provide a reconfigurable and parallel processing infrastructure that aligns well with CA-based models, allowing the development of secure, high-speed, and resource-efficient encryption solutions [16].

The use of FPGA technology in cryptographic hardware design has gained momentum due to its ability to accelerate performance while preserving flexibility. Several recent studies have demonstrated the effectiveness of implementing cryptographic algorithms, including AES, stream ciphers, and chaos-based schemes on FPGA to achieve improved throughput, reduced latency, and stronger hardware-level security [17,18,19,20]. These advancements motivate the exploration of alternative cryptographic paradigms that can be natively mapped onto FPGA architectures, such as the reversible cellular automata-based system proposed in this work.

While previous work has demonstrated the feasibility and theoretical strength of RCA-based encryption through software simulation [21], relatively few studies have addressed the practical realization of such systems in hardware. This work presents the design and implementation of a multi-layer RCA encryption algorithm on an FPGA platform. The proposed system integrates five RCA components with distinct neighborhood radii and roles, coordinated through iterative rounds and controlled by a 256-bit key.

The purpose of this study is to demonstrate that the structural and functional properties of cellular automata, when deployed on an FPGA, can provide a viable and efficient framework for secure hardware-level encryption. The implementation confirms that multi-layer RCA logic can be synchronized, evolved, and controlled through modular hardware design, maintaining the reversibility and rule-dependence required for secure encryption and decryption. These results support the broader investigation of bio-inspired and rule-based computing models in cryptographic hardware applications.

Our research introduces key advancements in the field of hardware cryptographic systems. These contributions, which highlight the unique aspects and strengths of our proposed system, are outlined below:

• Development of an innovative multi-layer encryption algorithm entirely based on reversible cellular automata, leveraging a cascade of RCA modules to strengthen diffusion and security characteristics of the cipher;
• Full integration of cellular automata principles in both encryption logic and random state generation, ensuring structural consistency and alignment with CA-based design methodology validated in prior studies;
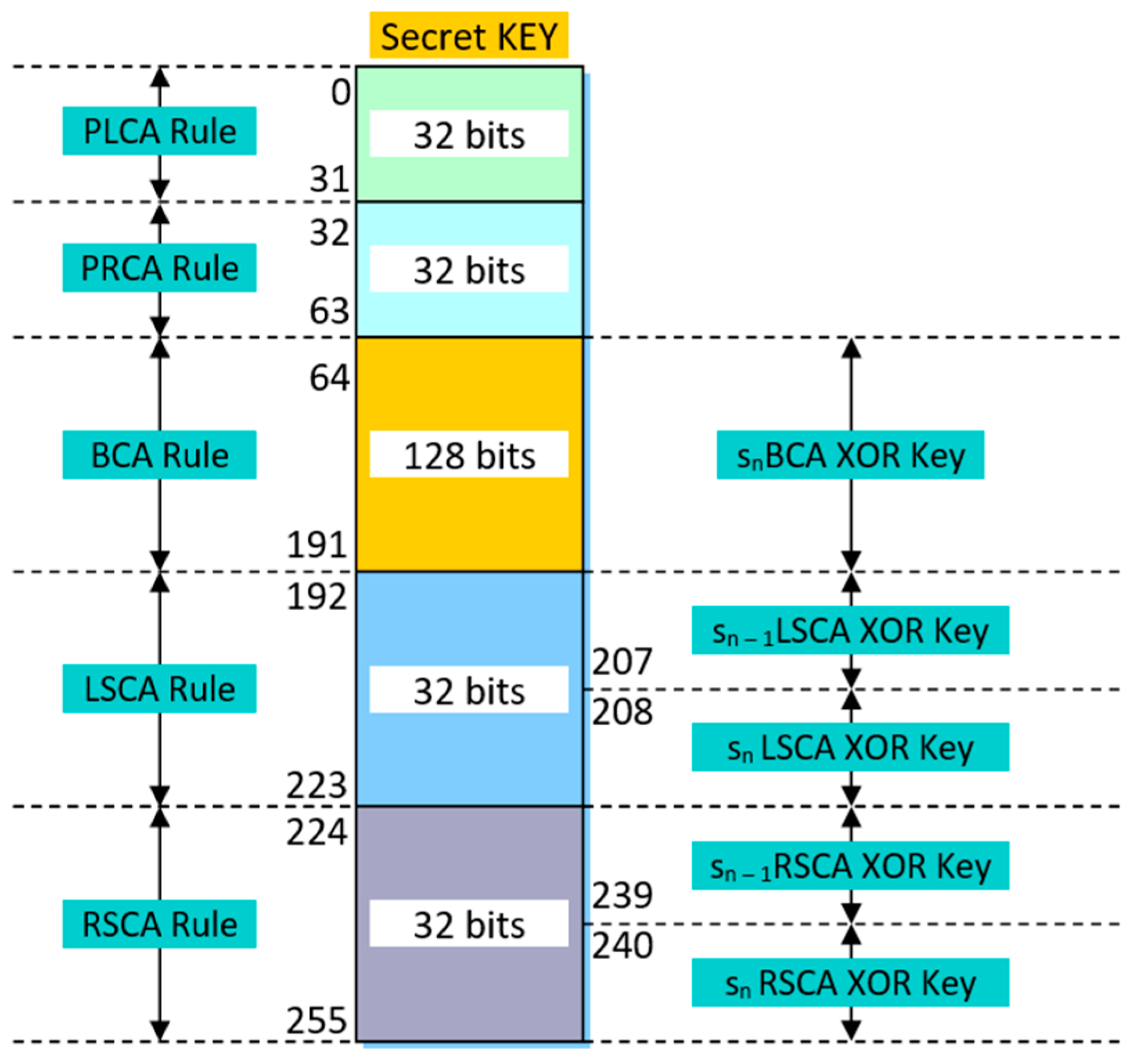
• Design of a robust key structure consisting of 256-bits, enabling dynamic rule configuration for each RCA and securing critical recovery data, thereby significantly expanding the cryptographic keyspace;
• FPGA-based hardware implementation optimized for parallelism and reversibility, utilizing modular RCA units along with the inclusion of a custom PC–FPGA communication interface allowing seamless encryption/decryption operations and secure key/data handling;
• Application of NIST statistical tests to assess ciphertext randomness along with visual evaluation techniques and performance analysis confirming high entropy and resistance to pattern-based attacks, further demonstrating the cryptosystem’s effectiveness.

The remainder of this paper is organized as follows. Section 2 presents the materials and methods used in the design of the proposed cryptosystem. It begins with a brief overview of key cellular automata principles, followed by the introduction of hybrid cellular automata (HCA) and reversible cellular automata, highlighting their specific roles in the encryption process. This section also details the architecture of the multi-layer encryption algorithm, explaining its operational logic from individual block processing within a single round to the system’s overall encryption and decryption flow. Section 3 focuses on the hardware implementation of the cryptosystem, describing the FPGA-based design from a top-level perspective and elaborating on the main architectural modules responsible for RCA evolution, communication, and control. Section 4 presents the experimental results obtained from the hardware system, along with a discussion evaluating the performance, behavior, and reliability of the implemented cryptosystem. Finally, Section 5 concludes the paper by summarizing key findings.

2. Materials and Methods of the Cryptosystem

This section introduces the fundamental principles and structural design underpinning the proposed encryption algorithm. The first subsection outlines the theoretical background of cellular automata, highlighting core concepts such as neighborhood radius, boundary conditions, and rule representation. It then focuses on two specific classes of CA used within the system: hybrid cellular automata (HCA), which are utilized for random number generation based on alternating rule patterns (90/150), and reversible cellular automata, which form the core mechanism for secure data transformation. The second subsection presents the design methodology of the multi-layer encryption algorithm, detailing how multiple RCA components are integrated across the rounds to achieve data confidentiality. This includes graphical representations and explanatory sequences that describe both encryption and decryption workflows.

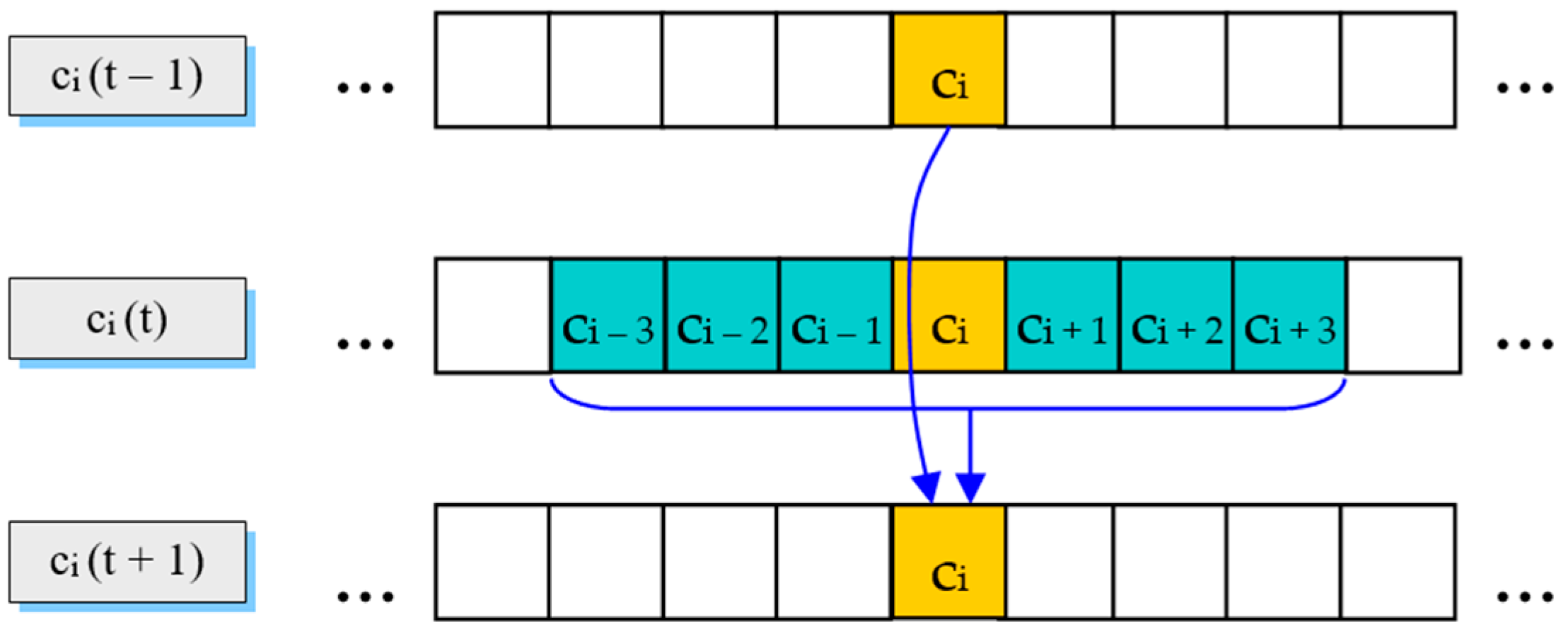
2.1. Cellular Automata Models

Cellular automata are discrete dynamic systems composed of a regular lattice of identical cells, where each cell holds a state from a finite set (often binary, {0,1}). The evolution of the system occurs in discrete time steps, and at each step, the state of a cell is updated simultaneously across the grid based on a local transition rule. This rule considers the state of the cell and its surrounding neighbors, defined collectively as the neighborhood [22]. The number of neighboring cells that influence a given cell is defined by the radius of the automaton. The radius r of a one-dimensional CA determines the span of this neighborhood: a cell located at position i in the array will have a neighborhood defined as

N(c_i) = {c_i−r, c_i−(r−1), …, c_i, …, c_i+(r−1), c_i+r}

(1)

where c_i denotes the state of the cell at position i. Consequently, the total number of cells considered for the update of a single cell is 2r + 1. For example, a radius-1 CA uses 3 cells per neighborhood, while radius-2 and radius-3 CAs use 5 and 7 cells, respectively.

Another fundamental concept in CA design is the treatment of boundary conditions, which defines how the CA handles the edge cells that may lack sufficient neighbors [23]. Among the most commonly used are fixed boundaries, also known as null boundaries where edge neighbors are assumed constant, typically zero, periodic boundaries, in which the grid is treated as circular, allowing the first and last cells to be neighbors, and reflective boundaries where edge neighbors mirror the value of the adjacent internal cell.

Each rule in a cellular automaton specifies a mapping from every possible neighborhood configuration to a new cell state. For binary CA, the number of possible rules increases exponentially with the neighborhood size—for instance, a radius-1 CA has 2³ = 8 possible neighborhood configurations and 2⁸ = 256 total rules commonly referred to by Wolfram’s numbering convention (e.g., Rule 90, Rule 150). These rule definitions can be encoded as binary strings of length 2^2r+1, where each bit corresponds to the output for a specific neighborhood configuration. Increasing the radius of a cellular automaton expands the number of possible rule configurations. Specifically, a radius-2 CA produces 2³² unique rules, while a radius-3 CA results in 2¹²⁸ distinct rule combinations.

A distinct class within the broader family of cellular automata is the hybrid cellular automaton, which extends the conventional uniform CA by allowing different cells to evolve according to different local rules. Unlike uniform CA, where a single evolution rule is applied uniformly across all cells, HCAs assign a specific rule to each cell individually, enabling greater diversity and adaptability in their behavior [24]. This heterogeneity makes HCAs particularly suitable for tasks requiring increased randomness or complexity, such as cryptographic applications. Binary HCAs commonly include linear rules such as rule 90 and rule 150, both of which are known for producing complex, pseudo-random patterns.

Table 1. Binary representation of two evolution rules (90 and 150).

Rule 1	111	110	101	100	011	010	001	000
90	0	1	0	1	1	0	1	0
150	1	0	0	1	0	1	1	0

¹ Rule in decimal form. Evolution of central cell is considered in each case.

illustrates the binary representations of these two rules for a radius-1 CA, where each bit corresponds to the output for a particular neighborhood configuration ordered from highest to lowest value.

Linear cellular automata (LCA) operate using rules defined by XOR-based logic applied over a cell’s neighborhood. Rules 90 and 150 fall in this category because their evolution is governed by XOR operations applied over specific neighborhoods. Rule 90 calculates the next state of a cell using the XOR of its immediate left and right neighbors, while Rule 150 includes the cell itself in the XOR computation along with its two neighbors. To offer a clearer understanding of how these rules operate and how their evolution functions are constructed, a graphical representation is provided in Figure 1 along with the corresponding Boolean equations used for state transitions, defined as follows:

c_i (t + 1) = c_i–1(t) ⊕ c_i+1(t); Rule 90.

(2)

c_i (t + 1) = c_i–1(t) ⊕ c_i(t) ⊕ c_i+1(t); Rule 150.

(3)

The assignment of these rules across the lattice can follow a fixed pattern or a dynamically generated scheme, depending on the intended application. Due to their increased entropy and ability to produce unpredictable sequences, HCAs have been widely explored as building blocks in random number generators. In the context of this work, a hybrid CA combining rules 90 and 150 is utilized for generating initial random states within the cryptographic algorithm, taking advantage of its structural simplicity and inherent randomness. A detailed explanation of how these HCAs are incorporated into the cryptosystem is provided in the following subsection.

Reversible cellular automata represent a subclass of cellular automata in which the evolution process is reversible, meaning that each configuration of the system has a unique predecessor. This bijective nature enables both forward and backward traversal of states, making RCAs particularly suitable for symmetric cryptographic systems where decryption is essentially the reverse of encryption. While some elementary CA rules inherently support reversibility, their number is limited, and many do not offer the complexity or randomness necessary for secure cryptographic applications [25].

To overcome the limitations of simple reversible rules, this work employs second-order reversible cellular automata, a more flexible and powerful approach. In this model, the next state of each cell is influenced not only by its neighborhood at the current time step (t), but also by its own state at the previous time step (t − 1), as described by the evolution function:

c_i(t + 1) = f [N(c_i(t)), c_i(t − 1)]

(4)

In this work, the term reversible refers specifically to the ability of the cellular-automata-based cryptographic system to deterministically reproduce previous configurations when both the initial states and the secret key are known. This form of reversibility differs from the broader theoretical concept of reversibility often associated with pseudo-random number generators in cellular automata, which may suffer from degeneration at certain configurations, rendering backward reconstruction infeasible. This ensures that both encryption and decryption processes are symmetric and reliable, without requiring the storage of intermediate states.

A graphical representation of this concept is provided in Figure 2, illustrating the evolution of a single cell within a one-dimensional reversible cellular automaton using a radius-3 neighborhood.

The reversible rule is constructed by defining two complementary evolution rules: one applied when the previous state of the cell is ‘1’, and the other, its bitwise complement, when the previous state is ‘0’. This mechanism preserves reversibility while increasing the rule space and enabling more intricate evolution behavior for cryptographic operations. From a mathematical standpoint, the second rule is derived from the first, as expressed below, where r denotes the radius of the cell.

CR₂ = 2^m − CR₁ − 1

(5)

m = 2^2*r+1

(6)

Complementary rules enable precise two-way evolution in reversible cellular automata, ensuring that previous states can be accurately reconstructed. This reversibility is founded on the principle of bijectivity, requiring the update function to be both injective, so that no two inputs yield the same output, and surjective, ensuring every output results from some valid input. As a result, each configuration leads to a unique next state, and any state can be reliably traced back to its origin, maintaining the system’s reversible behavior.

A single RCA following these principles can be used for encrypting data by initializing it with two configurations: one derived from the plaintext and one randomly generated. The RCA is then evolved over a fixed number of iterations. The final two states produced by this evolution represent the encrypted output. For decryption, the process is reversed: the last two configurations are used as starting points, and the automaton is iterated backward using the same rules and the same number of iterations. In each case, the secret key consists of the reversible rule applied during the encryption and decryption process. Figure 3 illustrates how reversible cellular automata are applied within cryptographic systems, depicting the operational flow of both encryption and decryption processes. This symmetric structure guarantees that the original data can be precisely reconstructed, maintaining both confidentiality and reversibility.

The encryption and decryption process using reversible cellular automata is structured around symmetric forward and backward evolution. In the encryption phase, the system starts with two initial configurations: a random state s₀ and the plaintext represented by s₁ state. These are passed through the RCA evolution, which processes them over a fixed number of iterations to produce two final states, s_n−1 and s_n. The state s_n−1 becomes the ciphertext, while s_n serves as recovery data, which are subsequently encrypted using an XOR operation with a secret key, in accordance with the Vernam algorithm [26], to enhance security. During decryption, this encrypted recovery data are first decrypted using the same XOR key to retrieve s_n, which, along with s_n−1, is fed back into the RCA evolution in reverse order. Through backward evolution, the algorithm reconstructs the original initial states, effectively recovering the original plaintext.

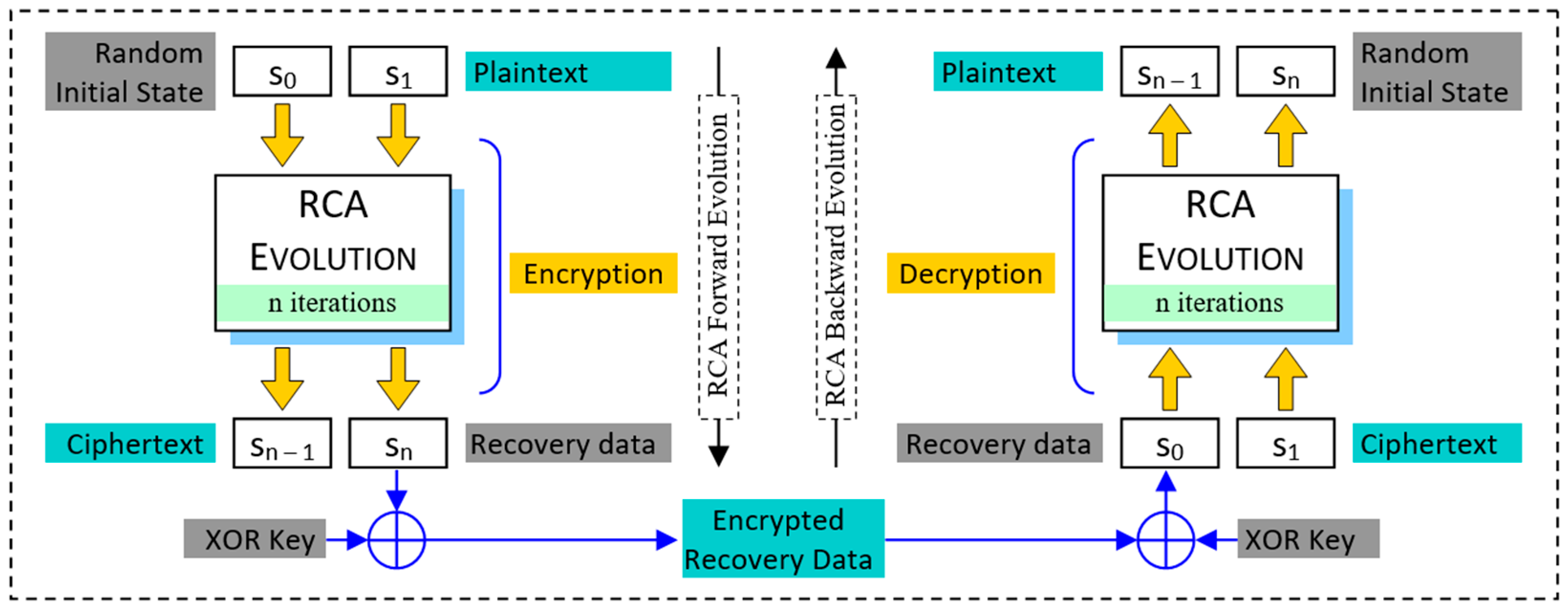
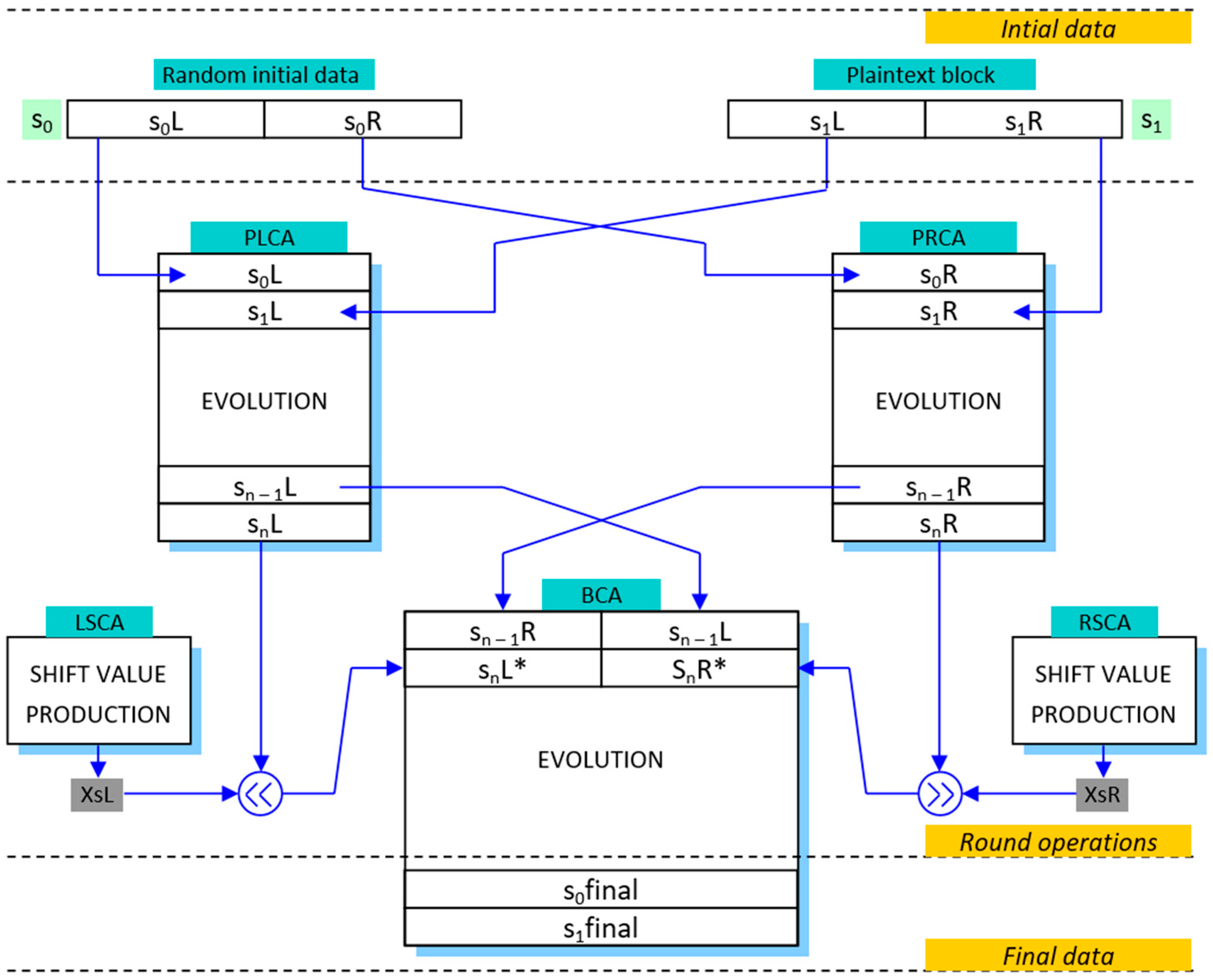
2.2. Multi-Layer RCA-Based Encryption Design

The proposed encryption algorithm is structured around a multi-layer framework that integrates five reversible cellular automata across three distinct functional layers, forming a cascading encryption process. This layered architecture is designed to enhance diffusion, key sensitivity, and reversibility, making it suitable for secure block encryption. Each layer contributes a specific transformation role within the system, working together to ensure the integrity of the encrypted output and the accurate reconstruction of the original data during decryption. The algorithm consists of the following layers built from RCA components:

• Primary Transformation Layer: consists of two parallel RCA modules (denoted as PLCA and PRCA), each processing a separate half of the input data block;
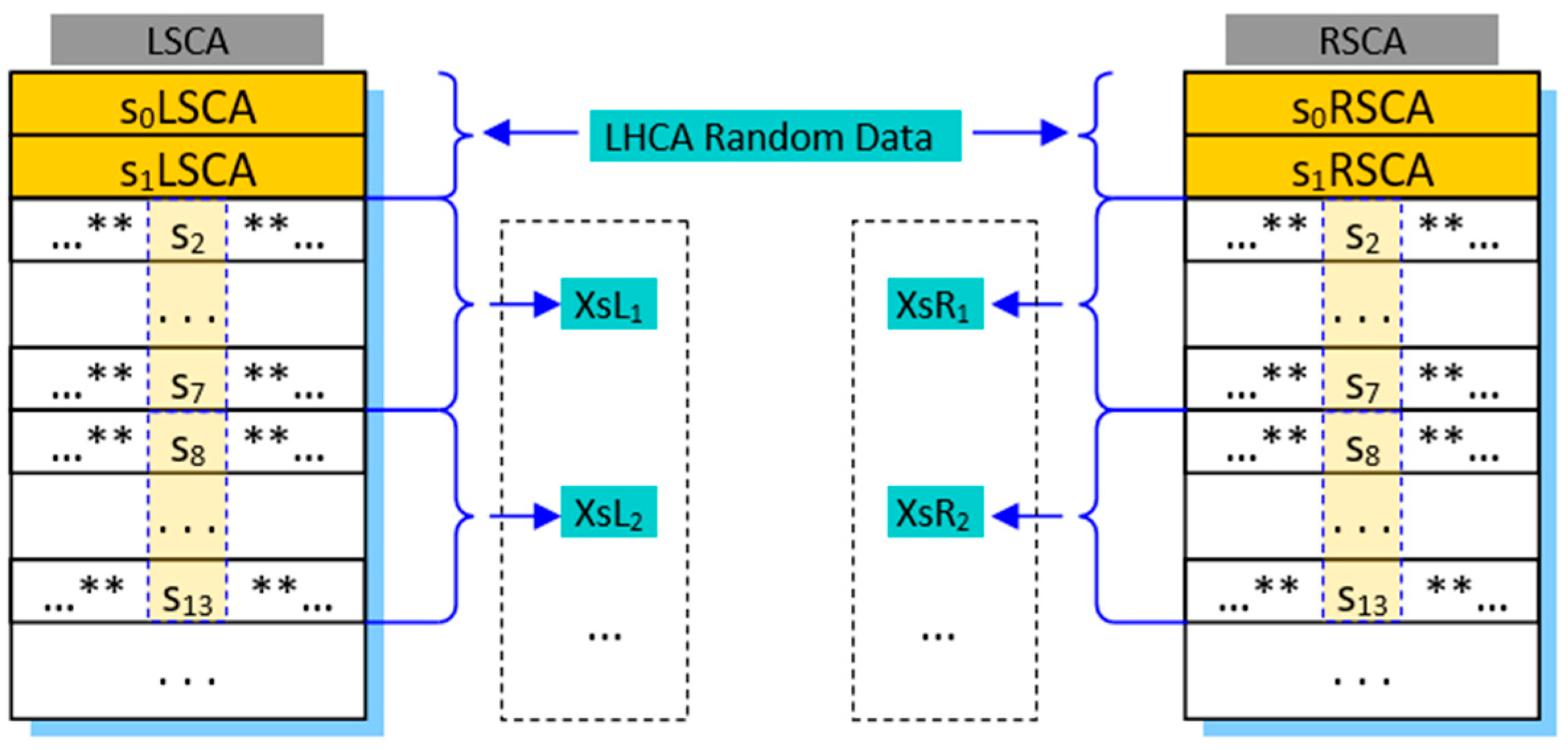
• Shift Computation Layer: introduces controlled variability in the data flow by employing additional RCA modules (LSCA and RSCA) to dynamically generate shift values in order to increase dispersion and eliminate symmetry in the data;
• Binding Layer: performs the recombination of the processed data using another RCA module (BCA) operating over the entire block length, resulting in a final encrypted output for the current round and an additional state used for the next block encryption.

The flow of data through these layers is repeated over multiple rounds, reinforcing complexity and resistance to cryptanalytic attacks. This iterative design principle aligns with modern symmetric encryption standards such as the Data Encryption Standard or Advanced Encryption Standard, which also rely on multiple transformation rounds to strengthen security through confusion and diffusion. Following this approach, the proposed algorithm performs 16 consecutive rounds of reversible transformations for each 128-bit plaintext block, using the multi-layer RCA structure to progressively obscure the original data. Figure 4 illustrates the internal architecture of a single encryption round within the proposed multi-layer RCA-based algorithm. The diagram highlights the sequential flow of data, showing how intermediate transformations are applied and how each RCA component interacts to produce the encrypted output for the current round.

To support a secure and reversible transformation process within each encryption round, the algorithm integrates five distinct reversible cellular automata across its multi-layer structure. These RCAs are configured using extended neighborhood radius to expand the complexity and variability of their rule sets. Specifically, the RCAs in the primary transformation layer and the shift computation layer utilize a radius-2 neighborhood, while the RCA responsible for binding operations employs a larger radius-3 neighborhood. The automata differ in size based on their functional role: the two RCAs in the primary layer are each composed of 64 cells; the shift control automata each consist of 16 cells, optimized for generating the shift values and the binding RCA operates over a full 128-cell structure, accommodating the merged results of previous layers. To ensure seamless evolution of cell states and avoid edge anomalies, all RCAs in the system are governed by periodic boundary conditions, which treat the first and last cells as neighbors, maintaining consistency and preserving the circular nature of the automaton evolution. Figure 5 below illustrates the process of successive block encryption, emphasizing the chaining mechanism, where the final state of one block directly influences the initialization of the next, ensuring data diffusion and enhancing security.

As depicted in Figure 4, the encryption of a single 128-bit plaintext block in one round of the proposed RCA-based cryptosystem follows a structured and layered sequence of operations. The process begins with two initial inputs: a 128-bit block of plaintext denoted as s₁init and a 128-bit random initialized value labeled as s₀init. These two states are divided into two equal halves, forming four 64-bit segments: s₀L, s₁L, s₀R, and s₁R. The left halves (s₀L, s₁L) are fed into the primary left cellular automaton, while the right halves (s₀R, s₁R) are sent into the primary right cellular automaton. Both PLCA and PRCA evolve their respective states using specific RCA rules defined in the encryption key. The evolution produces the outputs s_n−1L and s_nL from PLCA and s_n−1R and s_nR from PRCA.

Next, the outputs s_nL and s_nR are subjected to a bitwise circular shift. The amount by which each is shifted, left for s_nL and right for s_nR, is dynamically determined by the two instances of the shift computation layer that compute the shift values XsL and XsR. The shifted results are labeled s_nL* and s_nR*, respectively. To provide a clearer understanding of how these values are derived, the process is illustrated in Figure 6 below.

Following this, the binding cellular automaton, which operates with a wider neighborhood and 128-bit states, is initialized. Its inputs are a combination of earlier outputs, the first one obtained from swapping the position and concatenation of the states s_n−1L and s_n−1R, and the second one obtained from the concatenation of state s_nL* with state s_nR*.

This layer is responsible for reconstructing and further transforming the output from the primary and shift layers, enhancing diffusion and increasing resistance to statistical attacks. The BCA is evolved for 22 generations using its own rule defined in the encryption key, ultimately producing the final outputs for the current round s₀final and s₁final. These values serve two purposes: if the current round is not the last, they become the new initialization values (s₀init and s₁init) for the next round, and if it is the final round, s₀final is designated as the ciphertext block, while s₁final is stored as recovery data necessary for decryption. This round-based design ensures strong confusion and diffusion throughout the encryption process and forms the foundation of the reversible transformation scheme used in the system.

At the start of the encryption process, each of the two SCAs is initialized a single time using predefined configurations derived from the same random source responsible for the initial state of the first plaintext block in round one (s₀init). Prior to every encryption round, both SCAs undergo six iterations of evolution. During this process, the central cell in each SCA produces one bit per iteration, collectively forming a 6-bit shift value referred to as XsL (for LSCA) or XsR (for RSCA). This mechanism ensures that the value can range from 0 to 2⁶, enabling flexible and dynamic shifting of the 64-bit outputs from the primary RCAs. The generated shift values are used to perform circular bit shifts, left and right, on the respective outputs, ensuring full or partial rotation, depending on the calculated value.

The random 128-bit initial value required to initiate the encryption process is generated using a linear hybrid cellular automaton (LHCA) configured with rules 90 and 150. This setup consists of four independent LHCA instances, each operating as a 32-cell CA. Each LHCA follows a specific rule configuration pattern derived from Hortensius’s rule order combinations, which are known to achieve maximal-length cycles and strong pseudo-random behavior [27]. In this pattern, each bit position in the 32-bit LHCA is assigned either rule 90 or 150 based on a predefined sequence that ensures optimal linear complexity and avoids short repetitive cycles. This predefined sequence is expressed as a binary string, where a value of ‘0’ indicates the use of rule 90 and a value of ‘1’ indicates the use of rule 150 for the corresponding cell position, respectively, as detailed in

Table 2. Rule combination order for maximum cycle length.

Number of Cells	Maximum Cycle Length	Rule
32	232	01000110000010011011101111010101

. The generated values not only serve as the initial state for the encryption algorithm but also contribute to the initialization of key RCA components such as the shift control automata (SCA), ensuring secure initialization.

The seed used to initialize the LHCA-based random number generator is set arbitrarily with a predefined value during the first use. For subsequent encryption operations, the system updates its seed by assigning the last generated state of the LHCA as the new starting point. This approach is viable because the initial random state used for encryption does not need to be stored or remembered for decryption, ensuring both randomness and efficiency without compromising the reversibility of the encryption process. The usage of randomly generated data in the developed cryptosystem is depicted in Figure 7 below.

The secret key is a fundamental component of the proposed encryption system, directly influencing the behavior and security of the multi-layer reversible cellular automata architecture. It is composed of 256-bits and is responsible for configuring the evolution rules for each of the five RCA modules used across the multi-layer structure of the cryptosystem. These rules govern the way each RCA updates its cell states during the encryption and decryption processes. To better illustrate the structure of the secret key and how each segment corresponds to the rule configuration of a specific RCA, Figure 8 provides a breakdown of the key layout. The diagram illustrates the exact bit ranges allocated to each of the five RCA modules, highlighting their association with the respective neighborhood radius and functional role within the encryption algorithm.

The first 32 bits of the key define the rule used by the primary left cellular automaton, followed by the next 32 bits, which correspond to the primary right cellular automaton. Both PLCA and PRCA utilize a radius-2 neighborhood, which results in 2^2r+1 = 2⁵ = 32 possible neighborhood configurations, thus requiring a 32-bit rule for full definition. Similarly, the left and right shift cellular automata (LSCA and RSCA) also use radius-2, and each is allocated 32 bits from the key. The final 128 bits are dedicated to the binding cellular automaton, which operates on a larger radius of 3. This extended radius leads to 2^2r+1 = 2⁷ = 128 distinct neighborhood patterns, and therefore necessitates a 128-bit rule definition.

These rule segments are not just arbitrary bitstrings but represent reversible evolution rules that determine how a cell’s next state is computed based on its current neighborhood and its own previous state. The system adheres to second-order reversible cellular automata principles, where two complementary rules are used to ensure bidirectional evolution. Specifically, the 256-bit key explicitly provides only the rule corresponding to the case when a cell’s state in the previous generation (t − 1) is 1. The complementary rule, which applies when the previous state is 0, is derived by bitwise negation of the provided rule. This method guarantees reversibility and simplifies key design, as it reduces the amount of information that must be stored and transmitted while still supporting complete reconstruction of prior states during decryption.

In addition to governing the evolution of the cellular automata throughout the encryption process, the secret key plays a pivotal role in securing the final states of the system once all plaintext blocks have been processed. Specifically, the algorithm protects five critical RCA outputs: the final state of the binding cellular automaton, referred to as the recovery data, and the last two configurations of each of the two shift cellular automata (LSCA and RSCA). These elements are collectively sensitive, as they contain information essential for correctly reversing the encryption and reconstructing the original data. If exposed, they could potentially be exploited by adversaries to infer the internal state transitions of the system.

To prevent such vulnerabilities, these final states are secured through a transformation process resulting in a 192-bit string called Encrypted Recovery Data (ERd). This string is formed by applying a bitwise XOR operation between the sensitive states and specific segments of the 256-bit secret key. The precise derivation of the ERd and its component contributions are detailed below, clearly illustrating how key-dependent transformations enhance security by protecting the most crucial internal states of the system.

ERd [0..127] = s_n BCA [0..127] XOR Key [64..191]

(7)

ERd [128..143] = s_n−1 LSCA [0..15] XOR Key [192..207]

(8)

ERd [144..159] = s_n LSCA [0..15] XOR Key [208..223]

(9)

ERd [160..175] = s_n−1 RSCA [0..15] XOR Key [224..239]

(10)

ERd [176..191] = s_n RSCA [0..15] XOR Key [240..255]

(11)

This construction ensures that without knowledge of the key, the original states remain inaccessible. The ERd value is appended to the ciphertext as a final output of the encryption phase and is required during decryption to accurately initialize the system for reverse evolution. The XOR operation offers a simple yet powerful cryptographic mechanism, enhancing security by obscuring critical data while maintaining low computational overhead. This efficiency, combined with its protective function, highlights the essential role the secret key plays in reinforcing the overall security framework of the encryption system.

The decryption process is designed to mirror the encryption logic, ensuring accurate and complete reconstruction of the original plaintext. Due to the reversible nature of the cellular automata used, each transformation applied during encryption can be undone by following the backward evolution path, starting from the final system state. Decryption requires three critical inputs: the final ciphertext block, the 192-bit Encrypted Recovery Data, and the original 256-bit secret key.

The decryption begins with extracting the original internal system states needed to initiate the reverse process, which are obtained by decrypting the ERd using an XOR operation with specific segments of the secret key. These recovered states serve as the starting point for backward evolution. The decryption of ciphertext blocks proceeds in reverse order, starting from the last encrypted block and moving backward to the first. This is necessary because the encryption process uses chaining, where each block’s initial state depends on the final state of the previous round. For each block, the same number of rounds is executed using the same RCA configurations and key-defined rules as during encryption. However, in each round, the data flow through the three RCA layers in the reverse order compared to encryption, starting from the binding layer to the shifting layer and ending with the primary layer. The outputs from these stages progressively reconstruct the earlier plaintext configurations. After completing all rounds in reverse and processing all ciphertext blocks from last to first, the original plaintext is fully restored.

This design not only ensures data recoverability but also maintains high resistance to cryptanalysis, as each round depends on tightly coupled RCA state transitions, key-dependent behavior, and shift operations. The overall structure thus preserves both confidentiality and reversibility, aligning with the principles of secure symmetric block encryption systems.

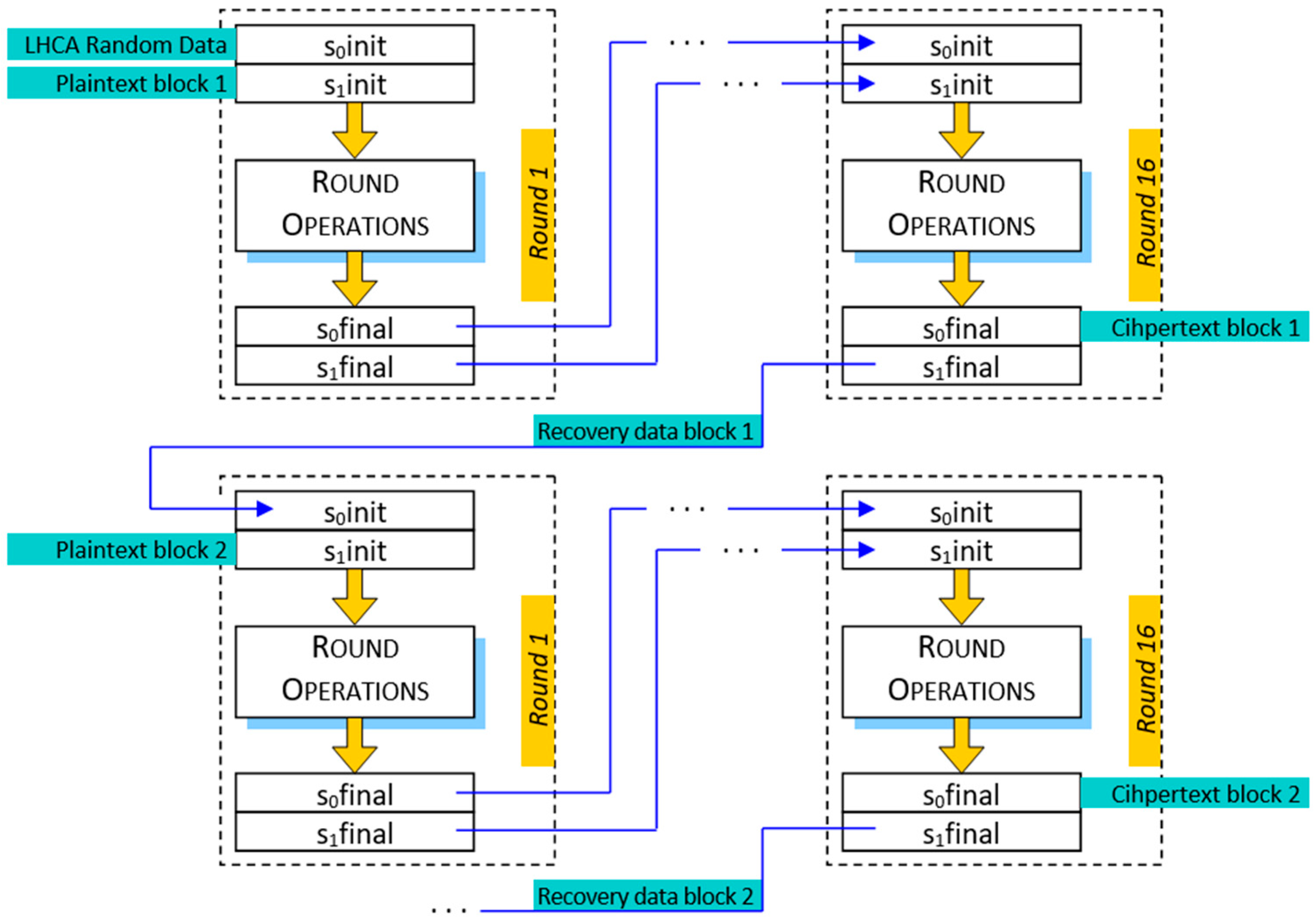
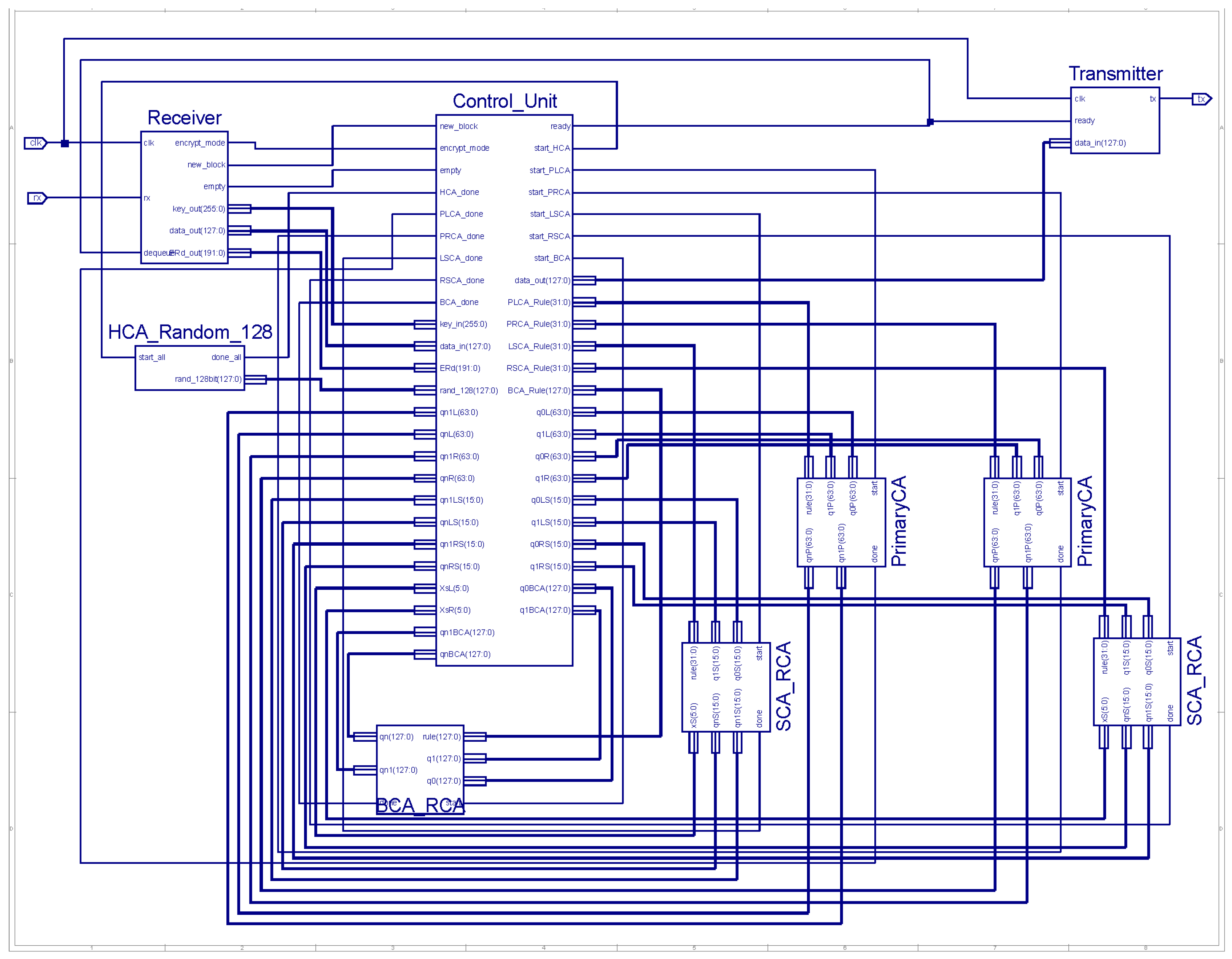
3. Hardware Architecture and Implementation

This section presents the hardware-level design and implementation of the proposed multi-layer RCA-based encryption algorithm, realized on a field programmable gate array platform. The FPGA was chosen for its inherent parallel processing capabilities, which align naturally with the structural and operational properties of cellular automata. This compatibility allows the algorithm to take full advantage of parallel evolution, enabling efficient execution and enhanced security. The section begins by describing the top-level hardware architecture, followed by detailed explanations of the core components that make up the cryptosystem. These include the individual reversible cellular automata modules responsible for encryption logic and the control unit that handles data flow and process sequencing. In addition, the system integrates a UART-based communication interface that facilitates interaction with an external environment. A dedicated software application, developed as part of the project, enables users to control encryption and decryption operations by sending and receiving data to and from the FPGA board. Figure 9 presents the block diagram that includes the overall integration of the system components.

The first block is the Communication Unit (COMM_UNIT), which manages the data exchange between the software application and the FPGA board. This unit is composed of two modules: a receiving module that handles incoming data from the PC to the FPGA, such as encryption keys and plaintext or ciphertext blocks, and a transmitting module that sends the processed data, either encrypted or decrypted, back to the PC.

The second block is the Encryption Unit (ENC/DEC_UNIT), which performs the core encryption and decryption operations. This unit is subdivided into two key subcomponents: the control unit, responsible for managing the data flow and sequencing of operations across the algorithm’s multiple rounds, and the CA units, which house dedicated modules for each of the hybrid and reversible cellular automata layers involved in the encryption structure. As shown in Figure 10, the top-level design provides a clear overview of the internal architecture of the cryptosystem.

The hardware implementation of the cryptosystem includes dedicated communication modules that facilitate reliable data transfer between the PC and the FPGA. This is achieved through a serial UART communication interface divided into two main components: the receiver module and the transmitter module. The receiver module is responsible for capturing incoming data from the PC, including the secret key, plaintext blocks for encryption, or ciphertext blocks for decryption. It stores the received bytes and ensures data are correctly forwarded to the processing unit. The transmitter module handles the outbound communication by sending back the processed data to the PC. Once a complete 128-bit block has been processed, the transmitter breaks it into bytes and sends it serially.

In addition to handling raw data reception, the receiver module plays a critical role in defining the operational mode of the cryptosystem, specifically, whether the system should perform encryption or decryption. This functionality is facilitated through the encrypt_mode output signal, which is used by the control unit to determine the appropriate processing flow for the incoming data. The operational mode is configured from the software application interface, shown in Figure 11, where the user can toggle between encryption and decryption using a checkbox control. Based on the selected mode, the application automatically appends an identifier character to the transmitted data: ‘P’ for plaintext (encryption mode), ‘C’ for ciphertext (decryption mode), and ‘K’ to indicate the transmission of the secret key. These characters correspond to well-known ASCII codes, which can be easily recognized by the receiver module in hardware. Once identified, these prefix characters are stripped before the actual data are passed to the encryption/decryption unit, ensuring clean and correctly formatted input. This mechanism simplifies the control logic and provides an efficient and user-friendly way to dynamically configure system behavior without requiring additional signals or complex hardware protocols.

In order to manage multiple 128-bit data blocks efficiently, the receiving module stores incoming blocks in a FIFO-like buffer structure. This ensures that blocks are maintained in the correct processing order. The structure is controlled by two key signals: dequeue, which is issued by the control unit to remove a processed block, and empty, which signals when no further blocks remain to be processed. An important observation regarding the decryption process is that since decryption operates in reverse, starting from the last ciphertext block and proceeding backward, the reordering of the ciphertext is efficiently handled at the software level. This approach eliminates the need for complex hardware control logic for data reversal, thereby optimizing resource usage and simplifying the hardware design. The reversing operation is lightweight and introduces negligible overhead in software, ensuring a seamless integration with the hardware-based decryption flow. Another important aspect of the decryption process concerns the encrypted recovery data, required to reconstruct the final system states necessary for reverse operations. In the hardware flow, this 192-bit ERd is identified by the receiving module, which extracts the first 192 bits from the incoming ciphertext stream and routes them appropriately for decryption initialization. This mechanism ensures seamless separation between recovery data and the actual ciphertext blocks, simplifying state recovery.

The HCA_Random_128 module serves as the system’s random state generator, responsible for producing the first 128-bit initial configuration required to begin the encryption process. This module is composed of four individual hybrid cellular automata, each operating on 32-bit and evolving according to a hybrid rule set based on rules 90 and 150. The selection of these rules follows a specific binary pattern known to generate maximum-length cycles, ensuring high entropy and unpredictability in the generated states. Each of the four HCAs is initialized with a predefined 32-bit value, serving as the seed for the random number generation process. The final 32-bit output of each HCA serves the role of a new seed for a subsequent encryption process, and it is also concatenated to produce a complete 128-bit value. This combined output forms the initial random state used by the cryptosystem to begin processing the first block of plaintext.

The encryption process in the proposed hardware implementation is coordinated by the control unit based on the HCA random generator and the collection of RCA units. These components are tightly integrated, each fulfilling a specific role that contributes to the overall functioning of the encryption operation. At the core of the system lies the control unit, which orchestrates the entire encryption process. It manages the flow of data, sequencing of operations, and the activation of each CA module. Based on inputs such as encrypt_mode and key_in, the control unit determines the operational mode, identifies the key and plaintext/ciphertext inputs, and generates the appropriate control signals (start_PLCA, start_PRCA, start_LSCA, start_RSCA, start_BCA) to trigger the corresponding RCA modules. Additionally, it handles the readiness signals (PLCA_done, PRCA_done, LSCA_done, RSCA_done, BCA_done, and HCA_done) that indicate the completion of evolution cycles in each RCA block, allowing it to manage transitions between stages and rounds. The control unit also handles the generation and forwarding of intermediate data like rotated outputs and shift values, along with the distribution of key segments to each RCA, ensuring data dependencies between layers are maintained across all rounds of encryption. To better illustrate the process of securing data, Algorithm 1 below presents the logic of the overall operation flow of the hardware implementation, using pseudocode:

Algorithm 1: FPGA-Based Multi-Layer RCA Overall Operation Logic Flow

Initialize UART Communication Initialize RCA Units with Key Rules Load Secret Key (256-bit) Generate Initial Random State (128-bit) while (Receiver detects new data block) if Received Data Identifier = ‘K’ Store Secret Key from Incoming Stream else if Received Data Identifier = ‘P’ OR ‘C’ Store Input Block into Buffer Set encrypt_mode Flag Accordingly end if while (Buffer Not Empty) Dequeue 128-bit Block from FIFO if encrypt_mode = ENCRYPT for Round = 1 to 16 Evolve PLCA and PRCA in Parallel Compute Shift Values using LSCA and RSCA Apply Circular Shifts to PLCA and PRCA Outputs Evolve BCA Using Shifted Outputs end for Store Final BCA State Generate Encrypted Recovery Data (ERd) Append ERd to Final Cipher Block Transmit Cipher Block via UART else if encrypt_mode = DECRYPT Extract ERd and Restore Last States for Round = 1 to 16 Reverse BCA Evolution Reverse Shifts and Primary RCAs Evolutions end for Transmit Decrypted Plaintext Block end if end while end while end

The system contains five distinct reversible cellular automata units, each fulfilling a specialized role based on their position in the encryption architecture as described in Section 2.2. Together, these units implement the layered RCA-based encryption process over 16 rounds. Each RCA module is activated by control signals from the control unit, and the results are sequentially routed to the next stages. The system architecture ensures efficient data management, synchronization, and secure reversible transformation of data, assured through the modular design of the implementation.

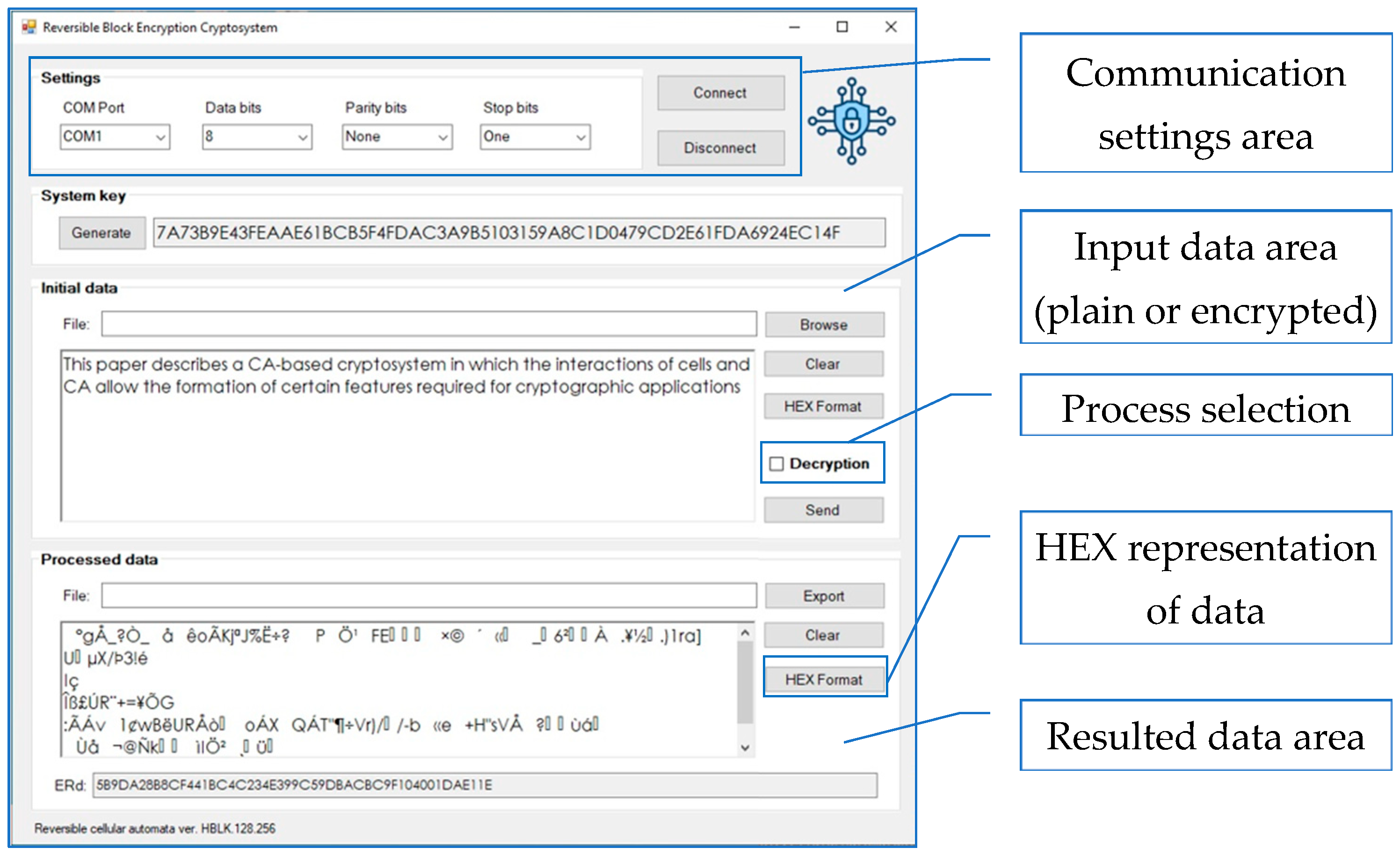
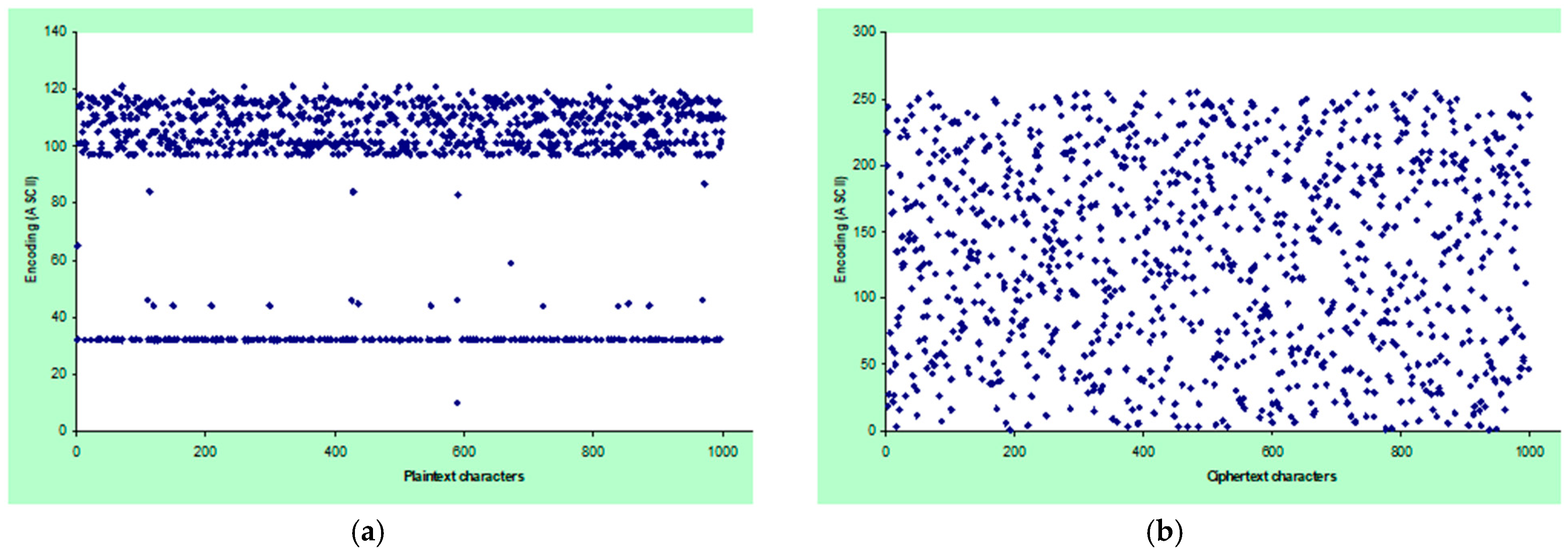
4. Results and Discussion

This section presents and analyzes the experimental results obtained following the complete design and hardware implementation of the proposed RCA-based encryption system. The discussion focuses on evaluating the cryptographic strength and operational effectiveness of the system through a series of assessments aligned with essential security properties. These include statistical analysis of the encrypted output to evaluate data randomness, graphical inspection of ciphertext dispersion relative to the original plaintext, and evaluation of key sensitivity and diffusion characteristics. In addition, implementation-specific results are discussed, including hardware resource utilization. The resilience of the system to attacks is also addressed, supported by evidence from the algorithm’s design characteristics and test outputs. Collectively, these analyses provide a comprehensive view of the cryptosystem’s performance and its suitability for secure, hardware-level data protection.

The proposed cryptosystem was developed and tested using a combination of software and hardware components. The software application, responsible for system control and communication, was implemented on a desktop computer equipped with an Intel Core i5-14600K processor and 32 GB of RAM. On the hardware side, the encryption algorithm was developed using Xilinx ISE version 10.1, and it was deployed on a Xilinx Spartan-3E FPGA board, specifically the Digilent Nexys 2 model.

The current research and hardware-level implementation of the cryptosystem using FPGA builds upon a previously conducted study in which the encryption algorithm was developed and validated at the software level [21]. In that earlier work, a custom-designed desktop application was created to simulate and test the core principles of the multi-layer RCA-based encryption system. The software platform enabled a comprehensive evaluation of the algorithm’s functionality, correctness, and security features through various experimental scenarios. The promising results obtained, including strong key sensitivity, data diffusion, and accurate decryption, served as a solid foundation and motivation for transitioning the design to a hardware environment. This shift aimed to harness the parallel processing strengths of FPGA technology to further enhance performance and demonstrate the feasibility of deploying the cryptosystem in practical applications.

To assess the quality and security of the encrypted data produced by the proposed cryptosystem, a series of statistical evaluations were conducted using the National Institute of Standards and Technology (NIST) Statistical Test Suite. These tests are specifically designed to measure the randomness of binary sequences generated by cryptographic systems, a critical factor in ensuring resistance against various forms of cryptanalysis. Randomness in encrypted data is essential because it prevents the appearance of detectable patterns that could be exploited by attackers to infer information about the plaintext or the encryption key.

The NIST Statistical Test Suite consists of 14 distinct tests, each designed to evaluate a different dimension of randomness within binary sequences generated by encryption systems. These tests apply a range of analytical approaches to detect potential irregularities or patterns that could compromise data confidentiality. Each test within the suite evaluates a different aspect of randomness and outputs a p-value, which indicates the probability that a truly random generator would produce a sequence less random than the one being tested. For the current study, a total of 1,000,000 bits of encrypted data were collected and analyzed as 10 bitstreams of 100,000 bits each, in accordance with the input size requirements specified by the NIST guidelines [28]. A significance level of α = 0.01 was used, meaning that sequences are considered statistically random if their p-value is greater than or equal to 0.01, providing a 99% confidence level in the validity of the randomness results. The detailed outcomes of these tests are summarized in

Table 3. NIST-based randomness validation of encrypted bitstreams.

NIST Statistical Test	p-Value	Test Result—Proportion
Frequency (monobits)	0.122325	SUCCESS—10/10
Block frequency	0.534146	SUCCESS—10/10
Runs	0.350485	SUCCESS—10/10
Longest run of one in a block	0.350485	SUCCESS—9/10
Cumulative sums (forward)	0.035174	SUCCESS—10/10
Cumulative sums (reverse)	0.739918	SUCCESS—10/10
Rank	0.213309	SUCCESS—10/10
FFT	0.739918	SUCCESS—9/10
Non-overlapping template	0.066882	SUCCESS—10/10
Overlapping template	0.911413	SUCCESS—10/10
Approximate entropy	0.739918	SUCCESS—10/10
Serial 1	0.122325	SUCCESS—10/10
Serial 2	0.350485	SUCCESS—10/10
Linear complexity	0.534146	SUCCESS—9/10

below.

In addition to evaluating statistical randomness, the suite also provides insights into the distribution of binary values, specifically the proportion of ones and zeroes, across the analyzed ciphertext sequences. Ensuring a nearly equal distribution of these binary values is a fundamental characteristic of a secure cryptographic system, as it contributes to the elimination of recognizable structures that adversaries might exploit. A balanced output not only reflects the strength of the underlying encryption mechanism but also reinforces its resistance to statistical attacks.

Table 4. Binary value distribution analysis of encrypted sequences.

	BS 1	BS 2	BS 3	BS 4	BS 5	BS 6	BS 7	BS 8	BS 9	BS 10
No. of 0s	50,030	50,270	49,970	50,327	49,793	50,002	50,008	50,120	50,028	50,386
No. of 1s	49,970	49,730	50,030	49,673	50,207	49,998	49,992	49,880	49,972	49,614

presents the proportion of ones and zeroes obtained for each of the 10 analyzed bitstreams (BS), offering an additional metric to validate the robustness of the encryption algorithm.

According to NIST’s guidelines, the minimum requirement for passing each statistical test is around 8 for a sample size of 10 binary sequences when using a significance level α = 0.01. In this study, the encrypted data were divided into 10 sequences of 100,000 bits each and analyzed accordingly. The results align with the expectations of high potential randomness, and all applied tests met or exceeded the required confidence thresholds, thereby validating the cryptographic quality of the generated ciphertext.

In addition to evaluating the randomness of the encrypted output, the NIST statistical test suite was also applied to validate the quality of the HCA-based random number generator used in the proposed cryptosystem. The test results confirmed that the HCA generator produces statistically sound random sequences, meeting the required criteria for cryptographic randomness. This validation supports its use as a reliable source of initial data for encryption processes. Moreover, the choice of HCA as the random number generator reinforces the system’s conceptual consistency, as it ensures that all components of the cryptosystem are founded on cellular automata principles.

To further assess the encryption system’s effectiveness in concealing meaningful patterns, an analysis of the ciphertext distribution across the ASCII interval was conducted. While the original plaintext is constrained within the alphanumerical range of the ASCII table, the encrypted output generated by the system exhibits a broad dispersion across the entire ASCII interval. This uniform distribution contributes significantly to the unpredictability and confidentiality of the encrypted data, as it removes recognizable structures that could otherwise compromise data security. As illustrated in Figure 12, the ciphertext does not exhibit clustering or repetitions that could be linked to the original message, highlighting the system’s capacity to prevent data sensitivity and potential exposure through statistical observation.

To evaluate the feasibility and efficiency of implementing the proposed cryptosystem at the hardware level, resource utilization statistics were collected after synthesizing the design on the selected FPGA platform. These statistics provide insight into the area and logic consumption associated with deploying the complete system, including both communication modules and the internal RCA-based processing units.

Table 5. Hardware implementation summary.

Resource	Used/Total	Area (%)
No. of slices	3771/4656	81
No. of slice flip-flops	5587/9312	60
No. of 4 input LUTs	7449/9312	80
No. of bonded IOBs	62/232	27
No. of GCLKs	1/8	12
Timing	Value
Minimum period	13,28 ns
Maximum frequency	75,301 MHz

below summarizes the utilization of key FPGA resources.

In the FPGA implementation, each reversible cellular automata rule is stored as a binary value corresponding to its respective neighborhood size, and the evolution of each cell is computed in parallel through combinational logic blocks. This design enables one-step full-state updates, aligned with the CA’s parallelism model. Each RCA unit, whether 16, 64, or 128 cells wide, is instantiated using modular entities that permit straightforward scalability. The synthesis report shows moderate resource consumption, with logic slice utilization remaining within device capacity even for the complete system. The resource utilization may be further optimized using approaches such as parallelization of program instructions using techniques like genetic algorithms [29], which could help streamline instruction execution and logic placement. While the UART-based serial communication was used in this study to validate functionality and enable testing from a PC interface, the architecture can be extended to more robust high-speed protocols such as PCI Express or Ethernet, especially for integration into networked or embedded environments. This highlights the design’s adaptability and its suitability for practical secure hardware applications beyond conceptual validation.

A comparative efficiency evaluation was carried out by calculating the throughput of the proposed encryption algorithm, expressed in Mbps, to determine its performance improvements when implemented at the hardware level. This analysis aimed to assess whether the hardware implementation, developed in the current study, outperforms the earlier software-based version described in previous research. Additionally, the algorithm’s performance was benchmarked against other encryption algorithms, with the average results presented in

Table 6. Comparative analysis results.

Algorithm	[30]	[31]	[32]	Software Version [13]	Proposed Cryptosystem
Mbps (avg.)	6.3558	10.3303	21.7254	19.4357	67.3265

below. These results are derived from synthesis reports and a series of empirical tests conducted across different input data scenarios. The findings confirm that the transition to hardware significantly enhances performance due to the inherent parallelism and optimized resource utilization of FPGA platforms.

The proposed cryptographic system demonstrates strong resistance to various forms of cryptanalytic attacks, like brute-force and reverse engineering techniques. The foundation of this resistance lies primarily in the system’s large key space and the inherent complexity introduced by its multi-layer RCA structure. With a secret key length of 256-bits, the algorithm offers a key space of 2²⁵⁶ possible combinations, making exhaustive key search computationally infeasible using current or near-future computing resources.

While the results from the NIST statistical test suite confirm the high degree of randomness in the generated ciphertext, a critical attribute for resisting statistical and differential attacks, it is important to acknowledge that such validation alone does not constitute formal proof of cryptographic strength. Thus, beyond the statistical test results, the robustness of the system is supported by its large key space (2²⁵⁶), the high number of possible configurations of each RCA module due to their extended radius and size, and the dynamic evolution mechanism that diffuses input data across multiple layers and rounds. These features collectively contribute to the algorithm’s resistance against brute-force and pattern-based attacks.

The strength of the proposed encryption algorithm also lies in the enormous configuration space of each reversible cellular automaton used throughout its multi-layer architecture. While the secret key governs the evolution rules, the state space of each RCA is determined by the number of cells composing it: PLCA and PRCA each have a configuration space of 2⁶⁴ possible states, LSCA and RSCA each have a configuration space of 2¹⁶ possible states, while the BCA has a total of 2¹²⁸ possible states. This plays a vital role in preventing attacks as it ensures a vast number of potential internal states. This analysis shows that each RCA, beyond the complexity introduced by its evolution rule (defined in the key), brings a massive number of internal configurations to the encryption system. The high-dimensional state space ensures that even if an attacker knows the rule, determining the initial or intermediate configuration remains computationally impractical.

Additionally, since encryption evolves across 16 rounds, and each round involves transitions across these large configuration spaces, the complexity grows exponentially. One critical feature of the encryption algorithm is its ability to prevent identical plaintext blocks from producing the same ciphertext. This is accomplished through the chaining mechanism, in which the encryption of each block is influenced by the final states generated from the encryption of the previous block. As a result, even if the same plaintext block appears multiple times, the algorithm produces distinct ciphertexts for each occurrence. This is achieved without the need to store or transmit the initial random state, as the reversibility of RCA ensures that decryption can reconstruct all required intermediate states from the final configurations alone. This chaining effect, combined with the secret key structure and the reversible nature of the RCA rules, further strengthens resistance to attacks, particularly in cases where partial information may be available to adversaries. The approach results in highly nonlinear and diffused transformations of the plaintext, a fact that is validated by the presented statistical and structural test results.

Although the proposed cryptosystem uses reversible cellular automata and XOR-based rule structures commonly found in linear CA, the system cannot be accurately described as simply reversible coding or pseudo-random masking. The architecture leverages a multi-layer configuration of RCA modules, extended radii for richer rule spaces, and iterative evolution rounds governed by a 256-bit secret key, thereby ensuring high entropy and strong data diffusion. These design choices introduce non-linearity and interdependency across rounds, elevating the transformation beyond simple XOR operations. Therefore, despite using CA rules as primitives, the overall mechanism fulfills the structural expectations of an encryption system. This distinguishes the presented approach from basic reversible encoding schemes, reinforcing its applicability in secure data communication contexts.

The proposed cryptographic system is particularly suited for deployment in scenarios that require secure and efficient data exchange within constrained hardware environments. These include embedded systems, Internet of Things (IoT) devices, industrial control systems, and secure hardware-level communication channels. Such applications demand lightweight, parallelizable encryption solutions capable of operating in real time without extensive computational overhead. The use of FPGA-based implementation not only enables parallel processing in alignment with the cellular automata model but also offers adaptability and reconfigurability, making it well-suited for integration into custom secure hardware designs. This combination of efficiency and security supports the cryptosystem’s applicability in domains where both performance and protection against data compromise are essential.

5. Conclusions

This paper presents the design and hardware-level implementation of a multi-layer encryption system based on reversible cellular automata, using an FPGA platform to fully leverage the intrinsic parallelism of CA structures. The proposed cryptosystem was carefully structured into three RCA-driven layers, each contributing to the transformation, diffusion, and binding of data across multiple encryption rounds. The system integrates five RCAs of varying lengths and radii, coordinated through a control unit and supported by a lightweight communication interface with a desktop application for user interaction.

The implementation successfully demonstrates the feasibility of deploying a complex RCA-based algorithm on reconfigurable hardware while preserving the theoretical principles of cellular automata models. The use of a 256-bit secret key ensures strong protection against brute-force attacks and supports secure rule-based RCA evolution. Statistical analysis of the encrypted outputs, including tests with the NIST Suite, confirmed the randomness and uniform bit distribution of the cipher data, validating their resistance to cryptanalysis. The hardware-level FPGA-based implementation proved capable of achieving secure encryption and decryption, further underlining the practical potential of RCA-based designs in embedded or high-performance cryptographic applications.