1. Introduction
The implementation of artificial intelligence (AI) and robotics in smart agricultural equipment offers innovative solutions for enhancing yield and optimizing resource utilization efficiency. Several critical soil attributes, including nitrogen (N), phosphorus (P), and potassium (K) contents, are vital for optimal crop growth and development. Nitrogen is essential for photosynthesis; however, excessive nitrogen application can adversely affect plant health by elevating osmotic pressure [
1]. Likewise, optimal phosphorus concentrations are crucial for development and efficient resource utilization in precision farming contexts, where the adaptive regressor plays a key role in dynamic nutrient adjustment, whereas adequate potassium improves photosynthesis and resistance to lodging [
2]. In contrast, excessive potassium application might hinder the absorption of other vital cations, such as calcium and magnesium. Consequently, ensuring the adequate provision of nutrients is essential for optimizing productivity while mitigating environmental hazards linked to excessive application, including non-point-source pollution [
3]. Consistent and precise monitoring of sample attributes using AI-driven equipment, supported by an adaptive regressor, is vital for timely intervention and maximizing overall yield.
Despite considerable progress in sample property prediction technologies in recent years, several challenges persist. The geographical variability in sample attributes markedly influences the forecasting accuracy, particularly at extensive scales where the soil composition can vary dramatically due to disparities in climatic, topographical, and land use factors [
4]. Secondly, although conventional laboratory analyses yield highly precise outcomes, their substantial expense and time requirements restrict their widespread adoption in real-time farming devices. Traditional procedures are often expensive, labor-intensive, environmentally harmful, or insufficiently timely for effective intervention.
Deep learning methods are garnering increasing attention as rapid and non-destructive techniques for spectral data detection. Their benefits include minimizing sample degradation and enhancing detection efficiency. For example, convolutional neural network (CNN)-based transfer learning has been applied to a small-sample red grape appearance grading model [
5]. Nonetheless, although deep learning techniques exhibit significant promise for predicting sample properties, their efficacy is constrained by the generalization capacity and feature extraction efficiency of the resulting models, which are negatively affected by data scarcity. The masked autoencoder (MAE) has achieved significant advancements in image processing due to its robust feature learning capabilities [
6,
7]. Nonetheless, the implementation of the MAE method in spectral data feature learning requires additional investigation [
8,
9].
To address concerns surrounding data privacy in agricultural applications, especially in cases where soil nutrient profiles can be linked to specific geolocations or proprietary land management practices, our approach prioritizes privacy preservation. Although nutrient data may not be inherently sensitive, sharing such data across multiple stakeholders—such as farms, cooperatives, or governmental bodies—could inadvertently expose confidential insights. Therefore, our use of federated learning ensures data locality and mitigates potential privacy risks. Once privacy is safeguarded, we further improve the computational efficiency and scalability of the developed model, especially considering the limitations in terms of network connectivity and computing resources characterizing rural environments. We propose a federated learning framework, called FedMAE regressor, to tackle the challenges associated with sample nutrient prediction, for which we employ a masked autoencoder (MAE) methodology. This framework seeks to improve the precision and effectiveness of predicting sample attributes such as nitrogen, phosphorus, and potassium levels in diverse environments, especially in scenarios involving collaborative data analysis across regions and devices. Conventional approaches frequently encounter challenges when dealing with incomplete or non-independent data. The integration of federated learning and deep learning techniques helps to effectively mitigate these issues. This research contributes to advancements in model stability and convergence, alongside improved training efficiency, achieved through the implementation of sophisticated architectural features and optimization methods. These innovations enhance the model’s generalization capacity for nutrient content prediction tasks.
This study utilizes a neural network architecture in the design of a non-federated regressor to model the nonlinear relationships between the input data and target variables. The training process is refined to improve the stability and efficiency of the model. Experimental results indicate that the proposed method demonstrates superior performance compared to both traditional approaches and existing techniques in terms of predicting sample attributes, including nitrogen, phosphorus, and potassium contents. This study presents an effective solution for predicting nutrient contents, thereby supporting the implementation of precision agriculture. This study’s primary contributions are as follows:
An adaptive normalization strategy is designed; in particular, to enhance the model’s robustness under non-IID client data distributions, we introduce an adaptive normalization scheme prior to local training. Unlike standard normalization techniques, this module adjusts dynamically to each client’s feature distribution.
A feature transformation allocation module is designed, which combines multi-layer feature transformation with balanced data allocation. This structure can achieve a more compact and meaningful feature representation in edge scenarios, thereby improving the prediction accuracy and model efficiency for clients with heterogeneous data.
This study adapts the masked autoencoder (MAE) framework for federated regression tasks on high-dimensional spectral data. Unlike prior works, which have used MAEs primarily for vision or representation learning, our architecture integrates an MAE as a central encoder to extract robust features from partially observed spectra across decentralized nodes. Compared to traditional federated learning models, which rely on shallow encoders or fixed statistical features, our MAE-based framework enables deeper representation learning, better tolerance to missing or noisy data, and improved generalization under non-IID conditions.
The remainder of this paper is organized as follows:
Section 2 reviews the related work in the fields of spectral analysis, deep learning, and federated learning.
Section 3 introduces the problem formulation and outlines the overall system design.
Section 4 describes the proposed FedMAE regressor model and the experimental setup in detail.
Section 5 presents the results and compares the performance of the proposed method against baseline models.
Section 6 discusses the limitations and potential improvements. Finally,
Section 7 concludes the paper and outlines directions for future research.
2. Background
The expansion of precision agriculture practices is accompanied by challenges relating to the management of extensive, geographically dispersed data and increasing concerns regarding data privacy. The integration of advanced machine learning techniques in decentralized environments presents an opportunity to address these issues. Implementing these technologies necessitates careful consideration of the associated technical and ethical challenges, particularly concerning data sharing and privacy protection. Federated learning approaches are well-suited to tackle these challenges and provide innovative solutions for efficient data processing.
2.1. Advancement of Machine Learning Techniques in Sample Attribute Prediction
The use of machine learning technology in agricultural production contexts allows for the enhanced prediction of sample attributes such as nutrient contents, optimized application of fertilizers, increased crop yields, and supports sustainable farming practices. Systems designed for purposes such as automated attribute sampling and fertilization utilize sensor data and spectral analysis to monitor and optimize sample attribute conditions in real-time. The spatiotemporal variability in sample attribute properties results in data heterogeneity across regions, complicating generalization efforts [
10]. The small sample size and high-dimensional characteristics of the spectral data present challenges in terms of improving model performance [
11]. Most models, even when trained on well-balanced datasets, fail to adequately represent the diversity of sample attribute types.
2.2. The Potential for Federated Learning in Agriculture
In this study, federated learning is primarily employed due to its ability to support decentralized model training and accommodate heterogeneous data distributions across edge devices. Privacy is a secondary benefit derived from the federated learning architecture. While privacy protection [
12] is one of the recognized advantages of federated learning (FL), it is not the dominant concern in the context of soil nutrient prediction. Unlike personal or medical data, soil nutrient and spectral data are not inherently sensitive. Instead, the adoption of FL in this study is driven by the need to accommodate heterogeneous and geographically distributed data sources, as well as to enable localized training on devices with limited communication or storage capabilities. In FL, participants collaboratively train models by sharing only model updates—not raw data—with a central server. This not only helps to preserve the locality of data but also reduces bandwidth usage and computational overhead [
13]. Leveraging information across multiple data sources without centralized collection, FL enables the developed model to capture diverse environmental patterns and improve generalization performance [
14].
In addition, federated learning is superior to traditional centralized learning methods in terms of communication efficiency. With traditional methods, a large amount of raw data must be transmitted frequently; however, in federated learning, only model update information needs to be exchanged, dramatically reducing bandwidth consumption and communication overhead [
15]. This feature is vital in resource-limited agricultural environments, especially in rural areas far from central servers. Through reducing the frequency and amount of data transferred, federated learning not only improves computational efficiency but also enables collaborative training on distributed data which, in turn, promotes both scalability and privacy protection in precision agriculture contexts.
2.3. The Potential of Masked Autoencoder
The masked autoencoder (MAE) was initially applied to image processing tasks [
6]. It learns reconstruction features by processing partial masks of input data, allowing for the extraction of robust feature representations. Compared with traditional methods, MAEs can mine potential data features when data are missing or incomplete, thus improving the robustness of the model.
The introduction of an MAE for spectral data analysis provides significant advantages [
16]. The high dimensionality and redundancy of spectral data make it difficult for traditional methods to extract key features efficiently. In contrast, an MAE can effectively remove redundant information and retain necessary signals by forcing the network to learn the core features of data through the mask mechanism. This method provides a new idea for the effective extraction of information from spectral data in federated learning environments.
3. Related Work
3.1. Development of Sample Attributes Analysis Techniques
Traditional methods for nutrient content detection mainly rely on chemical analysis and laboratory determination. For example, Stevens [
17] used visible and near-infrared reflectance spectroscopy and partial least squares regression to predict soil organic carbon content in large-scale European soil surveys, finding that unbiased predictions can be made over large geographic areas. Although these methods are highly accurate, they often require a complex sample preparation process, which is time-consuming and may cause irreversible damage to the sample. Researchers are exploring more efficient and non-destructive methods for the detection of sample nutrient contents to overcome these limitations. To alleviate these problems, researchers have proposed a number of improvements. Rinnan [
18] reviewed the ability of spectral preprocessing techniques—such as multivariate scattering correction and standard normal variable transformation—to improve the performance of models and proved that these methods are effective, to a certain extent. However, these methods rely on manual feature extraction and data preprocessing, which are inflexible and make it difficult to deal with high-dimensional complex data.
Deep learning technology can provide significantly improved prediction accuracy through nonlinear modeling in tasks such as sample attribute prediction, achieving good results. Yang et al. [
19] combined a convolutional neural network and a recurrent neural network to analyze the spectral data of mineral soil, providing a new technical path for building a more robust spectral prediction model. Khan et al. [
20] successfully extracted information highly similar to real data using a cyclic GAN, while Zhao [
21] effectively solved the shadow problem in hyperspectral images using periodic consistency adversarial networks. In the field of UV-VIS spectroscopy, UV-VIS spectrophotometers combined with artificial intelligence technologies such as machine learning, neural networks, and deep learning can achieve high-precision compound identification and quantitative analysis, especially in terms of the detection of low concentrations of target substances [
22]. The advantages of these methods include rapid analysis, high sensitivity, and high data reliability. They have been extensively utilized across various domains, including the quality assessment of formaldehyde in industrial products [
23], the measurement of ammonia levels in environmental water samples [
24], the identification of ethanol concentrations in alcoholic beverages [
25], analysis of the targeted extraction of veterinary pharmaceuticals [
26], and the quantification of glutathione for evaluation of oxidative stress levels [
27]. Although deep learning technology has shown great potential in spectral analysis, its high equipment costs and operational complexity still limit its widespread application in agricultural production.
3.2. The Development of Federated Learning
Many scholars have conducted in-depth research on the development status in federated learning. Yang et al. summarized the basic principles and application scenarios of federated learning, particularly emphasizing the advantages of data privacy protection and distributed computing environments. They also explored the application of federated learning in emerging fields such as edge computing and the Internet of Things, providing essential directions for future research. In addition, Zhao et al. [
28] proposed a multi-source domain adversarial adaptation framework based on federated learning. Through minimizing the feature distribution differences between data from different clients and data from the central server, the negative transfer phenomenon was effectively reduced via federated learning. Arooj proposed FedWindT, a transformer-based federated learning model designed for decentralized wind power forecasting [
29]. This model leverages the self-attention mechanism of transformers to capture temporal dependencies in wind data while preserving data privacy through federated training across wind farms.
As the technology continues to evolve, the application scenarios of federated learning have expanded from the initial mobile device scenario to a wider range of fields. In the process of development, researchers gradually began to study the problems of non-IID data and data heterogeneity. Wang [
30] proposed Federated Learning with Matched Averaging (FedMA), a federated learning method for aligning the structure of client models in a non-independent and non-IID environment. Through introducing a model alignment mechanism, FedMA effectively improves the aggregation performance and training stability under the condition of data heterogeneity. Xiao et al. [
31] proposed a secure and privacy-protecting federated learning system named BCE-FL, which is specifically used for the non-independent and identically distributed conditions characterizing device fault diagnosis in the industrial Internet of Things context. FedMask [
32] allows for the efficient computation and communication of personalized federated learning on heterogeneous devices. However, FedMask does not consider changes in network and computational conditions that affect training or the resource-constrained nature of IoT devices. Moreover, the formulation of the neural network mask will influence the precision of the ultimate training outcome. Guo proposed a novel federated learning framework named FedMLP [
33]. Through constructing multi-level prototypes (including prototypes and semantic prototypes) and designing multi-level regularization methods, this framework effectively solves the problems of local catastrophic forgetting and global concept drift in dynamic heterogeneous federated learning, significantly improving the performance and stability of the resulting model in heterogeneous data environments. Fed3R [
34] introduces a recursive ridge regression method tailored for federated settings using strong pre-trained models. While effective in linear tasks, its representational capacity is limited when applied to nonlinear, high-dimensional data. In Federated Bayesian Neural Regression [
35], a global Gaussian process approach combining Bayesian inference with federated training is utilized. This method offers quantification of uncertainties and scalability but incurs significant computational overhead and requires complex hyperparameter tuning. In Federated Block-Term Tensor Regression [
36], low-rank tensor decompositions are applied for regression across decentralized medical datasets. While FBTTR is well-suited for structured clinical tensors, its block-term assumptions may not generalize well to agricultural spectral data, which are typically characterized by high noise and variability. Despite substantial progress in the theory and practice of federated learning, the majority of research has focused on classification problems, with very minimal investigation into intricate regression tasks such as spectral data processing. At the same time, existing studies have generally ignored the problem of model interpretation; furthermore, it is difficult to make full use of unlabeled data to improve model performance, especially in fields such as the spectral analysis of sample attributes, where obtaining large amounts of labeled data is often costly and time-consuming.
3.3. Application of Masked Autoencoder in Spectral Data Analysis
Masked autoencoder technology allows for the extraction of a robust feature representation through partial mask processing of input data and the learning of reconstruction features. The high dimensionality and complex correlation structure of spectral data make it necessary to use an approach which is capable of processing incomplete and noisy data. SS-MAE [
37] is an innovative spatial–spectral masked autoencoder that adeptly amalgamates spatial and spectral data from diverse remote sensing sources, demonstrating enhanced efficacy in image classification tasks relative to conventional approaches. Wang et al. [
38] introduced a novel feature-guided mask self-coding technique that selectively masks significant spectral features rather than employing random masks, thus enhancing the learning of representations for remote sensing data classification. Cao et al. [
39] developed an innovative approach to apply a transformer-based masked autoencoder to hyperspectral image classification. This approach demonstrated superior feature extraction capabilities by utilizing local and global spectral–spatial information, maintaining strong performance even with limited labeled samples. Wan et al. [
40] introduced the near-infrared masked autoencoder technique, utilizing the LUCAS 2009 dataset as prior knowledge to enhance the reconstruction of spectral data and markedly increase the robustness of spectral features through strategic random masking, thereby improving the prediction accuracy for nutrient contents.
Based on the research of Wan, this study extends the MAE-NIR method to the federated learning context. As a result, FedMAE regressor is proposed: an automatic mask coding method for distributed environments with heterogeneous data distribution characteristics. The proposed method combines the advantages of federated learning and deep learning to construct an innovative regressor architecture designed to improve model accuracy in sample attribute property prediction tasks.
4. Methodology
This chapter systematically explains our federated system for spectral data regression tasks. The system covers the complete process, from data preprocessing to model construction and optimization. It underscores the enhancement of performance in federated settings, striving to fully actualize the promise of federated learning in distributed contexts.
4.1. Data Preprocessing
This study adopts a set of systematic data preprocessing strategies to lay a foundation for subsequent model training. First, we use an adaptive normalization scheme, which can effectively adjust the degree of influence of outliers to keep each feature dimension within a comparable numerical interval. This kind of processing significantly reduces the interference of extreme data points on the training stability of the model, thus improving the algorithm’s convergence efficiency and prediction consistency. Compared with standard normalization methods such as z-score [
41] and min–max scaling [
42], our adaptive normalization approach dynamically adjusts to local feature distributions, making it more suitable for federated settings with non-IID data. Similarly, the proposed multi-layer feature transformation extends beyond classical PCA [
43] by incorporating nonlinear mappings that better capture hierarchical spectral representations under varying input conditions.
For feature engineering, we develop a multi-layer feature transformation method to provide a higher-order feature representation of the original spectral data via nonlinear mapping. This transformation enhances the expressive capacity of the data and allows the model to discern the intricate associative structure within the data, hence augmenting its predictive and generalization capabilities. Through integrating these higher-order characteristics, we augment the dataset’s information and enhance the model’s effectiveness in capturing complex nonlinear interactions.
We design a balanced data distribution mechanism to meet the special needs of the distributed learning environment. This mechanism ensures that the data subsets obtained by each node are consistent and represent the distribution of target variables in the multi-client architecture. This data segmentation strategy can reduce the problem of distribution migration, to a certain extent, and promotes the comprehensive performance of the global model, leading to stronger robustness and generalization ability in heterogeneous data environments. The pseudo-code for data processing is as follows Algorithm 1:
| Algorithm 1: Data preprocessing framework. |
| Input: |
| Output: |
| 1: |
| 2: |
| 3: |
| 4: |
| 5:
|
| 6:
|
| 7:
|
| 8:
|
| 9:
|
| 10: then |
| 11: |
| 12: |
| 13: else |
| 14: |
| 15: end if |
| 16: |
| 17: |
| 18: then |
| 19: |
| 20: |
| 21: else |
| 22: |
| 23: end if |
| 24: |
| 25:end function |
4.2. Design of Model Architecture
Our model design incorporates a centralized model for individual device utilization and a federated model for comparative evaluation. We present an innovative regressor design that integrates the advantages of federated learning and deep learning to improve the accuracy and robustness of sample attribute property prediction tasks. We performed numerous adjustments to address the issues caused by the variety and non-independent co-distribution of the data. These enhancements are explicitly intended to enhance upon the efficacy of traditional regression models while tackling the distinct challenges faced in federated learning contexts.
4.2.1. Federated Learning Regressor Design
Building on Wan’s pioneering work [
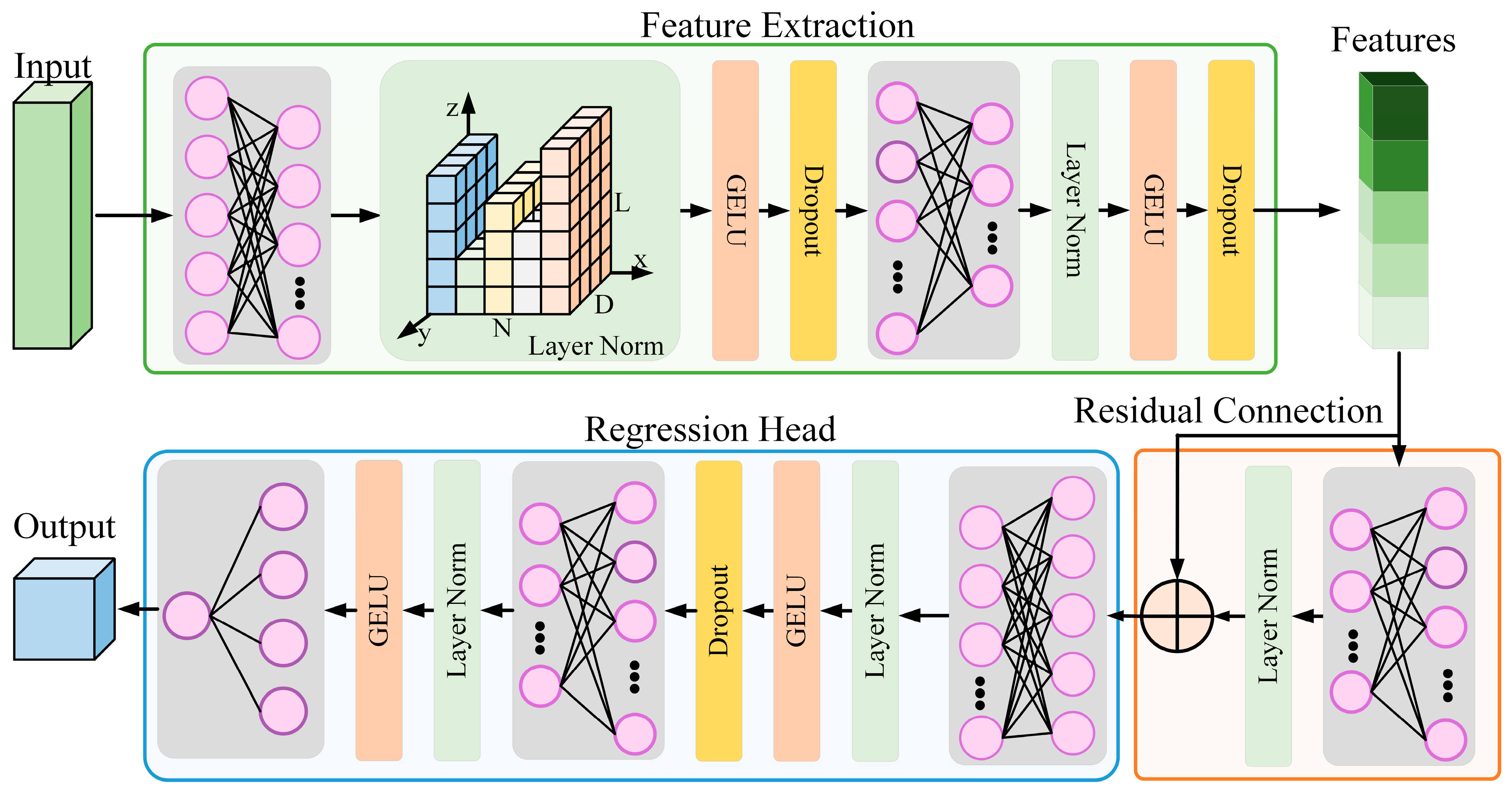
40], in which they introduced the MAE-NIR method, we developed an advanced federated architecture using the LUCAS 2009 dataset as prior knowledge to enhance spectral data reconstruction. Their method improves the robustness of spectral features through strategic random masking techniques, thereby improving the accuracy of nutrient content prediction. Extending this conceptual framework to the federated learning context, we propose the FedMAE regressor method: an approach for masked automatic coding designed explicitly for distributed environments with heterogeneous data distribution characteristics. This method provides a powerful way to process incomplete and noisy data efficiently. The term “regression head” in the proposed FedMAE regressor refers to the fully connected neural layer (or sequence of layers) attached after the encoder, which maps the learned feature representation to the real-valued output. As shown in
Figure 1, the model architecture combines several key innovations to improve the model’s performance, stability, and training efficiency in a federated learning setting:
To ensure stable training across varying client data distributions, we implement LayerNorm, which normalizes data across the feature dimensions. This strategy contributes to consistent convergence behaviors regardless of the unique data traits of different clients, maintaining the model’s integrity and performance.
The model integrates residual connections to improve gradient flow during backpropagation. These connections add the layer’s input to its output, facilitating smoother gradient propagation, leading to faster convergence, and improving the overall stability of the deep network throughout the training process. In addition, we utilize GELU for the activation function, which generates smoother gradients and incorporates randomness, leading to more continuous and differentiable nonlinearities.
We design the model architecture to separate feature extraction from the regression head. This structure enables the network to learn complex, higher-level features from the input data before predicting sample attribute properties. The model can better generalize to new data by isolating these two tasks, enhancing its performance on previously unseen inputs.
The calculation formula for the Layer Normalization layer is shown in Formula (1) as follows:
where
and
are calculated as shown in Formulas (2) and (3), respectively, and N represents the number of float values output by the LayerNorm layer; in this study, N is taken as 256. The GELU and dropout layer formulas are shown in Formula (4) as follows:
The calculation methods for GELU and m are shown as Formulas (5) and (6), respectively:
The formula for the residual connection part is shown in Formula (7) as follows:
Among them, represents the output of the input vector x after passing through a fully connected layer, while represents the output of after passing through the LayerNorm layer. The calculation method for LayerNorm is shown as the aforementioned Formula (1). The input and output of the residual connection part are both 128 float values, thereby ensuring the effective retention of information during the multi-layer transmission process.
These improvements are combined into a computationally efficient federated learning framework that models complex data relationships while maintaining robustness with respect to the challenges faced in federated learning environments, including non-homogeneous data distributions and variable client computing resources.
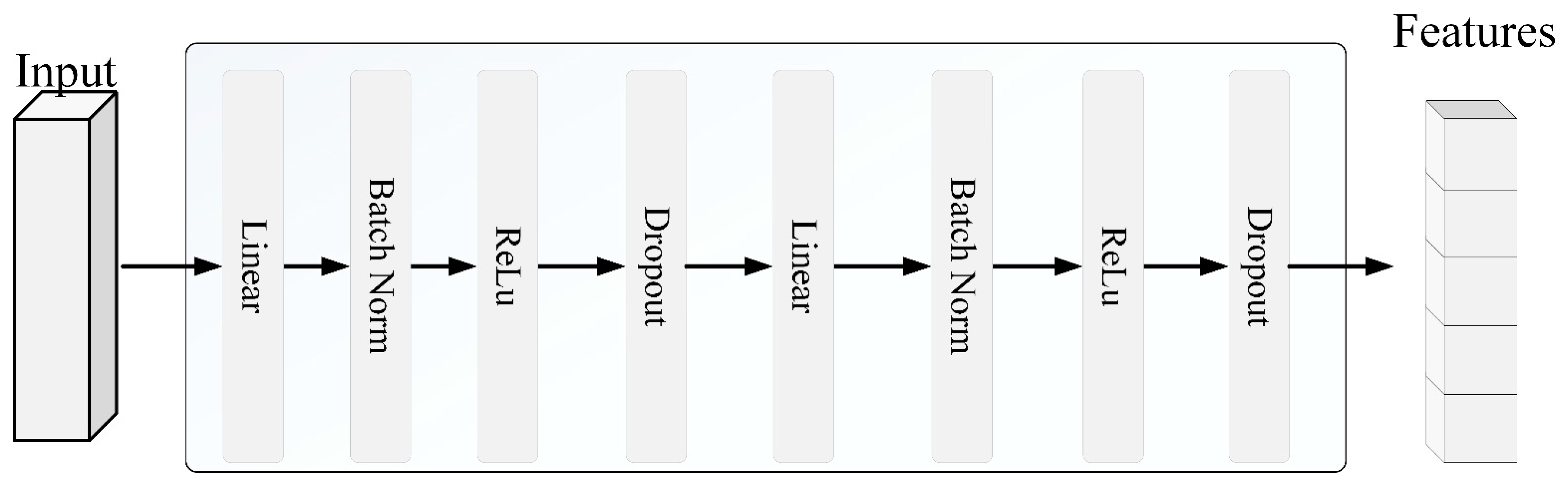
Compared with the traditional architecture in
Figure 2, the FedMAE regressor incorporates a federated structure that supports decentralized training. It utilizes feature extraction to extract the spectral feature distribution from spectral data, and residual connections and regression heads are introduced to enhance the model’s ability to capture nonlinear patterns in heterogeneous data. These architectural differences enable FedMAE to generalize better in distributed environments, especially those in which the data are not independently and identically distributed (non-IID).
4.2.2. Non-Federated Regressor Design
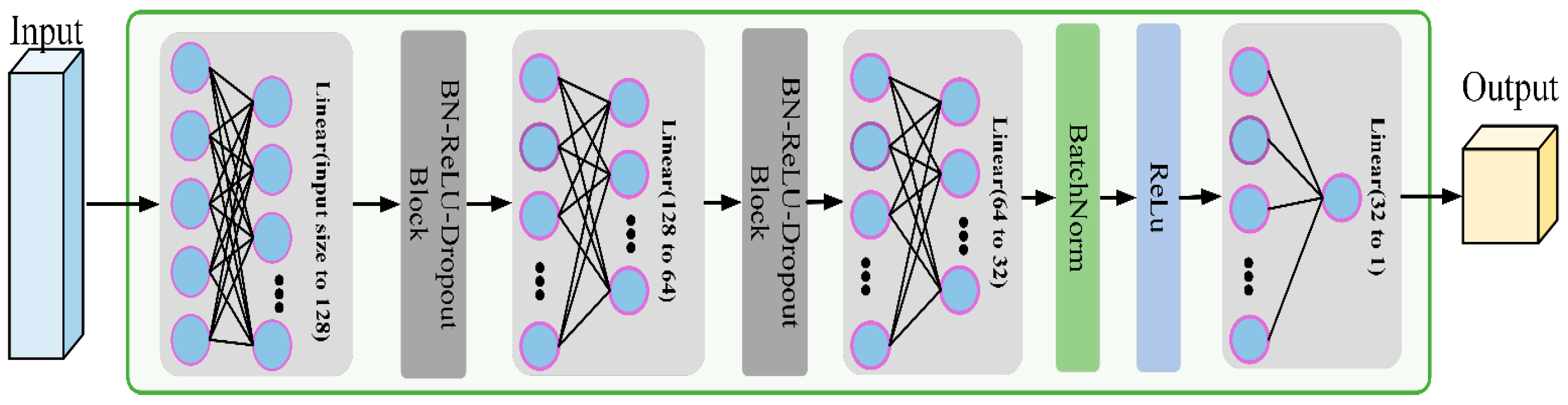
To establish a performance baseline, this study used a traditional fully connected neural network (FCNN) architecture as a centralized model, which was trained on the entire dataset. This centralized FCNN served as a benchmark to evaluate the effectiveness of the proposed FedMAE regressor under federated settings. The single-device regressor was implemented as a traditional fully connected neural network (FCNN), consisting of the following architecture: Input Layer: The number of input neurons corresponds to the dimensionality of the spectral feature input.
Hidden Layer 1: A linear layer with 32 neurons, followed by a ReLU activation function to introduce nonlinearity.
Dropout Layer: Applied with a dropout rate of 0.2 to mitigate overfitting.
Hidden Layer 2: A second linear layer with 16 neurons (i.e., half of the previous layer), followed by another ReLU activation.
Output Layer: A linear layer with one neuron to output the final prediction value.
As illustrated in
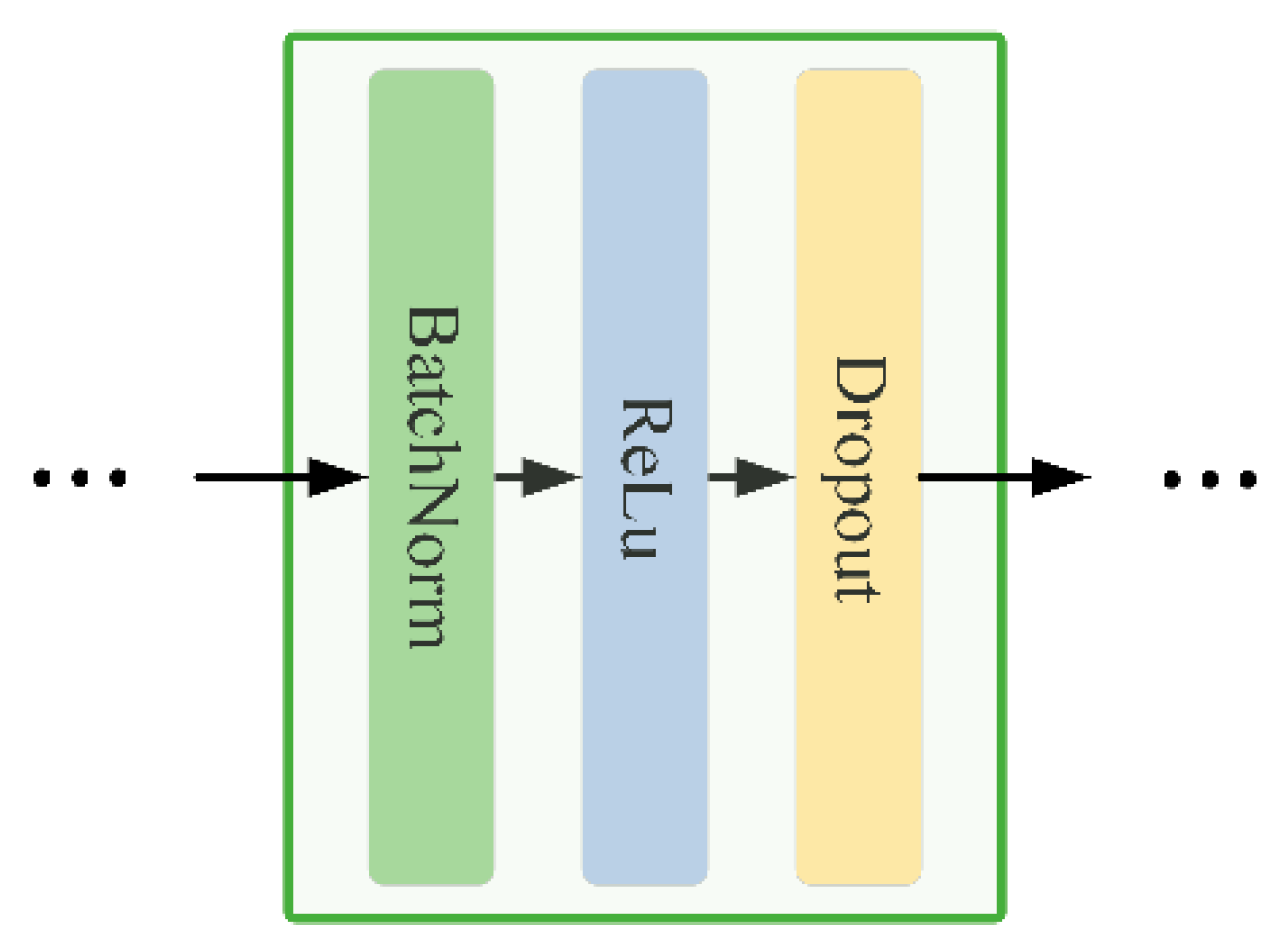
Figure 3, the model consists of multiple linear layers with ReLU activation functions behind each layer, while Dropout layers are used between hidden layers to reduce the risk of overfitting. The core block structure, consisting of BatchNorm, ReLU activation, and Dropout, is shown in
Figure 4. This model can effectively capture the nonlinear relationship between the input data and target variables through this structural design.
In terms of weight initialization in the model, we adopted the Xavier initialization method, which selects initial values for the weights based on the input and output dimensions of the layer such that the output of each layer has reasonable variance at the early stage of training. This initialization strategy helps the network to converge quickly at the beginning of training while reducing the risk of gradient disappearance or explosion. Through this initialization method, each model layer can maintain a relatively stable gradient flow during the forward propagation process, thus speeding up the training process. The model was trained using the Adam optimizer, with the Mean Squared Error (MSE) as the loss function. The batch size was set to 64, and training was run for 200 epochs. Spectral features were standardized prior to training. This network served as a centralized baseline for comparison with the federated FedMAE regressor and single-client models.
4.3. Federated Learning Training Workflow
The federated learning training process consists of three key stages:
Local Model Training
Each client trains a local model using its assigned data partition. Local epochs are implemented to ensure stability, where clients perform multiple training iterations on their datasets. Gradient clipping is applied to prevent gradient explosion during deep neural network training. In terms of model architecture, the federated regression model is used to learn from the local data of each client. Local model training involves a combination of MSE and L1 losses to enhance robustness to outliers and improve generalization ability.
Model Aggregation Strategy
After local training, client model parameters are aggregated to form a global model. As different clients may have varying amounts of data, a weighted averaging approach is employed, where each client’s contribution is proportional to its dataset size. Maintaining consistency between local and global models is essential for ensuring the stability of convergence.
Communication Efficiency Optimization
Communication overhead is a critical factor in federated learning, as frequent data exchanges between clients and the central server can be costly in terms of bandwidth and latency. For efficiency optimization, we use a compressed update strategy. Instead of transmitting full model parameters, clients send only the difference between local and global models, reducing the data transferred in each training round. A sparse communication strategy is also applied, where only the most crucial model updates are sent to the server, further decreasing communication overhead. This process ensures that federated learning remains scalable across multiple clients while maintaining reasonable communication costs and computational efficiency.
4.4. Optimization Methods
The implementation combines several optimization techniques to enhance the model’s convergence and mitigate training instabilities in federated learning environments. The AdaBelief optimizer, utilized in gradient-based optimization for model updating, exhibits superior convergence performance compared to conventional Adam optimizers. This optimizer dynamically modifies the learning rate according to the historical gradient variance to facilitate more efficient and reliable training updates. This study further employs a dynamic learning rate scheduling technique to systematically alter the learning rate throughout the training period, hence enhancing the learning process. In our experiments, the scheduler started with an initial learning rate of 0.0001, which was gradually decreased based on training progress. As the training progresses, this method gradually reduces the learning rate, promotes convergence, and avoids overshooting minimum. The scheduler systematically adjusts the learning rate for the entire training trajectory, initially accelerating convergence using larger step sizes and then gradually reducing them to promote fine-grained optimization. This periodic modulation effectively navigates loss landscapes and bypasses sub-optimal convergence points. While communication-efficiency-promoting techniques—such as compressed model updates and periodic synchronization—greatly reduce transmission overhead in the federated setting, they are not without limitations. First, compressed updates may lead to a loss of precision in parameter representation, which can affect convergence stability and result in slower training or sub-optimal accuracy, especially for sensitive regression tasks. Additionally, asynchronous or infrequent aggregation can introduce client drift, where local models diverge too far from the global optimum, requiring more rounds to stabilize. These trade-offs must be carefully balanced: in low-bandwidth or resource-constrained environments, communication savings may justify minor performance degradation; however, in high-precision scenarios such as nutrient quantification, this could impact the real-world usability of the resulting models. Future work may explore the use of adaptive compression schemes or error feedback mechanisms to mitigate these issues.
In order to prevent overfitting of models and improve their generalization ability, this study adopted an early stop mechanism. The method monitors validation losses during training and stops the training process if the losses do not improve over a certain number of iterations. This approach is designed to avoid unnecessary training when the model’s performance on the validation set begins to level off or deteriorate.
In addition, this study adopted gradient amplitude control measures to ensure the stability of the numerical values. Specifically, the gradient clipping technique constrains extreme parameter updates by applying a maximum threshold on the gradient specification. In contrast, the gradient scaling technique adjusts the numerical representation of the gradient during backpropagation on GPU-accelerated systems. These mechanisms are fundamental in federated environments, where gradient features can exhibit high variability between distributed clients.
4.5. Training and Validation
This section details the training and validation procedures, covering dataset selection, federated data partitioning, and model evaluation strategies.
Dataset: The dataset used in this study is the publicly available Anhui Soil Dataset, which contains 1360 soil samples collected from Huangshan and Shitai County in Anhui Province, China. Each sample includes spectral reflectance data spanning 161 spectral bands in the near-infrared (NIR) range from 900 nm to 1700 nm. The spectral data were collected using a calibrated laboratory spectrometer and preprocessed following standard protocols. The corresponding nutrient labels—nitrogen (N), phosphorus (P), and potassium (K) contents—were obtained through standard laboratory chemical analysis methods, as described in [
44,
45]. The dataset is organized in CSV format, with each row representing one sample and columns containing the spectral band values and target nutrient concentrations. This structure makes it suitable for both centralized and federated learning settings, especially when evaluating models under heterogeneous data distribution scenarios.
Data Partitioning: A critical aspect of federated learning is the data distribution across multiple clients. The dataset was divided into multiple subsets using a stratified sampling technique to emulate such a scenario. This method ensures that each client receives a representative subset of data, preserving the distribution of target variables. We used 80% of the data for training and 20% for testing. This configuration mitigates the training bias arising from imbalanced client datasets by emulating authentic decentralized data distribution conditions.
Experimental Set: The training process is controlled by hyperparameters, including the number of training cycles, batch size, learning rate, and optimization method. The proposed FedMAE regressor model was trained on the spectral dataset with a fixed masking rate of 75%, randomly setting half of the input features during the training process to encourage robust feature reconstruction. The following parameter settings were used during the training process: In order to ensure sufficient convergence of the federated model, the model was trained for 2000 epochs, and the batch size for each client was set to 32. These values were chosen to balance the computational efficiency and stability of the gradient updates during local model training. The initial learning rate for model training was set to 0.0001, which was subsequently adjusted using the dynamic learning rate scheduler described in
Section 4.4. This strategy helps to enhance the convergence speed during early training and enables finer optimization in later stages. Additionally, in order to prevent overfitting, an early stopping mechanism was used to monitor the validation loss. Training was stopped early if the validation loss did not improve after 20 consecutive passes. During the training process, the gradient was clipped to a maximum value of 5.0 to prevent the model from making excessive updates, ensuring the stability of convergence. The model was implemented using Pytorch 2.5.1 and trained on a CPU.
Refinement of the Training Process: To enhance the stability and efficiency of training, several refinements were incorporated into the model training pipeline. First, the batch size was set to 32 for the MAE-based models and 64 for the FCNN baseline, striking a balance between memory efficiency and gradient stability. Second, training was conducted for 200 to 500 epochs, depending on the model, with early stopping based on the validation loss employed to prevent overfitting and reduce unnecessary computation. In addition, dropout layers (p = 0.2) were inserted after key hidden layers for regularization, mitigating the risk of overfitting on small or noisy subsets. Finally, model checkpoints were saved periodically, enabling training recovery and performance monitoring. These refinements collectively contributed to smoother training dynamics and improved the models’ generalization performance in both centralized and federated settings.
Validation and Evaluation: The global model was evaluated using retained test data after completing federated training. The following metrics were used to assess performance: R-Square (R2), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE). These metrics allowed for a comprehensive evaluation of the model’s accuracy in predicting sample attributes. The results were also compared to those obtained using traditional centralized models, ensuring that the federated model is competitive and effectively leverages the advantages of distributed learning.
Through the incorporation of these stringent assessment methodologies, the study guarantees that the federated model not only aligns with but also exceeds conventional centralized models, providing a scalable and privacy-preserving approach for spectral data analysis, enabling sample property prediction.
5. Results
Our experimental evaluation revealed apparent performance differences between the federated learning and centralized approaches for three target nutrient elements: potassium (K), phosphorus (P), and nitrogen (N). Based on 32 repeated iterations and subsequent statistical analyses, the R2, RMSE, and MAE indicators demonstrated divergent patterns of predictive effectiveness, highlighting variations in model performance evaluation.
5.1. Federated Learning Versus Single-Client Performance
In
Figure 5,
Figure 6 and
Figure 7 and
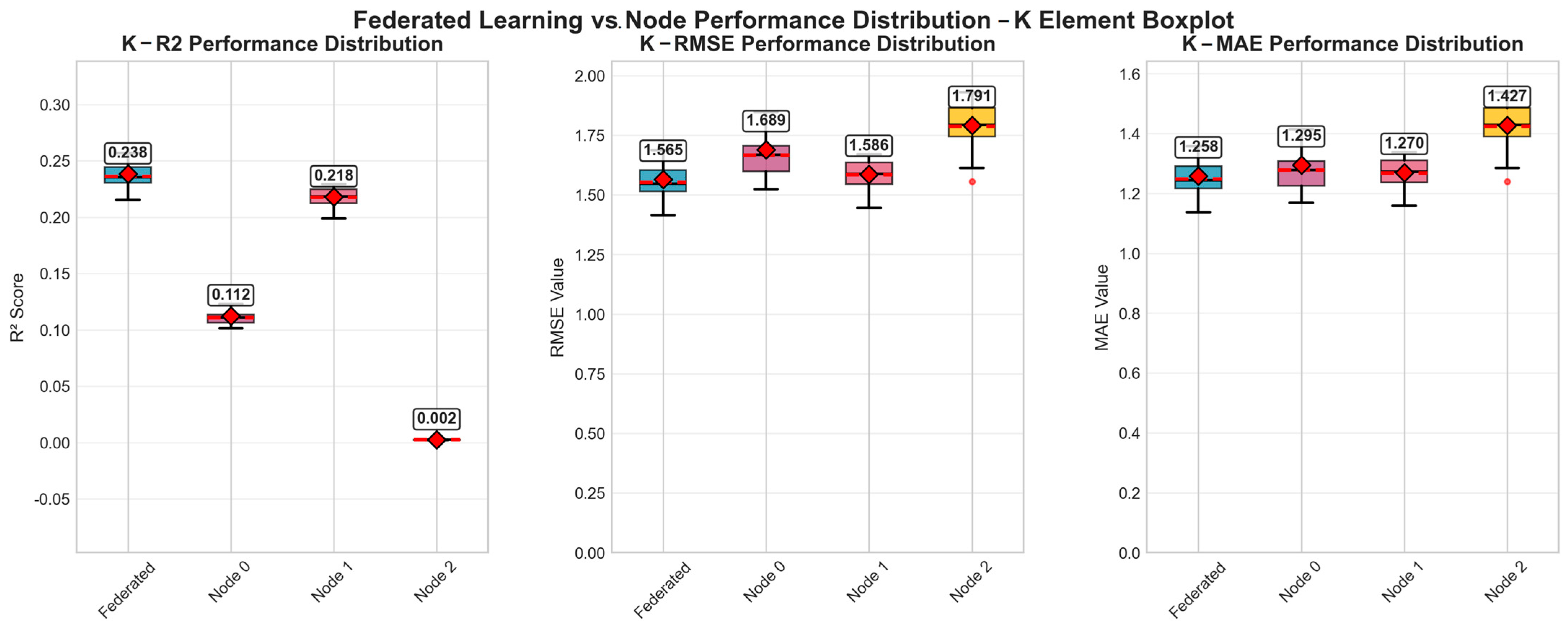
Section 5.1, the labels Node 0, Node 1, and Node 2 refer to centralized models that were each trained independently using only their respective local data subsets without participating in the federated aggregation process. These models simulate standalone client-side learners under isolated data conditions and are intended to serve as baseline comparisons to the proposed FedMAE regressor. This setting allows us to evaluate the performance benefits of federated learning by comparing it against purely local training scenarios with no cross-client collaboration.
For potassium (K) estimation, the R
2 value of the federated learning model was 0.24378, superior to the performance of all single-client models. This indicates a moderate predictive ability. Meanwhile, the relatively average error indicators shown by the federated model with respect to all single clients include an RMSE of 1.560 and MAE of 1.252. As shown in
Figure 5, the error metric of the federated model was superior to those of the single-client models. The performance of each client varied greatly, with Node 2 presenting the poorest performance, indicating a significant heterogeneity of data among the various collection sites.
The predictive performance for phosphorus (P) and nitrogen (N) showed a similar trend, with the federated learning model being basically superior to all single-client models in all evaluation metrics. These improvements achieved through the federated method highlight its ability to effectively utilize distributed data and enhance the resulting model’s generalization ability and robustness.
5.2. Federated Learning Versus Centralized Learning Performance
In this evaluation, the centralized FCNN model described in
Section 4.2.2 was used as a baseline, which was trained on the full dataset. As shown in
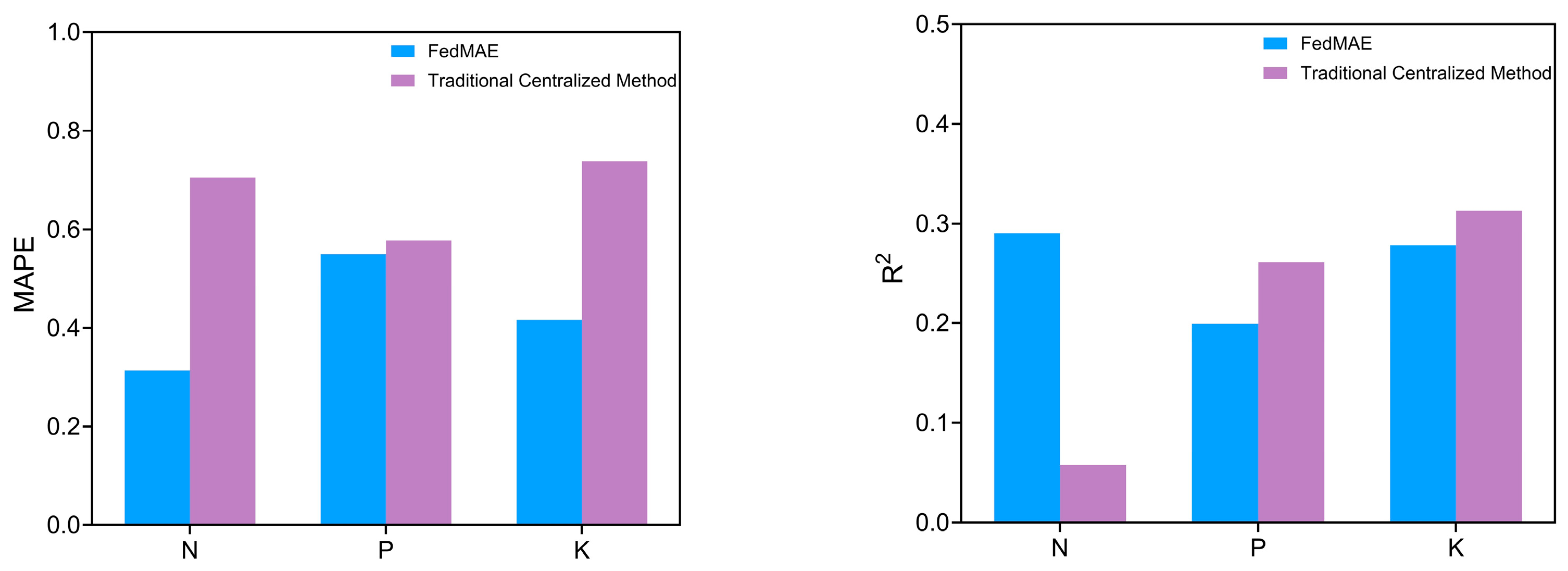
Figure 8, its performance was compared against that of the proposed FedMAE regressor in order to assess the advantages of federated learning in distributed environments.
For phosphorus (P) prediction, R2 values of 0.199 and 0.261 were achieved by the federated and non-federated models, respectively. However, despite this minor drawback, the federated learning model showed excellent performance in MAE and MAPE, consistently achieving lower errors compared to the non-federated model. Client performance was significantly inconsistent, with negative R2 values for Node 1 and Node 2, indicating challenges in generalizing phosphorus content across different samples.
Similar results were observed for potassium (K) predictions, as the R2 value derived from the federated learning framework was inferior to that of the centralized model, signifying a marginally diminished capacity of the model to elucidate the variance in the target variable in a distributed context. The RMSE values for the federated learning model were somewhat greater than those recorded for the centralized model, while the overall prediction accuracy was somewhat diminished. These enhancements indicate that although federated learning may encounter some challenges in accurately reflecting the complete spectrum of potassium concentration variations, it improves the overall robustness and stability of forecasts, especially in terms of mitigating extreme biases.
The nitrogen (N) estimates showed the most promising results, with the federated model achieving the highest overall R2 value of 0.290, substantially better than that of the non-federated approach. The federated model also showed superior error metrics compared to those of the non-federated implementation. This suggests that the federated learning model is particularly beneficial for nitrogen prediction, possibly due to the capture of different nitrogen fixation models under different sample conditions.
According to the results shown in
Figure 8, nitrogen was the most favorable predictor among all methods, with the lowest error values and the highest coefficients of determination. This suggests that the inherent characteristics of nitrogen content may make it more suitable for spectral analysis and subsequent machine-learning-based predictions. Conversely, phosphorus prediction demonstrated the most arduous qualities, characterized by persistently elevated error metrics and consistently low R
2 values in both federated and non-federated implementations. Phosphorus compounds typically display intricate spectral features that fluctuate markedly with the mineral composition and pH level of samples.
To evaluate the computational efficiency of the proposed FedMAE regressor in comparison with the traditional centralized regression model, we conducted a resource profiling experiment measuring peak memory usage, system memory occupancy, and runtime, the results of which are summarized in
Table 1. The FedMAE regressor demonstrated clear advantages in terms of resource consumption. Specifically, it achieved a 44.4% reduction in peak memory usage and a 25.2% decrease in peak system memory utilization when compared to the traditional centralized regression model. Additionally, the FedMAE approach completed training in 36 min, which is 22% faster than the 46 min required by the baseline. These improvements can be attributed to the federated architecture, which distributes computational workloads across multiple clients, thus reducing the memory and processing burden on any single device.
5.3. Ablation Study
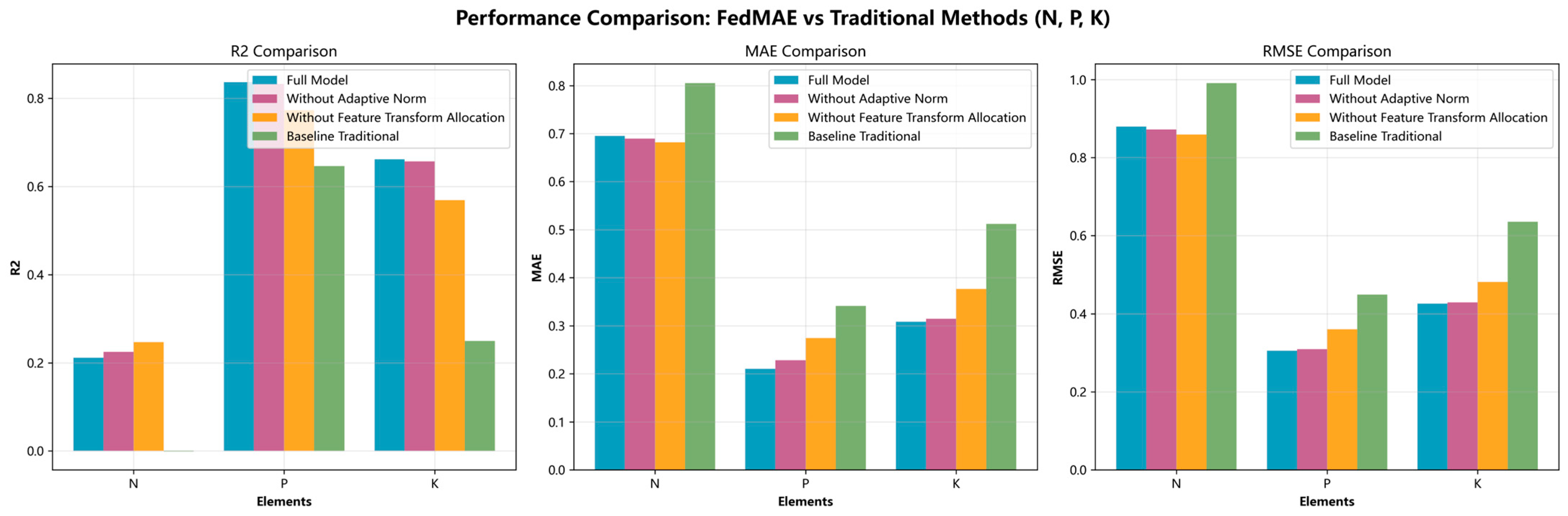
To evaluate the individual contributions of key components in the proposed FedMAE regressor, we conducted ablation experiments focusing on the following modules: adaptive normalization, and multi-layer feature transformation and balanced data allocation. In particular, due to the structural dependency between the multi-layer feature transformation and balanced data allocation components—specifically, the change in feature dimensionality from 200 to 64—these two modules were evaluated jointly as a single block (denoted as feature transform allocation).
Figure 9 presents the results of the ablation study, evaluating the contributions of the two key architectural components in the FedMAE regressor mentioned above. The baseline included the full model, and comparisons were made against two ablated versions—one with adaptive normalization removed and one without the feature transform allocation block—as well as against a traditional regression model. Removing adaptive normalization resulted in performance degradation, particularly in the phosphorus (P) and potassium (K) prediction tasks. For instance, in the potassium prediction scenario, the R
2 dropped from approximately 0.67 to 0.66, accompanied by a slight increase in RMSE. This indicates that adaptive normalization plays an important role in stabilizing feature distributions across clients with heterogeneous data.
Excluding the feature transform allocation module led to a more substantial decline in performance. This ablation caused a clear drop in R2 scores and increases in both MAE and RMSE values. These results suggest that the integration of richer feature representation with a balanced client data allocation mechanism is critical for improving model generalization in non-IID federated environments.
Overall, the findings confirm that both the adaptive normalization and feature transform allocation modules enhance the robustness and accuracy of predictions, particularly in the presence of heterogenous data, as is typical in edge device-based federated learning applications.
5.4. Hyperparameter Tuning Analysis
To evaluate the sensitivity and robustness of the FedMAE regressor to key hyperparameters, we conducted a series of experiments in which the batch size and learning rate were varied. The goal was to identify parameter configurations that optimize the model’s predictive performance across the nitrogen (N), phosphorus (P), and potassium (K) estimation tasks. The results, as summarized in
Table 2 and
Table 3, are reported in terms of performance metrics including the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and coefficient of determination (R
2) for each configuration.
Based on the results in
Table 2 and
Table 3, the configuration with batch size = 32 and learning rate = 0.0001 consistently achieved the best (or near-best) performance across all nutrient prediction tasks. These settings provided a stable training process with minimal error metrics and strong generalization capability. Therefore, these hyperparameter values were adopted as the default configuration in all experiments.
5.5. Comparative Evaluation with Traditional Regression Models
To further highlight the effectiveness of our proposed FedMAE regressor, we com-pared its performance against two widely used traditional regression models: Gradient Boosting Decision Trees (GBDT) and Extreme Gradient Boosting (XGBoost). Both models were trained in a centralized manner using the aggregated dataset. The comparison was conducted for all three target attributes—nitrogen (N), phosphorus (P), and potassium (K)—using two standard metrics: Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE).
As shown in
Table 4, our FedMAE model consistently outperformed both comparative models across all nutrient prediction tasks. The improvements were particularly notable in the nitrogen prediction task, in which FedMAE achieved the lowest error metrics, demonstrating its superior capability to capture complex spectral patterns in a decentralized setting.
6. Analysis
The results allowed for a comparison of the prediction effects for three target nutrients (N, P, K) in different training environments, revealing several important implications regarding the comparative performance of federated and single-client learning approaches.
6.1. Performance Analysis of Federated Versus Centralized Learning
The federated model for nitrogen (N) predictions obtained an R2 value of 0.290, which was markedly superior to those of the centralized method (0.058) and all single-client models. The error metrics further illustrate the benefits of the federated model, which attained the lowest RMSE (0.571) and MAE (0.369) values. This variation in performance can be ascribed to the variety of sample attributes (i.e., nitrogen distribution) across several geographic locations, as represented by the unique clients. The FedMAE regressor architecture efficiently consolidates several nitrogen models without direct data sharing, thus safeguarding data privacy while encompassing a broader spectrum of nitrogen variation attributes.
The combined model was outperformed in terms of R2 by the centralized model in the phosphorus (P) prediction task. This anomaly can be explained by the error metrics, where the federated model maintained competitive RMSE (1.160) and MAE (0.798) values. The apparent contradiction between R2 and the error metrics suggests that while the federated model captures general trends in phosphorus content, it struggles with extreme values (or outliers) that disproportionately affect the coefficient of determination. This observation is consistent with the pre-treatment strategy, where phosphorus values showed higher variance and required more extensive normalization. Although the federated model obtained competitive error indicators, its performance was still not optimal compared to the non-federated approach. This result demonstrates that phosphorus compounds have complex spectral characteristics and are highly sensitive to the pH and mineral content attributes of samples. Furthermore, due to their aggregation of information across diverse data distributions, local models may fail to sufficiently represent the complete spectrum of phosphorus fluctuations.
The federated model’s potassium (K) predictions demonstrated enhanced performance relative to all single-client models, although it exhibited marginally inferior performance when compared to the non-federated method. However, the federated model achieved the lowest RMSE (1.010) of all the methods, indicating better overall error minimization. This result indicates that the optimization effectively mitigates the oscillations in the federated aggregation process, which is especially beneficial for potassium prediction, for which the variability in sample attributes affects the stability of measurements.
A comparative evaluation of the federated and centralized learning approaches revealed subtle performance characteristics. While the federated model excelled in terms of nitrogen predictions, the predictions for potassium and phosphorus exhibited certain variations. This heterogeneity may have resulted from the inherent characteristics of the data distribution between different collection points. The R2 values observed for specific single-client models suggest that these local models performed worse than simply predicting the mean, highlighting the challenge of developing robust nutrient prediction models from limited, geographically constrained data sets. The federated learning approach successfully mitigated these limitations for nitrogen prediction, demonstrating its efficacy when considering nutrients with consistent spectral characteristics under different sampling conditions.
6.2. Limitations and Uncertainties of Results
The experiments presented in this study highlight the potential benefits of FL for nutrient prediction tasks, especially regarding nitrogen (N). However, some limitations of the methods and results warrant further discussion. Federated learning alleviates privacy issues by keeping data localized to customers; nonetheless, it encounters challenges when datasets display uneven distribution or significant fluctuations in attributes, such as those observed for nutrient contents. The inadequate performance metrics for potassium and phosphorus were particularly apparent for single-client models exhibiting more extreme data distributions, such as Node 2 for potassium forecasting. This indicates that additional research is required to enhance the optimization of federated learning models in order to more effectively manage these data discrepancies. Methods such as domain adaptation and transfer learning may be investigated to tackle the obstacles associated with heterogeneous data distributions, hence enhancing the applicability of models across various sample types.
To further interpret the relatively lower prediction performance for phosphorus (P) and potassium (K), several factors must be considered. First, phosphorus compounds exhibit complex interactions with soil components such as calcium, iron, and aluminum oxides, leading to highly variable absorption patterns that are difficult to capture through NIR spectra alone. Similarly, potassium tends to have weaker and less distinct spectral signatures in the NIR range compared to nitrogen, making accurate modeling inherently more challenging. Additionally, the data distributions for P and K are more imbalanced, with a higher proportion of extreme values and outliers, thus adversely affecting the generalization ability of regression models.
To address these issues, future improvements can include: (1) enhancing the extraction of features through targeted spectral band selection or transformation techniques (e.g., derivative spectra, wavelet transform); (2) employing outlier-robust loss functions such as Huber loss or quantile loss to reduce sensitivity to abnormal values; and (3) designing nutrient-specific sub-modules in the FedMAE architecture to allow for feature specialization by nutrient type. Such refinements are expected to enhance the model’s capacity to handle the spectral and statistical complexities associated with phosphorus and potassium prediction.
While this study focused on nutrient prediction using soil spectral data, the proposed FedMAE Regressor framework is designed to be modular and adaptable to a wide range of agricultural sensing tasks. For instance, it can be extended to other types of continuous-valued data such as soil moisture, temperature, or vegetation indices, for which spatial heterogeneity and incomplete data are also common. Additionally, the model’s ability to learn robust representations from partially observed inputs makes it suitable for applications involving sensor failures or intermittent data collection, which are frequent in real-world agricultural deployments. Future research may explore the application of the proposed framework for cross-region yield estimation, plant disease progression modeling, or in multimodal fusion scenarios involving image and spectral inputs. These extensions demonstrate the framework’s potential as a general-purpose solution for intelligent, decentralized agricultural analytics.
7. Conclusions
This study proposed the FedMAE regressor framework based on a masked autoencoder (MAE) to improve the prediction of sample attributes while effectively protecting data privacy. The model architecture incorporates several key innovations to enhance the performance stability and training efficiency in federated learning environments. The experimental results validated that federated learning helps to improve the prediction of nutrient contents through collaborative model development while maintaining data privacy. Performance improvements were found to correlate with nutrient properties, particularly for nutrients with high spatiotemporal variability such as nitrogen, where the model obtained using the federated approach showed significant advantages due to the aggregation knowledge from different environments without the need for direct data sharing. In addition, this study employed the AdaBelief optimizer to enhance training stability and convergence speed by adapting the step size based on gradient variance. Adaptive aggregation strategies were also used to address data heterogeneity and reduce communication overhead by weighting client updates in federated learning environments. Through these innovations, our approach was shown to achieve improved prediction accuracy for certain sample attributes. The proposed FedMAE regressor demonstrated strong predictive performance and robustness in heterogeneous, decentralized environments, making it a promising candidate for real-world agricultural applications. Its federated architecture inherently supports privacy preservation and decentralized deployment across edge devices such as in-field sensors, drones, or mobile agricultural terminals. This sets a precedent for future federated learning applications in agricultural and environmental sciences, where privacy and heterogeneously distributed data are critical issues.
Although the FedMAE regressor method proposed in this study has made significant progress in terms of sample attribute prediction, some limitations still remain to be addressed in future studies. First, to mitigate the impacts of biased nutrient distributions—particularly for phosphorus and potassium—future studies should adopt more balanced data sampling or data augmentation techniques, such as SMOTE or synthetic spectra generation, to improve the stability of the resulting regression models. Second, given the low spectral distinguishability among nutrients in the 900–1700 nm range, further research should explore extended spectral ranges (e.g., mid-infrared), feature engineering methods (e.g., spectral derivatives), or band selection algorithms to extract more informative features. Moreover, integrating physicochemical properties (e.g., pH, cation exchange capacity, organic matter) alongside spectral inputs may improve the model’s explainability and nutrient prediction accuracy, especially for weakly represented nutrients. In federated settings, non-IID data distributions remain a challenge. Developing client-specific adaptation modules or personalized federated learning strategies could improve performance consistency across heterogeneous clients. These research directions are expected to contribute to the aim of systematically overcoming the proposed model’s shortcomings and lay a solid foundation for deploying practical, privacy-preserving, and accurate soil analysis systems in real-world agricultural scenarios.
Author Contributions
Conceptualization, C.Z.; methodology, C.Z., Y.L., B.S. and T.S.; validation, Y.L.; supervision, B.S.; project administration, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shandong Province Higher Education Young Innovative Talents Cultivation Program Project (Grant No. TJY2114), Jinan City-School Integration Development Strategy Project (Grant No. JNSX2023015), Natural Science Foundation of Shandong Province (Grant No. ZR2021MF074), and University of Jinan Disciplinary Cross-Convergence Con (Grant No. XKJC-202408).
Data Availability Statement
Conflicts of Interest
Author Chuan’gang Zhao was employed by the company Shandong University Electric Power Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Haj-Amor, Z.; Araya, T.; Kim, D.-G.; Bouri, S.; Lee, J.; Ghiloufi, W.; Yang, Y.; Kang, H.; Jhariya, M.K.; Banerjee, A.; et al. Soil salinity and its associated effects on soil microorganisms, greenhouse gas emissions, crop yield, biodiversity and desertification: A review. Sci. Total Environ. 2022, 843, 156946. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Guo, Z.; Chen, H.; Yang, X.; Geng, J. Effects of different potassium fertilizer types and dosages on cotton yield, soil available potassium and leaf photosynthesis. Arch. Agron. Soil Sci. 2021, 67, 275–287. [Google Scholar] [CrossRef]
- Vejan, P.; Khadiran, T.; Abdullah, R.; Ahmad, N. Controlled release fertilizer: A review on developments, applications and potential in agriculture. J. Control. Release 2021, 339, 321–334. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, M.; Zhu, Y.; Liu, Z. Impacts of land use and plant characteristics on dried soil layers in different climatic regions on the loess plateau of china. Agric. For. Meteorol. 2011, 151, 437–448. [Google Scholar] [CrossRef]
- Zha, Z.; Shi, D.; Chen, X.; Shi, H.; Wu, J. Classification of appearance quality of red grape based on transfer learning of convolution neural network. Agronomy 2023, 13, 2015. [Google Scholar] [CrossRef]
- Feichtenhofer, C.; Fan, H.; Li, Y.; He, K. Masked autoencoders as spatiotemporal learners. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2022; Volume 35, pp. 35946–35958. [Google Scholar]
- Shi, Y.; Siddharth, N.; Torr, P.; Kosiorek, A.R. Adversarial masking for self-supervised learning. In International Conference on Machine Learning; PMLR: Baltimore, MD, USA, 2022; pp. 20026–20040. [Google Scholar]
- Wei, C.; Fan, H.; Xie, S.; Wu, C.-Y.; Yuille, A.; Feichtenhofer, C. Masked feature prediction for self-supervised visual pre-training. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 14668–14678. [Google Scholar]
- Xie, Z.; Zhang, Z.; Cao, Y.; Lin, Y.; Bao, J.; Yao, Z.; Dai, Q.; Hu, H. Simmim: A simple framework for masked image modeling. In Proceedings of the IEEE/CVF Conference On Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9653–9663. [Google Scholar]
- Wang, Y.; Shao, M. Spatial variability of soil physical properties in a region of the loess plateau of pr china subject to wind and water erosion. Land Degrad. Dev. 2013, 24, 296–304. [Google Scholar] [CrossRef]
- Dou, B.; Zhu, Z.; Merkurjev, E.; Ke, L.; Chen, L.; Jiang, J.; Zhu, Y.; Liu, J.; Zhang, B.; Wei, G.-W. Machine learning methods for small data challenges in molecular science. Chem. Rev. 2023, 123, 8736–8780. [Google Scholar] [CrossRef] [PubMed]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.Y. Communication-efficient learning of deep networks from decentralized data. In International Conference Artificial Intelligence and Statistics; PMLR: Fort Lauderdale, FL, USA, 2017; pp. 1273–1282. [Google Scholar]
- Bonawitz, K.; Eichner, H.; Grieskamp, W.; Huba, D.; Ingerman, A.; Ivanov, V.; Kiddon, C.; Konecn, J.; Mazzocchi, S.; McMahan, B.; et al. Towards federated learning at scale: System design. In Proceedings of the Machine Learning and Systems, Palo Alto, CA, USA, 31 March–2 April 2019; Volume 1, pp. 374–388. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Talwalkar, A.; Smith, V. Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 2020, 37, 50–60. [Google Scholar] [CrossRef]
- Zhu, L.; Wu, J.; Biao, W.; Liao, Y.; Gu, D. Spectralmae: Spectral masked autoencoder for hyperspectral remote sensing image reconstruction. Sensors 2023, 23, 3728. [Google Scholar] [CrossRef]
- Stevens, A.; Nocita, M.; Tóth, G.; Montanarella, L.; van Wesemael, B. Prediction of soil organic carbon at the european scale by visible and near infrared reflectance spectroscopy. PLoS ONE 2013, 8, e66409. [Google Scholar] [CrossRef]
- Rinnan, Å.; Van Den Berg, F.; Engelsen, S.B. Review of the most common preprocessing techniques for near-infrared spectra. TrAC Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Wang, R.; Wang, H. Combination of convolutional neural networks and recurrent neural networks for predicting soil properties using vis–nir spectroscopy. Geoderma 2020, 380, 114616. [Google Scholar] [CrossRef]
- Khan, A.; Lee, C.-H.; Huang, P.Y.; Clark, B.K. Leveraging generative adversarial networks to create realistic scanning transmission electron microscopy images. npj Comput. Mater. 2023, 9, 85. [Google Scholar] [CrossRef]
- Zhao, M.; Yan, L.; Chen, J. Hyperspectral image shadow compensation via cycle-consistent adversarial networks. Neurocomputing 2021, 450, 61–69. [Google Scholar] [CrossRef]
- Rial, R.C. Ai in analytical chemistry: Advancements, challenges, and future directions. Talanta 2024, 274, 125949. [Google Scholar] [CrossRef] [PubMed]
- Loh, H.C.; Chong, K.W.; Ahmad, M. Quantitative analysis of formaldehyde using uv-vis spectrophotometer pattern recognition and artificial neural networks. Anal. Lett. 2007, 40, 281–293. [Google Scholar] [CrossRef]
- Ling, T.L.; Ahmad, M.; Heng, L.Y. Uv-vis spectrophotometric and artificial neural network for estimation of ammonia in aqueous environment using cobalt (ii) ions. Anal. Methods 2013, 5, 6709–6714. [Google Scholar] [CrossRef]
- Martelo-Vidal, M.J.; Vázquez, M. Application of artificial neural networks coupled to uv–vis–nir spectroscopy for the rapid quantification of wine compounds in aqueous mixtures. CyTA-J. Food 2015, 13, 32–39. [Google Scholar] [CrossRef]
- Nezhadali, A.; Shadmehri, R.; Rajabzadeh, F.; Sadeghzadeh, S. Selective determination of closantel by artificial neural network-genetic algorithm optimized molecularly imprinted polypyrrole using uv–visible spectrophotometry. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 243, 118779. [Google Scholar] [CrossRef]
- Revignas, D.; Amendola, V. Artificial neural networks applied to colorimetric nanosensors: An undergraduate experience tailorable from gold nanoparticles synthesis to optical spectroscopy and machine learning. J. Chem. Educ. 2022, 99, 2112–2120. [Google Scholar] [CrossRef]
- Zhao, K.; Hu, J.; Shao, H.; Hu, J. Federated multi-source domain adversarial adaptation framework for machinery fault diagnosis with data privacy. Reliab. Eng. Syst. Saf. 2023, 236, 109246. [Google Scholar] [CrossRef]
- Arooj, Q. FedWindT: Federated learning assisted transformer architecture for collaborative and secure wind power forecasting in diverse conditions. Energy 2024, 309, 133072. [Google Scholar] [CrossRef]
- Wang, H.; Yurochkin, M.; Sun, Y.; Papailiopoulos, D.; Khazaeni, Y. Federated learning with matched averaging. arXiv 2020, arXiv:2002.06440. [Google Scholar]
- Xiao, Y.; Shao, H.; Lin, J.; Huo, Z.; Liu, B. BCE-FL: A secure and privacy-preserving federated learning system for device fault diagnosis under non-IID condition in IIoT. IEEE Internet Things J. 2023, 11, 14241–14252. [Google Scholar] [CrossRef]
- Li, A.; Sun, J.; Zeng, X.; Zhang, M.; Li, H.; Chen, Y. Fedmask: Joint computation and communication-efficient personalized federated learning via heterogeneous masking. In Proceedings of the 19th ACM Conference on Embedded Networked Sensor Systems, Coimbra, Portugal, 15–17 November 2021; pp. 42–55. [Google Scholar]
- Guo, S.; Wang, H.; Geng, X. Dynamic heterogeneous federated learning with multi-level prototypes. Pattern Recognit. 2024, 153, 110542. [Google Scholar] [CrossRef]
- Fanì, E.; Camoriano, R.; Caputo, B.; Ciccone, M. Fed3R: Recursive Ridge Regression for Federated Learning with strong pre-trained models. In Proceedings of the International Workshop on Federated Learning in the Age of Foundation Models in Conjunction with NeurIPS 2023, 2023. [Google Scholar]
- Yu, H.; Guo, K.; Karami, M.; Chen, X.; Zhang, G.; Poupart, P. Federated bayesian neural regression: A scalable global federated gaussian process. arXiv 2022, arXiv:2206.06357. [Google Scholar]
- Faes, A.; Pirmani, A.; Moreau, Y.; Peeters, L.M. Federated Block-Term Tensor Regression for decentralised data analysis in healthcare. arXiv 2024, arXiv:2412.06815. [Google Scholar]
- Lin, J.; Gao, F.; Shi, X.; Dong, J.; Du, Q. SS-MAE: Spatial–spectral masked autoencoder for multisource remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Wang, Y.; Hernández, H.H.; Albrecht, C.M.; Zhu, X.X. Feature guided masked autoencoder for self-supervised learning in remote sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 321–336. [Google Scholar] [CrossRef]
- Cao, X.; Lin, H.; Guo, S.; Xiong, T.; Jiao, L. Transformer-based masked autoencoder with contrastive loss for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Wan, M.; Yan, T.; Xu, G.; Liu, A.; Zhou, Y.; Wang, H.; Jin, X. Mae-nir: A masked autoencoder that enhances near-infrared spectral data to predict soil properties. Comput. Electron. Agric. 2023, 215, 108427. [Google Scholar] [CrossRef]
- Al Shalabi, L.; Shaaban, Z.; Kasasbeh, B. Data mining: A preprocessing engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Mining, W.I.D. Data Mining: Concepts and Techniques; Morgan Kaufinann: Burlington, MA, USA, 2006; Volume 10, pp. 559–569. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- RVestergaard, J.; Vasava, H.B.; Aspinall, D.; Chen, S.; Gillespie, A.; Adamchuk, V.; Biswas, A. Evaluation of optimized preprocessing and modeling algorithms for prediction of soil properties using vis-nir spectroscopy. Sensors 2021, 21, 6745. [Google Scholar] [CrossRef]
- Breure, T.; Prout, J.; Haefele, S.M.; Milne, A.; Hannam, J.; Moreno-Rojas, S.; Corstanje, R. Comparing the effect of different sample conditions and spectral libraries on the prediction accuracy of soil properties from near-and mid-infrared spectra at the field-scale. Soil Tillage Res. 2022, 215, 105196. [Google Scholar] [CrossRef]
Figure 1.
The input data is processed through a feature extraction module (green), followed by a regression head (blue) and a residual connection (orange) to enhance prediction. GELU refers to Gaussian Error Linear Unit, Layer Norm is layer normalization, and Dropout is used for regularization. Purple circles and their connecting lines denote fully connected layers, which map extracted features to the final prediction outputs.
Figure 1.
The input data is processed through a feature extraction module (green), followed by a regression head (blue) and a residual connection (orange) to enhance prediction. GELU refers to Gaussian Error Linear Unit, Layer Norm is layer normalization, and Dropout is used for regularization. Purple circles and their connecting lines denote fully connected layers, which map extracted features to the final prediction outputs.
Figure 2.
The traditional model architecture.
Figure 2.
The traditional model architecture.
Figure 3.
The proposed centralized architecture.
Figure 3.
The proposed centralized architecture.
Figure 4.
BN–ReLU–Dropout Block.
Figure 4.
BN–ReLU–Dropout Block.
Figure 5.
Performance comparison of federated and single-client models for potassium (K) prediction, based on R², RMSE, and MAE metrics. The performance data represent the average results from 32 independent training runs and have been statistically validated. Red dots indicate outlier values that deviate from the typical range, reflecting the variability and stability of performance across different clients.
Figure 5.
Performance comparison of federated and single-client models for potassium (K) prediction, based on R², RMSE, and MAE metrics. The performance data represent the average results from 32 independent training runs and have been statistically validated. Red dots indicate outlier values that deviate from the typical range, reflecting the variability and stability of performance across different clients.
Figure 6.
Performance comparison of federated and single-client models for nitrogen (N) prediction based on R2, RMSE, and MAE metrics.
Figure 6.
Performance comparison of federated and single-client models for nitrogen (N) prediction based on R2, RMSE, and MAE metrics.
Figure 7.
Performance comparison of federated and single-client models for phosphorous (P) prediction based on R2, RMSE, and MAE metrics.
Figure 7.
Performance comparison of federated and single-client models for phosphorous (P) prediction based on R2, RMSE, and MAE metrics.
Figure 8.
Federated versus non-federated (single device) model performance (single optimal performance).
Figure 8.
Federated versus non-federated (single device) model performance (single optimal performance).
Figure 9.
Ablation study comparing the full FedMAE model with versions excluding adaptive normalization or feature transformation and balanced allocation modules.
Figure 9.
Ablation study comparing the full FedMAE model with versions excluding adaptive normalization or feature transformation and balanced allocation modules.
Table 1.
Comparative analysis of resource consumption between FedMAE regressor and traditional regression model.
Table 1.
Comparative analysis of resource consumption between FedMAE regressor and traditional regression model.
| Method | Peak Memory (MB) | Peak System Memory (%) | Runtime (Minutes) |
|---|
| Traditional Centralized | 5322.1 | 75.3 | 46 |
| FedMAE Regressor | 2956.72 | 50.2 | 36 |
Table 2.
Performance of FedMAE under different batch sizes across nutrient prediction tasks.
Table 2.
Performance of FedMAE under different batch sizes across nutrient prediction tasks.
| Element | Batch Size | R2 | MAE | RMSE |
|---|
| N | 4 | 0.2850 | 0.3614 | 0.5806 |
| 8 | 0.2795 | 0.3648 | 0.5929 |
| 16 | 0.2819 | 0.3648 | 0.5775 |
| 32 | 0.2903 | 0.3686 | 0.5712 |
| P | 4 | 0.1507 | 0.8647 | 1.1832 |
| 8 | 0.1421 | 0.8758 | 1.1741 |
| 16 | 0.1420 | 0.8142 | 1.1941 |
| 32 | 0.1993 | 0.7983 | 1.1597 |
| K | 4 | 0.2503 | 0.7588 | 0.9977 |
| 8 | 0.2377 | 0.7722 | 1.0102 |
| 16 | 0.2526 | 0.7488 | 1.0151 |
| 32 | 0.2783 | 0.7014 | 1.0109 |
Table 3.
Performance of FedMAE under different learning rates across nutrient prediction tasks.
Table 3.
Performance of FedMAE under different learning rates across nutrient prediction tasks.
| Element | Learning Rate | R2 | MAE | RMSE |
|---|
| N | 0.001 | 0.1284 | 0.3801 | 0.6225 |
| 0.0005 | 0.1974 | 0.3739 | 0.5852 |
| 0.0003 | 0.2660 | 0.3664 | 0.5845 |
| 0.0001 | 0.2903 | 0.3686 | 0.5712 |
| P | 0.001 | 0.1453 | 0.8123 | 1.1771 |
| 0.0005 | 0.1555 | 0.8145 | 1.1945 |
| 0.0003 | 0.1779 | 0.7827 | 1.1641 |
| 0.0001 | 0.1993 | 0.7983 | 1.1597 |
| K | 0.001 | 0.3204 | 0.6690 | 1.0173 |
| 0.0005 | 0.3095 | 0.6751 | 1.0086 |
| 0.0003 | 0.3192 | 0.6687 | 0.9886 |
| 0.0001 | 0.2783 | 0.7014 | 1.0109 |
Table 4.
Performance comparison of FedMAE, GBDT, and XGB in nutrient prediction tasks.
Table 4.
Performance comparison of FedMAE, GBDT, and XGB in nutrient prediction tasks.
| Element | Model | MAE | RMSE |
|---|
| N | XGB | 1.612 | 3.193 |
| GBDT | 0.828 | 1.806 |
| FedMAE | 0.368 | 0.571 |
| P | XGB | 3.433 | 6.928 |
| GBDT | 1.483 | 3.196 |
| FedMAE | 0.798 | 1.159 |
| K | XGB | 2.907 | 5.465 |
| GBDT | 1.764 | 3.434 |
| FedMAE | 0.701 | 1.010 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).