An Intrusion Detection System for the CAN Bus Based on Locality-Sensitive Hashing

Abstract

As the Internet of Vehicles (IoV) rapidly gains popularity, the Controller Area Network (CAN) faces increasingly severe security threats. Most of the existing research on protecting the CAN bus has been based on artificial intelligence models, which require complex feature extraction and training processes and are too resource-intensive for deployment in resource-constrained CAN environments. To address these challenges, we propose a lightweight intrusion detection system based on locality-sensitive hashing that achieves efficient security protection without relying on complex machine learning and deep learning frameworks. We employ the Nilsimsa algorithm to compute hash digests of the data, using the similarity scores of these digests as anomaly scores to identify abnormal traffic. Evaluations show that our method achieves an accuracy of 98%, and tests of the system’s overhead confirm its suitability for deployment in resource-limited CAN scenarios.

1. Introduction

As vehicle technology increasingly becomes more intelligent, the Controller Area Network (CAN) has become an indispensable component in modern automobiles. The CAN bus is responsible for transmitting critical operational data among various Electronic Control Units (ECUs) within a vehicle [1]. However, the CAN bus has no secure authentication mechanism, making it susceptible to external attacks that could jeopardize both vehicle operations and passenger safety [2]. Therefore, developing effective Intrusion Detection Systems (IDSs) to protect the CAN bus from malicious activities is crucial. Most existing IDSs fail to detect new or zero-day attacks, as there is no corresponding attack data during model training. Thus, anomaly-based IDSs are the most suitable option for protecting the CAN bus, as they can identify both existing and new attacks by learning the patterns in normal data and modeling deviations from this normalcy as anomalies.

Although various anomaly-based IDS solutions for the CAN bus currently exist, these methods typically rely on machine learning or deep learning, which require significant computing resources and storage space. They also rely on continuous data training and model updates, potentially encountering concept drift. Moreover, AI-based approaches often necessitate feature engineering, and if the chosen features are unsuitable, the detection performance can be severely impacted; in practice, deploying such methods on the CAN bus entails complex feature extraction. Given the limited resources of in-vehicle systems, these requirements are often difficult to satisfy in real-world vehicle environments [3]. A typical low-end ECU usually has only a single computing core with a clock speed of a few hundred megahertz and a memory capacity of a few hundred kilobytes [4]. Notably, the current research often remains confined to single-vehicle scenarios and does not fully exploit the potential of cloud–edge collaborative architectures in connected vehicle environments. The powerful computing capabilities and global threat intelligence repositories in the cloud can support distributed model training and knowledge sharing, while lightweight algorithms at the edge enable low-latency responses. The collaboration of these two sides provides a novel approach to overcoming the existing resource constraints. Addressing these challenges, a cloud–edge collaborative architecture offers unique advantages: on the one hand, edge nodes (e.g., on-board ECUs) can perform lightweight real-time detection to meet low-latency requirements, only needing to upload suspicious data fragments to the cloud, which significantly reduces the communication overhead; on the other hand, the cloud can continuously optimize the detection models by aggregating data from multiple vehicles.

To address the aforementioned issues, we propose a novel lightweight anomaly-based IDS designed specifically for CAN bus environments that uses locality-sensitive hashing (LSH). By employing low-overhead algorithms and data processing flows, this approach significantly reduces the memory and computational costs while ensuring fast response times and detection accuracy. Unlike methods that rely on complex machine learning frameworks, ours does not require large training datasets yet still maintains a reliable detection rate. Moreover, it can be adopted as a lightweight anomaly detection solution at the edge nodes within a cloud–edge collaborative architecture.

This paper begins by introducing the relevant background, followed by a review of the existing IDS technologies. We then present our intrusion detection method in detail, along with a series of tests and experiments to evaluate its performance. Finally, we discuss the advantages and limitations of our approach and outline potential directions for future improvements.

2. Background

2.1. The CAN Bus and Its Security

Since its debut in 1986, the Controller Area Network (CAN) has become an indispensable communication protocol in modern automobiles. This network design supports hostless communication among various Electronic Control Units (ECUs) within a vehicle, greatly simplifying the internal wiring layout, reducing the manufacturing costs, and enhancing the overall reliability and efficiency of the system. The CAN protocol utilizes a broadcast mechanism that allows each node within the vehicle to randomly access the bus and transmit data between nodes. It also employs a mechanism called arbitration to manage situations where multiple nodes access the bus simultaneously, ensuring the sequentiality and correctness of data transmissions. Through arbitration, nodes transmit messages according to priority, with higher-priority messages able to interrupt the transmission of lower-priority ones. This is crucial for automotive control systems that have stringent real-time requirements. Based on the importance of the applications and bandwidth needs, the CAN bus is divided into the high-speed CAN (HS CAN) and the low-speed CAN (LS CAN). The HS CAN is typically used to connect sensors and ECUs performing critical tasks, such as engine control and braking systems, while non-critical or less critical nodes, such as in-car entertainment systems and air conditioning controls, may be connected via the LS CAN. This tiered approach ensures that critical systems maintain high communication efficiency and reliability while allocating adequate communication resources to less critical applications.

The standard frame format for a CAN frame primarily consists of an 11-bit CAN ID, a 4-bit data length code (DLC), and a data segment of 0–8 bytes. Figure 1 illustrates the structure of a standard CAN frame.

Although the CAN bus is widely used in the automotive industry due to its low cost, ease of installation, and low communication overhead, it lacks encryption and user authentication mechanisms and allows the use of message priority to gain the right to send messages. As a result, it is vulnerable to data eavesdropping and tampering threats. Attackers can send forged CAN messages to manipulate or disrupt critical vehicle functions, posing serious security risks [5].

2.2. Locality-Sensitive Hashing

A hash function maps an input of an arbitrary length to a fixed-length output. Traditional hash functions can distribute different data points (vectors) into various hash buckets, making non-uniformly distributed data points appear nearly uniformly in these buckets. However, such hash functions do not preserve the similarity relationships between data points. To enable the rapid retrieval of similar data points, the similarity among feature vectors should be reflected in their hashed values. Hence, locality-sensitive hashing (LSH), which retains the similarity relationships among data points, has been widely adopted [6], with applications to spam detection [7], image retrieval [8], and IoT traffic fingerprinting [9], among others.

In this work, we employ the Nilsimsa algorithm [7], a variant of LSH designed to produce summaries (digests) that are insensitive to minor, automatically generated changes while maintaining a low false positive rate. It generates a 32-byte code to represent the distribution of triplets in the data. The Nilsimsa algorithm processes data using a five-character sliding window, scanning one character at a time. Whenever a new character enters the window, the corresponding triplet is generated and passed to a hash function $h\left(\right)$. This hash function produces an output i within the range $[0,255]$, denoted by $i=h\left(trigram\right)$. The frequency of i is recorded in a 256-element integer array called the accumulator. After the analysis, each position in the accumulator holds the number of times the corresponding triplet hash value appeared. Dividing the total number of processed triplets by 256 yields an average triplet count per position, which serves as a threshold. A triplet whose frequency exceeds this threshold is deemed significant. When comparing each triplet’s frequency to the threshold, if the frequency in the accumulator exceeds the threshold, the corresponding position in the digest is marked as 1; otherwise, it is marked as 0. Finally, a flip operation is performed to produce the final digest. Figure 2 illustrates the workflow of the Nilsimsa algorithm.

Two Nilsimsa digests can be compared to determine whether they represent the same message. Specifically, the digests’ comparison value is calculated as the number of matching bits minus 128; a higher comparison value indicates greater similarity between the two digests. Thus, the similarity range for two hash digests is [−128, 128]. In our approach, we expect normal data to exhibit relatively high similarity, whereas abnormal data should be less similar to normal data.

3. Related Works

In recent years, as the functionality of connected vehicles has continuously improved and the application scenarios have expanded, the Internet of Vehicles (IoV) has shown robust growth. However, behind the automotive industry’s gradual move toward digitalization, electrification, connectivity, and intelligence, cybersecurity and data security risks are emerging. Common internet threats—such as Trojan viruses, network attacks, and personal privacy leaks—are gradually extending into the realm of IoV, creating a complex and severe security landscape.

Research on IoV security is thus attracting increasing attention. Some studies focus on enhancing the security of the CAN message itself. For instance, Ref. [10] proposes a method for encrypting the 8-byte payload data, but this approach may incur a substantial performance overhead and is difficult to deploy, especially for vehicles already on the market. Ref. [4] identifies the anomalies in different ID payload sequences by computing the Hamming distance between consecutive payloads. Ref. [11] models the message sequences within a given time interval as a graph structure, using the cosine similarity and Pearson’s correlation to measure the similarity between consecutive graphs, and applies thresholding, change-point detection, and an LSTM (Long Short-Term Memory) recurrent neural network to detect and predict malicious messages injected into the CAN bus.

Thanks to their strong generalization capability, artificial intelligence (AI)-based solutions provide an excellent means of defending against automotive network attacks, and numerous machine learning (ML) and deep learning (DL) models have been proposed for this purpose. For instance, Ref. [12] introduces a new universal intrusion detection method that leverages convolutional attention and a Gated Recurrent Unit (GRU) network to detect intrusions on the CAN bus. Ref. [13] proposes a novel semi-supervised convolutional adversarial autoencoder model which uses large amounts of unlabeled data along with smaller quantities of labeled data, thereby reducing the need for extensive labeled datasets. Ref. [14] employs Generative Adversarial Networks (GANs) to artificially generate noisy data for adversarial training. Ref. [15] uses an LSTM-based RNN to detect anomalies in the CAN bus by predicting the next packet’s data value, with the prediction error serving as the anomaly signal. Ref. [16] puts forward a distributed anomaly detection system using Hierarchical Temporal Memory (HTM) but at a high computational cost. Ref. [17] adopts an LSTM autoencoder for anomaly detection in both in-vehicle and external networks, yielding a good performance yet lacking an assessment of the runtime overhead. In addition, some studies have also focused on lightweight intrusion detection for in-vehicle networks. For example, [18] presents an ultra-lightweight and energy-efficient Intrusion Detection System (IDS) for in-vehicle networks based on pruned Binarized Neural Networks (BNNs). The proposed system adopts a two-stage Coarse-to-Fine (C2F) architecture to reduce the inference time and is deployed across CPU, GPU, and FPGA platforms. However, the method relies entirely on supervised learning, requiring labeled data for all known attack types. Ref. [19] proposes a wavelet-based Intrusion Detection System for CAN networks that identifies malicious traffic by detecting behavior changes in transmission patterns, which can detect an anomaly in milliseconds. Ref. [20] proposes a lightweight intrusion detection system that transforms CAN ID time series into images (using MTF, RP, and GASF encoding) and utilizes a convolutional neural network with efficient channel attention (ECACNN) to accurately and efficiently detect abnormal communication in connected autonomous vehicles.

In previous work [9], locality-sensitive hashing (LSH) has been successfully applied to traffic-based device identification, demonstrating its potential to capture distinguishing patterns in network traffic. This suggests that LSH-based methods are not limited to similarity detection in unstructured data but can also be adapted to classifying structured traffic streams—motivating our exploration of LSH for anomaly detection in CAN bus networks. Compared to the traditional machine-learning-based intrusion detection systems, which often rely on labeled data and high computational overheads, LSH offers a lightweight, training-free alternative that performs similarity-based detection with minimal resource consumption. This makes it particularly suitable for in-vehicle environments, where embedded ECUs have strict constraints in terms of their memory and processing power. Various related works are summarized and compared as shown in

Table 1. Summary of various related works.

Research Work	Contributions	Complex Data Pre-Processing	High Cost	Testing On Public Dataset
[10]	Encryption of CAN frames	✗	✓	✗
[4]	Based on the Hamming distance	✗	✗	✗
[11]	Based on consecutive message sequence graphs	✓	✗	✓
[12]	Mixed intrusion detection	✗	✓	✓
[13]	First using convolutional adversarial autoencoders	✓	✓	✓
[14]	Based on a GAN	✓	✓	✓
[15]	Based on LSTM	✓	✓	✗
[16]	Continuous online learning	✓	✓	✗
[17]	Detecting both internal and external attacks	✓	✓	✓
[18]	Based on pruned Binarized Neural Networks	✓	✗	✓
[19]	Based on wavelet	✗	✗	✓
[20]	Based on a neural network with efficient channel attention	✓	✗	✓

.

Compared with related work, our approach offers the following advantages:

(1)

Anomaly-based intrusion detection: It does not require labeled data and provides a better detection capability for unknown attacks;

(2)

Independence from AI frameworks: No feature extraction is needed, minimizing the runtime overhead and facilitating real-world deployment on in-vehicle networks;

(3)

A high detection performance with low overhead: It achieves robust detection results while maintaining minimal system resource consumption.

4. The Proposed Architecture

We hypothesize that the locality-sensitive hash values of normal data exhibit high similarity to previously observed normal traffic, while abnormal data produce significantly divergent hash values. Based on this, we propose an anomaly detection mechanism that uses the similarity of the LSH digests as a lightweight indicator of the behavioral deviation. Since each CAN frame contains at most 8 bytes of data, the individual frame-level differences may be too subtle to produce meaningful hash distinctions. To address this, we aggregate the ID and payload fields for every n consecutive CAN frame into a single message sequence, from which we compute the LSH digest. This aggregation enhances the semantic richness and helps capture higher-level behavioral patterns. Given that a typical in-vehicle ECU generates approximately 2000 CAN frames per second [14], setting n in the range of 50 to 200 is both computationally reasonable and effective for temporal context modeling. Choosing a value for n that is too large may dilute the temporal locality and increase the detection latency, whereas a small value for n may reduce the ability to detect anomalous behavior effectively.

To ensure real-time applicability and memory efficiency, we maintain a sliding window of the k most recent LSH digests representing nominal behavior. Rather than storing all historical digests, which is impractical for embedded ECUs, we use a limited-size buffer that captures the most up-to-date normal patterns. Storing the latest digests ensures that the detection is responsive to the current operational context, while older digests may no longer reflect the system’s recent state due to behavioral drift or environmental changes. At system startup, the sliding window is populated with LSH digests computed exclusively from a subset of clean, benign CAN traffic. This “cold-start” procedure ensures that the sliding window contains no anomalous hashes at the outset, preventing any initial contamination of the reference model.

To set the threshold $\theta$, we use a configurable percentile of the similarity score distribution derived from normal data. Specifically, we adopt the $\alpha$-th percentile (e.g., the fifth percentile) as a hyperparameter to control the detection sensitivity. The impact of this hyperparameter on the detection performance is systematically evaluated in the experimental section.

Figure 3 illustrates the overall architecture of our proposed intrusion detection system.

Algorithm 1 describes the LSH-based anomaly detection method.

Algorithm 1 LSH-based anomaly detection

Input:      $F=\{f_1,f_2,\dots \}$: Stream of incoming CAN frames      n: Number of frames to aggregate      k: Sliding window size for LSH digest history      $\alpha$: Percentile for similarity threshold Output:      Anomaly alerts Initialization:      $B\leftarrow \left[\right]$         # Temporary buffer of size n      $W\leftarrow \left[\right]$         # Sliding window of size k      Compute the threshold $\theta$ as the $\alpha$-th percentile of the similarity scores on normal data Detection Loop: for each CAN frame $f_t$ do    Extract ID and data from $f_t$, append to B    if length(B) == n then      $h\leftarrow$Hash(B)      Clear buffer B      if window W is not empty then         $s\leftarrow$ average similarity between h and all digests in W         if $s<\theta$ then           Raise anomaly alert         end if      end if      Append h to W      if length(W) > k then         Remove oldest digest from W      end if    end if end for

5. Evaluation

5.1. The Experimental Setup

Our experiments are conducted in an offline setting using pre-collected datasets. Each CAN frame stream is processed sequentially, simulating the online update to the digest buffer and real-time anomaly decisions. The key hyperparameters in our method are the aggregation length n and the digest buffer size k. We conduct a grid search using the AUROC as the selection criterion. The sensitivity analyses for these parameters are shown in Section 5.2.4.

5.1.1. The Dataset

We utilize two datasets to evaluate the proposed method. The primary dataset is the Car-Hacking Dataset released by the HCRL [21], which was collected from a real vehicle’s OBD-II port during a series of information injection attacks. It contains 300 instances of injected intrusions, each lasting approximately 3 to 5 s, with every dataset spanning 30 to 40 min of CAN traffic. The dataset includes four types of attacks—DoS, fuzzing, gear spoofing, and RPM spoofing—along with features such as timestamps, CAN IDs, data lengths, data values, and labels.

The Car Hacking: Attack & Defense Challenge 2020 dataset [22], also released by the HCRL, was developed as part of a competition aimed towards advancing the attack and detection techniques for Controller Area Network (CAN) systems. It includes several subsets: a preliminary training set, a preliminary evaluation set, and a final submission set. We employ the final submission dataset for testing.

The two datasets used in our experiments are summarized in

Table 2. Overview of the car hacking dataset.

Attack Type	Total Messages	Normal Messages	Injected Messages
DoS attack	3,665,771	3,078,250	587,521
Fuzzy attack	3,838,860	3,347,013	491,847
Spoofing the drive gear	4,443,142	3,845,890	597,252
Spoofing the RPM gauze	4,621,702	3,966,805	654,897

and

Table 3. Overview of the Car Hacking: Attack & Defense Challenge 2020 dataset.

Round	Total Messages	Normal Messages	Attack Messages
Preliminary	3,672,151	3,372,743	299,408
Final	1,270,310	1,090,312	179,998

.

Our proposed method is training-free and does not require learning from labeled or unlabeled data. During evaluation, it operates directly on the test set by maintaining a sliding window of recent similarity digests. To ensure a fair comparison, we provide each baseline with 80% of the normal data for training. The remaining 20% of the normal data, together with all of the attack data, are used for testing. This distinction also highlights the efficiency of our method, which avoids the model training time and storage overhead associated with large parameterized models.

5.1.2. The Evaluation Metrics

To comprehensively assess the detection performance of our proposed method, we employ several key evaluation metrics: the accuracy, F1-score, AUROC, false positive rate (FPR), and false negative rate (FNR). Each of these metrics ranges from 0 to 1.

Accuracy measures the overall performance of a classification model, representing the proportion of correctly classified samples among the total number of samples. While it is a direct indicator of the model performance, it may be misleading under class imbalances.

$$\mathrm{Accuracy}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(1)

The $F_1$-score is the harmonic mean of the precision and recall, reflecting both the precision and recall of the model. This metric is particularly informative for imbalanced datasets, as it accounts for both the classifier’s ability to correctly detect positive cases and minimize false alarms.

$$\mathrm{F}1={\displaystyle \frac{2\times \mathrm{Precision}\times \mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}}$$

(2)

The AUROC (Area Under the Receiver Operating Characteristic Curve) evaluates a classification model’s performance by calculating the area under the ROC curve. The ROC curve depicts the relationship between the true positive rate (TPR) and the false positive rate (FPR) at various thresholds. A higher AUROC value indicates a stronger classification capability. An AUROC of 1 is ideal, and 0.5 typically signifies a performance no better than random guessing. Since AUROC is independent of specific decision thresholds, it provides a comprehensive assessment of model performance unaffected by the threshold selection.

$$\mathrm{AUROC}={\int }_{x=0}^{1}TPR\left(\mathrm{d}x\right)$$

(3)

The FPR (false positive rate) is the proportion of actual negative samples that is incorrectly classified as positive. It measures how often the system triggers false alarms under normal conditions. A high FPR leads to frequent false alarms, increasing the management burden and potentially causing genuine attacks to be overlooked. Maintaining a low FPR is therefore critical in practical deployments.

$$\mathrm{FPR}={\displaystyle \frac{FP}{FP+TN}}$$

(4)

The FNR (false negative rate) is the proportion of actual positive samples that is misclassified as negative. It reflects how frequently the IDS fails to detect real attacks. A higher FNR indicates that the system overlooks more actual attacks.

$$\mathrm{FNR}={\displaystyle \frac{FN}{FN+TP}}$$

(5)

5.1.3. Baseline Methods

To evaluate the performance of our proposed method, we compare it against several common anomaly detection approaches: Isolation Forest (iForest), an autoencoder (AE), and Empirical Cumulative Distribution Functions for Outlier Detection (ECOD).

iForest [23] is a tree-based unsupervised anomaly detection method. It constructs multiple isolation trees by randomly selecting the features and split values. Its core principle is that the anomalies are easier to isolate because they differ significantly from the majority of normal data points.

AE [24] is a neural-network-based unsupervised learning technique, often employed for feature extraction and anomaly detection. It consists of two parts—an encoder and a decoder—and is trained to minimize the reconstruction error (the difference between the input and reconstructed output). Since the model learns the normal patterns during training, anomalous data typically exhibits a high reconstruction error, making it detectable via a preset error threshold.

ECOD [25] is an anomaly detection method based on empirical cumulative distribution functions. It computes the outlier score for each data point by examining the empirical cumulative distributions for each feature independently. Assuming feature independence, ECOD can efficiently detect anomalies in high-dimensional datasets. It has relatively low computational complexity, making it suitable for large-scale data.

To ensure a fair comparison, the input to all of the above methods consists of frame sequences formed by n consecutive CAN frames.

We manually extract the numerical features from each aggregated sequence of n CAN frames. Each frame includes the ID, DLC (data length code), and up to 8 bytes of data. The extracted features include

• The statistical features of the CAN IDs: The maximum, minimum, mean, and standard deviation of the n message IDs;
• DLC statistics: The maximum, minimum, mean, and standard deviation of the DLC values across the sequence;
• Data byte statistics: The maximum, minimum, mean, and standard deviation over all bytes in the frame payloads;
• The ID frequency features: The number of unique IDs and the maximum, minimum, mean, and standard deviation of their occurrence counts within the sequence;
• The data distribution features: A normalized histogram over all 256 possible byte values (0–255), representing the distribution of the byte frequencies in the payload data.

These features are concatenated into a fixed-length vector for each input segment and serve as the input to anomaly detection models. This approach captures both the statistical properties and byte-level distributional characteristics of CAN traffic. Prior to training, all of the feature vectors are processed using min–max normalization to ensure consistent scaling across dimensions.

Table 4. Hyperparameters for ECOD, autoencoder, and Isolation Forest.

Algorithm	Hyperparameters
ECOD	contamination = 0.4
AE	input_dim = 273, hidden_layers = (128, 64, 32, 16), batch_size = 64, epochs = 30
iForest	n_estimators = 100, contamination = 0.4

provides a summary of the hyperparameters used for all of the baseline models in our experiments.

5.2. Results

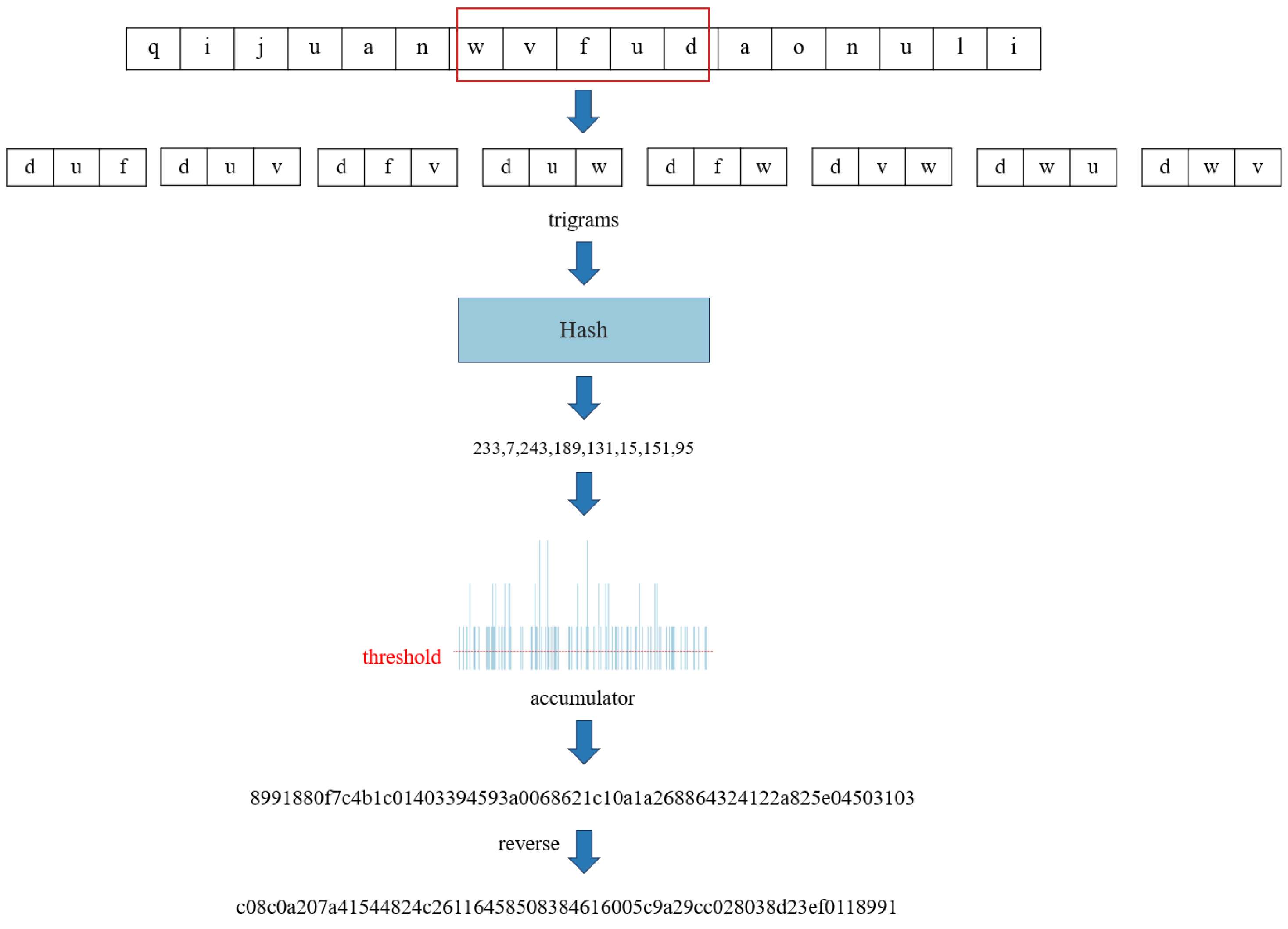
5.2.1. The Detection Capability

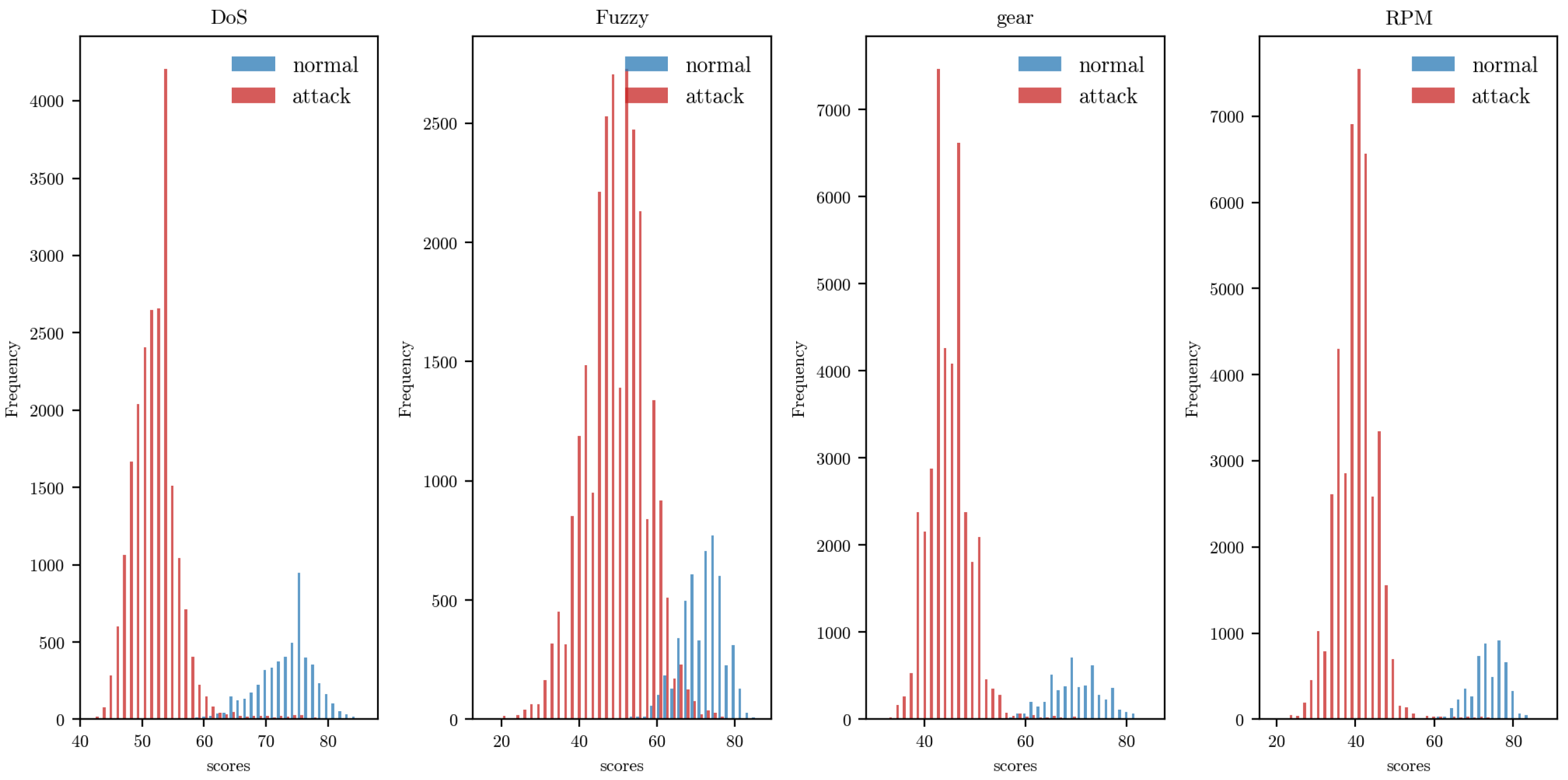
Under the experimental setting with $n=50$, $\alpha =5$, and $k=100$, we evaluate the detection performance across all four attack types in the car hacking dataset. To analyze the behavior of the similarity-based detection mechanism further, we present boxplots and histograms (see Figure 4 and Figure 5) illustrating the distribution of the similarity scores for both normal and anomalous samples. The visualizations show clear separation between the two distributions, indicating that the proposed method effectively differentiates between normal and attack patterns.

Table 5. The detection performance for different methods and attack types in the Car-Hacking Dataset. The bold formatting highlights the best results.

Method	Attack	Accuracy	F1	AUROC	FPR	FNR
iForest [23]	DoS	0.9403	0.9019	0.9766	0.0514	0.0788
	Fuzzy	0.9037	0.8575	0.9525	0.0731	0.1416
	Gear	0.8627	0.8377	0.9198	0.1118	0.1712
	RPM	0.8824	0.8666	0.9428	0.0929	0.1481
ECOD [25]	DoS	0.9764	0.9612	0.9848	0.0255	0.0188
	Fuzzy	0.9974	0.9962	0.9999	0.0006	0.0060
	Gear	0.8129	0.7699	0.8358	0.1268	0.2677
	RPM	0.7569	0.7267	0.7987	0.2123	0.2805
AE [24]	DoS	0.9985	0.9975	0.9998	0.0025	0.0042
	Fuzzy	0.9899	0.9808	0.9971	0.0071	0.0122
	Gear	0.9917	0.9949	0.9907	0.0092	0.0077
	RPM	0.9973	0.9970	0.9995	0.0010	0.0076
WINDS [19]	DoS	0.9497	0.9602	-	-	-
	Fuzzy	0.8778	0.9017	-	-	-
	Gear	0.9883	0.9901	-	-	-
	RPM	0.9944	0.9938	-	-	-
GIDS [14]	DoS	0.9790	-	0.9990	-	-
	Fuzzy	0.9800	-	0.9990	-	-
	Gear	0.9620	-	0.9960	-	-
	RPM	0.9800	-	0.9990	-	-
Proposed	DoS	0.9845	0.9904	0.9954	0.0127	0.0160
	Fuzzy	0.9656	0.9794	0.9906	0.0745	0.0268
	Gear	0.9918	0.9953	0.9984	0.0085	0.0082
	RPM	0.9950	0.9972	0.9989	0.0044	0.0051

compares the performance of our proposed method with five representative baseline approaches. Among them, iForest [23], ECOD [25], and the AE [24] are the baseline methods we implemented as part of our evaluation framework. In contrast, the remaining two WINDS [19] and GIDS [14] are included based on results reported in the prior literature.

The proposed method outperforms all of the non-AI baselines across most of the attack types and evaluation metrics, demonstrating clear advantages in both accuracy and robustness. Although the AE method achieves a slightly higher performance, the proposed method maintains comparable scores. In particular, for gear spoofing attacks, the proposed method achieves the best results on all metrics except the FNR. iForest performs poorly across all scenarios, with consistently low F1- and AUROC scores, indicating its limited suitability. ECOD achieves excellent results in detecting fuzzy attacks (F1 = 0.9962), but its overall performance is hindered by weak results for gear and RPM spoofing. WINDS shows a relatively good performance for gear and RPM attacks but still falls short of the proposed method. These results suggest that the method offers a favorable trade-off between a lightweight implementation and detection effectiveness.

One notable limitation of the proposed method is its comparatively lower performance on fuzzy attacks, with slightly reduced AUROC and F1-scores relative to those of the AE and ECOD. Fuzzy attacks operate by injecting randomly generated CAN frames into the network, which may inadvertently trigger unintended ECU behaviors. We hypothesize that due to their randomized yet structurally valid nature, fuzzy attack frames exhibit traffic patterns that are more similar to benign CAN messages compared to other attack types. This resemblance may reduce the contrast in the similarity scores and make anomaly detection more challenging for similarity-based methods. Supporting this, we observe that the average similarity score for fuzzy attack samples is significantly higher than that for the other attack types, indicating that these messages are more likely to be mistaken as normal under the proposed hash-based detection mechanism. The following table reports the mean similarity scores for both normal and attack segments.

Since the proposed method computes locality-sensitive hashes over aggregated sequences of n consecutive CAN frames, we further investigate how the proportion of attack frames within each segment affects the resulting similarity score.

Table 6. The mean similarity scores and coefficients for different types of attacks in the car hacking dataset.

Type	Mean Similarity (Normal)	Mean Similarity (Attack)	Coefficient
DoS	78.80	47.404	−0.72
Fuzzy	78.30	60.09	−0.56
Gear	75.72	44.53	−0.59
RPM	79.78	40.22	−0.57

also presents the Pearson’s correlation coefficients between the number of attack frames and the corresponding detection scores across the four attack types. The results show a negative correlation in all cases, meaning that the more attack frames are included in a segment, the less similar it becomes to normal data. The correlation coefficients range from −0.57 to −0.72, indicating at least a moderate to strong negative linear relationship across all attack types. This indicates a moderate to strong inverse linear relationship: as more attack frames are included in a segment, the less similar it becomes to normal data. These findings validate the scoring mechanism for our method—segments that contain more abnormal behavior tend to diverge more significantly from the learned normal profile.

However, among the four attacks, the correlation is weakest for fuzzy attacks. This aligns with the earlier observation that fuzzy attack frames, though malicious, are syntactically valid and randomly distributed, making them more likely to be blended into normal segments without drastically altering the hash-based similarity. As a result, even segments containing multiple fuzzy attack frames may retain relatively high similarity scores, contributing to the reduced detection sensitivity observed for this attack type.

To validate the generalization capability of our method further, we also conducted experiments on the Car Hacking: Attack & Defense Challenge 2020 dataset. This dataset presents a different set of attack scenarios and vehicle configurations, providing a complementary evaluation setting for assessing the robustness of our approach.

Table 7. The detection performance on the 2020 Car Hacking Challenge dataset. The bold formatting highlights the best results.

Method	Accuracy	F1	AUROC	FPR	FNR
Proposed	0.9759	0.9803	0.9974	0.0399	0.0137
AE [24]	0.9819	0.9791	0.9959	0.0066	0.0326
iForest [23]	0.6837	0.6606	0.7616	0.2493	0.0143
ECOD [25]	0.5403	0.6092	0.5530	0.0483	0.0026
CAVIDS [26]	0.9700	0.9000	-	0.0280	0.0390
XGBoost [22]	-	0.864	-	-	-

presents the overall detection performance of our proposed method and that of several baseline approaches. We set $n=100$, $k=50$, and $\alpha =5$. The proposed method achieves a high AUROC of 0.9974, indicating its excellent discriminative ability. Its F1-score (0.9801) and accuracy (0.9758) are also competitive, closely matching those of the autoencoder (AE), which slightly outperforms in accuracy but exhibits a higher false negative rate. This suggests that our method is more sensitive to anomalous patterns, reducing missed detections. Traditional anomaly detection methods such as Isolation Forest and ECOD perform considerably worse in this setting, with ECOD achieving only 54.0% accuracy and a 55.3% AUROC. Isolation Forest yields a better AUROC (0.7616) but suffers from a high false positive rate (FPR = 0.2493), limiting its practical usability. CAVIDS [26] is a lightweight intrusion detection method designed specifically for connected autonomous vehicles (CAVs). It is based on Logical Analysis of Data (LAD), a rule-based two-class classification technique that constructs partially defined Boolean functions (pdBfs) from historical CAN message data. CAVIDS shows a strong performance in its accuracy (0.9700) but lags behind in its F1-score. The XGBoost-based method from [22] reports only the F1-score (0.864), which is significantly lower than that of the proposed method.

Overall, our method demonstrates robust generalization to a dataset with different characteristics and attack patterns, maintaining a strong detection capability without relying on deep learning or model retraining.

5.2.2. The Runtime and Resource Overhead

Table 8. Computation times and estimated storage overheads of different methods.

Method	Runtime	Estimated Storage
Proposed	0.93 ± 0.01 ms	3.2 KB
AE	1.53 ± 0.04 ms	21 MB
iForest	0.70 ± 0.02 ms	1440 KB
ECOD	1.23 ± 0.02 ms	-

summarizes the average runtime per sample and the estimated storage overhead for each evaluated method. Our method involves computing a locality-sensitive hash digest for each test frame series and comparing it against the most recent k stored digests, which demonstrates low computational latency (0.93 ms) and minimal memory usage (3.2 KB), as it only stores a fixed-size sliding window of $k=100$ LSH digests. In contrast, the autoencoder (AE) introduces a higher storage overhead (21 MB), mainly due to its trained neural network parameters. As a deep learning model, the AE contains a large number of parameters and requires substantial matrix computations, making it unsuitable for deployment on resource-constrained devices such as in-vehicle ECUs [27]. iForest also requires moderate memory (1.44 MB), reflecting the number and depth of the isolation trees.

Notably, ECOD differs from the other methods in that it retains the full training dataset as part of its model representation. This design makes its storage requirements directly dependent on the training data size and thus difficult to express as a fixed overhead in kilobytes or megabytes. As such, we omit its estimated storage value in the table.

Therefore, our method demonstrates significant advantages in both the storage and runtime overhead, making it particularly well suited to deployment on the CAN bus.

5.2.3. The Ablation Study

To verify the effectiveness of each component in our proposed method, we conducted a fine-grained ablation analysis, removing or modifying specific parts of the approach to assess their individual contributions.

Table 9. Results of the ablation experiments on the car hacking dataset.

Method	Accuracy	F1	AUROC
Full Model	0.98	0.99	0.99
‐ Flow Concatenation ‐ Storing the Latest	0.70	0.60	0.60
‐ Storing the Latest	0.89	0.90	0.96

compares the performance when removing flow concatenation and omitting the step of storing the k most recent LSH digests or disabling storing the latest digests.

The results indicate that when neither flow aggregation nor storing the latest digests is performed, the LSH-based method exhibits a very poor performance, with an accuracy of about 70% and the F1-score and the AUROC both at around 0.6, far lower than the values for the baseline methods in Table 5. Furthermore, omitting only the step of storing the k most recent LSH digests yields metrics above 90%, yet its accuracy and F1-score remain suboptimal. These findings underscore the importance of combining both flow aggregation and recent digest storage to achieve the best detection performance.

5.2.4. The Influence of the Hyperparameters

We examine how varying the hyperparameters n (the number of CAN frames concatenated to form a frame series) and k (the number of recent LSH digests stored) affects the detection performance. Figure 6 and Figure 7 depict the AUROC, accuracy, and F1-score under different values of n and k.

The Car Hacking Dataset:All three metrics (AUROC, accuracy, and F1-score) show a consistent decline as n increases. This indicates that aggregating too many CAN frames into a single sequence may blur the temporal locality and dilute the distinction between normal and anomalous patterns. Notably, extreme values of k also hurt the performance: setting $k=10$ leads to significant fluctuations—particularly at $n=150$—while $k=500$ introduces visible degradation, likely due to the inclusion of outdated behavioral patterns in the reference window. The best trade-off is observed when $n=50$ to 100 and $k=100$ to 200.

The Car Hacking Challenge dataset: The performance trends are less monotonic but still reflect similar sensitivities. All three metrics generally peak at $n=100$ across most k values and drop sharply at $n=200$. The AUROC for $k=100$ reaches its maximum at $n=100$, while both the accuracy and F1-score also show the optimal performance in the n = 100–150 range. At $n=200$, the performance deteriorates across the board, especially for $k=200$, confirming that excessive aggregation combined with a large reference window weakens anomaly separability.

Summary and recommendations: These results demonstrate that both hyperparameters affect the performance in a coupled manner. A small aggregation window ($n\le 100$) ensures a good temporal resolution, while a moderately sized reference set ($k=100\sim 200$) balances the memory usage with detection robustness.

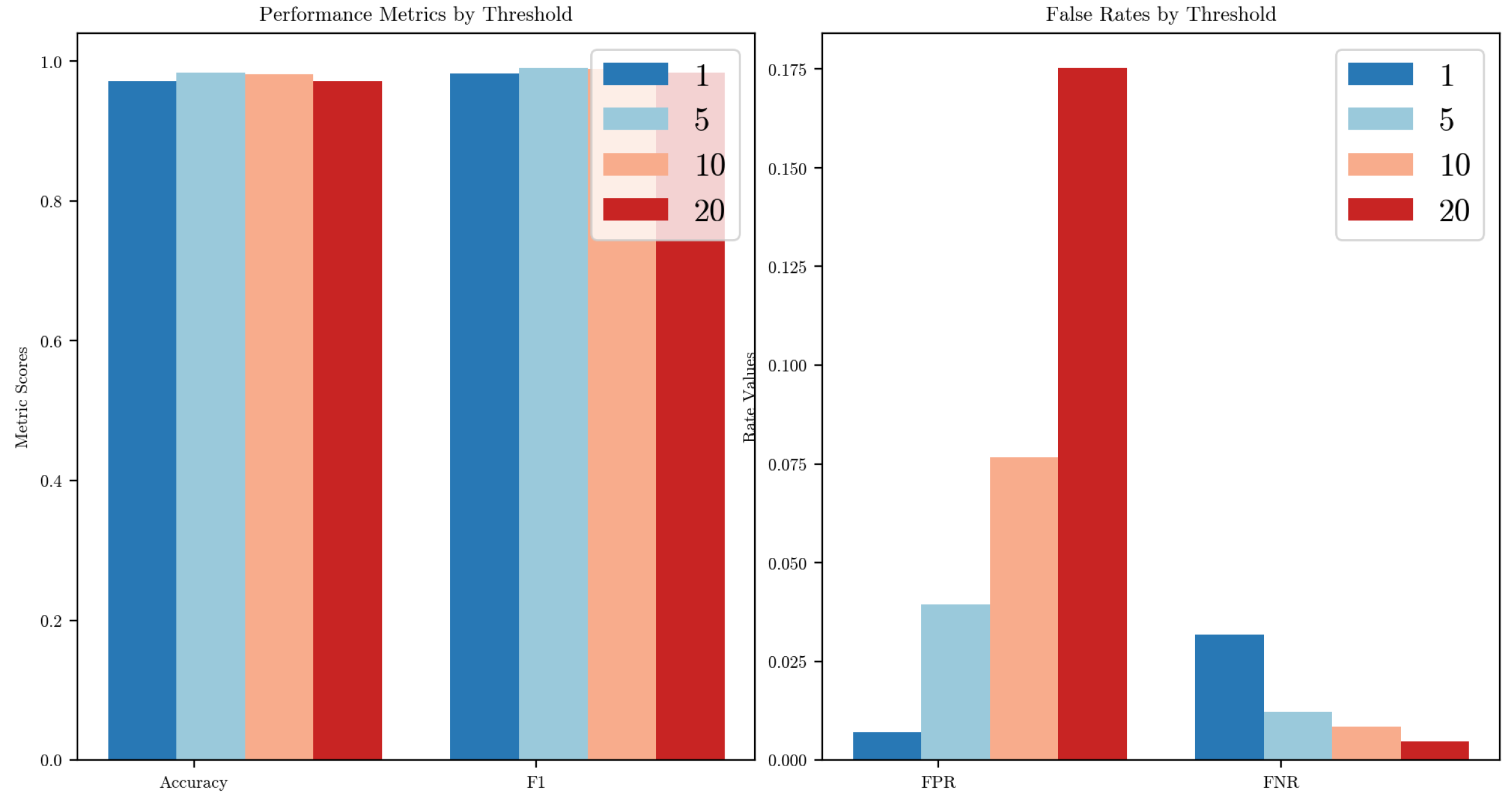
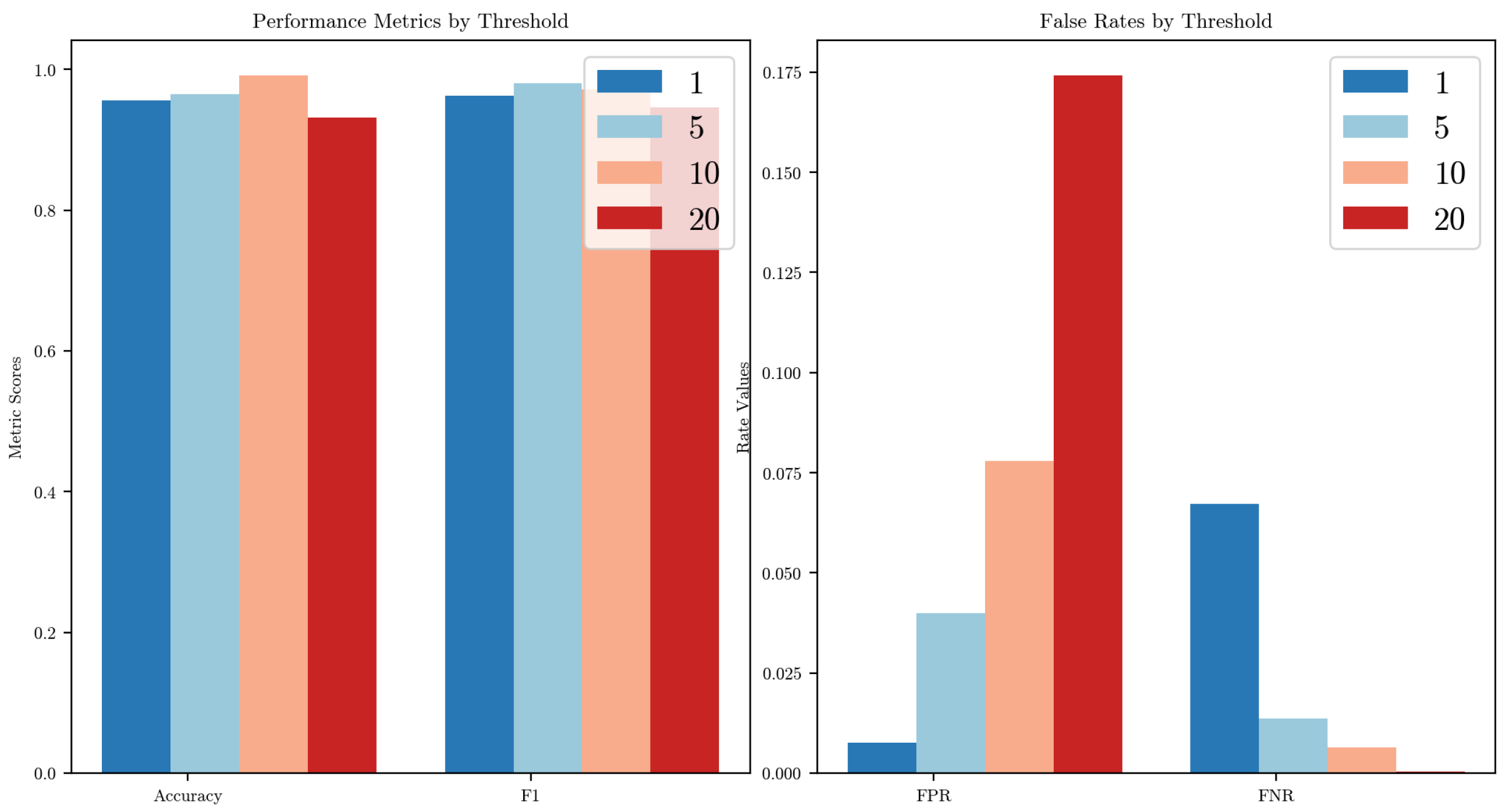
Figure 8 and Figure 9 illustrate the effects of varying the detection threshold $\theta$ performance metrics and error rates across the two datasets. We define $\theta$ as the $\alpha$-th percentile of the similarity score distribution computed from a set of normal data. Specifically, thresholds corresponding to the 1st, 5th, 10th, and 20th percentiles were evaluated.

In both cases, setting $\alpha =5$ yields the most balanced performance: the accuracy and F1-score remain high, while both the false positive rate (FPR) and false negative rate (FNR) are kept at acceptable levels. When $\alpha$ is too low (e.g., 1), the threshold $\theta$ becomes overly strict, increasing the FNR slightly, as more anomalies are misclassified as normal. Conversely, as $\alpha$ increases to 10 or 20, the threshold becomes more permissive, leading to a noticeable increase in the FPR, particularly evident in the car hacking dataset, where the FPR exceeds 17% at $\alpha =20$.

The patterns are consistent in the Car Hacking Challenge dataset, though the performance curves are flatter. This indicates that the method is relatively robust to threshold variations but still benefits from a carefully chosen $\alpha$. Based on these observations, we adopt $\alpha =5$ as the default setting for all experiments.

5.2.5. The Impact of the Choice of LSH Algorithm

In addition to Nilsimsa, we also selected another locality-sensitive hashing algorithm, TLSH [28], to evaluate its effectiveness. TLSH is an improved variant of Nilsimsa that uses a Pearson hash to compute trigram hash values. Instead of the average used by Nilsimsa, TLSH adopts quartiles for thresholding. The final TLSH digest incorporates a checksum, length information, and quartile-based statistical information, while the similarity is determined by the Hamming distance between Bloom filters.

Table 10. Performance metrics for different LSHs in the car hacking dataset.

Method	Accuracy	F1	AUROC	FPR	FNR
TLSH	0.9585	0.9761	0.9792	0.1952	0.0166
Nilsimsa	0.9832	0.9902	0.9966	0.0268	0.0152

shows the comparative performance of these two LSH algorithms. The experimental results demonstrate that Nilsimsa outperforms TLSH across all metrics. For TLSH, the AUROC, accuracy, and F1-score fall below 0.98, and its FPR is notably higher than that of Nilsimsa—indicating a higher tendency towards false alarms. However, the FNR for both algorithms is roughly similar, remaining below 0.02.

We also note that TLSH only considers hash values in the range of 0–127, whereas Nilsimsa uses 256 possible outputs in its bucket mapping. In smaller- to medium-scale datasets, Nilsimsa’s finer-grained distribution allows it to detect minor variations in the input data, capturing more subtle features. Consequently, Nilsimsa’s performance proves superior to that of TLSH in this scenario.

6. Conclusions

In summary, this work makes the following contributions:

(1)

We propose a novel intrusion detection method for CAN bus systems based on locality-sensitive hashing (LSH), which enables training-free and real-time anomaly detection;

(2)

We adapt the Nilsimsa hashing algorithm for structured CAN traffic by aggregating the frame sequences and evaluating the similarity scores against recent normal behavior.

We validated our method on the widely used Car-Hacking Dataset and the Car Hacking Challenge dataset, and the results showed its strong performance in terms of the accuracy, F1-scores, and AUROCs. Compared with other baseline methods, our approach remains lightweight while preserving a reliable detection performance. In addition, we systematically evaluated the impact of key hyperparameters (n, k, and $\alpha$) on the detection performance across the two datasets, confirming the importance of careful parameter selection for balancing the detection accuracy, robustness, and resource efficiency. We also compared Nilsimsa against another locality-sensitive hashing algorithm, TLSH, and demonstrated Nilsimsa’s superior efficacy for CAN bus intrusion detection. While our method demonstrates a promising performance in detecting various types of attacks, we acknowledge its potential vulnerability to low-frequency or stealthy intrusions. Such attacks may gradually contaminate the sliding window used for reference, reducing the detection sensitivity over time. In future work, we aim to enhance the resilience of our approach by exploring adaptive or decay-based windowing strategies, hybrid reference models, and anomaly scoring methods that account for long-term behavioral drift. And we aim to optimize the Nilsimsa algorithm’s workflow to further enhance its performance in network traffic intrusion detection scenarios. We also intend to explore more advanced or automated parameter tuning strategies to further enhance the detection generalization and usability in real-world vehicular systems.

As connected vehicles become increasingly prevalent, their underlying technologies often lack sufficient security—rendering them vulnerable to numerous attacks. This paper provides a novel, lightweight, and effective method for safeguarding CAN bus security in connected vehicles, thus offering algorithm-level support for real-time edge-side detection within a cloud–edge collaborative architecture.