KPV-UNet: KAN PP-VSSA UNet for Remote Image Segmentation

Abstract

Semantic segmentation of remote sensing images is a key technology for land cover interpretation and target identification. Although convolutional neural networks (CNNs) have achieved remarkable success in this field, their inherent limitation of local receptive fields restricts their ability to model long-range dependencies and global contextual information. As a result, CNN-based methods often struggle to capture the comprehensive spatial context necessary for accurate segmentation in complex remote sensing scenes, leading to issues such as the misclassification of small objects and blurred or imprecise object boundaries. To address these problems, this paper proposes a new hybrid architecture called KPV-UNet, which integrates the Kolmogorov–Arnold Network (KAN) and the Pyramid Pooling Visual State Space Attention (PP-VSSA) block. KPV-UNet introduces a deep feature refinement module based on KAN and incorporates PP-VSSA to enable scalable long-range modeling. This design effectively captures global dependencies and abundant localized semantic content extracted from complex feature spaces, overcoming CNNs’ limitations in modeling long-range dependencies and inter-national context in large-scale complex scenes. In addition, we designed an Auxiliary Local Monitoring (ALM) block that significantly enhances KPV-UNet’s perception of local content. Experimental results demonstrate that KPV-UNet outperforms state-of-the-art methods on the Vaihingen, LoveDA Urban, and WHDLD datasets, achieving mIoU scores of 84.03%, 51.27%, and 62.87%, respectively. The proposed method not only improves segmentation accuracy but also produces clearer and more connected object boundaries in visual results.

1. Introduction

With the rapid development of remote sensing imaging technology, remote sensing technology has become a necessary means of obtaining information about the Earth’s surface. As a fundamental task in remote sensing image processing, semantic segmentation has shown broad application prospects in recent years. Remote sensing images contain rich surface information, and the semantic segmentation of high-resolution remote sensing images has been widely applied in various fields, such as environmental monitoring [1,2,3], urban planning [4,5,6], and meteorological observation [7,8,9]. Semantic segmentation classifies images at the pixel level and assigns a corresponding category label to each pixel, thereby enabling a fine-grained division of complex surface scenes.

In recent years, Convolutional Neural Network (CNN)-based methods have significantly advanced semantic segmentation, surpassing traditional approaches and gradually becoming the dominant paradigm. Fully Convolutional Networks (FCNs) [10] marked a foundational shift by enabling end-to-end dense prediction. Building on this, a series of representative architectures have been proposed to improve segmentation performance further. The encoder–decoder framework has gained widespread adoption due to its modular design and effectiveness in capturing low-level and high-level features [11,12]. In this architecture, the encoder is responsible for extracting semantic features. At the same time, the decoder progressively restores spatial resolution. U-Net [12] introduced skip connections between corresponding encoder and decoder layers, effectively integrating low-level spatial details with high-level semantic representations. DeepLabV3+ [13], an extension of DeepLabV3 [14], enhanced spatial recovery by integrating a decoder module that refines object boundaries.

However, semantic segmentation faces challenges for remote sensing images due to complex boundaries and small object scales. As shown in Figure 1, ABCNet [15] is a CNN-based method, UNetformer [16] is a Transformer-based method, and RS3Mamba [17] is a Mamba-based method. The above CNN-based methods cannot segment objects well. In addition, the segmented object boundaries have poor consistency. For example, the segmentation effect of the building boundaries in the prediction results of each method is inadequate. In the first row, the CNN-based method fails to accurately identify the tiny building components in the remote sensing image, resulting in suboptimal segmentation performance. Similarly, in the second row, none of the methods given in the figure separates adjacent cars. The above shortcomings may be due to the fact that the convolution operation of the CNN fails to preserve boundary information well when expanding the receptive field, making the final prediction result so poor. Therefore, sufficient global context information may be the key to solving the above problems. Due to the size limitation of the convolution kernel, CNN cannot build global context information. However, the emergence of Transformer [18] provides new insights. ST-UNet [19] uses the global attention mechanism of Swin Transformer [20] to enhance the understanding of complex remote sensing scenes through a dual encoder structure. GDBNet [21] proposes a three-branch semantic segmentation network that extracts context information by combining a Swin Transformer and CNN. However, these methods still rely on a CNN for feature extraction in essence, then indirectly derive context information through the attention mechanism of the Transformer rather than directly building global context encoding. Therefore, it is not easy to obtain sufficient global semantic associations. Although Transformers can learn long-distance dependencies, their high computational complexity poses significant challenges when considering model efficiency and memory usage.

Recently, a new architecture based on the spatial state model has been proposed. Mamba [22] has shown significant advantages in efficiently modeling long sequence dependencies by introducing a selective scanning mechanism, hardware aware optimization strategies, and parallel scanning operations. Subsequently, Vision Mamba [23] extended Mamba to the image field and provided a two-dimensional selective scanning mechanism (SS2D), enabling Mamba to capture long-range dependencies in images effectively. At the same time, with the continuous evolution of neural network architectures, researchers have begun to pay attention to the balance between the expressive power and generalization performance of the model. As an emerging neural network structure, the Kolmogorov–Arnold Network (KAN) [24] is based on the Kolmogorov–Arnold representation theorem and replaces traditional weight connections with explicit function representation, showing stronger function approximation ability and interpretability. Compared with the MLP, KAN uses spline interpolation functions as neuron building blocks, enabling it to perform superior tasks such as low-sample learning and complex pattern modeling. In addition, KAN shows faster convergence speeds and stronger anti-overfitting abilities during training, providing new ideas for improving the accuracy of remote sensing image segmentation.

In this paper, we propose a new remote sensing image segmentation framework, KPV-UNet. This framework adopts a multistage ResNet18 [25] backbone structure and introduces a Mamba-based Pyramid Pooling Visual State Space Attention (PP-VSSA) block at the head end stage to model long-distance semantic dependencies across stages; a two-layer tokenized Kolmogorov-Arnold network (Tok-KAN) is introduced at the end stage to enhance the nonlinear modeling capability of the channel dimension and improve the recognition effect of boundaries and small targets. In addition, to solve the problems of texture blur and ground interference in remote sensing images, this paper also designs an Auxiliary Local Monitoring (ALM) block to guide the main branch training from the intermediate features to promote detail recovery and semantic consistency. The main contributions of this paper can be summarized as follows:

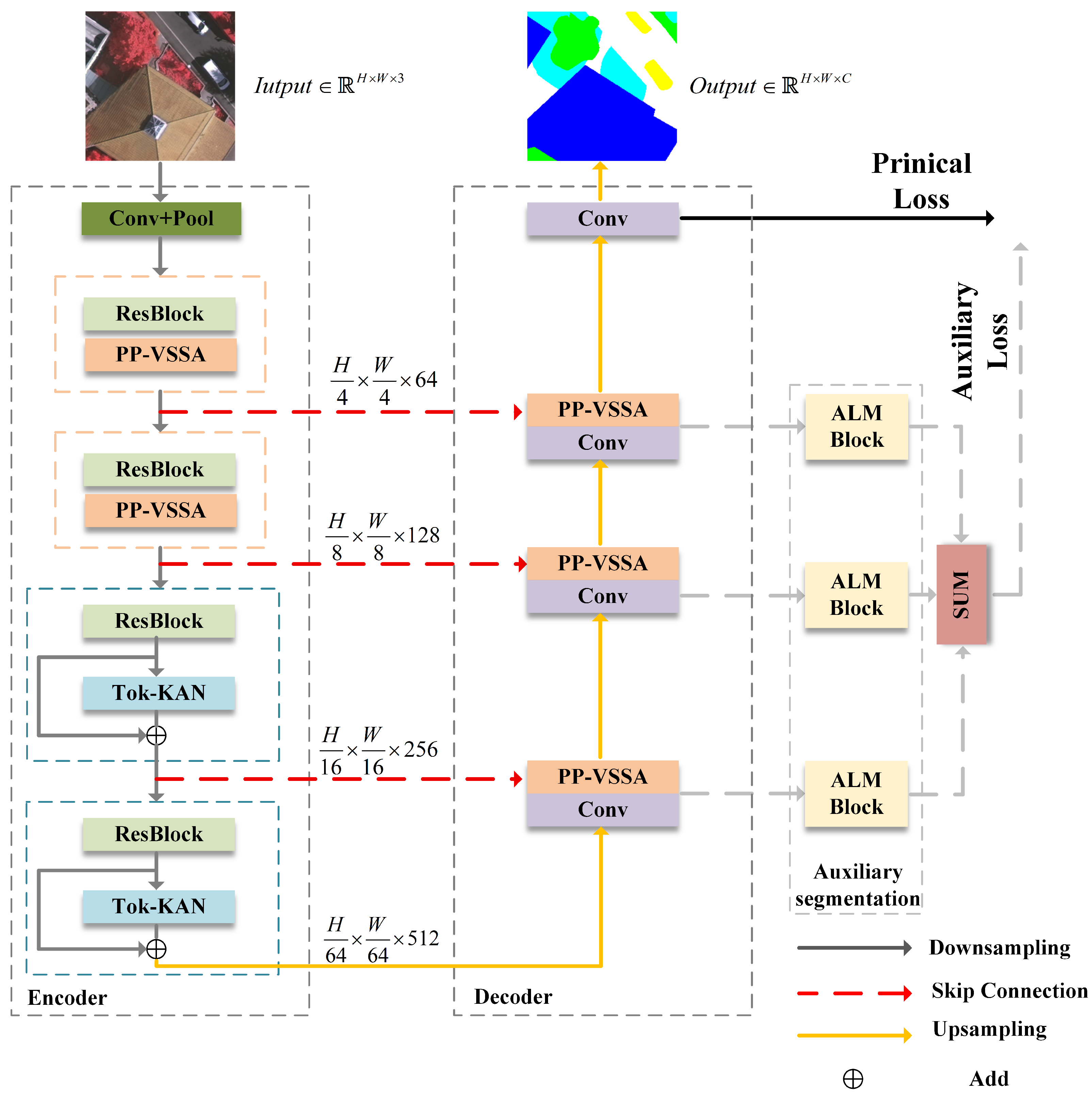
• A dual-branch encoding structure is proposed, integrating CNN, Mamba, and KAN. This design fully leverages the local modeling capability of CNNs, Mamba’s long range dependency modeling, and KAN’s nonlinear representation power to accurately recognize small objects and blurred boundaries in remote sensing images. As a result, it effectively enhances the synergy between local detail perception and global context understanding.
• We propose the Pyramid Pooling Visual State Space Attention (PP-VSSA) module, which fuses the efficient global dependency modeling capability of the EMA attention mechanism with the multi-scale context fusion capability of pyramid pooling, aiming to make up for the deficiencies of Mamba in terms of local detail portrayal and cross-scale semantic associations.
• We propose an Auxiliary Local Monitoring (ALM) block to address the decoder’s insufficient perception of local information. By using two convolution operations of different scales and introducing an auxiliary loss function, the model’s perception of local semantic information is enhanced with the help of supervised training. The restrictive configuration is only performed during the training phase, which saves inference costs and ensures overall application efficiency.

The remainder of this paper is organized as follows: Section 2 presents the related work. Section 3 introduces our proposed methodology and modules. Section 4 experimentally validates the proposed method on the Vaihingen, LoveDA Urban and WHDLD datasets. Finally, conclusions are drawn in Section 5.

2. Related Work

2.1. Remote Sensing Image Semantic Segmentation

Early studies mainly relied on combining manual features and traditional machine learning. Researchers extracted spectral, texture, and geometric features from remote sensing images. They combined them with classifiers such as support vector machines (SVMs) [26] and random forests (RFs) [27] to achieve segmentation. However, the representational ability of manual features is limited, and it is difficult to cope with the multi-scale changes and complex background interference of remote sensing data. With the emergence of deep learning, global context modeling and local detail modeling have always been the core factors affecting accuracy and generalization ability in the semantic segmentation of remote sensing images. Existing studies have explored solutions from the following three directions: Local feature modeling based on CNN: Traditional convolutional neural network structures (such as UNet [12], SegNet [11]) rely on local receptive fields and layer-by-layer stacking to obtain context information. Models such as UNet++ [28] and MAResUNet [29] enhance feature propagation and detail retention capabilities through dense connections and residual structures but have limited performance in cross-regional semantic understanding and global consistency. Global modeling methods based on Transformer: The Transformer structure introduces a self-attention mechanism that can capture the relationship between pixels at any position in the image and is suitable for processing large-scale semantic contexts. Representative methods such as ST-UNet [19] and SegFormer [30] reduce computational complexity through window division, adaptive nested structure, etc., while maintaining global modeling capabilities. However, there are still deficiencies in boundary clarity and small target recognition, and they rely heavily on computing resources. Hybrid modeling and structural optimization: To overcome the above problems, some methods try to fuse local add global features. For example, GBDNet [21] takes into account both features by coordinating the global modeling capabilities of Swin Transformer and the local detail extraction capabilities of CNNs; UNetFormer introduces the Transformer module in the encoder to take into account both features; PPM [31]/ASPP [14] uses multi-scale pooling or dilated convolution to achieve coarse-grained context perception.

2.2. Mamba

The Mamba [22] architecture was introduced as an alternative to the Transformer, aiming to reduce computational complexity while retaining the ability to model long-distance dependencies in visual data. The Mamba architecture is based on the structured state space model (SSM). It has shown significant advantages in long sequence modeling tasks through the selective scanning mechanism and linear time complexity design.

In recent years, many architectures based on SSM have been widely used in many fields, including computer vision and remote sensing. Vmamba [32] and Vision Mamba [23] demonstrate innovative practices based on SSM architectures in computer vision. Vmamba achieves linear computational complexity while retaining the global receptive field by introducing a Cross Scanning Module (CSM). This module optimizes information modeling capabilities by scanning in the spatial dimension to reconstruct non-causal visual images into an ordered sequence of patches. In addition, Vision Mamba effectively compresses image information by using bidirectional Mamba blocks that embed position information and a bidirectional state space modeling method, verifying that efficient visual feature learning can be achieved without a self-attention mechanism.

In remote sensing, researchers have also integrated Mamba into various tasks. RS3Mamba [17] was one of the first SSM models used for remote sensing semantic segmentation. It introduces a dual branch collaborative decoder and combines the local global attention fusion strategy to improve the segmentation effect significantly. PPmamba [33] adds a multi-scale pyramid pooling mechanism based on RS3Mamba, effectively integrating local details with global context information and considerably improving the segmentation accuracy in complex scenes. However, the complex architecture of RS3Mamba brings huge computational overhead. Although PPmamba and UNetMamba reduce the computational overhead, they still have certain deficiencies in target boundary detection, especially in the edge area of the object, which is prone to blur or unclear contours, affecting the effect of refined segmentation.

2.3. KAN

Although current mainstream methods have made significant progress in overall segmentation performance, there are still some deficiencies in object boundary detection, especially in the edge areas of objects, which are prone to blur or unclear outlines, affecting the effect of refined segmentation. Therefore, introducing modules with stronger nonlinear expression capabilities and higher interpretability has become a key path to improving boundary perception capabilities. The KAN [24] architecture is derived from the Kolmogorov–Arnold theorem. It replaces the traditional activation function with a learnable one-dimensional spline function and decomposes high-dimensional complex mapping into several single variable continuous functions. It has exceptionally high nonlinear expression capabilities and dramatically enhances the interpretability of the model. The modular design of KAN makes up for CNNs’ shortcomings in modeling complex nonlinear relationships. It establishes a more direct connection between physical features and empirical performance, which can help to better understand the model decision process. U-KAN [34] incorporates the KAN layer into the U-Net framework in medical images. By introducing self-learning nonlinear activation functions, the model improves the prediction accuracy while enhancing the transparency of the decision logic based on the parameter interpretability path. In addition, the KM-UNet [35] model, by integrating KAN and Mamba into the U-Net architecture, realizes the coordinated optimization of global long-range dependency modeling and local nonlinear feature expression for the first time in medical image segmentation. In the early exploration of remote sensing images, Cheon [36] replaced the traditional MLP with KAN for optical image classification, verifying its potential in improving classification accuracy and reducing computational complexity; AEKAN [37] first realized multimodal change detection through a pure KAN architecture and achieved excellent performance; WavKAN [38] used wavelet functions as an activation mechanism to perform efficient nonlinear mapping of hyperspectral spectral signatures. Although these studies have demonstrated the advantages of KAN in classification and change detection tasks, KAN is still in the exploratory stage in scenarios such as remote sensing image segmentation and semantic understanding, which require deep semantic refinement and restoration.

In summary, Mamba’s efficient global modeling capabilities and KAN’s nonlinear expression and interpretability advantages complement each other, helping to enhance the contextual understanding and boundary recognition capabilities in remote sensing image semantic segmentation. To this end, this paper further explores the architectural potential of the fusion of the two to achieve better segmentation performance.

3. Materials and Methods

The overall architecture of the proposed KPV-UNet is shown in Figure 2. The architecture adopts a four-stage encoder–decoder structure, including a ResNet18 network, the Pyramid Pooling Visual State Space Attention (PP-VSSA) block stage, and the Tokenized Kolmogorov–Arnold (Tok-KAN) block stage.

In the encoder part, the input image is extracted through four layers of ResNet18, two layers of PP-VSSA, and two layers of Tok-KAN stage. The decoder consists of three convolutional blocks and three PP-VSSA blocks. Each encoder module reduces the feature resolution by half, while each decoder module doubles the feature resolution.

3.1. Tok-KAN Architecture Design for Remote Sensing Image Semantic Segmentation

In this study, to address the challenges of fuzzy boundaries and multi-scale feature coupling of complex objects in remote sensing images, we introduced Tok-KAN, based on the Kolmogorov–Arnold network (KAN), as a hierarchical feature extractor in the U-Net encoding path. Tok-KAN uses KAN’s powerful nonlinear modeling capabilities and its learnable univariate activation function structure to improve feature expression capabilities and model interpretability effectively. The overall structure of Tok-KAN is shown in Figure 3b, which is divided into two main stages: Tokenization and KAN embedding calculation. Given an input feature map $\mathbb{R}\in H\times W\times C$, we first divide it into N non-overlapping patches of P and project it into a D-dimensional embedding space:

$$Z_0=[x_{1}E;x_{2}E;\dots ;x_{N}E]\in {\mathbb{R}}^{N\times D},$$

(1)

where $x_i$ represents the i patch vector, and E is a trainable linear projection matrix implemented by the convolution to enhance the expression of position information. In the KAN module, a set of learnable univariate activation functions is used to transform the features. The structure of the KAN layer can be expressed as:

$$\mathrm{KAN}\left(Z\right)=\left({\mathrm{\Phi }}_{K-1}\circ {\mathrm{\Phi }}_{K-2}\circ \dots \circ {\mathrm{\Phi }}_1\circ {\mathrm{\Phi }}_0\right)Z,$$

(2)

where each ${\mathrm{\Phi }}_i$ consists of learnable univariate activation functions. After each layer of the KAN operation, Tok-KAN introduces lightweight depth-wise separable convolution (DwConv) and normalization to enhance the spatial modeling capability of the model and adopts residual connection to maintain gradient flow:

$$Z^{\prime }=\mathrm{LN}\left(Z+\mathrm{DwConv}\left(\mathrm{KAN}\right(Z\left)\right)\right),$$

(3)

where $\mathrm{LN}$ represents layer normalization, $\mathrm{DwConv}$ represents depthwise convolution, and $\mathrm{KAN}\left(Z\right)$ represents the output of the KAN layer.

Unlike MLP, Tok-KAN does not rely on fixed activation functions and linear weight matrices but achieves efficient nonlinear modeling through a learnable function approximation mechanism. In addition, its structure is naturally interpretable: each connection is controlled by a univariate function, which facilitates visualization and analysis of model behavior. This enables the network to better capture the nonlinear relationship between multidimensional features in complex scenes in remote sensing images, thereby improving the segmentation accuracy of targets such as roads, buildings, vegetation, and vehicles. Introducing the Tok-KAN module enables KPV-UNet to simultaneously maintain the image’s global object association features and local detail texture information, which is particularly critical for accurately dividing complex surface targets with similar spectral characteristics, such as vegetation coverage areas and building complexes. This innovative approach, in which KAN replaces the linear transformation matrix, not only significantly reduces the parameter overhead but also enhances the model’s ability to capture long-range contextual information and multi-scale feature expression, which is of great significance for handling a wide range of object scales and scene diversity present in remote sensing images.

3.2. PP-VSSA: Pyramid Pooling Visual State Space Attention Module

In this study, we designed the Pyramid Pooling Visual State Space Attention (PP-VSSA) block to enhance the feature extraction and attention mechanism at the encoder and decoder levels of the U-Net network. The module consists of two parts: feature extraction and attention.

Figure 4a shows the structure of the conventional visual SSM block, where the input is processed by the VSS block, followed by the Layer Normalization (LN) block and MLP block. However, the conventional visual SSM block has many limitations in capturing global spatial features from remote sensing images. In sharp contrast, the PP-VSSA block shown in Figure 4b is a hierarchical feature extractor in our KPV-UNet model, which uses multi-branch auxiliary and attention methods for remote sensing image semantic segmentation. In order to allow the model to perceive four types of contextual information from “extreme field of view” to “detailed texture” at the same time, PP-VSSA guides the input features along four parallel paths: first, adaptive average pooling to 1 × 1 (the mean of the entire feature map) to extract the most macroscopic global semantics; pooling to 1 + H/4 to capture the uneven distribution of large scale objects; pooling to 1 + H/2 to take into account the intermediate scale between macro and micro; pooling to 1 + 3H/4 to focus on local details and edge information. The pooling results on each path are subjected to 1 × 1 convolution to reduce the number of channels to 1/4 of the original input to control the number of parameters and then upsampled back to the original resolution through bilinear interpolation. The weighting ratio $\lambda$ is a learnable parameter that reflects the dependency of features at different depths on global information. Let $X\in {\mathbb{R}}^{C\times N\times N}$ represent the feature map entering KPV-UNet, where PP-VSSA can be defined as follows:

$$P_i=\mathrm{Conv}\left({\mathrm{AvgPool}}_i\left(X_{in}\right)\right),i\in \mathit{range}(1,N,N//4),$$

(4)

$$U_i=\mathrm{BilinearUp}\left(P_i\right),$$

(5)

$$X_p=\mathrm{Concat}(U_1,U_2,U_3,U_4),$$

(6)

$$X_p=(1-\lambda )·X_{in}+\lambda ·X_p,$$

(7)

where ${\mathrm{AvgPool}}_i$ represents the average pooling operation with pooling size i, and Conv represents a standard convolutional layer with kernel size 1.

However, uniformly using bilinear interpolation for multi-scale features extracted from the same feature map will introduce significant redundancy, resulting in a high degree of information duplication between the features of each scale. Subsequently, we introduced the Mamba and Efficient multi-scale attention module (EMA) [39] mechanisms in this module. Mamba effectively extracts core semantic features across scales through its selective filtering mechanism; the extracted features are processed by layer normalization and SS2D modules, in turn, to further decouple cross-scale dependencies. Finally, these enhanced features are fused with the original features through residual connections. At the same time, the introduced EMA attention mechanism performs dynamic calibration in the channel dimension, suppresses noise interference through smooth updates of historical weights, and improves feature stability and robustness. The formula is:

$$X_{out}=\mathrm{EMA}\left(X+\mathrm{SS}2\mathrm{D}\left(X_p\right)\right),$$

(8)

where X is the original feature map and $X_p$ denotes its pooled version, $\mathrm{SS}2\mathrm{D}$ is the extracted global contextual features from $X_p$ through multi-directional sequence scanning and state-space modeling, and $\mathrm{EMA}$ denotes the efficient multi-scale attention module that reweights and refines the combined features to produce the output $X_{out}$.

Notably, the incorporation of four distinct pooling layers allows the block to capture a broader spectrum of local features across multiple scales. The use of varying pooling sizes plays a critical role in extracting comprehensive local representations from the input image, which is essential for achieving accurate semantic segmentation.

3.3. Loss Function

During the training process, this paper adopts an enhancement strategy that uses the main features to refine the segmentation head and incorporates the Auxiliary Local Monitoring (ALM) block as an auxiliary head to optimize the model performance further. The main loss function $L_{\mathrm{p}}$ used in this model is a weighted sum of Dice loss $L_{\mathrm{dice}}$ and cross-entropy loss $L_{\mathrm{ce}}$, and the auxiliary loss function $L_{\mathrm{a}}$ uses cross-entropy loss $L_{\mathrm{ce}}$. The specific expressions of $L_{\mathrm{dice}}$ and $L_{\mathrm{ce}}$ are as follows:

$$L_{\mathrm{dice}}=1-{\displaystyle \frac{2}{N}}\sum _{n=1}^N\sum _{k=1}^K{\displaystyle \frac{{\widehat{y}}_k^{\left(n\right)}{y}_k^{\left(n\right)}}{{\widehat{y}}_k^{\left(n\right)}+y_k^{\left(n\right)}}},$$

(9)

$$L_{\mathrm{ce}}=-{\displaystyle \frac{1}{N}}\sum _{n=1}^N\sum _{k=1}^K{\widehat{y}}_k^{\left(n\right)}log{y}_k^{\left(n\right)},$$

(10)

where N represents the number of samples, K represents the total number of categories, $y_k^{\left(n\right)}$ indicates the k element in the one-hot encoding of the actual label of sample n, and ${\widehat{y}}_k^{\left(n\right)}$ indicates the confidence that the sample belongs to.

The Auxiliary Local Supervision (ALM) block is shown in Figure 5. It uses two parallel convolution branches. One path uses the convolution kernel of 1 × 1, and the other uses the convolution kernel of 3 × 3 to process the input features. Subsequently, the feature maps processed by the two branches are spliced in the channel dimension. The spliced features are adjusted by the 1 × 1 convolution to optimize the feature representation, and the SE attention [40] module is introduced to model the channel dependency. Finally, after 1 × 1 convolution processing and upsampling, the final output feature is obtained.

$$F_{i1}=ReLU6\left(BN\left({Conv}_{1\times 1}\left(F_i\right)\right)\right),$$

(11)

$$F_{i2}=ReLU6\left(BN\left({Conv}_{3\times 3}\left(F_i\right)\right)\right),$$

(12)

$$F_i^{\prime }=Upsample({Conv}_{1\times 1}^{″}\left(SE\left({Conv}_{1\times 1}^{\prime }\left(Concat(F_{i1},F_{i2})\right)\right)\right),$$

(13)

where BN is batch normalization, ReLU6 is the activation function, and $F_i$ represents the output features of the decoder at the corresponding stage. To more effectively coordinate the primary loss function, we introduce a weight parameter to adjust the importance of the auxiliary loss. Therefore, the total loss can be expressed as:

$$L=L_p+\alpha L_a=(L_{\mathrm{dice}}+L_{\mathrm{ce}})+\alpha L_{\mathrm{ce}},$$

(14)

where the weight factor $\alpha$ is set as 0.4 [16].

4. Experiments and Results

4.1. Dataset

4.1.1. ISPRS Vaihingen

The ISPRS Vaihingen dataset consists of 33 high-resolution remote sensing images of varying sizes, each cropped from top-level orthophotos while avoiding invalid data regions. Both the orthophotos and their corresponding digital surface models (DSMs) have a spatial resolution of 9 cm. The images are provided in 8-bit TIFF format, containing three spectral bands: near-infrared (NIR), red, and green. All images are semantically annotated based on the SIC classification scheme. For our experiments, we selected 12 images (IDs: 1, 3, 7, 11, 13, 17, 23, 26, 28, 32, 34 and 37) for training and 4 images (IDs: 5, 15, 21 and 30) for testing.

4.1.2. LoveDA Urban

The LoveDA Urban [41] dataset is based on urban scenes in Nanjing, Changzhou, and Wuhan, China, and contains 1833 high-resolution RGB images (1024 × 1024 pixels, GSD 0.3 m) for complex urban feature analysis. The data covers seven types of features: buildings, roads, water bodies, bare land, forests, farmland, and background, and it is optimized for the areas where densely built areas and vegetation intersect in the city. In this study, we used 1156 images for training and 677 for testing.

4.1.3. WHDLD

The WHDLD [42] dataset, released by Wuhan University, is an open-source remote sensing image segmentation dataset consisting of 4940 RGB images with a resolution of 256 × 256 × 3. It includes six semantic categories: bare soil, buildings, pavement, roads, vegetation, and water. For our experiments, the dataset was randomly divided into a training set (80%, 3952 images) and a test set (20%, 988 images).

4.2. Experimental Setup

The training process of these models is simplified by using the AdamW optimizer. We adopt a polynomial decay learning rate schedule, where the power parameter is configured to 0.9. The initial learning rate is set to $6\times {10}^{-4}$, while the learning rate of the backbone is specifically specified to be $6\times {10}^{-5}$. The batch size and weight decay are configured to 4 and 0.01, respectively. The training is performed for a total of 50 epochs, with 2 tests and 2 evaluation metrics calculated for each epoch, and the first 5 epochs are dedicated to the warm-up training strategy. The experiments are conducted on a server node running the Ubuntu 20.10 operating system, which is equipped with an NVIDIA GeForce RTX 4070 Ti GPU with a video memory size of 12 GB. Two widely used metrics are recorded to quantitatively evaluate the proposed method: the mean F1 score (mF1) and the mean intersection over union (mIoU). The values of mIoU and mF1 are calculated as follows:

$$mIoU={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{I{P}_i}{T{P}_i+F{P}_i+F{N}_i}},$$

(15)

$$mF1={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{2\ast T{P}_i}{2\ast T{P}_i+F{N}_i+F{P}_i}},$$

(16)

where N is the number of classes, $T{P}_i$, $F{P}_i$, and $F{N}_i$ represent the true positives, true negatives, and false negatives of objects indexed as class i, respectively.

4.3. Performance Comparison

To assess the performance of KPV-UNet, we carried out comparative experiments with seven representative state-of-the-art models. PPMamba [33] was selected as the baseline for these evaluations. The comparison encompassed CNN-based approaches such as ABCNet [15] and MAResUNet [29], a hybrid CNN-Transformer model including UNetFormer [16], ST-UNet [19], and GBDNet [21], as well as another Mamba-based method, RS3Mamba [17].

• ABCNet [15]: A bilateral network with a spatial path for detail preservation and a Res-Net-18-based context path enhanced by linear attention (AEM). Features are fused via channel-weighted aggregation (FAM) to combine local and global information.
• MAResUNet [29]: MAResUNet proposes a linear attention mechanism (LAM), which reduces the computational complexity of dot product attention from O(N²) to O(N) through first-order Taylor expansion approximation and feature normalization, and based on this, reconstructs U-Net jump connections to construct a multistage attention ResU-Net (MAResU-Net).
• UNetFormer [16]: UNetFormer proposes a UNet-like Transformer architecture, which works together with a lightweight ResNet18 encoder and a global–local attention decoder to form global–local collaborative optimization.
• ST-UNet [19]: ST-UNet adopts a dual encoder architecture in which the CNN-based main encoder and the Swin Transformer auxiliary encoder are processed in parallel. The auxiliary encoder embeds the spatial interaction module (SIM) to enhance the spatial information encoding through pixel-level correlation, and the feature compression module (FCM) retains small-scale feature details in patch token downsampling and hierarchically integrates global dependencies into the main encoder features through the relationship aggregation module (RAM).
• GBDNet [21]: GDBNet proposes a three-branch semantic segmentation network that optimizes boundary segmentation by working together with the global branch (Swin Transformer), detail branch (ResNet), and boundary branch (ResNet), combined with the feature preservation module (FPM), spatial interaction module (SIM), and balanced feature module (BFM).
• RS3Mamba [17]: RS3Mamba is a dual-branch semantic segmentation framework that extracts local features through the main branch based on ResNet. It models global dependencies through the auxiliary branch based on the VSS module (Mamba architecture) and realizes feature adaptive fusion in combination with the Collaborative Completion Module (CCM).
• PPMamba [33]: PPmamba utilizes a lightweight CNN–Mamba hybrid architecture to achieve global context modeling with linear complexity through the SS2D module.

4.3.1. Performance Comparison on ISPRS Vaihingen

As shown in

Table 1. Experimental results on the ISPRS Vaihingen dataset. This paper proposes OA with five foreground classes and two overall performance metrics. The accuracy of each class is listed in the IoU table.

Method	Impsurf	Building	Low veg	Tree	Car	mIoU	mFl
MAResUNet [29]	85.45	91.74	67.22	82.56	74.11	80.22	88.76
ST-UNet [19]	76.19	83.42	57.02	72.54	62.21	70.28	79.77
ABCNet [15]	85.80	92.73	67.31	83.50	80.73	82.01	89.88
UNetFormer [16]	84.46	91.73	67.59	84.00	83.88	82.33	90.09
GBDNet [21]	84.52	91.58	66.78	82.56	81.35	81.37	89.03
RS3Mamba [17]	86.30	93.75	67.11	83.70	83.01	82.77	90.32
PPMamba [33]	86.60	93.49	67.06	83.59	84.38	83.03	90.47
KPV-UNet	87.03	94.16	68.68	84.12	86.16	84.03	91.09

Bold values indicate the best performance in each column.

, KPV-UNet achieves a significant improvement over the baseline PPMamba model: its mIoU and mF1 scores increase by 1.00% and 0.62%, respectively. This result confirms that PPMamba suffers from insufficient local-detail capture and weak object edge modeling in remote sensing image semantic segmentation, which can blur or lose boundary information and thus degrade segmentation accuracy. In contrast, KPV-UNet effectively overcomes these shortcomings. As shown in the first and third rows of Figure 6, KPV-UNet demonstrates an exceptional ability to capture fine building-edge details and to accurately recognize small objects. Notably, KPV-UNet excels across five classes—impervious surface, building, low vegetation, tree, and car. In the building category, it outperforms the baseline model by 0.67% and UNetformer by 2.43%, indicating that KPV-UNet is particularly adept at modeling complex building geometries and precisely delineating their boundaries. In the low vegetation class, KPV-UNet surpasses PPMamba by 1.62%, underscoring its effectiveness in accurately delineating areas of grass, shrubs, and other low-stature vegetation. Moreover, KPV-UNet achieves the highest F1 and IoU scores in the car and tree categories; for cars, its IoU reaches 86.16%, at least 2% higher than other models and 1.78% higher than PPMamba. This improvement reflects KPV-UNet’s enhanced capacity for capturing local details, particularly in detecting cars that occupy only a small fraction of the Vaihingen images. These results highlight KPV-UNet’s capability to accurately identify and segment a broad spectrum of object categories.

Figure 6 visually compares the segmentation results on the ISPRS Vaihingen dataset, including the output of all models, NIRRG images, and ground truth. The visualization results show that KPV-UNet provides more accurate and detailed segmentation, especially in building boundaries, vehicles, and low-vegetation areas. It is worth noting that in the third row of Figure 6, it is significantly marked that only KPV-UNet correctly identifies vehicles covered by a large amount of low vegetation and trees. In addition, in the first and fourth rows of Figure 6, KPV-UNet’s building segmentation (blue area) is more realistic, reduces misjudgment, and improves the accurate recognition of targets. In contrast, white and yellow misidentification areas appear in the other comparison models.

4.3.2. Performance Comparison on LoveDA Urban

As shown in

Table 2. Experimental results on the LoveDA Urban dataset. This paper proposes OA with seven foreground classes and two overall performance metrics. The accuracy of each class is listed in the IoU table.

Method	Background	Building	Road	Water	Barren	Forest	Agriculture	mIoU	mF1
MAResUNet [29]	34.70	49.75	42.45	49.84	32.31	37.10	6.38	36.08	51.30
ST-UNet [19]	34.57	52.12	46.45	50.12	35.23	40.23	30.12	41.26	52.24
ABCNet [15]	36.96	55.62	50.87	54.71	38.75	33.55	32.80	43.32	53.36
UNetFormer [16]	37.53	59.15	52.63	69.10	30.13	44.94	39.90	47.63	63.57
GBDNet [21]	38.45	56.76	56.33	66.34	31.45	44.15	46.45	48.56	64.15
RS3Mamba [17]	40.53	59.08	57.36	67.01	26.45	44.76	47.96	49.02	64.80
PPMamba [33]	39.45	63.17	61.56	66.83	38.07	41.00	38.46	49.79	65.60
KPV-UNet	37.84	61.79	59.99	69.56	32.44	46.55	50.75	51.27	66.82

Bold values indicate the best performance in each column.

, experiments were conducted on the LoveDA Urban dataset as a supplementary benchmark to verify KPV-UNet’s performance further. Similar to the results of the previous datasets, KPV-UNet achieved the highest mIoU and mF1 scores among the six models. Its performance is significantly better than the baseline model, with mIoU and mF1 improved by 1.48% and 1.22%, respectively. It is worth noting that KPV-UNet performs very well in the agricultural category, as seen from the third and fourth rows of Figure 7. Specifically, KPV-UNet achieved 50.75% IoU and 66.88% F1 scores in the agricultural category, ranking the best among all models. This highlights that KPV-UNet can effectively and accurately capture and distinguish agricultural features from adjacent categories. Although our model did not achieve the best overall IoU for the building and road categories, it can be seen from the first row of Figure 7 that compared with PPMamba, which achieved the highest IoU in the road category, our method did not have the road break phenomenon. Similarly, in the second row of Figure 7, compared with the effect of PPMamba in the building category, our method can more clearly distinguish the boundaries of adjacent buildings instead of connecting them together like PPMamba. Although there is still room for improvement in the IoU of these two small object categories, we have achieved significant improvements in the segmentation accuracy and connectivity of boundary details, further verifying the advantages and innovation of the proposed method in local feature modeling and detail preservation.

4.3.3. Performance Comparison on WHDLD

To better verify our KPV-UNet model, we also verified the WHDLD data, as shown in

Table 3. Experimental results on the WHDLD dataset. This paper proposes OA with six foreground classes and two overall performance metrics. The accuracy of each class is listed in the IoU table.

Method	Bare Soil	Water	Pavement	Road	Vegetation	Building	mIoU	mF1
MAResUNet [29]	38.63	93.23	42.17	59.12	79.48	54.82	61.24	74.21
ST-UNet [19]	38.72	93.21	41.69	58.16	78.91	54.98	60.94	73.93
ABCNet [15]	38.38	93.71	41.85	58.88	79.66	54.56	61.17	74.11
UNetFormer [16]	39.06	93.81	43.00	59.62	79.76	55.15	61.73	74.61
GBDNet [21]	41.77	94.25	42.03	58.76	80.32	56.77	62.32	74.88
RS3Mamba [17]	39.49	94.02	42.29	58.39	80.31	56.08	61.76	74.61
PPMamba [33]	39.65	94.15	44.11	61.08	80.41	56.05	62.58	75.30
KPV-UNet	38.96	94.55	44.59	61.37	80.55	57.11	62.87	75.52

Bold values indicate the best performance in each column.

. Consistent with the results above, KPV-UNet obtained the highest mIoU and mF1 scores among the five models. Its performance was significantly better than the baseline model PPMamba, with mIoU and mF1 increased by 0.29% and 0.22%, respectively, and it performed best among the five categories. It is worth noting that in the third row of Figure 8, compared with the other models, our model shows significant optimization in terms of boundary positioning accuracy for the contour segmentation of the building category, which effectively improves the semantic segmentation performance of the target area.

4.3.4. Ablation Experiments

Table 4. Ablation experiment results on Vaihingen and WHDLD.

Dataset	Model	PP-VSSA	Tok-KAN	ALM	mFl	mIoU
Vaihingen	PPMamba [33]				90.47	83.03
Vaihingen	KPV-UNet	×	×	×	89.51	81.39
Vaihingen	KPV-UNet	✓	×	×	90.00	82.57
Vaihingen	KPV-UNet	✓	✓	×	90.53	83.09
Vaihingen	KPV-UNet	✓	✓	✓	91.09	84.03
WHDLD	PPMamba [33]				75.30	62.58
WHDLD	KPV-UNet	×	×	×	73.93	61.51
WHDLD	KPV-UNet	✓	×	×	73.93	61.51
WHDLD	KPV-UNet	✓	✓	×	74.57	62.01
WHDLD	KPV-UNet	✓	✓	✓	75.52	62.87

Bold values indicate the best performance in each column. ✓: Enabled; ×: Disabled.

compares the performance of all four configurations. KPV-UNet achieves significant performance improvements on multiple datasets through module combination: in the Vaihingen dataset, after gradually enabling PP-VSSA, Tok-KAN, and ALM, mF1 increases from 89.51% to 91.09%, and mIoU increases from 81.39% to 84.03%; in the LoveDA Urban dataset, module collaboration increases mF1 by 3.02% and mIoU by 3.22%; in the WHDLD dataset, mF1 and mIoU increase by 1.59% and 1.36%, respectively. Among them, PP-VSSA strengthens the capture of local details through multiscale feature fusion, Tok-KAN refinement processing enhances the recognition effect of small targets, and the ALM module combines the main head for multilevel supervision to improve the edge feature representation capability, verifying the effectiveness of the three module designs for semantic segmentation of remote sensing images. Combining the two components overcomes the problems of the traditional Mamba architecture, such as insufficient multi-scale feature fusion and blurred edge recognition.

To intuitively demonstrate the contribution of each module, we present a comparative visualization of segmentation results for four representative test regions in Figure 9, covering challenging scenarios including shadow occluded cars (Case #1), boundaries of adjacent objects (Case #2), and complex road networks (Cases #3 and Case #4). The results clearly indicate that PP-VSSA significantly enhances target recognition—as shown in Row 2 of Figure 9, its integration enables more accurate identification of small targets like cars compared to the baseline network, demonstrating that multi-scale fusion and attention complementarity improve recognition accuracy. Tok-KAN achieves efficient nonlinear modeling through a learnable function approximation mechanism, enhancing the model’s ability to capture local variations and nonlinear patterns, which is particularly advantageous for identifying small or camouflaged objects. For instance, in Row 1 of Figure 9, Tok-KAN correctly detects shadowed vehicles for the first time, while the baseline model overlooks these details. Serving as an auxiliary supervision head for shallow features, ALM further refines object contours and enhances edge detail recognition, with its improvements most evident in complex road segmentation (Rows 3–4 of Figure 9). As illustrated in Figure 9, our model demonstrates superior performance in identifying small objects (e.g., vehicles and rooftops) compared to baseline methods. The visual results highlight its capability to localize small targets while effectively handling adjacent object boundaries accurately, conclusively validating the efficacy of PP-VSSA, Tok-KAN, and ALM in enhancing small target recognition and resolving ambiguous object boundaries.

4.3.5. Model Complexity Analysis

The computational complexity of KPV-UNet is evaluated based on three indicators: floating point operation count (FLOPs), model parameters, and memory footprint. FLOPs are used to measure the computational complexity of the model; the parameter reflects the network scale, and the memory footprint reflects the memory requirements. An ideal model should have low values for FLOPs, parameters, and memory footprint.

In

Table 5. Parallel complexity analysis was measured using 2 images of 256 × 256 pixels on a single NVIDIA Geforce RTX 4070Ti GPU. The median value is the result of the ISPRS Vaihingen dataset.

Method	FLOPs (G)	Parameter (M)	Memory (MB)	mIoU (%)
MAResUnet [29]	35.18	26.28	279	80.22
ABCNet [15]	15.69	13.41	207	82.01
ST-UNet [19]	79.73	187	4167	70.28
UNetFormer [16]	11.74	11.68	219	82.33
GBDNet [21]	113.90	199	4434	81.37
RS3Mamba [17]	63.97	49.65	499	82.77
PPMamba [33]	56.32	30.23	1006	83.03
KPV-UNet	63.18	28.01	1043	84.03

Bold values indicate the best performance in each column.

, parallel complexity analysis was measured using two 256 × 256 images on a single NVIDIA GeForce RTX 4070 Ti GPU. Intermediate values are the results of the ISPRS Vaihingen dataset.

Based on the data in Table 5, we systematically analyzed the complexity and performance of eight mainstream semantic segmentation models. The table reports FLOPs, parameter counts, memory footprints, and mIoU scores, offering a comprehensive evaluation of their remote sensing image segmentation capabilities. In terms of computational complexity (FLOPs), our proposed KPV-UNet requires 63.18 G—second only to RS3Mamba—Caused by the Tok-KAN module’s block-wise feature maps for large-scale linear projections, multi-channel nonlinear mappings, depth-wise separable convolutions, and normalization operations. Although this adds only 6.26 G FLOPs compared with the baseline PPMamba, it yields a 1.00% mIoU improvement, a trade-off that is reasonable and acceptable in offline or cloud-based batch-processing scenarios where multi-GPU distributed training and inference can be employed. Moreover, despite its higher computational cost, KPV-UNet maintains a modest parameter count of 28.01 M—significantly lower than RS3Mamba’s 49.65 M and PPMamba’s 30.23 M—demonstrating an optimized architecture that reduces parameter redundancy while preserving expressive power, which is vital for deployment and scalability in resource-constrained remote-sensing applications.

5. Conclusions

In this paper, we propose KPV-UNet, a hybrid architecture that synergistically integrates the local function representation capability of Kolmogorov–Arnold Network (KAN) with the efficient long-distance modeling advantage of the Mamba structure. This integration effectively solves the problem of accurate localization of tiny objects and accurate delineation of adjacent boundaries with fuzzy edges. Extensive experiments confirm that the proposed KPV-UNet achieves superior performance in semantic segmentation on the Vaihingen, WHDLD and LoveDA Urban benchmarks. However, there are still some limitations. First, as a fully supervised method, KPV-UNet may be difficult to generalize to images from unseen sensors, geographic regions, or significantly different resolutions; second, the composite design of PP-VSSA, Tok-KAN, and ALM, although effective, will lead to additional FLOPs. In the future, we will significantly improve the generalization ability of the model to unknown sensors and new geographic regions, reduce model complexity, and improve inference efficiency.