Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation
Abstract
1. Introduction
2. Mathematical Models
2.1. Spoofing Attacks Model
2.2. GNSS/INS Tightly Coupled Navigation System Model
2.3. Analysis of Impact of Spoofing on Kalman Filter Innovation
2.4. Spoofing Detection Algorithm Based on EWMA Control Chart and Robust Estimation
3. Spoofing Detection Algorithm Based on Shewhart Control Chart
4. Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation
4.1. Joint Spoofing Detection Metric for Spoofing End Moment Detection
4.1.1. Construction of Joint Spoofing Detection Metric
4.1.2. Validation of Joint Spoofing Detection Metric Effectiveness
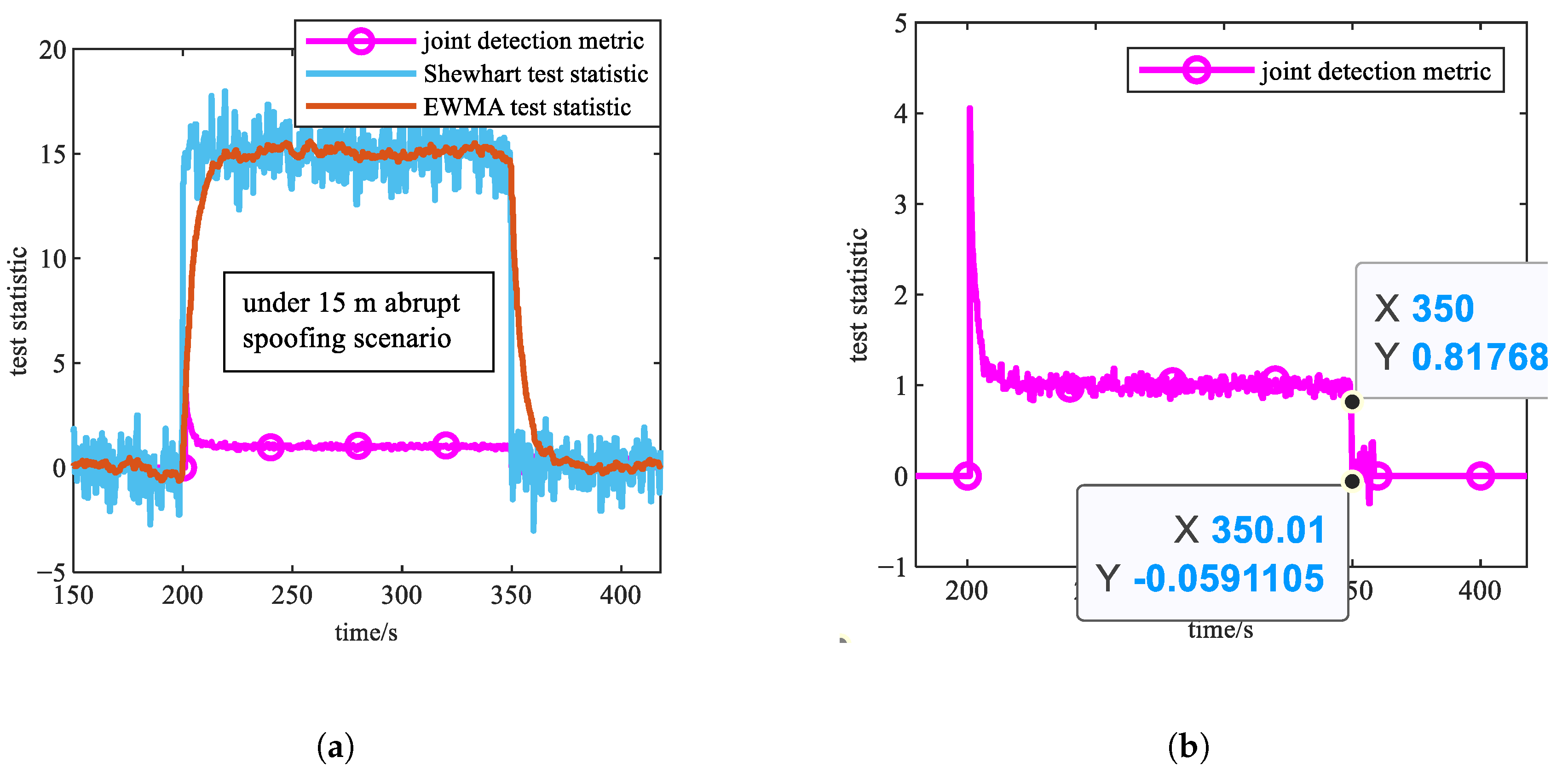
- Experiment 1: Slowly varying spoofing with a pseudorange spoofing rate of 0.2 m/s and abrupt spoofing with a pseudorange bias of 15 m are separately applied to visible satellite PRN1. These scenarios represent typical slowly varying and abrupt spoofing attacks that present high detection difficulty. During the spoofing period, the curves of , , and are shown in Figure 2 and Figure 3, where Figure 2b and Figure 3b provide magnified views of , specifically marking the abrupt change around 350 s when spoofing terminates.
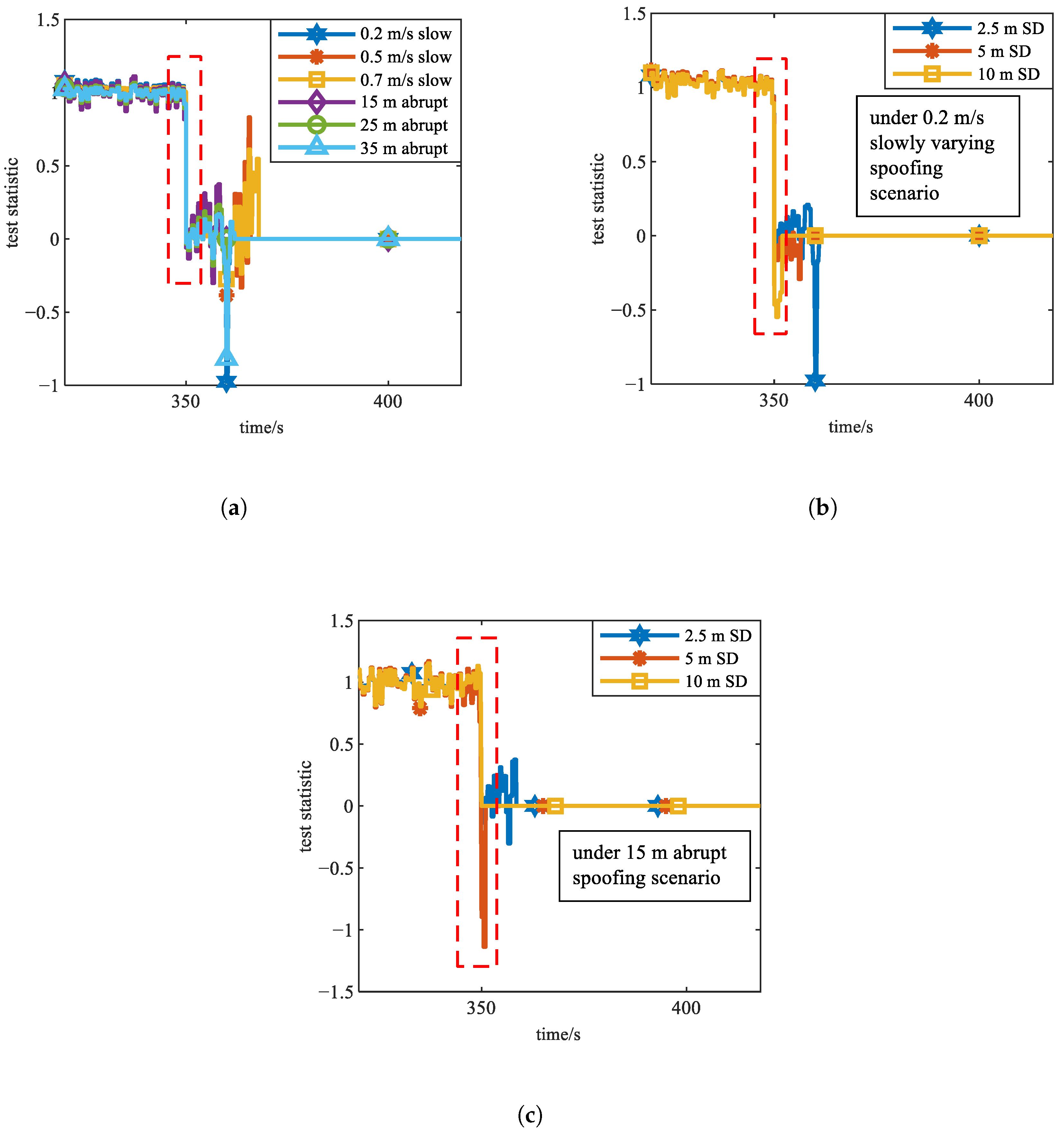
- Experiment 2: Under conditions where the pseudorange observation noise standard deviation is 2.5 m (favorable signal conditions), curves across different spoofing intensities and types are compared, as shown in Figure 4a.
- Experiment 3: Under a slowly varying spoofing scenario with a pseudorange rate of 0.2 m/s, the curves are compared across different pseudorange observation noise levels, as shown in Figure 4b.
- Experiment 4: Under a abrupt spoofing scenario with a pseudorange bias of 15 m, curves are compared across different pseudorange observation noise levels, as shown in Figure 4c.
4.2. Spoofing End Moment Detection Method Based on Sample Quantiles
4.2.1. Anomaly Detection Based on Sample Quantiles
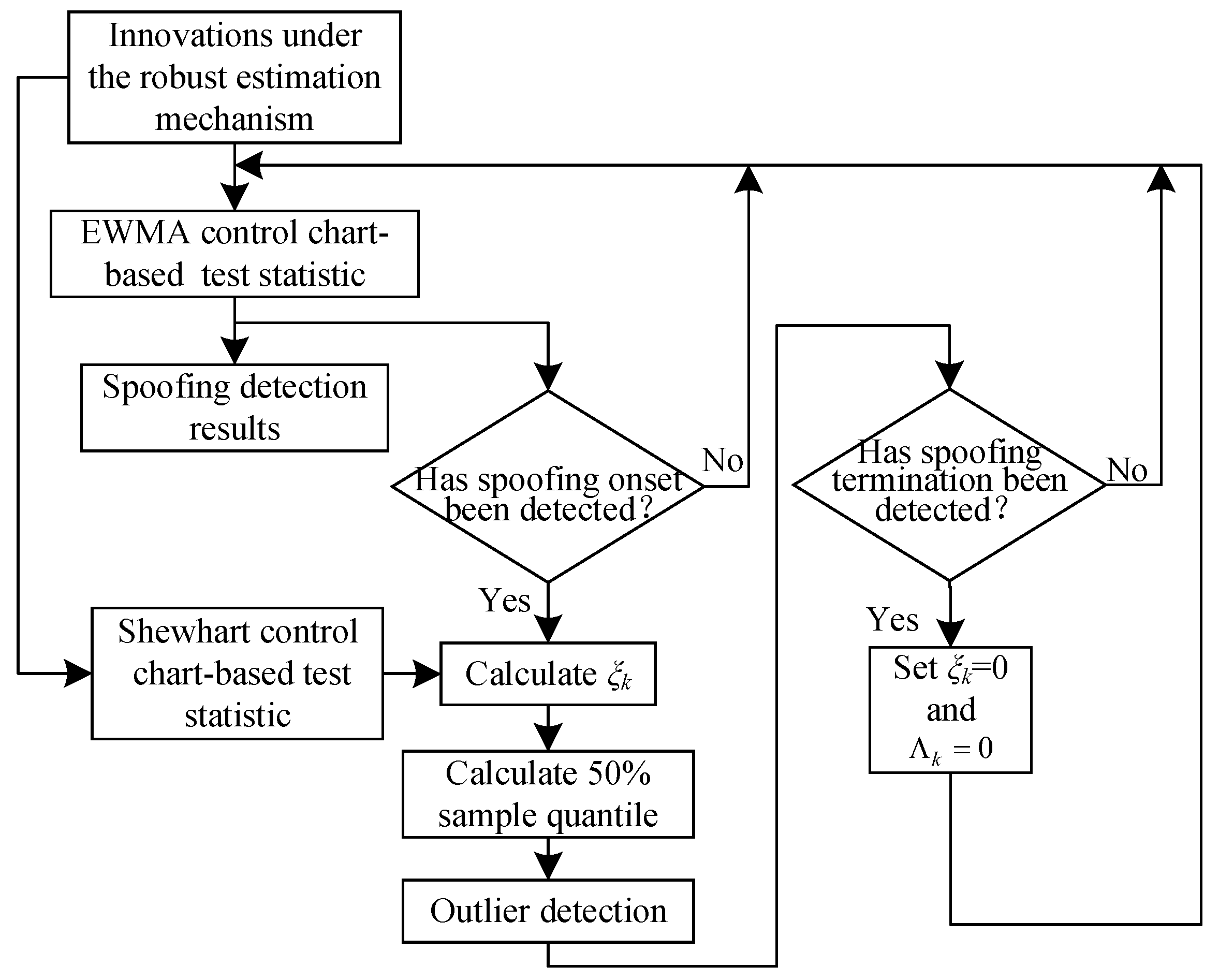
4.2.2. Procedures of Spoofing End Moment Detection Method Based on Sample Quantiles
- Compute at each epoch after spoofing onset detection, generating sequence Y:
- Select a sliding time window size l to form multiple sequence segments like . The choice of l depends on the employed sample quantile and the distribution characteristics of the time-series data. If the window is too large, the calculation of sample quantiles may miss anomalies; if it is too small, it cannot determine the statistical significance of sample quantiles. This paper selects .
- A new sequence is formed based on all of the obtained sequence segments:
- For each sequence segment in Equation (21), the sample quantile is calculated. Considering the characteristics of sequence Y, this paper employs the 50% sample quantile (also known as the median) for computation. The median corresponds to the 50th percentile value when all sample data are sorted in ascending order. The resulting sequence composed of all calculated medians M is
- For each sequence segment in Equation (21), compute the absolute difference between every element and the corresponding median of that segment, and take out the maximum value among all the absolute differences. Take the ith sequence segment as an example. That is, , . The values corresponding to each sequence segment are combined in time order to obtain the absolute difference sequence :compare each absolute difference value in sequentially with the preset threshold . When an absolute value exceeds , it can be identified as an outlier, and the corresponding epoch is the spoofing end moment .
4.2.3. Validation of Spoofing End Moment Detection Method Based on Sample Quantiles
4.3. Process of Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation
5. Experiments and Results
- Experiment 6: satellites subjected to abrupt spoofing attacks at varying intensities.
- Experiment 7: satellites subjected to slowly varying spoofing attacks at varying intensities.
- Experiment 8: satellites subjected to intermittent spoofing attacks across multiple time intervals.
5.1. Simulation Settings
5.2. Results and Analysis
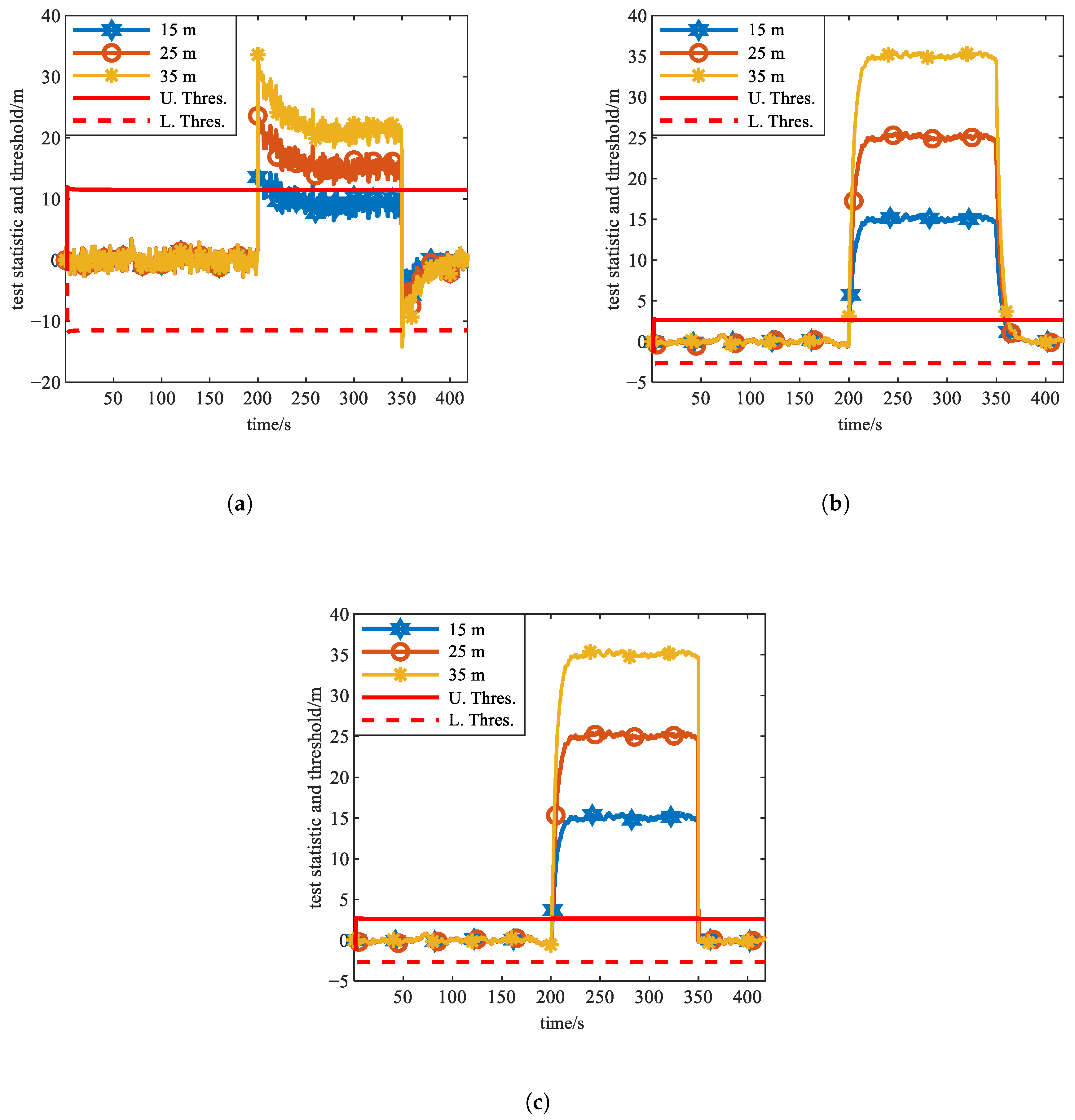
5.2.1. Experiment 6
5.2.2. Experiment 7
5.2.3. Experiment 8
6. Conclusions
- A Shewhart control chart-based detection algorithm is proposed to achieve the rapid and precise detection of minor spoofing termination, later utilized as a baseline method for the joint algorithm.
- The limitations of the individually applied EWMA control chart- and robust estimation-based algorithm (M2) and Shewhart control chart-based detection algorithm (M1) are analyzed. A joint spoofing detection algorithm is introduced, integrating dual control charts and robust estimation. Two components, including a joint detection metric for indicating spoofing termination and a spoofing end moment detection method based on sample quantiles, are designed.
- Simulation are subsequently conducted, demonstrating the proposed joint algorithm’s superiority over M1 and M2 across slowly varying, abrupt, and intermittent spoofing attack scenarios due to three key advantages: (1) the timely detection of all minor spoofing while complying with ICAO’s 30 s cruise phase alert requirement; (2) significantly accelerated spoofing termination detection; and (3) effective intermittent minor spoofing detection and accurate duration identification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Pseudocode Description of the Joint Spoofing Detection Algorithm
| Algorithm 1: Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation |
 |
References
- Rothmaier, F.; Chen, Y.H.; Lo, S.; Walter, T. GNSS spoofing detection through spatial processing. Navigation 2021, 68, 243–258. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, J. Synthesis algorithm for effective detection of GNSS spoofing attacks. Int. J. Aeronaut. Space Sci. 2020, 21, 251–264. [Google Scholar] [CrossRef]
- Habler, E.; Bitton, R.; Shabtai, A. Assessing Aircraft Security: A comprehensive survey and methodology for evaluation. ACM Comput. Surv. 2023, 56, 96. [Google Scholar] [CrossRef]
- Miralles, D.; Bornot, A.; Rouquette, P.; Levigne, N.; Akos, D.M.; Chen, Y.H.; Lo, S.; Walter, T. An assessment of GPS spoofing detection via radio power and signal quality monitoring for aviation safety operations. IEEE Intell. Transp. Syst. Mag. 2020, 12, 136–146. [Google Scholar] [CrossRef]
- Li, J.; Zhu, X.; Ouyang, M.; Li, W.; Chen, Z.; Dai, Z. Research on multi-peak detection of small delay spoofing signal. IEEE Access 2020, 8, 151777–151787. [Google Scholar] [CrossRef]
- Gu, N.; Xing, F.; You, Z. GNSS Spoofing Detection Based on Coupled Visual/Inertial/GNSS Navigation System. Sensors 2021, 21, 6769. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, M.; Lee, J. CUSUM-based GNSS spoofing detection method for users of GNSS augmentation system. Int. J. Aeronaut. Space Sci. 2020, 21, 513–523. [Google Scholar] [CrossRef]
- Shang, X.; Sun, F.; Liu, B.; Zhang, L.; Cui, J. GNSS spoofing mitigation with a multicorrelator estimator in the tightly coupled INS/GNSS integration. IEEE Trans. Instrum. Meas. 2022, 72, 8500112. [Google Scholar] [CrossRef]
- Jin, X.; Zhang, X.; Li, S.; Zheng, S. Detection of slowly varying spoofing using weighted Kalman gain in GNSS/INS tightly coupled systems. GPS Solut. 2024, 28, 54. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Fu, Q.; Liu, Z. Impact assessment of GNSS spoofing attacks on INS/GNSS integrated navigation system. Sensors 2018, 18, 1433. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, X.; Pang, C.; Wang, Y.; Zhang, L.; Feng, B. Improved fault detection method based on robust estimation and sliding window test for INS/GNSS integration. J. Navig. 2020, 73, 776–796. [Google Scholar] [CrossRef]
- Yimin, W.; Hong, L.; Mingquan, L. Spoofing profile estimation-based GNSS spoofing identification method for tightly coupled MEMS INS/GNSS integrated navigation system. IET Radar Sonar Navig. 2020, 14, 216–225. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J. Kalman-filter-based integrity evaluation considering fault duration: Application to GNSS-based attitude determination. GPS Solut. 2022, 26, 51. [Google Scholar] [CrossRef]
- Zhong, L.; Yue, W.; Xueyan, L. Spoofing interference detection algorithm based on EWMA control chart and robust estimation. Acta Aeronaut. Astronaut. Sin. 2024, 45, 329655. [Google Scholar]
- Liu, Y.; Li, S.; Fu, Q.; Liu, Z.; Zhou, Q. Analysis of Kalman filter innovation-based GNSS spoofing detection method for INS/GNSS integrated navigation system. IEEE Sens. J. 2019, 19, 5167–5178. [Google Scholar] [CrossRef]
- Liang, W.; Li, K.; Li, Q. Anti-spoofing Kalman filter for GPS/rotational INS integration. Measurement 2022, 193, 110962. [Google Scholar] [CrossRef]
- Zhong, L.; Liu, J.; Li, R.; Wang, R. Approach for detecting soft faults in GPS/INS integrated navigation based on LS-SVM and AIME. J. Navig. 2017, 70, 561–579. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, H.; Sun, C.; Bai, L.; Feng, W. Enhanced GNSS spoofing detector via multiple-epoch inertial navigation sensor prediction in a tightly-coupled system. IEEE Sens. J. 2022, 22, 8633–8647. [Google Scholar] [CrossRef]
- Ke, Y.; Lv, Z.; Zhang, C.; Deng, X.; Zhou, W.; Song, D. Tightly Coupled GNSS/INS Integration Spoofing Detection Algorithm Based on Innovation Rate Optimization and Robust Estimation. IEEE Access 2022, 10, 72444–72457. [Google Scholar] [CrossRef]
- Jorani, R.M.; Haddar, M.; Chaari, F.; Haddar, M. Gear Crack Detection Based on Vibration Analysis Techniques and Statistical Process Control Charts (SPCC). Machines 2023, 11, 312. [Google Scholar] [CrossRef]
- Harrou, F.; Taghezouit, B.; Khadraoui, S.; Dairi, A.; Sun, Y.; Hadj Arab, A. Ensemble Learning Techniques-Based Monitoring Charts for Fault Detection in Photovoltaic Systems. Energies 2022, 15, 6716. [Google Scholar] [CrossRef]
- Gao, Y.; Li, G. A slowly varying spoofing algorithm avoiding tightly-coupled GNSS/IMU with multiple anti-spoofing techniques. IEEE Trans. Veh. Technol. 2022, 71, 8864–8876. [Google Scholar] [CrossRef]
- Roberts, S. Control chart tests based on geometric moving averages. Technometrics 2000, 42, 97–101. [Google Scholar] [CrossRef]
- Chai, D.; Ning, Y.; Wang, S.; Sang, W.; Xing, J.; Bi, J. A robust algorithm for multi-gnss precise positioning and performance analysis in urban environments. Remote Sens. 2022, 14, 5155. [Google Scholar] [CrossRef]
- Marais, H.L.; Zaccaria, V.; Odlare, M. Comparing statistical process control charts for fault detection in wastewater treatment. Water Sci. Technol. 2022, 85, 1250–1262. [Google Scholar] [CrossRef]
- Morales, V.H.; Panza, C.A. Control Charts for Monitoring the Mean of Skew-Normal Samples. Symmetry 2022, 14, 2302. [Google Scholar] [CrossRef]
- ICAO. International Standards and Recommended Practices: Annex 10 to the Convention on International Civil Aviation, Volume I—Radio Navigation Aids, Amendment 89. International Civil Aviation Organization. 2018. Available online: https://www.icao.int (accessed on 10 March 2025).
- Umsonst, D.; Ruths, J.; Sandberg, H. Finite sample guarantees for quantile estimation: An application to detector threshold tuning. IEEE Trans. Control Syst. Technol. 2022, 31, 921–928. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Book Review; IEEE Aerospace and Electronic Systems Magazine; Artech: Morristown, NJ, USA, 2015; Volume 30, pp. 26–27. [Google Scholar]






| Experiment Number | Spoofed Satellite | Standard Deviation of Pseudorange Observation Noise (m) | Pseudorange Bias Under Abrupt Spoofing (m) | Pseudorange Rate Under Slowly Varying Spoofing (m/s) | Spoofing Duration (s) |
|---|---|---|---|---|---|
| 1 | PRN1 | 2.5 | 15 | 0.2 | 200∼350 |
| 2 | 2.5 | 15/25/35 | 0.2/0.5/0.7 | ||
| 3 | 2.5/5/10 | 0 | 0.2 | ||
| 4 | 2.5/5/10 | 15 | 0 | ||
| 5 | 2.5/5/10 | 15/25/35 | 0.2/0.5/0.7 |
| Sensor | Parameter | Parameter Value |
|---|---|---|
| GNSS | Masking angle | 10° |
| Standard deviation of signal propagation error | 1 m | |
| Standard deviation of code tracking error | 1 m | |
| Standard deviation of range rate tracking error | 0.02 m/s | |
| Standard deviation of pseudorange observation noise | 2.5 m | |
| IMU | Gyro biases | (−0.0009, 0.0013, −0.0008) (°)/h |
| Gyro random noise | 0.002 (°)/ | |
| Accelerometer biases | (30, −45, 26) mg | |
| Accelerometer random noise | 20 mg/ |
| Experiment Number | Spoofed Satellite | Pseudorange Bias Under Abrupt Spoofing (m) | Pseudorange Rate Under Slowly Varying Spoofing (m/s) | Spoofing Duration (s) |
|---|---|---|---|---|
| 6 | PRN1 | 15/25/ 35 | 0 | 200∼350 |
| 7 | PRN1 | 0 | 0.2/0.5/0.7 | 200∼350 |
| 8 | PRN1 | 0 25 | 0.5 0 | 200∼270 280∼350 |
| Pseudorange Bias (m) | Spoofing Onset Detection Delay (s) | Spoofing Termination Detection Delay (s) | Spoofing Duration Identification Results (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | |
| 15 | 0.01 | 1.01 | 1.01 | −92.51 | 8.51 | 0.01 | 200.01~257.49 | 201.01~358.51 | 201.01~350.01 |
| 25 | 0.01 | 0.51 | 0.51 | 0.01 | 10.01 | 0.01 | 200.01~350.01 | 200.51~360.01 | 200.51~350.01 |
| 35 | 0.01 | 0.01 | 0.01 | 0.01 | 12.01 | 0.01 | 200.01~350.01 | 200.01~362.01 | 200.01~350.1 |
| Pseudorange Rate (m/s) | Spoofing Onset Detection Delay (s) | Spoofing Termination Detection Delay (s) | Spoofing Duration Identification Results (s) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M1 | M2 | M3 | M1 | M2 | M3 | M1 | M2 | M3 | |
| 0.2 | 98.51 | 21.01 | 21.01 | 0.01 | 11.01 | 0.01 | 298.51~350.01 | 221.01~361.01 | 221.01~350.01 |
| 0.5 | 32.51 | 10.01 | 10.01 | 0.01 | 16.01 | 0.01 | 232.51~350.01 | 210.01~366.01 | 210.01~350.01 |
| 0.7 | 26.01 | 8.51 | 8.51 | 0.01 | 18.01 | 0.01 | 226.01~350.01 | 208.51~368.01 | 208.51~350.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Yuan, X.; Yue, W. Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation. Electronics 2025, 14, 2505. https://doi.org/10.3390/electronics14132505
Zhong L, Yuan X, Yue W. Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation. Electronics. 2025; 14(13):2505. https://doi.org/10.3390/electronics14132505
Chicago/Turabian StyleZhong, Lunlong, Xu Yuan, and Wenjing Yue. 2025. "Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation" Electronics 14, no. 13: 2505. https://doi.org/10.3390/electronics14132505
APA StyleZhong, L., Yuan, X., & Yue, W. (2025). Joint Spoofing Detection Algorithm Based on Dual Control Charts and Robust Estimation. Electronics, 14(13), 2505. https://doi.org/10.3390/electronics14132505






