GSTD-DETR: A Detection Algorithm for Small Space Targets Based on RT-DETR

Abstract

Ground-based optical equipment for detecting geostationary orbit space targets typically involves long-exposure imaging, facing challenges such as small and blurred target images, complex backgrounds, and star streaks obstructing the view. To address these issues, this study proposes a GSTD-DETR model based on Real-Time Detection Transformer (RT-DETR), which aims to balance model efficiency and detection accuracy. First, we introduce a Dynamic Cross-Stage Partial (DynCSP) backbone network for feature extraction and fusion, which enhances the network’s representational capability by reducing convolutional parameters and improving information exchange between channels. This effectively reduces the model’s parameter count and computational complexity. Second, we propose a ResFine model with a feature pyramid designed for small target detection, enhancing its ability to perceive small targets. Additionally, we improve the detection head and incorporate a Dynamic Multi-Channel Attention mechanism, which strengthens the focus on critical regions. Finally, we designed an Area-Weighted NWD loss function to improve detection accuracy. The experimental results show that compared to RT-DETR-r18, the GSTD-DETR model reduces the parameter count by 29.74% on the SpotGEO dataset. Its AP₅₀ and AP_50:95 improve by 1.3% and 4.9%, reaching 88.6% and 49.9%, respectively. The GSTD-DETR model demonstrates superior performance in the detection accuracy of faint and small space targets.

1. Introduction

Geostationary orbit (GEO) hosts numerous critical space assets, such as communication and navigation satellites. Monitoring resident space objects in these orbits is crucial for achieving space situational awareness and safeguarding important space assets [1]. However, due to factors such as the distant target distance, clouds, atmospheric effects, light pollution, sensor noise, and star background interference [2], the ground-based detection of geostationary orbit targets faces significant challenges.

As shown in Figure 1, under the staring observation mode of ground-based telescopes, geosynchronous orbit satellites typically exhibit Gaussian-like point spread functions with radii spanning 2–5 pixels or manifest as multi-pixel clustered point sources.

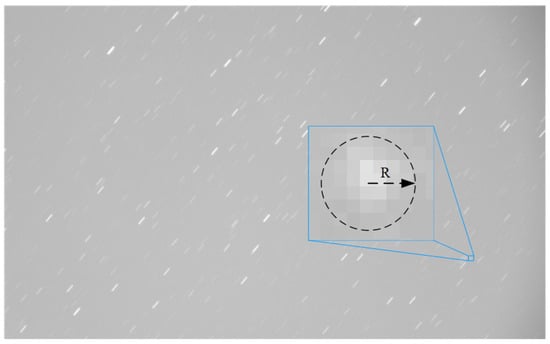
Figure 1. Morphology of space targets in images under telescope’s staring mode.

The goal of detecting geostationary orbit space targets is to accurately detect and recognize small targets amidst complex backgrounds. Traditional object detection methods are typically optimized for large targets and are constrained by receptive field limitations, which present significant challenges in detecting small targets. In recent years, deep learning methods, particularly convolutional neural networks (CNNs) and Transformer models, have led to significant progress in object detection. However, these methods often face limitations in small target detection and are frequently hindered by insufficient local feature extraction capabilities and high computational complexity [3,4].

To address the above issues and enhance the capability of detecting small space targets in complex environments, this paper proposes an improved space small target detection model based on the RT-DETR-r18 model. The structural improvements introduced over RT-DETR aim to optimize the model for small target detection tasks while maintaining computational efficiency. The main improvements are as follows:

(1)

We propose a DynCSP architecture as the backbone network. This backbone not only extracts high-quality feature representations but also significantly reduces the number of parameters and computational costs. By splitting the feature map and processing each part separately, the DynCSP architecture improves information exchange between channels and enhances the network’s feature extraction capability, which is particularly useful for small target detection.

(2)

We propose a ResFine model to enhance the network’s ability to perceive small targets, especially in feature extraction and information fusion. The model incorporates a feature pyramid structure, which improves the ability to capture small-scale details. Additionally, we design an SEK module for feature integration, allowing for a more efficient fusion of multi-scale features and enhancing detection accuracy.

(3)

We introduce a Dynamic Multi-Channel Attention (DMCA) mechanism, which is an improvement over the original Moment Channel Attention (MCA) mechanism. The DMCA mechanism dynamically adjusts the importance of feature channels, helping the model focus on critical regions while maintaining computational efficiency. Additionally, we modify the network’s neck by removing the P5 layer and retaining only the P3 and P4 layers, enabling the model to focus on high-resolution features that are better at preserving small target details, thus improving small target detection accuracy.

(4)

We propose an Area-Weighted NWD (AWNWD) loss function, which builds on the Normalized Wasserstein Distance (NWD) loss function. This loss function introduces small target-aware enhancements and scale difference terms, improving the model’s focus on small targets. By incorporating both the area and scale differences, this loss function improves the robustness and precision of small object detection, particularly in complex environments.

These structural improvements work synergistically to enhance the detection of small space targets and low signal-to-noise ratios while maintaining a reasonable computational cost.

The structure of this paper is as follows: Section 2 reviews the related research in the field of space target detection, introducing both traditional methods and deep learning-based approaches. Section 3 provides a detailed description of our proposed GSTD-DETR model, focusing on its core architecture, innovative modules, and method improvements. Section 4 presents the experimental setup, dataset, and evaluation metrics, along with the comparative experimental results, analyzing the advantages of our method. Section 5 concludes this paper by summarizing the main contributions, discussing the limitations of the model, and outlining future research directions.

2. Related Works

In space object detection, traditional methods include morphological recognition, star map matching, matched filtering, background masking, multi-frame stacking, frame difference, trajectory correlation, and multi-level hypothesis testing. For instance, Gao et al. proposed a target extraction method based on Time Energy Selective Scaling (TESS) and three-dimensional Hough transform [5]. Kong et al. introduced multi-frame masking techniques and a morphological dilation-based weak target extraction algorithm [6]. Han Luyao et al. proposed a real-time detection method through morphological processing and inter-frame matching that is suitable for targets with known prior motion information but with performance degradation under low signal-to-noise ratios (SNRs) [7]. Yang et al. proposed a hierarchical exposure strategy and a star map target sequence-based celestial object removal method, which is only applicable to natural targets [8]. Yao et al. improved the adaptive inter-frame difference detection algorithm by enhancing the detection effect through median and Kalman filtering, but the accuracy decreased in complex noisy environments [9]. Wang et al. proposed a target detection method based on both time-domain and spatial-domain correlations; however, the method suffers from low computational efficiency and heavy reliance on prior information [10]. Miao et al. proposed an improved multi-level hypothesis testing algorithm, although the computational load increases under low-SNR conditions [11]. PAN et al. proposed a small, weak target detection method based on time series images, achieving efficient detection through SNR enhancement and adaptive background noise suppression, but it performs poorly in dynamic scenarios [12].

With the development of deep learning, traditional image processing methods have gradually shown their limitations in detecting targets with complex backgrounds and low contrast [13,14]. Consequently, deep learning methods have gradually become mainstream in the field of target detection [15,16]. Deep learning-based target detection methods can be classified into two main categories: two-stage algorithms (such as SPP-Net and Faster R-CNN) and one-stage algorithms (such as the You Only Look Once series) [17]. For example, Rasit Abay et al. achieved high-altitude target detection with a feature fusion pyramid network, achieving an F1 score of 92% [18]. Meanwhile, Vittori et al. proposed a U-Net-based method for target trajectory extraction, which showed limited effectiveness in detecting small target trajectories [19]. Jia et al. enhanced the detection and classification capability for celestial targets by improving the Faster R-CNN algorithm [20]. Additionally, the methods proposed by Guo et al., which incorporate channel and spatial attention networks [21], and by Chen et al., who combined LSTM and CNNs for space target detection and tracking [22], demonstrated good performance in multi-task scenarios. To address the challenges of small targets and complex backgrounds, Liu et al. proposed an improved algorithm based on attention mechanisms [23], though it struggles with detecting targets with blurred edges.

In recent years, both the YOLO series and the DETR model have made significant progress in space target detection, but they still face a trade-off between computational efficiency and accuracy, particularly in noisy environments where performance remains to be improved [24,25]. Yuan et al. [24] improved the YOLOv5 model by integrating cross-layer context, adaptive weighting, and spatial information enhancement modules, which enhanced the detection capability for small space targets, though at the cost of increased computational burden. Wang et al. [25] enhanced the DETR model by introducing diverse attention mechanisms into the backbone network and encoder, significantly improving the detection of spacecraft and space debris, though this approach requires considerable computational overhead and yields suboptimal performance for tiny targets.

Despite these advances, the detection of small space targets still faces challenges such as high computational complexity and poor real-time performance. Therefore, further improvements in detection accuracy, reductions in computational costs, and enhancement in the robustness of these methods in dynamic and low-signal-to-noise-ratio environments are still necessary.

3. Methodology

3.1. GSTD-DETR Model

Figure 2 illustrates the GSTD-DETR framework proposed in this paper. This method is based on RT-DETR, an advanced end-to-end object detector known for balancing speed and accuracy across various tasks [26]. The RT-DETR model has several versions, including RT-DETR-r18, RT-DETR-r34, RT-DETR-r50, RT-DETR-r101, and RT-DETR-x [27]. Among these, RT-DETR-r18 achieves a good trade-off between speed and accuracy. Therefore, we chose RT-DETR-r18 as the base model for developing our network. As shown in Figure 2, the GSTD-DETR framework consists of a backbone, a hybrid encoder, a decoder, and a prediction head.

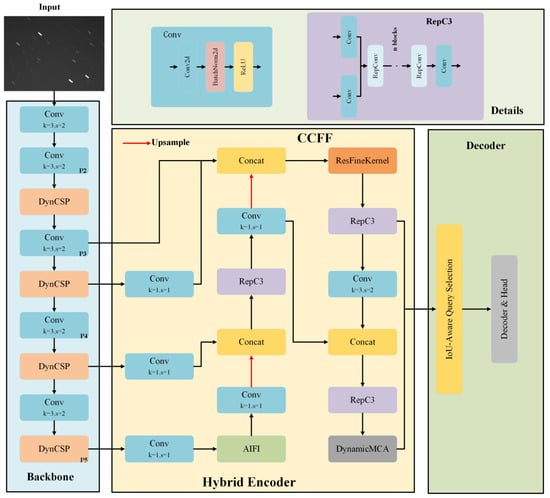
Figure 2. GSTD-DETR framework diagram.

First, the backbone network captures key information from the input image and generates feature maps at different scales. These feature maps are then fused through an efficient hybrid encoder. Next, the IoU (Intersection over Union)-aware query selection mechanism is used to select a fixed number of image features as the initial queries for the decoder. In the decoder, with the help of auxiliary heads, the queries are gradually refined, ultimately generating bounding boxes with confidence scores.

3.2. DynCSP Backbone Network

The RT-DETR model offers two different backbone network options: ResNet and HGNetv2 [27,28]. However, both networks rely heavily on the use of full-channel standard convolutions (SCs) in deep layers, leading to significant computational burdens, large parameter counts, the loss of spatial information, and a lack of optimization for small-scale targets when handling small targets. Therefore, for small target detection tasks, network design should place greater emphasis on addressing these issues and adopt more lightweight and adaptable backbone networks.

The Cross-Stage Partial network (CSPNet) is a network architecture designed to enhance the learning capability and computational efficiency of convolutional neural networks (CNNs). The core idea of CSPNet is to split the feature map into two parts: one part is processed through residual networks (ResNet-like blocks), while the other part is passed directly through, with the results of both parts being merged. This design reduces computational load, as not all features are processed through complex residual blocks, while still maintaining the model’s learning capacity [29]. The DynCSP block proposed in this paper is inspired by the CSP architecture. The structure of the DynCSP backbone network is shown in Figure 3.

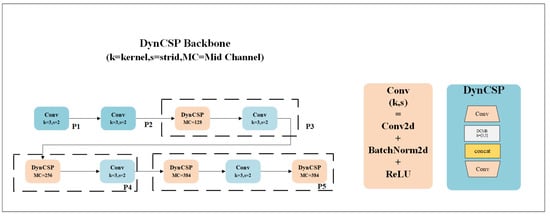
Figure 3. DynCSP backbone structure diagram.

The DynCSP block splits the input feature map, performs convolution operations on each part separately, and then generates the output feature map by concatenating the channels. This structure facilitates the flow of information while also avoiding information bottlenecks, thereby enhancing the network’s feature extraction capability. It also improves gradient propagation, allowing the network to be better optimized during training, especially in very deep networks, thus avoiding issues such as vanishing or exploding gradients [30,31]. The structure of this module is shown in Figure 4.

Figure 4. DynCSP block.

Considering the small scale and varying shapes of small targets in images, traditional convolutional kernels (such as 3 × 3 kernels) may struggle to capture the detailed features of these small targets. Therefore, the DCMB module introduces multiple convolution kernels of different sizes, combining them to capture more scale-specific information.

Traditional convolution operations use fixed convolution kernel weights, while dynamic convolution adjusts the weights of the kernels based on the features of the input data [32]. The DCMB module optimizes the use of convolution kernels by dynamically adjusting their weights, enhancing sensitivity to small targets. Through this mechanism, the network can dynamically select the most suitable convolution operation based on the features of the current input.

The DCMB module fuses the features extracted by different convolution kernels, allowing the features of each channel to incorporate information from other scales, thereby improving the model’s ability to recognize targets. To prevent the issue of gradient vanishing in deep networks while maintaining information flow, the DCMB module incorporates residual connections, enabling smooth information flow across multiple modules. These residual connections allow input information to be directly passed to the output, preventing information loss in complex network layers and enhancing the network’s training stability.

The design of the DCMB module primarily addresses the issues of multi-scale feature fusion and computational efficiency in small target detection through the combination of multi-scale convolutions, dynamic convolution kernel weight adjustment, and residual connections. This module has strong adaptability and flexibility, dynamically selecting the most suitable convolution kernel based on the input features, thus improving the detection accuracy of small targets in complex environments. The structure is shown in Figure 5.

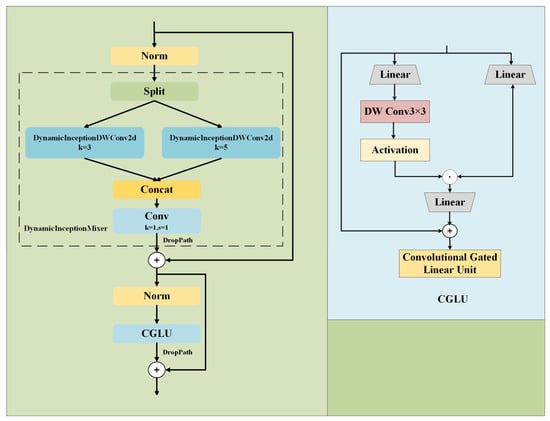
Figure 5. DCMB module.

The DynamicInceptionMixer part of the DCMB module optimizes feature extraction by using multiple convolution kernel sizes and dynamically adjusting channels, enabling the network to capture small target features at different scales. By introducing the Convolutional GLU (CGLU) activation function, the network’s nonlinear representation capability is enhanced, while the DropPath mechanism effectively mitigates overfitting, thus improving the network’s robustness. The formula for the CGLU activation function is as follows.

$$\mathrm{CGLU}(x)=x\odot \sigma (W_{g}x+b_g)$$

(1)

Here, $\odot$ denotes element-wise multiplication, $\sigma$ represents the sigmoid activation function, $x$ is the input vector, and $W_{\mathrm{g}}$ and $b_g$ are the weight matrix and bias vector of the gating layer, respectively.

This part splits the input into two sub-tensors, each containing half of the original input’s channel count. The split operation divides the input tensor along the channel dimension (dim = 1) into two parts. Each sub-tensor, containing half of the channels, is passed through a set of dynamic convolutions. The input tensor is processed using DynamicInceptionDWConv2d with two different kernel sizes. Finally, the outputs of all convolution paths are concatenated using a concat operation to form a larger feature map. A 1 × 1 convolution is then applied to the concatenated feature map to reduce its channel count and restore it to the original channel count of the input.

The core idea of DynamicInceptionDWConv2d is to capture multi-scale information by combining convolution kernels of different sizes while enhancing the network’s sensitivity to key features by dynamically adjusting the weights of the convolution kernels. Dynamic convolution adapts the convolution kernel weights based on the input data, making the convolution operation more flexible and targeted. Its structure is shown in Figure 6.

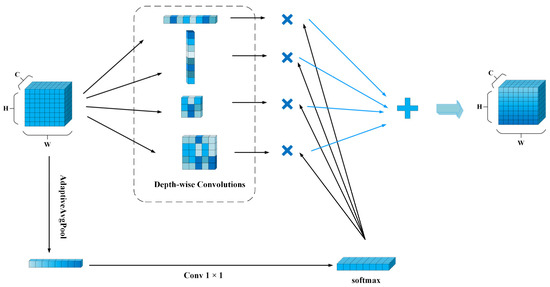
Figure 6. DynamicInceptionDWConv2d.

The DynamicInceptionDWConv2d module combines depth-wise separable convolutions with dynamic convolution kernel adjustment mechanisms to reduce the number of parameters and improve computational efficiency. This module employs a multi-scale feature fusion strategy, making it particularly suitable for small target detection tasks and significantly enhancing detection accuracy. The key feature of this module is its ability to dynamically adjust the convolution strategy based on the input feature map. This is achieved through the Dynamic Kernel Weights mechanism. First, the input feature map is processed by an adaptive average pooling layer (AdaptiveAvgPool), which aggregates each channel into a single statistic. Then, a convolution layer generates the weights for four different convolution kernels. These weights are dynamically adjusted based on the scale and feature distribution of the input data, allowing the system to select the most suitable convolution operation for small target detection.

The dynamic adjustment of the convolution strategy is realized by normalizing the kernel weights using a Softmax operation, ensuring that the sum of all weights equals 1. By dynamically adjusting the convolution kernel weights, the model can flexibly adapt to different input scenarios, improving its robustness in handling diverse and varying inputs.

3.3. ResFine Model

Small targets often perform poorly on the conventional P3, P4, and P5 detection layers. A traditional approach to improving small target detection capability is to add a P2 detection layer, but this also introduces a range of issues, such as excessive computational load and more time-consuming post-processing [33,34]. To effectively fuse feature information from different channels and improve network performance and accuracy, this paper proposes a feature pyramid structure based on the DynCSP block, along with improvements to the original CCFF. As shown in Figure 7, the ResFineKernel module is introduced. First, the P3 layer features and the features processed through the DynCSP block are fused, and then the ResFineKernel module is applied to integrate the features.

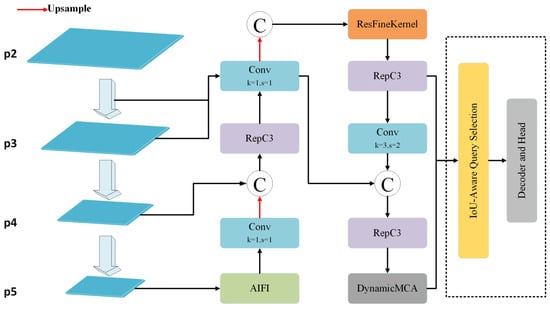
Figure 7. ResFine model structure.

Figure 8 shows the structure of the ResFineKernel module. The core design goal of the ResFineKernel module is to enhance the model’s ability to perceive small targets, especially in feature extraction and information fusion. The module achieves its functionality through the Squeeze-and-Excitation Kernel (SEK) and residual connections. Specifically, the workflow of the ResFineKernel module consists of two main parts: feature extraction and feature fusion.

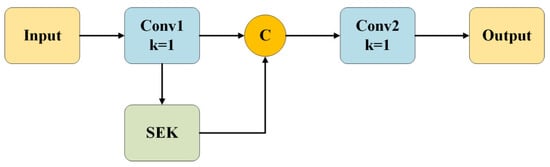
Figure 8. ResFineKernel module.

Residual connections effectively mitigate the vanishing gradient problem, especially in small target detection tasks, where retaining high-resolution details is crucial for accurate target localization. Through this feature fusion approach, the model can more precisely extract and integrate key information.

The SEK proposed in this paper is an improved multi-scale convolution branch module. The core idea is to enhance the expression capability of local details through multi-scale feature extraction and an adaptive channel attention mechanism (Squeeze-and-Excitation, SE), thereby improving detection accuracy.

The SEK module uses multiple convolution kernels of different sizes to extract features at different scales, efficiently capturing feature representations from local to global contexts and enhancing small target detection performance through feature fusion. This method not only solves the computational overhead introduced by the P2 layer but also further improves small target detection performance through effective feature integration. The SEK module consists of multiple parallel convolution branches, with each branch using different kernel sizes and dilation settings to capture image information from multiple scales and directions. The specific design is shown in Figure 9. This design ensures that fine-grained information is preserved while balancing global context.

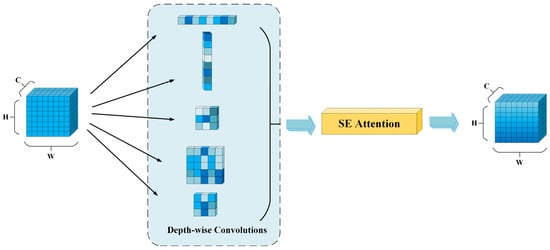
Figure 9. Squeeze-and-Excitation Kernel.

The outputs from each branch are fused through pixel-wise addition, resulting in a comprehensive feature map that contains multi-scale and multi-angle information, providing rich detail expressions for subsequent detection.

After the multi-scale convolution results are fused, the SE module is introduced to perform channel-wise adaptive re-calibration on the fused features. By using adaptive average pooling, the spatial information of each channel is compressed into global statistics, thereby capturing the global feature distribution. The global description is then reduced and re-expanded through two layers of 1 × 1 convolutions (with a ReLU activation in between), and finally, the channel weights are generated using a sigmoid activation function. The channel weights obtained are multiplied by the multi-scale fused features, enabling the adaptive enhancement of key information.

3.4. Dynamic Multi-Channel Attention

Due to the small size of the targets, lower-level features (P3 and P4) contain more spatial information and are better at preserving target details. The P5 layer, however, undergoes multiple downsampling operations, resulting in lower spatial resolution and the loss of small target details. Therefore, removing the P5 layer reduces reliance on low-resolution features and increases the utilization of high-resolution features. In this paper, the P5 layer is removed from the neck part, and only the P3 and P4 layers are retained. The DynamicMCA (DMCA) module is introduced to enhance the focus on important features, making the network more dependent on lower-level feature maps. Figure 10 illustrates three prediction head structures.

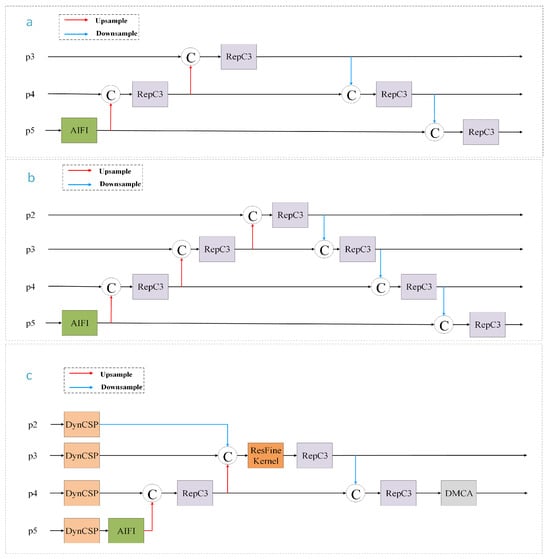
Figure 10. Schematic diagram of prediction heads: (a) original prediction head of RT-DETR-r18; (b) prediction head of RT-DETR-r18-p2; (c) prediction head of GSTD-DETR.

Compared to the other two, the proposed improvement is effective without introducing excessive computational costs. By removing the P5 layer, the network reduces reliance on low-resolution features, allowing for the increased utilization of high-resolution features, which are better at preserving small target details. Additionally, the introduction of the DMCA module further enhances feature extraction without adding significant computational burden. The lightweight adaptive weighting mechanism of DMCA, combined with Dynamic Channel Reorganization and Spatial Attention Enhancement, ensures that the network focuses on relevant features while maintaining computational efficiency.

We propose DMCA as an improvement over the original Moment Channel Attention (MCA) mechanism [35]. DMCA inherits the channel attention mechanism of MCA and enhances it through lightweight adaptive weighting to adjust the importance of feature channels. It captures spatial dependencies by integrating both average and max pooling features. Channel and spatial attention are computed in parallel to form complementary enhancements, and feature self-calibration is achieved via sigmoid activation.

The DMCA structure consists of two main parts: Dynamic Channel Reorganization (DCR) and Spatial Attention Enhancement. The structure is shown in Figure 11.

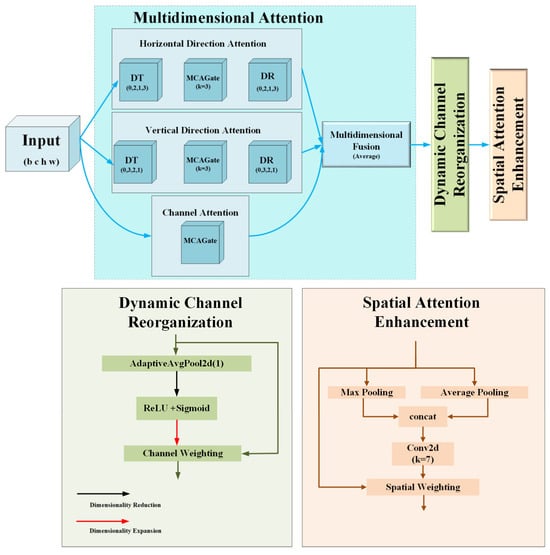
Figure 11. DMCA module.

The input feature map undergoes initial feature extraction and channel weighting through the basic MCA process. It is then processed through the DCR and Spatial Attention Enhancement modules.

Dynamic Channel Reorganization is a mechanism that dynamically adjusts the importance of features along the channel dimension, allowing the weight of each channel to be automatically adjusted based on the specific content of the input feature map. Unlike traditional static channel attention mechanisms, DCR uses adaptive average pooling to learn feature channel weights at each layer, enabling more refined control over the influence of each channel in the network.

The Spatial Attention Enhancement mechanism further improves the representation capability of the feature map by weighting the spatial dimensions. First, average pooling and max pooling operations are applied to the feature map of each channel, obtaining different statistical features of the spatial information. These two pooling operations capture important regions along the spatial dimension. After concatenating the results of average and max pooling, the combined feature is input into a 7 × 7 convolution layer to generate a spatial attention weight map. This weight map is normalized using a sigmoid function. Finally, the spatial attention weights are applied to the spatial dimension of the input feature map, enhancing the model’s focus on important spatial locations and reducing attention on less relevant areas.

3.5. Area-Weighted NWD Loss Function

Traditional IoU-based bounding box regression methods (such as IoU, GIoU, and CIoU) primarily focus on the geometric relationship between the predicted box and the ground truth (GT) box when computing the loss, such as the overlap area and center distance, while neglecting the influence of the bounding box’s shape and scale on the regression results [36,37,38,39]. In small target detection scenarios, the sensitivity of these methods to IoU values becomes more pronounced.

The IoU is calculated using the following formula:

$$\mathrm{IoU}={\displaystyle \frac{\left|B\cap B^{gt}\right|}{\left|B\cup B^{gt}\right|}}$$

(2)

The numerator represents the intersection between the predicted bounding box $B$ and the ground truth bounding box $B^{gt}$. The denominator represents the area of the union of the predicted bounding box $B$ and the ground truth bounding box $B^{gt}$, which is the total area covered by both boxes.

Small objects occupy fewer pixels in an image, and their features are relatively less distinct, making the accurate detection of small objects more challenging. Therefore, there is a need for a method that can more precisely describe the bounding box regression loss for small objects to improve the performance of small object detection.

Through an analysis of the characteristics of bounding box regression, it has been observed that differences in the shape and scale of bounding boxes in regression samples lead to variations in IoU values under the same bias conditions [40]. For small-scale bounding boxes, the impact of shape and bias on the IoU value is more significant. Consequently, when designing the bounding box regression loss function for small object detection, it is essential to take both shape and scale factors into account.

To address this issue, this paper proposes an Area-Weighted NWD (AWNWD) loss function based on the Normalized Wasserstein Distance (NWD) [41] loss function. This loss function introduces small object-aware enhancement and scale difference terms. It takes into account the weighted influence of the bounding box position, size, and object area, thereby strengthening the impact of small objects in the loss function. This approach enhances the model’s attention to small objects while ensuring that the model balances the importance of targets at different scales during the loss calculation, thus improving the model’s robustness.

The traditional NWD formula is as follows:

$$D=\sqrt{{(x_c-x_c^{gt})}^2+{(y_c-y_c^{gt})}^2+{\displaystyle \frac{{(w-w^{gt})}^2+{(h-h^{gt})}^2}{weigh{t}^2}}}$$

(3)

$$\mathrm{NWD}=e^{-{\displaystyle \frac{D}{C}}}$$

(4)

where $\left(x_c,y_c\right)$ and $\left(x_c^{gt},y_c^{gt}\right)$ represent the center coordinates of the predicted bounding box and the ground truth (GT) box, respectively; $w$ and $h$ are the width and height of the predicted bounding box, while $w^{gt}$ and $h^{gt}$ are the width and height of the ground truth (GT) box, respectively; $weight$ and $C$ are constants related to the dataset.

The basic form of AWNWD is as follows:

First, the sigmoid function is used to map the area to a range between 0 and 1, resulting in an area weight. The area weight, computed using the sigmoid function, dynamically adjusts based on the size of the object, allowing the model to place more emphasis on smaller target details. By applying this weight to the Wasserstein distance, the model’s focus on small objects is enhanced by increasing the importance of small target regions during the distance calculation. This adjustment improves the model’s ability to detect small objects by making the loss function more sensitive to small-scale variations.

Next, the logarithmic difference in the area ratio between the predicted bounding box and the ground truth bounding box is computed and normalized using the sigmoid function. Incorporating this difference term into the loss function helps the model focus on the impact of scale variations on detection performance. By combining both the area weight and the scale difference, this approach ensures that the model can better handle target scale variations and enhance detection performance, especially for small objects.

The formula for the sigmoid activation function is as follows:

$$\sigma (x)={\displaystyle \frac{1}{1+e^{-x}}}$$

(5)

The calculation of the area weight is as follows:

$$are{a}_{weight}=\sigma \left(1-{\displaystyle \frac{w\times h+w^{gt}\times h^{gt}}{2}}\right)$$

(6)

The calculation of scale difference is as follows:

$$scal{e}_{diff}=\left|\ln \left({\displaystyle \frac{w\times h}{w^{gt}\times h^{gt}+\epsilon }}\right)\right|$$

(7)

The calculation of the weighted Wasserstein distance is as follows:

$$D_{weight}=\sqrt{\left({(x_c-x_c^{gt})}^2+{(y_c-y_c^{gt})}^2+{\displaystyle \frac{{(w-w^{gt})}^2+{(h-h^{gt})}^2}{weigh{t}^2}}\right)}\times (1+are{a}_{weight})$$

(8)

The final loss is calculated as follows:

$$\mathrm{AreaWeightedNWD}=e^{-{\displaystyle \frac{D_{weight}}{C}}}+\alpha \times scal{e}_{diff}$$

(9)

Here, $\alpha$ and $C$ are hyperparameters. The computational flow of the AWNWD loss is illustrated in Figure 12.

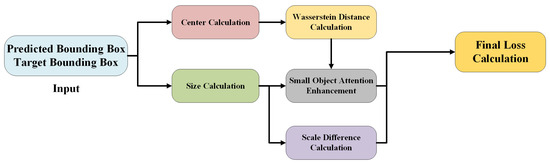
Figure 12. AWNWD computational flowchart.

4. Results

4.1. Dataset and Experimental Setup

The SpotGEO dataset [42,43], released by the European Space Agency (ESA) in June 2020, serves as the official dataset for the GEO satellite object detection competition. This dataset was acquired from multiple nighttime observations using ground-based telescopes located at various sites, ensuring the richness of the data. Each frame of the dataset had a resolution of 640 × 480 pixels.

In this experiment, the dataset was divided into training, validation, and testing sets at a ratio of 7:1:2. Specifically, 4480 images were used for the training set, 640 for the validation set, and 1280 for the testing set. Figure 13 illustrates some images from the dataset.

Figure 13. Sample images from the SpotGEO dataset.

Table 1 presents the experimental environment and parameter settings for the RT-DETR-related experiments in this paper. To ensure a fair comparison and facilitate reproducibility, both the proposed GSTD-DETR model and the baseline RT-DETR-r18 model were trained using identical hyperparameter settings, including learning rate, batch size, optimizer type, and momentum. All detection models were trained under the same hardware and software conditions, utilizing identical training, validation, and testing datasets. The initial learning rates for the comparison models were set consistently with their respective original papers, with a momentum value of 0.9. Training for all models was terminated upon the convergence of accuracy.

Table 1. Experimental environment and parameter settings.

Experimental Environment		Parameter Setting of DETR
GPU	RTX4090	Batch size	16
CPU	AMD EPYC 7352	Momentum	0.9
Development environment	Python 3.10.0 Pytorch 2.3.0 CUDA 12.1	Optimizer	AdamW
		Learning rate	0.0001
		Weight decay coefficient	0.0001
		Input size	640 × 480

Regarding the selection of parameters $\alpha$ and $C$ in the Area-Weighted NWD loss function, the parameter $C$ adopted the default NWD value of 12.8. According to the experimental data shown in Table 2, the model achieved optimal performance when $\alpha$ was set to 0.1.

Table 2. Performance (AP_50:95) under different $\alpha$ values.

$\alpha$	0.01	0.05	0.1	0.15	0.2
AP50:95	0.365	0.412	0.499	0.451	0.401

4.2. Evaluation Metrics

Due to the small number of pixels corresponding to targets in images and the susceptibility of detection to noise and image quality, stricter evaluation criteria are required to ensure the precise detection of small spatial targets. The AP_50:95 metric provides a more rigorous evaluation standard, which more accurately reflects the model’s ability to detect small targets at different IoU thresholds. Additionally, the recall rate directly reflects the model’s detection completeness for small targets. Therefore, this paper selected the precision, recall, AP₅₀, and AP_50:95 metrics to evaluate the detection accuracy of the model.

In this paper, average precision (AP) was used as a metric to evaluate the accuracy of the object detection model. AP represents the area under the precision–recall curve, and its calculation formula is as follows:

$$AP={\displaystyle {\int }_0^1\mathrm{Precision}}(\mathrm{Recall})d(\mathrm{Recall})$$

(10)

where Precision represents the probability that a sample predicted as a positive sample is actually a positive sample, and Recall represents the probability that a sample that is actually a positive sample is correctly predicted as positive. The related calculation formulas are as follows:

$$\begin{array}{l}\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}\\ \mathrm{Recall}={\displaystyle \frac{TP}{TP+FN}}\end{array}$$

(11)

In object detection tasks, the evaluation metrics are defined as follows: true positives (TPs) refer to the number of positive samples that are correctly identified; false positives (FPs) denote negative samples that are erroneously classified as positive; and false negatives (FNs) represent positive samples that are not successfully detected. Detection performance is commonly assessed by the IoU between the predicted bounding box and the ground truth bounding box, with respect to a predetermined threshold. A higher IoU threshold imposes stricter criteria for detection accuracy. The AP at an IoU threshold of 0.5 is referred to as AP₅₀, whereas the mAP over a range of IoU thresholds from 0.5 to 0.95, with a step size of 0.05, is referred to as AP_50:95. In the case of single-object detection, the mAP_50:95 value is equivalent to the AP_50:95 value. The calculation of AP_50:95 is formally defined as follows:

$$A{P}_{50:95}={\displaystyle \frac{1}{10}}{\displaystyle \sum _{i=0}^{9}A}{P}_{5i+50}$$

(12)

where AP_5i+50 represents the average precision when the IoU threshold is 0.05i + 0.5.

4.3. Ablation Experiments

In the ablation experiments, the RT-DETR-r18 model was employed as the baseline network, and the performance of the GSTD-DETR network was evaluated on the SpotGEO dataset.

Table 3 provides a detailed presentation of the performance metrics under different model configurations. By listing the network’s layers, parameters, and GFLOPs, it visually demonstrates the contribution of each module. The GSTD-DETR network had 29.74% fewer parameters than the baseline RT-DETR-r18. Although the computational cost increased by 3.26%, the overall AP_50:95 improved by 4.9%.

Table 3. Ablation experiment results.

DynCSP	ResFineKernel	DMCA	AWNWD	Layers	Parameters (M)	GFLOPs	AP50:95
-	-	-	-	295	19.97	58.3	0.45
√	-	-	-	439	13.31	43.9	0.478
	√	-	-	317	20.48	64.3	0.458
-	-	√	-	297	18.65	56.0	0.452
√	√	-	-	483	15.21	61.2	0.49
√	√	√	-	488	14.03	60.2	0.497
√	√	√	√	488	14.03	60.2	0.499

By improving the backbone network, feature extraction module, feature fusion method, and the prediction head and loss function, the AP, AR, and AP_50:95 metrics of GSTD-DETR significantly improved, demonstrating the effectiveness of the enhanced modules. Although the computational costs increased, this increase is deemed acceptable given the performance gains.

As shown in Figure 14, the partial detection results demonstrate that the model can accurately detect small spatial targets in images under various conditions, exhibiting good robustness. The algorithm is capable of recognizing targets, with the detection results showing high accuracy and stability. The detection performance under star occlusion conditions indicates that the algorithm can detect most occluded targets; however, a small number of targets were not correctly identified, suggesting that there is still room for further optimization in handling brighter star occlusion issues. Overall, the small spatial target detection algorithm performs well in complex environments.

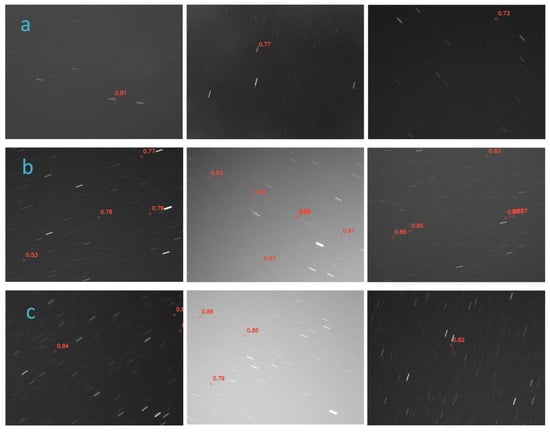
Figure 14. Partial detection results: (a) stellar streak occlusion; (b) multiple targets; (c) complex background.

4.4. Comparative Experiments

This paper compared the performance of GSTD-DETR with several state-of-the-art object detection models using the same dataset. Table 4 presents the qualitative results of GSTD-DETR compared to YOLOv8m, YOLOv11m [44], RT-DETR-r18, RT-DETR-r18-p2 with the P2 detection head, RT-DETR-r34, and RT-DETR-r50 [27]. As shown in Table 4, GSTD-DETR achieved superior accuracy among all of the comparison models, with an improvement of 1.9% over the RT-DETR-r18-p2 model. This result effectively demonstrates the model’s performance in detecting small spatial targets.

Table 4. Comparison of different detection models.

Model	Backbone	File Weights (MB)	Parameters (M)	GFLOPs	AP	AR	AP50	AP50:95
YOLOv8m	CSPDarknet	49.6	25.90	79.3	0.820	0.651	0.765	0.402
YOLOv11m	CSPDarknet	38.6	20.11	68.5	0.811	0.671	0.775	0.408
RT-DETR-r18	ResNet18	38.6	19.97	58.3	0.904	0.787	0.873	0.45
RT-DETR-r18-p2	ResNet18	40.8	20.94	78	0.907	0.775	0.858	0.480
RT-DETR-r34	ResNet34	60.09	31.32	90.2	0.914	0.8	0.875	0.464
RT-DETR-r50	ResNet50	654	42.78	134.4	0.911	0.801	0.878	0.471
ours	DynCSP	27.2	14.03	60.2	0.925	0.805	0.886	0.499

GSTD-DETR performed excellently in small object detection, achieving significant improvements: AP increased by 1.8% compared to RT-DETR-r18-p2; AR was 80.5%, an improvement of 1%; AP₅₀ reached 88.6%, an increase of 2.8%; and AP_50:95 was 49.9%, improved by 1.9%. These enhancements demonstrate that GSTD-DETR’s detection capability for small objects was strengthened. Compared to RT-DETR-r18-p2, GSTD-DETR strikes a good balance between performance and efficiency.

GSTD-DETR has a GFLOPs of 60.2M, which is higher than that of some lightweight models but lower than that of more computationally intensive models like RT-DETR-r50 (134.4 GFLOPs). This indicates that GSTD-DETR achieves a moderate computational overhead while maintaining performance. The model has 14.03M parameters, and the trained weights are 27.2 MB, which is significantly smaller than those of r18, r34, and r50. This ensures high accuracy while also ensuring efficient training and deployment. Compared to more computationally expensive models, the smaller parameter size of GSTD-DETR provides higher efficiency in terms of inference speed and storage requirements, making it suitable for practical applications with limited computational resources. The three-dimensional scatter plot of model performance shown in Figure 15 clearly demonstrates that GSTD-DETR achieves a good balance between high accuracy and an appropriate model size.

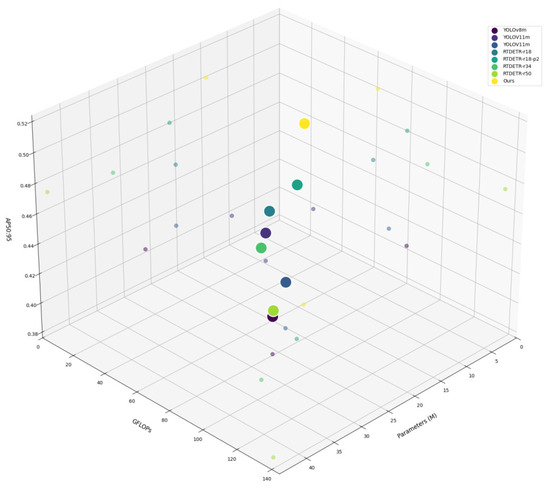
Figure 15. Three-dimensional scatter plot of model performance across multiple evaluation metrics.

Figure 16 illustrates a comparison of the detection capabilities of the proposed GSTD-DETR method with other state-of-the-art detectors. This comparison highlights the effectiveness of GSTD-DETR in complex scenarios. The first column shows the name of each method.

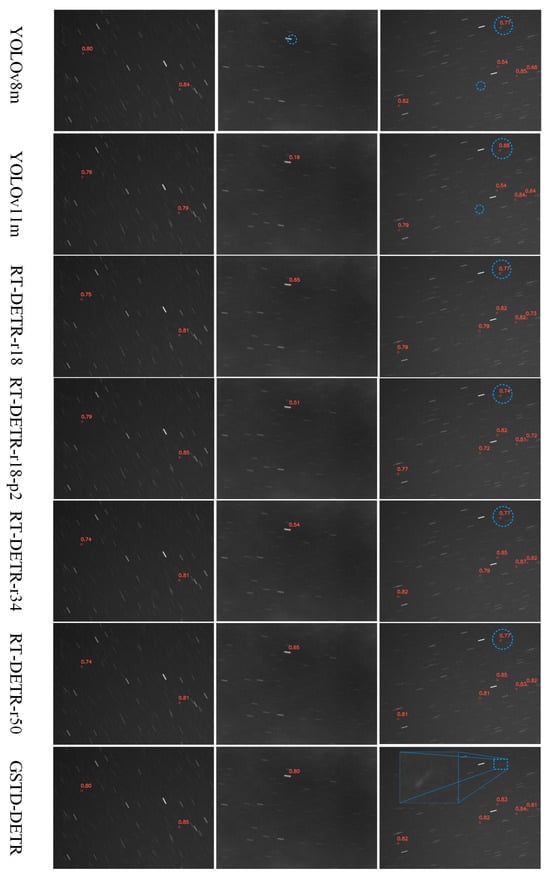
Figure 16. Detection results of different types of spatial targets.

Compared to other object detectors (YOLOv8m, YOLOv11m, RT-DETR-r18, RT-DETR-r18-p2, RT-DETR-r34, and RT-DETR-r50), GSTD-DETR demonstrates superior performance across all metrics.

In the first column of the resulting images, it is visually evident that all models successfully identified the target; however, GSTD-DETR demonstrated notably higher confidence scores. The second column presents the target detection performance under stellar background occlusion. Under such challenging conditions, GSTD-DETR maintained strong robustness and accuracy, whereas the confidence levels of the other models dropped significantly. The final column illustrates scenarios where the background contains blurred objects that resemble the detection targets. Our model is still capable of accurately distinguishing the true target. Enlarged view analysis confirms that the interference object was not a geostationary target; however, the other models incorrectly classified it as a target with high confidence, resulting in false positives.

In summary, GSTD-DETR demonstrates robust detection capabilities under complex backgrounds and occlusion scenarios. With its efficient architecture and reliable performance, the algorithm holds significant promise for real-time detection tasks and exhibits strong potential for deployment in practical operational environments.

5. Conclusions

This paper proposed a GSTD-DETR model based on RT-DETR-r18, aiming to achieve high detection accuracy under various conditions while keeping the model size within a reasonable range. First, a DynCSP architecture was introduced as the backbone network, which not only extracted high-quality feature representations but also significantly reduced the number of parameters and computational costs. Second, to enhance the model’s ability to perceive small targets, a ResFineKernel module was proposed, along with an SEK module for feature integration. Subsequently, an improved DMCA mechanism based on MCA was introduced, and modifications to the network’s neck were made, including the removal of the P5 layer, retaining only the P3 and P4 layers, allowing the model to more effectively focus on key feature regions. Finally, an AWNWD loss function based on the NWD loss function was proposed. This loss function increased the model’s focus on small targets.

Under complex external conditions, small object detection tasks are influenced by various factors, including but not limited to atmospheric effects, light pollution, sensor noise, and star background occlusion. To address these challenges, we evaluated the performance of the improved model across various scenarios. The results indicated that the enhanced model outperformed other detection algorithms in terms of accuracy.

However, despite its strong performance, GSTD-DETR has certain limitations. It is designed for single-frame detection, which may be beneficial for real-time detection tasks, but it does not leverage inter-frame information. Additionally, the algorithm’s effectiveness on high-resolution images still requires further validation. In the future, we plan to conduct real-time target detection experiments on hardware platforms, further fine-tuning the model to ensure its capability for high-resolution real-time target detection.