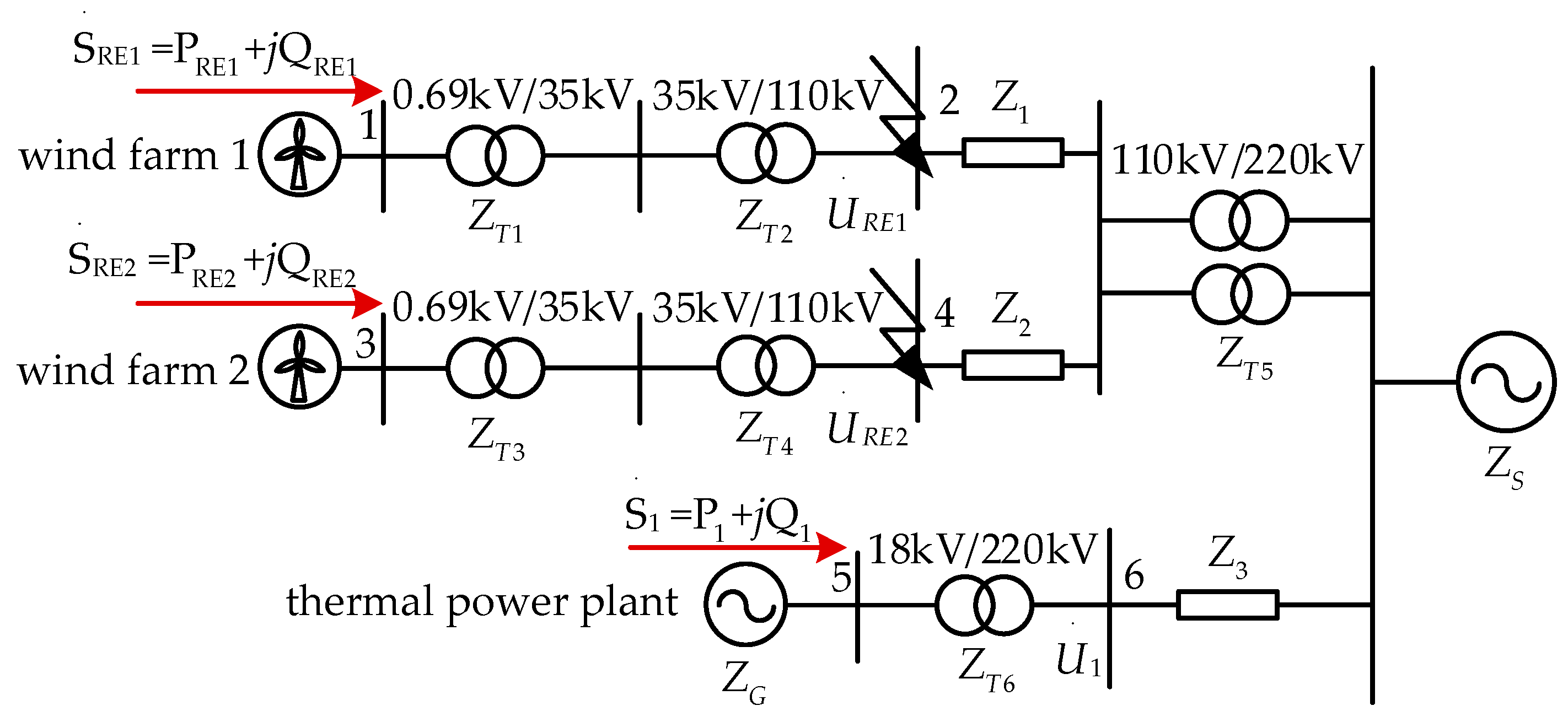
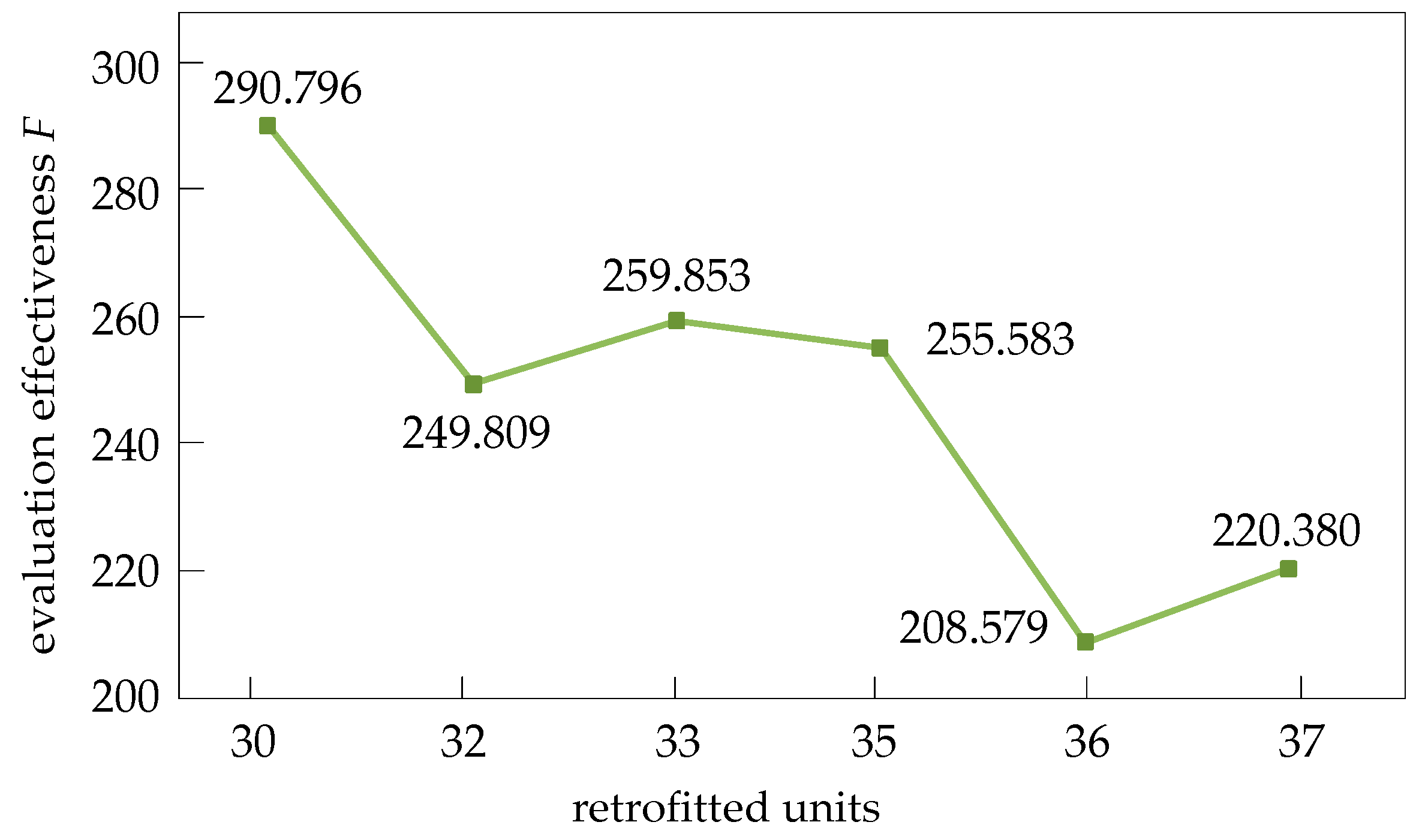
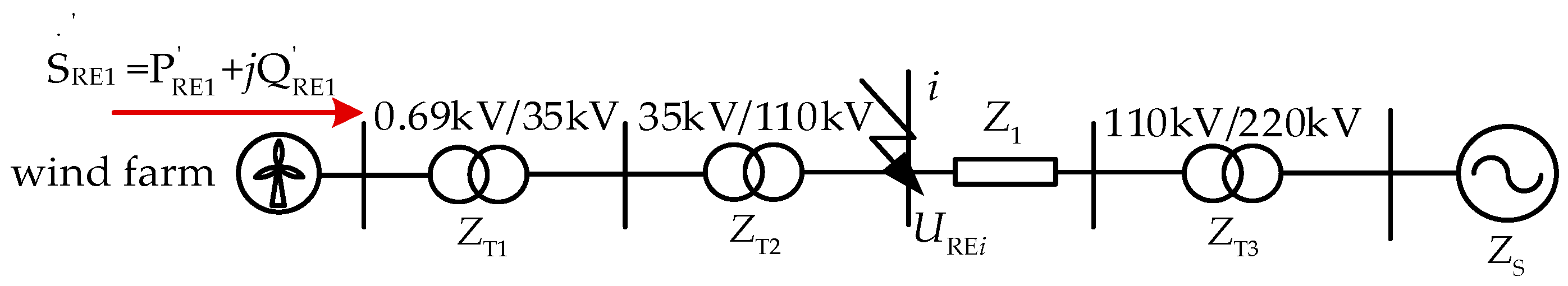Appendix A
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected points (nodes 41, 45, 49) when the thermal power units are shut down at node 32 were calculated, and the specific data are shown in
Table A1 and
Table A2.
Table A1.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 32 is Shut Down.
Table A1.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 32 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7005 | 1.6675 | 1.6240 |
| 2.50 | 2.70 | 2.90 | 1.6682 | 1.6347 | 1.5926 |
| 2.55 | 2.75 | 2.95 | 1.6370 | 1.6032 | 1.5624 |
| 2.60 | 2.80 | 3.00 | 1.6068 | 1.5727 | 1.5332 |
Table A2.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 32 is Shut Down.
Table A2.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 32 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2519 | 2.1639 | 2.0924 |
| 2.50 | 2.70 | 2.90 | 2.2083 | 2.1210 | 2.0517 |
| 2.55 | 2.75 | 2.95 | 2.1664 | 2.0796 | 2.0124 |
| 2.60 | 2.80 | 3.00 | 2.1258 | 2.0396 | 1.9745 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected point (nodes 41, 45, 49) when the thermal power unit at node 32 is in synchronous condenser operation were calculated, and the specific data are shown in
Table A3 and
Table A4.
Table A3.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 32.
Table A3.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 32.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7128 | 1.6823 | 1.6335 |
| 2.50 | 2.70 | 2.90 | 1.6802 | 1.6493 | 1.6019 |
| 2.55 | 2.75 | 2.95 | 1.6488 | 1.6175 | 1.5715 |
| 2.60 | 2.80 | 3.00 | 1.6185 | 1.5868 | 1.5422 |
Table A4.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 32.
Table A4.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 32.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2913 | 2.2008 | 2.1199 |
| 2.50 | 2.70 | 2.90 | 2.2470 | 2.1573 | 2.0786 |
| 2.55 | 2.75 | 2.95 | 2.2043 | 2.1152 | 2.0389 |
| 2.60 | 2.80 | 3.00 | 2.1631 | 2.0747 | 2.0005 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected points (nodes 41, 45, 49) when the thermal power units are shut down at node 33 were calculated, and the specific data are shown in
Table A5 and
Table A6.
Table A5.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 33 is Shut Down.
Table A5.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 33 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7067 | 1.6553 | 1.6188 |
| 2.50 | 2.70 | 2.90 | 1.6744 | 1.6230 | 1.5876 |
| 2.55 | 2.75 | 2.95 | 1.6432 | 1.5919 | 1.5576 |
| 2.60 | 2.80 | 3.00 | 1.6131 | 1.5618 | 1.5286 |
Table A6.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 33 is Shut Down.
Table A6.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 33 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2740 | 2.1035 | 2.0715 |
| 2.50 | 2.70 | 2.90 | 2.2304 | 2.0622 | 2.0315 |
| 2.55 | 2.75 | 2.95 | 2.1884 | 2.0223 | 1.9928 |
| 2.60 | 2.80 | 3.00 | 2.1478 | 1.9839 | 1.9556 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected point (nodes 41, 45, 49) when the thermal power unit at node 33 is in synchronous condenser operation were calculated, and the specific data are shown in
Table A7 and
Table A8.
Table A7.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 33.
Table A7.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 33.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7135 | 1.6983 | 1.6492 |
| 2.50 | 2.70 | 2.90 | 1.6811 | 1.6653 | 1.6277 |
| 2.55 | 2.75 | 2.95 | 1.6498 | 1.6334 | 1.5872 |
| 2.60 | 2.80 | 3.00 | 1.6196 | 1.6027 | 1.5579 |
Table A8.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 33.
Table A8.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 33.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2931 | 2.2306 | 2.1533 |
| 2.50 | 2.70 | 2.90 | 2.2491 | 2.1869 | 2.1121 |
| 2.55 | 2.75 | 2.95 | 2.2068 | 2.1447 | 2.0724 |
| 2.60 | 2.80 | 3.00 | 2.1659 | 2.1041 | 2.0341 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected points (nodes 41, 45, 49) when the thermal power units are shut down at node 35 were calculated, and the specific data are shown in
Table A9 and
Table A10.
Table A9.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 35 is Shut Down.
Table A9.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 35 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.6966 | 1.6541 | 1.6112 |
| 2.50 | 2.70 | 2.90 | 1.6643 | 1.6219 | 1.5870 |
| 2.55 | 2.75 | 2.95 | 1.6332 | 1.5908 | 1.5570 |
| 2.60 | 2.80 | 3.00 | 1.6031 | 1.5608 | 1.5281 |
Table A10.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 35 is Shut Down.
Table A10.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 35 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2739 | 2.1016 | 2.0702 |
| 2.50 | 2.70 | 2.90 | 2.2304 | 2.0603 | 2.0303 |
| 2.55 | 2.75 | 2.95 | 2.1884 | 2.0206 | 1.9917 |
| 2.60 | 2.80 | 3.00 | 2.1478 | 1.9822 | 1.9545 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected point (nodes 41, 45, 49) when the thermal power unit at node 35 is in synchronous condenser operation were calculated, and the specific data are shown in
Table A11 and
Table A12.
Table A11.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 35.
Table A11.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 35.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7142 | 1.7016 | 1.6321 |
| 2.50 | 2.70 | 2.90 | 1.6818 | 1.6685 | 1.6088 |
| 2.55 | 2.75 | 2.95 | 1.6505 | 1.6366 | 1.5784 |
| 2.60 | 2.80 | 3.00 | 1.6203 | 1.6058 | 1.5491 |
Table A12.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 35.
Table A12.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 35.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2946 | 2.2264 | 2.1362 |
| 2.50 | 2.70 | 2.90 | 2.2507 | 2.1827 | 2.0950 |
| 2.55 | 2.75 | 2.95 | 2.2083 | 2.1405 | 2.0553 |
| 2.60 | 2.80 | 3.00 | 2.1675 | 2.0998 | 2.0169 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected points (nodes 41, 45, 49) when the thermal power units are shut down at node 36 were calculated, and the specific data are shown in
Table A13 and
Table A14.
Table A13.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 36 is Shut Down.
Table A13.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 36 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7094 | 1.6718 | 1.6264 |
| 2.50 | 2.70 | 2.90 | 1.6771 | 1.6394 | 1.5951 |
| 2.55 | 2.75 | 2.95 | 1.6459 | 1.6081 | 1.5650 |
| 2.60 | 2.80 | 3.00 | 1.6159 | 1.5779 | 1.5360 |
Table A14.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 36 is Shut Down.
Table A14.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 36 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2819 | 2.1565 | 2.0964 |
| 2.50 | 2.70 | 2.90 | 2.2383 | 2.1144 | 2.0560 |
| 2.55 | 2.75 | 2.95 | 2.1963 | 2.0738 | 2.0171 |
| 2.60 | 2.80 | 3.00 | 2.1556 | 2.0346 | 1.9795 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected point (nodes 41, 45, 49) when the thermal power unit at node 36 is in synchronous condenser operation were calculated, and the specific data are shown in
Table A15 and
Table A16.
Table A15.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 36.
Table A15.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 36.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7151 | 1.7058 | 1.6423 |
| 2.50 | 2.70 | 2.90 | 1.6826 | 1.6727 | 1.6107 |
| 2.55 | 2.75 | 2.95 | 1.6514 | 1.6408 | 1.5803 |
| 2.60 | 2.80 | 3.00 | 1.6212 | 1.6101 | 1.5510 |
Table A16.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 36.
Table A16.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 36.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2968 | 2.2448 | 2.1407 |
| 2.50 | 2.70 | 2.90 | 2.2529 | 2.2010 | 2.0995 |
| 2.55 | 2.75 | 2.95 | 2.2106 | 2.1588 | 2.0598 |
| 2.60 | 2.80 | 3.00 | 2.1697 | 2.1181 | 2.0215 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected points (nodes 41, 45, 49) when the thermal power units are shut down at node 37 were calculated, and the specific data are shown in
Table A17 and
Table A18.
Table A17.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 37 is Shut Down.
Table A17.
Short-Circuit Ratio at the Machine End of the New Energy Field Station when the Thermal Unit at Node 37 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7071 | 1.6786 | 1.6283 |
| 2.50 | 2.70 | 2.90 | 1.6748 | 1.6460 | 1.5970 |
| 2.55 | 2.75 | 2.95 | 1.6437 | 1.6146 | 1.5668 |
| 2.60 | 2.80 | 3.00 | 1.6136 | 1.5842 | 1.5377 |
Table A18.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 37 is Shut Down.
Table A18.
Short-Circuit Ratio at the Grid-connected Points of the New Energy Field Station when the Thermal Unit at Node 37 is Shut Down.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.2616 | 2.1902 | 2.1006 |
| 2.50 | 2.70 | 2.90 | 2.2183 | 2.1474 | 2.0601 |
| 2.55 | 2.75 | 2.95 | 2.1766 | 2.1061 | 2.0210 |
| 2.60 | 2.80 | 3.00 | 2.1364 | 2.0662 | 1.9833 |
The short-circuit ratio at the machine end of the new energy field station (nodes 43, 47, 51) and the short-circuit ratio at the grid-connected point (nodes 41, 45, 49) when the thermal power unit at node 37 is in synchronous condenser operation were calculated, and the specific data are shown in
Table A19 and
Table A20.
Table A19.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 37.
Table A19.
Short-Circuit Ratio at the Machine End of the New Energy Field Station during Synchronous Condenser Operation of Thermal Power Units at Node 37.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 1.7275 | 1.6890 | 1.6430 |
| 2.50 | 2.70 | 2.90 | 1.6948 | 1.6562 | 1.6114 |
| 2.55 | 2.75 | 2.95 | 1.6634 | 1.6246 | 1.5810 |
| 2.60 | 2.80 | 3.00 | 1.6330 | 1.5941 | 1.5517 |
Table A20.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 37.
Table A20.
Short-Circuit Ratio at the Grid-connected Points of New Energy Field Stations during Synchronous Condenser Operation of Thermal Power Units at Node 37.
| | | | | |
|---|
| 2.45 | 2.65 | 2.85 | 2.3264 | 2.2136 | 2.1424 |
| 2.50 | 2.70 | 2.90 | 2.2820 | 2.1704 | 2.1012 |
| 2.55 | 2.75 | 2.95 | 2.2391 | 2.1287 | 2.0614 |
| 2.60 | 2.80 | 3.00 | 2.1978 | 2.0885 | 2.0230 |