Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion
Abstract
1. Introduction
2. Signal Model
3. DOA Estimation Algorithm via DFNeT
3.1. Data Management and Labeling
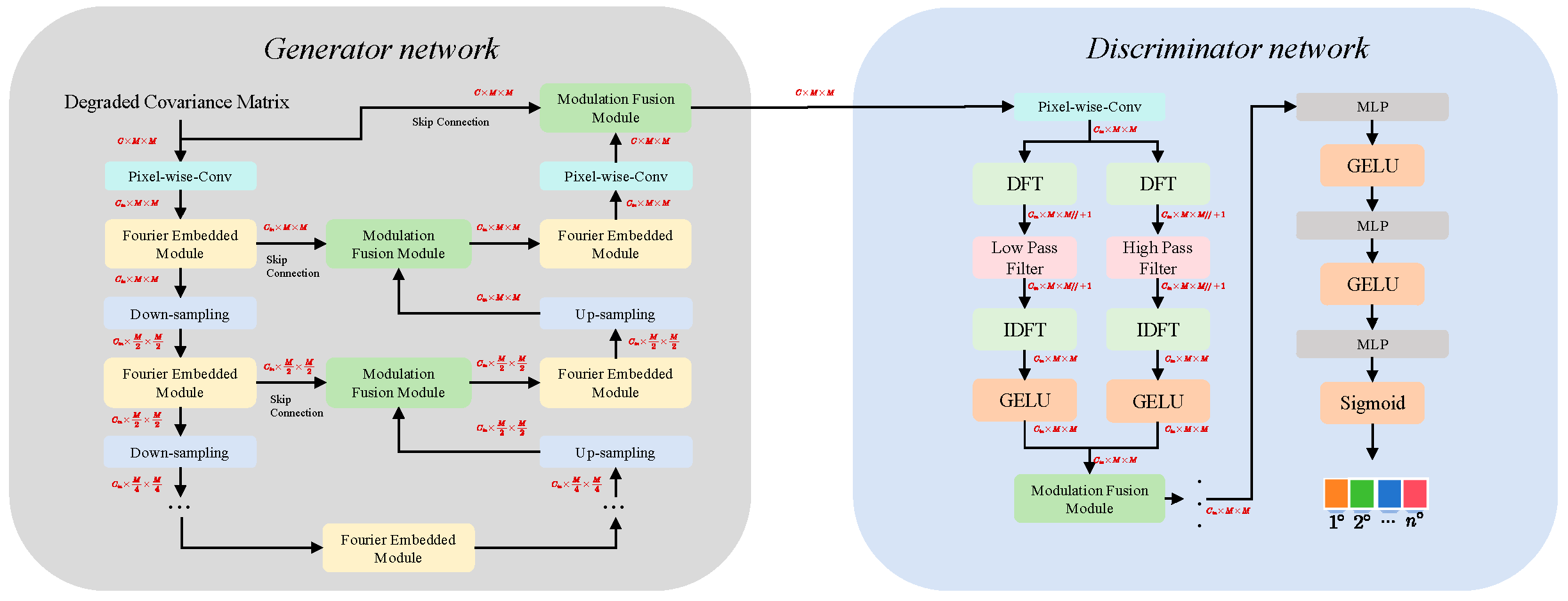
3.2. Neural Network Structure
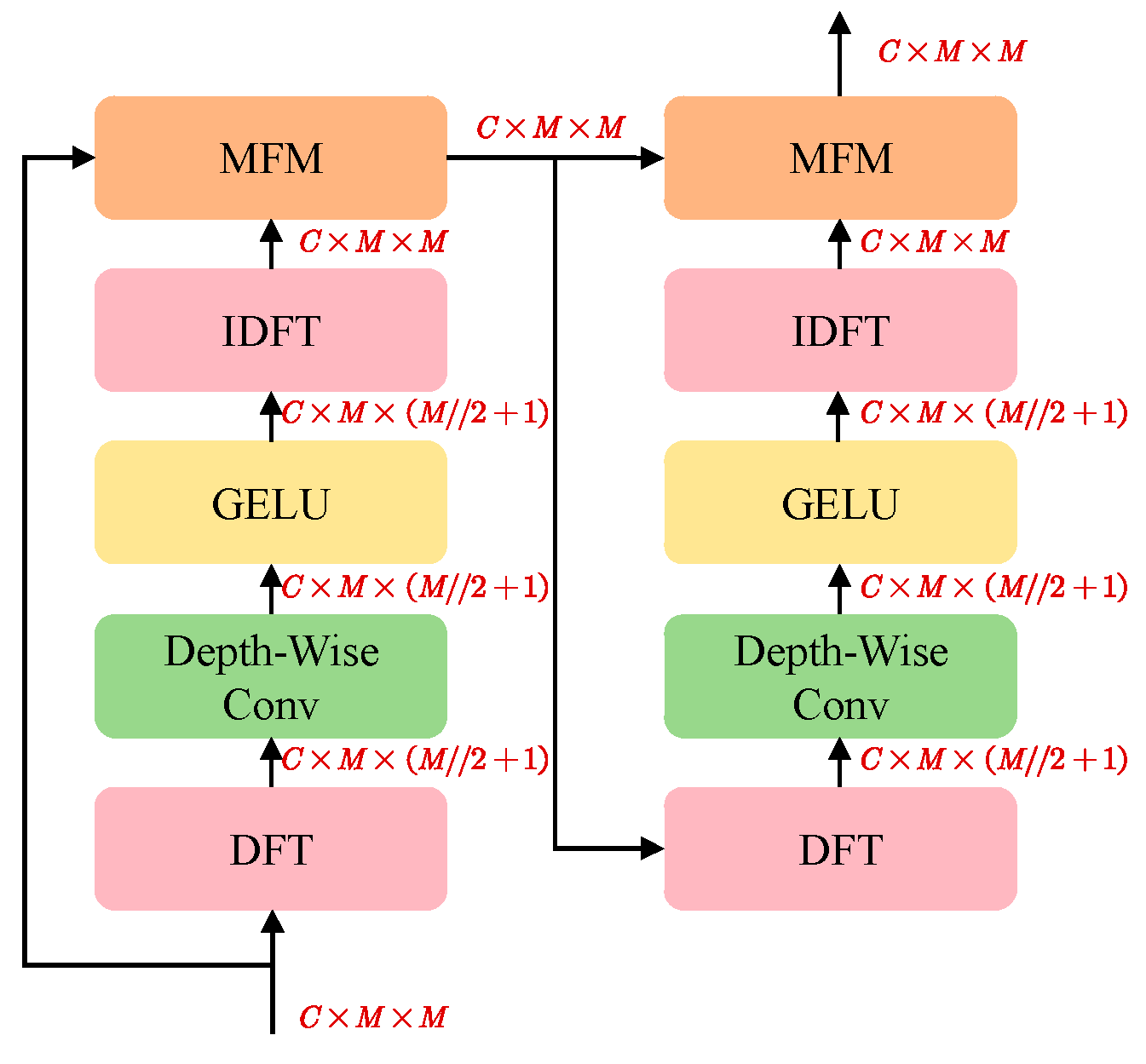
3.2.1. Generator Network Structure
3.2.2. Discriminator Network Structure
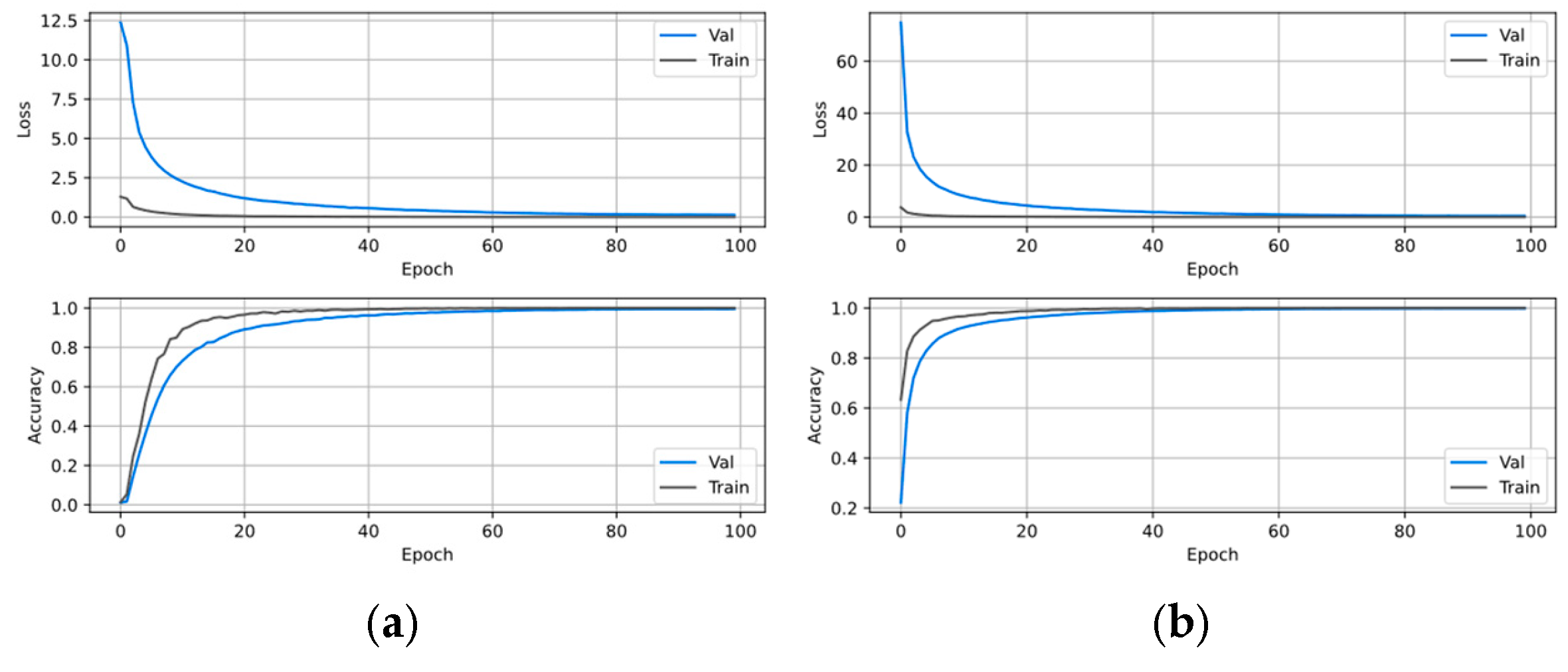
3.3. Network Training
3.3.1. Generator Network Training
3.3.2. Discriminator Network Training
4. Simulation Results
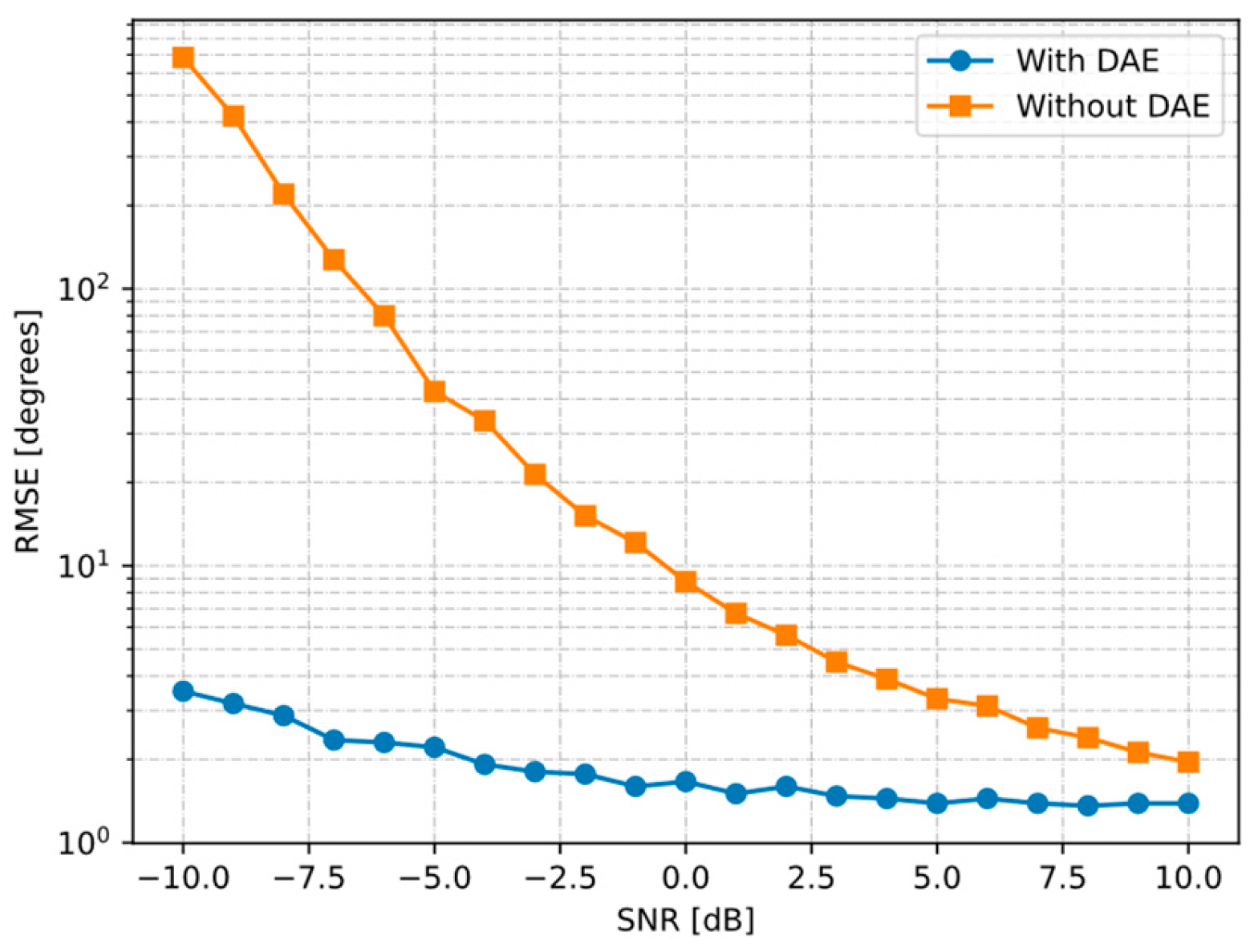
4.1. Performance of DAE
4.2. Comparison to Other Methods
4.3. Operational Performance with Two Simultaneous Emitters
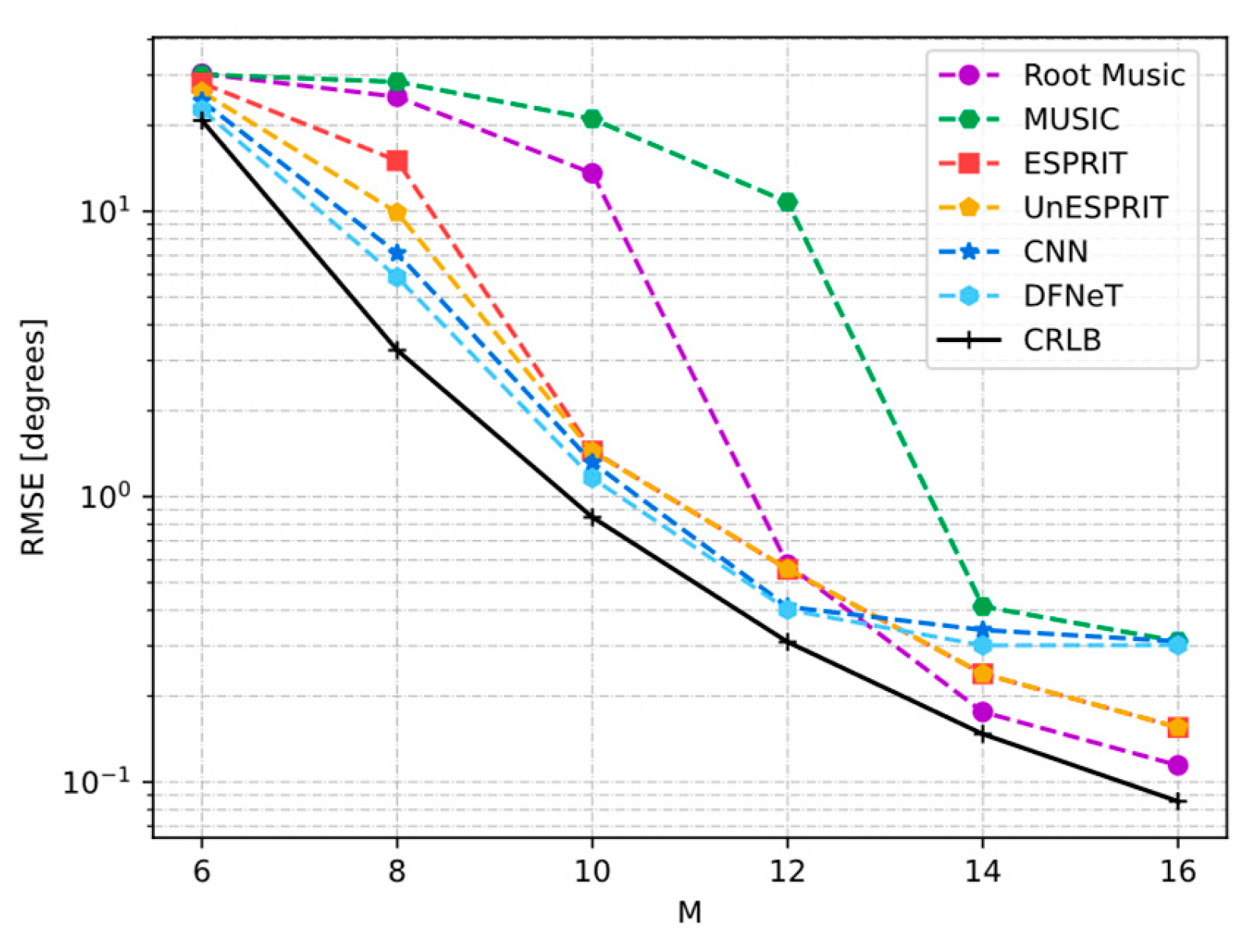
4.3.1. Cross-Method Performance Benchmarking
4.3.2. RMSE Under Different SNR with K = 2
4.3.3. Parametric RMSE Dependence on Snapshot Quantity with K =2
4.3.4. Dual Stochastic Angular RMSE Performance
4.4. Results with Three Sources
4.4.1. Comparison of Different Methods
4.4.2. RMSE Under Different SNR with K = 3
4.4.3. Parametric RMSE Dependence on Snapshot Quantity with K = 3
4.4.4. Triple Stochastic Angular RMSE Performance
4.4.5. RMSE Under Different Number of Array Elements
4.5. Number of Sources Unknown
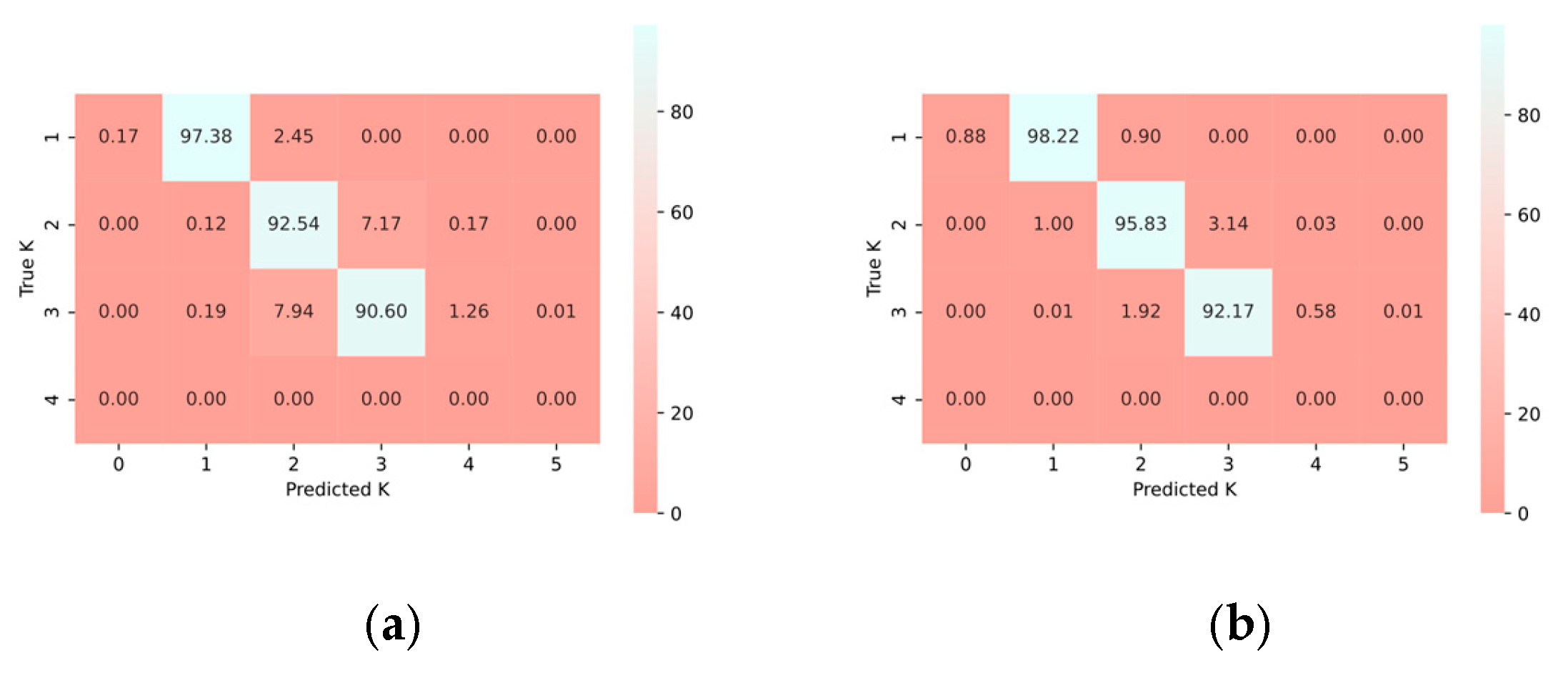
4.5.1. Estimate the Number of Signal Sources
4.5.2. DOA Estimation with Mix Number of Source
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Jaffer, A.G. Maximum likelihood direction finding of stochastic sources: A separable solution. In ICASSP-88. International Conference on Acoustics, Speech, and Signal Processing; IEEE Computer Society: New York, NY, USA, 1988; Volume 5, pp. 2893–2896. [Google Scholar]
- Song, Y.; Zheng, G. Height Measurement for Meter Wave Polarimetric MIMO Radar with Electrically Long Dipole under Complex Terrain. Remote Sens. 2023, 15, 1265. [Google Scholar] [CrossRef]
- Zheng, G.; Tang, J.; Yang, X. ESPRIT and Unitary ESPRIT Algorithms for Coexistence of Circular and Noncircular Signals in Bistatic MIMO Radar. IEEE Access 2016, 4, 7232–7240. [Google Scholar] [CrossRef]
- Huang, H.; Yang, J.; Huang, H.; Song, Y.; Gui, G. Deep Learning for Super-Resolution Channel Estimation and DOA Estimation Based Massive MIMO System. IEEE Trans. Veh. Technol. 2018, 67, 8549–8560. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, Y.; Gong, Y.; Kumar, N.; Wang, L.; Rodrigues, J.J.P.C. Joint multipath channel estimation and array channel inconsistency calibration for massive MIMO systems. IEEE Internet Things J. 2024, 11, 37407–37420. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, P.; Li, X. Channel Parameter Estimation of mmWave MIMO System in Urban Traffic Scene: A Training Channel based Method. IEEE Transations Intell. Transp. Syst. 2022, 25, 754–762. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, C.; Song, Y. Height Measurement for Meter Wave MIMO Radar based on Matrix Pencil Under Complex Terrain. IEEE Trans. Veh. Technol. 2023, 72, 11844–11854. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F.; He, J.; Truong, T.-K. EMVS-MIMO Radar With Sparse Rx Geometry: Tensor Modeling and 2-D Direction Finding. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8062–8075. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, Z.; Wen, F.; He, J.; Truong, T.K. Coarray tensor train decomposition for bistatic MIMO radar with uniform planar array. IEEE Trans. Antennas Propag. 2025. [Google Scholar] [CrossRef]
- Kuang, M.; Wang, Y.; Wang, L.; Xie, J.; Han, C. Localisation and classification of mixed far-field and near-field sources with sparse reconstruction. IET Signal Process. 2022, 16, 426–437. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, Y.; Dai, T.; Wang, L. DOA estimation based on smoothed sparse reconstruction with time-modulated linear arrays. Signal Process. 2024, 214, 109229. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low Complexity MIMO-FBMC Sparse Channel Parameter Estimation for Industrial Big Data Communications. IEEE Trans. Ind. Inform. 2021, 17, 3422–3430. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Andrew, Z. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Cao, W.; Ren, W.; Zhang, Z.; Huang, W.; Zou, J.; Liu, G. Direction of Arrival Estimation Based on DNN and CNN. Electronics 2024, 13, 3866. [Google Scholar] [CrossRef]
- Li, N.; Zhang, X.; Lv, F.; Zong, B.; Feng, W. A Bayesian Deep Unfolded Network for the Off-Grid Direction-of-Arrival Estimation via a Minimum Hole Array. Electronics 2024, 13, 2139. [Google Scholar] [CrossRef]
- Dong, H.; Suo, J.; Zhu, Z.; Li, S. Improved Underwater Single-Vector Acoustic DOA Estimation via Vector Convolution Preprocessing. Electronics 2024, 13, 1796. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q. MD-DOA: A Model-Based Deep Learning DOA Estimation Architecture. IEEE Sens. J. 2024, 24, 20240–20253. [Google Scholar] [CrossRef]
- Hinton, G.E. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Burger, H.C.; Schuler, C.J.; Harmeling, S. Image denoising: Can plain neural networks compete with BM3D? In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2392–2399. [Google Scholar]
- Papageorgiou, G.K.; Sellathurai, M. Direction-of-Arrival Estimation in the Low-SNR Regime via a Denoising Autoencoder. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, J.; Zhou, Z. Two-Dimensional Coherent Polarization–Direction-of-Arrival Estimation Based on Sequence-Embedding Fusion Transformer. Remote Sens. 2024, 16, 21. [Google Scholar] [CrossRef]
- Cao, Y.; Zhou, T.; Zhang, Q. Gridless DOA Estimation Method for Arbitrary Array Geometries Based on Complex-Valued Deep Neural Networks. Remote Sens. 2024, 16, 3752. [Google Scholar] [CrossRef]
- Papageorgiou, G.K.; Sellathurai, M.; Eldar, Y.C. Deep Networks for Direction-of-Arrival Estimation in Low SNR. IEEE Trans. Signal Process. 2021, 69, 3714–3729. [Google Scholar] [CrossRef]
- Shmuel, D.H.; Merkofer, J.P.; Revach, G.; Sloun, R.J.G.V.; Shlezinger, N. SubspaceNet: Deep Learning-Aided Subspace Methods for DoA Estimation. IEEE Trans. Veh. Technol. 2024, 74, 4962–4976. [Google Scholar] [CrossRef]
- Adavanne, S.; Politis, A.; Virtanen, T. Direction of Arrival Estimation for Multiple Sound Sources Using Convolutional Recurrent Neural Network. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 1462–1466. [Google Scholar]
- Wen, F.; Shi, J.; Gui, G.; Yuen, C.; Sari, H.; Adachi, F. Joint DOD and DOA Estimation for NLOS Target using IRS-aided Bistatic MIMO Radar. IEEE Trans. Veh. Technol. 2024, 73, 15798–15802. [Google Scholar] [CrossRef]
- Wu, L.-L.; Huang, Z.-T. Coherent SVR Learning for Wideband Direction-of-Arrival Estimation. IEEE Signal Process. Lett. 2019, 26, 642–646. [Google Scholar] [CrossRef]
- Zheng, R.; Sun, S.; Liu, H.; Chen, H.; Li, J. Interpretable and Efficient Beamforming-Based Deep Learning for Single-Snapshot DOA Estimation. IEEE Sens. J. 2024, 24, 22096–22105. [Google Scholar] [CrossRef]
- Nie, W.; Zhang, X.; Xu, J.; Guo, L.; Yan, Y. Adaptive Direction-of-Arrival Estimation Using Deep Neural Network in Marine Acoustic Environment. IEEE Sens. J. 2023, 23, 15093–15105. [Google Scholar] [CrossRef]
- Cho, S.; Jeong, T.; Kwak, S.; Lee, S. Complex-Valued Neural Network for Estimating the Number of Sources in Radar Systems. IEEE Sens. J. 2025, 25, 1746–1755. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Z.; Zhang, W.; He, Z. End-to-End Regression Neural Network for Coherent DOA Estimation with Dual-Branch Outputs. IEEE Sens. J. 2024, 24, 4047–4056. [Google Scholar] [CrossRef]
- Gao, N.; Jiang, X.; Zhang, X.; Deng, Y. Efficient Frequency-Domain Image Deraining with Contrastive Regularization. In European Conference on Computer Vision; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Frigo, M.; Johnson, S.G. FFTW: An adaptive software architecture for the FFT. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 15 May 1998; Volume 3. [Google Scholar]
- Gondara, L. Medical Image Denoising Using Convolutional Denoising Autoencoders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 241–246. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, S.; Li, H. Depth information assisted collaborative mutual promotion network for single image dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024. [Google Scholar]
- Zhou, M.; Huang, J.; Guo, C.L.; Li, C. An efficient global modeling paradigm for image restoration. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Rao, B.D.; Hari, K.V.S. Performance analysis of Root-Music. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Li, L. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antennas Wirel. Propag. Lett. 2004, 3, 129–132. [Google Scholar]
- Haardt, M.; Nossek, J.A. Unitary ESPRIT: How to obtain increased estimation accuracy with a reduced computational burden. IEEE Trans. Signal Process. 2002, 43, 1232–1242. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Jansson, M.; Goransson, B.; Ottersten, B. A subspace method for direction of arrival estimation of uncorrelated emitter signals. IEEE Trans. Signal Process. 1999, 47, 945–956. [Google Scholar] [CrossRef]


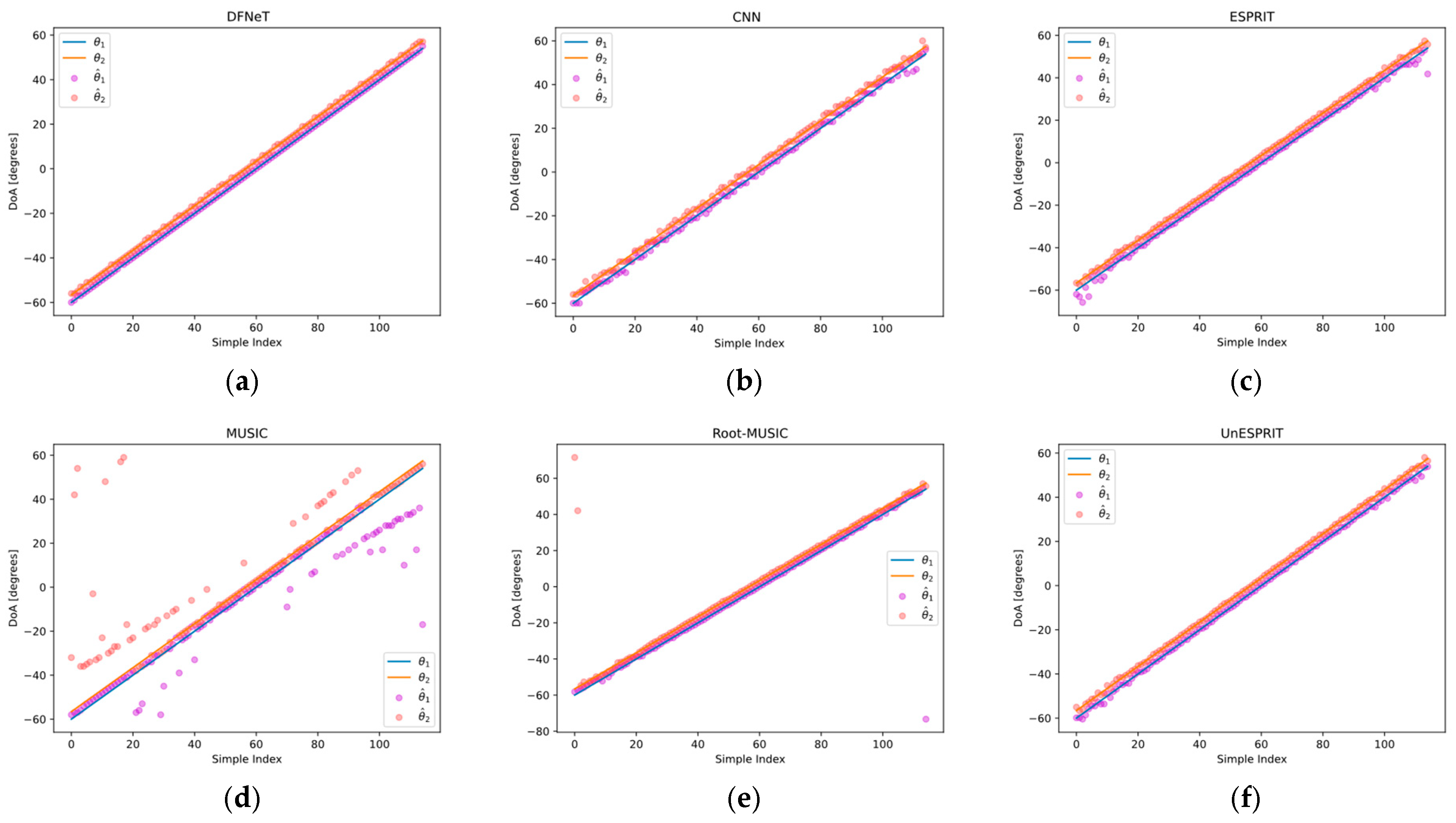
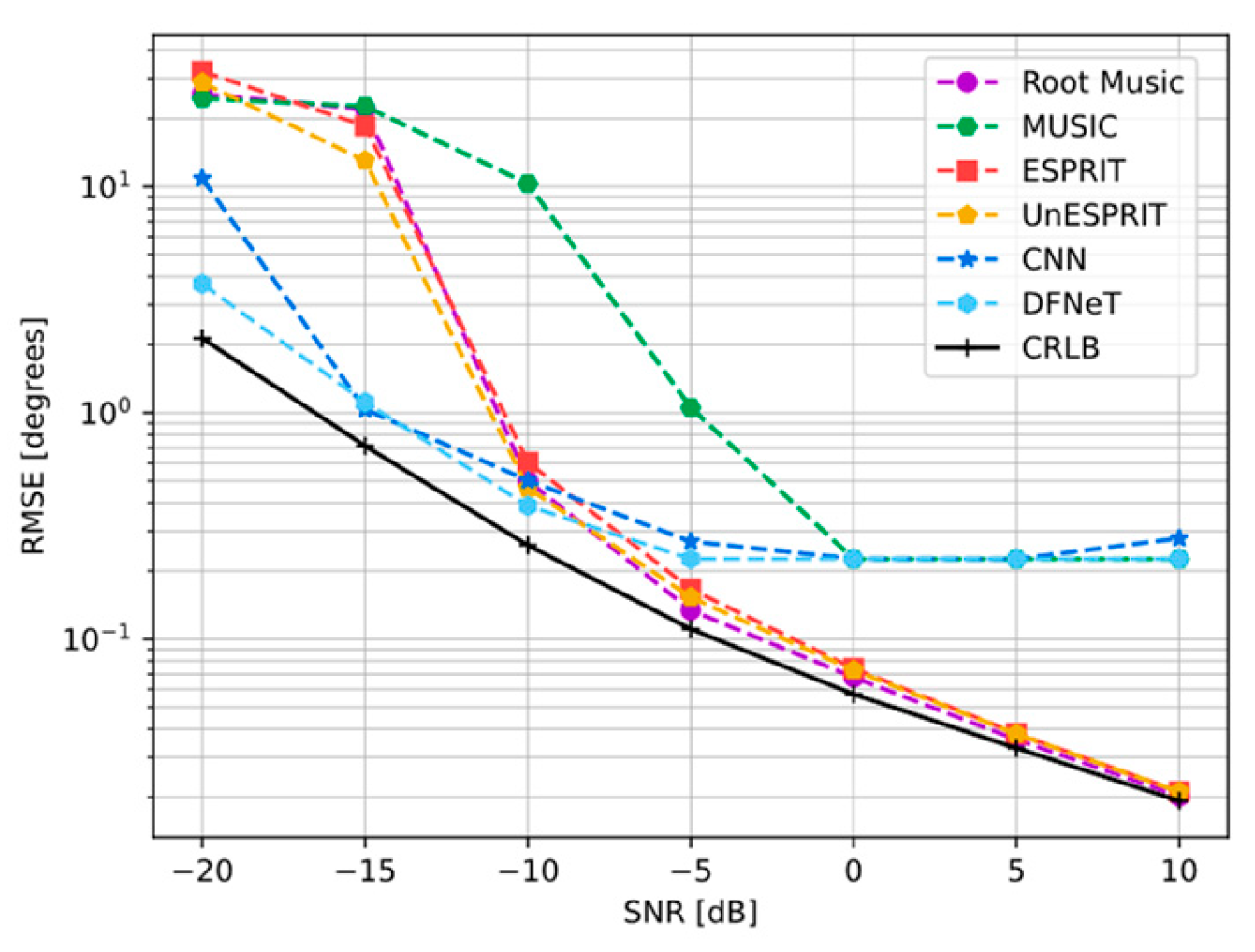
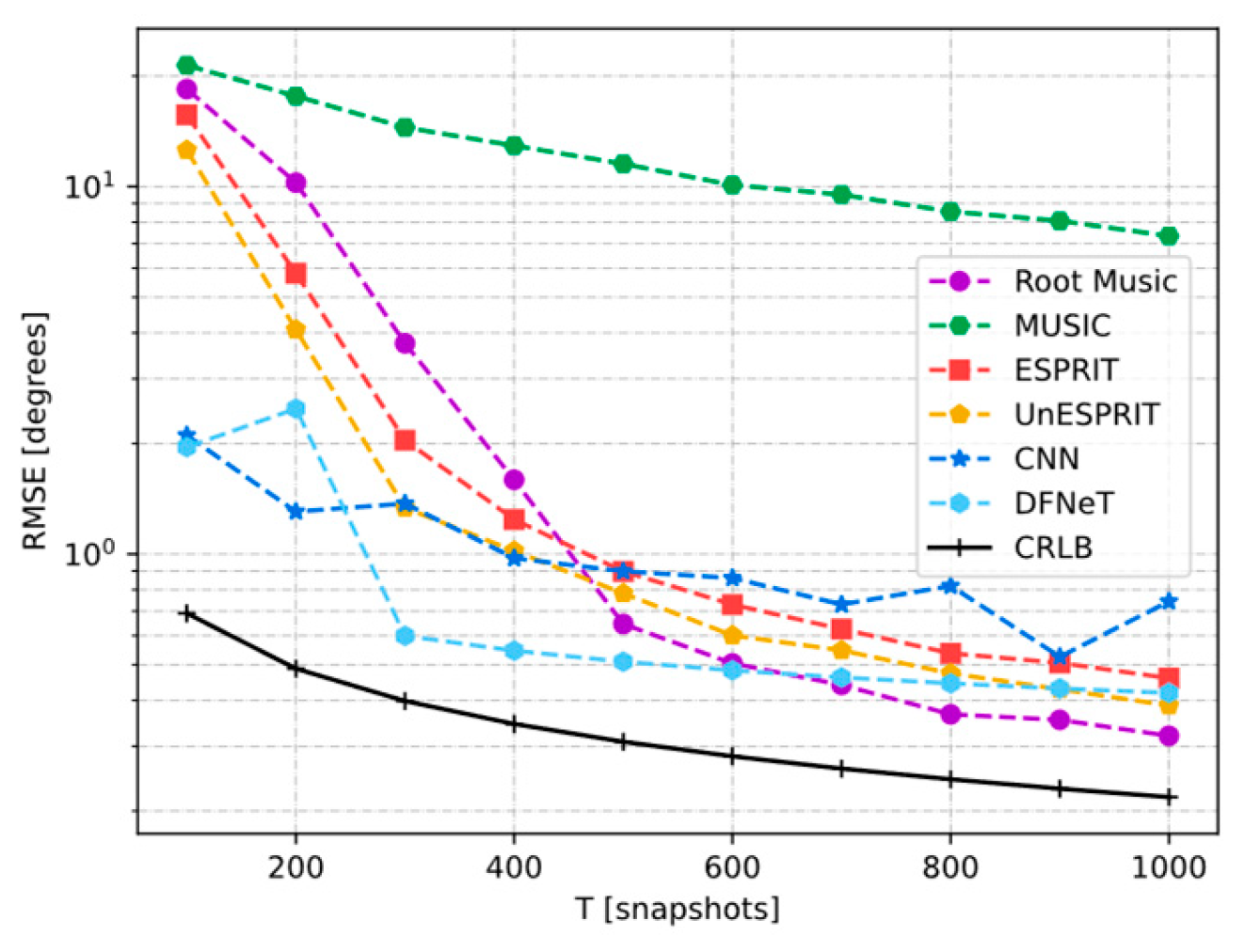

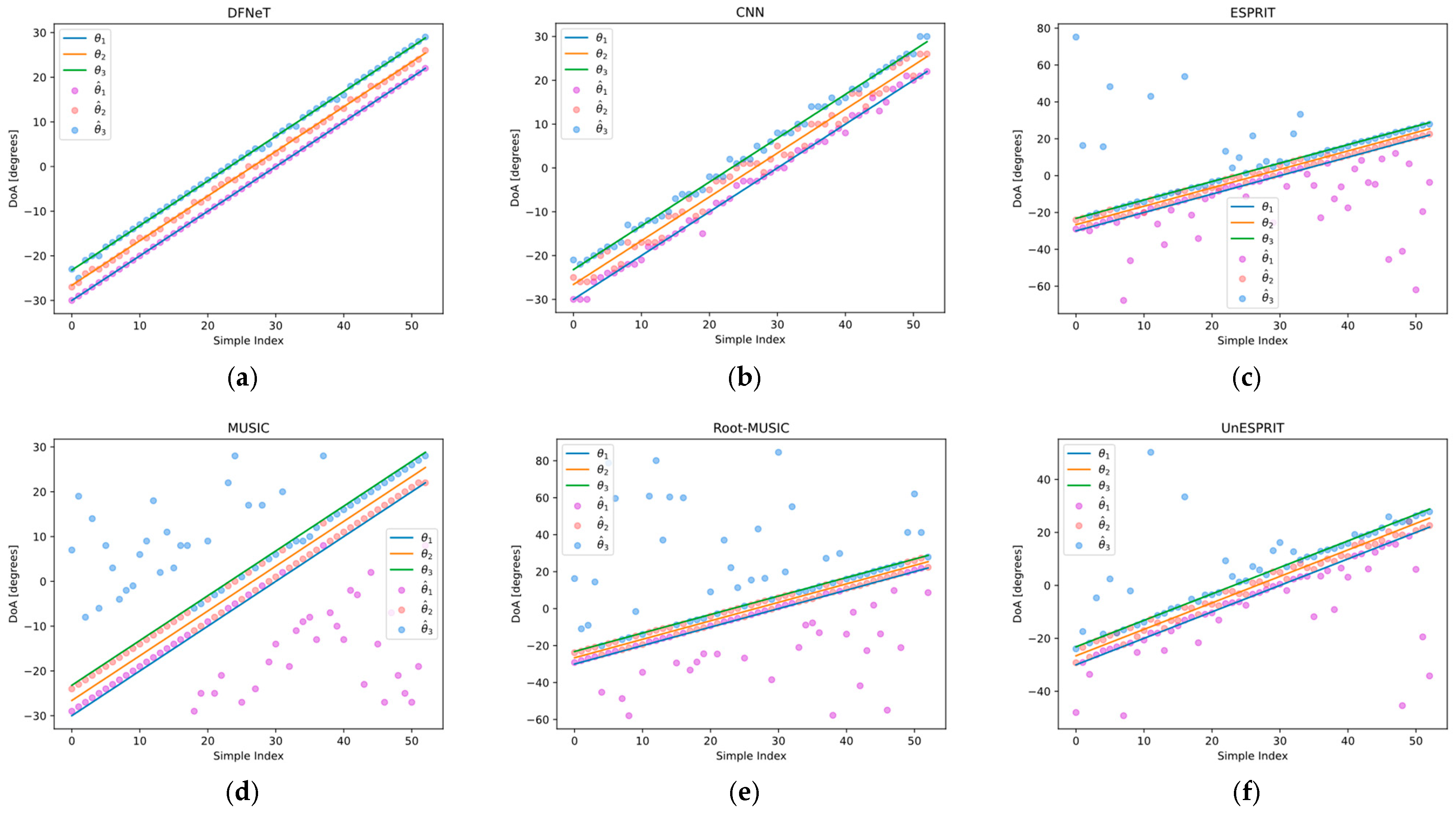




| Methods | Absolute Error | RMSE | Runtime |
|---|---|---|---|
| MUSIC | 71.0 | 18.156996495542 | 5.2713 × 104 s |
| Root-MUSIC | 127.33102461862 | 13.559954773844 | 4.4995 × 104 s |
| ESPRIT | 12.205500438346 | 1.3089848606459 | 1.1502 × 104 s |
| UnESPRIT | 2.6026574864040 | 0.6014306026930 | 3.6746 × 104 s |
| CNN in [27] | 4.0 | 1.1791669867362 | 2.2422 × 104 s |
| DFNeT | 0.4 | 0.0304347826086 | 2.6461 × 104 s |
| Methods | Absolute Error | RMSE | Runtime |
|---|---|---|---|
| MUSIC | 47.0 | 13.342324012813 | 5.4774 × 104 s |
| Root-MUSIC | 70.95549396180607 | 22.791004616156 | 4.6732 × 104 s |
| ESPRIT | 81.96869387724863 | 17.588607263825 | 1.1574 × 104 s |
| UnESPRIT | 63.42179344323082 | 10.608104099319 | 1.1451 × 104 s |
| CNN in [27] | 4.0 | 1.3754358943153 | 1.1978 × 104 s |
| DFNeT | 2.799999999999997 | 0.0226415094339 | 1.2814 × 104 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Zheng, G.; Song, Y.; Xiao, L.; Qin, C. Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion. Electronics 2025, 14, 2449. https://doi.org/10.3390/electronics14122449
Zheng H, Zheng G, Song Y, Xiao L, Qin C. Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion. Electronics. 2025; 14(12):2449. https://doi.org/10.3390/electronics14122449
Chicago/Turabian StyleZheng, He, Guimei Zheng, Yuwei Song, Liyuan Xiao, and Cong Qin. 2025. "Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion" Electronics 14, no. 12: 2449. https://doi.org/10.3390/electronics14122449
APA StyleZheng, H., Zheng, G., Song, Y., Xiao, L., & Qin, C. (2025). Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion. Electronics, 14(12), 2449. https://doi.org/10.3390/electronics14122449





