Powerful Sample Reduction Techniques for Constructing Effective Point Cloud Object Classification Models
Abstract
1. Introduction
2. Related Work
2.1. Three-Dimensional Point Cloud Classification
2.2. Downsample Methods
3. Methodology
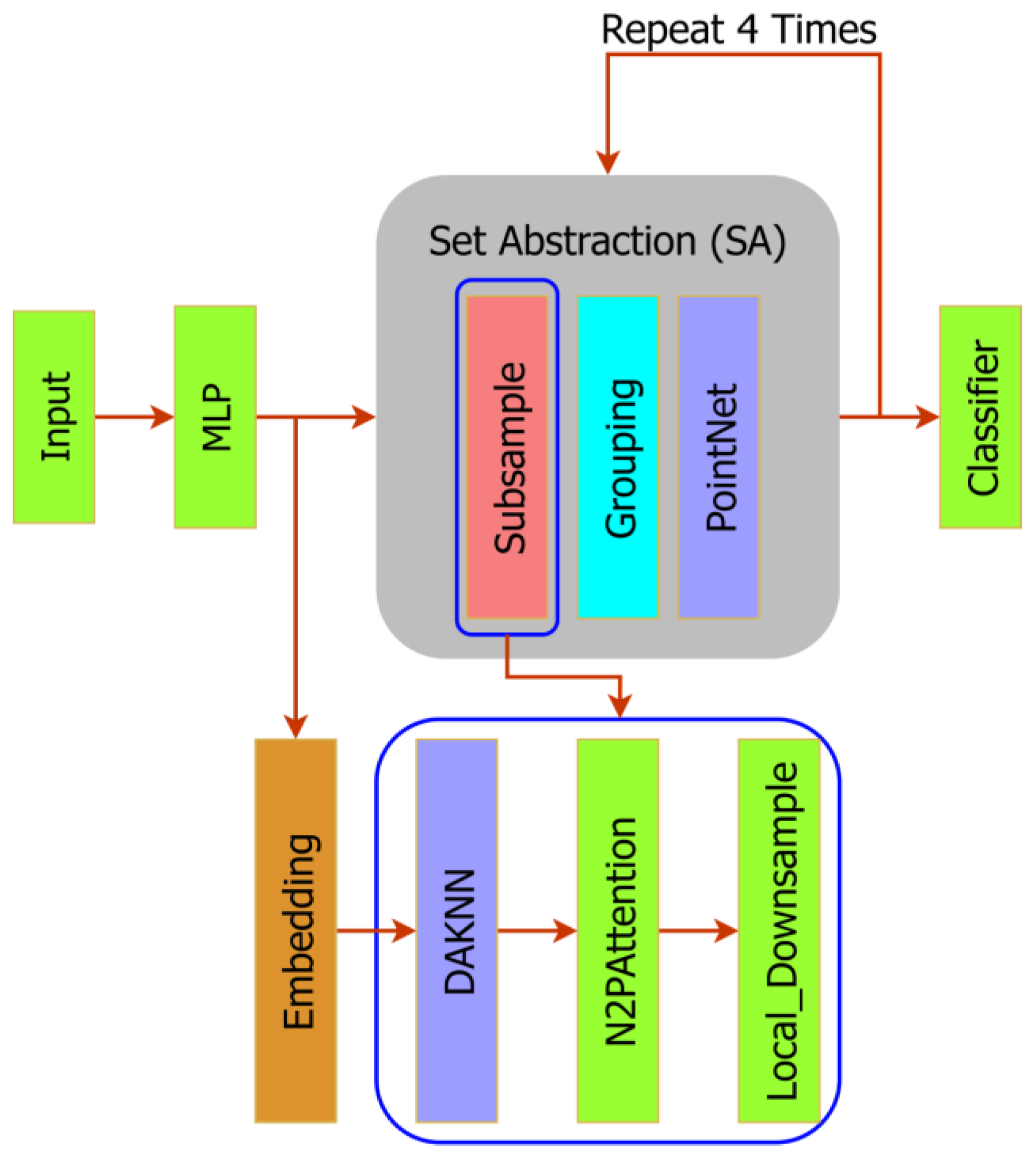
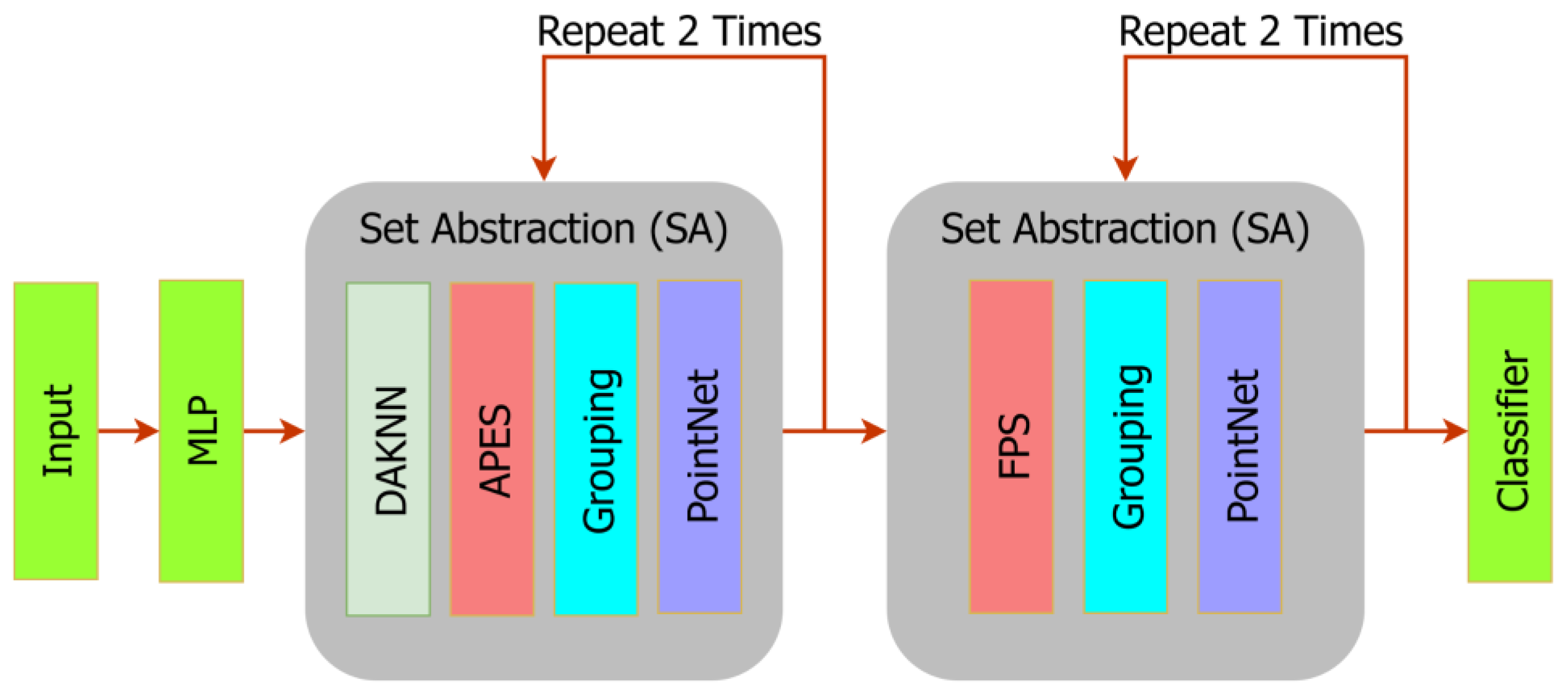
3.1. System Architecture
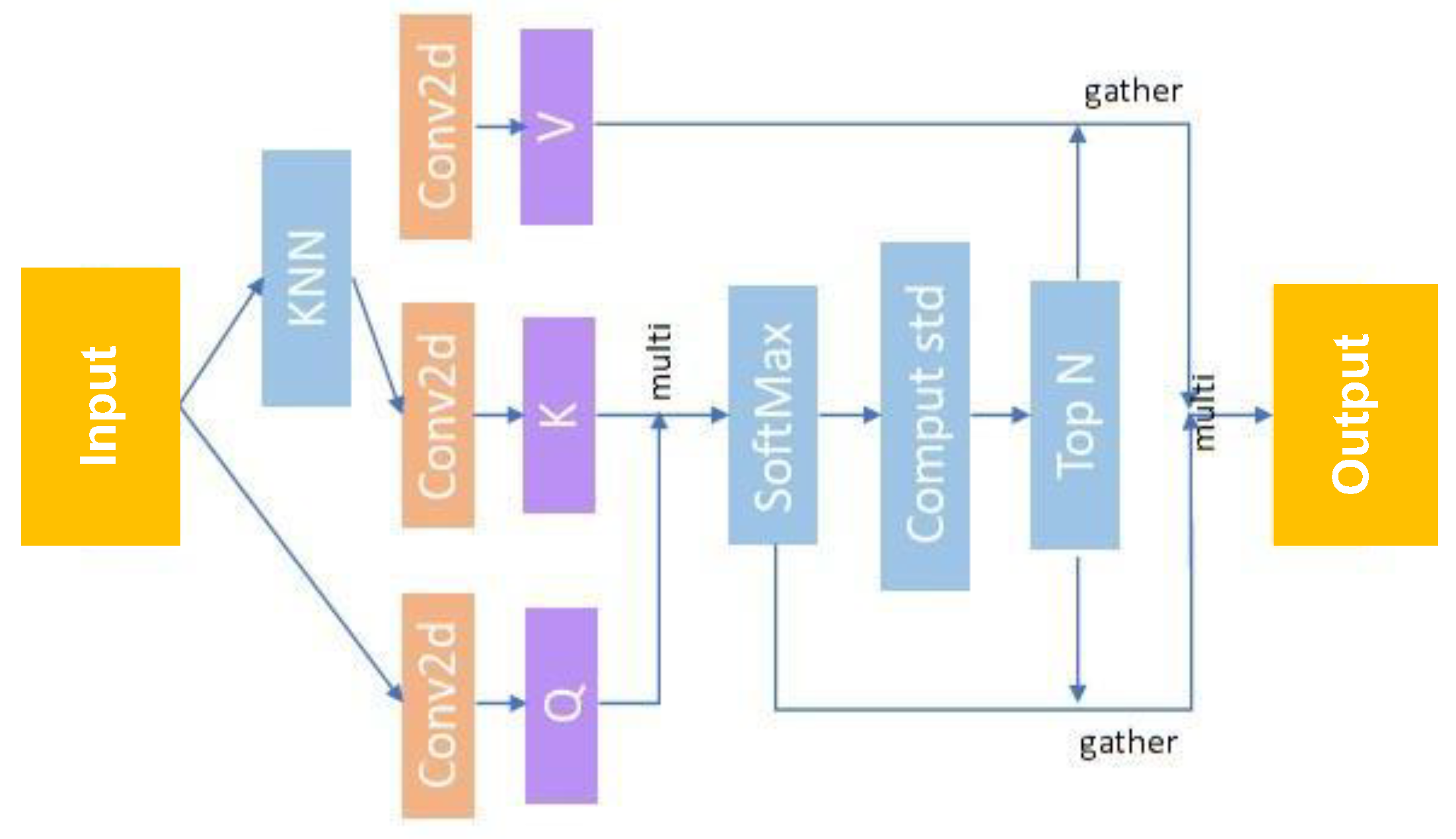
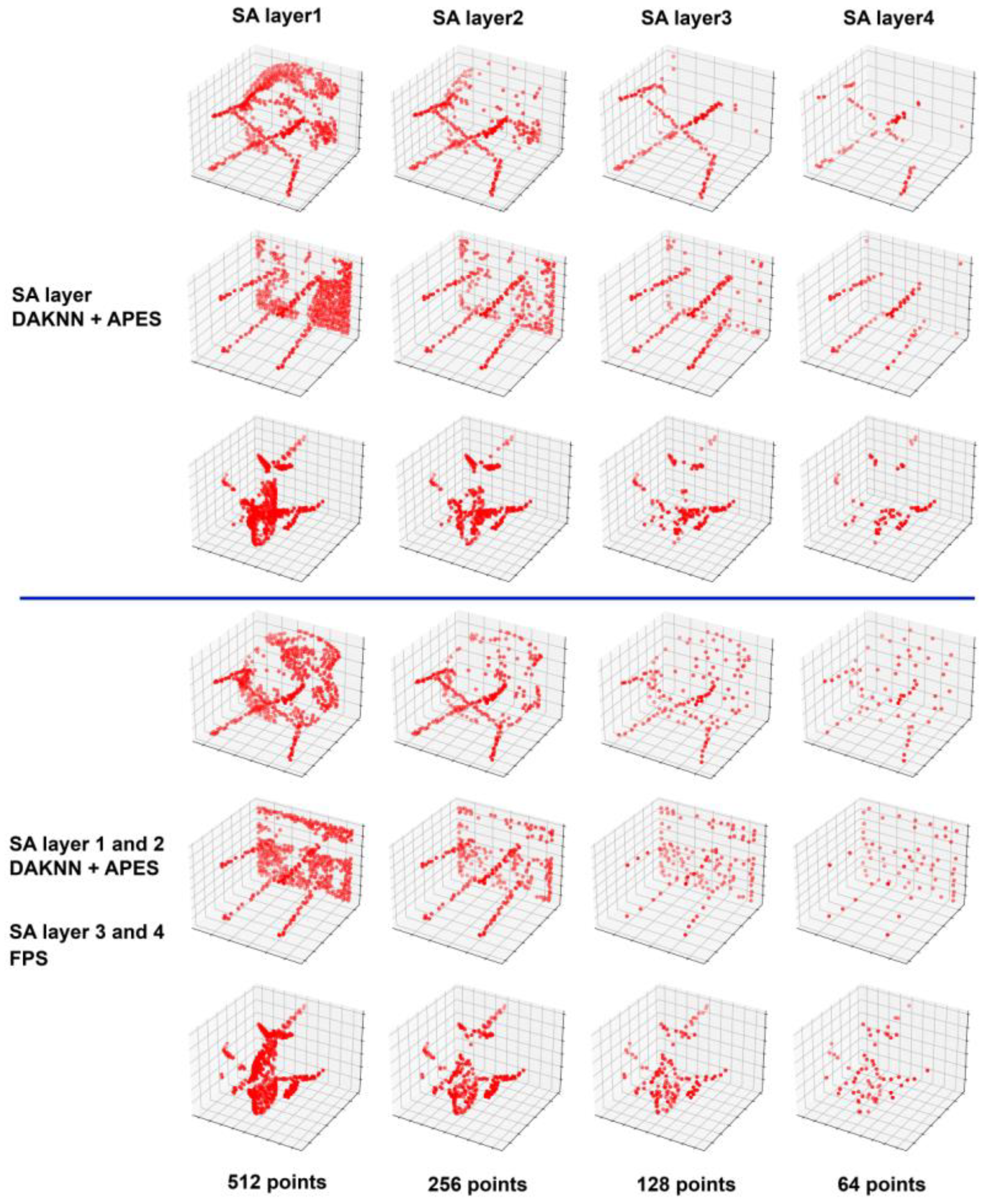
3.2. Attention-Based Point Cloud Edge Sampling
3.2.1. Neighbor to Point (N2P) Attention Layer
3.2.2. Local Downsample Layer
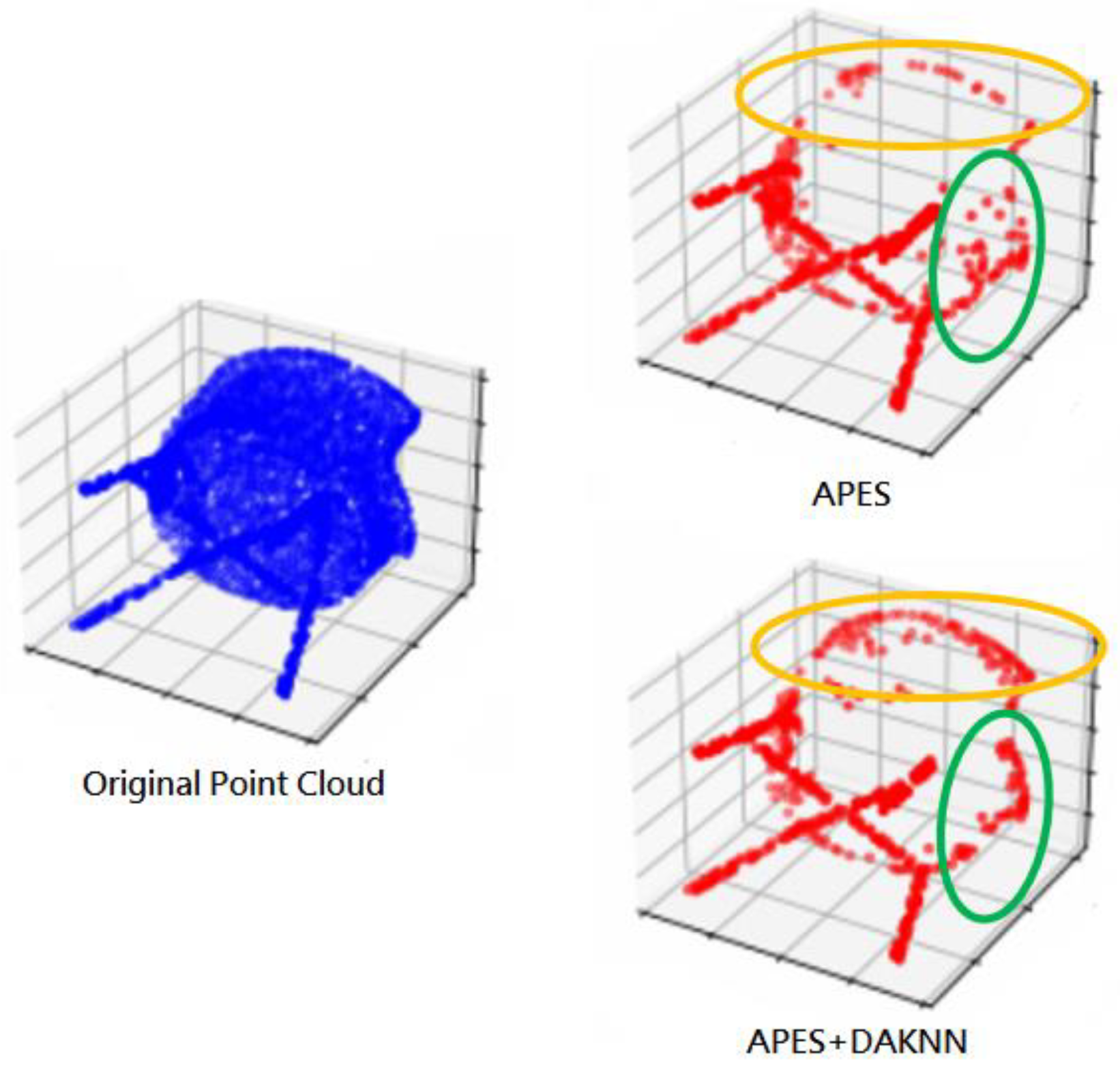
3.3. Density-Adaptive K Nearest Neighboring
3.4. Network Architecture Adjustment
4. Experiment
4.1. Dataset
4.2. Experiment Platform
4.3. Method Integration and Evaluation
4.4. Experiment in Kernel Density Estimation
4.5. Subsample Using the APES and FPS Methods
4.6. Point Cloud Data Augmentation
4.7. The Range of K Values for DAKNN
4.8. Final Experimental Results
4.9. Comparison with Transformer-Based Architectures
4.10. Comparison of Time at Different K Values
4.11. Adaptive Kernel Density Experiment
5. Conclusions
- By using the DAKNN approach to calculate the K value, the original APES downsampling method better captures the edge points of the point cloud, making the contours more complete.
- The combination of two downsampling methods, along with effective data augmentation techniques, enhances computational efficiency and effectively improves accuracy.
- In addition to changing the original PointNext-s downsampling method, we also adjusted the hyperparameters. As a result, our method not only successfully improved accuracy but also reduced the model’s average training time by approximately 15% compared to the original PointNext-s.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. Adv. Neural Inf. Process. Syst. 2017, 30, 5105–5114. [Google Scholar]
- Ma, X.; Qin, C.; You, H.; Ran, H.; Fu, Y. Rethinking network design and local geometry in point cloud: A simple residual MLP framework. arXiv 2022, arXiv:2202.07123. [Google Scholar]
- Qian, G.; Li, Y.; Peng, H.; Mai, J.; Hammoud, H.; Elhoseiny, M.; Ghanem, B. Pointnext: Revisiting pointnet++ with improved training and scaling strategies. Adv. Neural Inf. Process. Syst. 2022, 35, 23192–23204. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef] [PubMed]
- Mirbauer, M.; Krabec, M.; Křivánek, J.; Šikudová, E. Survey and evaluation of neural 3d shape classification approaches. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8635–8656. [Google Scholar] [CrossRef]
- Camuffo, E.; Mari, D.; Milani, S. Recent advancements in learning algorithms for point clouds: An updated overview. Sensors 2022, 22, 1357. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Tian, S.; Lu, B.; Zhang, L.; Ning, X.; Bai, X. Deep learning-based 3D point cloud classification: A systematic survey and outlook. Displays 2023, 79, 102456. [Google Scholar] [CrossRef]
- Kyaw, P.P.; Tin, P.; Aikawa, M.; Kobayashi, I.; Zin, T.T. Cow’s Back Surface Segmentation of Point-Cloud Image Using PointNet++ for Individual Identification. In Genetic and Evolution-Ary Computing; Pan, J.S., Zin, T.T., Sung, T.W., Lin, J.C.W., Eds.; Springer: Singapore, 2025; Volume 1321. [Google Scholar] [CrossRef]
- Li, J.; Chen, B.M.; Lee, G.H. So-net: Self-organizing network for point cloud analysis. In Proceedings of the IEEE Conference on Computer Vision And Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhao, H.; Jiang, L.; Fu, C.-W.; Jia, J. Pointweb: Enhancing local neighborhood features for point cloud processing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Hu, Q.; Yang, B.; Xie, L.; Rosa, S.; Guo, Y.; Wang, Z.; Trigoni, N.; Markham, A. Randla-net: Efficient semantic segmentation of large-scale point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Xu, M.; Zhang, J.; Zhou, Z.; Xu, M.; Qi, X.; Qiao, Y. Learning geometry-disentangled representation for complementary understanding of 3d object point cloud. In Proceedings of the AAAI Conference on Artificial Intelligence, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Guo, M.-H.; Cai, J.-X.; Liu, Z.-N.; Mu, T.-J.; Martin, R.R.; Hu, S.-M. Pct: Point cloud transformer. Comput. Vis. Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Devlin, J.; Chang, M.-W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Yu, X.; Tang, L.; Rao, Y.; Huang, T.; Zhou, J.; Lu, J. Point-bert: Pre-training 3d point cloud transformers with masked point modeling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Berg, A.; Oskarsson, M.; O’Connor, M. Points to patches: Enabling the use of self-attention for 3d shape recognition. In Proceedings of the 2022 26th International Conference on Pattern Recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022. [Google Scholar]
- Tao, W.; Chen, H.; Moniruzzaman, M.; Leu, M.C.; Yi, Z.; Qin, R. Attention-Based Sensor Fusion for Human Activity Recognition Using IMU Signals. arXiv 2021, arXiv:2112.11224. [Google Scholar]
- Dovrat, O.; Lang, I.; Avidan, S. Learning to sample. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–19 June 2019. [Google Scholar]
- Lang, I.; Manor, A.; Avidan, S. Samplenet: Differentiable point cloud sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Lin, Y.; Huang, Y.; Zhou, S.; Jiang, M.; Wang, T.; Lei, Y. DA-Net: Density-adaptive downsampling network for point cloud classification via end-to-end learning. In Proceedings of the 2021 4th International Conference on Pattern Recognition and Artificial Intelligence (PRAI), Yibin, China, 20–22 August 2021. [Google Scholar]
- Qian, Y.; Hou, J.; Zhang, Q.; Zeng, Y.; Kwong, S.; He, Y. Mops-net: A matrix optimization-driven network fortask-oriented 3d point cloud downsampling. arXiv 2020, arXiv:2005.00383. [Google Scholar]
- Wang, X.; Jin, Y.; Cen, Y.; Lang, C.; Li, Y. Pst-net: Point cloud sampling via point-based transformer. In Proceedings of the Image and Graphics: 11th International Conference, ICIG 2021, Haikou, China, 6–8 August 2021; Springer: New York, NY, USA, 2021. [Google Scholar]
- Wang, X.; Jin, Y.; Cen, Y.; Wang, T.; Tang, B.; Li, Y. Lightn: Light-weight transformer network for performance-overhead tradeoff in point cloud downsampling. IEEE Trans. Multimed. 2023, 27, 832–847. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, J.; Pfrommer, J.; Beyerer, J. Attention-based Point Cloud Edge Sampling. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Wang, L.; Chen, Y.; Song, W.; Xu, H. Point Cloud Denoising and Feature Preservation: An Adaptive Kernel Approach Based on Local Density and Global Statistics. Sensors 2024, 24, 1718. [Google Scholar] [CrossRef]





| Experiment Platform | |
|---|---|
| CPU | i7-13700 2.10 GHz |
| GPU | NVDIA GrForce RTX 4090 |
| CPU Memory | 32 |
| GPU Memory | 24 |
| OS | Windows 11 (23.10.1) |
| Python Version | 3.8.18 |
| PyTorch Version | 1.10.0 |
| CUDA Runtime Version | 11.8.89 |
| Methods | Input Points | K-Neighbor (Downsample) | Batch Size | Embedding Feature Size | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|---|---|
| PointNext-s | 1024 | - | 32 | - | 93.11% | 89.96% |
| +Local_downsample | 1024 | 32 | 32 | - | 91.17% | 87.62% |
| +Embedding, Local_downsample | 1024 | 32 | 32 | 128 | 92.42% | 88.47% |
| +Embedding, Local_downsample, N2PAttention | 1024 | 32 | 32 | 128 | 92.62% | 89.36% |
| +Embedding, Local_downsample, N2PAttention, DAKNN | 1024 | 8~32 | 32 | 128 | 93.23% | 90.76% |
| Methods | Input Points | BandWidth | Batch Size | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|---|
| Ours | 1024 | 0.05 | 32 | 93.07% | 90.20% |
| 1024 | 0.1 | 32 | 93.23% | 90.76% | |
| 1024 | 0.15 | 32 | 93.15% | 91.17% | |
| 1024 | 0.2 | 32 | 93.07% | 90.36% | |
| 1024 | 0.25 | 32 | 93.03% | 90.49% | |
| 1024 | 0.3 | 32 | 93.15% | 90.58% |
| Methods | Input Points | Batch Size | SA Layers 1 and 2 | SA Layers 3 and 4 | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|---|---|
| PointNext-s | 1024 | 32 | FPS | FPS | 93.11% | 89.96% |
| Ours | 1024 | 32 | APES | APES | 92.38% | 89.70% |
| 1024 | 32 | DAKNN APES | DAKNN APES | 93.23% | 89.36% | |
| 1024 | 32 | DAKNN APES | FPS | 93.35% | 90.71% |
| Methods | Input Points | Batch Size | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|
| PointCloud_Scale PointCloud_Translate | 1024 | 32 | 93.35% | 90.71% |
| PointCloud_Scale PointCloud_Translate +PointCloud_rotation | 1024 | 32 | 93.44% | 90.97% |
| PointCloud_Scale PointCloud_Translate +PointCloud_Jitter | 1024 | 32 | 92.79% | 90.16% |
| PointCloud_Scale PointCloud_Translate+ Random_Dropout (10%) | 921 | 32 | 93.23% | 90.92% |
| Methods | Input Points | Max K | Min K | Value | Batch Size | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|---|---|---|
| Ours | 1024 | - | 8 | 1024 | 32 | 93.25% | 90.58% |
| 1024 | 32 | 8 | 512 | 32 | 93.44% | 90.85% | |
| 1024 | 24 | 8 | 512 | 32 | 93.23% | 90.76% |
| Methods | Input Points | Batch Size | Epochs | SA Layers 1 and 2 | SA Layers 3 and 4 | Overall Accuracy | Average Accuracy |
|---|---|---|---|---|---|---|---|
| PointNext-s | 1024 | 32 | 600 | FPS | FPS | 93.11% | 89.96% |
| 1024 | 6 | 200 | FPS | FPS | 92.54% | 89.79% | |
| +APES | 1024 | 32 | 600 | APES | APES | 92.62% | 89.36% |
| +DAKNN | 1024 | 32 | 600 | DAKNN APES | FPS | 93.44% | 90.85% |
| 1024 | 8 | 200 | DAKNN APES | FPS | 93.49% | 90.70% | |
| 1024 | 6 | 200 | DAKNN APES | FPS | 93.57% | 91.14% |
| Method | Architectures | Input Point | Overall Acc. |
|---|---|---|---|
| Point Transformer | Transformer | - | 93.70% |
| [ST] Point-BERT (1k) | Transformer-based | 1024 | 93.20% |
| [ST] Point-BERT (8k) | Transformer-based | 8192 | 93.80% |
| PointNext-s + APES + DAKNN | CNN + DAKNN/APES | 1024 | 93.57% |
| K Value | Epoch | Time | Accuracy |
|---|---|---|---|
| 8 | 600 | 08:14:58 | OA: 92.63 mAcc: 90.15 |
| 300 | 04:05:24 | OA: 92.79 mAcc: 90.13 | |
| 16 | 300 | 04:18:08 | OA: 92.67 mAcc: 90.35 |
| 32 | 300 | 04:49:58 | OA: 92.71 mAcc: 89.90 |
| 600 | 10:05:54 | OA: 92.38 mAcc: 89.54 | |
| Adaptive (8~32) | 300 | 05:25:30 | OA: 92.91 mAcc: 90.12 |
| 600 | 10:55:54 | OA: 92.50 mAcc: 89.30 | |
| Adaptive (8~16) | 300 | 05:14:27 | OA: 92.63 mAcc: 90.43 |
| Epoch | K Value | |||
|---|---|---|---|---|
| Adaptive | 8 | 16 | 32 | |
| 300 | 5.3 h | 4.10 h | 4.30 h | 4.80 h |
| 600 | 10.9 h | 8.25 h | - | 10.10 h |
| Bandwidth | Epoch | Time | Accuracy |
|---|---|---|---|
| 0.1 | 200 | - | OA: 92.63 mAcc: 90.30 |
| 600 | 10:55:54 | OA: 92.50 mAcc: 89.30 | |
| Adaptive (0.1~0.2) | 200 | 03:42:08 | OA: 92.59 mAcc: 90.50 |
| 600 | 11:01:28 | OA: 92.18 mAcc: 90.12 | |
| Adaptive (0.12~0.17) | 200 | 03:54:54 | OA: 92.59 mAcc: 89.44 |
| Noise Ratio | Offset | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.10 | ||
| 1% | OA | 93.03 | 92.46 | 92.87 | 92.42 | 92.26 | 92.30 | 92.26 | 92.22 | 92.50 | 92.54 |
| mAcc | 90.60 | 89.04 | 90.00 | 89.30 | 89.40 | 89.20 | 89.03 | 89.63 | 90.03 | 89.59 | |
| 2% | OA | 92.50 | 92.10 | 92.26 | 92.26 | 92.14 | 91.25 | 91.09 | 91.21 | 91.45 | 91.33 |
| mAcc | 89.87 | 89.37 | 89.82 | 89.40 | 89.53 | 88.47 | 88.24 | 87.95 | 88.72 | 88.41 | |
| 4% | OA | 92.46 | 92.26 | 92.06 | 91.61 | 91.17 | 91.29 | 90.68 | 89.71 | 89.34 | 89.30 |
| mAcc | 89.82 | 89.28 | 89.29 | 88.69 | 87.93 | 88.05 | 86.93 | 87.06 | 85.79 | 85.06 | |
| 7% | OA | 92.30 | 92.10 | 91.37 | 90.92 | 90.19 | 89.87 | 88.37 | 87.52 | 86.26 | 85.05 |
| mAcc | 89.14 | 89.28 | 88.00 | 87.60 | 85.95 | 85.64 | 83.96 | 81.86 | 81.90 | 79.00 | |
| 10% | OA | 92.59 | 91.73 | 90.92 | 89.99 | 88.98 | 87.88 | 86.51 | 84.24 | 82.09 | 79.54 |
| mAcc | 89.81 | 88.92 | 87.60 | 85.85 | 83.80 | 83.33 | 80.06 | 78.06 | 74.20 | 71.91 | |
| Testing SNR | Training SNR | |||||
|---|---|---|---|---|---|---|
| 0% | 5% | 10% | 15% | 20% | ||
| 0% | OA | 92.71 | 93.23 | 93.15 | 93.11 | 92.87 |
| mAcc | 89.90 | 90.84 | 90.29 | 91.01 | 90.09 | |
| 5% | OA | 92.14 | 92.95 | 93.64 | 93.19 | 92.38 |
| mAcc | 89.52 | 90.51 | 90.72 | 90.90 | 89.86 | |
| 10% | OA | 92.83 | 92.83 | 93.31 | 93.07 | 92.91 |
| mAcc | 90.17 | 89.58 | 90.49 | 90.87 | 90.05 | |
| 15% | OA | 92.75 | 92.54 | 92.59 | 93.27 | 93.27 |
| mAcc | 90.49 | 90.05 | 89.23 | 90.73 | 90.75 | |
| 20% | OA | 91.98 | 92.63 | 93.07 | 92.38 | 92.59 |
| mAcc | 89.86 | 89.80 | 90.03 | 89.76 | 89.90 | |
| Avg. | OA | 92.55 | 92.88 | 93.00 | 92.97 | 92.77 |
| mAcc | 90.11 | 90.12 | 90.02 | 90.51 | 90.29 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-L.; Yang, H.-W.; Chuang, C.-H. Powerful Sample Reduction Techniques for Constructing Effective Point Cloud Object Classification Models. Electronics 2025, 14, 2439. https://doi.org/10.3390/electronics14122439
Lin C-L, Yang H-W, Chuang C-H. Powerful Sample Reduction Techniques for Constructing Effective Point Cloud Object Classification Models. Electronics. 2025; 14(12):2439. https://doi.org/10.3390/electronics14122439
Chicago/Turabian StyleLin, Chih-Lung, Hai-Wei Yang, and Chi-Hung Chuang. 2025. "Powerful Sample Reduction Techniques for Constructing Effective Point Cloud Object Classification Models" Electronics 14, no. 12: 2439. https://doi.org/10.3390/electronics14122439
APA StyleLin, C.-L., Yang, H.-W., & Chuang, C.-H. (2025). Powerful Sample Reduction Techniques for Constructing Effective Point Cloud Object Classification Models. Electronics, 14(12), 2439. https://doi.org/10.3390/electronics14122439








