A Research Study on an Entropy-Weighted Multi-View Fusion Approach for Agricultural WSN Data Based on Fuzzy Clustering
Abstract
1. Introduction
2. Introduction to the Entropy Weight-Collaborative Partition Multi-View Fuzzy Clustering Algorithm
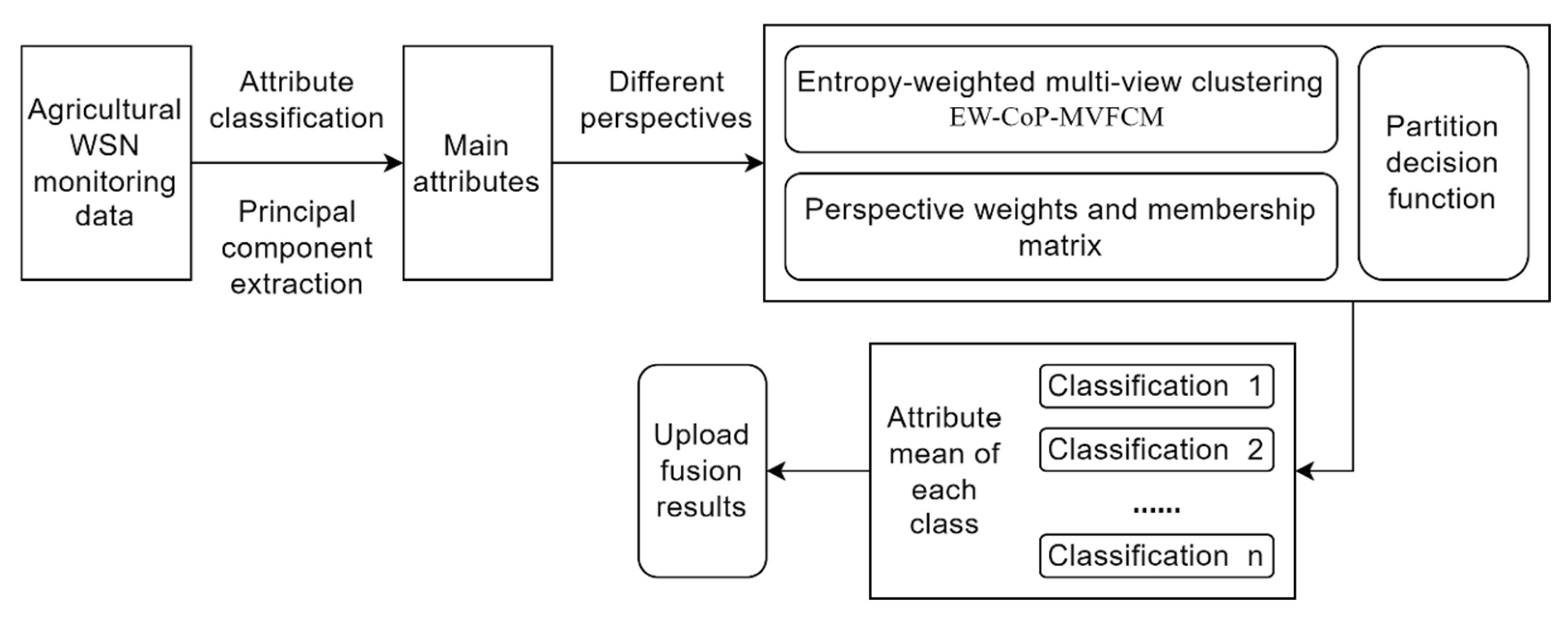
3. Multi-View Data Fusion Algorithm Based on Main Attributes
3.1. Attribute Reduction
- (1)
- Normalizes all attributes and calculates their variances;
- (2)
- Defines a variance threshold m0; attributes with variance above m0 are main attributes, others are secondary.
3.2. Parameters Setting
4. Implementation Steps
| Algorithm 1: Multi-View Collaborative Fusion Algorithm for Agricultural WSN Data Based on Main Attributes |
| Input: At the same time, a cluster head node receives sensor data from N nodes, including node address, air temperature, air humidity, precipitation, wind force, and solar radiation. Output: Data fusion result. #Step 1: Data Registration data_structs = [] FOR EACH data IN sensor_data_list: struct = { ‘address’: data.node_address, ‘‘temperature’: data.air_temp, ‘humidity’: data.air_humidity, ‘precipitation’: data.daily_precip, ‘wind’: data.wind_speed, ‘radiation’: data.solar_rad } data_structs.append(struct) # Step 2: Identify Main Attributes (Exemplar Values) primary_attrs = [‘temperature’, ‘precipitation’, ‘radiation’] secondary_attrs = [‘humidity’, ‘wind’] # Step 3: Multi-view Collaborative Clustering k = determine_optimal_clusters(data_structs, primary_attrs) # Determine the k-value with reference to the target range centers = init_random_centers(k, primary_attrs) # Random initialization of cluster prototypes membership_matrix = init_normalized_matrix(len(data_structs), k) # Normalization of the fuzzy membership matrix view_weights = init_normalized_weights(len(primary_attrs)) # Weight normalization across views # Iterative refinement DO: prev_centers = copy(centers) # Update cluster prototypes (Mathematical implementation details are provided in Section 2 and Section 3 of the paper) centers = update_cluster_centers(data_structs, membership_matrix, view_weights, primary_attrs) # update fuzzy membership matrix membership_matrix = update_membership_matrix(data_structs, centers, view_weights, primary_attrs) # update view weights view_weights = update_view_weights(data_structs, centers, membership_matrix, primary_attrs) WHILE convergence_check(centers, prev_centers) < THRESHOLD # Step 4: Generate Consensus Values cluster_results = assign_to_clusters(membership_matrix) # Assign data points to clusters via membership fused_data = [] FOR EACH cluster IN cluster_results: fused_entry = { ‘addresses’: [struct[‘address’] FOR struct IN cluster.members], ‘fused_values’: {} } # Compute fused main attributes (intra-class mean) FOR attr IN primary_attrs + secondary_attrs: values = [struct[attr] FOR struct IN cluster.members] fused_entry[‘fused_values’][attr] = mean(values) fused_data.append(fused_entry) # Step 5: Output Fused Results RETURN fused_data # Auxiliary function example FUNCTION determine_optimal_clusters(data, attrs): # Determine optimal k within the reference range using the elbow method or the silhouette coefficient k_range = range(2, 10) # Target reference range best_k = elbow_method(data, attrs, k_range) RETURN best_k FUNCTION update_view_weights(data, centers, membership, attrs): # Update view weights using Section 3 formulae weights = [] total_weight = 0.0 FOR attr_idx, attr IN enumerate(attrs): weight = calculate_view_weight(attr, data, centers, membership) weights.append(weight) total_weight = weight # Normalization procedure RETURN [w/total_weight FOR w IN weights] |
5. Simulation Results and Analysis
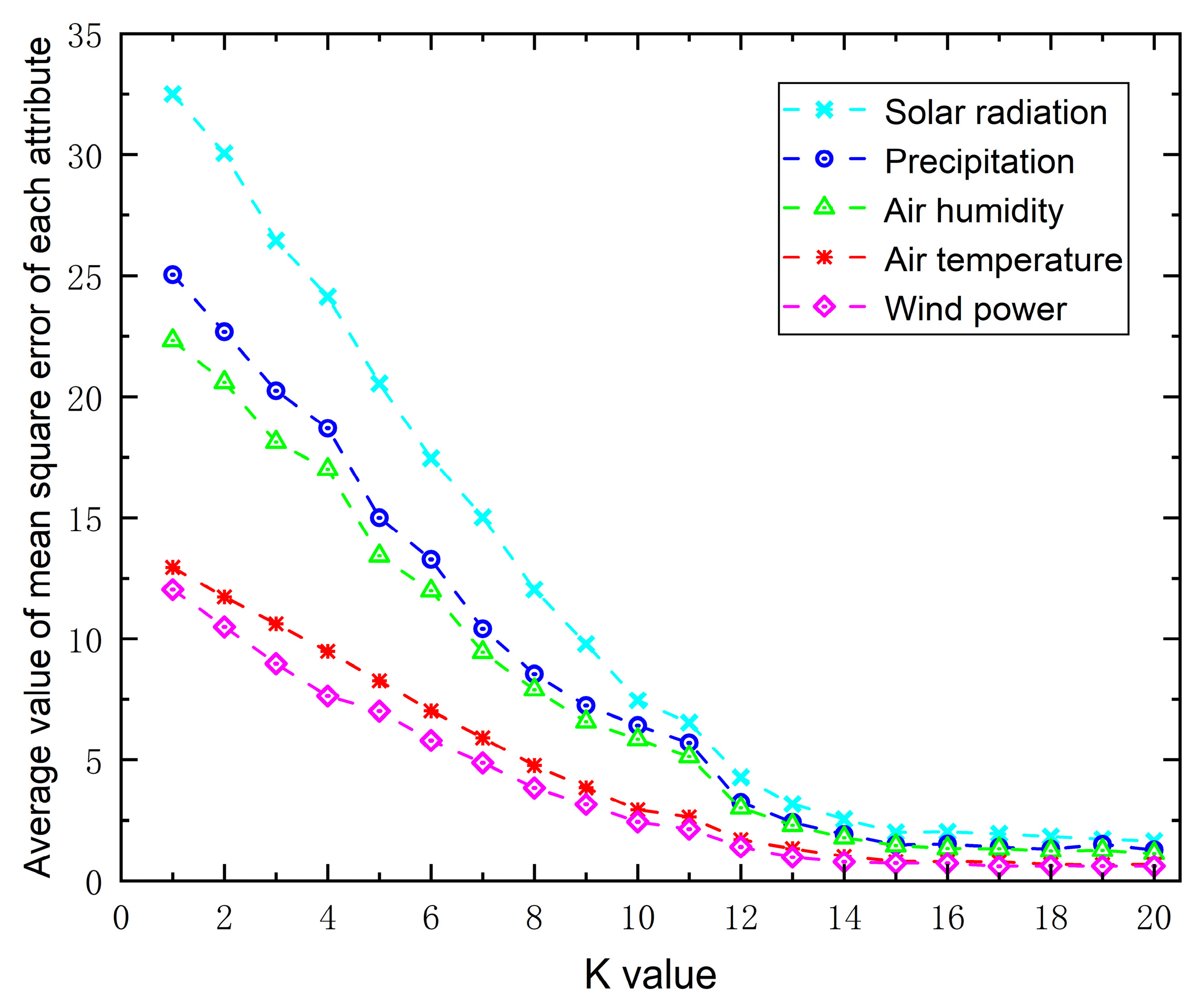
5.1. Analysis of Different Cluster Center Numbers
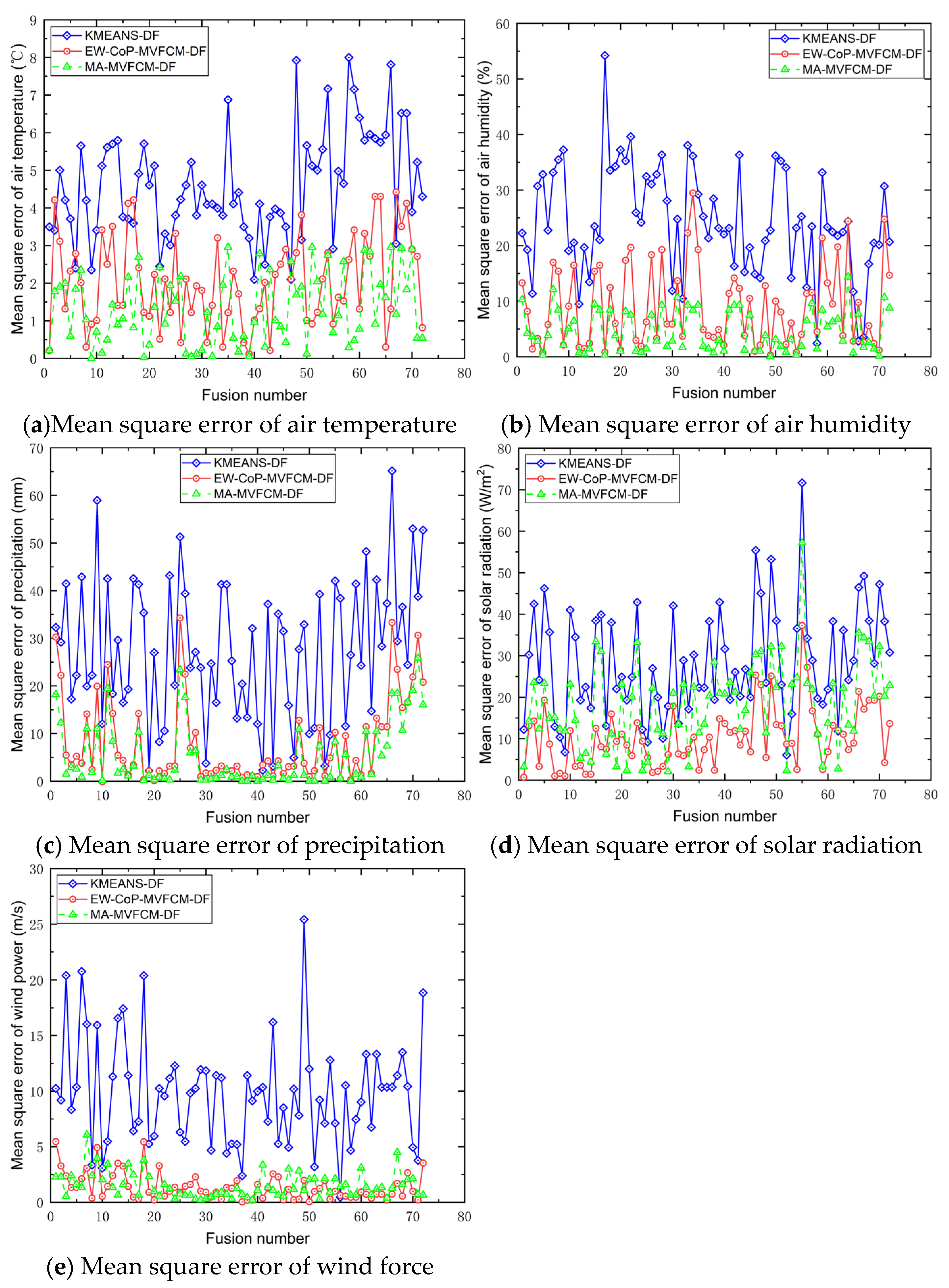
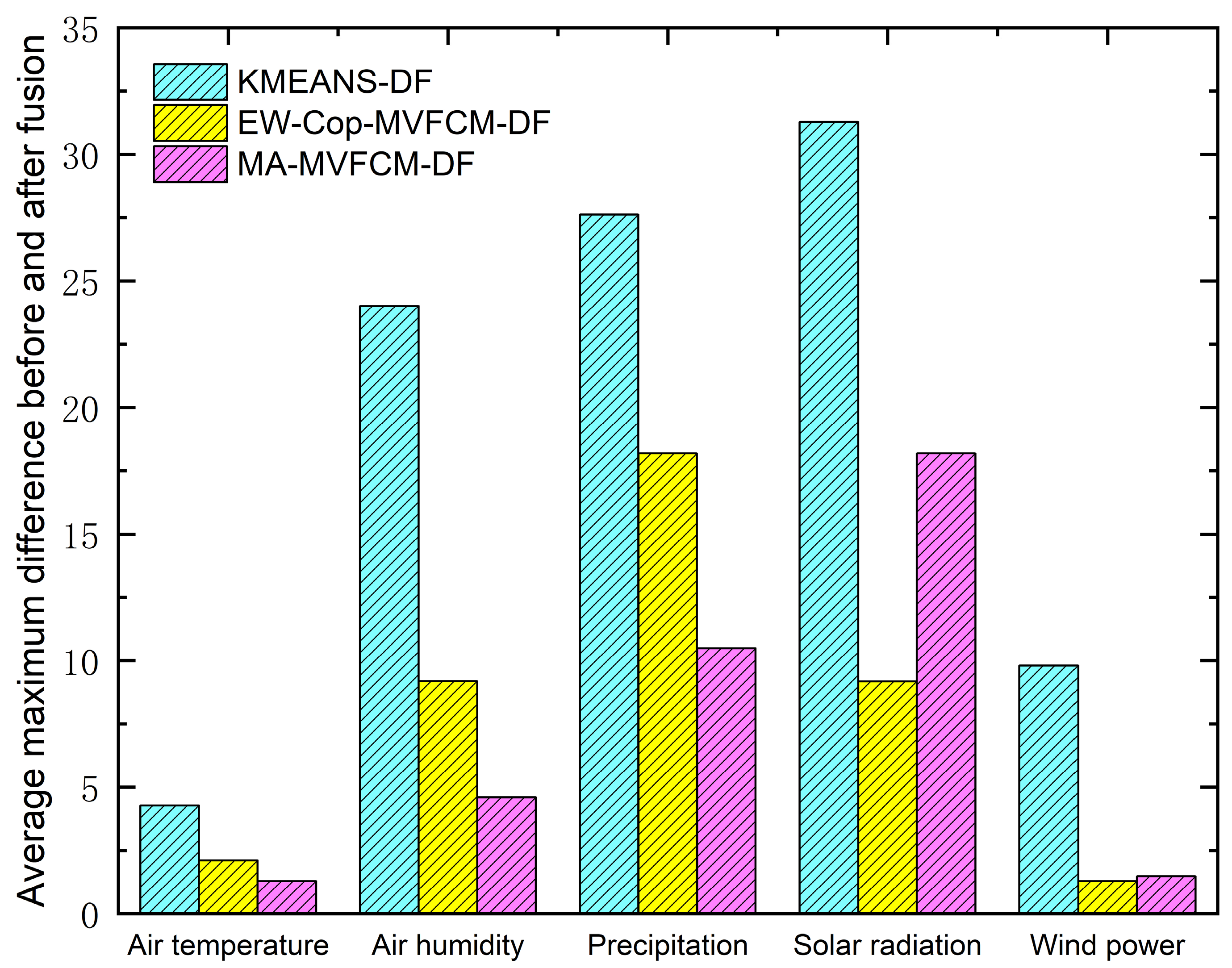
5.2. Data Fusion Accuracy
6. Conclusions
- (1)
- Determining main parameters: Considering the computational cost of WSNs and data characteristics, identifying key parameters based on the relationships among agricultural parameters is crucial and deserves further exploration.
- (2)
- Optimizing the objective function: When fusing multiple parameters, combining fuzzy or rough set theory to address uncertainties can enhance the efficiency of the fusion process.
- (3)
- Handling secondary attributes: Simply discarding secondary attributes is a crude approach. Future work can focus on optimizing clustering results using secondary attributes to achieve better data fusion outcomes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WSN | Wireless sensor network |
| BSBL | Block-sparse Bayesian learning |
| EW-CoP-MVFCM | Entropy Weight-Collaborative Partition Multi-View Fuzzy Clustering Algorithm |
| FCM | Fuzzy C-means algorithm |
| MA-MVFCM-DF | Main-attribute-based multi-view data fusion algorithm |
| KMEANS-DF | K-means-based data fusion algorithm |
| MSE | Mean squared error |
References
- Zhao, C.; Wu, H.; Zhu, L. A ZigBee-based energy saving routing algorithm for farmland wireless sensor networks. Chin. High Technol. Lett. 2013, 23, 368–373. [Google Scholar]
- Aldalahmeh, S.A.; Ciuonzo, D. Distributed detection fusion in clustered sensor networks over multiple access fading channels. IEEE Trans. Signal Inf. Process. Over Netw. 2022, 8, 317–329. [Google Scholar] [CrossRef]
- Tian, Q.; Edward, J.C. Optimal distributed detection in clustered wireless sensor networks. IEEE Trans. Signal Process. 2007, 55, 3892–3904. [Google Scholar] [CrossRef]
- Wu, L.; Sahu, N.; Xu, S.; Babu, P.; Ciuonzo, D. Optimization based sensor placement for multi-target localization with coupling sensor clusters. IEEE Trans. Signal Inf. Process. Over Netw. 2023, 9, 596–611. [Google Scholar] [CrossRef]
- Gao, H.; Liu, Y.; Chen, S. Fusion of WSN Cluster Head Data Based on Improved K-means Clustering Algorithm. Trans. Chin. Soc. Agric. Mach. 2015, s1, 162–167. [Google Scholar]
- Bhasker, B.; Murali, S. An Energy-Efficient Cluster-based data aggregation for agriculture irrigation management system using wireless sensor networks. Sustain. Energy Technol. Assess. 2024, 65, 103771. [Google Scholar] [CrossRef]
- Kong, L.; Xia, M.; Liu, X.Y.; Chen, G.; Gu, Y.; Wu, M.Y.; Liu, X. Data Loss and Reconstruction in Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2818–2828. [Google Scholar] [CrossRef]
- Sun, J.; Yu, Y.; Wen, J. Compressed-Sensing Reconstruction Based on Block Sparse Bayesian Learning in Bearing-Condition Monitoring. Sensors 2017, 17, 1454. [Google Scholar] [CrossRef]
- Al-Qurabat, A.K.M.; Salman, H.; Finjan, A.A.R. Important extrema points extraction-based data aggregation approach for elongating the WSN lifetime. Int. J. Comput. Appl. Technol. 2022, 68, 357–368. [Google Scholar] [CrossRef]
- Alper, S.S.; Abdullah, A.; Adnan, Y. A Two-Tier Distributed Fuzzy Logic Based Protocol for Efficient Data Aggregation in Multi-Hop Wireless Sensor Networks. IEEE Trans. Fuzzy Syst. 2018, 26, 3615–3629. [Google Scholar] [CrossRef]
- Sreedevi, P.; Venkateswarlu, S. An Efficient Intra-Cluster Data Aggregation and finding the Best Sink location in WSN using EEC-MA-PSOGA approach. Int. J. Commun. Syst. 2022, 35, e5110. [Google Scholar] [CrossRef]
- Gao, F.; Yu, L.; Wang, Y.; Lu, S.; Zhang, W.A.; Yu, L. Development of host computer software for crop water status monitoring system based on wireless sensor networks. Chin. Soc. Agric. Eng. 2010, 26, 175–181. [Google Scholar]
- Shastry, K.A.; Sanjay, H.A. A modified genetic algorithm and weighted principal component analysis based feature selection and extraction strategy in agriculture. Knowl.-Based Syst. 2021, 232, 107460. [Google Scholar] [CrossRef]
- Torres, A.B.; da Rocha, A.R.; da Silva, T.L.C.; de Souza, J.N.; Gondim, R.S. Multilevel data fusion for the internet of things in smart agriculture. Comput. Electron. Agric. 2020, 171, 16. [Google Scholar] [CrossRef]
- Sun, G.; Zhang, Z.; Zheng, B.; Li, Y. Multi-Sensor Data Fusion Algorithm Based on Trust Degree and Improved Genetics. Sensors 2019, 19, 2139. [Google Scholar] [CrossRef]
- Yang, X.; Hua, Z.; Li, L.; Huo, X.; Zhao, Z. Multi-source information fusion-driven corn yield prediction using the Random Forest from the perspective of Agricultural and Forestry Economic Management. Sci. Rep. 2024, 14, 4052. [Google Scholar] [CrossRef]
- Jiang, Y.Z.; Deng, Z.-H.; Wang, J.; Qian, P.-J.; Wang, S.-T. Collzborative Partition Multi-View Fuzzy Clustering Algorithm using Entropy Weighting. J. Softw. 2014, 25, 2293–2311. [Google Scholar]
- Hu, J.; Pan, Y.; Li, T.; Yang, Y. TW-Co-MFC: Two-Level Weighted Collaborative Fuzzy Clustering Based on Maximum Entropy for Multi-View Data. Tsinghua Sci. Technol. 2021, 26, 185–198. [Google Scholar] [CrossRef]
- Cleuziou, G.; Exbrayat, M.; Martin, L.; Sublemontier, J.-H. CoFKM: A Centralized Method for Multiple-View Clustering. In Proceedings of the Ninth IEEE International Conference on Data Mining, Miami Beach, FL, USA, 6–9 December 2009. [Google Scholar] [CrossRef]
- Chao, G.; Sun, S.; Bi, J. A Survey on Multi-View Clustering. IEEE Trans. Artif. Intell. 2017, 2, 146–168. [Google Scholar] [CrossRef]
- Ruan, S. A Quantitative Comparison between Shannon and Tsallis–Havrda–Charvat Entropies Applied to Cancer Outcome Prediction. Entropy 2022, 24, 436. [Google Scholar] [CrossRef]
- Zhu, C.; Miao, D. Entropy-based multi-view matrix completion for clustering with side information. Pattern Anal. Appl. 2020, 23, 359–370. [Google Scholar] [CrossRef]
- Qian, P.; Zhou, J.; Jiang, Y.; Liang, F.; Zhao, K.; Wang, S. Multi-View Maximum Entropy Clustering by Jointly Leveraging Inter-View Collaborations and Intra-View-Weighted Attributes. IEEE Access 2018, 6, 28594–28610. [Google Scholar] [CrossRef] [PubMed]
- Kassim, M.R.M.; Harun, A.N. Applications of WSN in agricultural environment monitoring systems. In Proceedings of the International Conference on Information & Communication Technology Convergence, Jeju, Republic of Korea, 19–21 October 2016; pp. 344–349. [Google Scholar] [CrossRef]
- Ruipeng, T.; Jianbu, Y.; Jianrui, T.; Aridas, N.K.; Talip, M.S. Design of agricultural wireless sensor network node optimization method based on improved data fusion algorithm. PLoS ONE 2024, 19, e0308845. [Google Scholar] [CrossRef]
- Wang, L.; Fu, C.; Qi, J. The Multisensor Data Fusion Method Based on Improved Fuzzy Evidence Theory in the Coal Mine Environment. J. Sens. 2024, 2024, 5581891. [Google Scholar] [CrossRef]
- Khoiri, I.B.; Erfianto, B. The Application Of Multi-Sensor Data Fusion Method with Fuzzy Time Series Model to Improve Indoor Water Prediction Accuracy Quality. Build. Inform. Technol. Sci. (BITS) 2023, 4, 1805–1814. [Google Scholar] [CrossRef]

| Single-view data fusion methods | Based on k-means | Disadvantage: The output lacks reliability and comprehensiveness |
| Based on block-sparse Bayesian learning | ||
| Based on important extrema points extraction | ||
| Based on the distributed fuzzy logic protocol | ||
| Multi-view data fusion methods | Based on the improved genetic algorithm | Disadvantage: fail to consider different clustering characteristics of various attributes |
| Based on the multilevel data fusion method | ||
| Based on the trust degree | ||
| Based on the random forest model |
| The initial number of cluster centers | k = 5 | k = 10 | k = 15 |
| Data compression rate | 4.24% | 8.47% | 12.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; You, X. A Research Study on an Entropy-Weighted Multi-View Fusion Approach for Agricultural WSN Data Based on Fuzzy Clustering. Electronics 2025, 14, 2424. https://doi.org/10.3390/electronics14122424
Wang X, You X. A Research Study on an Entropy-Weighted Multi-View Fusion Approach for Agricultural WSN Data Based on Fuzzy Clustering. Electronics. 2025; 14(12):2424. https://doi.org/10.3390/electronics14122424
Chicago/Turabian StyleWang, Xun, and Xiaohu You. 2025. "A Research Study on an Entropy-Weighted Multi-View Fusion Approach for Agricultural WSN Data Based on Fuzzy Clustering" Electronics 14, no. 12: 2424. https://doi.org/10.3390/electronics14122424
APA StyleWang, X., & You, X. (2025). A Research Study on an Entropy-Weighted Multi-View Fusion Approach for Agricultural WSN Data Based on Fuzzy Clustering. Electronics, 14(12), 2424. https://doi.org/10.3390/electronics14122424






