DRL-Based Fast Joint Mapping Approach for SFC Deployment

Abstract

The rapid development of Network Function Virtualization (NFV) enables network operators to deliver customized end-to-end services through Service Function Chains (SFCs). However, existing two-stage deployment strategies fail to jointly optimize the placement of Virtual Network Functions (VNFs) and the routing of service traffic, resulting in inefficient resource utilization and increased service latency. This study addresses the challenge of maximizing the acceptance rate of service requests under resource constraints and latency requirements. We propose DRL-FJM, a novel dynamic SFC joint mapping orchestration algorithm based on Deep Reinforcement Learning (DRL). By holistically evaluating network resource states, the algorithm jointly optimizes node and link mapping schemes to effectively tackle the dual challenges of resource limitations and latency constraints in long-term SFC orchestration scenarios. Simulation results demonstrate that compared with existing methods, DRL-FJM improves total traffic served by up to 42.6%, node resource utilization by 17.3%, and link resource utilization by 26.6%, while achieving nearly 100% SFC deployment success. Moreover, our analysis reveals that the proposed algorithm demonstrates strong adaptability and robustness under diverse network conditions.

1. Introduction

The rapid advancement of information technology has presented significant challenges to traditional network architectures, largely due to the growing complexity and diversity of network communications. Network Function Virtualization (NFV) has emerged as a promising solution to address these challenges [1]. NFV enables the virtualization of network functions, allowing them to operate on general-purpose servers instead of relying on dedicated hardware. In the NFV paradigm, network operators often utilize Service Function Chains (SFCs) to deliver personalized network services to users [2]. An SFC consists of a series of Virtual Network Functions (VNFs) arranged in a specific sequence [3], providing flexibility in adding or removing VNFs as needed. VNFs are deployed in virtual machines hosted on physical servers, enabling efficient and flexible resource utilization, thereby maximizing the benefits for service providers.

The orchestration of SFCs has been a major focus of research, with numerous studies aiming to optimize network service deployment to minimize operational costs or reduce energy consumption [4]. However, the emergence of new applications, such as autonomous driving, AR/VR, and large-scale IoT, has significantly increased the demand for lower latency and higher quality network services. End-to-end latency constraints have thus become a critical factor in determining the quality of SFCs, presenting new challenges for their deployment.

Specifically, SFC deployment can be divided into two parts: VNF placement and traffic routing path selection. Current research typically addresses these two aspects sequentially, resulting in two distinct approaches, namely node mapping and link mapping. In the node mapping approach, optimal nodes are selected for VNF placement, after which the VNFs are connected to form the SFC, while this method effectively utilizes computational resources across the network, it often disregards latency, which may result in selecting longer routing paths that fail to meet latency requirements and lead to bandwidth wastage. Alternatively, the link mapping approach assigns a candidate path for traffic flow first, then deploys VNFs along that path. Although this method can achieve shorter routing paths, it may suffer from insufficient computational resources to fulfill the SFC requirements.

Since these approaches solve one aspect of the problem independently and subsequently use the result to address the other, they lack an integrated consideration of the multiple resources, elements, and constraints involved, leading to suboptimal performance in complex network environments. Thus, there is a need for a more comprehensive solution to this complex problem.

Fortunately, DRL has emerged as a powerful technique for solving complex decision-making problems, enabling efficient VNF embedding and traffic routing in dynamic networks. However, solving the SFC deployment problem in a single step remains challenging due to the massive combined action space, making agent training extremely difficult.

In this paper, we propose a Deep Reinforcement Learning-based Fast Joint Mapping (DRL-FJM) approach for SFC deployment, designed to improve the acceptance rate of SFCs while meeting latency constraints. First, we introduce a Comprehensive Resource-Aware Deployment and Routing (CRADR) method, which considers the overall impact of each SFC deployment plan to directly select an appropriate solution. We then propose a Proximal Policy Optimization (PPO)-based algorithm that leverages DRL’s ability to dynamically perceive network resources to select a long-term optimal SFC deployment plan. Our main contributions are as follows:

1.

We formulate the latency-constrained SFC deployment problem as a multi-constraint joint node-link mapping task, and model it as a long-term Markov Decision Process (MDP) with the objective of maximizing the SFC acceptance rate under resource and delay constraints;

2.

We propose DRL-FJM, a DRL-based Fast Joint Mapping Approach for SFC Deployment. We first design an evaluation metric for SFC deployment schemes to quantify the impact of network resource potential and joint mapping strategies. By directly searching this metric within the joint solution space of node and link mappings, we obtain a set of feasible end-to-end SFC deployment schemes. On this basis, we propose a method based on Proximal Policy Optimization (PPO) to dynamically capture network resource states and evaluate the long-term effects of deployment decisions, thereby selecting the optimal scheme. This joint design integrates model-driven candidate generation with learning-based global policy optimization;

3.

We conduct extensive experiments comparing DRL-FJM with existing DRL-based node mapping, link mapping algorithms. The results demonstrate that DRL-FJM achieves a higher acceptance rate under varying workloads.

The remainder of this paper is organized as follows: Section 2 reviews related work. Section 3 describes the system model and problem formulation for SFC deployment. Section 4 presents the DRL-FJM algorithm. Section 5 evaluates and analyzes the performance of DRL-FJM. Finally, Section 6 concludes the paper.

2. Related Work

In recent years, much research has focused on determining the placement of all VNFs before sequentially connecting them. In reference [5], the authors proposed a minimum residual heuristic algorithm to solve the VNF placement problem in multi-cloud environments with deployment cost constraints. In reference [6], the problem was formulated as a Markov Decision Process (MDP) to capture dynamic network state transitions, using an attention-based DRL model to jointly optimize latency and cost. A distributed reinforcement learning-based service chain energy management framework was introduced in [7], which dynamically adjusted VNF placement to reduce latency and improve energy efficiency. In reference [8], a heuristic algorithm based on complex network theory was proposed to minimize total resource usage cost while considering latency-aware and reliable VNF placement. Zeng et al. [9] developed a rule-based DRL algorithm that first generates a fractional solution for VNF deployment and then refines this solution using a rule-based algorithm to meet all constraints. In reference [10], Yue et al. focus on the VNF placement problem and propose an affinity-based heuristic mapping algorithm to achieve higher network throughput and resource utilization. Varasteh et al. [11] present an online heuristic framework that sequentially addresses the SFC deployment problem by first placing VNFs and then performing traffic routing. A Lagrangian relaxation-based aggregated cost heuristic algorithm is employed to solve the delay-constrained minimum-cost shortest-path routing subproblem. In reference [12], Qiu et al. investigate the placement of VNFs and their redundant backups in Fault-Prone Mobile Edge Cloud (FP-MEC) environments, and propose a two-stage online scheme to maximize the accepted request throughput while minimizing the acceptance cost. Fan et al. [13] proposed selecting VNF placement nodes based on global resource capacity probabilities and connecting nodes using the shortest path, with DRL used to select the final deployment plan from the generated set of solutions.

Several studies have adopted an alternative approach by determining the traffic routing path first, followed by choosing VNF placement along that path. In reference [14], due to the complexity of the SFC deployment problem, the authors proposed solving the two subproblems separately. They utilized a pointer network-based Actor–Critic algorithm for the traffic routing problem and then applied the resulting solution to the VNF placement problem. Tian et al. [15] presented a two-stage method in which a graph-based resource aggregation routing approach was used to identify candidate paths under latency constraints, followed by DRL to determine VNF placement. In reference [16], Wang et al. transform the network representation into a virtual layered graph that incorporates NFV processing delay, and then solve the problem using a traditional shortest-path algorithm. In reference [17], Pei et al. propose a novel graph-based routing algorithm to enable differentiated routing for SFC request flows, and design a relative cost metric to balance resource consumption and prevent congestion in the network. Duan et al. [18] focused on optimizing traffic routing paths by proposing an SFC path optimization strategy based on network function placement clustering, which employed a multi-head attention mechanism to optimize various types of SFC layouts.

However, the aforementioned approaches address VNF placement and traffic routing separately rather than jointly, resulting in a decoupled decision-making process. Due to the sequential nature of service chains, making placement decisions first and then routing VNFs via shortest paths can lead to inefficient detours, which increase link resource consumption and violate latency constraints. Conversely, determining traffic routing paths first may result in insufficient computing resources along the selected path to satisfy the VNF deployment requirements. In both cases, the second decision is overly constrained by the first, leading to suboptimal deployment results.

Moreover, these methods typically optimize one component while holding the other fixed, which fails to fully exploit the solution space. In contrast, our proposed DRL-FJM approach jointly considers node and link mapping combinations, evaluates multiple complete SFC deployment candidates, and employs a DRL agent to select the optimal plan by perceiving real-time network resource status. This unified framework enables global resource-awareness and dynamic adaptation to network conditions, overcoming the inherent limitations of decoupled strategies.

3. System Model Furthermore, Problem Formulation

3.1. System Model

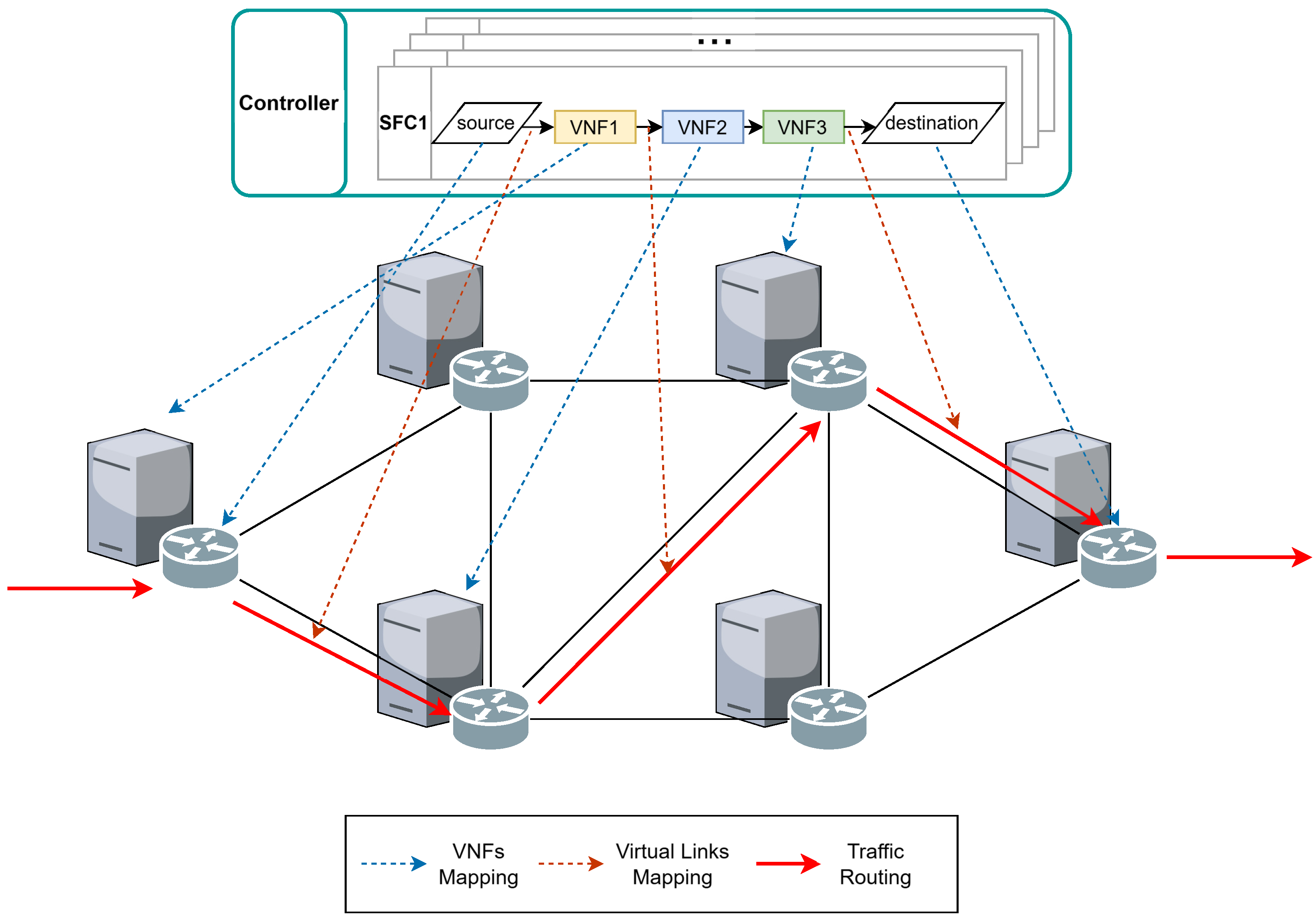
As illustrated in Figure 1, our system model consists of NFV infrastructure, VNFs, and a centralized controller. The NFV infrastructure includes multiple servers and switching nodes, where VNFs can be instantiated on servers to provide services to users. Each SFC flow must traverse a series of VNFs in a specified order, from an ingress node to an egress node, with VNF placement and traffic routing paths determined by the controller. The controller has access to network resource states and can compute the end-to-end delay for SFCs. Upon the arrival of an SFC request, the centralized controller computes a mapping plan that satisfies both resource and latency requirements, deploying the SFC in the network. Once the SFC service is completed, its occupied resources are released.

3.2. Physical Network and SFCs

The underlying physical network is typically represented as an undirected graph $G^S=(N^S,E^S)$, consisting of nodes with computing resource capacities denoted as $C=\left\{c_n\right|n\in N^S\}$ and edges with bandwidth denoted as $B=\left\{b_{u,v}\right|u,v\in N^S,e_{u,v}\in E^S\}$, respectively. Here, $u,v\in N^S$ represents the nodes, while $e_{u,v}$ represents the bidirectional links between them.

All user service demands in the network can be represented as a set of Service Function Chains $G^V$, where $G_i^V\in G^V$ represents the i-th SFC, which contains source and destination nodes as well as a set of ordered network function requirements, represented as a directed graph $G_i^V=(N_i^V,E_i^V)$. $N_i^V=\{sr{c}_i,v_{i,1},v_{i,2},\cdots ,v_{i,j},\cdots ,ds{t}_i\}$ represents the set of virtual nodes, where $sr{c}_i$ and $ds{t}_i$ denote the source and destination nodes, respectively. $V_i^v=\langle v_{i,1},v_{i,2},\cdots ,v_{i,|V_i^v|}\rangle$ represents the ordered sequence of VNFs, with each type of VNF having its own computational resource requirements ${\phi }_{i,j}^{cpu}$. Thus, an SFC request can be defined as $req=\{G_i^V,f_i,t_i^a,t_i^h,t_i^d\}$, where $t_i^a$ and $f_i$ denote the arrival time and traffic demand of the SFC, respectively. $t_i^h$ represents the SFC’s lifetime, after which the SFC task ends and the physical resources occupied are released. $t_i^d$ represents the delay requirement, and if the delay exceeds the constraint, the service will be rejected. Therefore, it is crucial to meet resource requirements and effectively plan paths to satisfy the delay constraint.

3.3. The Problem Formulation

The SFC deployment problem can be defined as mapping the directed graph $G^V$ representing the set of SFCs onto the undirected graph $G^S$ of the underlying network while satisfying service latency and traffic requirements: $M:G^V(N^V,E^V)\to G^S(N^S,E^S)$. A binary variable $x_{i,j}^{n,\iota }$ defines the embedding location of the j-th VNF $v_{i,j}$ in the i-th SFC, and another binary variable $y_{i,e}$ represents whether the i-th SFC $G_i^V$ passes through link $e_{u,v}$. $z_i$ denotes whether the SFC request $G_i^V$ is accepted, as shown in the following equations.

$$x_{i,j}^{n,\iota }=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{v}_{i,j}\mathrm{is}\mathrm{embedded}\mathrm{on}\mathrm{node}n\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(1)

$$y_i^{u,v,\iota }=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{SFC}{G}_i^V\mathrm{traverses}\mathrm{link}{e}_{u,v}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(2)

$$z_i=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\mathrm{SFC}{G}_i^V\mathrm{is}\mathrm{accepted}\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

The mapping process involves two parts: node mapping and link mapping.

For node mapping, we need to find physical nodes that meet the VNF requirements for the SFC request, considering two main constraints:

Node Resource Constraint: The computational resources required by a VNF must not exceed the corresponding available resources of the physical node:

$$\sum _{v_{i,j}\in V_i^v}{x}_{i,j}^{n,\iota }{\phi }_{i,j}^{cpu}\le {\omega }_n^{cpu},\forall n\in N^S$$

(4)

Node Deployment Constraint: Each VNF can only be deployed on a single physical node:

$$\sum _{n\in N^S}{x}_{i,j}^{n,\iota }=1$$

(5)

For link mapping, we need to find physical links between the mapped nodes, considering two main constraints:

Bandwidth Constraint: The total bandwidth mapped to the physical link $e_{u,v}$ should not exceed its remaining bandwidth $w_{u,v}^{bw}$:

$$y_i^{u,v,\iota }{f}_i\le {\omega }_{u,v}^{bw},\forall e_{u,v}\in E^S$$

(6)

Path Constraint: If the SFC $G_i^V$ is accepted, the traversed physical links must be sequentially connected, and splitting is not allowed. We use $P_i^{\tau ,\iota }=\langle n_{i,1}^{\tau ,\iota },n_{i,2}^{\tau ,\iota },\dots ,n_{i,\left|P_i^{\tau ,\iota }\right|}^{\tau ,\iota }\rangle$ to denote the selected deployment path for the SFC $G_i^V$, and $I_{i,n}^{\tau ,\iota }$ and $O_{i,n}^{\tau ,\iota }$ represent the number of incoming and outgoing flows at each node n, respectively. Thus, for each node $n\in P_i^{\tau ,\iota }$, we have the following constraint:

$$O_{i,n}^{\tau ,\iota }-I_{i,n}^{\tau ,\iota }=\left\{\begin{array}{cc}1,\hfill & n=sr{c}_i^{\tau ,\iota }\hfill \\ -1,\hfill & n=ds{t}_i^{\tau ,\iota },\forall n\in P_i^{\tau ,\iota }\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(7)

Delay Constraint: the delay experienced by the SFC flow must not exceed its maximum tolerable delay. We primarily consider propagation delay and packet queuing delay, as expressed in the following equation:

$$d_{u,v}^{\tau }=d_{u,v}^p+d_{u,v}^{q,\tau }$$

(8)

Propagation delay $d_{u,v}^p$ is defined as the time required for a message to propagate through the transmission medium between nodes, proportional to the length of the medium between the endpoints. Queuing delay $d_{u,v}^{q,\tau }$ refers to the time packets spend waiting in a queue before being processed, which depends on the current link traffic. In this paper, we model queuing delay using an M/M/1 queuing model [19], where ${\omega }_{u,v}^{bw}$ represents the remaining bandwidth of the link $e_{u,v}$. According to the M/M/1 model, the queuing delay for a link is calculated using the following formula:

$$d_{u,v}^{q,\tau }={\displaystyle \frac{b_{u,v}-{\omega }_{u,v}^{bw}}{{\omega }_{u,v}^{bw}}}{d}_o^{u,v}$$

(9)

We denote ${\mathcal{G}}_{\tau }$ as the set of all deployed and active SFCs at time $\tau$, and thus the delay constraint can be expressed as follows:

$$\sum _{j=1}^{\left|P_i^{\tau ,\iota }\right|-1}{y}_i^{n_{i,j}^{\tau ,\iota },n_{i,j+1}^{\tau ,\iota },\iota }{d}_{n_{i,j}^{\tau ,\iota },n_{i,j+1}^{\tau ,\iota }}^{\tau }\le t_i^{d,\tau ,\iota },\forall G_i^{\tau ,\iota }\in {\mathcal{G}}_{\tau }$$

(10)

In this paper, our optimization objective is to maximize the number of successfully deployed SFCs, i.e.,

$$max\sum _{G_i^V\in G^V}{z}_i$$

s.t.(1), (2), (3), (4), (5), (6), (7), (8), (9), (10),

$$x_{i,j}^{n,\iota }\in \{0,1\},y_i^{u,v,\iota }\in \{0,1\},\forall n\in N^S,e_{u,v}\in E^S$$

The above formulation defines a constrained optimization problem for the online SFC deployment scenario, where the objective is to maximize the number of successfully deployed SFC requests while satisfying computational, bandwidth, and delay constraints. This problem structure provides the theoretical foundation for the DRL-based orchestration method introduced in the next section.

4. Algorithm

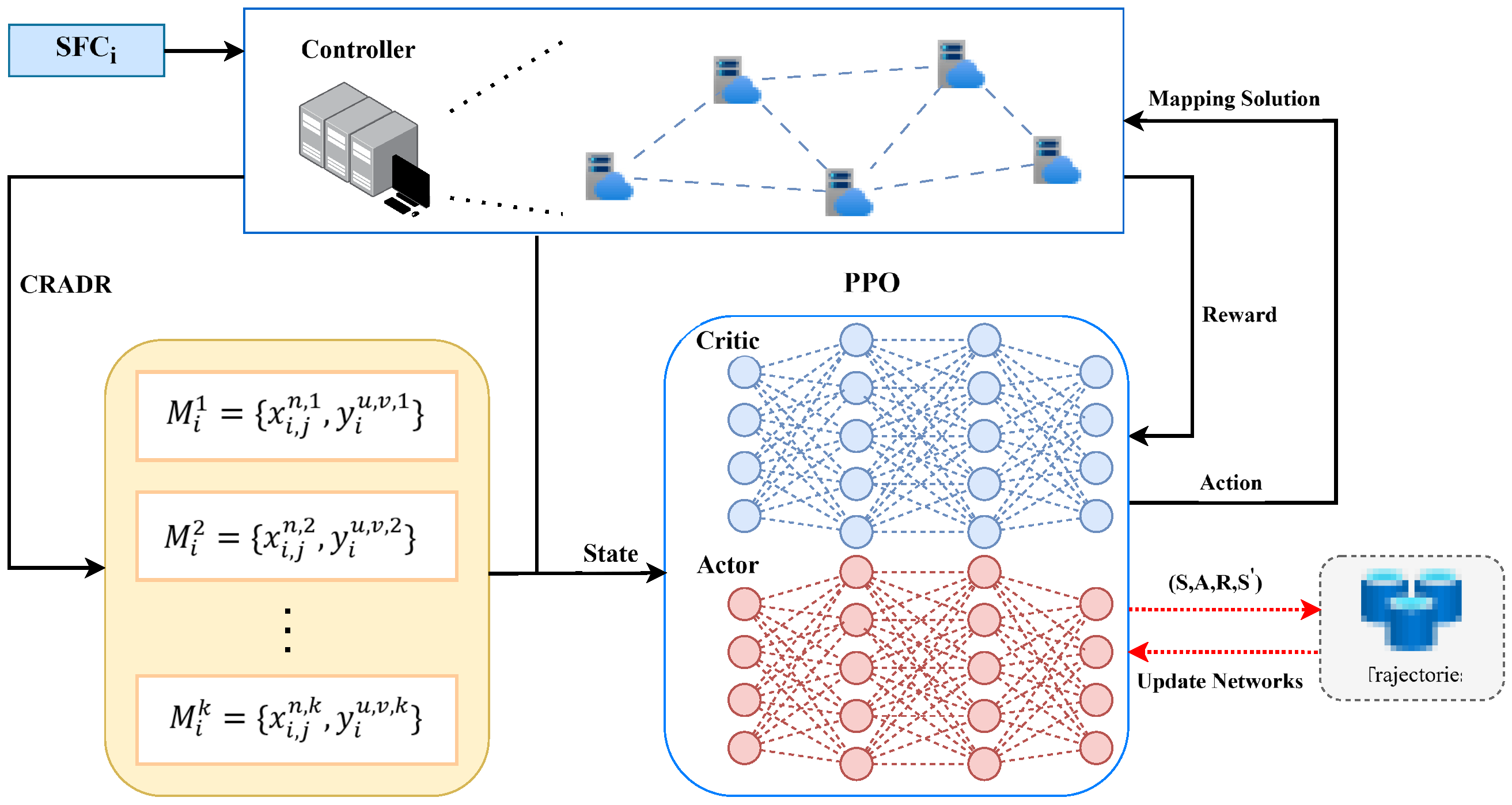
In this section, we first propose a Comprehensive Resource-Aware Deployment and Routing Method (CRADR) to directly obtain an SFC deployment plan. We then introduce a DRL-based Fast Joint Mapping Approach for SFC Deployment (DRL-FJM). The overall workflow is illustrated in Figure 2, which will be detailed after introducing the necessary components.

4.1. Comprehensive Resource-Aware Deployment and Routing Method

A complete SFC deployment solution involves both VNF node mapping and traffic routing path mapping. To serve more SFC requests, it is crucial to ensure the efficient utilization of both node computational resources and link bandwidth resources while meeting latency requirements. This necessitates a comprehensive evaluation of both node mapping and link mapping impacts.

To achieve this, we need to ensure that the mapping scheme has adequate computational and bandwidth resources and satisfies latency constraints, while also considering the availability of neighboring resources. Specifically, during the SFC mapping process, the service capacity of a single node or link depends not only on its own capacity but also on the capacity of neighboring nodes or links. Therefore, we use ${\omega }_u^{\prime \mathit{cpu}}$ and ${\omega }_{u,v}^{\prime bw}$ to evaluate the resource potential of nodes and links, respectively.

$${\omega }_u^{\prime \mathit{cpu}}={\omega }_u^{cpu}+{\displaystyle \frac{{\sum }_{v\in N}s{\chi }_{u,v}{\omega }_v^{cpu}}{{\sum }_{v\in N^s}{\chi }_{u,v}}}·(1-{\widehat{\omega }}^{cpu})$$

(11)

$${\omega }_{u,v}^{\prime bw}={\omega }_{u,v}^{bw}+\left({\displaystyle \frac{{\sum }_{n\in N^s}{\chi }_{u,n}{\omega }_{u,n}^{bw}}{{\sum }_{n\in N^s}{\chi }_{u,n}}}+{\displaystyle \frac{{\sum }_{n\in N^s}{\chi }_{v,n}{\omega }_{v,n}^{bw}}{{\sum }_{n\in N^s}{\chi }_{v,n}}}\right)(1-{\widehat{\omega }}^{bw})$$

(12)

where ${\chi }_{u,n}$ indicates whether nodes u and n are neighbors, ${\widehat{\omega }}^{cpu}$ represents the average remaining resource rate of all nodes in the network, and ${\widehat{\omega }}^{bw}$ represents the average remaining resource rate of all links in the network:

$${\chi }_{u,n}=\left\{\begin{array}{cc}1,\hfill & \mathrm{node}u\mathrm{is}\mathrm{a}\mathrm{neighbor}\mathrm{of}\mathrm{node}n\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(13)

$${\widehat{\omega }}^{cpu}={\displaystyle \frac{{\sum }_{n\in N^S}\frac{{\omega }_n^{cpu}}{c_n}}{|N^S|}}$$

(14)

$${\widehat{\omega }}^{bw}={\displaystyle \frac{{\sum }_{e_{u,v}\in E^s}\frac{{\omega }_{u,v}^{bw}}{b_{u,v}}}{|N^S|}}$$

(15)

Next, we propose an SFC Deployment Solution Metric (DSM) to evaluate the overall impact of the deployment plan. The DSM consists of two components: the Node Mapping Metric (NMM) and the Link Mapping Metric (LMM), where NMM assesses the impact of node mapping, and LMM assesses the impact of link mapping. Thus, for a mapping plan $M_i^k=\{x_{i,j}^{n,k},y_i^{u,v,k}|v_{i,j}\in V_i^v,n\in N^S,e_{u,v}\in E^S\}$ of an SFC $G_i^V$, we have:

$$DSM=(1-{\widehat{\omega }}^{cpu})·NMM+(1-{\widehat{\omega }}^{bw})·LMM$$

(16)

$$NMM=\sum _{j=1}^{|V_i^p|}{\displaystyle \frac{{\phi }_{i,j}^{cpu}}{{\sum }_{n\in N^S}{\omega }_n^{\prime cpu}·x_{i,j}^{n,k}-{\sum }_{m=1}^{j-1}{\sum }_{n\in N^S}{\phi }_{i,m}^{cpu}·x_{i,j}^{n,k}·x_{i,m}^{n,k}}}$$

(17)

$$LMM=\sum _{e_{u,v}\in E^S}{y}_i^{u,v,k}·(1-{\displaystyle \frac{{\omega }_{u,v}^{\prime bw}}{b_{u,v}}})$$

(18)

DSM dynamically considers changes in computational and bandwidth resources based on the network resource status. When the selected node for deployment has fewer available computational resources, the value of DSM will be higher. Similarly, a longer path or lower available bandwidth will result in a higher DSM value. Therefore, by directly searching this metric within the joint solution space of node and link mappings, we can select deployment plans with lower DSM values. This enables a more comprehensive evaluation of the mapping impact and allows us to directly determine the joint node and link mapping plan.

4.2. Definition of DRL Environment

The CRADR method can identify an optimal deployment plan based on the DSM metric for the current network environment. However, due to the rapid and complex variations in network resource states, a plan based on a single fixed metric may not yield a globally optimal deployment. To address this challenge, we employ DRL, which offers strong feature-extraction and decision-making capabilities to determine a long-term optimal SFC deployment plan, maximizing resource utilization and SFC acceptance rates over time.

DRL combines reinforcement learning and deep learning, allowing an agent to learn policies in complex, high-dimensional environments. Through interaction with the environment, the DRL agent takes actions and adjusts based on reward signals, aiming to maximize the expected cumulative reward. Deep neural networks act as function approximators in DRL, helping the agent efficiently estimate state values or action values, thus overcoming the limitations of traditional reinforcement learning in large-scale state spaces. We use a Markov Decision Process (MDP) to model the sequential decision-making of SFC deployment, with three main definitions: state, action, and reward, detailed as follows:

State: In DRL, the state represents the information obtained by the agent from the environment. This includes node resource information, link resource information, current delay information of deployed SFCs, and the characteristic information of the deployment plan returned by CRADR.

Node resource information is represented as $s_i^{node}$, where ${\displaystyle \frac{{\omega }_u^{cpu}}{c_u}}$ represents the remaining resource rate of the node u, and ${\displaystyle \frac{{\omega }_u^{bw}}{b_u}}$ represents the remaining bandwidth resource rate of neighboring nodes:

$$s_i^{node}=\left\{{\displaystyle \frac{{\omega }_u^{cpu}}{c_u}}\right\}\cup \left\{{\displaystyle \frac{{\omega }_u^{bw}}{b_u}}\right\},u\in N^S$$

(19)

$${\omega }_u^{bw}=\sum _{v\in N^S}{\chi }_{u,v}{\omega }_{u,v}^{bw}$$

(20)

$$b_u=\sum _{v\in NS}{\chi }_{u,v}{b}_{u,v}$$

(21)

Link resource information $s_i^{link}$ includes the remaining bandwidth resource rate of the link:

$$s_i^{link}=\left\{{\displaystyle \frac{{\omega }_{u,v}^{bw}}{b_{u,v}}}\right\},e_{u,v}\in E^S$$

(22)

Delay information $s_i^{delay}$ is composed of the maximum delay constraint ratio of non-expired SFCs traversing a given node or link in the current network, indicating the urgency of delay at each node or link:

$$s_i^{delay}=\left\{max\left\{{\displaystyle \frac{{\sum }_{v_{i,j}\in V_i^p}{x}_{i,j}^{n_i}{d}_i\left(t\right)}{t_i^d}}|G_i^V\in G^V\left(t\right)\right\}\right\}\cup \left\{max\left\{{\displaystyle \frac{{\sum }_{v_{i,j}\in V_i^p}{y}_i^{u,v,t}{d}_i\left(t\right)}{t_i^d}}|G_i^V\in G^V\left(t\right)\right\}\right\},n\in N^S,e_{u,v}\in E^S$$

(23)

Deployment information $s_i^{solutions}$ indicates the expected usage of node computational resources and link bandwidth resources by each deployment plan:

$$s_i^{solutions}=\left\{{\displaystyle \frac{{\sum }_{v_{i,j}\in V_i^v}{x}_{i,j}^{n,k}{\phi }_{i,j}^{cpu}}{c_n}}\right\}\cup \left\{{\displaystyle \frac{y_i^{u,v,k}{f}_i}{b_{u,v}}}\right\},n\in N^S,e_{u,v}\in E^S,M_i^k\in M_i$$

(24)

Therefore, the final state information $s_i$ can be represented as:

$$s_i=s_i^{node}\cup s_i^{link}\cup s_i^{delay}\cup s_i^{solutions}$$

(25)

These elements are chosen to ensure that the agent has a complete and dynamic view of both the current network conditions and the implications of each possible action. This design enables the agent to effectively evaluate trade-offs between resource usage, path selection, and latency compliance, thus aligning with the goal of maximizing SFC acceptance under multiple constraints.

Action: DRL-FJM aims to perceive network load status and SFC deployment information and select an SFC deployment plan among K options. Thus, the decision space is defined as $A=(0,1,...,K-1)$.

Reward: The DRL agent improves its performance by continually receiving rewards from the environment. The reward function reflects the extent to which the current action meets the objectives and is used to evaluate the action taken. Our goal is to maximize the acceptance of SFC requests, thus the reward is defined as $r_i=z_i$, where $z_i$ is the deployment result defined in Equation (3). This design directly reflects the optimization objective, as the accumulated reward corresponds to the total number of successful deployments.

4.3. DRL-Based Fast Joint Mapping Approach for SFC Deployment

We use a Proximal Policy Optimization (PPO)-based DRL algorithm to make deployment plan decisions for SFCs [20]. Proximal Policy Optimization is a policy-gradient-based deep reinforcement learning algorithm that is widely used to solve complex decision optimization problems. PPO introduces a clipping mechanism to control the change in policies during updates effectively, ensuring stability and efficiency in policy updates. PPO employs an Actor–Critic architecture, which includes two core neural networks: an Actor network and a Critic network. The Actor network is responsible for generating a probability distribution of actions, while the Critic network estimates the value of the current state.

The Actor network generates a probability distribution ${\pi }_{\theta }\left(a_t\right|s_t)$ of actions $a_t$ based on the current state $s_t$. Its primary goal is to update the policy by maximizing a clipped objective function, ensuring that the change between the new and old policies is not too large. The objective function for updating the policy network is defined as:

$$L^{CLIP}\left(\theta \right)={\mathbb{E}}_t\left[min\left(r_t\left(\theta \right){\widehat{A}}_t,\mathrm{clip}\left(r_t\left(\theta \right),1-ϵ,1+ϵ\right){\widehat{A}}_t\right)\right]$$

(26)

where $r_t\left(\theta \right)$ is the probability ratio between the new and old policies, and ${\widehat{A}}_t$ is the advantage function, which measures the superiority of taking a specific action in the current state:

$$r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{\mathrm{old}}}\left(a_t\right|s_t)}}$$

(27)

$${\widehat{A}}_t=r_t+\gamma V_{\varphi }\left(s_{t+1}\right)-V_{\varphi }\left(s_t\right)$$

(28)

PPO introduces clipping to control the magnitude of policy updates, limiting the update ratio $r_t\left(\theta \right)$ to the range $[1-ϵ,1+ϵ]$, to prevent instability due to drastic changes in the policy. By maximizing $L^{CLIP}\left(\theta \right)$, the Actor network gradually improves the policy, converging to a better policy over multiple iterations.

The Critic network estimates the value of the current state $s_t$ as $V_{\varphi }\left(s_t\right)$ to assist the Actor network in making better action choices. The Critic network updates its parameters by minimizing the Mean Squared Error (MSE) of value estimation, enhancing the accuracy of state value prediction. Its optimization objective function is:

$$L^{VF}\left(\varphi \right)={\mathbb{E}}_t\left[{\left(V_{\varphi }\left(s_t\right)-{\widehat{R}}_t\right)}^2\right]$$

(29)

where ${\widehat{R}}_t$ represents the target return, given by:

$${\widehat{R}}_t=r_t+\gamma V_{\varphi }\left(s_{t+1}\right)$$

(30)

By minimizing the MSE between the state value $V_{\varphi }\left(s_t\right)$ and the target return ${\widehat{R}}_t$, the Critic network continuously corrects its value estimation, providing more accurate value references for policy optimization.

The overall optimization goal of PPO is to optimize both the Actor network and the Critic network while incorporating an entropy regularization term to enhance exploration and prevent the policy from prematurely converging to a local optimum. The overall loss function of PPO can be expressed as:

$$L^{PPO}(\theta ,\varphi )=L^{CLIP}\left(\theta \right)-c_1{L}^{VF}\left(\varphi \right)+c_{2}H\left({\pi }_{\theta }\right)$$

(31)

where $H\left({\pi }_{\theta }\right)$ is the entropy regularization term, used to increase the randomness of the policy, defined as:

$$H\left({\pi }_{\theta }\right)=-\sum _a{\pi }_{\theta }\left(a\right|s)\log {\pi }_{\theta }\left(a\right|s)$$

(32)

In the above equation, $c_1$ and $c_2$ are important coefficients that adjust the value loss and the entropy regularization term. By optimizing this overall loss function, PPO adjusts both the Actor and Critic networks simultaneously, ensuring that policy optimization and value estimation improve in tandem, striking a balance between exploration and exploitation.

Based on the above design, we propose the DRL-FJM algorithm (as shown in Algorithm 1). Figure 2 illustrates its workflow. First, at the beginning of each time step, we release resources occupied by expired SFCs in the network. Then, we use CRADR to generate a set of deployment plans $M_i=\langle M_i^1,M_i^2,\dots ,M_i^K\rangle$ (steps 7–8 in Algorithm 1), obtaining deployment plans based on network resource information and delay information. Next, the deployment plan is executed, obtaining a new state and immediate reward, and recording the transition.

During the network parameter update phase, we jointly optimize the networks through gradient ascent for the Actor network and gradient descent for the Critic network (steps 16–19 in Algorithm 1), simultaneously improving the policy performance and the accuracy of value prediction in each epoch.

The computational complexity of DRL-FJM is primarily determined by two components: the candidate deployment generation and the PPO-based decision step. The CRADR module generates K candidate deployment schemes in polynomial time relative to the size of the substrate network. The PPO model then selects the final deployment from these K candidates with a forward pass through the neural network. Therefore, the approach remains efficient and applicable in real-time deployment scenarios.

Algorithm 1 DRL-FJM Algorithm

Require:  Learning rate $\alpha$, remaining bandwidth and computational resources, SFC requests, maximum steps per epoch Ensure:  Actor network parameters $\theta$, Critic network parameters $\varphi$   1: Initialize policy network $\theta$ and value network $\varphi$   2: Initialize an empty replay buffer D   3: for episode $=1$ to MaxEpisodes do   4:     Reset environment   5:     for $t=1$ to MaxTimeSteps do   6:         Release expired SFCs and receive request ${\mathrm{req}}_i$   7:         Use CRADR to generate candidate deployment plans $M_i$   8:         Obtain resource state and compute current state $s_t$   9:         Input $s_t$ to policy network to obtain ${\pi }_{\theta }\left(a_t\right|s_t)$ 10:         Sample action $a_t\sim {\pi }_{\theta }\left(a_t\right|s_t)$ 11:         Execute action $a_t$ and deploy in simulator 12:         Observe $r_t$, $s_{t+1}$, and completion flag 13:         Store transition $(s_t,a_t,r_t,s_{t+1})$ in D 14:         if $tmodK=0$ then 15:            Compute ${\widehat{A}}_t$ and ${\widehat{R}}_t$ for each transition in D 16:            Update parameters: 17:                $\theta \leftarrow \theta +{\alpha }_A{\nabla }_{\theta }{L}^{PPO}(\theta ,\varphi )$ 18:                $\varphi \leftarrow \varphi +{\alpha }_C{\nabla }_{\varphi }{L}^{PPO}(\theta ,\varphi )$ 19:         end if 20:         Update old policy ${\theta }_{\mathrm{old}}\leftarrow \theta$ 21:         Clear buffer D 22:     end for 23: end for

5. Performance Evaluation

In this section, we evaluate the performance of our proposed DRL-FJM algorithm. All simulations were conducted on a computer equipped with a 12th Gen Intel^® Core™ i9-12900H CPU @ 2.50 GHz and an NVIDIA GeForce RTX 3070 GPU.

5.1. Simulation Environment

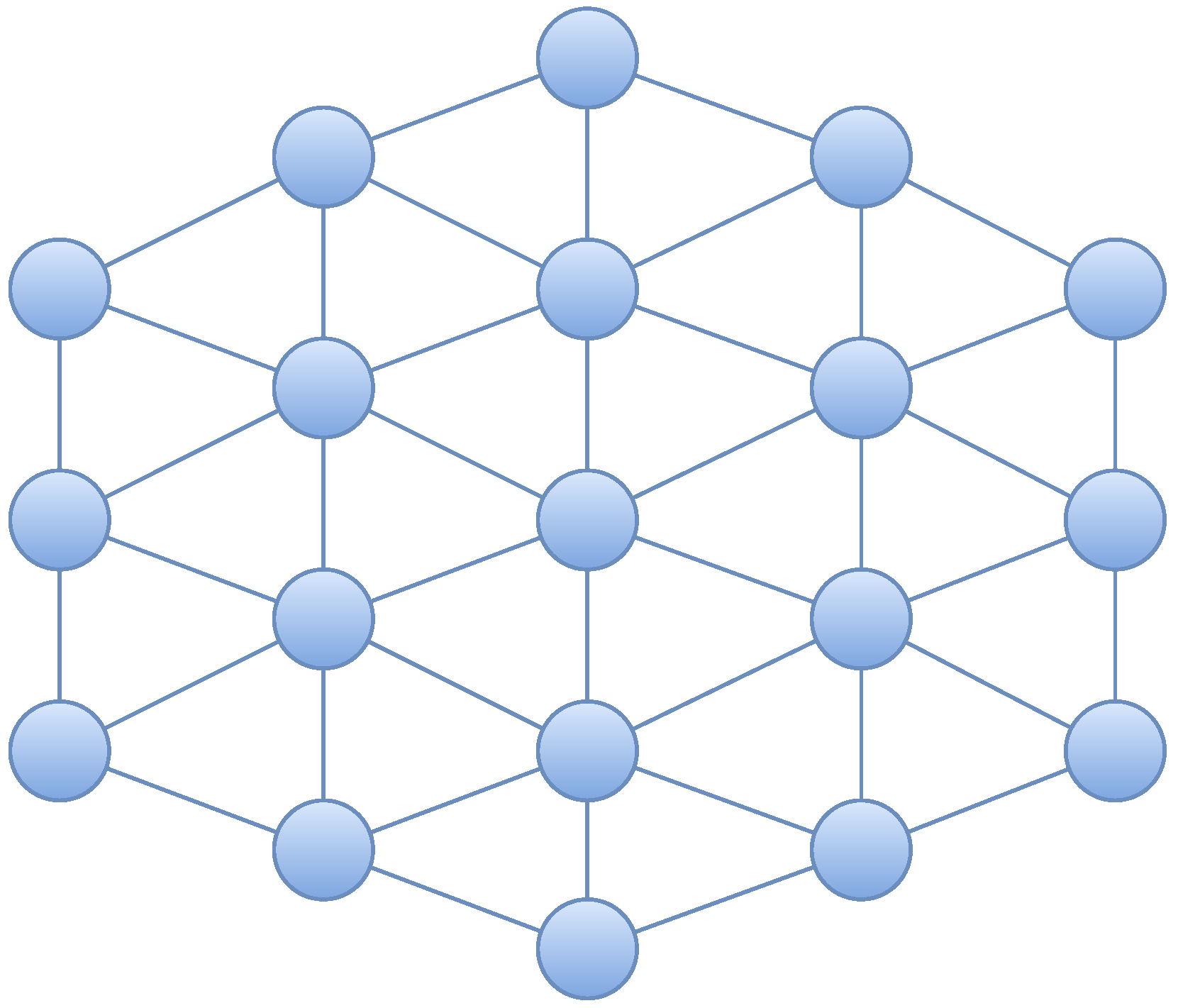
The simulation experiments were conducted using SFCSim [21], an open-source service function chain orchestration simulation tool, which is built on the NetworkX network simulation library. The simulation employed a cellular network topology, as shown in Figure 3. The cellular network contains 19 nodes and 42 links, with each node capable of establishing links with its neighboring nodes. Each network node is accompanied by an edge computing node with 80 CPU cores. The link bandwidth between nodes is 1 Gbps, the propagation delay is 0.4 ms, and the transmission delay for a single packet is 0.2 ms.

The network provides eight types of VNFs. The CPU resource coefficient for processing each Mbps of traffic by each VNF is uniformly distributed between 0.02 and 0.04 cores. Additionally, we assume that SFC requests arrive sequentially following a Poisson process with an average arrival rate $\lambda =2$. The source and destination nodes of user service chains are randomly generated in the network topology, and the traffic demand follows a uniform distribution U (40 MBps, 50 MBps). The number of VNFs that the traffic needs to pass through ranges between 2 and 5.

Furthermore, DRL is implemented using PyTorch 2.2.1, and the relevant parameter settings are shown in

Table 1. Parameters of the DRL model.

Parameter	Value	Description
${\alpha }_A$	$1\times {10}^{-4}$	The learning rate of $\theta$
${\alpha }_C$	$3\times {10}^{-4}$	The learning rate of $\varphi$
$\gamma$	$0.995$	The discount factor
$c_1$	$0.5$	The value function coefficient
$c_2$	$0.01$	The entropy coefficient
U	256	The number of units in fully-connected layers

. The Actor and Critic networks are built using three fully connected layers, with ReLU activation functions. The learning rates for the Actor and Critic networks were selected empirically. A higher learning rate was used for the Actor network to facilitate efficient policy exploration, while a lower rate for the Critic network ensured stable and accurate value estimation. This configuration aligns with common settings in Actor–Critic reinforcement learning methods. In testing phase, we evaluate the performance using 2000 SFC requests.

5.2. Compared Algorithms

To validate the effectiveness of DRL-FJM, we compare it with the following four baselines:

• PPO-Deployment: A node mapping algorithm that uses a PPO-based DRL model to select suitable VNF deployment nodes and then connects the VNFs using the shortest path.
• PPO-Routing: A link mapping scheme that uses a PPO-based DRL model to select appropriate traffic routing paths, followed by selecting nodes with the highest remaining computational resources along the path to deploy VNFs.
• CRADR-Random: Randomly selects one deployment plan from K generated by the CRADR algorithm.
• CRADR-Greedy: Selects the optimal deployment plan computed by the CRADR algorithm for deployment.

5.3. Performance Comparison

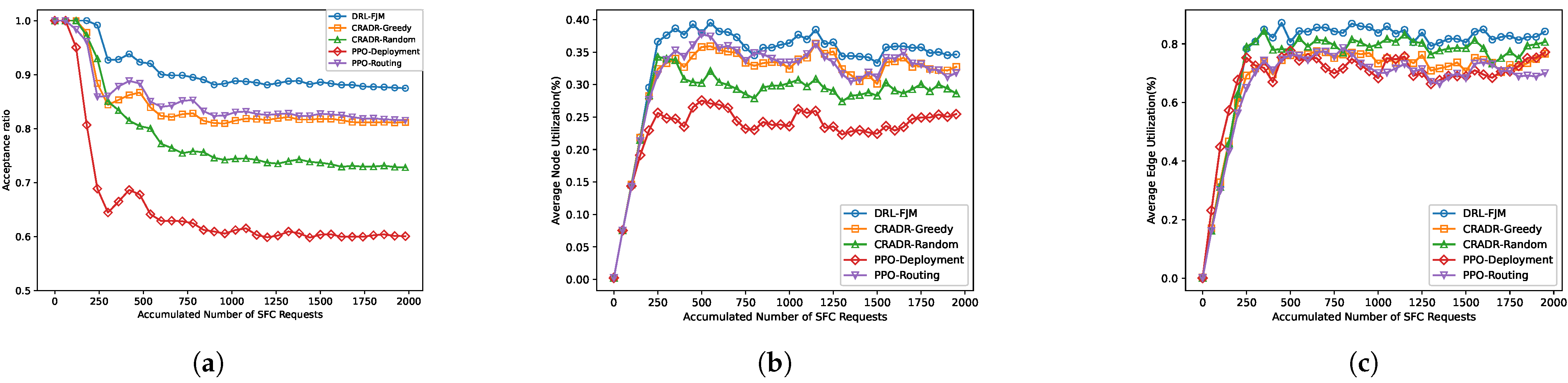
As shown in Figure 4, we evaluate the performance of the DRL-FJM algorithm under balanced network resource conditions. Figure 4a shows the acceptance ratio of SFC requests as they arrive sequentially. It can be observed that, when the number of SFC arrivals reaches 2000, CRADR-Random and CRADR-Greedy outperform the DRL-based node and link mapping algorithms, indicating that the CRADR approach effectively considers both computational and bandwidth resources, enabling a more reasonable end-to-end SFC deployment solution. Furthermore, the DRL-FJM algorithm dynamically perceives resource and latency conditions in the network, selecting a more optimal SFC deployment solution, achieving an acceptance rate close to 100%, which is superior to CRADR-Greedy (89%) and CRADR-Random (85%). This high acceptance ratio is not an isolated result. As demonstrated in Figure 5, Figure 6, Figure 7 and Figure 8, DRL-FJM consistently demonstrates superior adaptability and resource awareness under varying constraints and traffic patterns. These results jointly confirm that the excellent acceptance performance observed in Figure 4 reflects a robust and generalizable policy, rather than case-specific overfitting. This demonstrates the effectiveness of the neural network structure and reinforcement learning’s feature extraction and decision-making capabilities in DRL-FJM for improving deployment outcomes.

Figure 4b shows the total traffic served by different algorithms over time slots. It can be seen that DRL-FJM can serve more SFC requests simultaneously under the same network resources, with an average service traffic 42.6% higher than that of the PPO-Deployment algorithm and 30.7% higher than that of the PPO-Routing algorithm.

Figure 4c,d show the average utilization of node computational resources and link bandwidth resources, respectively, as SFC requests continue to arrive. As can be seen, while the PPO-Deployment algorithm takes node computing capabilities into account, it can cause detours, resulting in bandwidth wastage. The PPO-Routing algorithm, while effectively considering path length, leads to rapid depletion of resources on some nodes and links, resulting in lower overall resource utilization. Our DRL-FJM algorithm comprehensively perceives global network resources to intelligently decide deployment plans, ensuring efficient utilization of both node and bandwidth resources.

Figure 5 and Figure 6 evaluate the performance of the algorithms under limited computing resources and limited bandwidth scenarios, respectively. In Figure 5, when computing resources are scarce and bandwidth resources are abundant, the deployment success rates of CRADR-Random, CRADR-Greedy, and DRL-FJM are 3.7%, 7.4%, and 10.5% higher, respectively, compared to the node and link mapping algorithms. Regarding resource utilization, PPO-Routing and PPO-Deployment have similar acceptance rates but use less bandwidth, demonstrating some advantage in link resource utilization. DRL-FJM selects paths that better satisfy computational resource requirements, improving SFC acceptance rates under scarce computing resources. In Figure 6, when computing resources are sufficient but bandwidth resources are limited, node-first mapping schemes perform poorly. DRL-FJM achieves higher overall resource utilization and SFC acceptance rates.

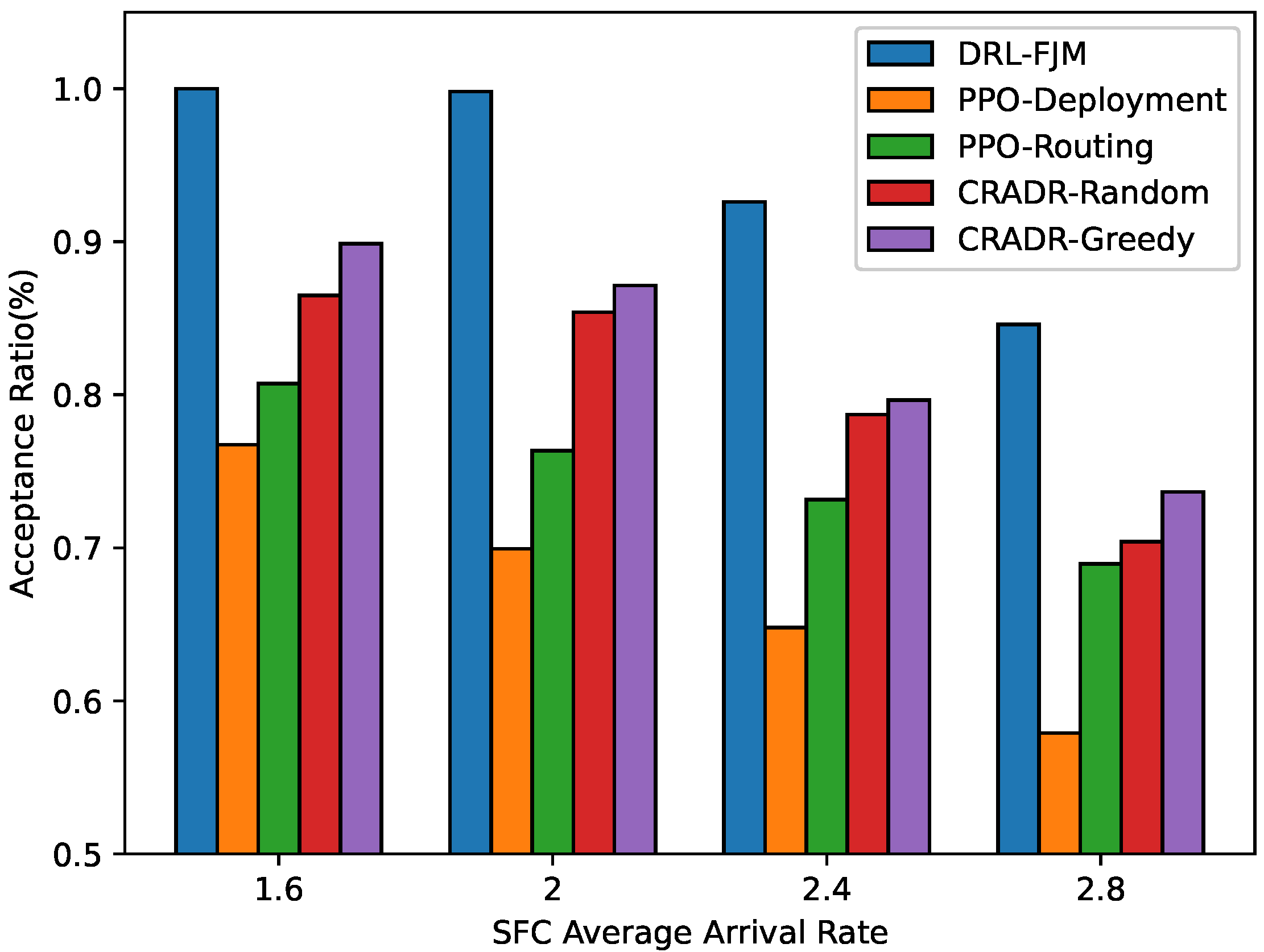
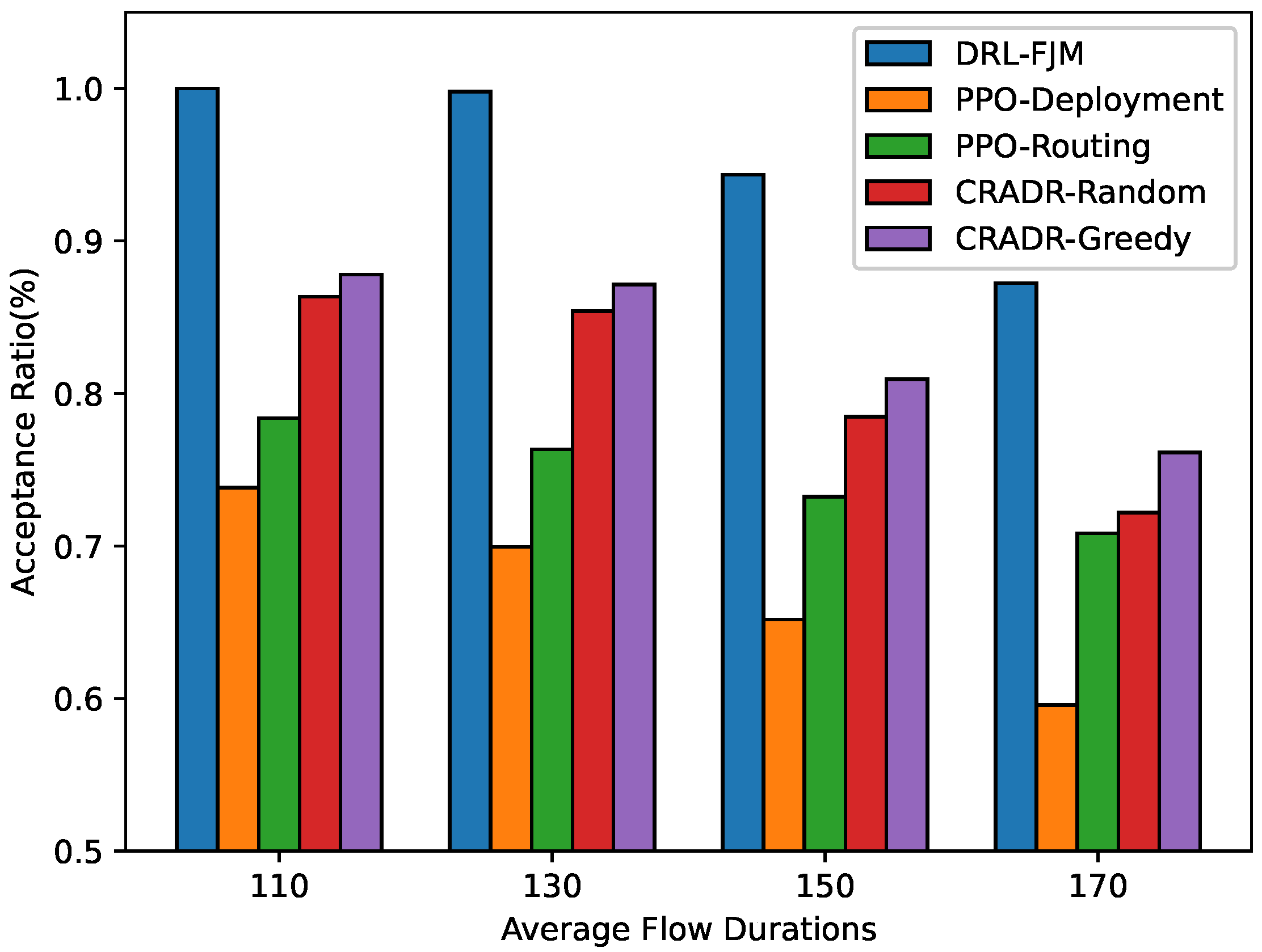
We also examine the impact of different average SFC arrival rates and flow durations, as shown in Figure 7 and Figure 8. As the arrival rate increases, the SFC acceptance ratio gradually decreases. It is noteworthy that increasing the average SFC arrival rate and average flow duration has a similar effect on the acceptance ratio. This is because, assuming sufficient computing and bandwidth resources, Little’s Law indicates that the expected number of SFCs present in the network at each time slot is proportional to the product of the average arrival rate and average flow duration. Thus, increasing these parameters results in a greater number of pending SFCs, leading to resource shortages and a decrease in new SFC acceptance. Our DRL-FJM algorithm outperforms other algorithms under different SFC arrival rates and flow durations, demonstrating superior performance and robustness.

6. Conclusions

This paper focuses on the challenges of SFC online deployment, proposing a deep reinforcement learning-based algorithm, called DRL-FJM. The algorithm is designed to maximize the acceptance rate of SFCs while satisfying network resource and latency constraints. First, it searches the evaluation metric for SFC deployment schemes within the joint solution space of node and link mappings to generate multiple end-to-end joint deployment candidates. Based on this, a PPO-based DRL model is employed to select the final deployment plan. By holistically evaluating the network resource state, the algorithm jointly optimizes node and link mappings, effectively capturing the multi-resource and multi-constraint characteristics of the network and enabling more efficient intelligent deployment. Extensive experiments demonstrate that the proposed DRL-FJM algorithm significantly outperforms existing methods, achieving up to 42.6% higher total network service traffic, 17.3% higher node resource utilization, and 26.6% higher link bandwidth utilization. It also reaches a near-100% SFC deployment success rate and demonstrates strong adaptability and robustness across different network resource environments.

For future work, we plan to further assess the algorithm’s performance in ultra-large-scale networks and enhance its speed and efficiency by employing deep reinforcement learning to prune the joint mapping space. Our objective is to achieve faster and more effective deployment solutions. Additionally, we aim to explore dynamic SFC migration and readjustment strategies, thereby extending the applicability of the proposed method to broader business scenarios.