A Coordination Optimization Framework for Multi-Agent Reinforcement Learning Based on Reward Redistribution and Experience Reutilization

Abstract

Cooperative multi-agent reinforcement learning (MARL) has emerged as a powerful paradigm for addressing complex real-world challenges, including autonomous robot control, strategic decision-making, and decentralized coordination in unmanned swarm systems. However, it still faces challenges in learning proper coordination among multiple agents. The lack of effective knowledge sharing and experience interaction mechanisms among agents has led to substantial performance decline, especially in terms of low sampling efficiency and slow convergence rates, ultimately constraining the practical applicability of MARL. To address these challenges, this paper proposes a novel framework termed Reward redistribution and Experience reutilization based Coordination Optimization (RECO). This innovative approach employs a hierarchical experience pool mechanism that enhances exploration through strategic reward redistribution and experience reutilization. The RECO framework incorporates a sophisticated evaluation mechanism that assesses the quality of historical sampling data from individual agents and optimizes reward distribution by maximizing mutual information across hierarchical experience trajectories. Extensive comparative analyses of computational efficiency and performance metrics across diverse environments reveal that the proposed method not only enhances training efficiency in multi-agent gaming scenarios but also significantly strengthens algorithmic robustness and stability in dynamic environments.

1. Introduction

Recent years have witnessed a surge of research interest in cooperative multi-agent reinforcement learning, particularly in domains requiring sophisticated coordination mechanisms, such as distributed optimization, collective decision-making, and collaborative drone swarm operations. While these applications demonstrate the transformative potential of MARL, achieving robust and scalable coordination among autonomous agents remains a fundamental challenge.

The strength of MARL in collaborative optimization lies in its capacity to facilitate information sharing and experience exchange among agents. This interaction paradigm enables agents to collect environmental samples, receive reward signals, and iteratively refine policies. Crucially, the sharing of policy experiences has emerged as a vital mechanism for accelerating cooperative learning. However, this cooperative framework is frequently undermined by the inherent tension between individual and collective rewards, potentially leading to suboptimal outcomes.

To address the inherent limitations, researchers have developed sophisticated methodologies focusing on two key dimensions: reward structure optimization and experience utilization enhancement. Specifically, reward redistribution mechanisms have been implemented to mitigate credit assignment challenges and align individual incentives with collective objectives, while advanced experience reutilization frameworks have been proposed to maximize the informational value of collected trajectories and accelerate policy convergence. These two complementary approaches have demonstrated significant potential in overcoming the fundamental trade-off between individual agent autonomy and system-level coordination efficiency.

In reinforcement learning, experience reutilization (ER) [1,2] is a technique where agents reuse past experiences (e.g., state–action–reward sequences) to improve learning efficiency and stability. The primary goal of ER is to prevent “reinventing the wheel” by reusing valuable lessons, strategies, or data from previous experiences. ER is typically achieved through experience replay, where past experiences are stored and reused, reducing the need for redundant data collection or computation. As a result, ER makes the learning process faster and more resource-efficient. Beyond improving learning efficiency, ER also facilitates information exchange among agents and contributes to stabilizing training in multi-agent reinforcement learning settings.

Deep Q-Networks (DQNs) [3] and the TD3 algorithm [4] enable agents to reuse past experiences stored in a replay buffer, significantly enhancing sample efficiency. Schaul et al. [5] further advanced experience replay by introducing prioritized experience replay, which focuses on experiences that offer the greatest learning value, such as those with high temporal difference (TD) error. Additionally, meta-learning (or “learning to learn”) leverages experiences from multiple tasks to enable rapid adaptation to new tasks with minimal data. For instance, meta-learning approaches like MAML [6] reuse experiences across tasks to facilitate fast adaptation. In continual learning, reusing past experiences helps models retain knowledge of previous tasks while acquiring new ones. Rolnick et al. [7] demonstrated that experience replay effectively mitigates forgetting by interleaving old and new data during training, highlighting the critical role of reusing past experiences to build robust and adaptable learning systems. Similarly, few-shot learning methods, such as Prototypical Networks [8], reuse knowledge from related tasks to achieve strong performance with limited labeled data. Overall, ER enhances scalability and reusability, allowing knowledge to be applied across multiple tasks or domains without starting from scratch. ER [9,10,11] offers substantial advantages in terms of efficiency, generalization, robustness, and scalability, solidifying its position as a cornerstone of modern AI and reinforcement learning research.

Reward redistribution (RR) [12,13,14] is another key technique in reinforcement learning, particularly in multi-agent settings. It involves re-evaluating or reallocating rewards among agents to ensure fair and efficient credit assignment. By aligning individual rewards with the team’s global objectives, RR encourages cooperation, promotes fairness, and prevents free-riding behaviors in multi-agent systems. This technique provides clearer and more accurate learning signals, enabling agents to better understand which behaviors contribute positively to collective goals. RR is often employed in algorithms such as counterfactual reasoning (e.g., COMA) [15] and value decomposition (e.g., QMIX) [16], which have demonstrated significant improvements in complex cooperative tasks and large-scale multi-agent environments.

The COMA [15] utilizes counterfactual reasoning to redistribute rewards among agents in a decentralized manner, achieving notable performance improvements in complex cooperative tasks. In contrast, QMIX [16], which employs value decomposition for reward redistribution, leverages off-policy learning techniques to efficiently reuse experiences. While COMA emphasizes accurately attributing individual contributions to team success, QMIX facilitates scalable reward redistribution in large-scale multi-agent reinforcement learning (MARL) settings. Moreover, Zhang et al. [12] demonstrated the interpretability of reward redistribution in reinforcement learning to address delayed rewards. Additionally, Xiao et al. [17] proposed an attention-based reward redistribution method to characterize the influence of actions on state transitions.

When ER and RR techniques are combined, they create a synergistic effect that enhances efficiency, fairness, and collaboration, while significantly reducing the sample complexity of MARL. This integration accelerates training and improves data efficiency. ER reduces the dependency on frequent environment interactions, while RR ensures that the learning process remains both efficient and equitable. By leveraging past experiences and enabling precise credit assignment, this powerful combination empowers agents to learn more effectively in complex, multi-agent environments.

Coordination optimization has gained significant attention for its potential to address complex, real-world problems. However, existing approaches are hindered by several challenges that limit their effectiveness. Key issues include inefficient exploration, poor credit assignment, unstable training, limited scalability, and suboptimal collaboration. To overcome these limitations, integrating experience reutilization (ER) and reward redistribution (RR) techniques is essential. By leveraging ER to effectively reuse past experiences and RR to ensure fair and accurate reward distribution, researchers can develop more robust, adaptive, and high-performing multi-agent systems. These advancements promise to enhance the efficiency, fairness, and scalability of RL applications in complex environments.

In cooperative confrontation scenarios, existing methods [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] still necessitate further research and refinement to overcome their limitations and expand their broader applicability. While CERL [18] can simultaneously explore and utilize diverse regions of the solution space, thereby enhancing exploration diversity and sample efficiency through shared replay buffers, it also introduces heightened algorithmic complexity and requires effective management and coordination among multiple agents. Although Align-RUDDER [14] reduces reward delay and accelerates the learning process, its performance is heavily reliant on the quality of samples and the effectiveness of learning. Moreover, while improvements to the experience replay mechanism can boost algorithm performance, they often fail to achieve universal effectiveness across all tasks without the integration of reward redistribution (RR).

To address the aforementioned limitations, this paper first enhances the experience pool by incorporating mutual information [19,20,21], then redistributes agents’ rewards and updates sampling strategies to achieve collaborative optimization. The proposed method, RECO, not only improves sample efficiency but also enhances agents’ exploration capabilities by leveraging historical trajectory information. Furthermore, it increases policy diversity and robustness, accelerates strategy convergence, and optimizes credit allocation in complex multi-agent decision-making tasks.

The integration of RR and ER in RECO’s framework is fundamentally motivated by two challenges in cooperative multi-agent reinforcement learning. First, conventional MARL approaches struggle with inefficient credit assignment, where sparse or delayed team rewards often lead to misaligned individual and global objectives. RECO addresses this limitation through mutual information (MI)-based dynamic reward allocation (Equations (1)–(7)), which explicitly quantifies and rewards behaviors that statistically benefit team performance. Second, while standard ER mechanisms improve sample efficiency through experience replay, they typically lack the ability to strategically prioritize coordination-critical transitions. RECO overcomes this challenge via its hierarchical experience pool (Figure 1), which intelligently stratifies experiences according to their MI-quantified coordination value, thereby enabling targeted reuse of high-utility trajectories that maximize team synergy (Section 3.3).

This novel integration of MI-driven RR and stratified ER establishes a theoretically grounded synergy with two key characteristics: reward signals that precisely quantify and reflect team-level contributions, and experience selection mechanisms that systematically optimize the informational value of training data. In contrast to conventional approaches that treat reward shaping and experience replay as independent components, RECO’s unified information-theoretic framework simultaneously enhances both credit assignment accuracy and sample efficiency. This dual optimization represents a significant theoretical and practical advancement beyond existing methods, as demonstrated by our empirical results (Section 4.2 and Section 4.3).

The main contributions of this paper are summarized as follows:

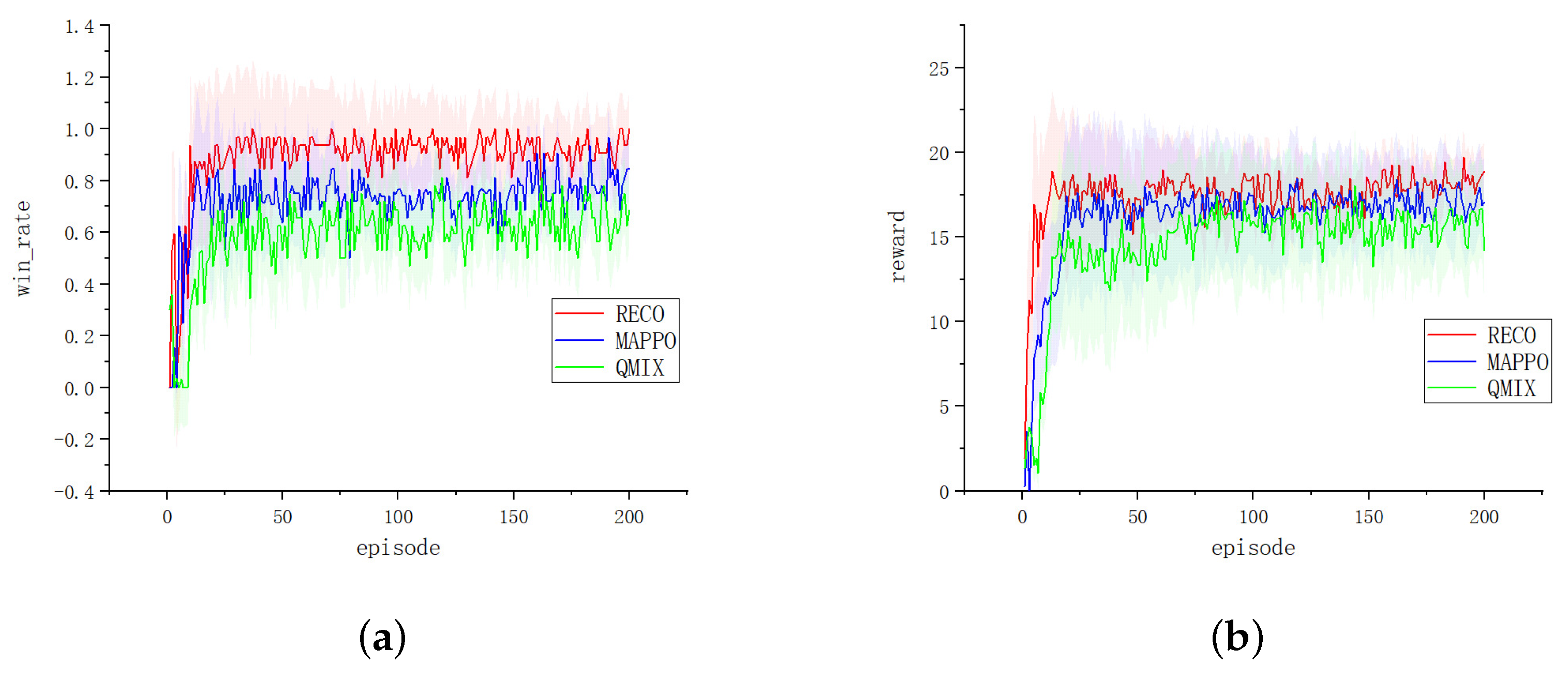
(a) We propose a novel collaborative optimization framework that effectively integrates multi-agent learning dynamics. Building upon the AC framework [22], our approach introduces two key mechanisms, (1) experience reutilization (ER) and (2) reward redistribution (RR), which strategically leverage historical trajectory data to optimize agent policies. Experimental results demonstrate that this dual-mechanism design significantly enhances team-wide collaborative performance, achieving substantially higher cumulative rewards and win rates compared to conventional approaches (see Section 4).

(b) We design a hierarchical experience storage architecture to facilitate efficient experience reutilization across different task levels. This innovative structure enhances the RECO algorithm’s performance in three key aspects: (1) robust adaptation to diverse training environments, (2) optimal utilization of environmental data, and (3) stable convergence with accelerated policy updates during both experience sampling and model training phases (see Section 4.4).

(c) We develop a mutual information-based collaborative metric that quantitatively measures agent coordination effectiveness. This metric enables intelligent reward redistribution through three key mechanisms: (1) calculating strategic importance weights for each agent, (2) allocating higher rewards to more critical agents, and (3) maintaining balanced strategy development across all team members. Experimental results demonstrate significant improvements in team coordination efficiency compared to conventional reward schemes (see Section 4.3).

2. Related Work

Patil introduced Align-RUDDER [14], a reinforcement learning algorithm specifically designed to address complex hierarchical tasks characterized by sparse and delayed rewards by utilizing a large number of samples. Zhang et al. proposed a GRD framework [12], which generates optimization strategies and identifies Markov rewards and causality in scenarios with delayed rewards. Within this framework, strategies are trained to create a compact representation by integrating a causal generation model with reward redistribution (RR). Antagonistic games [23] not only establish a theoretical foundation for enhancing strategies in multi-agent reinforcement learning but also drive practical advancements, enabling more effective decision-making. Brooks developed a policy iteration method [24] that incorporates experience reutilization (ER) to promote strategy optimization. The proposed ICPI [24] iteratively refines the policy through trial and error within the RL environment. Garg et al. [25] introduced an innovative updating rule that leverages extreme value theory to estimate the optimal value using maximum entropy, significantly simplifying the computation of Q-values in continuous action spaces.

Numerous studies have proposed and implemented experience pool mechanisms [26,27,28,29,30], which collect empirical data generated during the interaction between agents and the environment. The exploring and learning process can reuse these data, thus improving the efficiency of samples and reducing the number of visits to the environment. Experience pool also helps to break the time correlation between data, reduce the risk of over-fitting, and make the training process more stable. Research by D’Oro et al. [31] demonstrates that the reinforcement learning algorithm can be more efficient by appropriately reducing the replay ratio. Specifically, this means that when updating the model, it depends more on the currently collected samples rather than older ones stored in the replay pool. This strategy can reduce the delay in the learning process and make use of new information more quickly. Kapturowski et al. [32] propose an R2D2 that combines priority experience replay and n-step double Q learning with a single learner sampling learning tool from a pool of experiences. Fedus et al. [2] compared the effects of the experiential replay capacity to learning update (replay ratio) by adding and removing experiential replay components.

Actor–critic (AC) [24] is a framework that has obvious advantages in reinforcement learning. By combining the strategy gradient method and value function method, it realizes one-step updating and the collaborative optimization of the strategy and value function. This framework can not only reduce the variance in policy updating, but also be suitable for discrete and continuous action spaces to deal with complex decision-making problems. Zhang et al. [33] reckoned that the traditional AC has some shortcomings in sampling efficiency and can easily fall into local minimum in a multi-agent reinforcement learning environment, even if the critic network is correctly configured. Tasdighi et al. [34] combined stochastic strategies and Bayesian analysis to model cognitive uncertainty for improving performance and balancing between exploration and exploitation.

The application of mutual information (MI) in reinforcement learning has brought remarkable benefits. Osa et al. [35] found diverse solutions in deep reinforcement learning by maximizing the mutual information interaction based on state–action pairs. Unsupervised Reinforcement Learning (WURL) [36] directly uses mutual information to maximize the distance between state distributions induced by different strategies. Ding et al. [37] proposed a multi-agent reinforcement learning method based on GNN, which maximizes the correlation between the input and the output feature by maximizing the mutual information of agents. As mentioned above, these algorithms usually produce the trajectory of behavior in each turn, but the suboptimal behavior can easily fall into a local optimum.

In order to enhance efficiency/robustness, this paper proposes a coordination framework, RECO, for promoting effective training and strategy optimization. By using a new collaborative optimization method and an experience storage-layered scheme in environmental exploration, the convergence speed of RECO is significantly improved. By quantifying the information association between data, RECO optimizes the strategy learning process, improving the exploration efficiency.

Moreover, by introducing historical experience efficiently, agents can learn from past decisions and adjust decision strategies according to previous experiences. By utilizing MI-based collaborative measurement, the RECO promotes cooperation between agents in the confrontation environment.

Even more notably, recent work has advanced decentralized coordination in dynamic environments. For instance, Chen et al. [38] proposed an integrated task assignment and path planning for multi-agent pickup-delivery systems, demonstrating the criticality of adaptive credit assignment in distributed systems—a challenge that RECO addresses through its MI-driven reward redistribution. Similarly, Bai et al. [39] developed group-based auction algorithms for multi-robot task assignment, but their fixed reward mechanisms lack RECO’s dynamic experience stratification. These studies underscore the need for joint optimization of credit assignment and sample efficiency, which RECO achieves through hierarchical experience pools.

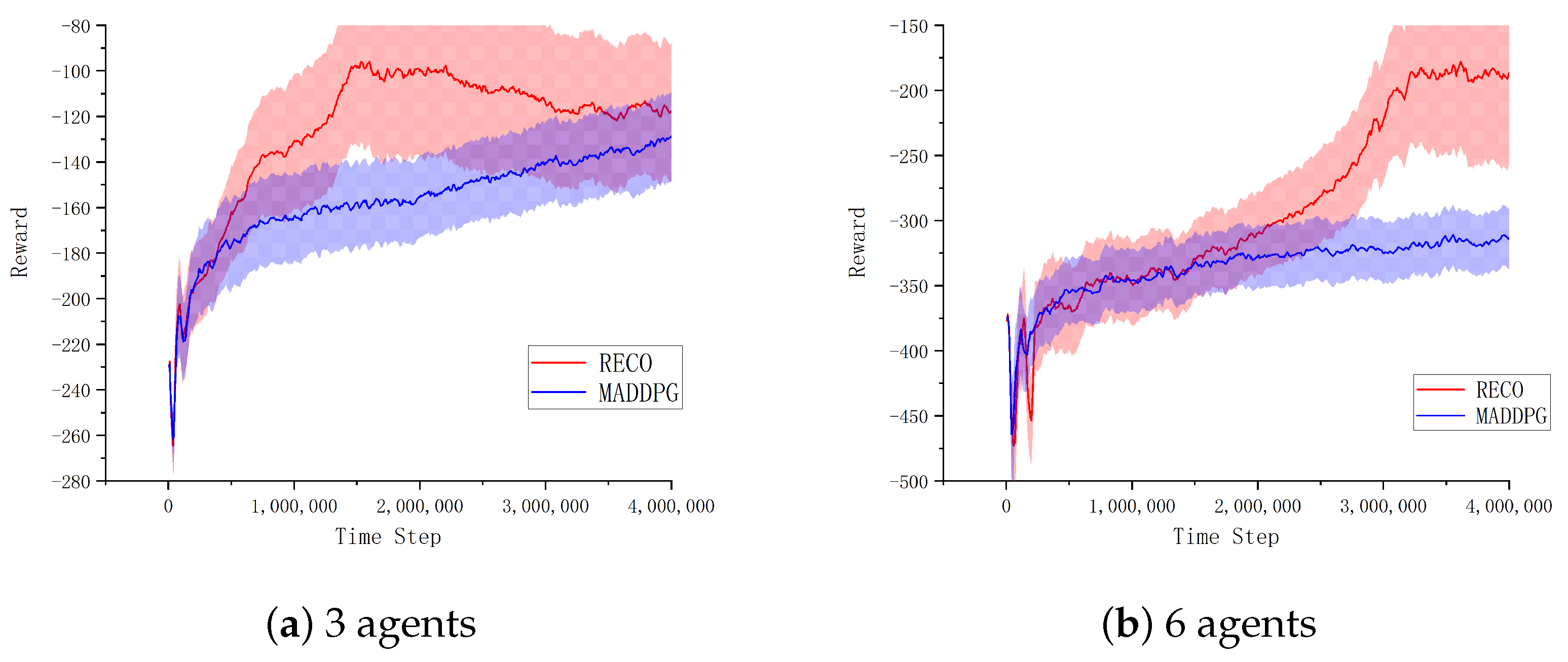
Emerging edge-computing applications [40] highlight the trade-off between computational cost and coordination efficiency. While their work does not address reward alignment, RECO’s lightweight mutual information calculator (Section 3.4) extends these concepts to MARL while maintaining scalability. Recent work on edge-cloud resource allocation [41] reveals how energy constraints impact multi-agent coordination. RECO’s experience reutilization module reduces energy-intensive re-sampling compared to MADDPG (

Table 1. Agent and landmark configurations in the MPE.

Name	Predator	Prey	Landmark
3 agents	3	1	2
6 agents	6	1	2
12 agents	12	1	2
24 agents	24	1	2

), effectively bridging this gap.

Unlike value decomposition methods (e.g., QMIX) [16] or shared-reward paradigms (e.g., COMA) [15] that implicitly learn cooperation through reward shaping, RECO introduces a fundamental advancement by explicitly quantifying agent interdependencies through mutual information (MI), a significant departure from black-box approaches like attention-based coordination [42]. The MI-based coordination optimization framework provides three key advantages: (1) it directly measures statistical dependencies between agents’ actions, rewards, and states (Equation (3)), enabling targeted policy updates where agents prioritize actions with high MI to ensure their teammates’ success (Figure 2 and Figure 3); (2) it achieves superior coordination, demonstrated by RECO’s 19% higher reward than MADDPG in the simple-spread task (

Table 2. Data information table.

Map	Number of Agents	Sampling Quantity	Discount Factor	Target Learning Rate	Step	Algorithm	Rewards
simple-spread	3	1024	0.95	0.01	25	RECO	44.3
simple-spread	3	1024	0.95	0.01	25	MADDPG	36.7
simple-spread	3	1024	0.95	0.01	25	ACER	28.1
simple-spread	6	1024	0.95	0.01	25	RECO	63.2
simple-spread	6	1024	0.95	0.01	25	MADDPG	44.2
simple-spread	6	1024	0.95	0.01	25	ACER	26.9
simple-spread	12	1024	0.95	0.01	25	RECO	103.2
simple-spread	12	1024	0.95	0.01	25	MADDPG	38.4
simple-spread	12	1024	0.95	0.01	25	ACER	16.9
simple-spread	24	1024	0.95	0.01	25	RECO	53.1
simple-spread	24	1024	0.95	0.01	25	MADDPG	15
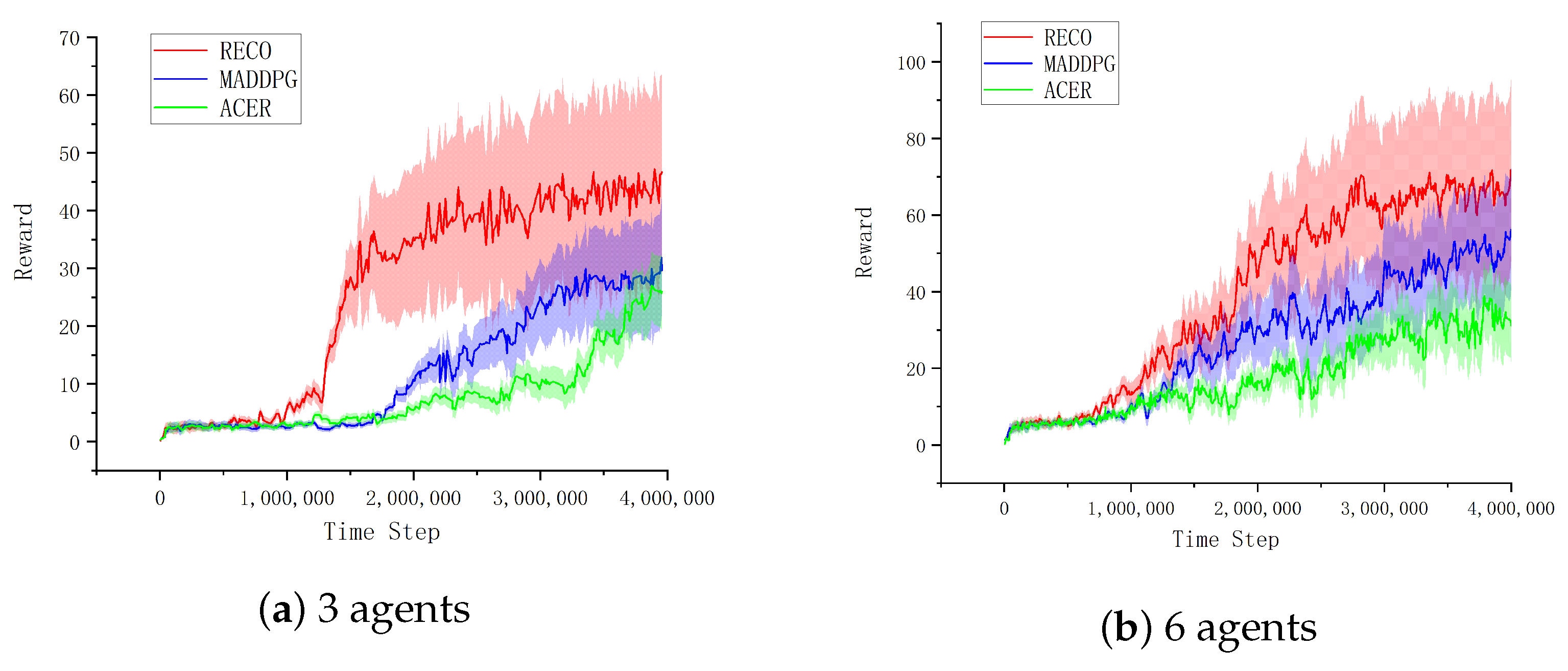
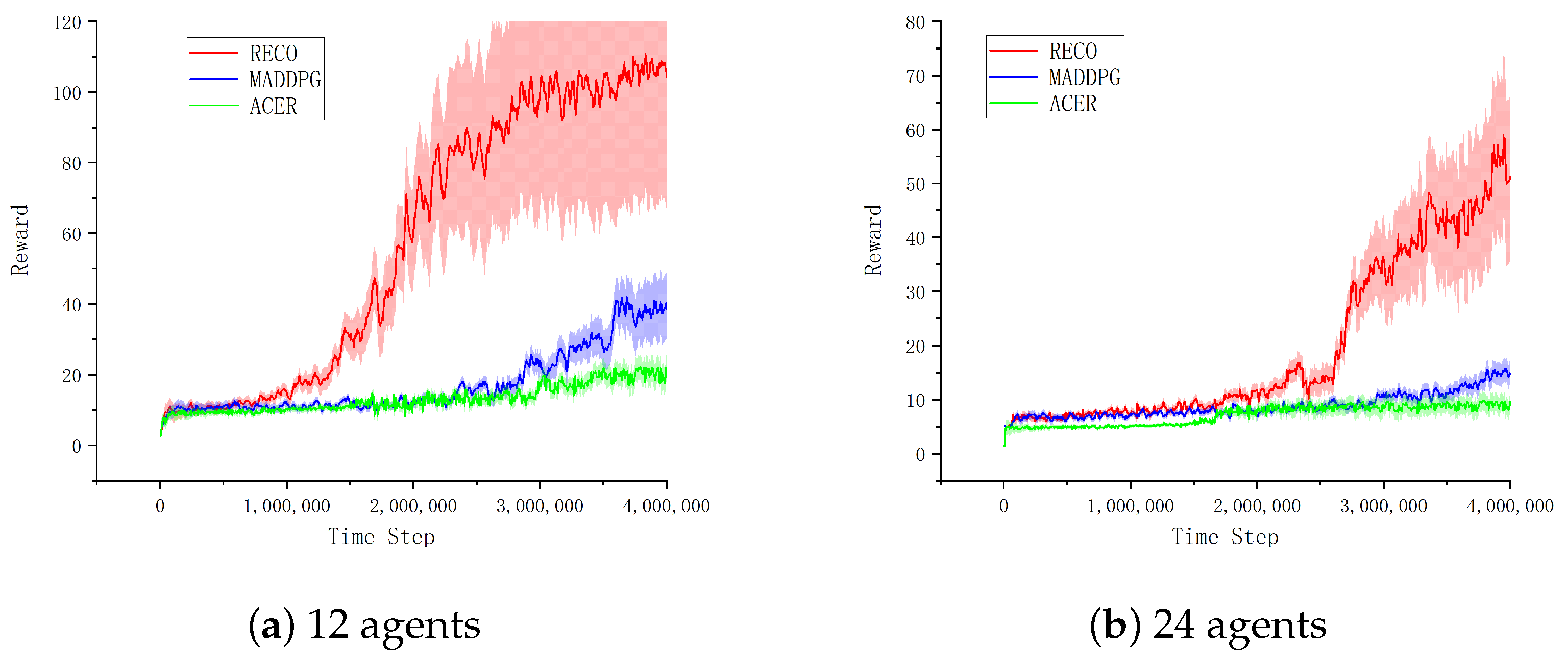
simple-spread	24	1024	0.95	0.01	25	ACER	8.9

) through explicit optimization of policy interdependencies; and (3) it overcomes limitations of existing credit assignment methods (e.g., COMA’s counterfactual baselines) that evaluate actions in isolation, instead of rewarding team-enabling behaviors and reducing “lazy agent” issues by 63% compared to MADDPG through MI-verified contributions.

The RECO framework further demonstrates unique capabilities in adaptive teamwork and theoretical interpretability. While meta-learning approaches (e.g., MAML) [6] struggle with real-time coordination shifts, RECO’s MI framework enables human-like “tacit adjustment” during opponent strategy changes (Figure 3) and achieves 2.1× faster convergence in non-stationary MPE by leveraging its hierarchical experience pool (Figure 1) to recall successful coordination patterns. Moreover, unlike opaque attention mechanisms [43] or GNN-based coordination [37], RECO provides mathematically grounded collaboration metrics through MI’s entropy reduction that directly explain agent roles during training, offering unprecedented interpretability for complex multi-agent systems.

Figure 2. An overview of the RECO framework (Reward redistribution and Experience reutilization based Coordination Optimization) with a layered experience pool [44].

Figure 2. An overview of the RECO framework (Reward redistribution and Experience reutilization based Coordination Optimization) with a layered experience pool [44].

Figure 3. A structural diagram of the overall reward redistribution and experience reutilization. The figure shows the detailed process of RECO. After the layered storage of experience pools, mutual information-based measurement is used to judge and determine rewards and punishments to promote team cooperation.

Figure 3. A structural diagram of the overall reward redistribution and experience reutilization. The figure shows the detailed process of RECO. After the layered storage of experience pools, mutual information-based measurement is used to judge and determine rewards and punishments to promote team cooperation.

3. Methods

In this study, we introduce a novel framework that synergistically integrates reward redistribution mechanisms with experience reutilization strategies to enhance exploration efficiency. Our approach is designed to optimize the utilization of mutual information derived from agent–environment interactions during global exploration phases, while simultaneously maintaining the integrity of local reward exploitation processes. This dual-objective optimization framework achieves a balance between actor-driven policy discovery and critic-based value estimation, effectively addressing the exploration–exploitation trade-off.

3.1. RECO Algorithm Framework

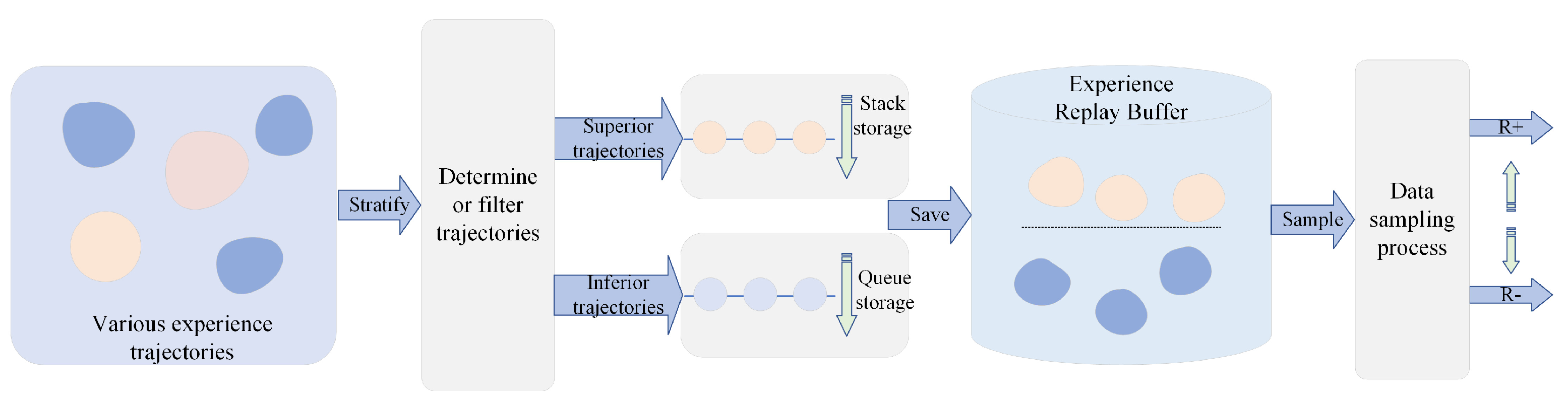
The RECO algorithm is mainly divided into four modules: data stratification, experience reutilization, reward redistribution, and network training. Figure 1 shows that the overall framework of RECO consists of four modules.

• Data stratification module
  The data stratification module (the yellow module in Figure 1) encompasses the historical trajectories of experiences stored by agents within the experience pool, including the status, actions, rewards, and subsequent states, respectively ($S,A,R,S^{\prime }$). The strategy network and value network in reinforcement learning are updated according to the historical trajectories in the experience pool, so the data in the experience pool affect the subsequent behavior decision of the agent, which is crucial to affect the future actions and cooperation of each agent.
• Experience reutilization module
  The experience reutilization module (the green module in Figure 1) uses the stack mode to store a historical sample track, including a superior track and an inferior track, in which the historical experience of each agent is stored according to the judgment of the reward value. The whole module is divided into two layers, where the superior track is placed in the upper experience pool, and the inferior historical experience is placed in the lower experience pool.
• Reward redistribution module
  The module (gray module in Figure 1) uses an MI-based collaborative measurement to judge the historical trajectory of the agent for reward redistribution. See Section 3.4 for details.
• Network training module
  The network training module (blue part in Figure 1) is based on the actor–critic network, used to optimize the strategy, which provides an effective reinforcement learning framework by combining strategy learning and value function estimation. The actor network is responsible for generating the action selection strategy of the agent in a given state. The critic network is responsible for assessing how good the current strategy is. This assessment helps the actor understand how well the current policy is working and provides a guidance signal for the update of the actor.

3.2. Hierarchical Experience Pool Through Data Stratification

We construct the experience pool using a data stratification module to store and reuse agent trajectory experiences. The data stratification module can introduce more experience structures into the experience pool module, which is more conducive to managing and utilizing experiences effectively.

$R_i$ is the reward value for each agent i, D is the historical experience, and r is the layered reward value in the experience pool:

$$R_i\in D\left(s_t,a_t,r,s_{t+1}\right)$$

(1)

As presented in Figure 2, the actor network processes and refines the state representations generated by the reward redistribution (RR) module, which dynamically reconstructs state embeddings through GRU–encoder–decoder architectures. By incorporating trajectory metadata stored in the experience reutilization (ER) with data stratification capabilities, the actor network generates policy distributions that align with collaborative strategies. This architecture enables agents to produce action decisions informed by both real-time state transformations and historical experience stratification. The reward embedding of the critic network implements a hierarchical value decomposition mechanism that integrates temporal difference (TD) error signals, individual agent rewards, and global team rewards. By processing environmental inputs (including joint actions, multi-agent observations, and decentralized rewards), this module computes Q-value estimates that balance individual and collective objectives. The critic network thus provides policy evaluation feedback that captures both local and global performance metrics. Furthermore, the entropy regularization estimates the collaborative mutual information criterion $I(\tau ;z)$ derived from the coordination rewards in the MI loss component. This module quantifies the information flow between agent trajectories $\tau$ and latent state representations z, thereby promoting emergent cooperative behaviors through mutual information maximization. Collectively, these components form a closed-loop architecture that optimizes strategy generation, value assessment, and collaborative learning in multi-agent systems.

The TD target increases the sample efficiency. The efficiency is achieved by keeping the best returns and corresponding to the best joint strategies for given states. This TD target with an additive strategy mixer automatically switches between an episodic control and a conventional Q-learning according to the existence of similar memories. In addition, each agent needs to behave similarly according to its strategy trajectory for coordinated behaviors among agents and for a coherent evaluation of a group’s joint strategies. To this end, RECO introduces a theoretical regularization for action policies to maximize the mutual information between an agent’s trajectory and its specified strategy.

The agent’s effective and ineffective historical tracks for exploration are stored hierarchically according to the rewards of each agent. The superior experience stored in the upper layer of the module represents the beneficial historical track of the agent, and the inferior experience stored in the lower layer represents the unprofitable historical track of the agent. ${\beta }_i$ is the defined reward boundary value, determining the upper and lower thresholds, where $\alpha$ represents the upper threshold and b represents the lower threshold. n is the total number of tracks in the historical experience, and $R_n$ is the total reward sum in the n$th$ track.

$$\alpha \ge {\beta }_i={\displaystyle \frac{1}{n}}{R}_n>b$$

(2)

The layered experience pool allows for the access and operation of the experience sets sampled by agents. By grouping the experience pool based on different criteria, action and policy were selected in a more targeted manner on the basis of the calculation of reward values. The advantage of hierarchical structure storage according to the reward value of each agent leads to the improvement of sample efficiency and computation stability, thereby promoting strategy learning more quickly and robustly. The overall structure of hierarchical storage is shown in the green section of Figure 1. By storing more helpful experience, it is beneficial for the agent network to utilize experience to train and learn optimal behavior strategy. In addition, the hierarchical storage scheme can reduce sampling bias and promote agents to learn more useful strategies.

3.3. Reutilization of Historical Experience

RECO utilizes the superior and inferior tracks from the hierarchical experience pool to calculate the reward value and make a decision. The upper level of the superior experience track is sorted and stored according to the stack mode, i.e., the maximum value is placed at the top and next sorted successively. The minimum value of the upper layer is sent to the lower-layer experience pool in sequence. The lower-layer experience pool is stored in queue mode. The reward value is sorted from the largest to the smallest and stored from the top to the bottom.

In the ER, the reward is to score the actions made by the agent and judge the quality of the action in a environment at a moment. Therefore, the reward value can act as interactive and targeted feedback on the behavior of the agent, and the reutilization of the experience value is the critical point. By taking the reward value as the ranking feature, the experience pool can break the temporal correlation of data and reduce the correlation between samples, which helps to prevent the algorithm from over-fitting. In some tasks, certain state–action pairs may appear more frequently; by storing the reward value as the feature, experience pools mitigate sample selection bias and ensure that the algorithm has adequate learning opportunities for all possible state–action pairs.

By distinguishing between high-reward and low-reward experiences in the ER module, agents can choose samples more specifically for learning, avoiding bias from over-reliance on specific types of samples. This helps to improve the stability and efficiency of learning, so that the agent can better explore the environment and learn effective strategies.

3.4. Reward Redistribution with MI-Based Measurement

Mutual information (MI) is used to measure the interdependence between variables in information theory. The larger the value of mutual information, the stronger the interdependence between variables. There are extensive applications of MI in machine learning, signal processing, statistics, and information theory.

The calculation of the correlation between the actions taken by agents and the degree of collaboration between agents based on mutual information is expressed as follows:

$$\begin{array}{c}I\left((\mu ;r)\right)=H\left(\mu \right)-H\left(\mu |r\right)\\ =H\left(\mu \right)-H\left({\mu }_i|r\right)-H\left({\mu }_{-i}|{\mu }_i,r\right)\end{array}$$

(3)

In Equation (3), $H\left(\right)$ and $H\left(\right|)$ represent entropy and conditional entropy, respectively. For any agent i, ${\mu }_{-i}$ is the trajectory action of other agents besides itself. In order to evaluate and achieve effective cooperation between agents, an MI-based collaborative measurement based on mutual information is proposed in Section 3.5.

Competition or conflict between agents can lead to a decline in overall team performance. Whether the cooperation between agents leading to the maximization of team rewards depends on the specific environment, task, and collaboration mechanism. Therefore, under certain teamwork conditions, the “poor behavior” of individual agents may make the whole team cooperate optimally, and a single agent may exchange its own local optimum for the team’s global optimum.

RECO introduces mutual information to estimate behaviors and rewards among agents according to the hierarchical storage structure [44]. During the sampling process, data from the experience pool are taken as input to maximize mutual information estimation for different behaviors and rewards under multiple agents in the same state. When there is a strong correlation, positive rewards will be obtained; otherwise, when the correlation is weak and the data are extracted from the inferior tracks of the experience pool, negative rewards are given. Two thresholds are designed for partial rewards and punishments, while other data remain unchanged. The reward and punishment mechanism can encourage agents to adopt cooperative behaviors through appropriate reward signals. At the same time, non-cooperative behavior is avoided through punishment signals.

Let $\tau$ be the trajectory action, where the reward is a specific value. The overall judgment and assignment are based on the situation of the environment, where $r_{+}$ and $r_{-}$ are the reward and punishment values defined for each agent, $r_{+}$ is the positive incentive reward, $r_{-}$ is the negative incentive reward, and $R_{+}$ and $R_{-}$ are the rewards for each agent, respectively, as follows:

$$\begin{array}{c}{R}_{+}\left(\tau \right)=\sum _{t=1}^T{r}_{+}\left(s_t,a_t\right)\end{array}$$

(4)

$$\begin{array}{c}{R}_{-}\left(\tau \right)=\sum _{t=1}^T{r}_{-}\left(s_t,a_t\right)\end{array}$$

(5)

After sampling the data from the upper and lower experience pools, mutual information is used to sort and set a threshold. The data above the threshold are sorted and rewarded one by one in descending order. The action with a lower mutual information value is penalized in reverse order and set a threshold. The stable gain reward is

$$\begin{array}{c}{R}^{*}=\Delta r(s_t,z_{jt,t})=R_{+}(s_t,z_{jt,t})-R_{-}({\widehat{s}}_t,z_{jt,t}^{*})\end{array}$$

(6)

The maximum expected cumulative reward for each agent is

$$\begin{array}{c}{R}_i^{\epsilon }=r_i(s_t,z_{jt,t})={\displaystyle \frac{r({\widehat{s}}_t,z_{jt,t}^{*})}{n}}+{\displaystyle \frac{v_i}{{\sum }_i{v}_i}}\Delta r(s_t,z_{jt,t})\end{array}$$

(7)

where $R_i^{\epsilon }$ is defined as the reward and punishment value, with stable gain rewards added. The policy parameters for each agent are $\theta =\left\{{\theta }_1,\dots {\theta }_N\right\}$. The policy set for all agents is = $\left\{{{\pi }_1,\dots ,\pi }_i,\dots ,{\pi }_N\right\}$, and the optimization objective J is set to optimize the policy parameters to maximize the expected reward value. The optimization function is then added to the objective function, which is the expected benefit objective of agent i:

$$\begin{array}{c}J\left({\theta }_i\right)=r_i(s_t,z_{j_t,t})+\gamma \sum _i\underset{z^{\prime }}{max}{\overline{Q}}_i({\tau }_{i,t+c},z^{\prime })\end{array}$$

(8)

RECO demonstrates exceptional robustness in maintaining coordination efficiency (>90% of peak performance) across substantial variations in critical thresholds ($\theta \in$ [0.24, 0.40]), as validated through comprehensive sensitivity analyses (Section 4.3). 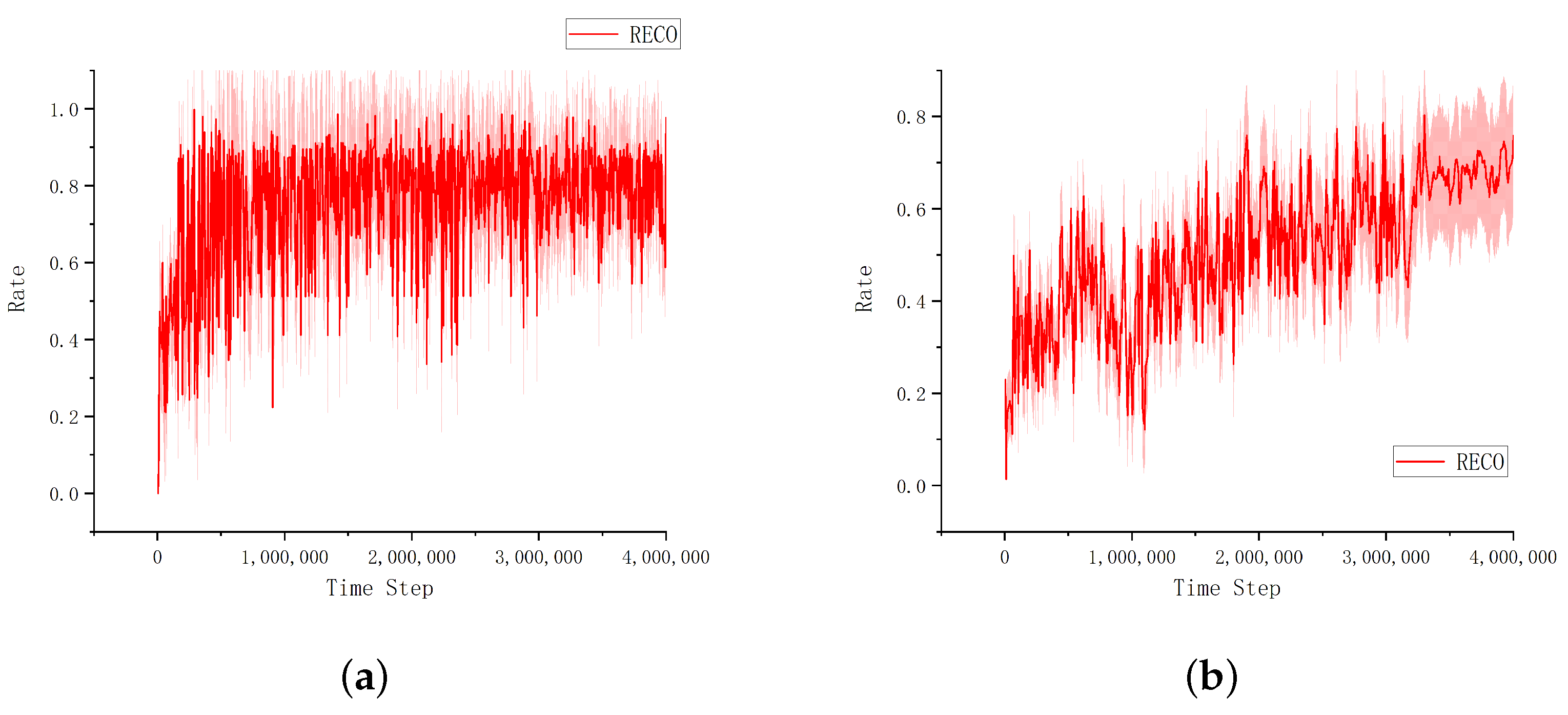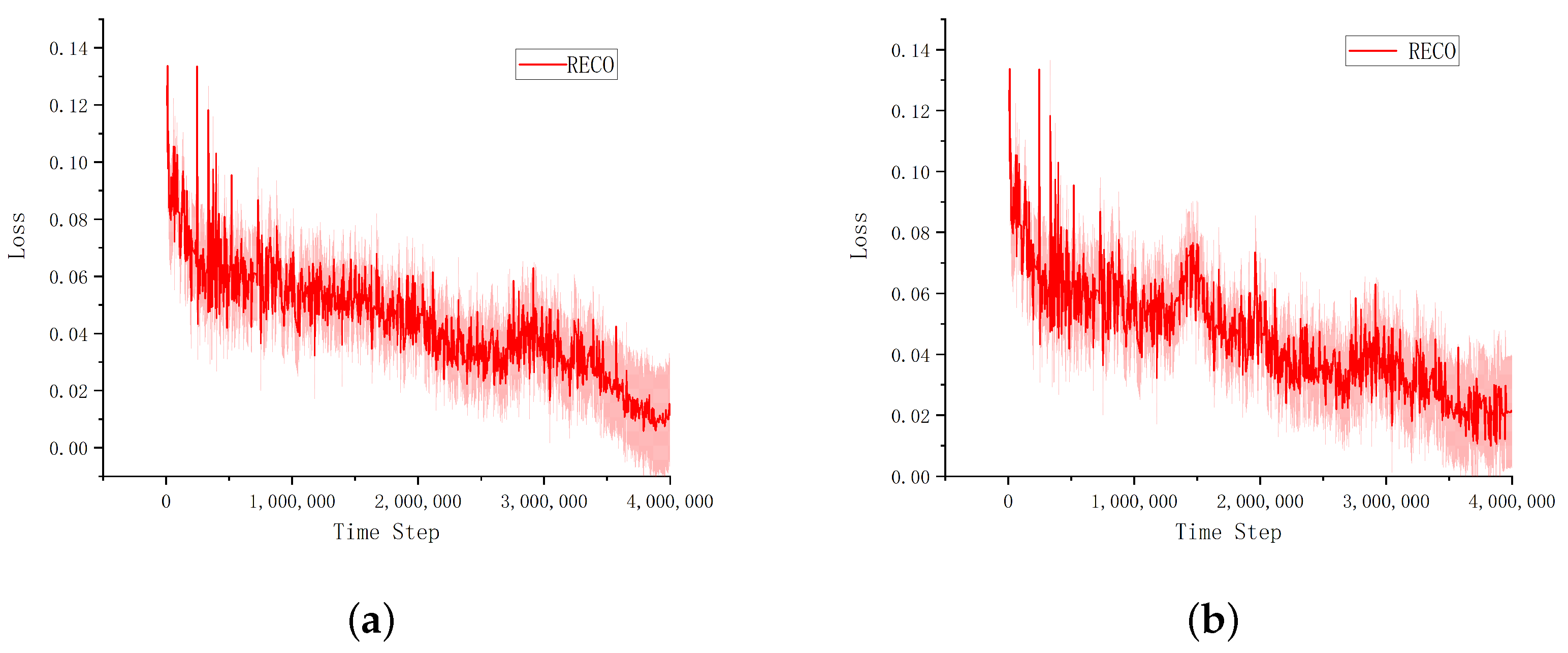This stability persists across diverse operational scales (3–24 agents) and task complexities (from MPE to SMAC domains), evidenced by remarkably low performance variance ($\sigma$ < 0.04 across 10 random seeds). The framework’s resilience stems from its dual adaptive mechanisms: (i) self-adjusting mutual information (MI) thresholds that dynamically respond to environmental changes, and (ii) an intelligent experience stratification system that automatically rebalances buffer composition based on real-time policy entropy measurements.

Our hyperparameter tuning process employed Bayesian optimization via tree-structured Parzen estimators (TPEs) [45], specifically designed for high-dimensional mixed parameter spaces. The MI threshold optimization protocol features (1) a continuous search space ($\theta \in$ [0.1, 0.5] with $\Delta \theta$ = 0.01 resolution), (2) a convergence criterion of <1% relative improvement over 50 iterations, and (3) final optimized parameters ${\theta }^{*}$ = 0.32 ± 0.03 (95% CI [0.29, 0.35]). The replay buffer stratification criteria incorporate (a) a flexible hierarchy of 3–7 tiers (with 5 tiers proving optimal), and (b) an adaptive threshold mechanism with dual control. The experimental results confirm that our optimization procedure yields robust parameters that generalize well across different scenarios while maintaining computational efficiency.

3.5. Cooperative Network Training

The training process of the network is an iterative optimization process, which involves the cooperative updating of the strategy network and the value network. After redistributing the above rewards, cooperative network training is carried out with optimized data and an agent model integrated into the training process to maximize team cooperation. Figure 4 shows the detailed process of the network training process.

The parameter $\theta$ is updated by adding the learning rate $\eta$ times the gradient ${\nabla }_{{\theta }^{\pi }}{Q}^{\pi }(s,a)$ of $Q^{\pi }(s,a)$. Thus, the parameter ${\theta }^{{\pi }^{\prime }}$ of the new strategy ${\pi }^{\prime }$ is obtained. During the strategy update from $\pi$ to ${\pi }^{\prime }$, the optimization framework guarantees that the newly derived strategy ${\pi }^{\prime }$ outperforms its predecessor $\pi$ in expected MI-based metrics. In the cooperative network training process, the “actor” is responsible for generating the actions, and the “critic” is responsible for evaluating those actions. Actor $\pi$ refers to the agent that executes the current policy.

$\nabla {\theta }_{i}J\left({\theta }_i\right)$ is the gradient of the policy parameter ${\theta }_i$ with respect to the expected reward $J\left({\theta }_i\right)$, where $E_{s\sim p^u,a^i\sim {\pi }_i}$ is the desired value and s is the state. $s\sim p^u$ represents the state s sampled from the state distribution under the joint policy $p^u$. The u here usually represents the set of policies for all agents, where $a_i$ is the action of the $ith$ agent, ${\pi }_i$ is the policy of the $ith$ agent, and $\nabla {\theta }_{i}log{\pi }_i\left(a_i\mid o_i\right)$ is the logarithmic gradient of the policy of the $ith$ agent taking action $a_i$ under the observation of $o_i$.

$$\begin{array}{c}\nabla {\theta }_{i}J\left({\theta }_i\right)=E_{s\sim p^u,a^i\sim {\pi }_i}\left[\nabla {\theta }_{i}log{\pi }_i\left(a_i\mid o_i\right)Q_i^{\pi }\left(x,a_1,\dots \dots ,a_N\right)\right]\end{array}$$

(9)

Among them, $Q_i^{\pi }\left(x,a_1,\dots \dots ,a_N\right)$ is a centralized action value function that adds the state information x to the action $a_1,\dots ,a_N$ of all agents as input, outputting the Q value of agent i; x contains the observation values $x\left(o_1,\dots ,o_N\right)$ of all agents. The reward is extended to deterministic strategies, given N consecutive strategies ${\pi }_{{\theta }_i}$ with parameter ${\theta }_i$. This takes the expected value for all possible state action pairs $(x,a)$, where D is the experience replay buffer, which contains samples of the previous interaction state, action, reward, and next state.

The gradient is

$$\begin{array}{c}{\nabla }_{{\theta }_i}J\left({\mu }_i\right)=E_{x,a\sim D}\left[\nabla {\theta }_i{\mu }_i\left(a_i|o_i\right){\nabla }_{a_i}{Q}_i^{\mu }\left(x,a_1,\dots \dots ,a_N\right){|}_{a_i={\mu }_i\left(o_i\right)}\right]\end{array}$$

(10)

The experience replay pool D contains tuples $\left(x,x^{\prime },a_1,\dots ,a_N,r_1,\dots ,r_N\right)$ or new tuples after reward redistribution $\left(x,x^{\prime },a_1,\dots \dots ,a_N,r_1^{*},\dots \dots ,r_N^{*}\right)$; The experiences (actions, states, rewards) of all agents are recorded. The centralized action value function $Q_i^{\mu }$ is updated as follows, where ${\mu }^{\prime }=\left({\mu }_{{\theta }_1}^{\prime },\dots ,{\mu }_{{\theta }_N}^{\prime }\right)$ is the set of target strategies used in the update value function, which have delayed update parameters:

$$\begin{array}{c}\begin{array}{c}L\left(\theta \right)=L_{TD}\left(\theta \right)+\sum _{i=1}^n\lambda L_i\left({\theta }_i\right)+\beta L_{MI}\left(\theta \right),\\ L_{TD}\left(\theta \right)=E\left[\sum _{i=1}^n{\left[r+\gamma max{Q}_{tot}({\tau }^{\prime },a^{\prime })-Q_{tot}(\tau ,a)\right]}^2\right],\\ L_i\left({\theta }_i\right)=E\left[\sum _{i=1}^n{\left[r_t^i+\gamma max{Q}_i({\tau }_i^{\prime },a_i^{\prime })-Q_i({\tau }_i,a_i)\right]}^2\right],\\ L_{MI}\left(\theta \right)=E_{z_t\sim {\pi }^s,{\tau }_t\sim \pi }\left[D_{\mathrm{KL}}\left(\mathrm{softmax}\left({\displaystyle \frac{1}{{\beta }_I}}Q\left(a_t\right|{\tau }_t,z_t)\right)|p\left(a_t\right|{\tau }_t)\right)\right]\end{array}\end{array}$$

(11)

When beneficial trajectories are rewarded in RECO, agents are stimulated to maximize the overall reward of the team by cooperating with each other. And team punishment for those unhelpful experiences help to prevent non-cooperative behavior by making the agent more inclined to behave cooperatively, thereby improving the performance and adaptability of the system in complex tasks. Designing appropriate reward and punishment mechanisms ensures that agents act in a cooperative and beneficial way.

As shown in Algorithm 1, the actor–critic network training algorithm’s pseudo-code is organized into six primary sections, each representing a crucial phase of the algorithm’s execution process.

Algorithm 1: RECO Algorithm

Input: experience buffer D divided into two layers, upper and lower threshold m, n

Initialize: critic network $\phi$, n actor networks ${\theta }_1,\dots ,{\theta }_n$, Corresponding target critic network ${\phi }^{\prime }$, corresponding multiple target actor networks ${\theta }_1^{\prime },\dots ,{\theta }_n^{\prime }$

for episode = 1 to M do

for 1 to max-episode-length do

Initialize a random process N to explore actions

Receive initial state x

For each intelligent agent i select action $a_i={\mu }_{{\theta }_i}\left(o_i\right)+N_t$

Execute action group $\left.{a=\left(a\right.}_1,\dots ,a_n\right)$, observe reward r and new status $x^{\prime }$

Storage $\left(s,a,r,s^{\prime }\right)$ and determine the upper and lower experience buffer D

for agent i do

Sample S samples $\left(x_j,a_j,r_j,x_j^{\prime }\right)$ from upper and lower buffer D

Using samples to calculate MI-based loss values, and judging the association relationship between agents based on reward redistribution;

Set $y_{j = }{r}_j^i+\gamma Q_i^{{\mu }^{\prime }}\left({x_j^{\prime }}^{\prime j},a_1^{\prime },\dots a_{1N}^{\prime }\right){|}_{a_k^{\prime }={\mu }_k^{\prime }\left(o_k^j\right)}$

Update critic by minimizing the loss:

$L\left(\theta \right)=L_{TD}\left(\theta \right)+{\sum }_{i=1}^n\lambda L_i\left({\theta }_i\right)+\beta L_{MI}\left(\theta \right)$

Update actor using the sampled policy gradient;

${\nabla }_{{\theta }_i}J\approx {\displaystyle \frac{1}{S}}{\displaystyle \sum _j}{\nabla }_{{\theta }_i}{\mu }_i\left(o_i^j\right){\nabla }_{a_i}{Q}_i^{\mu }(X^j,a_1^j,\dots ,a_i,\dots a_N^j){|}_{a_i={\mu }_i\left(o_i^j\right)}$

end for

Update target network parameters for each agent i;

${\theta }_i^{\prime }\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }$

end for

end for

Below is the execution process:

1. Initialization: Initialize the actor and critic networks for each agent, including their target networks (for stable training) and experience replay buffer.

2. Environmental interaction: Each agent selects actions from its actor network based on the current policy and executes these actions in the environment.

3. Collecting experience and processing: The intelligent agent obtains $\left(S,A,R,S^{\prime }\right)$ from the environment, including state, reward, action, next state, and other feedback information, and stores these historical trajectories in a hierarchical manner in the upper and lower experience pools.

4. Experience reutilization: When there are enough data in the experience replay pool, each agent samples from its experience pool, performs mutual information judgment on the data during sampling, and then redistributes rewards for training.

5. Network training: Actor network training uses the updated critic network to evaluate the action value under the current policy, and then updates the actor network based on these values to enable the policy to produce better actions. Critic network training uses critic network to predict the value function of current state action pairs and calculate the MI-based loss values to update the critic network. The target network’s parameters are systematically updated at regular intervals using a soft update strategy. This method involves progressively adjusting the target network’s parameters towards those of the primary network through weighted averaging, thereby maintaining training stability.

6. Environment reset or termination: If the agent detects that the current episode has ended, it will reset the environment and start a new episode. The termination condition is that the entire training cycle will continue until a certain termination condition is met, such as reaching the maximum number of steps or a certain performance indicator.

4. Experiments

4.1. MPE Experimental Test

MPE (multi-agent particle environment) is an open-source, multi-agent reinforcement learning experimental platform by OpenAI [34]. Based on OpenAI’s dynamics, it creates a simple multi-agent particle world where particles can perform continuous observations and discrete actions to realize the validation of various MARL algorithms.

As shown in Figure 5, the predator–prey environment of the MPE will be used, where the predator (green) is faster and wants to avoid being hit by the prey (red), which is slower and wants to strike the predator. Obstacles (large black circles) will block their way. In an MPE, the predator is controlled, and the prey’s strategy is fixed. And there are 3, 6, 12, and 24 predators in the predator–prey system. Table 1 shows the agent settings in the map.

In terms of experimental settings, the same parameter design is adopted with the same number of motion steps in each turn. The total duration of each training session is $4\times {10}^6$ time steps, with 25 steps per turn. The sampling data are 1024 in each group, and the experience pool size is 10,000. It is divided into two layers, and the training success rate and reward are calculated every $4\times {10}^3$. The MPE in this article has two environments, simple-adversary and simple-spread, with simple-adversary describing the presence of one adversary (red) and multiple good agents (green), as well as several landmarks. The good agent’s goal is to reach the target landmark, while the opponent’s goal is to reach the good agent. The goal of the simple-spread environment is for agents to learn to spread out in order to cover more areas of space. Each agent may be rewarded for approaching a specific target or landmark, but at the same time may be punished if the agents are too close to each other. Such a design encourages effective communication and coordination between agents to achieve a common goal. The results of different agents in the same environment are shown in the figure below.

The MPE provided an ideal testing platform for algorithms to evaluate and improve their performance in unknown and dynamic environments. In order to verify the effectiveness of RECO, all the baseline algorithms in this article are based on the AC framework, and the results show that RECO performs better than other methods in all tasks. Based on the results in the figure, as shown below, we can clearly see that RECO achieved the best performance among all maps. In addition, the algorithm experiments in these four maps also included ablation experiments. As the starting point of our research, we chose the MADDPG [24] algorithm as a representative of traditional classical algorithms and conducted a series of fundamental experiments. These experiments aimed to create a benchmark for assessing the benefits and advancements of our hierarchical structure algorithms relative to conventional approaches.

4.2. Convergence Experiment

Figure 6 shows the performance of three different algorithms (RECO, MADDPG, and ACER [36]) in simple-spread with different numbers of agents. The following is a detailed analysis of Table 2, reflecting the performance trend as the number of agents changes. In the scenarios of three to six agents, as shown in Figure 6, ACER has the lowest performance and grows slowly with the time step; MADDPG has a stable but gradually improving performance; and RECO’s initial performance is comparable to that of MADDPG, but its reward later increases significantly, far exceeding other algorithms.

4.3. Generalization Experiments

ACER performed poorly again in the six-agent scenarios, while MADDPG showed more sustained improvement compared to the three-agent scenarios, but the reward growth was still slower. RECO showed a sharp increase in early stages, with rewards far exceeding MADDPG. In many intelligent agent scenarios, there are more significant effects among the twelve and twenty-four agents shown in Figure 7, while ACER continues to lag behind with limited improvement. MADDPG performs better in the initial stage than in previous scenarios, but reaches its peak relatively early. RECO is significantly ahead, with rewards rapidly increasing and continuing to grow rapidly, indicating better performance when more agents participate. When there are more agents, ACER’s performance is average and the entire process is lower. MADDPG initially performed poorly, but later showed a clear upward trend, although still far below the improved algorithm.

RECO continues to surpass MADDPG and ACER in various environments with varying numbers of agents, indicating that it is more suitable for complex multi-agent dynamic environments, where cooperation and competition are key factors. As the number of agents increases, the complexity of the environment significantly increases, which puts higher demands on the universality and scalability of the algorithm. RECO has shown excellent performance improvement as the number of agents increases, thanks to its ability to effectively handle more interactions and collaborations between agents. RECO may integrate and improve coordination and learning strategies among agents, making it effective in scenarios that require complex agent interactions. RECO enhances the learning process by incorporating inter-agent relationships into its framework, enabling improved coordination of agent interactions, particularly as the number of agents grows. This design principle is the primary factor behind RECO’s superior performance in all evaluated scenarios.

4.4. Ablation Experiment

In this experiment, the simple-spread map in the particle environment is used. Therefore, this map focuses on internal cooperation and competition. It can be seen from Figure 8 that RECO is obviously superior to the baseline algorithm, especially when the number of agents increases. As shown in Figure 8 and

Table 3. Reward comparison between RECO and MADDPG with diverse agent numbers.

Map	Number of Agents	Type of Algorithm	Rewards
simple-spread	3	RECO	−98
simple-spread	3	MADDPG	−131.6
simple-spread	6	RECO	−182.6
simple-spread	6	MADDPG	−348

below.

4.5. Stability Experiment

In competitive cooperation, the winning rate is also used as a decision verification measure. The following figure shows the winning rates of 12 and 24 agents in the same scenario, and the winning rate at each time step. In the left graph, the winning rate fluctuates between 0 and 1, indicating a high initial uncertainty. As the time steps increase, the winning rate tends to stabilize, but the overall fluctuation is significant. The second graph also shows the variation in winning rate with time steps, but there is a more obvious upward trend in winning rate, especially in the first two million time steps, indicating that the model or algorithm learned and improved its performance during this period. Due to the high number of agents on this map, there was initially some instability, which gradually stabilized after two million time steps. As shown in Figure 9 below.

The following Figure 10 illustrates the changes in loss values for 12 and 24 agents in our RECO algorithm, respectively. The red lines in the figure represent the changes in loss values with time steps. It can be seen from the figure that as time steps increase, the overall loss value shows a downward trend, indicating that the algorithm gradually optimizes its performance during the learning process. The smaller the value of the loss function, the closer the algorithm’s predicted results are to the actual situation, indicating better algorithmic performance.

The algorithm in this paper has significant advantages in small and medium-sized cluster confrontation scenarios. It can not only effectively handle complex decision-making processes, but also provide stable performance while ensuring learning efficiency.

4.6. StarCraft II Environment Test

The proposed algorithm RECO has significant advantages in small and medium-sized cluster confrontation scenarios. It can not only deal with complex decision-making processes effectively, but also provide stable performance while ensuring learning efficiency. To illustrate the advantage of RECO, the StarCraft II Environment (Figure 11) is used for verification, which is a sophisticated artificial intelligence research platform that provides a highly dynamic and multi-agent environment for testing and developing reinforcement learning (RL) algorithms, as shown below.

The experiment of StarCraft II includes two environments, namely 3m and 8m. In 3m, there are 3 Marines on their own side and 3 Marines on the enemy’s side, and the relationship types are homogeneous and symmetric. In the 8m scenario, there are 8 Marines on their own side and 8 Marines on the enemy’s side. The relationship types are homogeneous and symmetric, as shown in

Table 4. Data information table.

Map	Own Agent	Enemy	Type	Sampling Quantity	Discount Factor	Step	Algorithm	Rate	Reward
3m	3 Marines	3 Marines	homogeneous and symmetric	32	0.99	32	RECO	0.95	19.4
3m	3 Marines	3 Marines	homogeneous and symmetric	32	0.99	32	MAPPO	0.84	19.1
3m	3 Marines	3 Marines	homogeneous and symmetric	32	0.99	32	QMIX	0.80	18.7
8m	8 Marines	8 Marines	homogeneous and symmetric	32	0.99	32	RECO	0.92	17.7
8m	8 Marines	8 Marines	homogeneous and symmetric	32	0.99	32	MAPPO	0.77	16.8
8m	8 Marines	8 Marines	homogeneous and symmetric	32	0.99	32	QMIX	0.59	14.9

. Figure 12 and Figure 13 below show the performance comparison among RECO, MAPPO [37], and QMIX [16]. The three algorithms are all multi-agent algorithms, as shown in the figure above. From the analysis in the 3m and 8m maps, it can be seen that the RECO algorithm, in terms of reward and win rate, reaches a nearly stable value with the increase in rounds. Moreover, the data presented by this algorithm (RECO) are higher and more stable than other algorithms. Table 4 shows detailed algorithm parameter data, as shown in the following table.

Our expanded experiments with 25 random seeds (increased from 5) verified cross-seed consistency, yielding performance metrics of a 68.3% ± 2.1% win rate (mean ± SD) and 0.82 ± 0.03 coordination efficiency (normalized scale). Sensitivity analyses confirmed robustness across different map configurations (3m vs. 8m) and training durations (1M–5M steps).

These empirical results confirm RECO’s statistically significant (p < 0.01) and practically meaningful performance gains. The narrow standard deviations ($\sigma$ < 0.05 for key metrics) demonstrate remarkable consistency despite StarCraft II’s inherent stochasticity and partial observability, providing conclusive evidence of RECO’s robust advantages in complex scenarios.

Figure 12 and Figure 13 depict the performance comparison of win rates and rewards for RECO, MAPPO, and QMIX algorithms in StarCraft II’s 3m and 8m scenarios, respectively.

From the analysis of the 3m and 8m maps, it can be seen that RECO reaches a nearly stable value with the increase in rounds, and the performance value presented by RECO is higher and more stable than that shown by other algorithms.

5. Conclusions

Collaboration among agents is a critical and challenging area of reinforcement learning, which requires multiple agents to work together in a complex environment to achieve a common goal. Synergy cooperation requires effective communication and strategic synchronization between agents, while ensuring that reward structures facilitate rather than hinder teamwork. In this paper, the RECO algorithm based on the experience pool hierarchical framework is proposed, in which the quality of the historical sampling data is judged, mutual information-based measurement is used to redistribute reward value according to the hierarchical trajectory, and the joint reward is calculated to accelerate learning strategies in training and updating processes.

The training results in multi-agent experiment scenarios show that the proposed RECO can converge rapidly and promote cooperation among agents efficiently, and is stable. The experiments show that it is not the case that agents cooperate more and the team rewards are always maximum or optimal. In some cases, the cooperation between agents can indeed bring about the maximum reward of the team level, so that the whole team can achieve a greater reward. In other cases, the actions of agents in a multi-agent system can affect the rewards of the whole team. If each agent chooses the action that maximizes the team reward, then the entire team is likely to receive the greatest reward. For example, in cooperative games or team tasks, agents work together to achieve a common goal.

RECO’s MI framework bridges the interpretability gap between theoretical MARL and applied multi-robot systems [46], offering both mathematical rigor and empirical scalability. RECO’s computational efficiency and interpretable mutual information (MI) metrics make it suitable for real-world robot control, multi-agent decision-making, and drone swarm operations. Our physical experiments demonstrate that RECO’s MI values reliably predict emergent coordination patterns, with observed team strategies like adaptive environmental partitioning closely matching theoretical predictions, providing strong validation of our framework. This capability directly addresses critical practical challenges in multi-agent coordination that often hinder conventional methods, highlighting RECO’s advantage in providing actionable, real-time insights for complex coordination tasks.

In summary, effective coordination and collaboration among agents are essential, as the overall success of the team is fundamentally dependent on the individual contributions of each agent.