Abstract
The temperature variations of interconnected coaxial connectors in RF circuits are strongly influenced by the contact surface characteristics and the ferromagnetic properties of the electroplated materials. In this study, specially structured N-DIN connectors with either magnetic or non-magnetic plating were designed. A dedicated high-frequency, high-power RF experimental platform was set up to monitor and measure the temperature and power of the connectors. Finite element analysis (FEA) was employed to simulate the current density and temperature distribution across the samples. Furthermore, an equivalent circuit model of the central conductor was established by integrating electrical contact theory with the magnetic hysteresis effect. Based on the voltage–temperature (V–T) relation and the derived magnetic field–magnetoresistance (H–M) relation, a predictive model for the temperature rise of the central conductor was formulated. Experimental results demonstrated good agreement with simulation predictions, validating the proposed model and highlighting the critical role of plating material properties in high-power RF connectors’ thermal effect.
1. Introduction
Electrical connectors are essential components of communication systems, serving as fundamental elements for energy transmission and information exchange between RF circuit modules. In engineering, connectors are viewed as extensions of transmission lines, exerting minimal impact on the signal transmission of circuits. However, from a reliability perspective, connectors often represent the weak link in electrical and communication systems due to the unique contact interfaces, which differ from typical transmission lines. Notably, as signal frequency and power increase, the heat generation of the connector increases, resulting in a rise in temperature. Excessive temperature can lead to accelerated aging and degradation of the contact structures of connectors, which may significantly alter transmitted signals, potentially compromising overall system performance and leading to failures. Hence, it is essential to evaluate the maximum operating temperature of RF coaxial connectors and investigate the factors influencing temperature variations.
At the microscopic scale, surface asperities render the contact interface uneven, resulting in localized current crowding at discrete contact spots and consequently giving rise to constriction resistance [1]. Constriction resistance and film resistance together determine the contact resistance, which serves as a critical indicator of connector degradation, particularly under direct current (DC) conditions [2]. To better quantify the effects of surface roughness on contact resistance, various analytical and statistical models have been proposed, establishing relationships among surface topography, real contact area, and electro-thermal behavior [3,4,5]. These models have facilitated deeper investigations into the mechanisms of contact aging and performance degradation [6,7].
However, in high-power applications, such as base stations, radar modules, and satellite transceivers, RF coaxial connectors are often subject to elevated currents and signal frequencies. This leads to significant heating at the contact interface, exacerbated by non-uniform current distribution due to the skin effect [8]. While the voltage–temperature (V–T) relation is widely used to estimate maximum contact temperatures, its accuracy declines under conditions where heat dissipation and frequency-dependent effects become significant [9]. In such cases, voltage-derived temperatures tend to overestimate actual values, but still serve as conservative benchmarks in engineering design.
Under RF excitation, contact impedance is no longer purely resistive; parasitic inductance and capacitance become non-negligible, affecting both signal integrity and thermal characteristics [10]. Finite element simulations have been employed to analyze these effects, revealing that temperature rise depends not only on input power and frequency but also on micro-asperity geometry at the contact spots [11]. This thermal instability can degrade connection quality and increase passive intermodulation distortion, thereby compromising the reliability of microwave communication systems [12]. Recent work has shown that thermally induced contact nonlinearity and magnetic hysteresis are key contributors to passive intermodulation (PIM) in coaxial connectors [13].
In recent years, materials science research has shown that magnetoresistance (MR) behavior in ferromagnetic materials can arise from internal domain structures, even in the absence of explicit magnetic phase transitions. For example, in perovskite manganites, the presence of ferromagnetic metal clusters and Griffiths phases can modulate resistance near room temperature [14]. These findings suggest that similar domain-level inhomogeneities in plated nickel layers may influence the RF electrical and thermal performance of connectors. Recognizing this, our study incorporates ferromagnetic effects into the modeling of contact resistance under high-frequency excitation, extending conventional contact theories into the domain of dynamic magnetic–electrical interactions.
Building upon the authors’ earlier studies [15,16] on the electrical and thermal behavior of coaxial connector interfaces under high-frequency, high-power excitation, the present work expands the investigation to include material-specific effects and domain-level magnetic interactions. A specialized set of N-DIN-type coaxial connectors, featuring varying electroplated materials and thicknesses, were designed to directly address the difficulty of identifying and measuring the internal temperature maximum. A dedicated experimental platform was developed to deliver high-frequency, high-power excitation while precisely measuring power dissipation and internal temperature distributions.
To capture the complex interplay between surface contact mechanics and thermal behavior, surface roughness was quantitatively characterized and used as the input for finite element models simulating current density, localized heating, and magnetic response at the contact interface. For non-magnetic coatings, the thermal prediction was improved by replacing the conventional voltage–temperature (V–T) relation with direct power-based temperature calculations, yielding more accurate results under high-power conditions. For magnetic coatings, an equivalent circuit model incorporating a field-dependent resistance term was introduced to represent hysteresis-induced magnetoresistance. This approach captures the fixed electromagnetic field mode in the plated region, providing a practical alternative to direct domain-level simulations.
By integrating experimental observations with multiphysics simulations and electrical contact theory, this work presents a novel temperature prediction framework that connects microscopic contact behavior with macroscopic thermal performance. The results reveal distinct thermal trends between magnetic and non-magnetic materials and demonstrate the importance of considering both electromagnetic properties and interfacial mechanics in the thermal design of RF connectors. The proposed method provides conservative yet accurate estimates suitable for engineering applications, advancing the modeling of RF connector reliability under realistic conditions.
2. Experimental Setup and Data Collection
2.1. Structure Analysis of Samples
Coaxial connectors, widely used in radio frequency (RF) circuits, are composed of a central conductor, an outer conductor, and an insulating layer. The outer conductors of connectors of the same type are mechanically interconnected via a threaded structure, thereby ensuring electrical contact between the pins and receptacles of the central conductors. Both the central and outer conductors are fabricated from copper alloys, typically coated with one or more layers of metal possessing superior electrical properties to enhance signal transmission and provide surface protection.
In this study, female DIN-to-female N and male N-to-male DIN connectors with various electroplating materials and thicknesses were selected as experimental samples for temperature measurements, as illustrated in Figure 1a. The N-DIN coaxial connector, characterized by a high power-conveying capability, can transmit up to 200 W when combined with a high-power load. Two electroplating schemes were implemented, utilizing nickel or silver as the coating materials on the copper alloy base. Both nickel and silver are widely employed in engineering electroplating, with nickel exhibiting ferromagnetic properties. The electroplated samples were further classified into three categories according to the plating thickness, as summarized in Table 1.
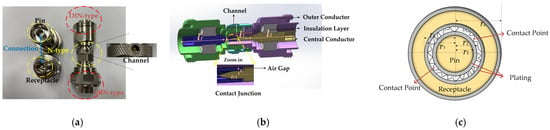
Figure 1.
Mechanical structure of the N-DIN coaxial connector: (a) External view; (b) internal view (l1 = 33.24 mm, l2 = 14.50 mm, l3 = 33.25 mm, r1 = 33.25 mm, ra = 1.42 mm); (c) schematic of the contact junction of the central conductor (r1 = 0.72 mm).

Table 1.
Three levels of electroplating material thickness.
The contact junction consists of a pair of N-DIN coaxial connectors with a pin and a receptacle, respectively. The receptacle of the coaxial connector is designed with a uniform six-part structure, which can effectively improve its opening degree and increase the contact area of the contact junction. It should be noted that the outer surface of the contact junction displays an air gap, as shown in Figure 1b. The schematic diagram of the cross-section of the central conductor contact junction of the coaxial connector is shown in Figure 1c, in which the contact area of the pin and the receptacle is highlighted.
To enable direct temperature measurement near the contact points, a channel with a radius of 1.2 mm was drilled by a high-speed CNC drilling machine within the outer conductor, oriented toward the central conductor, as shown in Figure 1a,b. A thermal resistor probe measuring 2 mm × 0.5 mm × 4.2 mm was used to investigate the thermal behavior of the central conductor through a dedicated channel. Considering that insertion of the thermal resistor probe could cause characteristic impedance mismatches in the channel region and potentially affect signal transmission, S-parameter measurements were performed on the sample with a thickness of level 2, using a standard connector as the control group.
2.2. High Frequency Characteristics of Samples
An Agilent vector network analyzer E5071C was used to measure the S parameters of the N-DIN connector. As a two-port network, the ratio of forward to reflected waves in the coaxial connector can be represented by the S parameters, as shown in Figure 2a. The relationship between the reflected and incident power waves is described as
where a1 and a2 represent a wave incident to Port 1 and Port 2, respectively. b1 and b2 represent a wave reflected from Port 1 and Port 2, respectively.
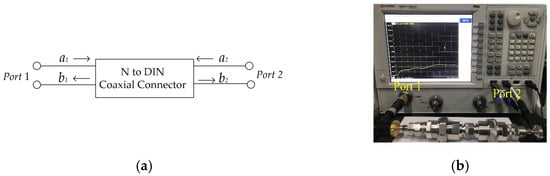
Figure 2.
(a) Forward and reverse waves on the N-DIN coaxial connector; (b) S-parameter measurement setup.
Port 1 was selected as the energy input port and Port 2 was selected as the energy output port, respectively. S11 represents the voltage reflection coefficient at Port 1, S21 represents the forward voltage gain, S12 represents the reverse voltage gain, and S22 represents the voltage reflection coefficient at Port 2. The measurement frequency range is from 100 MHz to 3 GHz, as shown in Figure 2b.
As seen in Figure 3, the value of the S11 parameter of the N-DIN connector with the channel closely matches that of the standard connector across most of the frequency range, indicating that the electromagnetic wave reflection at Port 1 is only slightly affected by the presence of the channel and the insertion of the thermal resistor probe. Similarly, the variation in the S21 parameter remains within a small range, demonstrating that signal transmission from Port 1 to Port 2 is not significantly impacted by the use of the thermal resistor probe.
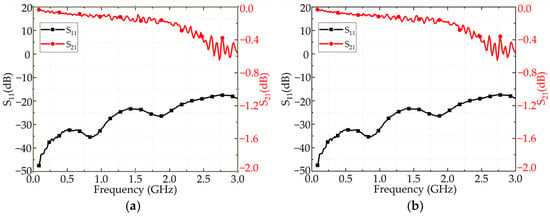
Figure 3.
(a) S-parameter measurement of the standard coaxial connector. (b) S-parameter measurement of the sample with the thermal resistor probe inserted into the channel.
2.3. Experimental Configuration and Data Collection
In order to measure the dissipated power and temperature data of the samples, a high-frequency and high-power RF experimental platform was designed and assembled, as shown in Figure 4. The experimental platform comprises a signal amplification system, a connector power consumption measurement system, and a thermal resistance temperature monitoring device.
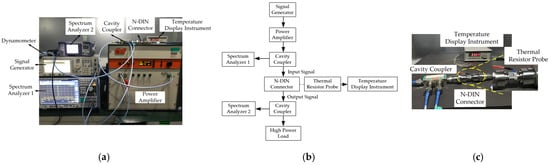
Figure 4.
Designed connector temperature and dissipated power measurement system. (a) Signal amplification system and power consumption measurement system; (b) steps to build the measurement platform; (c) thermal resistor temperature measurement device.
The signal amplification system consists of a signal generator, a power amplifier, a coaxial connector, and a high-power load. A Hewlett-Packard E4433B signal generator was used to produce a 3 GHz signal, which was subsequently amplified by an Amplifier-Research 100S1G4 power amplifier.
The connector power consumption measurement system includes a cavity coupler and two spectrum analyzers. The equivalent circuit of the system is depicted in Figure 4b. A cavity coupler with a coupling factor of 40 dB was employed to divide the input signal into two coupling ports and one output port. As the connector is a passive device, its input and output power were measured using two spectrum analyzers. The difference between the measured powers corresponds to the dissipated power within the connector.
The thermal resistance temperature monitoring device, shown in Figure 4c, consists of a thermal resistor probe and a temperature display instrument. A PT100 thermal resistor, with a measurement range of −50 °C to 300 °C, was utilized to monitor the temperature change of the central conductor.
The ambient temperature during the experiments was maintained at 293.55 K. Under mating conditions, the connector exhibited a maximum mating torque of 0.68 N·m, and the retention force of its locking mechanism was measured to be 450 N. A sinusoidal signal at a frequency of 3 GHz was amplified to 100 W by the signal amplification system. After a series of preliminary tests, it was observed that the temperature of the connectors, with different electroplating materials and thicknesses, reached a thermal steady state within approximately six minutes. During the experiments, the temperatures of the central conductor were measured and recorded every two minutes. For each combination of electroplating material and thickness level, three samples were prepared to ensure repeatability. Following the temperature measurements, the average temperature rise for each group was calculated. The power dissipation values of the connectors after reaching a steady state are summarized in Table 2.

Table 2.
Dissipated power of the connectors in experiment and circuit simulation.
The results presented in Figure 5a demonstrate a clear temperature rise of the central conductor under high-power conditions. The silver-plated connectors across the three thickness levels exhibited similar temperature evolution trends: the temperature increased rapidly within the first two minutes, rose more gradually between two and four minutes, and stabilized after approximately four to six minutes. The plating thickness had a pronounced effect on the magnitude of the temperature rise. Specifically, the maximum temperature rise at thickness level 1 was nearly twice that observed at level 3, indicating that increasing the silver plating’s thickness effectively mitigates heat generation in the N-DIN connector under high-power input. A negative correlation was observed between the silver plating’s thickness and the temperature rise of the central conductor. As seen in Figure 5b, the nickel-plated central conductor had a similar temperature trend to the silver-plated central conductor. In addition, the temperature of the nickel-plated central conductor rose sharply. Notably, the maximum steady-state temperature of plating thickness level 2 was higher than that of plating thickness level 1.
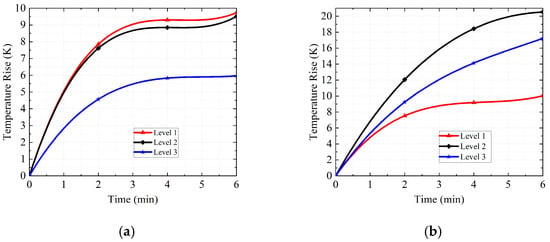
Figure 5.
The average temperature trend of the central conductor. (a) Silver-plated connectors. (b) Nickel-plated connectors.
2.4. Contact Surface Roughness of Samples
Structurally, the contact junction plays a critical role in the temperature rise of the coaxial connector, making it essential to characterize the surface morphology of the contact area. A ZYGO three-dimensional white light interference surface profilometer was employed to inspect the contact surface and to measure the roughness of the pins in N-DIN connectors with different plating materials and thickness levels.
As discussed previously, the actual surfaces of the silver-plated and nickel-plated N-DIN connectors are not smooth, but rather rough and uneven, as illustrated in Figure 6a. Notably, the shape of the contact surface of the pin resembles the side of a cylinder. A three-dimensional surface model was employed to quantify the roughness morphology of the pin surface, as shown in Figure 6b,c. The height variation along a line segment of the contact surface is within 1 μm, indicating that the contact between the pin and the receptacle occurs at discrete points formed by the mechanical engagement of surface asperities. The arithmetic mean height (Sa) and root mean square height (Sq) of a surface are used as metrics to characterize the surface roughness:
where A is the visual contact area of the N-DIN connector and can be measured by SEM analysis and h(x,y) is the height of the surface. It is noteworthy that the visual contact area of N-DIN connector samples with different thicknesses and materials exhibits a value of approximately 0.08 mm2. Three areas, each measuring 336.239 μm × 336.239 μm, were selected at equal intervals along the surface of the pin for roughness measurement. The measurement results show that the Sa values of the silver-plated samples range from 0.174 μm to 0.194 μm, and the Sq values range from 0.225 μm to 0.244 μm. For the nickel-plated samples, the Sa values range from 0.151 μm to 0.161 μm, and the Sq values range from 0.201 μm to 0.217 μm, respectively. For a given plating material, varying the thickness exhibited minimal influence on surface roughness, indicating that the size of surface asperities primarily depends on the electroplating process. Under the same thickness level, the nickel-plated surfaces exhibited lower average height and smoother morphology compared to the silver-plated surfaces. The average widths of the micro asperities were measured to be 3.63 μm for nickel plating and 3.72 μm for silver plating.
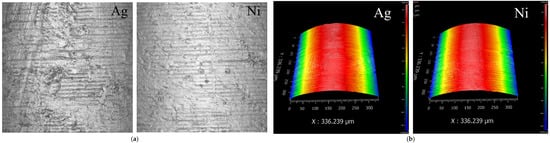
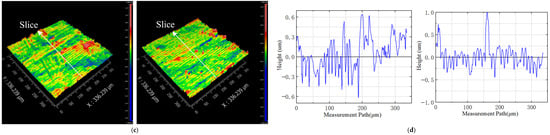
Figure 6.
Contact surface morphology of the N-DIN connector. (a) Real surface topography of the pin. (b) Three-dimensional model of a contact region. (c) Height distribution of the contact surface. (d) Height profile along a measurement path.
3. Simulation Model Field Analysis
A comprehensive understanding of the electromagnetic environment and contact interface conditions is essential for accurately predicting the maximum steady-state temperature at the contact junction of the connector. In this study, a finite element simulation model was first established to analyze the surface current density distribution on the central conductor with magnetic and non-magnetic plating materials, providing detailed insights into the electromagnetic characteristics of the connector. Additionally, the power dissipation of connectors with varying plating thicknesses was calculated and analyzed using circuit simulation tools to serve as a reference for evaluating thermal behavior. Finally, a finite element thermal simulation was performed to determine the temperature distribution across a simplified contact interface, supporting the prediction and assessment of the steady-state temperature at the actual contact region.
3.1. Distribution of Current Density
A finite element simulation model was established to analyze and calculate the current density at the contact junction, aiming to investigate the mechanism behind the generation of the maximum steady-state temperature in the connector samples. In the simulation, the pin of the central conductor was ideally simplified to a cylindrical conductor. The Magnetic and Electric Fields in AC/DC Module was employed to perform a frequency-domain stationary study, simulating the current density and local magnetization in the central conductor under a 3 GHz excitation. The base material of the conductor was set as copper alloy, with the plating material modeled as either silver or nickel. To correspond with the experimental sample conditions, the plating thicknesses in the simulation were set to 3 μm, 6 μm, and 9 μm, respectively. The surface of the coaxial connector was assumed to be smooth. The material parameters and calculation data used in the simulation are summarized in Table 3.

Table 3.
Material properties used in the FEA model.
The current distribution for silver plating and nickel plating with a thickness of 3 μm is shown in Figure 7. Notably, the current in the central conductor is primarily distributed near the surface, with a significant increase in current density towards the edge. The skin effect restricts the flow of current within the penetration depth. The skin depth, δ, is defined as
where f is the signal frequency, μr is the relative permeability of the conductor, μ0 is the magnetic permeability of free space, and ρ is the resistivity of the conductor.
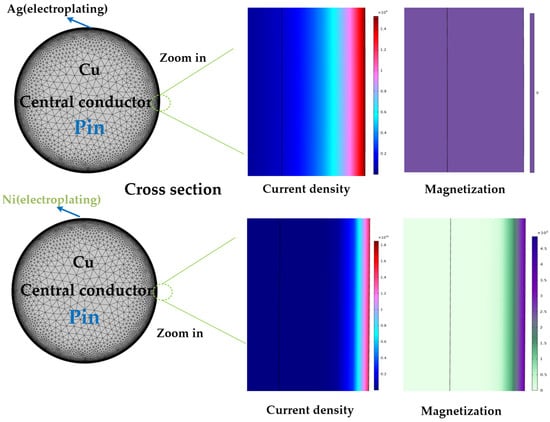
Figure 7.
Finite element simulation model for current distribution and magnetization intensity distribution of the central conductor of the connector.
A graph group was constructed to illustrate the radial trend of current density variation, starting from a point 0.02 mm inward from the boundary of the base material and extending to the boundary of the plating material. The results presented in Figure 8a,b reveal that the current density in the central conductor of connectors with different electroplating materials progressively increases as it approaches the boundary. Additionally, the currents in the central conductor of connectors with both electroplating materials remain confined within their respective electroplating layers, in accordance with the skin effect. Notably, the rate of change in current density along the radial path is significantly lower for the central conductor of silver-plated connectors compared to nickel-plated connectors. Furthermore, the peak current density in the central conductor of silver-plated connectors slightly decreased as the plating thickness increased, whereas in nickel-plated connectors, the peak current density showed a slight increase with thicker plating.
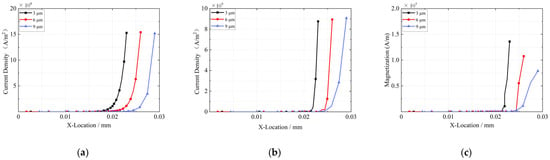
Figure 8.
Distribution of current density and magnetization of the central conductor. (a) Current density distribution of silver plating; (b) Current density distribution of nickel plating; (c) magnetization distribution of nickel plating.
Inspection of Figure 8c reveals that, analogous to the current density distribution, the magnetization intensity is notably higher at the boundaries of the electroplated layer compared to the interior of the conductor. As the thickness of the nickel plating increases, both the growth rate and the peak value of magnetization exhibit a marked decline. This observation indicates a strong dependence of the magnetization distribution on the plating thickness, suggesting that increased thickness effectively mitigates magnetic field concentration at the contact interface.
3.2. Power Differences on Simulation and Measurement
In order to calculate the theoretical dissipated power of connectors with different plating materials, a circuit simulation model was developed based on the temperature measurement circuit, as shown in Figure 9. The power input for the simulation circuit is set to 100 W with a frequency of 3 GHz. The dissipated power in the connector is calculated as the difference between probe 1 and probe 2. The S parameters of the connector samples were measured and incorporated into the simulation circuit to estimate the theoretical dissipated power. The results from the simulation, as shown in Table 3, allow a direct comparison with experimental data.
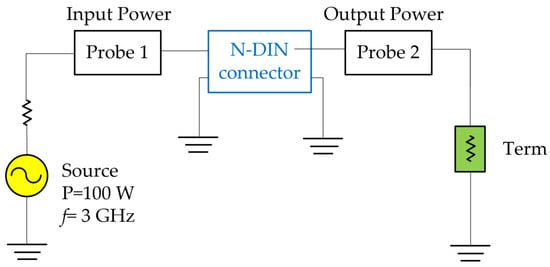
Figure 9.
Circuit simulation of N-DIN coaxial connectors.
The simulation results indicate that the dissipated power in the silver-plated connector decreases with an increase in plating thickness. Notably, the power difference between level 2 and level 3 is larger than that between level 1 and level 2, suggesting that the rate of power change increases as plating thickness increases. In contrast, for nickel-plated connectors, the dissipated power increases as plating thickness increases. Additionally, the power dissipation calculated in the circuit simulation is lower than that observed in the experimental results.
Based on the H–M relation, the variation in magnetization intensity with magnetic field strength follows a nonlinear pattern. Connectors plated with ferromagnetic materials show reduced magnetic resistance at lower external magnetic field strengths. The signal power used for measuring the S parameters with the vector network analyzer is approximately 10 dBm, which is significantly lower than the power in both the experimental and simulation circuits. As a result, the external magnetic field affecting the connector’s plating in the S parameter measurement circuit is much weaker compared to that in the experimental circuit. In the circuit simulations, the power dissipated by the connector is considered as a loss under conditions of low magnetic resistance. The discrepancy in power between the circuit simulations and experimental tests suggests that the magnetic resistance of the connector consumes a portion of the input power in the experimental setup. Conversely, for connectors plated with non-ferromagnetic materials like silver, the simulation and experimental results align closely, leading to minimal power differences.
3.3. FEA Simulation of Multi-Points Contacts
As previously discussed, the surface roughness occurs on the micron scale, which could influence the current distribution in the connector due to the micro asperities present on the surface. These asperities can also affect the temperature at the contact junction. To gain a deeper understanding of the relationship between the contact points and temperature distribution on the contact surface, an equivalent finite element model was developed.
In this model, the micro asperities on the contact surface are simplified to cylinders with varying radii, which represent the interactions between the pin and the receptacle at the contact points. Based on the roughness measurement results, the average width of the cylinders in the simulation is set to 3.63 μm. The AC/DC Module and the Heat Transfer Module were used. A stationary multiphysics simulation was performed, coupling the temperature field with current flow to evaluate the steady-state temperature at individual contact spots under a DC voltage of 0.1 V. The simulation demonstrates that the highest temperature is concentrated at the contact point itself, as shown in Figure 10. Additionally, the surrounding metal temperature increases in parallel with the contact point temperature, showing only a slight difference from the peak temperature. This model highlights the localized nature of the temperature rise at the contact junction and the small thermal gradient in the surrounding material.
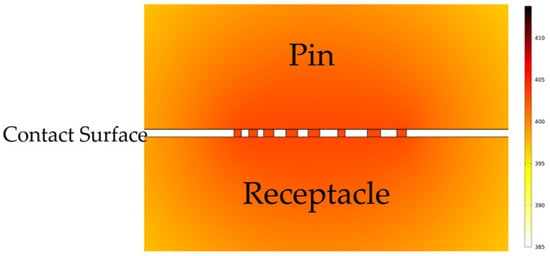
Figure 10.
Finite element simulation model for contact surface temperature distribution.
4. Electrical–Thermal Model Development
Based on the simulation and test, a physical basis for the current investigation was provided to consider and quantify the heat-generating part of the connector. For central conductor, this paper analyzed the maximum steady-state temperature of contact junction from the perspective of changes in current and voltage caused by connection resistance and magnetic resistance effect.
4.1. Electrical–Thermal Model Under DC Condition
The surface morphology measurements of the connector indicate that, under identical electroplating processes, variations in the thickness of plating material have minimal impact on the surface roughness. The contact between the pin and receptacle is essentially the compression of micro asperities on the contact surface. The average surface separation, d, can be modeled as a linear function of the contact roughness and contact force [17]
where F is the contact pressure. The relationship between the actual contact area, Ac, and the visual contact area, A, can be described as
where Φ(h) is the standard deviation of the surface heights, which is considered to conform to the Gaussian distribution. Based on the Greenwood and Williamson model [18], the surface asperity density, η, can be calculated by using the total number of asperities on the contact surface and actual contact area:
where Nc is the total number of asperities on the contact surface and was gained by surface topography instrument. For a given region, Aa, the relationship between the number of asperities, n, and is defined as follows:
Based on Holm’s electrical contact theory [1] and multiple contact a-spots theory [19], in the DC cases, the presence of a-spots reduces the volume of material for electrical conduction and restricts the flow of current, thus increasing resistance. The constriction resistance, Rc, can be expressed by
where H is the hardness of the material and ρ is the resistivity of the contact surface material. Relevant parameters of the contact surface are listed in Table 4. Notably, the contact pressure values presented in Table 4 were derived from experimental measurements of insertion and extraction forces, combined with the corresponding friction coefficient. At the same thickness level, the contact pressure of silver plating is lower than that of nickel plating, and the contact pressure for both plating materials slightly increases as the thickness of the contact surface increases. Silver plating, being relatively soft, exhibits a consistent hardness regardless of increasing thickness, while nickel plating, being harder, shows a significant increase in hardness with increased thickness. Additionally, the surface asperity density and root mean square height of silver plating are higher than those of nickel plating.

Table 4.
Relevant parameters of the contact surface.
According to Equation (8), the effects of contact pressure and contact asperity density on the contact resistance are shown in Figure 11. Within the selected thickness range, the contact resistance of the silver plating shows minimal variation, remaining between 1.08 mΩ and 1.14 mΩ. In contrast, the contact resistance of the nickel plating exhibits greater variability.
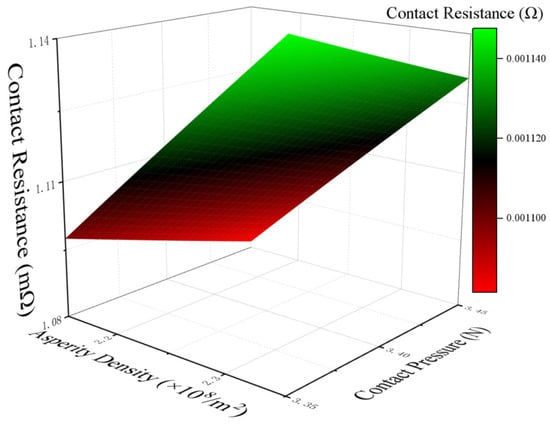
Figure 11.
The effects of contact pressure and contact asperity density on the contact resistance of the silver plating under DC conditions.
The simplified circuit of the connector is shown in Figure 12a. The bulk resistance and the constriction resistance together impede the flow of direct current (DC), and the relation can be expressed as
where RT is the connection resistance and Rbulk is the bulk resistance. The contact resistance of the entire contact surface is obtained by paralleling the resistance of the contact points, and the contact resistance is determined by the constriction resistance. The number and spatial distribution of a-spots are often not critical for assessing contact resistance in many practical applications, as electrical contact tends to occur fairly uniformly across the nominal contact area [20]. Based on the measured asperity density per unit area, the mean spacing between adjacent asperities at level 1 thickness was calculated to be 78.32 μm for the nickel plating and 67.26 μm for the silver plating. The characteristic asperity size is significantly smaller than the average spacing between contact points. To enable a reasonable simplification of the analytical model, the following assumptions were made in this study: (1) the contact spots are uniformly distributed over the entire contact surface and (2) each asperity is idealized as a cylindrical structure with identical dimensions.
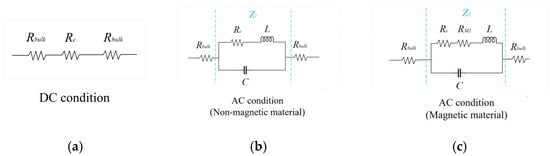
Figure 12.
Connection impedance network of the contact junction of the N-DIN coaxial connector under DC or AC conditions. (a) Connection resistance under DC conditions; (b) connection impedance of non-magnetic plating materials under AC conditions; (c) connection impedance of magnetic plating materials under AC conditions.
The span of each asperity is generally in the range of tens of microns, the voltage–temperature relation is valid under this contact condition [21]. The relationship between the voltage drop V across the asperity and the maximum steady-state temperature TM in the contact can be calculated by [19]
where T0 is the room temperature and λ1 and λ2 are the thermal conductivity of the two conductors in contact, respectively. ρ1 and ρ2 are the resistivity of the two conductors in contact, respectively. Consider the electroplating material of the pin and the receptacle are same, so λ1 = λ2 = λ, ρ1 = ρ2 = ρ. The V–T relation can be reduced to the form
Based on inspection and calculation of the properties of the materials presented in Table 4, silver and nickel conform to the Wiedemann–Franz law [1]
where L0 = 2.44 × 10−8 (V/K)2 is the Lorenz constant. Thus, Equation (15) can be simplified as
Equation (13) illustrates the relationship between the temperature change at the contact point and the applied voltage. Within the measured temperature range, the resistivity increases with rising temperature, while the thermal conductivity decreases with temperature; these effects tend to approximately neutralize each other. Therefore, within the temperature variation range of the connector studied in this paper, the change in the parameter L0 is negligible and is treated as a constant. Furthermore, Equation (13) is derived based on traditional contact theory, which assumes that the boundaries of the contact conductor are thermally insulated, and Joule heating is assumed to propagate only to the colder regions within the contact point. Under this assumption, the temperature of each heat-generating contact point changes synchronously, with no heat transfer occurring between contact points. This assumption implies that the highest temperature at any single contact point can represent the maximum temperature across the entire contact surface.
4.2. Derivation of the Maximum Steady-State Temperature of Connectors with Non-Magnetic Plating Material
Under high-frequency conditions, the skin effect confines the current flow to the surface of the contact, thereby increasing both the bulk resistance and the contact resistance of the connector relative to the direct current (DC) condition. The current density becomes concentrated and follows curved paths within the narrow regions of the contact interface, leading to the emergence of contact inductance. Furthermore, the non-contact regions within the contact surface contribute to the formation of parasitic capacitance [22]. For the silver-plated coaxial connector, the impedance network associated with a single contact spot between the pin and the receptacle is illustrated in Figure 13, and its corresponding network impedance parameters are as follows:
where ω = f/2π and f is the signal frequency. The connection resistance at an electrical interface is the sum of the contact resistance and the bulk resistance near the contact area, while the connection impedance of a single contact point of the silver plating layer is

Figure 13.
Derivation and verification scheme for the maximum steady-state temperature of non-magnetic material connectors.
As inductance and capacitance primarily function as energy storage and signal transmission elements within the network impedance, their magnitudes are typically in the order of pico-Henries and pico-Farads, respectively [23]. At a frequency of 3 GHz, the impedance relationships 1/ωC >> Rc and ωL << Rc hold, indicating that the capacitive path behaves approximately as an open circuit, while the inductive path behaves effectively as a short circuit, respectively. Accordingly, the connection impedance can be approximated as:
As shown in Equation (16), the current flowing through the contact resistance of a connector with a non-magnetic plating material is nearly identical to that through the bulk resistance in the vicinity of the contact point. The connection resistance of the connector impedes current flow, thereby dissipating a portion of the signal’s input power and causing an increase in the temperature at the contact interface. In contrast to the DC condition, where the system gradually reaches a maximum steady-state temperature, the degree of current obstruction caused by resistance is more pronounced under high-frequency excitation. As a result, the temperature variation at the contact point becomes more significant. The connection resistance in high frequency of two end-butted cylinders was estimated as follows [10]:
where g = ρ/2Rc-Ag is the constriction radius of silver plating, rcylinder = 100 μm is the dimension of the region of the contact point, and aAg is the average widths of the micro asperities of silver plating. It is important to note that, under high-frequency conditions, significant current constriction occurs in the vicinity of the contact region. Consequently, the bulk resistance considered here is limited to the material volume within a localized radius around the contact point. As indicated by Equation (17), the connection resistance at high frequencies is governed by multiple factors, including the contact resistance under DC conditions, the depth of the skin effect, the resistivity of the plating material, and the average widths of the micro asperities.
To assess the power dissipation due to the connection impedance in the contact point region, it is essential to consider the power dissipated by the bulk resistance in the non-contact areas of the N-DIN connector. Based on the skin effect and the law of resistance, the total bulk resistance of the conductor in the non-contact region of the connector is given by
where l2 is the length of the central conductor of the connector and ra is the radius of the central conductor; the values of l2 and ra are shown in Figure 1b. The thickness of the plating will affect ra, but the variation among different ra values is relatively minor compared to the overall radius of the central conductor.
The area of the plated contact region under high-frequency conditions is given by
The contact points are connected in parallel, so the voltage on a single contact point can be expressed as
where PT is the power dissipation of the connector in experimental test and n represents the number of contact points within the region through which the current flows across the contact surface. Consequently, the maximum steady-state temperature at contact point within the silver plating layer can be expressed as
Based on Equations (5)–(7), (11), and (21), the relationship between the microscopic structure of the connector contact surface and the temperature at the conductor contact points within the connector is established. By measuring the surface roughness, hardness, and contact pressure of the contact area, the contact resistance under direct current (DC) conditions can be theoretically calculated, which in turn allows for the estimation of the maximum steady-state temperature at the contact points of the non-magnetic material connector under high-frequency conditions.
4.3. Derivation of the Maximum Steady-State Temperature of Connectors with Magnetic Material Plating
When a connector with a ferromagnetic material electroplating is subjected to a magnetic field, the charge carriers (electrons or holes) within the material experience a Lorentz force. This force alters the trajectory of the charge carriers, thereby influencing the resistance of the ferromagnetic material. High-frequency and high-power signals propagate through the connector in transverse electric and magnetic (TEM) mode. The external bias magnetic field induces magnetic resistance in the material. Both magnetic resistance and contact resistance together impede the flow of current, resulting in a voltage drop across the contact area that exceeds the voltage drop generated by the contact resistance alone. According to the voltage–temperature (V–T) relationship, the actual temperature rise in the magnetic material contact area is theoretically greater than the temperature rise predicted by considering only the contact resistance. Figure 14 illustrates the derivation and verification scheme for determining the maximum steady-state temperature of connectors with magnetic material plating.
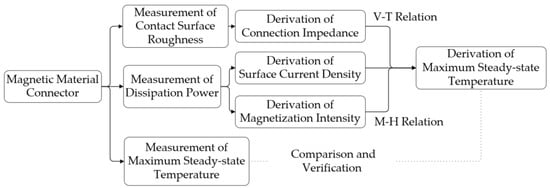
Figure 14.
Derivation and verification scheme for the maximum steady-state temperature of magnetic material connectors.
In the contact region formed by the pin and receptacle of a coaxial connector with a ferromagnetic material plating, the impedance network associated with a single contact point is illustrated in Figure 12c. The network impedance parameters can be expressed as follows:
The total connection impedance of the nickel-plated connector in a magnetic field is
Similarly to the calculation for non-magnetic materials, the capacitance can be approximated as an open circuit, while the inductance can be treated as a short circuit at 3 GHz. The total connection impedance of the nickel plating in the magnetic field is approximately
where ZT-Ni represents the resistance in magnetic field, Rbulk-Ni is the body resistance near the contact point, RM1 represents the magnetic resistance of the bulk resistance region, and RM2 represents the magnetic resistance at the contact point. In this paper, the sum of body resistance and contact resistance, 2 Rbulk-Ni + Rc-Ni, is called the conventional connection impedance, and the total magnetic resistance generated in the contact area, 2RM1 + RM2, is called the connection magnetic resistance.
The resistivity of nickel plating is significantly higher than that of the base metal, and its thickness is comparable to the radius of the contact point. Consequently, the current injected at the contact tends to diffuse preferentially into the base material rather than spreading laterally along the plating. This results in a lower voltage drop in the base metal near the contact point compared to the plating layer. To characterize this behavior, the concept of effective resistivity is introduced. Williamson and Greenwood demonstrated that the ratio of effective to intrinsic resistivity in nickel plating is influenced by plating thickness, contact size, and the resistivity contrast between the plating and base material [24].
where ρeff-Ni is the effective resistivity of nickel plating, ρNi is the resistivity of nickel plating, d is the thickness of the plating material, and aNi is the average width of the micro asperities of nickel plating. The f1 values corresponding to plating thicknesses of 3 μm, 6 μm, and 9 μm are 3.5, 4.0, and 4.0, respectively.
The concept of effective resistivity helps to explain the different power loss trends with plating thickness for nickel and silver observed in Table 2. For silver, its low hardness allows thicker coatings to form better contacts, reducing resistance and thus lowering power loss. In contrast, the effective resistivity of nickel increases with thickness under high-frequency conditions, which dominates over contact improvement and leads to higher power loss. Although level 2 and level 3 nickel coatings have similar resistivity, the thicker level 3 results in a longer current path and greater power loss.
Similarly to Equation (13), the total connection impedance of the nickel plating without magnetic field can be calculated by
where g = ρeff-Ni/2Rc-Ni is the constriction radius of nickel plating.
To accurately assess the impact of connection magnetic resistance on the temperature rise of the connector, it is crucial to understand the proportion of magnetic resistance within the total connection impedance. The ratio of connection magnetic resistance to conventional connection impedance is proportional to the square of the magnetization intensity [25]:
A hyperbolic tangent function can be used to describe the H–M relation [12]:
where k1, k2, and k3 are parameters related to the structure, dimensions, temperature, and other properties of the magnetic material. Both experimental and simulation approaches were integrated to calculate the parameters within the N-DIN coaxial connector. The direction of the magnetic domains within the nickel-plated contact surface () aligns with the direction of the applied bias magnetic field (). The magnetic flux density within the nickel plating layer is given by
It is worth noting that the maximum temperatures observed during RF operation are well below the Curie temperature of nickel (631 K), ensuring that the nickel plating retains its ferromagnetic properties. This supports the stability of internal magnetic domains and allows for persistent magnetoresistive behavior under excitation.
The magnetoresistance formulation employed in this study is based on magnetic hysteresis and the magnetic field dependence of resistance, which is theoretically supported by findings from manganite systems [14]. Although our study does not observe phase transitions, the underlying mechanism of magnetoresistance—modulation of electrical resistivity by magnetic domain interactions—applies similarly to nickel plating. Thus, our use of a simplified equivalent circuit with hysteresis-based resistance modeling remains physically meaningful for predicting the thermal response of RF connectors under high-power conditions.
Under high-frequency conditions, metallic nickel behaves as an excellent conductor, with its conduction current significantly greater than the displacement current. According to Ampere’s circuital theorem, the line integral of the magnetic field strength H along any closed curve L is equal to the algebraic sum of the currents enclosed by the closed curve. The relationship between the conduction current and the magnetic field strength can be calculated as
According to Figure 1c, the relationship between the distribution of magnetic field intensity and current density of the pin-receptacle in the cross section of the contact area can be quantified as
where represents the magnetic field strength in the base material, while and represent the magnetic field strength in the nickel plating of pin and receptacle, respectively. The represents the magnetic field strength around the contact point between the pin and the receptacle.
To facilitate the study of the electromagnetic environment at the contact surface, the integration path for the current in Equation (30) is chosen along the outer surface of the PIN. By combining the simulations of the surface current density for nickel plating layers of varying thicknesses, the external magnetic field strength at the pin-receptacle contact surface can be further calculated. Similarly to Equation (18), the body resistance of the non-contact area of the conductor in the nickel-plated connector is
The total power dissipated by the N-DIN connector in the transmission line is composed of the connection magnetic resistance in the contact point area, the conventional connection resistance, and the power consumed by the body resistance in the non-contact area. In the circuit simulation, the heat generated by magnetic resistance was not accounted for, and the total power dissipation of the connector can be expressed as
where PS is the dissipated power in circuit simulation.
In the experimental test, a significant magnetic resistance effect was observed. The power dissipation in the experimental test can be given by
where PT is the dissipated power in experimental test. When the input signal is characterized by a frequency of 3 GHz and a power of 100 W, the observed discrepancy between the experimentally measured power and the simulated circuit output can be attributed to the power losses incurred within the magnetic material coating. The current can be calculated by Equations (30) and (31):
The contact points are connected in parallel, so the voltage on a single contact point can be expressed as
where PT is the total power dissipation of the connector contact surface. Therefore, the maximum steady-state temperature of the conductor contact point in the nickel plating layer can be derived as
Based on the power difference between the experiment measurement and the circuit simulation, the parameters of the magnetic material with different plating thickness levels can be obtained, as shown in Table 5.

Table 5.
Relevant parameters of magnetic material plating.
The results presented in Table 5 indicate that connectors with different plating thicknesses exhibit similar H–M relations. This further suggests that, under the same high-frequency and high-power input signal, the magnetic resistance of connectors with varying plating thicknesses is primarily governed by the signal and remains unaffected by the contact surface environment. The significant variation in connection impedance among plating materials of different thicknesses leads to corresponding differences in maximum steady-state temperature.
4.4. Comparison of Calculation and Measurement
The thermal behavior of coaxial connectors under different plating materials exhibits distinct trends with respect to plating thickness. Table 6 presents the calculated and measured temperature variations of connectors with different plating materials and thicknesses. For silver-plated connectors, the maximum steady-state temperature decreases monotonically with increasing plating thickness. This reduction is primarily attributed to improved contact conditions, including enhanced contact pressure, diminished interfacial gaps, and an enlarged real contact area. These factors collectively lower the contact resistance, thereby reducing the voltage drop and associated temperature rise at the contact interface. This effect becomes increasingly pronounced at higher coating thicknesses. Both experimental observations and numerical simulations, as illustrated in Figure 15, consistently confirm this behavior.

Table 6.
Calculated and Measured Temperature Variations of Connectors with Different plating Materials and Thicknesses.
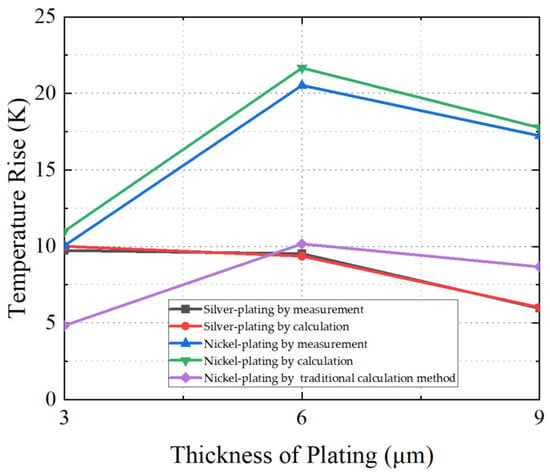
Figure 15.
Derivation and verification scheme for the maximum steady-state temperature of non-magnetic material connectors. Relationship between thickness of plating and temperature rise.
In contrast, nickel-plated connectors display a non-monotonic trend in maximum steady-state temperature with increasing plating thickness. Initially, the temperature rises due to the dominant influence of increasing effective resistivity, which offsets the effects of enhanced contact pressure and results in elevated connection resistance. However, beyond a critical thickness (from Level 2 to Level 3), the effective resistivity stabilizes, and the continued increase in contact pressure becomes the prevailing factor, leading to a reduction in connection resistance and, consequently, a decrease in the maximum steady-state temperature. This complex interplay between mechanical and electrical parameters highlights the material-specific nature of thermal responses in plated coaxial connectors.
In the traditional approach, the contact resistance is first calculated using Holm’s law and the Greenwood–Williamson (G–W) model. Then, the maximum steady-state temperature of the N-DIN RF coaxial connector is estimated based on Ohm’s law and the voltage–temperature (V–T) relationship. The predicted maximum temperatures for connectors with different nickel plating thicknesses are shown in Figure 15. As can be seen from the figure, the temperature rise predicted by the traditional method is significantly lower than the measured values. This discrepancy arises because the traditional model does not account for the skin effect or additional losses due to magnetic reluctance. These findings highlight that the proposed prediction framework markedly reduces the relative error in temperature estimation under high-frequency and high-power excitation. This improvement is attributed to the fact that classical models underestimate the contact voltage across rough surfaces at high frequencies, and consequently the resulting thermal effects.
Furthermore, in the case of connectors with magnetic plating materials, the presence of magnetic resistance under high-frequency conditions leads to an additional increase in connection resistance at the contact point. This elevated resistance contributes to a higher voltage drop and, consequently, a rise in the maximum steady-state temperature. The value of magnetic resistance varies with plating thickness, as different thickness levels alter the electromagnetic environment at the contact interface. These variations stem from changes in surface contact conditions, which affect the local magnetic field distribution. However, by calculating the characteristic parameters (k₁, k₂, k₃) of magnetic plating materials, the relationship between magnetic field strength (H) and magnetic resistance (M) at the contact interface can be quantitatively established, providing a foundation for analyzing the thermal behavior of connectors with magnetic plating materials. The calculated maximum steady-state temperature of the non-magnetic plating material model exhibits strong agreement with experimental measurements. In contrast, for magnetic plating materials, the predicted maximum temperature is slightly higher than the measured values. Nonetheless, this deviation remains within an acceptable range and does not compromise the engineering applicability of the model in evaluating the maximum steady-state temperature of RF coaxial connectors.
5. Conclusions
This study presents a novel multiphysics modeling framework for evaluating the steady-state thermal behavior of RF coaxial connectors under high-frequency, high-power excitation, with a particular emphasis on the role of plating material properties. By combining experimental temperature measurements, finite element simulations, and equivalent circuit modeling, a comprehensive relationship is established between microscopic contact mechanics and macroscopic thermal performance.
The experimental results and simulations consistently reveal distinct thermal behaviors between magnetic and non-magnetic plating materials. For non-magnetic silver coatings, increasing the plating thickness leads to improved contact quality and reduced interfacial resistance, resulting in a monotonic decrease in temperature. In contrast, ferromagnetic nickel coatings exhibit a non-monotonic temperature trend due to the combined effects of surface morphology, constriction resistance, and magnetically induced resistance variation. To account for the magnetoresistance effect in nickel coatings, a magnetic field-dependent resistance term was introduced into the equivalent circuit model, effectively capturing the hysteresis-induced nonlinearities observed in experimental data. Although slight overestimation of temperature was observed in the magnetic case, the model provides a conservative and practical margin for thermal reliability assessments.
Moreover, this work addresses several key technical challenges in the measurement and modeling of RF connector heating. A specially designed connector structure allowed the accurate localization and measurement of internal hot spots, while the experimental platform enabled precise power control and loss quantification. The modeling approach avoids the limitations of conventional V–T equations under high-power conditions by directly linking measured power dissipation to temperature rise. For ferromagnetic materials, the modeling bypasses domain-level magnetic simulations by capturing their electromagnetic response through macroscopic equivalent parameters, offering an efficient and scalable predictive framework.
In summary, this work advances the understanding of thermal behavior in high-power RF connectors, highlights the critical influence of material-specific electromagnetic properties, and introduces an experimentally validated modeling strategy that integrates electrical contact theory, magnetoresistive effects, and thermal analysis. The proposed framework provides a valuable tool for optimizing connector design and ensuring reliability in next-generation communication systems.
Author Contributions
Conceptualization, J.G. and Y.Z.; methodology, Y.Z. and T.Z.; software, Y.Z.; validation, Y.Z. and T.Z.; formal analysis, Y.Z.; investigation, J.L. and Y.Z.; resources, J.L.; data curation, Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z.; visualization, J.G. and T.Z.; supervision, J.G.; project administration, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Key R&D Program of China under grant number [2022YFF0605904] and in part by the Specialized Scientific Research Projects of Chinese Institute of Electronics and Beijing Smart-chip Microelectronics Technology Co., Ltd.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
Author Jie Lei was employed by the company FORSTAR S&T Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RF | Ratio frequency |
| FEA | Finite element analysis |
| DC | Direct current |
| AC | Alternating current |
| V–T | Voltage–temperature |
| H–M | Magnetic field strength–magnetization |
References
- Holm, R. Electric Contacts, Theory and Applications; Springer: Berlin, Germany, 1976. [Google Scholar]
- Jackson, R.L.; Ashurst, W.R.; Flowers, G.T.; Angadi, S.; Choe, S.-y.; Bozack, M.J. The effect of initial connector insertions on electrical contact resistance. In Proceedings of the 53th IEEE Holm Conference on Electrical Contacts, Pittsburgh, PA, USA, 16–19 September 2007; pp. 17–24. [Google Scholar] [CrossRef]
- Angadi, S.V.; Wilson, W.E.; Jackson, R.L.; Flowers, G.T.; Rickett, B.I. A Multi-Physics Finite Element Model of an Electrical Connector Considering Rough Surface Contact. In Proceedings of the 54th IEEE Holm Conference on Electrical Contacts, Orlando, FL, USA, 27–29 October 2008; pp. 168–177. [Google Scholar] [CrossRef]
- Singer, M.T.; Kshonze, K. Electrical resistance of random rough contacting surfaces using fractal surface modeling. In Proceedings of the 37th IEEE Holm Conference on Electrical Contacts, Chicago, IL, USA, 6–9 October 1991; pp. 73–82. [Google Scholar] [CrossRef]
- Michopoulos, J.G.; Young, M.; Iliopoulos, A. A Multiphysics Theory for the Static Contact of Deformable Conductors With Fractal Rough Surfaces. IEEE Trans. Plasma. Sci. 2015, 43, 1597–1610. [Google Scholar] [CrossRef]
- Lei, X.; Yu, Z.; Gao, Y.; Zhou, Y.; Xu, K.; Chen, Y.; Zhu, F. Investigation on Electrical and Thermal Performance of Electrical Connectors Under Rough Surface Contact. IEEE Trans. Compon. Packag. Manuf. Technol. 2025, 15, 281–287. [Google Scholar] [CrossRef]
- Wang, S.; Hu, F.; Su, B.; Zhai, G. Method for calculation of contact resistance and finite element simulation of contact temperature rise based on rough surface contact model. In Proceedings of the 26th International Conference on Electrical Contacts, Beijing, China, 14–17 May 2012; pp. 317–321. [Google Scholar] [CrossRef]
- Ren, W.; Wei, J.; Meng, X.; Zhi, H. Numerical Simulation of Temperature—Voltage Relation in Electrical Contacts and Correction of Classical Kohlrausch’s Equation. IEEE Trans. Electron Devices 2016, 63, 1217–1224. [Google Scholar] [CrossRef]
- Gatzsche, M.; Lücke, N.; Großmann, S.; Kufner, T.; Freudiger, G. Evaluation of Electric—Thermal Performance of High-Power Contact Systems With the Voltage—Temperature Relation. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 317–328. [Google Scholar] [CrossRef]
- Ji, R.; Flowers, G.T.; Gao, J.; Cheng, Z.; Xie, G. High-Frequency Characterization and Modeling of Coaxial Connectors with Degraded Contact Surfaces. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 447–455. [Google Scholar] [CrossRef]
- Timsit, R.S.; Luttgen, A. Temperature distribution in an ohmic-heated electrical contact at high signal frequencies. Appl. Phys. Lett. 2016, 108, 121603. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.; Yu, M. Thermal Effect Impact to Coaxial Connector in Microwave Connection Applications. In Proceedings of the 2020 IEEE Asia-Pacific Microwave Conference (APMC), Hong Kong, China, 8–11 December 2020; pp. 852–854. [Google Scholar] [CrossRef]
- Jin, Q.; Feng, Q. Passive Intermodulation Distortion in Connectors with Nonlinear Interaction in Electrical Contacts and Magnetic Materials. IEEE Trans. Microw. Theory Tech. 2022, 70, 1119–1131. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Wang, H.; Huo, D.; Tan, W. Room-temperature magnetoresistive and magnetocaloric effect in La1−xBaxMnO3 compounds: Role of Griffiths phase with ferromagnetic metal cluster above Curie temperature. J. Appl. Phys. 2022, 131, 043901. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, J.; Flowers, G.T. Modeling and Analysis of the Effect of Signal Frequency on the Contact Surface Temperature of Coaxial Connectors. In Proceedings of the 64th IEEE Holm Conference on Electrical Contacts, Milwaukee, WI, USA, 14–18 September 2019; pp. 270–277. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, J.; Flowers, G.T. Modeling and Analysis of Electrical-Thermal Performance of the Contact Surface of Coaxial Connectors at High Frequency and High Power. In Proceedings of the IEEE 67th Holm Conference on Electrical Contacts, Tampa, FL, USA, 23–26 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Q.; Liu, Y.; Chen, W.; Cao, J.; Xia, C.; Talwar, R.; Lederich, R. Analysis and Convenient Formulas for Elasto-Plastic Contacts of Nominally Flat Surfaces: Average Gap, Contact Area Ratio, and Plastically Deformed Volume. Tribol. Lett. 2007, 28, 27–38. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. In Proceedings of the Royal Society of London, London, UK, 6 December 1966; Volume 295, pp. 300–319. [Google Scholar] [CrossRef]
- Timsit, R.S. Electrical Contact Resistance: Properties of Stationary Interfaces. IEEE Trans. Compon. Packag. Technol. 1999, 22, 85–98. [Google Scholar] [CrossRef]
- Greenwood, J.A. Constriction resistance and the real area of contact. Brit. J. Appl. Phys. 1966, 17, 1621. [Google Scholar] [CrossRef]
- Timsit, R.S. On the Evalutation of Contact Temperature from Potential-Drop Measurements. IEEE Trans. Compon. Hybrids Manuf. Technol. 1983, 6, 115–121. [Google Scholar] [CrossRef]
- Malucci, R.D.; Panella, A.P. Contact Physics of Capacitive Interconnects. IEEE Trans. Compon. Packag. Manuf. Technol. 2013, 3, 377–383. [Google Scholar] [CrossRef]
- Timsit, R.S. High Speed Electronic Connectors: A Review of Electrical Contact Properties. IEICE Trans. Electron. 2005, E88-C, 1532–1545. [Google Scholar] [CrossRef]
- Williamson, J.B.P.; Greenwood, J.A. The constriction resistance between electroplated surfaces. In Proceedings of the International Conference on Electrical Contacts and Electromechanical Components, Appendix, Beijing, China, 9–12 May 1989; Pergamon Press: Oxford, UK, 1989. [Google Scholar]
- Ennen, I.; Kappe, D.; Rempel, T.; Glenske, C.; Hütten, A. Giant Magnetoresistance: Basic Concepts, Microstructure, Magnetic Interactions and Applications. Sensors 2016, 16, 904. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).