Abstract
This study generalizes and further develops methods for efficiently implementing artificial neural networks (ANNs) in the onboard computers of mobile robotic systems with limited resources, including unmanned aerial vehicles (UAVs). The neural networks are sped up by constructing a new unbounded activation function called “s-parabola”, which meets the requirements of twice differentiability and reduces computational complexity over sigmoid-based functions. An additional contribution to this acceleration comes from activation functions based on bit-parallel computational circuits. A comprehensive review of modern publications in this subject area is provided. For autonomous problem-solving using ANNs directly on board an unmanned aerial vehicle, a trade-off between the speed and accuracy of the resulting solutions must be achieved. For this reason, we propose using fast bit-parallel circuits with limited digit capacity. The special representation and calculation of activation functions is performed based on the transformation of Jack Volder’s CORDIC iterative algorithms for trigonometric functions and Georgy Pukhov’s bit-analog calculations. Two statements are formulated, the proofs of which are based on the equivalence of the results obtained using the two approaches. We also provide theoretical and experimental estimates of the computational complexity of the algorithms achieved with different operand summation schemes.
1. Introduction
Due to the active use of artificial neural networks (ANNs) in real-time systems and the availability of a wide class of typical nonlinearities as activation functions, there is an ongoing and relevant research interest in accelerating information processing. In this regard, various methods are used to speed up the computation of activation functions. For example, [1,2] are devoted to the special organization of “fast” neurons and neural networks. A detailed review of modern approaches to accelerating activation functions is provided in [3].
The CORDIC (Coordinate Rotation Digital Computer) family reduces the computation of complex functions to a set of simple iterations of algebraic addition and shift. It is often used as the basic algorithm for solving problems in onboard aerospace systems, providing a tradeoff between the accuracy and speed of computation with low memory costs [4,5]. The advantage of this implementation is that its accuracy is related to the number of iterations used, each of which adds one correct digit of the result. Modern applications of CORDIC algorithms that are useful on board UAVs mainly include fast and discrete Fourier transforms, discrete sine and cosine transforms, linear algebra algorithms, digital filtering, and image-processing algorithms. Despite their popularity, CORDIC algorithms have some disadvantages that prevent their effective use in parallel systems, including the iterative nature of calculations and the necessity of correcting the result. The solution may lie in constructing neurons with activation functions based on bit-parallel information-processing circuits using specialized computers with limited operand digit capacity [6].
Bit-parallel computing is a group of methods that calculate mathematical functions with high accuracy in floating-point formats. The problem with such calculations is multifaceted due to the diversity and specificity of the tasks solved on their basis. Bit-parallel computing is used, for example, in the onboard navigation and control systems of autonomous aerial vehicles. All existing approaches aim to increase the length of the processed binary operand, thus improving the computation speed. Of considerable interest is a series of works aimed at increasing the speed of solving various comparison problems, establishing correspondence between streams, and performing arithmetic operations on bit vectors, including the simultaneous processing of matrix columns [7,8,9,10].
The problem of achieving a high level of instruction parallelism in string-matching algorithms is considered in [11]. Two variants of the bit-parallel wide-window algorithm are presented, using parallel computation relying on the SIMD (Single Instruction Multiple Data) paradigm. As the experimental results show, this technique provides increased speed by doubling the size of window shifts.
Various architectural solutions have been proposed to speed up operations under computational resource constraints. In [12], a bit-parallel computing in-memory architecture based on SRAM 6T cells is presented to support reconfigurable bit precision, in which bit-parallel complex computations become possible by iterating low-latency operations. The proposed architecture provides 0.68 and 8.09 TOPS/W performance for parallel addition and multiplication, respectively. A specialized architecture designed for the parallel computation of bit patterns is proposed in [13]. That research assumes that all operations based on multi-bit data values are performed bit-serially, but at the same time, each operation is SIMD-parallel based on data, and -bit operations complete in clock cycles using only gates per clock.
Bit-analog computations of mathematical and logical functions are of interest. Thus, in [14], an alternative approach to a parallel solution is considered. Here, a bit stream is processed through digital logic to satisfy the required algorithm. Using elementary digital gates, classical elements such as integrators and differentiators required to implement a PID controller on an FPGA can be constructed. It is also worth noting the research on the bit-parallel modeling of combinational logic gates [15]. These results allow us to estimate the probability of the logical masking of a random circuit fault. The methods are compared in terms of accuracy and time cost using testing results for benchmark circuits.
The analog computation technique proposed by G.E. Pukhov is also of great interest. In [16], a method based on the differential Taylor transform (DT) was proposed, which was applied to the basic concepts and solutions of various mathematical problems, as well as to the creation of physical models. The results obtained using this method can be presented both numerically as spectra and analytically as an approximate sequential or functional dependence. The DT method is universal, allowing one to determine the original function in the form of various functions other than the Taylor expansion. In [17], differential transformations of functions and equations for the construction of linear and nonlinear circuits are presented. The authors of [18] consider the differential transform method for solving various types of differential equations in fluid mechanics and heat transfer. A method of approximate differential transformation and its combination with Laplace transforms and Padé approximation for finding the exact solutions of linear and nonlinear differential and integro-differential equations is presented in [19].
Let us proceed to a direct analysis of the work of G.E. Pukhov with respect to bit-parallel calculus [6]. The basis for constructing bit-parallel computing circuits is the concepts of a bit vector and matrix used in bit-analog schemes of inverse function calculation and square root extraction. For high-precision bit-parallel computing in the floating-point format, the modular–positional data representation format is used. It enables parallelizing arithmetic operations down to the level of individual digits of multi-digit mantissas. Mapping the result of a functional transformation into a bit-parallel circuit involves representing each digit of a number in the form of a bit formula. Analog and digital bit-parallel computing is used, for example, in onboard navigation and control systems, where it is important to ensure a real-time mode under limited resources.
Due to the limited number of mathematical functions representable by G.E. Pukhov’s method, we will turn to another theory regarding the construction of a variety of mathematical functions based on CORDIC family algorithms proposed by Jack Volder [20]. The algorithms efficiently calculate arithmetic, trigonometric, and hyperbolic functions and are currently used in various applications [21], such as image processing and communication. Full-fledged studies of CORDIC functions were performed in detail by V.D. Baykov [22,23]. CORDIC algorithms reduce the computation of complex functions to iterative procedures containing simple addition and shift operations [24,25,26]. A comparison and evaluation of methods for calculating the basic functions “square root” and “inverse function” is considered in [27]. The transition to bit-parallel computational schemes can be carried out formally by expanding the iterations. This study proposes solving the increasing problem of simultaneous derivation of Volder operators by comparing the obtained bitwise representations with similar ones proposed by G.E. Pukhov.
In [28], a low-latency CORDIC algorithm is proposed to accelerate the computation of arctangent functions. The authors stated that the novel method can effectively reduce the number of iterations through dedicated pre-rotation and comparison processes. The CORDIC IP Core User’s Guide [29] provides a block diagram of the CORDIC arithmetic unit, which is configurable and supports several functions, including “rotation”, . The device supports parallel mode, in which the output data are processed in one clock cycle, and serial mode, in which the output data are calculated in several clock cycles. The IP core supports variable precision and several rounding algorithms.
In the present study, we solve the problem of constructing bit-parallel computing circuits for the efficient implementation of neuron activation functions based on universal CORDIC algorithms. Such circuits can be constructed by extending the iterations and, on this basis, implementing computationally efficient activation functions of the “sigmoid” [30] and “s-parabola” [31] types. The circuits provide the necessary parallelism and expansion for the functional capabilities of onboard computers and can be obtained within the framework of the approaches proposed in [32,33]. An example of the construction of a “fast neuron” based on the calculation of the activation function using a tabular-algorithmic method with a focus on performing parallel representation and group summation operations is provided in [34].
To speed up computations in neural networks, specialized devices (ANN accelerators) are used [35]. ANN accelerators speed up two basic operations: multiplication and accumulation (MAC) and matrix–vector multiplication (MVM). The devices can be built using field-programmable gate arrays (FPGAs) or application-specific integrated circuits (ASICs). The authors of [36] propose a scalable convolutional neural network (CNN) accelerator architecture for devices with limited computing resources. It can be deployed on several small FPGAs instead of one large FPGA for better control over parallel processing. A low-power CNN accelerator using an FPGA designed for mobile and resource-constrained devices is proposed in [37]. Accelerators are used in various areas where neural network-based algorithms are employed: image and video processing, autonomous systems, and robotics [38].
Let us now turn to some modern development directions in the subject area. The problems in constructing fast onboard computers are of great interest and are considered, for example, in [39]. An analysis of the current state of the CubeSat Command and Data Handling (C&DH) subsystem is provided, covering both hardware components and flight software (FSW) development frameworks. The problems of applying modern neural network models in resource-constrained environments and accelerating inference time are considered in [40]. That study provides a comprehensive review of current advances in pruning techniques as a popular research direction in neural network compression.
A promising direction for further research is the construction of fuzzy neural networks (FNNs), which can be achieved using neural architecture search (NAS). Such networks provide high classification accuracy and good performance in the presence of uncertainties [41].
In this study, we rely on the creation of specialized computing structures without being tied to specific technologies.
Subsequent sections are organized as follows:
- Section 2 formulates and solves the problem of bit-parallel computation in the sigmoid activation function of a neural network using the CORDIC and Pukhov methods. This function is constructed based on corresponding representations of the inverse function (Section 2.1, Section 2.2 and Section 2.3) and exponent (Section 2.4). Two statements on the parallelism of the Volder operators for these functions are proven.
- Section 3 is devoted to constructing a bit-parallel scheme to compute a new activation function called “s-parabola”. For its implementation, bit-parallel schemes for extracting a square root using the CORDIC method (Section 3.1) and Pukhov’s method (Section 3.2) are presented. A statement on the parallel computability of Volder operators for implementing this function is proved. A parallel scheme for calculating Volder operators is also provided (Section 3.3).
- Section 4 presents theoretical estimates of the computational complexity of activation functions used in neural networks. Estimates of the time complexity of bit-parallel schemes for computing the sigmoid and s-parabola activation functions for different operand bit-widths are provided. The estimates consider the number of operations and the algebraic summation method used. Performance studies of the software implementation of the bit-parallel scheme using the example of the s-parabola are carried out.
- The final section contains the main conclusions and prospects for the practical application of bit-parallel computational circuits for the fast calculation of activation functions as a part of convolutional neural networks. We recommend that the algorithms be included in the mathematical support of onboard computing systems, taking into account the limitations of their computing resources.
2. Bit-Parallel Computation of the Activation Function of the “Sigmoid” Type
A limited number of constants; ; in CORDIC, the “rotate” and “vector” procedures; and the “logarithmic” operation, , in practical applications, can be calculated in advance and stored in a database/knowledge base. Having simultaneous access to all Volder operators, , in the “rotate”, “vector”, and “logarithm” operations, provides broad opportunities for organizing bit-parallel computations. A typical approach is to move away from the sequential nature of computations by expanding recurrent relations in time. Here, one should add the possibilities of bit-parallel circuits to find the inverse function and calculate the square root, obtained using G.E. Pukhov’s methodology.
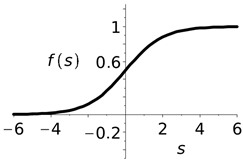
The sigmoid is a nonlinear function, , with parameter that outputs a real number in a range of 0 to 1; thus, if , then ; if , then [6]. The sigmoid is characterized by the saturation effect, which means that the network will be poorly trained at the boundaries. One disadvantage of neurons and ANNs is low computation speed. Let us consider the sigmoid (logistic) function of the following form:
In binary positional notation, the result can be represented as a convergent sum: . In practice, the upper limit of the sum is limited by the specific bit-width of the operands and the length of the digit grid of the computing device. We will consider the function , such that . The result of the calculation can be written in the usual positional form: .
The CORDIC family of computational algorithms can find one correct digit of the result at each iteration. Using the shift operation, addition, subtraction, and limited memory for storing constants, the algorithms implement the necessary functions [23]. The technology for performing CORDIC operations is based on the fundamental possibility of representing the result as a sum, , where are Volder operators (hereinafter referred to as operators) for cases of alternating iterations. The number of terms in the sum, , is associated with the number of iterations performed, which is determined by the bit-width of the operands, ; moreover, . The operators are obtained as a result of the corresponding iterative procedure, which forms the first stage of function computation. By analogy with [6], if we express the operators through the digits of the argument, we obtain a sum of the following form:
Since, in the general case, are not Volder operators, we will call them pseudo-operators.
The advantage of implementing these activation functions is the connection of accuracy with the number of iterations, at each of which, one correct digit of the result is added. The adjustable accuracy of the calculations, related to the number of iterations performed, allows us to choose a strategy depending on the time resource. The disadvantage of the given Formula (2) is the impossibility of the parallel calculation of the Volder operators, predetermining the sequential nature of the algorithms.
Let us consider the possibility of overcoming this disadvantage based on bit calculus [6]. Vector , whose components are the digits of a binary number (), is a normalized bit vector. The task of mapping the result of the functional transformation , where , into a bit-parallel circuit involves representing each th digit of a number, , in the form of a formula: In several cases typical of CORDIC algorithms, the digits of a mathematical function can be represented as a function of variables associated with the digits of the argument, for example, by Volder operators . Such schemes are also bit-parallel, provided that all operators are simultaneously available. Implementing the sigmoid in accordance with (1) is based on the schemes of the bit-parallel representation of functions and .
2.1. Bitwise Representation of the Inverse Function Using the CORDIC Method
The argument of the function must be presented in the form . Here, , are quantities called “Volder operators”, which are calculated by the following formula:
Given the operators (3), the result of the operation is obtained as follows:
By successively expanding the product (4), we obtain
Scheme (5) expresses the result of the operation through Volder operators, which can only be calculated sequentially. Of interest is the possibility of the parallel calculation of these operators.
2.2. Bitwise Representation of the Inverse Function Using G.E. Pukhov’s Method
Let us consider the function . Here, is a positive binary number represented in normalized form, is the mantissa, is the order of number , and is the value of the th digit of the mantissa with its own weight (); moreover, , and is the length of the digit grid.
The result of finding the reciprocal value is presented as , where is the mantissa of a number, . The relationship between and is set using a bit expression, , where is the bit vector. Here, is the square bit matrix, and is the inverse bit matrix [6].
The bit matrix is formed by bit vectors, and all known matrix inversion methods can be used to obtain the inverse bit matrix. Thus, we can obtain the following formulas:
Without losing generality, let us consider the order of calculations for . As a result of successive substitutions, given that , we obtain
Here, is expressed through the corresponding digit coefficients of . To make the form of the system (7) suitable for performing the group summation of operands, the corresponding elements should be moved from one digit to another, taking into account their weights. Thus, we have
The computing scheme is bit-parallel. In the general case, calculating each digit, , through the digits of the argument leads to values that do not belong to the set and, therefore, requires inter-bit alignment to form the binary code of the result. However, the summation of all elements with respect to their weights must be performed to obtain the final result.
From the system of bit coefficients (8), two groups of binary operands can be formed in accordance with their signs. The prepared binary numbers must be summed to obtain the final result.
2.3. Bit-Parallel Computation of Volder Operators for the Inverse Function
Statement 1.
Operators , for function can be calculated in parallel based on the equivalence of bit circuits (5) and (8).
Proof of Statement 1.
Computational Schemes (5) and (8) are equivalent since they lead to the same values of the function
. The validity of the statement is based on the identity of the bitwise equating of representations.
By bitwise equating Relations (5) and (8), we can obtain the Volder operators:
In accordance with Statement 1, scheme (9) demonstrates the fundamental possibility of obtaining the values of pseudo-operators directly from the binary argument, . Substituting the values of these operators into (8) provides the correct solution to the problem of calculating the inverse function in bit-parallel form.
2.4. Bitwise Representation of the Function
When calculating the exponential function with a base, we can assume that its argument, , is an -digit binary number. Therefore, the following representation of the result as a product is valid:
where .
Considering that is a vector consisting of zeros and ones, we obtain
For definiteness, let us set and . Substituting the set of constants, we obtain the formulas
From Expression (11), we derive bit vectors :
In accordance with (10), we obtain the result in the form of the following scheme:
The accuracy can be increased by moving to a higher bit-width. This approach can be applied to any other base.
According to the CORDIC approach, the function argument is represented by where the signs of the operators are found from the condition and the result is obtained in the following form:
Expanding the expression for , we obtain the following scheme for the bitwise representation:
By implementing the calculation scheme for an 8-bit argument, we obtain the results presented in Table 1.

Table 1.
Exponential function calculation.
In CORDIC, the simultaneous retrieval of operator values is a problem that can be eliminated based on the equivalence of bit schemes.
2.5. Parallel Computation of Volder Operators for the Function
Statement 2.
Operators , , for the function can be calculated in parallel based on the equivalence of bit circuits (14) and (16).
Proof of Statement 2.
By equating the expressions with the corresponding coefficients in Formulas (14) and (16), we express operators,
, through the digits of the argument:
This result is useful only from the perspective of demonstrating the fundamental possibility of obtaining bit-parallel circuits based on CORDIC.
Let us consider the calculation of the function , the result digits of which form a binary number, . To obtain this function in a bitwise form, we use the Volder relations. For a function of the form , the following recurrence relations are valid [23]:
Input values:
Result: .
However, in accordance with [6], we have
Considering the given relations, the result of calculating the function in bit-parallel form has the structure shown in Table 2.

Table 2.
Calculation of the function in bit-parallel form.
Thus, to perform the bit-parallel representation of the function , it is necessary to do the following:
- For each , calculate the corresponding set of operators, , for the base ;
- Create tables of logarithms, , , where the sign within a bracket is determined by the operator sign, ;
- Calculate the function using an adder that implements the summation operation.
Implementing the inverse function is performed as follows:
- The bit-parallel form (see Table 1) is modified by adding one . For this, we will use an approximate bitwise representation of the digit one (see Table 3).
 Table 3. Bitwise representation of the digit one.
Table 3. Bitwise representation of the digit one. - In accordance with Table 3, the digits for bitwise representation (8) are formed. As noted above, to move to the normalized binary representation, it is necessary to perform the summation operation.
- The inverse function, , according to scheme (8), and, finally, expression (1), are calculated.
3. Bit-Parallel Computation of the s-Parabola Activation Function
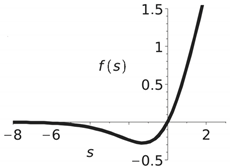
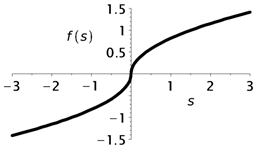
The approach proposed in this study is based on the idea of constructing models of fast neurons with an “s-parabola”-type activation function, in which the upper part (first quadrant) is the upper branch of the parabola, and the lower part is a mirror image of the lower part of the parabola relative to the ordinate axis (third quadrant). An example of such a curve compared with the swish (combining linear and nonlinear properties) and sigmoid functions is shown in Table 4.

Table 4.
Comparable nonlinear activation functions.
Note that the well-known SiLu (sigmoid linear unit) function is obtained by setting . Despite the significant advantages of the swish function, it has high computational complexity, which can affect the inference time for devices with limited computing resources. The sigmoid activation function in deep neural networks faces vanishing gradient and saturation problems. The “s-parabola” curve is smooth and monotonically increasing, and allows the model to train more efficiently and converge quickly to a solution [42]. The implementation relies on the bit-parallel representation of the function , forming the basis of the “s-parabola” nonlinearity.
3.1. Bit-Parallel Circuits for Calculating the Square Root Function Using Volder
According to the CORDIC approach [20,43], from which it follows that
By implementing the calculation scheme for an 8-bit argument, we obtain the results presented in Table 5.

Table 5.
Square root extraction method by J. Volder.
3.2. Pukhov’s Bit-Parallel Circuit for Square Root Extraction
Let be a positive binary number represented in the normalized form . The result of the operation , is represented by digits and is related to argument by the expression , where is a square bit matrix (bit-width ), and is bit vectors. Following the method of calculating the bit coefficients for [6], we obtain
By implementing the calculation scheme for an 8-bit argument, we obtain the results presented in Table 6.

Table 6.
Square root extraction method by G.E. Pukhov.
For the binary number system, it is true that . Therefore, after appropriate transformations, we obtain a bit-parallel computing circuit:
3.3. Parallel Computation of Volder Operators for the Square Root Function
Statement 3.
Operators , for the function can be calculated in parallel based on the equivalence of bit circuits (20) and (22).
Proof of Statement 3.
The relationship between the result and operand digits can be established based on the following equality:
The bit-parallel scheme for the inverse function was obtained earlier. By expanding the right-hand side of equality (23), we derive the bitwise representation of the function (see Table 7), taking into account the adopted constraints and weights.

Table 7.
Bitwise representation of the function .
Equating the mantissas of the obtained result and the result of the inverse operation (22), we obtain the values of pseudo-operators for square root extraction:
Substituting the obtained pseudo-operators into (20), we obtain
By redistributing the elements between adjacent digits, we obtain a normalized bit-parallel circuit:
4. Time Complexity Estimation for the Implementation of Bit-Parallel Circuits
Based on the developed bit-parallel circuits, the structure of a specialized processor unit is proposed, the operational part of which is shown in Figure 1.
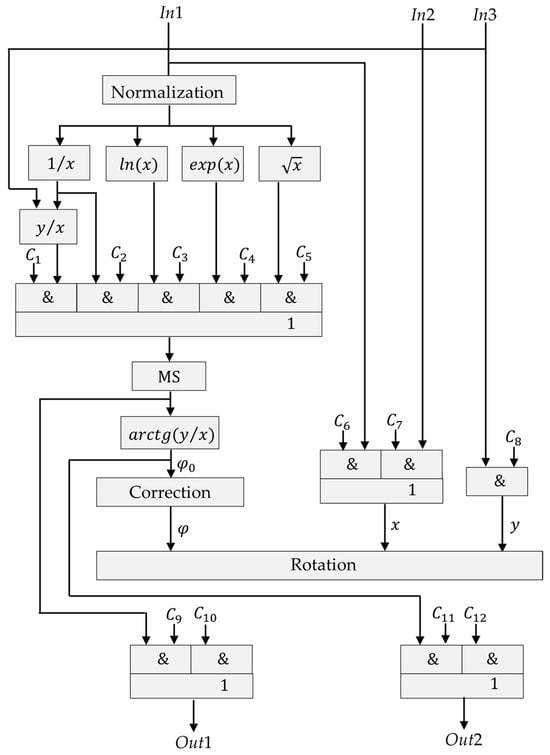
Figure 1.
Structure of a specialized processing unit.
The main emphasis is placed on tabular algorithmic calculations, with a significant role given to logic arrays that store pre-prepared information. Each operation is implemented in the processing unit by appropriately adjusting its structure. The structure is programmed by switching (assigning) individual blocks using control signals which are formed after the control device decodes the command codes. The use of pipelined and bit-parallel algorithms allows us to build calculators on a unified methodological basis with simple and convenient mathematical apparatuses combining cycles of information processing, which involves the group summation of operands with effective hardware support. The basic set of commands is presented in Table 8.

Table 8.
Basic set of commands for the geometric processor unit.
To select the required function, it is necessary to assign the path of information flow in the specified structure using control signals. The processor element hardware supports a specialized language, with the help of which the user can perform structured programming of algorithms.
The calculation of mathematical functions based on bit-parallel representation is reduced to the algebraic summation of binary operands in accordance with their signs and weights. The number of terms for , is estimated as , and for , as , where is the bit-width of the operands.
For bit-parallel circuits, a special data representation is used in the form of a table, which contains operands (columns) prepared for algebraic addition. An example of such a logical table for calculating the inverse function is presented in Table 9.

Table 9.
Bit-parallel circuit for calculating .
The table allows us to implement bit-parallel circuits based on FPGA and ASIC technologies. At this stage of the study, we limit ourselves to assessing the possible performance of such an approach.
Estimates of the computation complexity of various activation functions depending on the operand digits, , but without using bit-parallel computations are presented in Table 10.

Table 10.
Computational complexity of activation functions.
Table 10 shows that the theoretical estimation of computational acceleration using the s-parabola function compared with using sigmoid and swish can be more than 5.6-fold. At the same time, the s-parabola is significantly inferior to the ReLU function in terms of average performance (approximately 8-fold).
In [44], a theorem is formulated proving that the highest possible length of the sum of n m-bit integer numbers is equal to .
Using the cascade scheme of connecting parallel adders, the algebraic summation of operands can theoretically be performed for several clock cycles, , and the sequential summation will take cycles. The clock cycle here is equal to the time of one summation operation. Estimates of the complexity of calculating various functions according to Formulas (22) and (25) are provided in Table 11.

Table 11.
Complexity of bit-parallel computations (in cycles) of some functions.
Implementing bit-parallel circuits requires an increase in hardware costs. Of interest is summation technology based on fast multi-input adders [45,46]. Performance is determined by the formula , where the clock corresponds to the time when reading the operand from the permanent memory, and is the number of summands.
We simulated the computation of several mathematical functions for different input data in accordance with the CORDIC iteration formulas [29]. The average performance indicators obtained are given in Table 12.

Table 12.
Calculation time of mathematical functions using CORDIC algorithms.
The values are used to evaluate the performance indicators of the software implementations of activation functions. The corresponding computation time values are provided in Table 13. Testing was carried out on an Intel Core i7-7820X (3.6 GHz) processor using the assembler programming language.

Table 13.
Calculation time of activation functions.
Table 13 shows that the s-parabola activation function outperforms the sigmoid, SiLu, and swish activation functions by about 1.6-fold based on the test results. The transition to bit-parallel formulas to implement activation functions makes it possible to substantially equalize quantitative time estimations of various function calculations. Thus, program implementations of bit-parallel circuits provide acceleration in comparison with CORDIC implementations on an average of 1.5-fold. Better results can only be obtained with the hardware implementation of activation functions, but these studies are outside the scope of this study.
5. Discussion
We analyzed works devoted to the problem of implementing fast activation functions for artificial neural networks. We propose using “s-parabola” as an activation function along with the sigmoidal function. Computing the sigmoid as one of the main activation functions requires resource-intensive operations, such as raising to a power, division, or series expansion. Compared with the sigmoid, the proposed activation function is significantly simpler to implement and has certain advantages. To speed up calculations in systems with limited capabilities, we propose using Pukhov and Volder’s computational schemes with a fixed bit-width. The simultaneous use of these approaches ensures the parallel implementation of activation functions, demonstrating the possibility of constructing bit-parallel computational circuits that provide high performance.
The use of bit-parallel circuits and multiprocessor (multicore) devices allows us to significantly increase performance compared with implementation on a universal processor. The considered functions can be used in various multilayer ANNs, taking into account the specifics of the tasks being solved and the computing capabilities of the onboard computers. We recommend including the proposed algorithms in the mathematical software of onboard computers in the form of a library or implementing them as a universal computing module. The adjustable accuracy of calculations associated with the number of iterations performed allows us to choose a strategy depending on the time resource.
In the general case, studies have shown that applying the s-parabola function and its variations provides theoretical superiority in speed over the sigmoid, swish, hyperbolic tangent, and softsign functions, and that it is inferior only to the ReLU function. Software implementation with the swish, sigmoid, and s-parabola functions using CORDIC algorithms and bit-parallel circuits maintains this trend.
The results presented herein are subject to certain limitations, primarily attributable to the algorithmic and theoretical orientation of the study. The proposed bit-parallel computing circuits have not yet been directly implemented in hardware accelerators. The objective of this work was not to achieve direct hardware realization but rather to focus on algorithmic transformations and formal restructuring aimed at facilitating future hardware implementation. Due to this focus, no direct comparisons were conducted between the performance of neural networks using the newly proposed activation functions and those employing standard functions.
A distinguishing feature of the study lies in the development of a method for organizing bit-parallel algorithms as tabular structures defined by logical expressions. This representation provides a foundation for leveraging programmable logic arrays to accelerate the computation of activation functions in artificial neural networks. Additionally, an architecture of a specialized processing unit is proposed, featuring an instruction set capable of executing mathematical operations involved in fast activation functions. At this stage, a theoretical analysis of the computational complexity for both sequential and bit-parallel implementations of key activation functions has been carried out. Comparative software evaluations using assembly language confirm the potential and efficiency of the proposed approach for integration into hardware-based computing systems.
We plan to conduct experiments using hardware accelerators and specialized computers in subsequent studies. In addition, new activation functions will be used to solve many practical problems.
Funding
This research was funded by the Russian Science Foundation, grant number 25-21-00222 (https://rscf.ru/en/project/25-21-00222/, accessed on 6 May 2025).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nabavinejad, S.M.; Reda, S.; Ebrahimi, M. Coordinated Batching and DVFS for DNN Inference on GPU Accelerators. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 2496–2508. [Google Scholar] [CrossRef]
- Trusov, A.; Limonova, E.; Slugin, D.; Nikolaev, D.; Arlazarov, V.V. Fast Implementation of 4-bit Convolutional Neural Networks for Mobile Devices. In Proceedings of the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021. [Google Scholar] [CrossRef]
- Shatravin, V.; Shashev, D.; Shidlovskiy, S. Sigmoid Activation Implementation for Neural Networks Hardware Accelerators Based on Reconfigurable Computing Environments for Low-Power Intelligent Systems. Appl. Sci. 2022, 12, 5216. [Google Scholar] [CrossRef]
- Volder, J.E. The Birth of Cordic. J. VLSI Signal Process.-Syst. Signal Image Video Technol. 2000, 25, 101–105. [Google Scholar] [CrossRef]
- Chetana; Sharmila, K.P. VLSI Implementation of Coordinate Rotation Based Design Methodology using Verilog HDL. In Proceedings of the 2023 Third International Conference on Artificial Intelligence and Smart Energy (ICAIS), Coimbatore, India, 2–4 February 2023; pp. 1574–1581. [Google Scholar] [CrossRef]
- Pukhov, G.E.; Evdokimov, V.F.; Sinkov, M.V. Bit-Analog Computing Systems; Sovetskoe Radio: Moscow, Russia, 1978. [Google Scholar]
- Hyyro, H.; Navarro, G. Bit-Parallel Computation of Local Similarity Score Matrices with Unitary Weights. Int. J. Found. Comput. Sci. 2006, 17, 1307–1323. [Google Scholar] [CrossRef]
- Hyyro, H. Explaining and Extending the Bit-Parallel Approximate String-Matching Algorithm of Myers; Technical Report; Department of Computer Science, University of Tampere: Tampere, Finland, 2001. [Google Scholar]
- Hyyro, H.; Navarro, G. Faster bit-parallel approximate string matching. In Proceedings of the 13th Annual Symposium Combinatorial Pattern Matching (CPM’02), Fukuoka, Japan, 3–5 July 2002; pp. 203–224. [Google Scholar] [CrossRef]
- Hyyro, H.; Navarro, G. Bit-parallel witnesses and their applications to approximate string matching. Algorithmica 2005, 41, 203–231. [Google Scholar] [CrossRef]
- Cantone, D.; Faro, S.; Giaquinta, E. Bit-(Parallelism)2: Getting to the Next Level of Parallelism. In Proceedings of the 5th International Conference (FUN 2010), Ischia, Italy, 2–4 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 166–177. [Google Scholar] [CrossRef]
- Lee, K.; Jeong, J.; Cheon, S.; Choi, W.; Park, J. Bit Parallel 6T SRAM In-memory Computing with Reconfigurable Bit-Precision. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Dietz, H.G. Parallel Bit Pattern Computing. In Proceedings of the 2019 Tenth International Green and Sustainable Computing Conference (IGSC), Alexandria, VA, USA, 21–24 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Patel, N.; Coghill, G.; Nguang, S.K. Digital realization of analogue computing elements using bit streams. In Proceedings of the 3rd IEEE International Workshop on System-on-Chip for Real-Time Applications, Calgary, AB, Canada, 30 June–2 July 2003; pp. 76–80. [Google Scholar] [CrossRef]
- Telpukhov, D.V.; Nadolenko, V.V.; Gurov, S.I. Computing Observability of Gates in Combinational Logic Circuits by Bit-Parallel Simulation. Comput. Math. Model. 2019, 30, 177–190. [Google Scholar] [CrossRef]
- Abbasov, T.; Yalçınöz, Z.; Keleş, C. Differential (Pukhov) transform method analysis of transient regimes in electrical circuits. UNEC J. Eng. Appl. Sci. 2024, 4, 5–19. [Google Scholar] [CrossRef]
- Pukhov, G.E. Differential Transforms and Circuit Theory. J. Circuit Theory Appl. 1982, 10, 265–276. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Rabiei, F.; Naser, N.S.; Abbasbandy, S. A Review: Differential Transform Method for Semi-Analytical Solution of Differential Equations. Int. J. Appl. Mech. Eng. 2020, 25, 122–129. [Google Scholar] [CrossRef]
- Moosavi Noori, S.R.; Taghizadeh, N. Modified differential transform method for solving linear and nonlinear pantograph type of differential and Volterra integro-differential equations with proportional delays. Adv. Differ. Equ. 2020, 649, 1–25. [Google Scholar] [CrossRef]
- Volder, J.E. The CORDIC Trigonometric Computing Technique. IRE Trans. Electron. Comput. 1959, 8, 330–334. [Google Scholar] [CrossRef]
- Zechmeister, M. Solving Kepler’s equation with CORDIC double iterations. Mon. Not. R. Astron. Soc. 2021, 500, 109–117. [Google Scholar] [CrossRef]
- Baykov, V.D.; Seljutin, S.A. Elementary Functions Evaluation in Micro Calculators; Radio & Svyaz: Moscow, Russia, 1982. [Google Scholar]
- Baykov, V.D.; Smolov, V.B. Hardware Implementation of Elementary Function in Computers; Leningrad State University: St. Petersburg, Russia, 1975. [Google Scholar]
- Bhukya, S.; Inguva, S.C. Design and Implementation of CORDIC algorithm using Integrated Adder and Subtractor. In Proceedings of the 2021 6th International Conference for Convergence in Technology (I2CT), Maharashtra, India, 2–4 April 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, Z.L. CORDIC Algorithm and Its Applications. Bachelor’s Thesis, Università degli Studi di Padova, Department of Information Engineering, Padua, Italy, 2023. Available online: https://thesis.unipd.it/handle/20.500.12608/57115 (accessed on 28 May 2025).
- Vankka, J.; Halonen, K. CORDIC Algorithm. In Direct Digital Synthesizers; The Springer International Series in Engineering and Computer Science; Springer: Boston, MA, USA, 2001; Volume 614, pp. 23–32. [Google Scholar] [CrossRef]
- Vestermark, H. Fast Square Root and inverse calculation for Arbitrary Precision number. Preprint 2023, 1–29. [Google Scholar] [CrossRef]
- Li, K.; Fang, H.; Ma, Z.; Yu, F.; Zhang, B.; Xing, Q. A Low-Latency CORDIC Algorithm Based on Pre-Rotation and Its Application on Computation of Arctangent Function. Electronics 2024, 13, 2338. [Google Scholar] [CrossRef]
- Lattice Semiconductor Corp. CORDIC IP Core User’s Guide. FPGA-IPUG-02044 Version 1.4, July 2018. Available online: https://www.rxelectronics.jp/datasheet/0c/CORDIC-E5-UT.pdf (accessed on 28 May 2025).
- Mahima, R.; Maheswari, M.; Roshana, S.; Priyanka, E.; Mohanan, N.; Nandhini, N. A Comparative Analysis of the Most Commonly Used Activation Functions in Deep Neural Network. In Proceedings of the 2023 4th International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 6–8 July 2023; pp. 1334–1339. [Google Scholar] [CrossRef]
- Khachumov, M.; Emelyanova, Y.; Khachumov, V. Parabola-Based Artificial Neural Network Activation Functions. In Proceedings of the 2023 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 10–16 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 249–254. [Google Scholar] [CrossRef]
- Khachumov, V.M. Bit-Parallel Structures for Image Processing and Analysis. Pattern Recognit. Image Anal. 2003, 13, 633–639. [Google Scholar]
- Külekci, M.O. BLIM: A New Bit-Parallel Pattern Matching Algorithm Overcoming Computer Word Size Limitation. Math. Comput. Sci. 2010, 3, 407–420. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Khachumov, V.M. Bit-parallel Representation of Activation Functions for Fast Neural Networks. In Proceedings of the 7-th International Conference on Pattern Recognition and Image Analysis. V. 2 (PRIA-7-2004), St. Petersburg, Russia, 18–23 October 2004; pp. 568–571. [Google Scholar]
- Ghimire, D.; Kil, D.; Kim, S.-H. A Survey on Efficient Convolutional Neural Networks and Hardware Acceleration. Electronics 2022, 11, 945. [Google Scholar] [CrossRef]
- Neelam, S.; Amalin Prince, A. VCONV: A Convolutional Neural Network Accelerator for FPGAs. Electronics 2025, 14, 657. [Google Scholar] [CrossRef]
- Khalil, K.; Kumar, A.; Bayoumi, M. Low-Power Convolutional Neural Network Accelerator on FPGA. In Proceedings of the 2023 IEEE 5th International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hangzhou, China, 11–13 June 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Amid, A.; Kwon, K.; Gholami, A.; Wu, B.; Asanović, K.; Keutzer, K. Co-design of deep neural nets and neural net accelerators for embedded vision applications. IBM J. Res. Dev. 2019, 63, 1–14. [Google Scholar] [CrossRef]
- Cratere, A.; Gagliardi, L.; Sanca, G.; Golmar, F. On-Board Computer for CubeSats: State-of-the-Art and Future Trends. IEEE Access 2024, 12, 99537–99569. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, M.; Shi, J.Q. A Survey on Deep Neural Network Pruning: Taxonomy, Comparison, Analysis, and Recommendations. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10558–10578. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Xue, B.; Ma, L.; Zhang, M. Automatic Fuzzy Architecture Design for Defect Detection via Classifier-Assisted Multiobjective Optimization Approach. IEEE Trans. Evol. Comput. 2025. [Google Scholar] [CrossRef]
- Khachumov, M.V.; Emelyanova, Y.G. Parabola as an Activation Function of Artificial Neural Networks. Sci. Technol. Inf. Proc. 2024, 51, 471–477. [Google Scholar] [CrossRef]
- Kumar, P.A. FPGA Implementation of the Trigonometric Functions Using the CORDIC Algorithm. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; pp. 894–900. [Google Scholar] [CrossRef]
- Tyanev, D.S.; Popova, S.I.; Ivanov, A.I.; Yanev, D.V. Synthesis and Competitive Analysis of Multiple Inputs Parallel Adders. Available online: http://tyanev.com/resources/docs/Document_V_37_ENG.pdf (accessed on 13 April 2025).
- Ramírez, J.P. Simple and Linear Fast Adder of Multiple Inputs and Its Implementation in a Compute-In-Memory Architecture. In Proceedings of the 2024 International Conference on Artificial Intelligence, Computer, Data Sciences and Applications (ACDSA), Victoria, Seychelles, 1–2 February 2024; pp. 1–11. [Google Scholar] [CrossRef]
- Ramirez, J.P. Fast Addition for Multiple Inputs with Applications for a Simple and Linear Fast Adder/Multiplier And Data Structures. Preprint V1 2023, 1–23. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).