Modeling Pulsed Magnetic Core Behavior in LTspice
Abstract
1. Introduction
2. Materials and Methods
2.1. Background
2.1.1. Magnetic Hysteresis
2.1.2. Experimental Setup
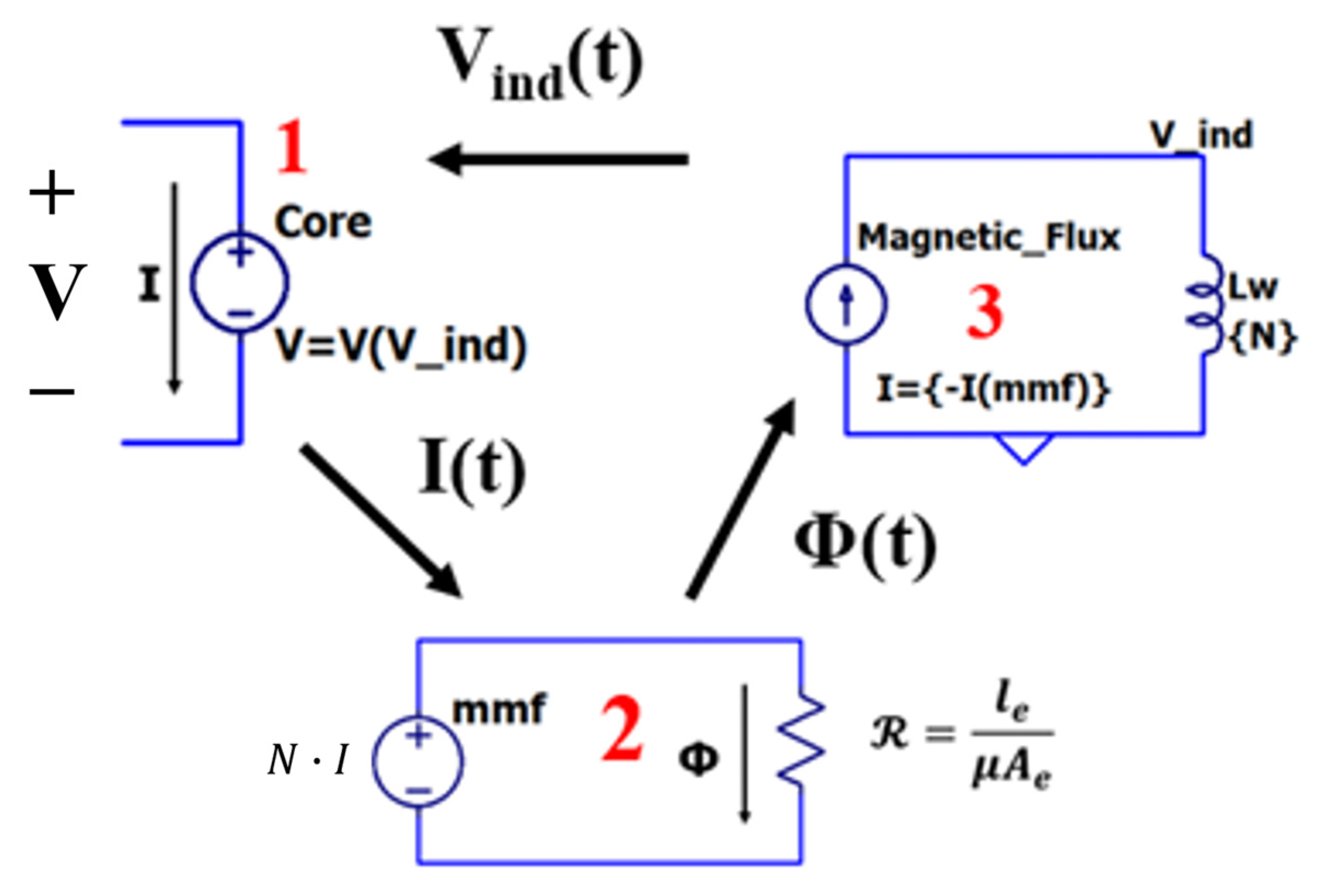
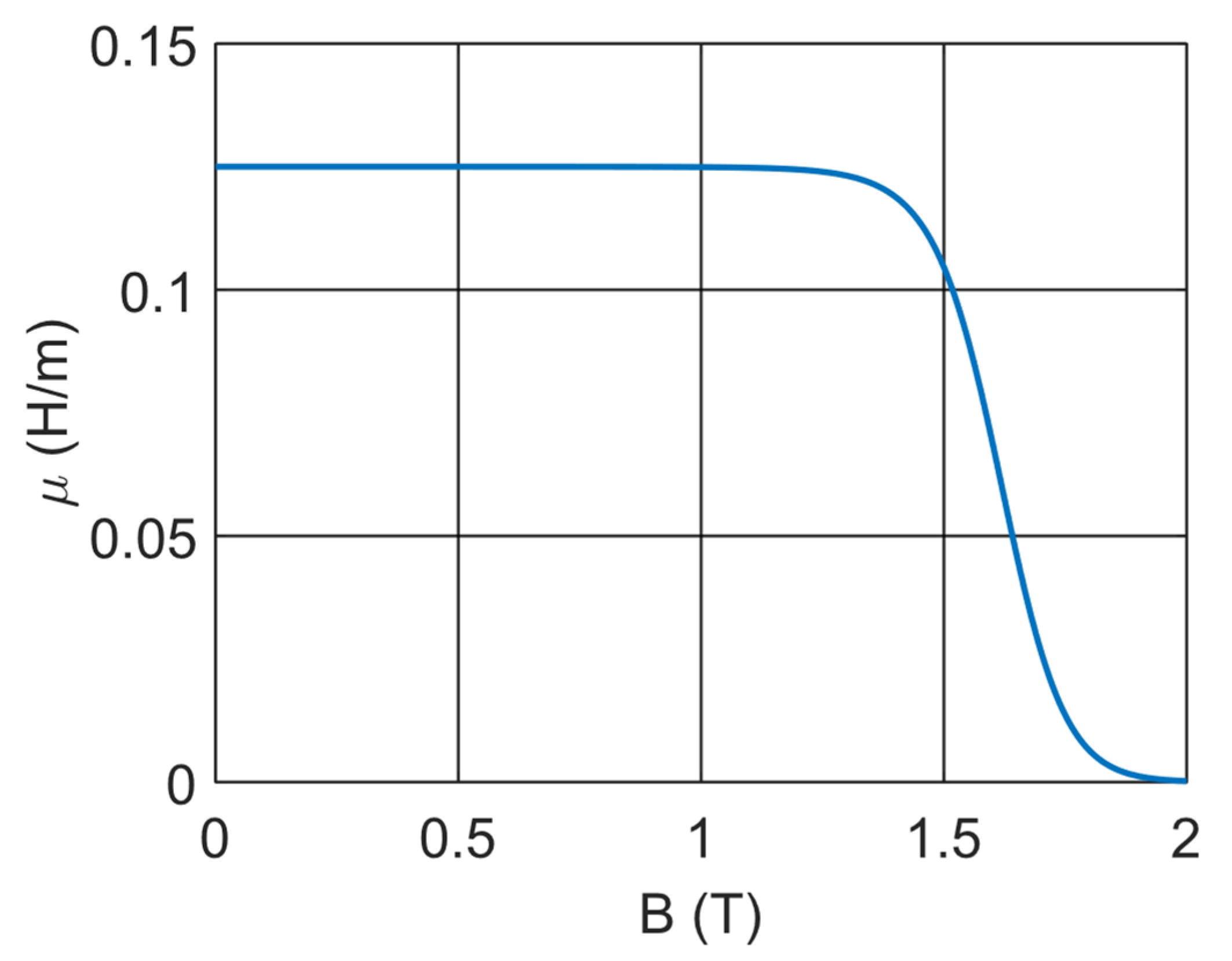
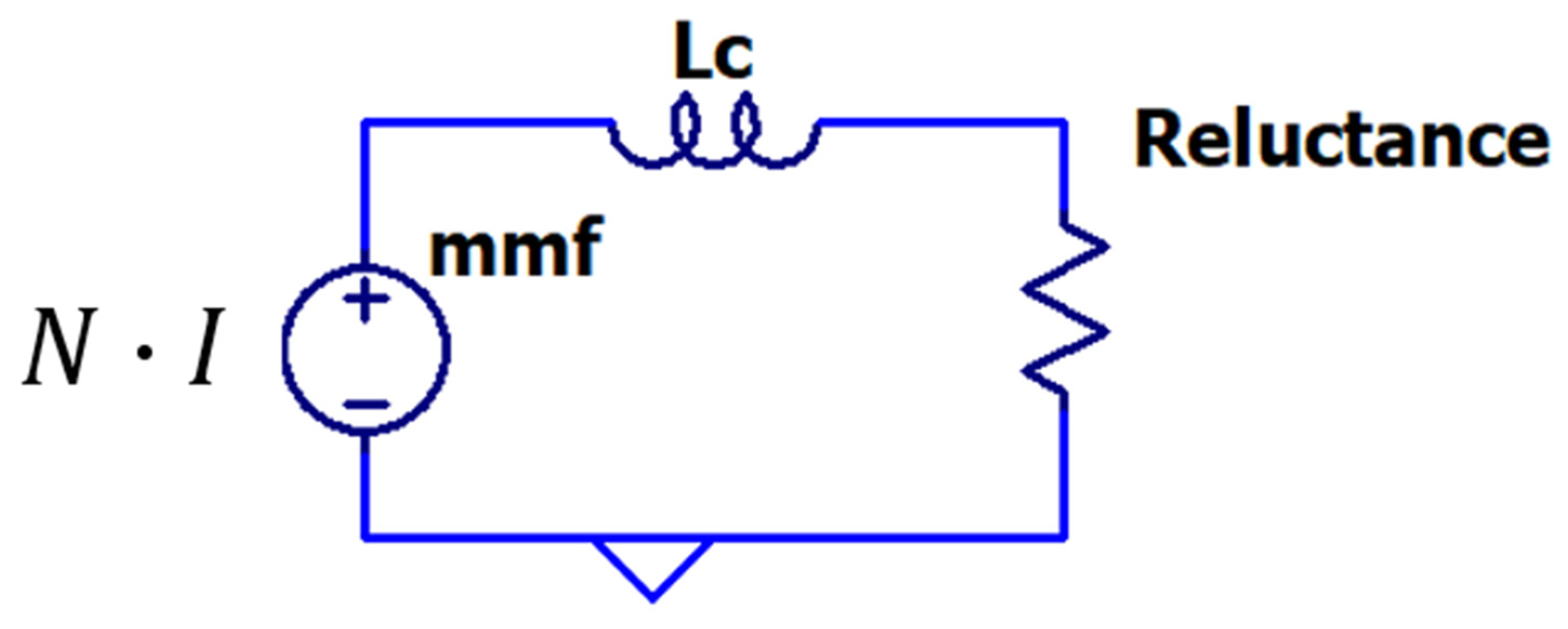
2.2. Magnetic Core Model Fundamentals
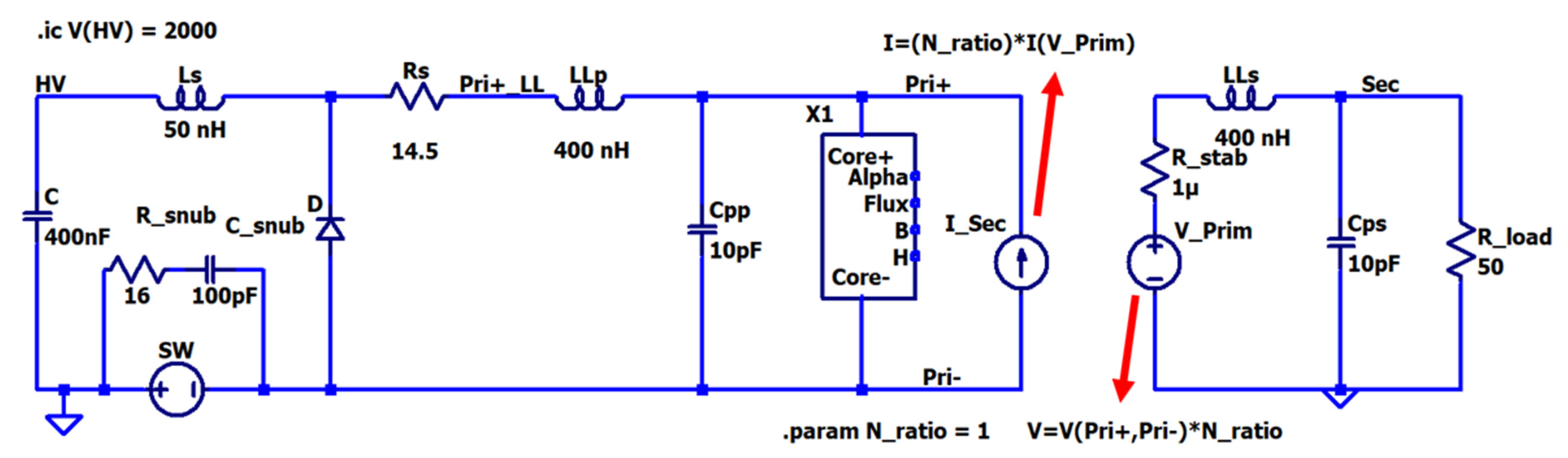
2.3. Core Model Implementation in LTspice
2.3.1. Basics
2.3.2. Core Behavior Modulation
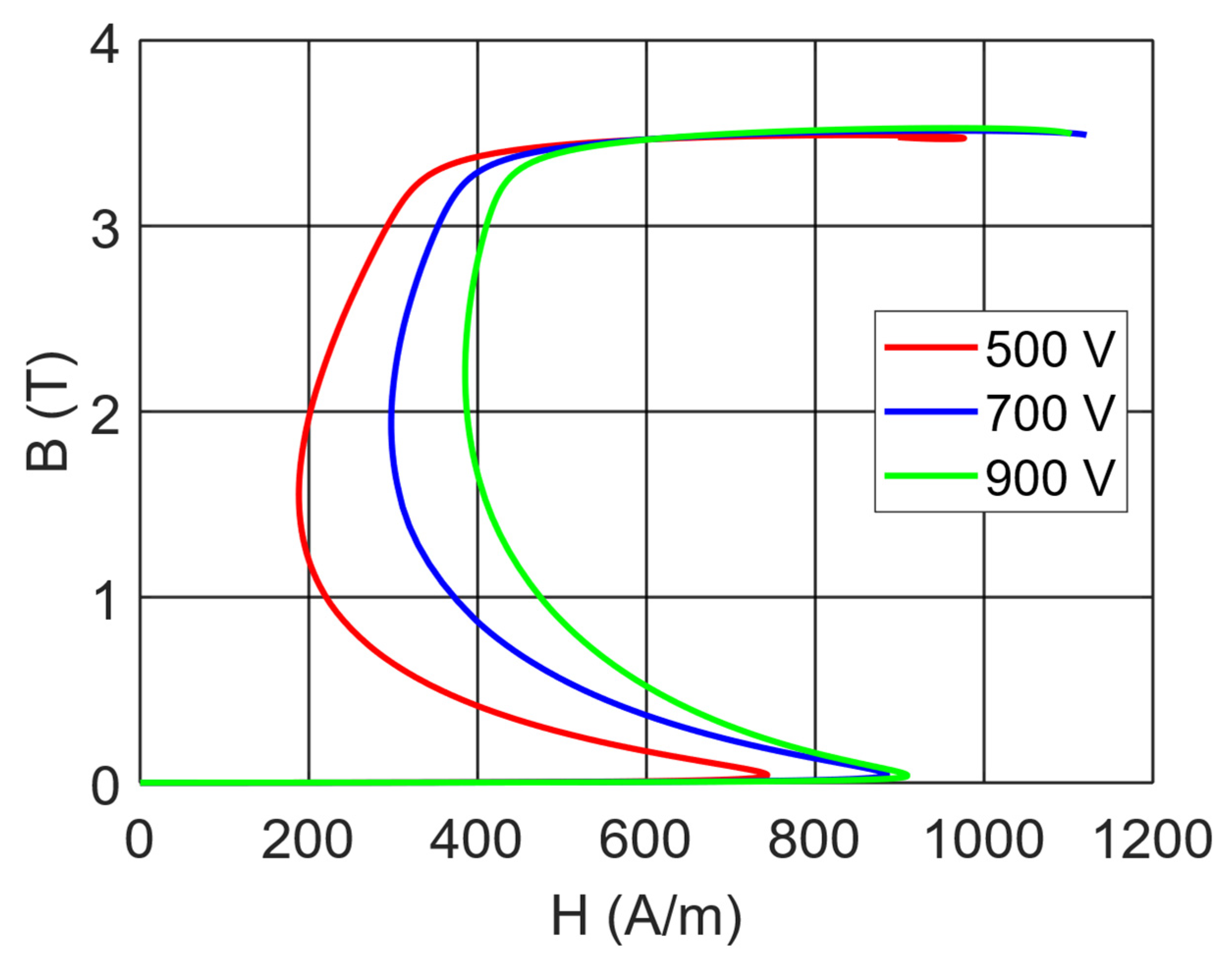
3. Results
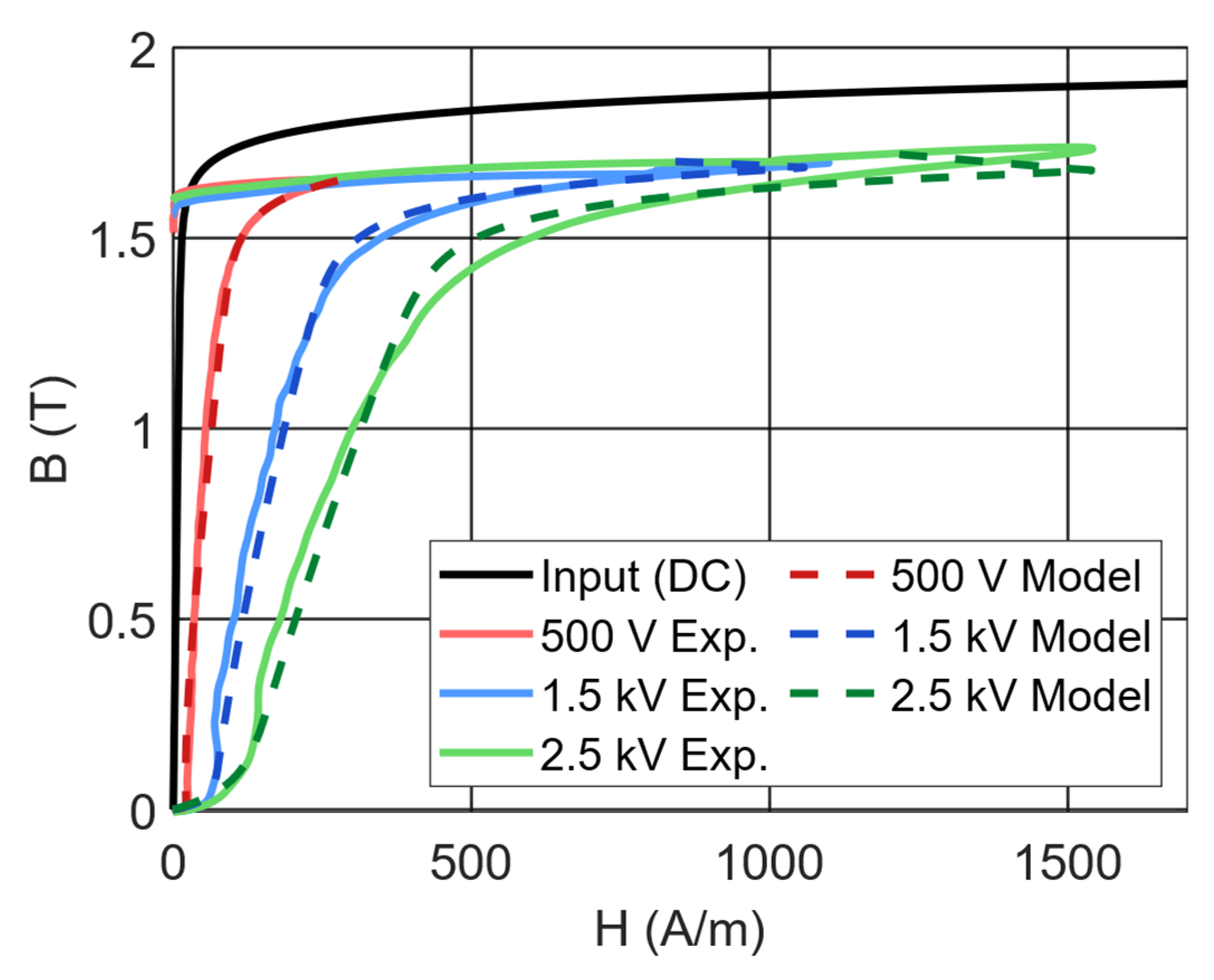
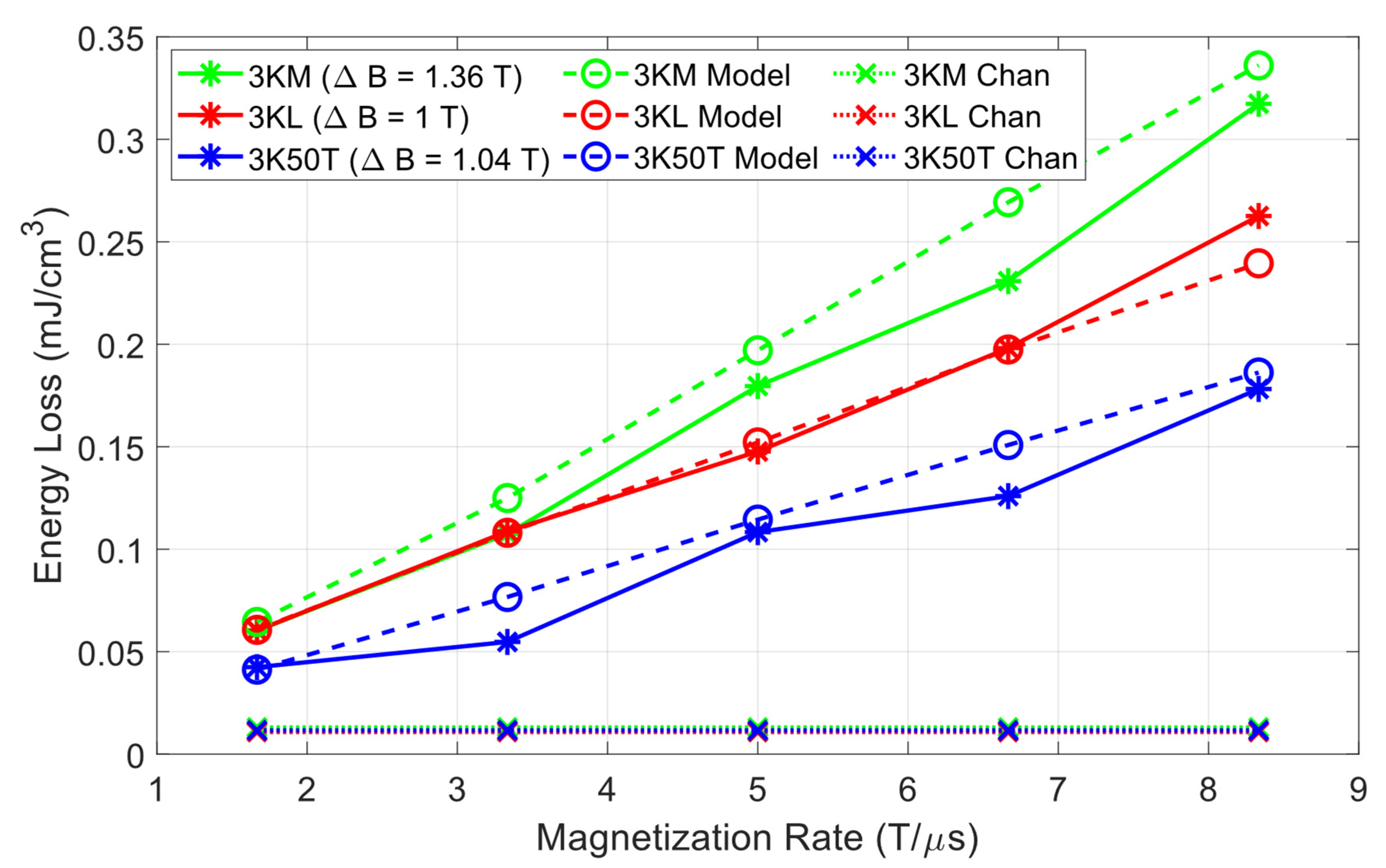
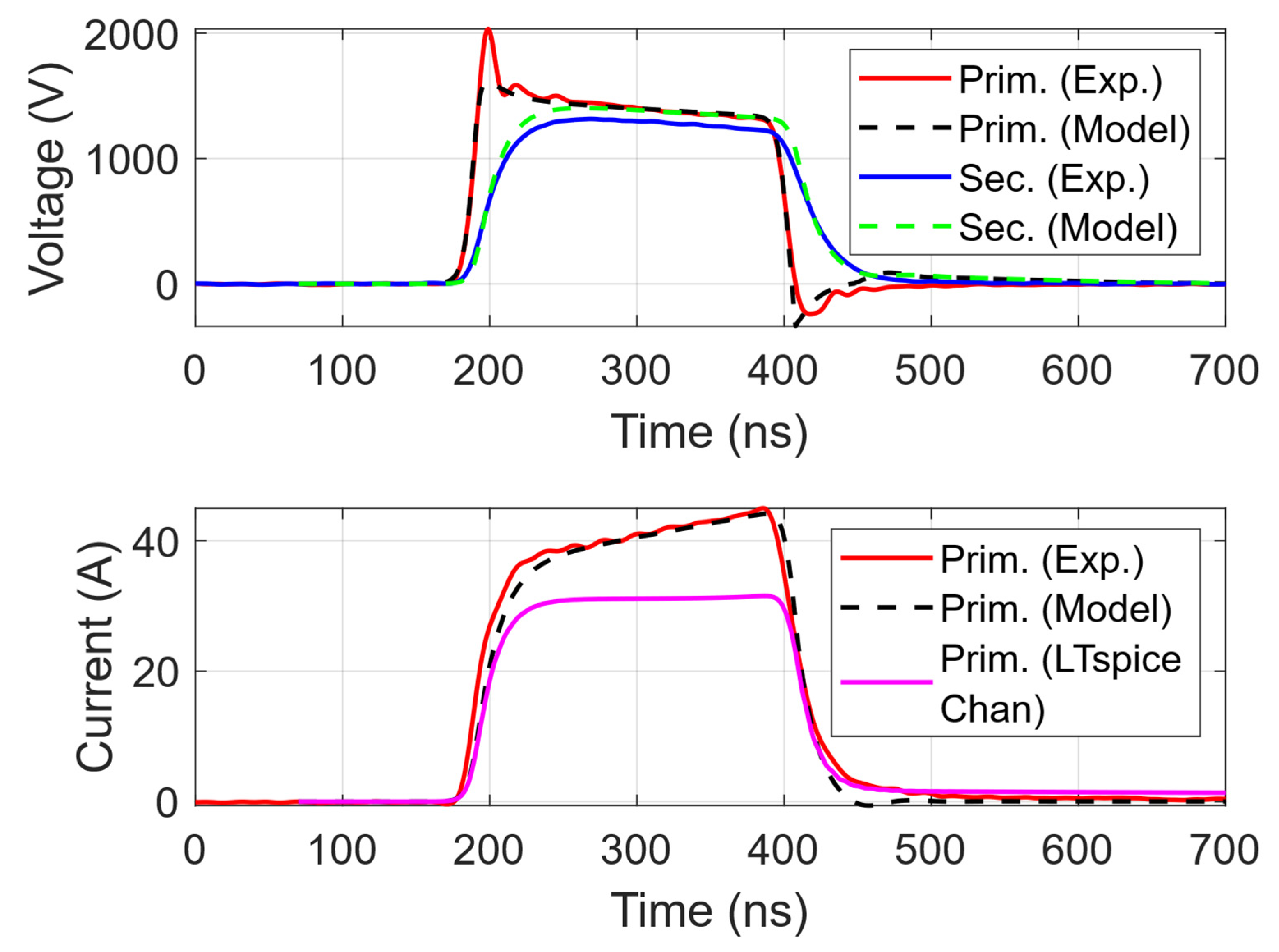
3.1. Model Evaluation
Model Application
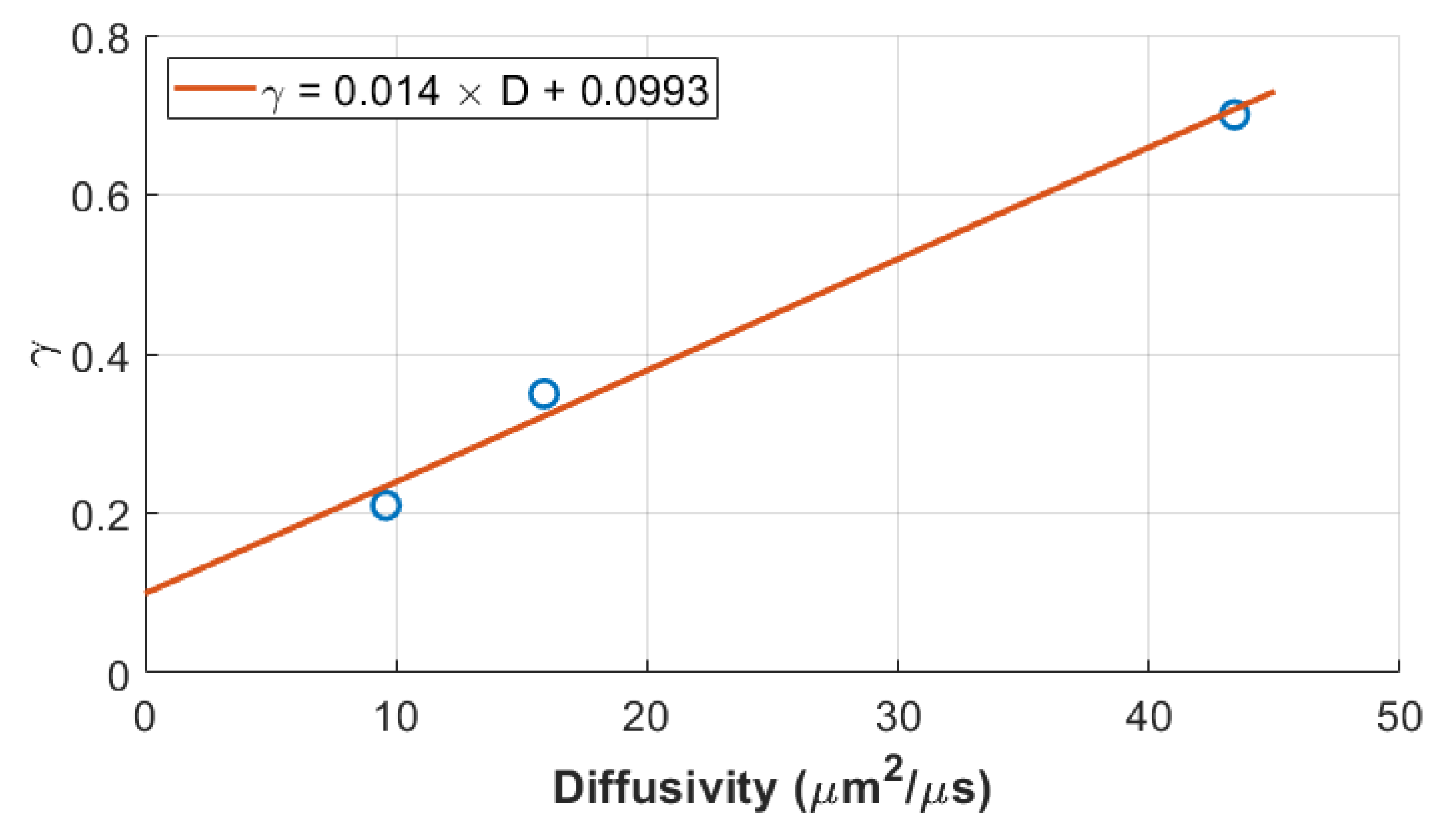
4. Discussion
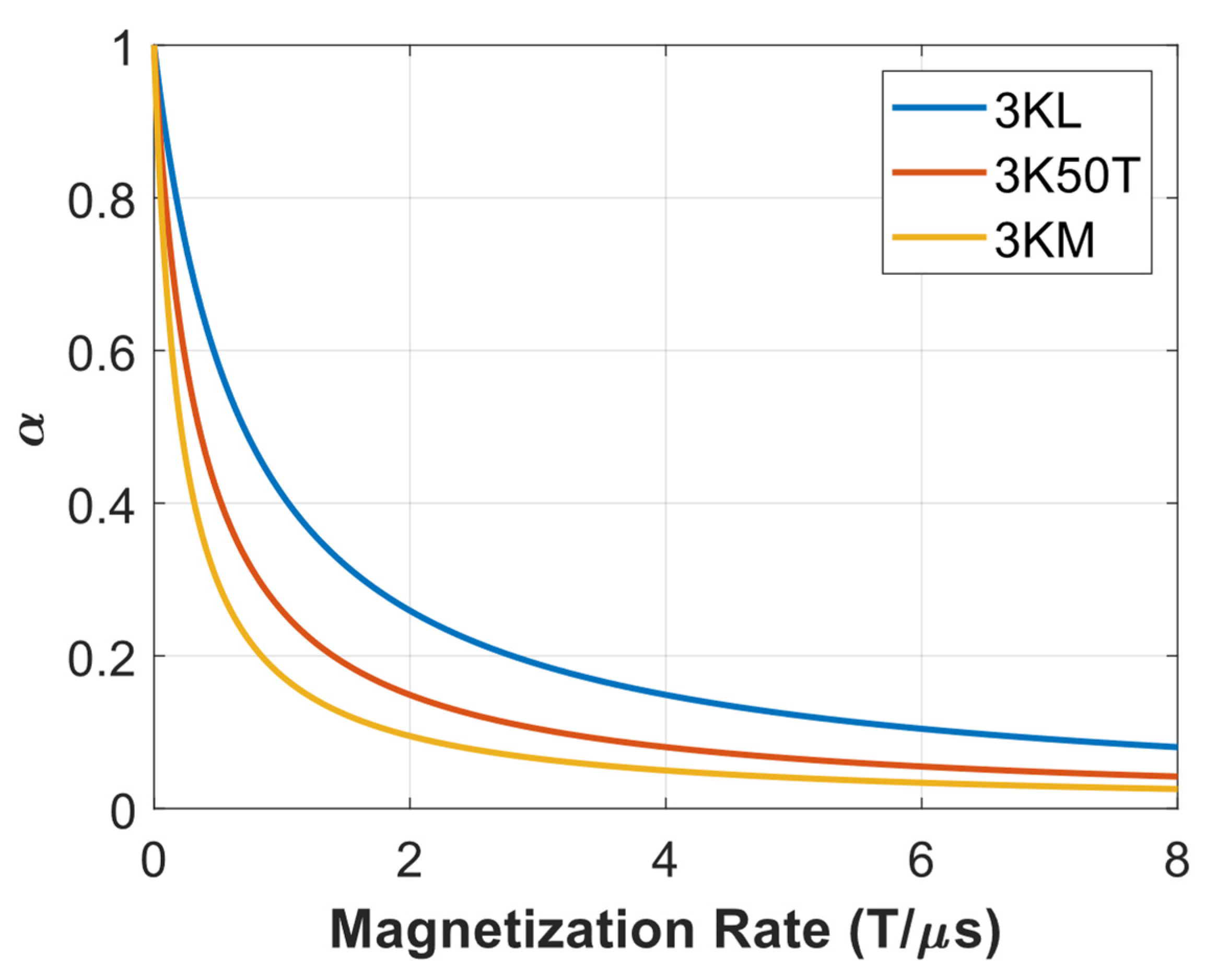
Model Parameter Trends
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SiC | Silicon Carbide |
| MOSFET | Metal Oxide Field Effect Transistor |
References
- Herzer, G. Modern Soft Magnets: Amorphous and Nanocrystalline Materials. Acta Mater. 2013, 61, 718–734. [Google Scholar] [CrossRef]
- Jiles, D.C.; Atherton, D.L. Theory of Ferromagnetic Hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Kanakgiri, K.; Ishan Bhardwaj, D.; Sai Ram, B.; Kulkarni, S.V. A Circuit-Based Formulation for Soft Magnetic Materials Using the Jiles–Atherton Model. IEEE Trans. Magn. 2024, 60, 7301107. [Google Scholar] [CrossRef]
- Chan, J.H.; Vladimirescu, A.; Gao, X.-C.; Liebmann, P.; Valainis, J. Nonlinear Transformer Model for Circuit Simulation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1991, 10, 476–482. [Google Scholar] [CrossRef]
- Engelhardt, M.T. Asymmetric Minor Hysteresis Loop Model and Circuit Simulator Including the Same. U.S. Patent 7,502,723, 10 March 2009. [Google Scholar]
- LTwiki. The Chan Model. Available online: https://ltwiki.org/index.php?title=The_Chan_model (accessed on 15 November 2024).
- Ghosh, M.K.; Gao, Y.; Dozono, H.; Muramatsu, K.; Guan, W.; Yuan, J.; Tian, C.; Chen, B. Numerical Modelling of Magnetic Characteristics of Ferrite Core Taking Account of Both Eddy Current and Displacement Current. Heliyon 2019, 5, e02229. [Google Scholar] [CrossRef] [PubMed]
- Hane, Y.; Nakamura, K. Dynamic Hysteresis Modeling for Magnetic Circuit Analysis by Incorporating Play Model and Cauer’s Equivalent Circuit Theory. IEEE Trans. Magn. 2020, 56, 6703306. [Google Scholar] [CrossRef]
- Petrescu, L.-G.; Petrescu, M.-C.; Cazacu, E.; Constantinescu, C.-D. Estimation of Energy Losses in Nanocrystalline FINEMET Alloys Working at High Frequency. Materials 2021, 14, 7745. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, M.; Li, Y. Measurement and Simulation of Magnetic Properties of Nanocrystalline Alloys under High-Frequency Pulse Excitation. Materials 2023, 16, 2850. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.; Clancy, T.; Houck, T.L.; Pogue, N. Pulsed Transformer Magnetic Core Comparison of Different Materials for Pulsed Power Applications. In Proceedings of the 2023 IEEE Pulsed Power Conference (PPC), San Antonio, TX, USA, 25–29 June 2023; pp. 1–4. [Google Scholar]
- Howard, A.B.; Curry, R.D.; Burdt, R.A. High- dB / Dt Square-Pulse Excitation of Finemet Magnetic Material. IEEE Trans. Plasma Sci. 2016, 44, 1914–1918. [Google Scholar] [CrossRef]
- Acosta-Lech, D.; Houck, T.L.; McHale, B.; Misch, M.K.; Sugihara, K. Multi-Pulse Performace of Amorphous Metal Magnetic Cores at High Magnetization Rates. In Proceedings of the 2019 IEEE Pulsed Power & Plasma Science (PPPS), Orlando, FL, USA, 23–28 June 2019; pp. 1–4. [Google Scholar]
- Goodenough, J.B. Summary of Losses in Magnetic Materials. IEEE Trans. Magn. 2002, 38, 3398–3408. [Google Scholar] [CrossRef]
- Alonso, J.M. Inductors: Variable and Controllable; Independently Published, 2021; ISBN 979-8-5002-4816-9. [Google Scholar]
- Brauer, J. Simple Equations for the Magnetization and Reluctivity Curves of Steel. IEEE Trans. Magn. 1975, 11, 81. [Google Scholar] [CrossRef]
- Zhang, D.M.; Li, E.P. Influence of Displacement Current on Magnetic Field Distribution in Ferrite Core within kHz–MHz Frequency Range. J. Magn. Magn. Mater. 2003, 256, 183–188. [Google Scholar] [CrossRef]
- Behavioral_Magnetic_Core_LTspice.exe. Available online: https://www.p3e.ttu.edu/BehavioralMagneticCoreLTspice (accessed on 1 May 2025).
- Ayachit, A.; Kazimierczuk, M.K. Transfer Functions of a Transformer at Different Values of Coupling Coefficient. IET Circuits Devices Syst. 2016, 10, 337–348. [Google Scholar] [CrossRef]
- Chemerys, V.; Borodiy, I. Influence of the Finite Speed of the Field Penetration into the Core on the Linearity of Transmission Function for the Pulsed Transformers (Numerical Investigation). 2021, 93–100. Available online: https://quickfield.com/publications/chemerys1.pdf (accessed on 4 June 2025).
- Chemerys, V.; Borodiy, I. Diffusion of the Pulsed Electromagnetic Field into the Multi-Layer Core of Inductor at Pulsed Devices. Proc. Natl. Aviat. Univ. 2008, 35, 44–51. [Google Scholar] [CrossRef]




| Parameter | FT-3KM | FT-3K50T | FT-3KL |
|---|---|---|---|
| Bs (T) | 1.23 | 1.23 | 1.23 |
| Br/Bs (%) | 50 | 10 | 5 |
| Hc (A/m) | 2.5 | 1.2 | 0.6 |
| ℓe (mm) | 204.2 | 205 | 205 |
| Ae (mm2) | 150 | 150 | 150 |
| T (μm) | 18 | 18 | 18 |
| DC–μr | 100,000 | 60,000 | 22,000 |
| σ (S/m) | 833,000 | 833,000 | 833,000 |
| Diffusivity (μm2/μs) | 9.6 | 15.9 | 43.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kelp, K.; Wright, D.; Stephens, J.; Dickens, J.; Mankowski, J.; Shaw, Z.; Neuber, A. Modeling Pulsed Magnetic Core Behavior in LTspice. Electronics 2025, 14, 2335. https://doi.org/10.3390/electronics14122335
Kelp K, Wright D, Stephens J, Dickens J, Mankowski J, Shaw Z, Neuber A. Modeling Pulsed Magnetic Core Behavior in LTspice. Electronics. 2025; 14(12):2335. https://doi.org/10.3390/electronics14122335
Chicago/Turabian StyleKelp, Keegan, Dawson Wright, Jacob Stephens, James Dickens, John Mankowski, Zach Shaw, and Andreas Neuber. 2025. "Modeling Pulsed Magnetic Core Behavior in LTspice" Electronics 14, no. 12: 2335. https://doi.org/10.3390/electronics14122335
APA StyleKelp, K., Wright, D., Stephens, J., Dickens, J., Mankowski, J., Shaw, Z., & Neuber, A. (2025). Modeling Pulsed Magnetic Core Behavior in LTspice. Electronics, 14(12), 2335. https://doi.org/10.3390/electronics14122335







