Based on the theoretical foundations of TabNet and Differential Privacy outlined previously, we designed and conducted experiments to evaluate the effectiveness of our privacy-preserving student behavior analysis model. This section outlines our experimental methodology, including dataset preparation, model implementation, and the training process.
3.1. Dataset Description and Processing
3.1.1. Dataset Overview
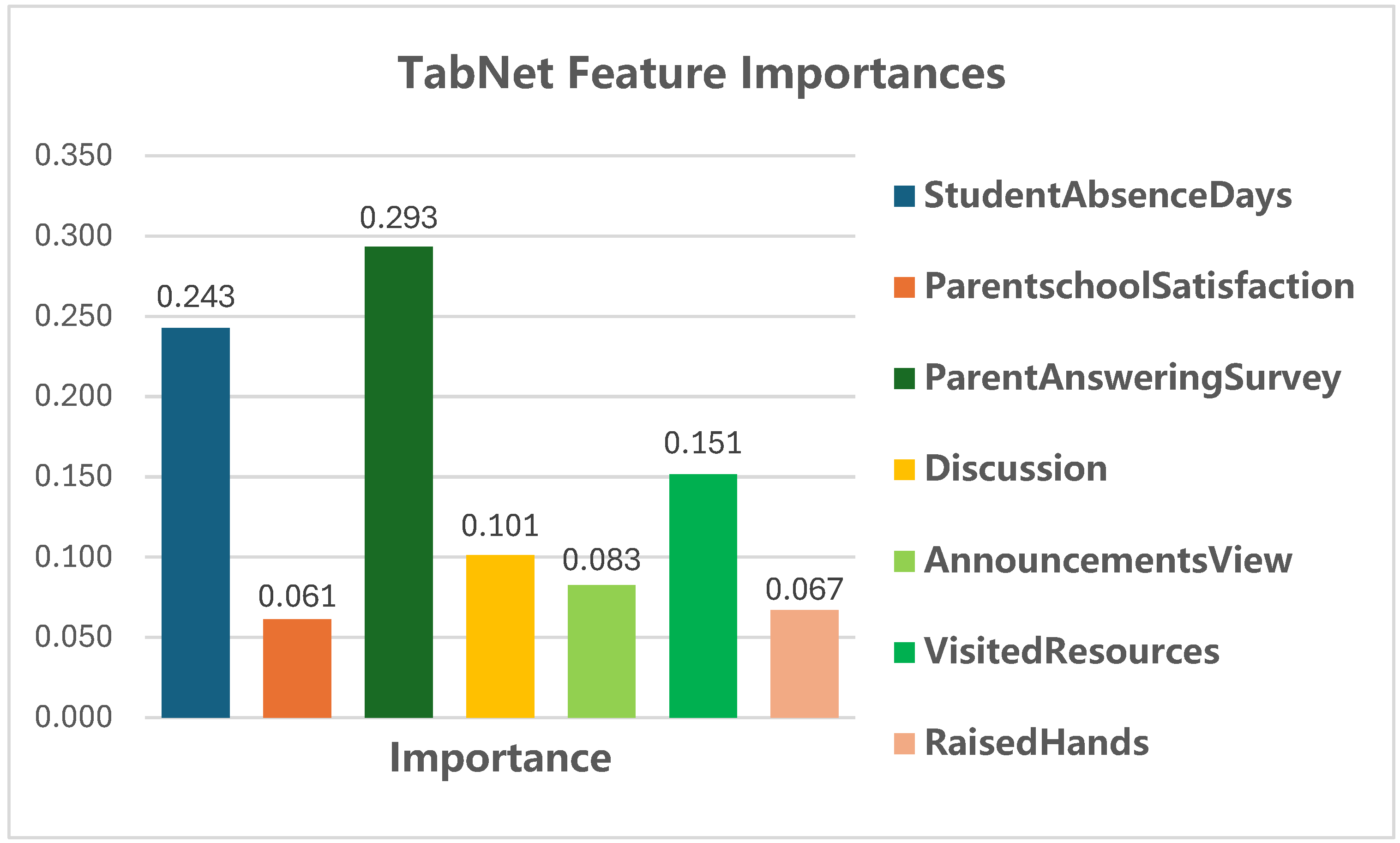
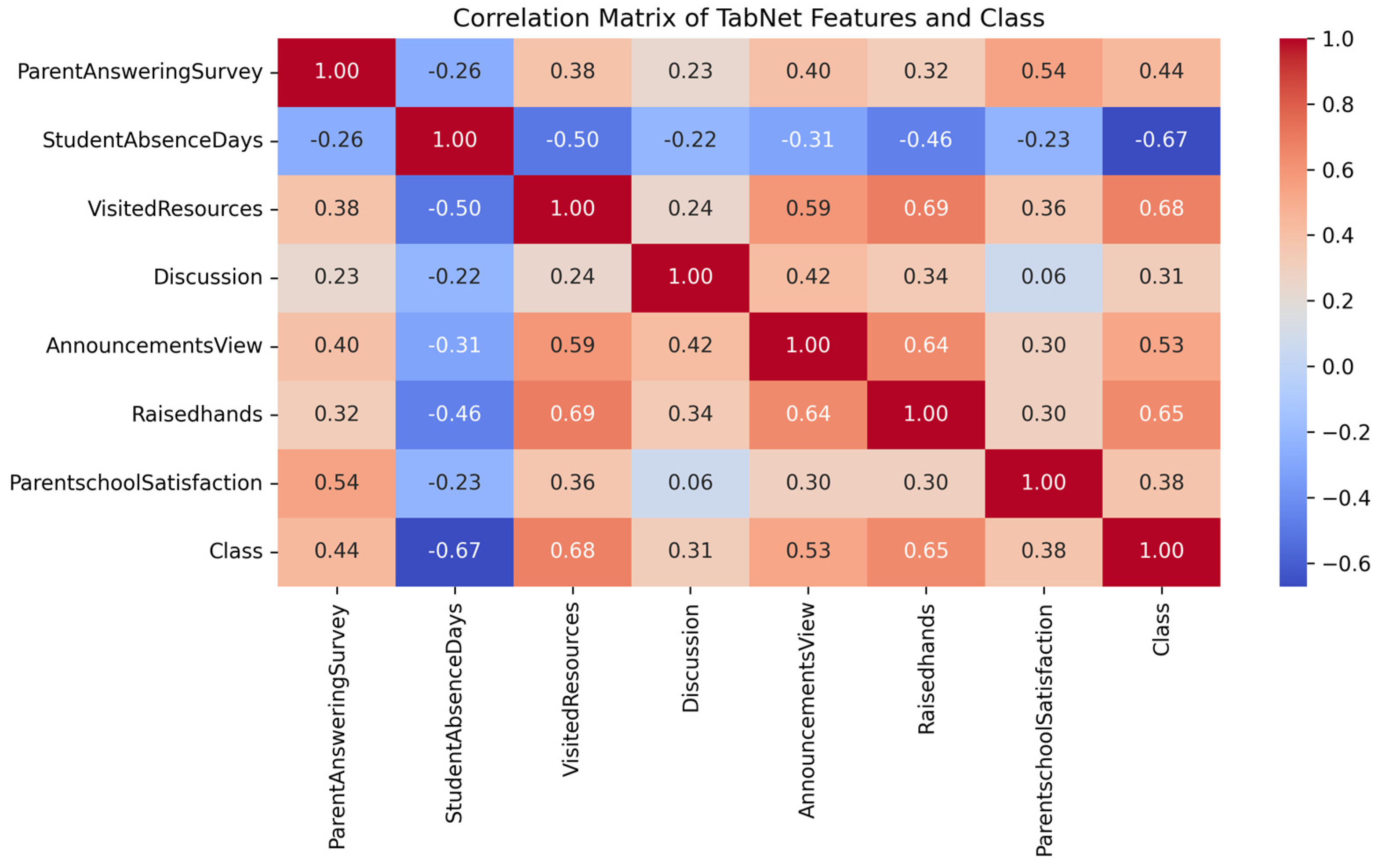
Our study uses a publicly accessible dataset from the Alibaba Cloud Tianchi platform, which contains multi-dimensional data on students’ online learning behaviors and performance records. After carefully selecting features based on their relevance to academic performance, we retained seven key features listed in
Table 1:
These features were selected from an initial set of 17 variables, excluding demo-graphic and administrative data such as gender, nationality, place of birth, and section identifiers, to focus on behavioral indicators directly related to academic performance.
3.1.2. Data Preprocessing
The data preprocessing phase involved three main stages:
First, we performed feature selection by removing non-behavioral attributes (such as gender, nationality, place of birth, state ID, grade ID, topic, semester, relation, and section ID) to focus on learning behavior indicators that directly influence academic performance.
Second, we conducted categorical variable encoding:
ParentAnsweringSurvey: “Yes” was converted to 1, and “No” was converted to 0;
ParentschoolSatisfaction: “Good” was converted to 1, and “Bad” was converted to 0;
StudentAbsenceDays: “Above-7” was converted to 1, and “Under-7” was converted to 0;
Class: “L” was converted to 0, “M” was converted to 1, and “H” was converted to 2.
Finally, we implemented data standardization and splitting:
The dataset was divided into training (80%) and testing (20%) sets;
Feature standardization was applied using StandardScaler to normalize the numerical features;
Data quality checks were performed to ensure consistency and integrity.
This preprocessing approach ensures that the data is adequately prepared for model training while preserving the essential characteristics of student learning behaviors. Standardization helps optimize the model’s performance by ensuring that all features contribute proportionally to the prediction task.
3.1.3. Ethical Considerations in Data Selection
While the preprocessing steps outlined above ensure data consistency and relevance for predictive modeling, the selection and exclusion of certain features raise important ethical considerations, particularly regarding fairness. In this study, demographic attributes such as gender, nationality, and place of birth were deliberately excluded from the dataset to focus on behavioral indicators of academic performance (e.g., Raisedhands, VisitedResources). However, this exclusion may inadvertently introduce fairness risks by overlooking systemic biases associated with underrepresented groups. For instance, if the data predominantly represent students from specific socioeconomic or cultural backgrounds, the model’s predictions might not generalize equitably across diverse populations, potentially leading to biased outcomes for certain demographics. Such risks could impact the responsible use of predictive models in educational settings, where equitable treatment is paramount. To mitigate these concerns, future iterations of this research will explore the inclusion of fairness-aware techniques, such as reweighting under-represented data or applying fairness constraints during model training, to ensure that the predictive outcomes do not perpetuate existing disparities.
3.2. Implementation of Differential Privacy Preserving Datasets
To protect student privacy, we integrate Differential Privacy (DP) into our data-processing pipeline before model training. We apply the Laplace Mechanism defined in
Section 2.2 (Equations (6) and (7)) to perturb the input data. This approach provides (
, 0)-DP guarantees. Choosing the privacy budget (
) and sensitivity (
) is critical for balancing privacy and data utility. We derive these parameters from rigorous theoretical foundations tailored to sensitive educational data.
We set the privacy budget
to 0.7. According to Equation (5) in
Section 2.2, this limits an adversary’s ability to distinguish two datasets differing by one record to a factor of
. This choice balances strong privacy guarantees with sufficient utility for predictive tasks, safeguarding sensitive educational data.
We analytically determine
as the maximum change in the input feature vector caused by altering a single record. This definition is formalized in Equation (7). We standardize features with StandardScaler to achieve zero mean and unit variance. Then, we compute
by evaluating the maximum impact of a single data point on the feature distribution. Under a normal distribution, standardized feature values lie within [−3, 3], covering about 99.7% of the data. For the
norm, the sensitivity of a single feature equals the maximum change from one record divided by the dataset size. Aggregating across all features, we conservatively set
= 0.1 as an upper bound to capture cumulative effects. This choice satisfies DP’s foundational requirement for a theoretically grounded sensitivity measure. We then compute the noise scale for the Laplace mechanism according to Equation (6):
This scale sets the noise magnitude for each feature. Noise is drawn from the Laplace distribution Lap(0, 0.1429) to meet the privacy budget.
We apply the Laplace mechanism to input data before model training. Noise is added independently to each standardized feature in both training and test sets. Noise generation follows the derived scale, strictly enforcing the privacy budget = 0.7 across the entire dataset perturbation. After input perturbation, TabNet’s sequential decision steps incur no additional privacy cost. Applying the privacy budget only at the input level removes the need for composition analysis. This approach ensures a clear, bounded privacy guarantee during data preprocessing. It effectively protects raw data before any model interaction.
Our implementation ensures DP-TabNet adheres to rigorous privacy principles. It also preserves practical utility for educational data analysis. We derive and using formal expressions and precise noise calibration. This process yields a robust privacy-preserving mechanism tailored to sensitive student data. It balances data protection with actionable insights for predictive modeling.
A key design consideration for DP-TabNet is whether TabNet’s sequential decision steps could accumulate privacy budget through iterative processing. In multi-stage architectures, each processing step can be treated as an additional data query. This may require composing privacy budgets under the DP framework. However, DP-TabNet achieves differential privacy by applying the Laplace Mechanism to input data before any model processing. As described earlier, we add noise to standardized features using = 0.7 and = 0.1. This enforces the privacy guarantee at the data level.Subsequent TabNet operations, such as feature selection and transformation, run on perturbed data without accessing the original dataset. As a result, no additional privacy cost occurs during internal processing, and the total budget is bounded by the initial perturbation. This approach ensures TabNet’s multi-step architecture stays within the predefined . It maintains a robust privacy guarantee for the entire framework.
Differential privacy applied via input perturbation with the Laplace Mechanism ( = 0.7, = 0.1) offers strong guarantees against direct exposure of individual data. However, its effectiveness against inference attacks, such as membership inference, where an adversary infers whether a specific record was in the training set, may be a concern during training or deployment. In DP-TabNet, such risks are significantly reduced by input perturbation. We add noise to raw data before any model interaction. This ensures that both the training process and the model parameters derive from perturbed data, inherently obscuring individual contributions. With = 0.7, the privacy guarantee is expressed by the bound . This bound limits an adversary’s ability to distinguish adjacent datasets by about 2.01, providing strong protection against direct re-identification. At this noise level (Lap(0, 0.1429)), inference attacks become less effective. The noise masks identifiable patterns, often reducing adversary confidence to near-random guessing (e.g., 50% for binary membership classification). TabNet’s sequential attention mechanism further mitigates inference risks. By dynamically selecting and processing features, it reduces overfitting to specific data points—a common vulnerability in inference attacks. Although no DP mechanism can eliminate all theoretical risks, DP-TabNet with = 0.7 maintains robust protection during training and deployment. The total privacy budget remains bounded by the initial perturbation, safeguarding sensitive educational data effectively.
3.3. Implementation of TabNet Model
Following the implementation of the differential privacy mechanism, we implemented the TabNet model for both the privacy-preserved and original datasets. The implementation follows the architectural design outlined in
Section 2.1, incorporating feature selection and processing mechanisms through sequential attention.
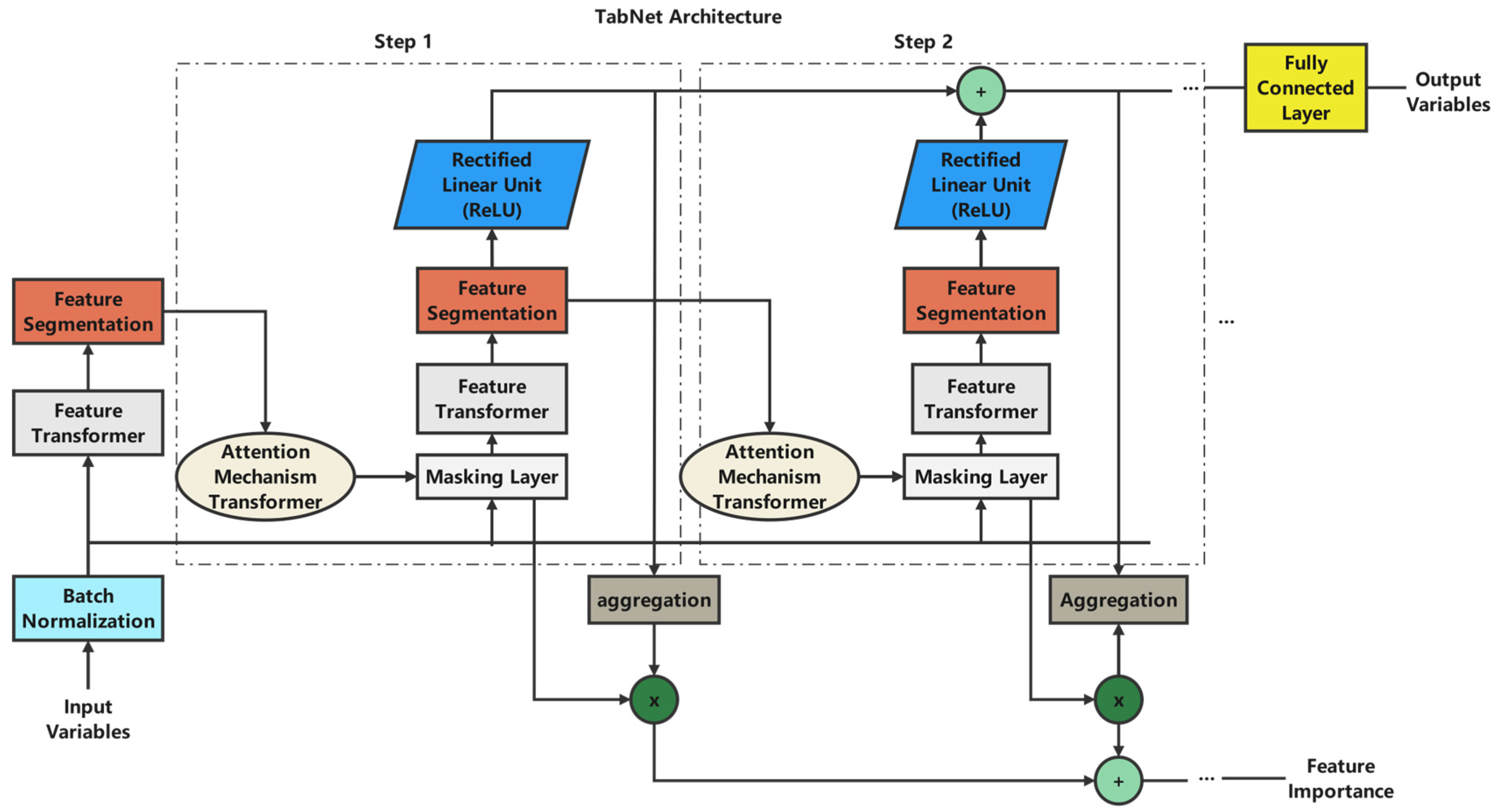
As shown in
Figure 3, the TabNet architecture processes student performance features through several sequential steps. The model groups input features into two main categories: Student Classroom Performance (including Raisedhands, VisitedResources, AnnouncementsView, and Discussion) and Student Extracurricular Activities (including ParentAnsweringSurvey, ParentschoolSatisfaction, and StudentAbsenceDays).
The feature processing flow in
Figure 3 illustrates how each feature group undergoes sequential transformations through:
Feature Selection: using the sparsemax attention mechanism from Equation (2). This selects the most relevant features at each decision step;
Input Processing: transforming selected features through the Feature Transformer layer as defined in Equation (1);
Attention Mechanism: the model employs transformers that process features while considering their relationships and importance. The aggregate feature importance is computed using Equation (4);
Information Aggregation: the processed features from both Student Classroom Performance and Student Extracurricular Activities are aggregated to form comprehensive representations for final prediction.
The feedback loops shown in the diagram implement the feature reuse mechanism controlled by the prior scale as defined in Equation (3).
This implementation allows the model to dynamically select and process features while preserving interpretability through explicit feature importance scores. The architecture’s parameters are carefully tuned, as shown in
Table 2, to optimize the model’s performance while preserving computational efficiency.
The TabNet model architecture is configured with carefully tuned hyperparameters to optimize performance while preserving model efficiency. The key architectural parameters are listed in
Table 2:
The key architectural parameters listed in
Table 2 are carefully calibrated to optimize the model’s performance:
Learning Rate (lr = 0.001): This value was determined through iterative experimentation within the range [0.0001, 0.01]. The selected learning rate represents an optimal balance between convergence stability and training efficiency. Lower values (≤0.0005) resulted in excessively slow convergence, while higher values (≥0.005) led to oscillation around local minima.
Decision Prediction Layer Width (n_d = 8): This parameter determines the dimensionality of feature transformers in each decision step. We conducted ablation studies with n_d values ranging from 4 to 16 and found that n_d = 8 provides sufficient representational capacity for the educational feature set while preventing overfitting on our dataset size. As formalized in Equation (1), this parameter directly influences the transformation matrix Wi dimensions and consequently affects the model’s capacity to capture complex feature interactions.
Attention Embedding Dimension (n_a = 8): We set n_a equal to n_d to ensure dimensional consistency throughout the network’s attention mechanism. This parameter governs the network’s capacity to focus on relevant features, directly impacting the sparsemax calculations in Equation (2). Our empirical testing showed minimal performance gain with larger values while incurring significant computational overhead.
Number of Decision Steps (n_steps = 3): This value was determined through cross-validation experiments comparing performance with n_steps {2, 3, 4, 5}. With n_steps = 3, the model achieves optimal performance by balancing depth (for capturing complex feature interactions) with parsimony (to prevent overfitting). Adding more steps (n_steps > 3) produced negligible accuracy improvements (<0.7%) while substantially increasing computational complexity. This parameter directly influences the sequential feature selection process described in Equations (2) and (3).
Feature Reuse Coefficient (gamma = 1.2): The γ parameter in Equation (3) governs feature sharing across decision steps. We evaluated performance across the range [1.0, 1.5] at 0.1 increments. The value = 1.2 was selected based on validation performance, as it allows moderate feature reuse while preventing excessive redundancy in feature selection, which is particularly important given the limited dimensionality of our educational dataset.
Number of Independent GLU Layers (n_independent = 2): Three independent Gated Linear Unit layers per step provide sufficient non-linear transformation capacity while preserving model efficiency. This affects the feature transformation process described in Equation (1).
Sparsity Regularization (lambda_sparse = 0.1): This parameter controls the strength of the sparsity constraint on feature selection. The value of 0.1 encourages the model to select relevant features while preventing over-reliance on individual features.
To mitigate overfitting risks from TabNet’s complexity and the small dataset size, we applied 5-fold cross-validation on the training set (80% of the data) prior to final model training. We evaluated using the same hyperparameters as the final model (see
Table 2) and applied early stopping based on validation accuracy with a patience of 30 epochs. Cross-validation assesses model generalization and ensures robustness against overfitting—a critical issue when applying deep learning to small datasets.
Figure 3 illustrates the feature processing flow, where each feature group undergoes sequential transformations:
Feature Selection: Applying the Sparsemax attention mechanism (Equation (2)) to select the most relevant features at each decision step.
Input Processing: transforming selected features via the Feature Transformer layer (Equation (1)).
Attention Mechanism: employing transformers to process features based on their relationships and importance, with aggregate importance computed by Equation (4).
Information Aggregation: aggregating processed features from both student classroom performance and extracurricular activities to form comprehensive representations for final prediction.
Feedback loops in the diagram implement the feature reuse mechanism controlled by the prior scale (Equation (3)).
This implementation enables dynamic feature selection and processing, while preserving interpretability via explicit feature importance scores. As shown in
Table 2, we carefully tuned the architecture parameters to optimize performance while maintaining computational efficiency.
These hyperparameter values work synergistically to enable effective feature selection and transformation while preserving model interpretability and computational efficiency. The systematic optimization process involved grid search and ablation studies to identify the parameter combination that maximizes predictive performance on educational data while maintaining robust generalization capabilities, as validated through cross-validation.
3.4. Baseline Models
To comprehensively evaluate the performance of our proposed TabNet model, we implemented multiple machine learning algorithms as baseline models, including both traditional tree-based methods and deep learning approaches. These models were chosen for their proven effectiveness in educational data mining and distinct approaches to feature processing and prediction tasks.
Random Forest, an ensemble learning method, constructs multiple decision trees and outputs the class that is the mode of the classes of the individual trees. The model can be represented as:
where
is the ensemble predictor,
represents individual decision trees, and
is the number of trees.
We used RandomizedSearchCV with a predefined parameter space to tune hyperparameters for the Random Forest model and ensure optimal performance. The parameter search space comprised six hyperparameters: number of trees (n_estimators) from 50 to 500; tree depth (max_depth) set to None or 10–90 in steps of 10; minimum samples to split (min_samples_split) from 2 to 20; minimum samples per leaf (min_samples_leaf) from 1 to 20; maximum features for splits (max_features) from 0.1 to 1.0; and bootstrap sampling (bootstrap) either True or False. We performed 100 iterations of randomized search with 5-fold cross-validation, optimizing for accuracy. The optimal hyperparameters were: n_estimators = 393; max_depth = 30; min_samples_split = 3; min_samples_leaf = 3; max_features = 0.23; bootstrap = True. This tuning improved model generalization, as evidenced by cross-validation results.
The Random Forest classifier implementation ensures consistency in predictions through fixed random state initialization while leveraging its advantage in handling both numerical and categorical features present in our educational dataset. The model’s inherent feature importance mechanism provides additional insights into the relative significance of different educational parameters.
XGBoost (eXtreme Gradient Boosting) uses a gradient-boosting decision tree algorithm with additional optimization and regularization techniques. The model follows the principle of additive training:
where
is the prediction for the i-th instance,
represents the
-th tree, and
is the space of regression trees.
The objective function being optimized can be expressed as:
where
is the loss function and
represents the regularization term.
Similarly, we tuned XGBoost hyperparameters with RandomizedSearchCV over 100 iterations and five-fold cross-validation, optimizing for accuracy. The parameter search space included key hyperparameters: number of estimators (n_estimators) from 50 to 600; maximum tree depth (max_depth) from 3 to 10; learning rate (learning_rate) from 0.01 to 1.0; subsample ratio (subsample) from 0.6 to 1.0; column sampling ratio (colsample_bytree) from 0.6 to 1.0; regularization terms (reg_alpha, reg_lambda) from 0 to 1.0; and minimum child weight (min_child_weight) from 1 to 10. The optimal hyperparameters were: n_estimators = 171; max_depth = 7; learning_rate = 0.67; subsample = 0.95; colsample_bytree = 0.75. This selection balances model complexity and performance.
In addition to tree-based models, we implemented a Multilayer Perceptron (MLP) as a representative deep learning baseline. The MLP consists of an input layer, multiple hidden layers with nonlinear activation functions, and an output layer with softmax activation for classification. The forward propagation through the network can be described as:
where
is the weighted input to layer
,
is the weight matrix,
is the activation from the previous layer,
is the bias vector, and
is the activation function.
The MLP model was configured with two hidden layers of 64 and 32 neurons, respectively, using ReLU activation functions and dropout regularization (rate = 0.2) to prevent overfitting. The model was trained using the Adam optimizer with a learning rate of 0.001 and a categorical cross-entropy loss function.
These baseline implementations provide a solid foundation for the comparative analysis presented in
Section 4, where we evaluate each approach’s relative strengths and limitations in the context of educational data analysis and privacy preservation. The selection of these diverse baseline models allows for a thorough evaluation of traditional ensemble methods (Random Forest), modern gradient boosting approaches (XGBoost), and neural network architectures (MLP) against the TabNet architecture in both standard and privacy-preserving configurations.
We include Differentially Private Stochastic Gradient Descent (DP-SGD) as an independent privacy-preserving model alongside baseline models evaluated under standard and input-perturbation DP settings. This setup allows us to assess training-time privacy mechanisms. DP-SGD integrates differential privacy into the training process by clipping gradients and adding noise during optimization. This approach provides privacy guarantees at the parameter level instead of the input data level [
25]. We implement DP-SGD as a standalone model with a privacy budget of
= 0.7 for consistency with the input-perturbation approach used in other models.We tune gradient clipping thresholds and noise scales to balance privacy and utility. However, this method may incur greater computational overhead and degrade performance compared to input perturbation. Including DP-SGD allows comprehensive evaluation of different DP strategies in educational data prediction. It offers insights into their relative impacts on model performance.