Building Electricity Prediction Using BILSTM-RF-XGBOOST Hybrid Model with Improved Hyperparameters Based on Bayesian Algorithm
Abstract
1. Introduction
Contribution
- A new hybrid model is proposed by integrating the advantages of three single models, which can effectively deal with the complex characteristics of high-dimensional, high-noise and nonlinear energy consumption data.
- The model hyperparameters are improved by a Bayesian algorithm to overcome the limitations of traditional methods while achieving optimal model performance.
- Using SHAP as the main tool for feature significance analysis reveals the key factors affecting electricity consumption, quantifies the positive and negative influence of different feature factors on model predictions, and provides a transparent and reliable basis for the development of energy management strategies.
2. Related Work
3. Experimental Design and Research Methodology
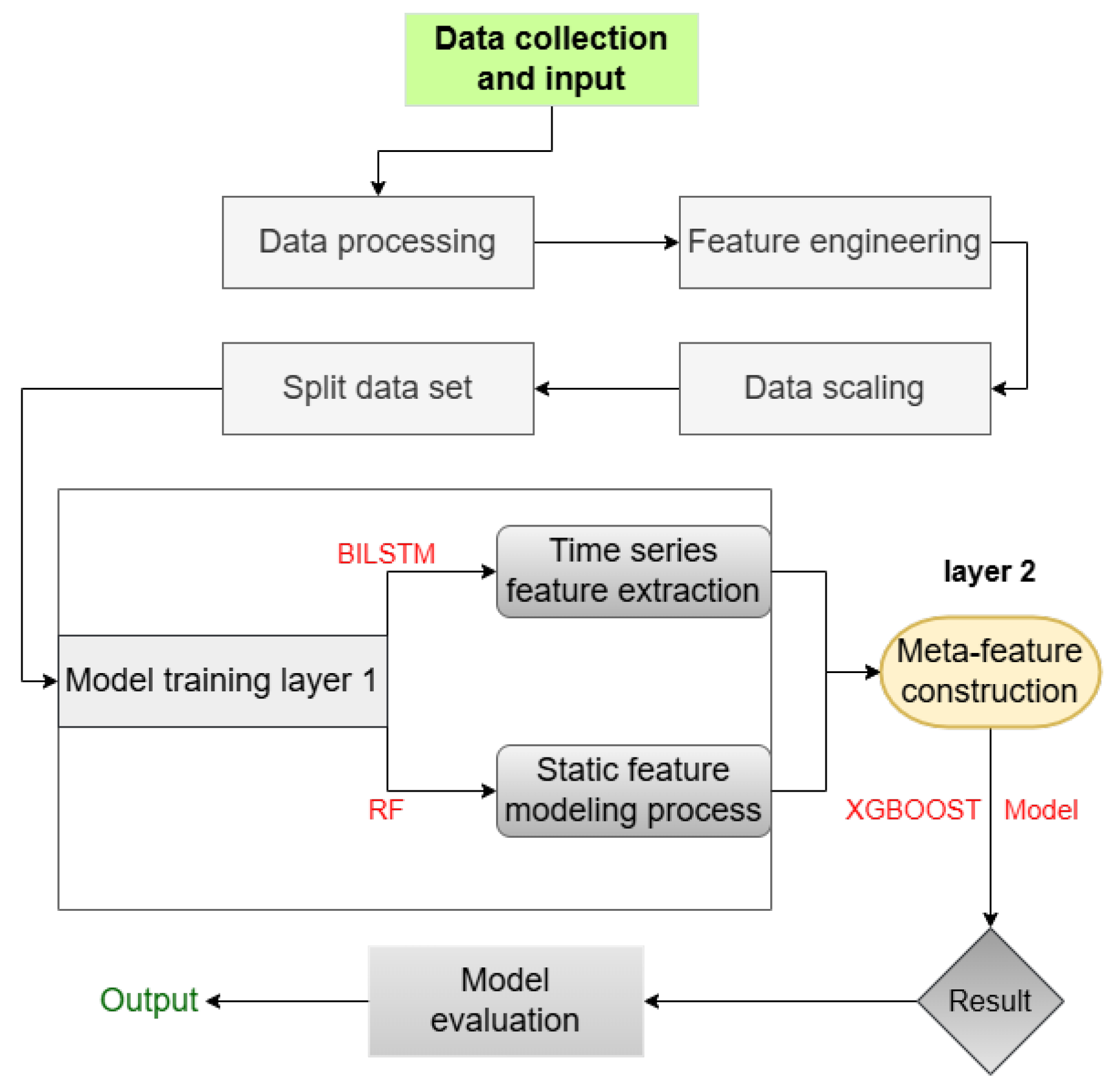
3.1. Model Structure
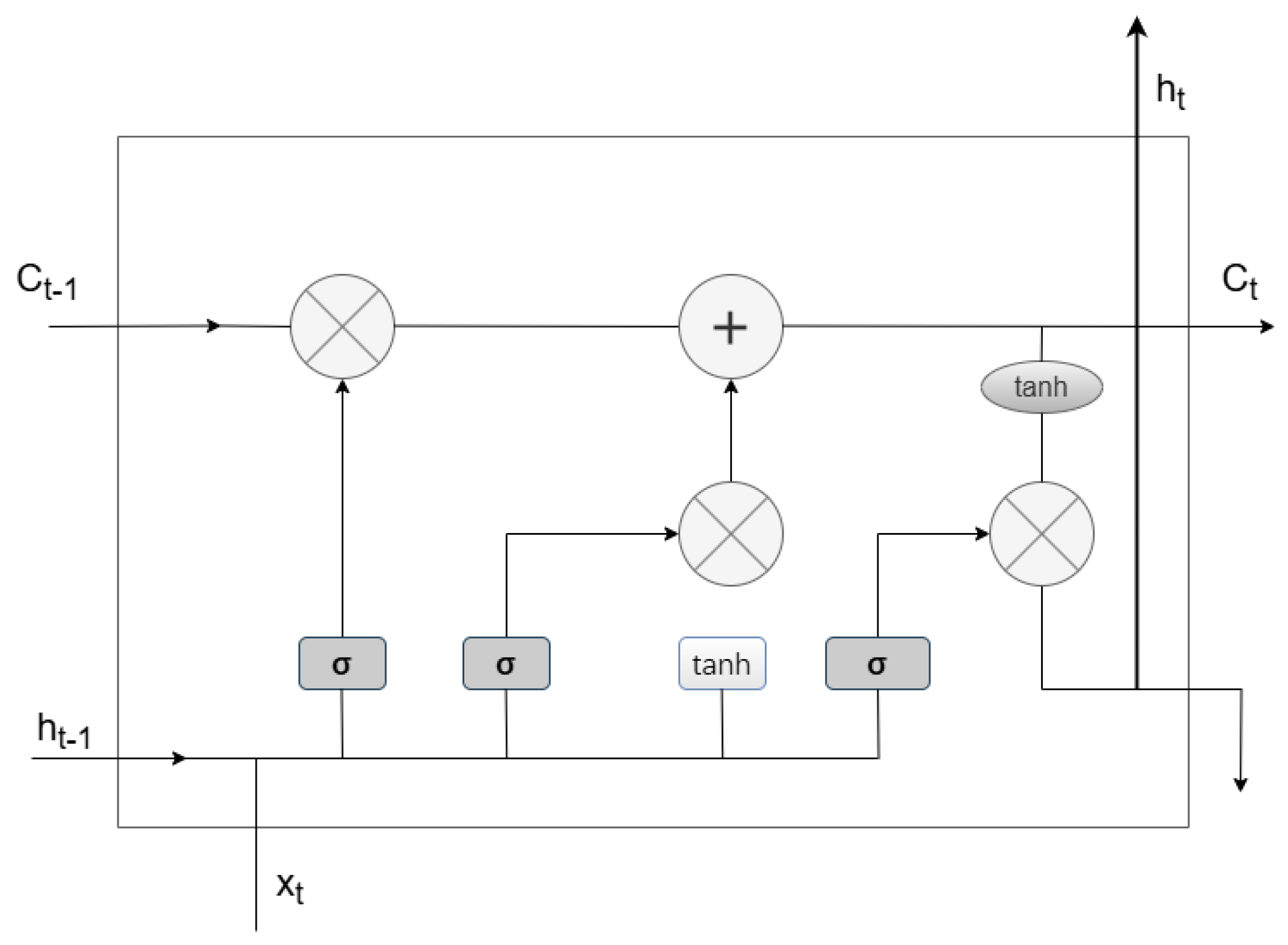
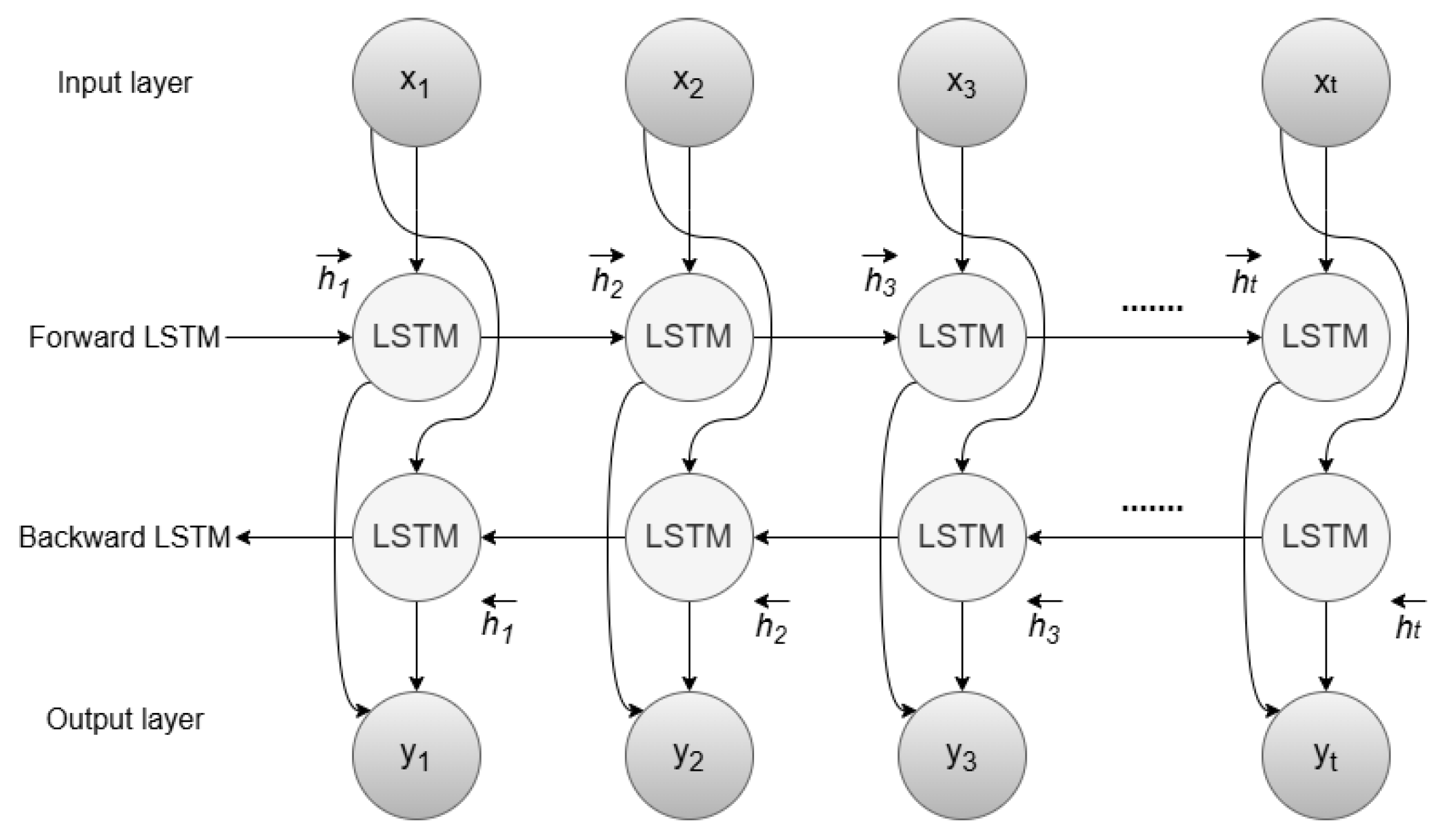
3.1.1. Bidirectional Long Short-Term Memory Neural Network (BILSTM) Model
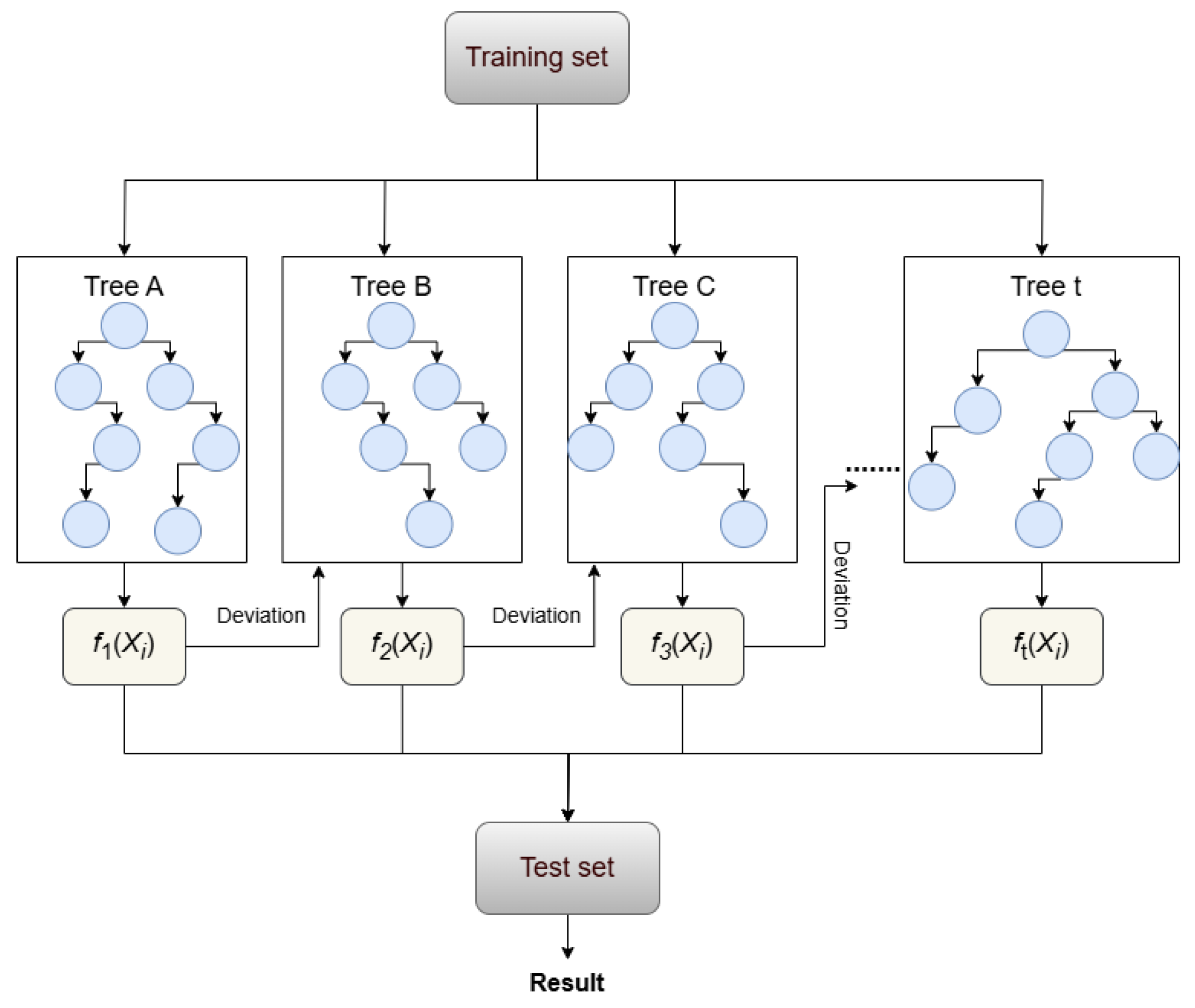
3.1.2. Random Forest (RF) Model
3.1.3. Extreme Gradient Boosting (XGBOOST) Model
3.1.4. BILSTM-RF-XGBOOST Hybrid Model
3.2. Bayesian Optimization Algorithm Under K-Fold Cross-Validation
3.2.1. Gaussian Process (GP) Surrogate Model
3.2.2. Expected Improvement (EI) Collection Function
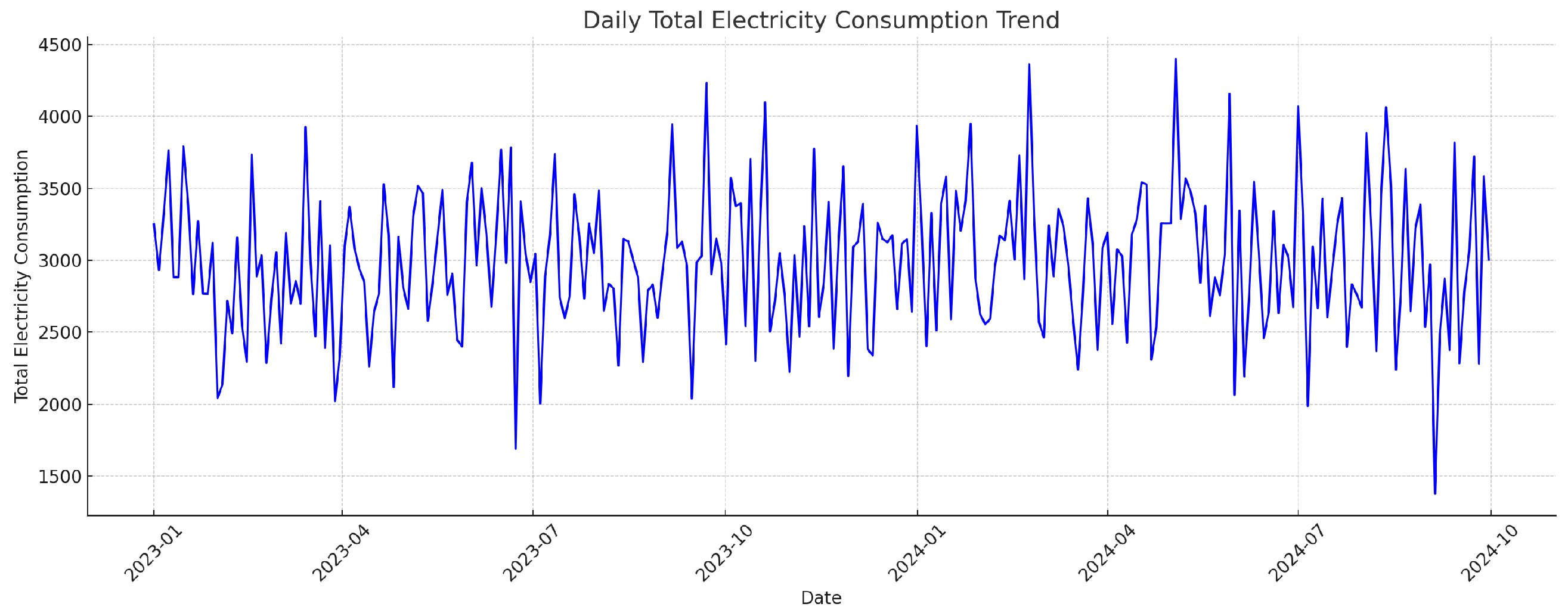
3.3. Data Collection and Pre-Processing
3.3.1. Data Sources and Pre-Processing
3.3.2. Feature Engineering
4. Experimental Setup and Analysis of Results
4.1. Model Evaluation Criteria
4.2. Optimal Hyperparameter Setting
4.3. Experimental Results and Analysis
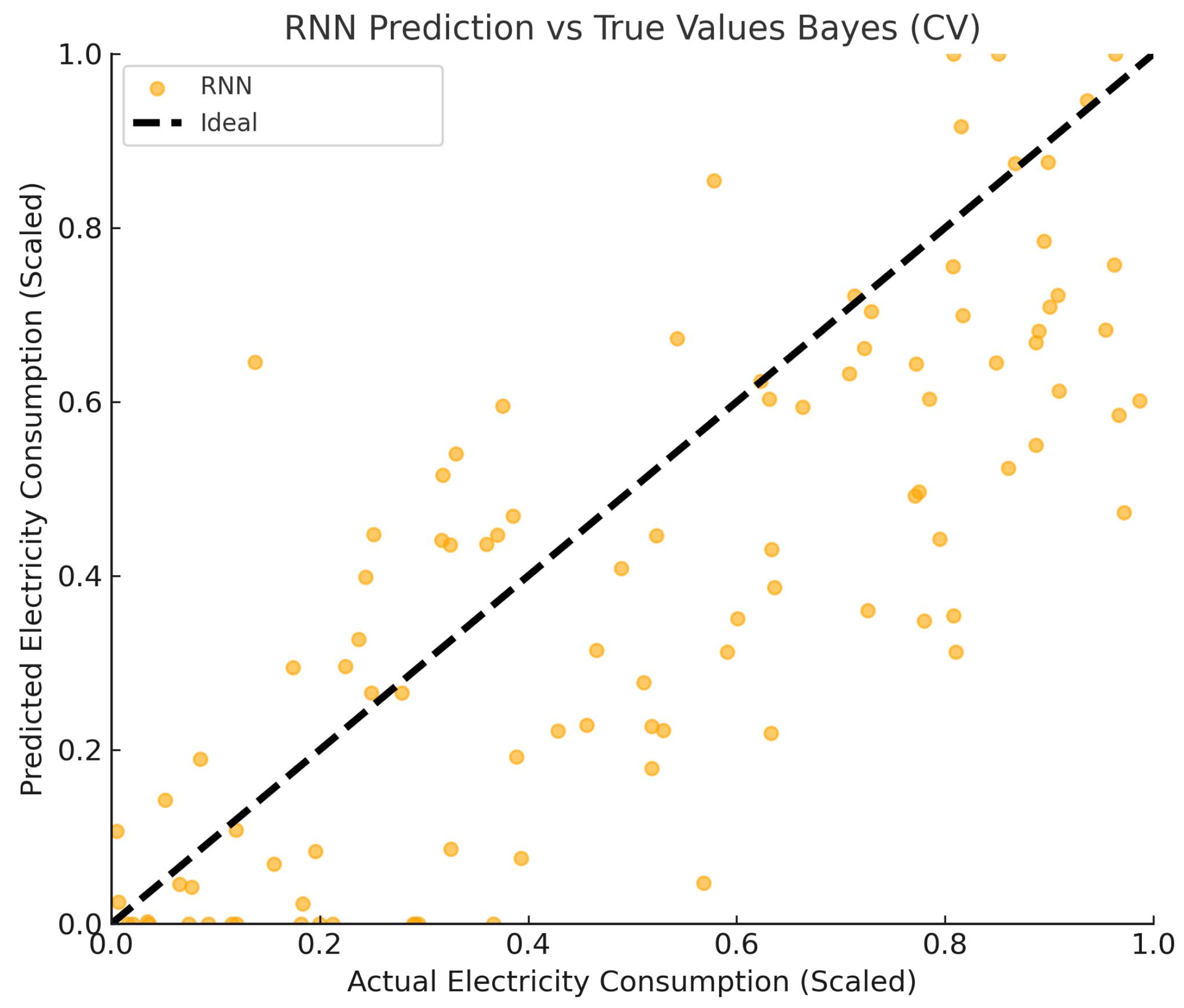
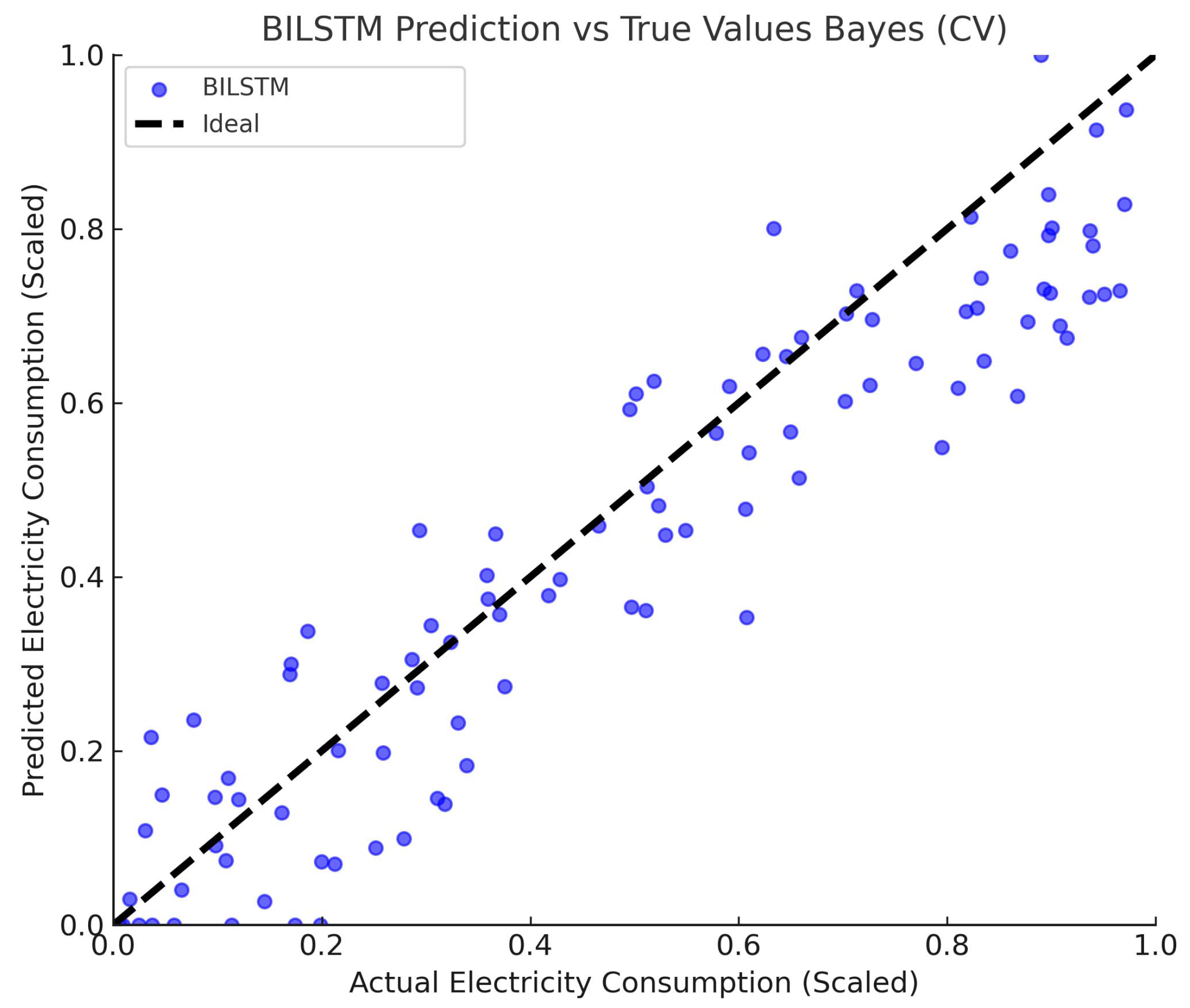
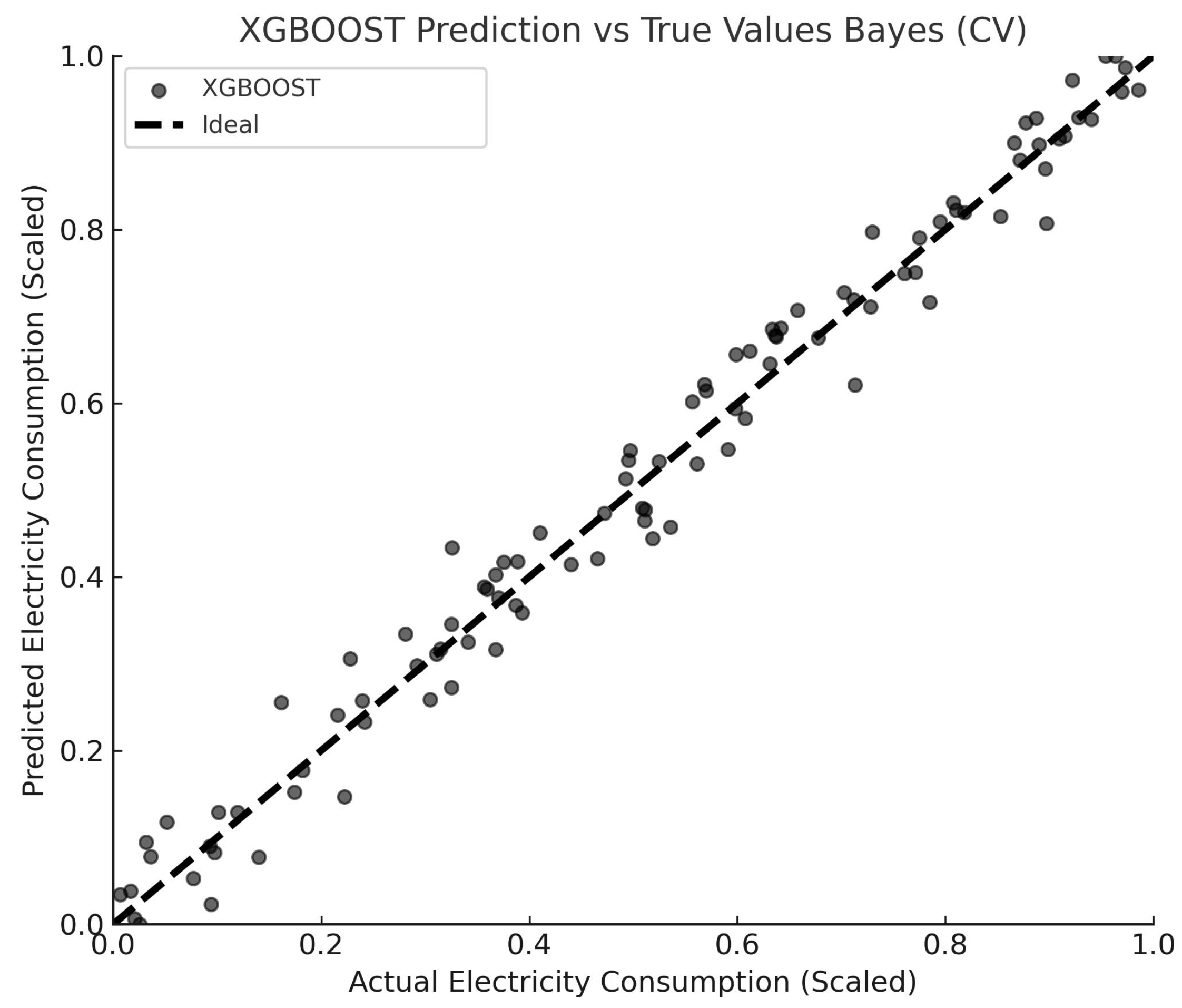
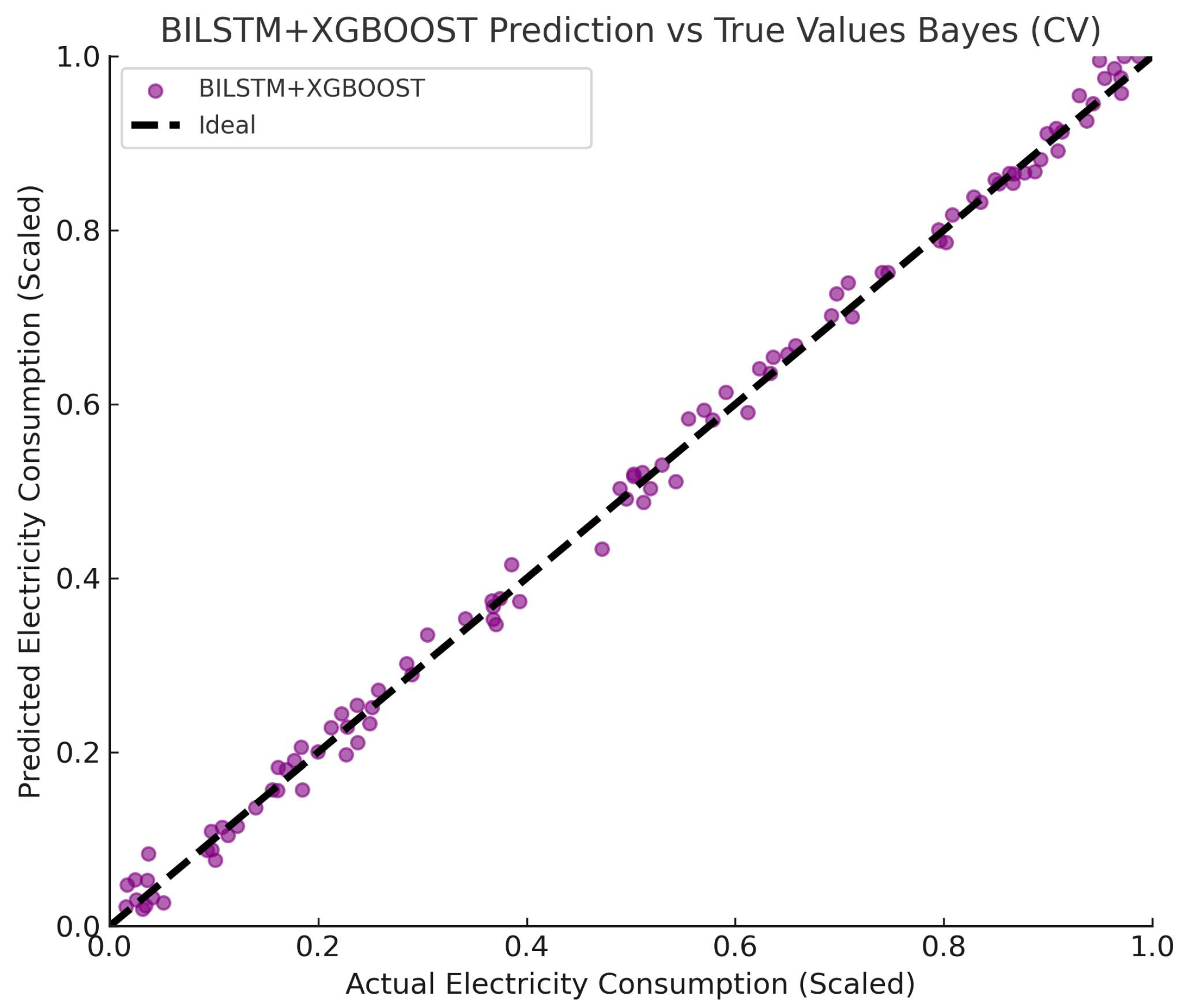
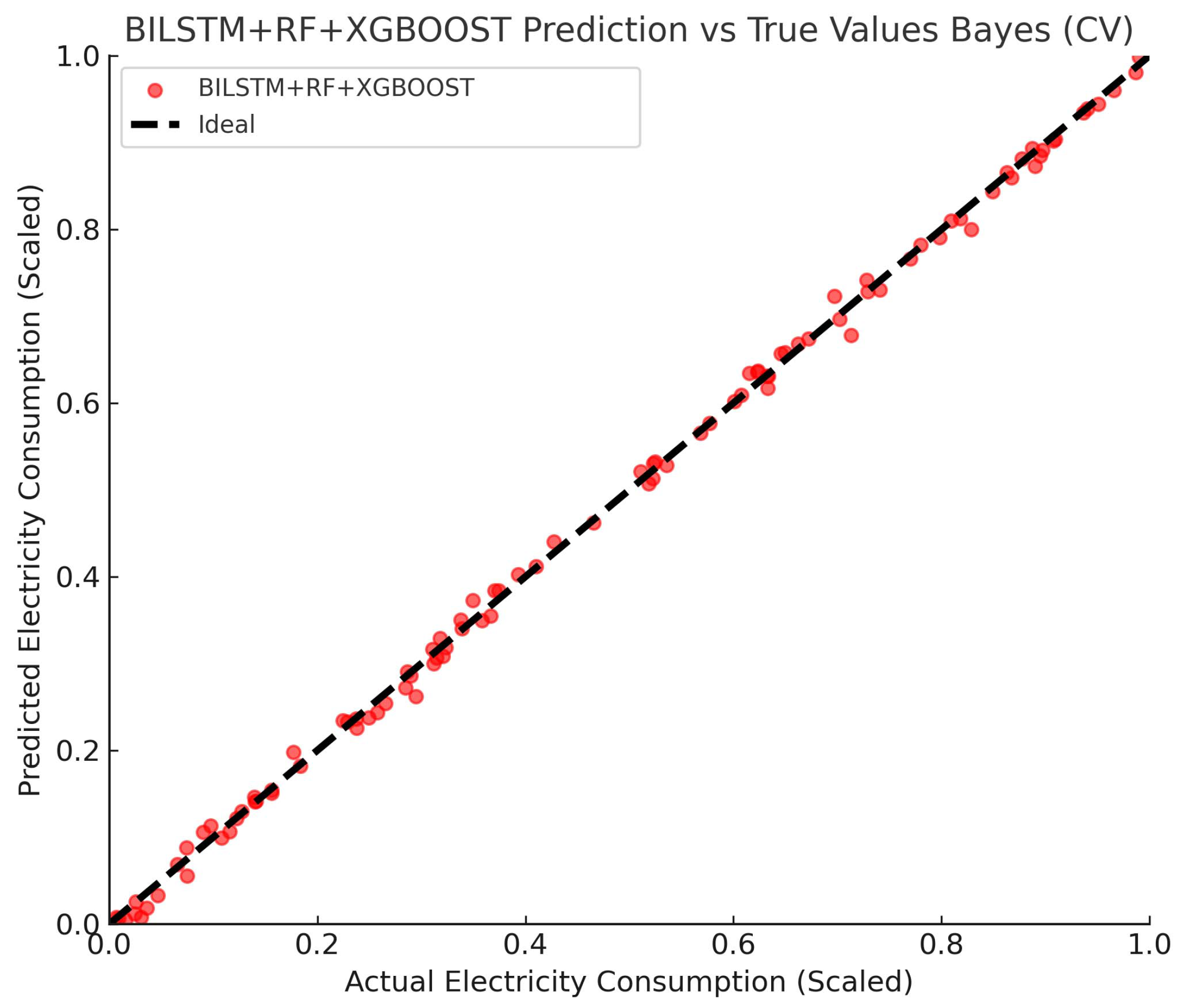
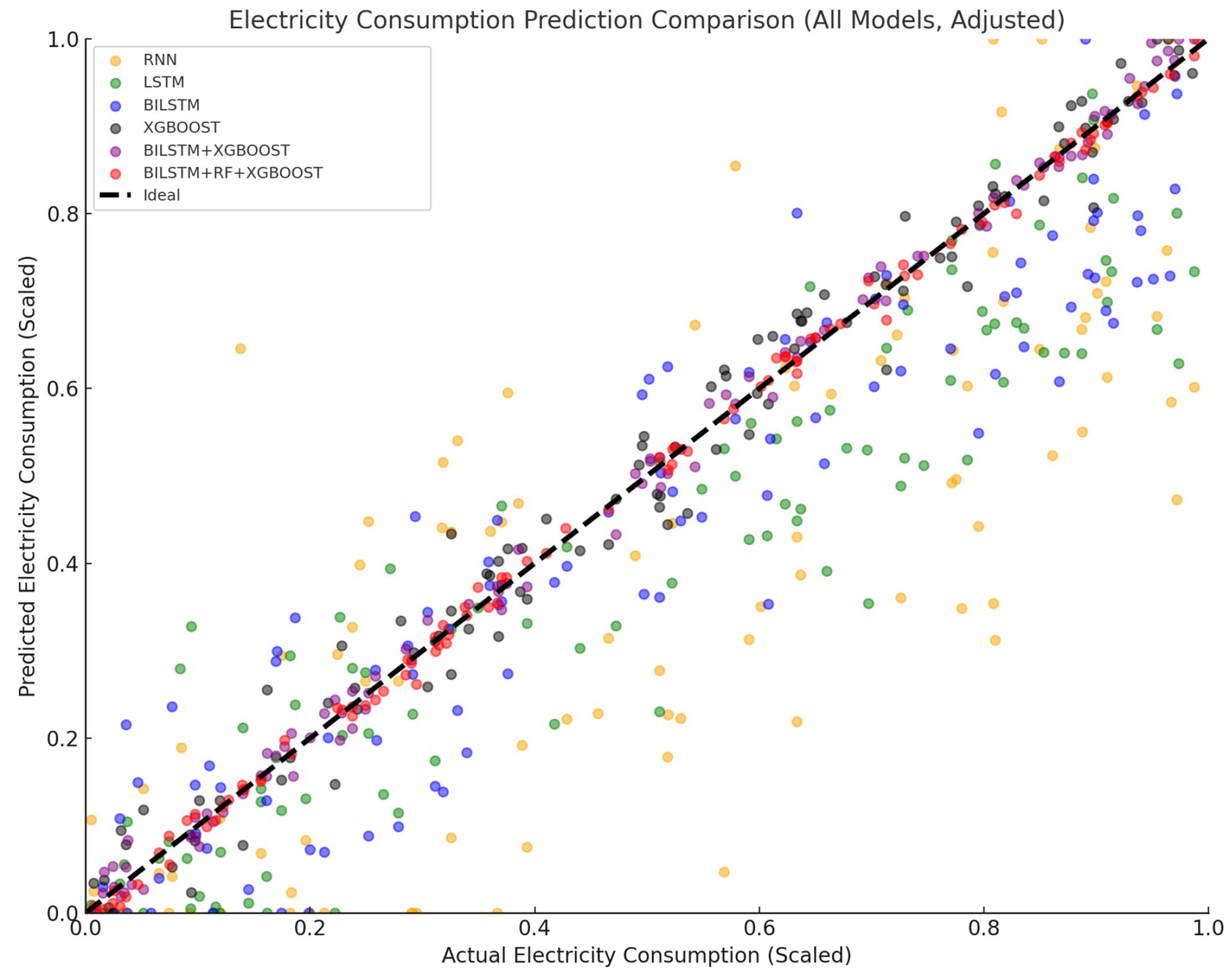
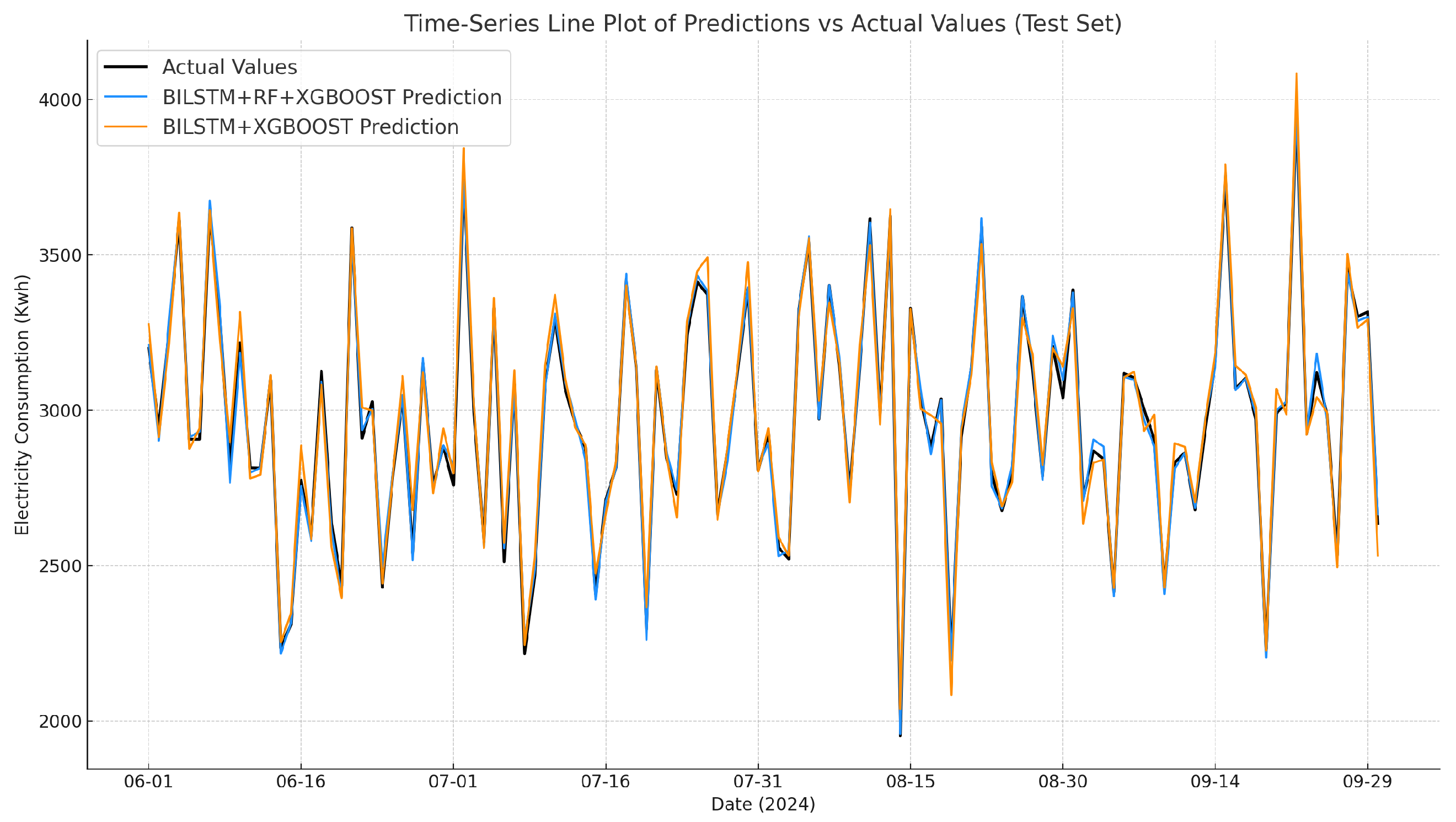
4.3.1. Analysis of Projected Results
4.3.2. Analysis of Model Evaluation Metrics
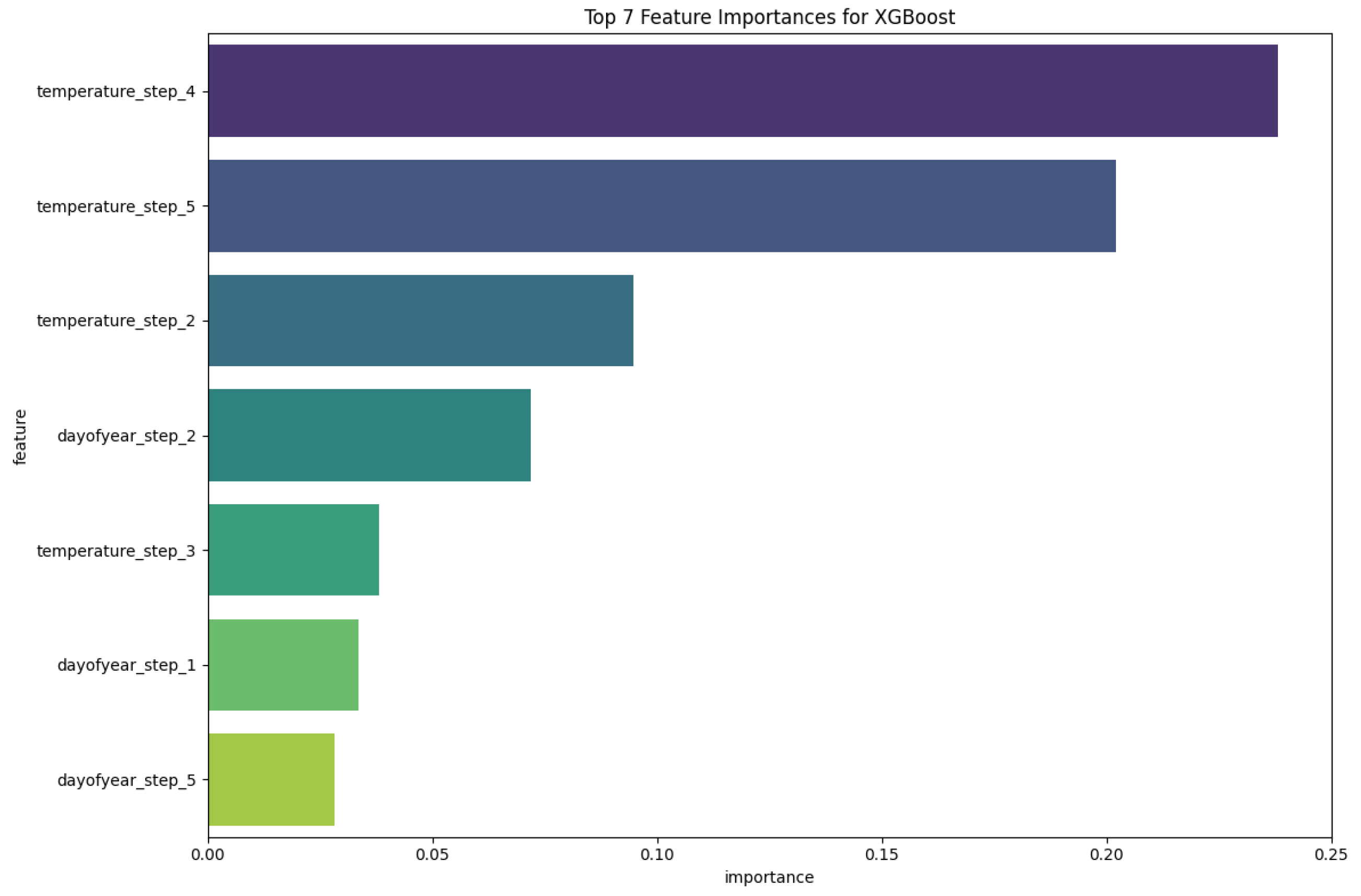
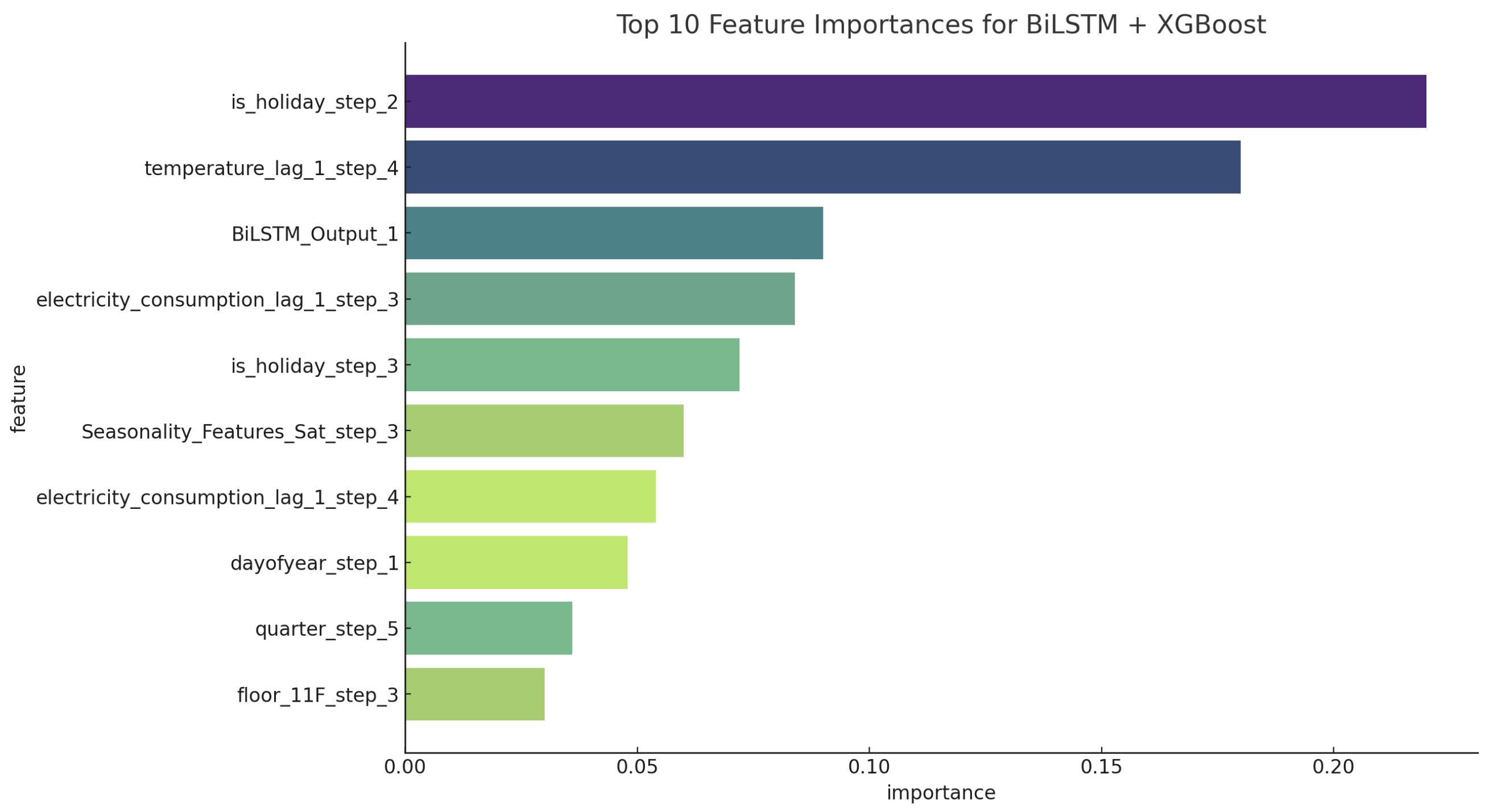
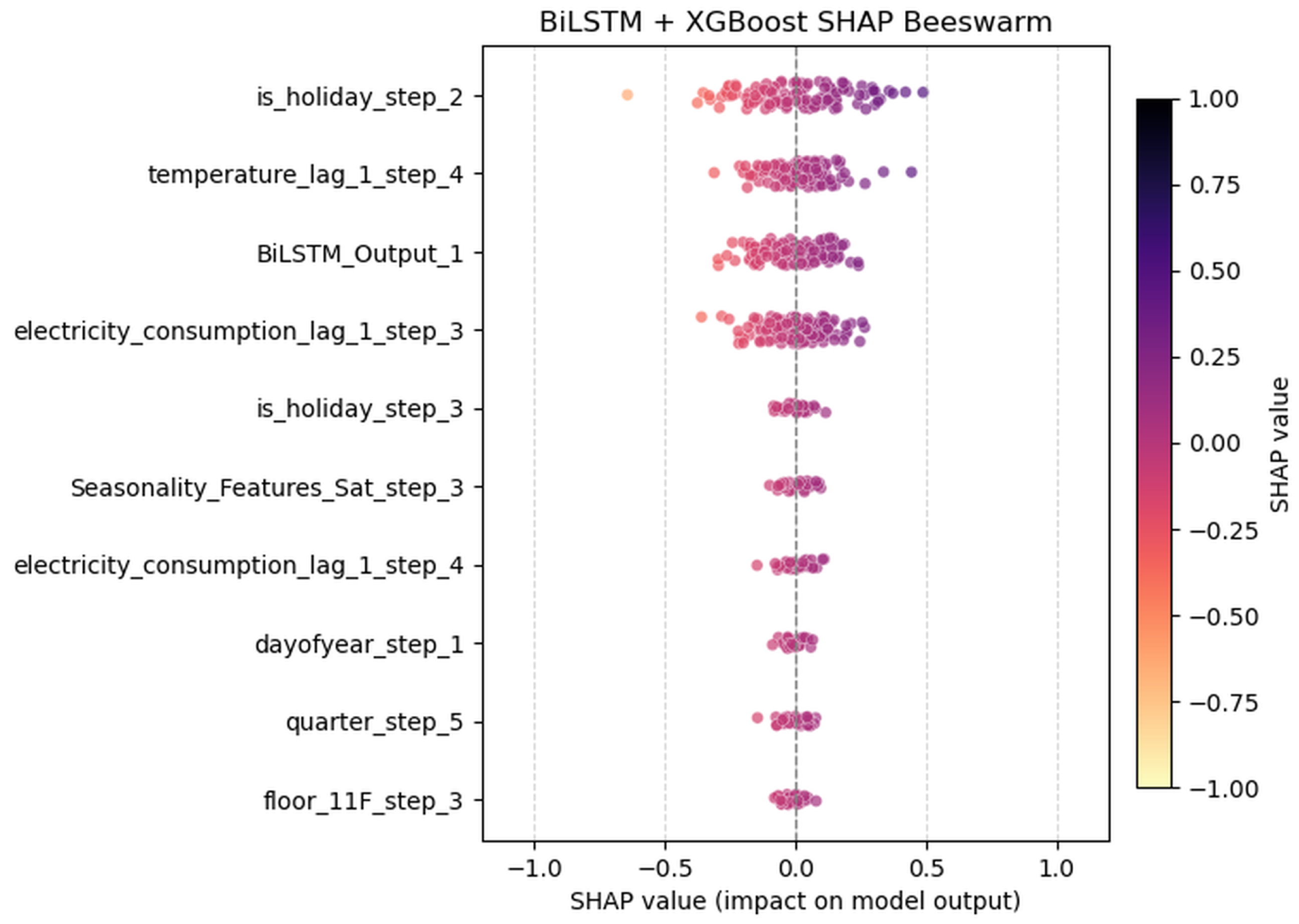
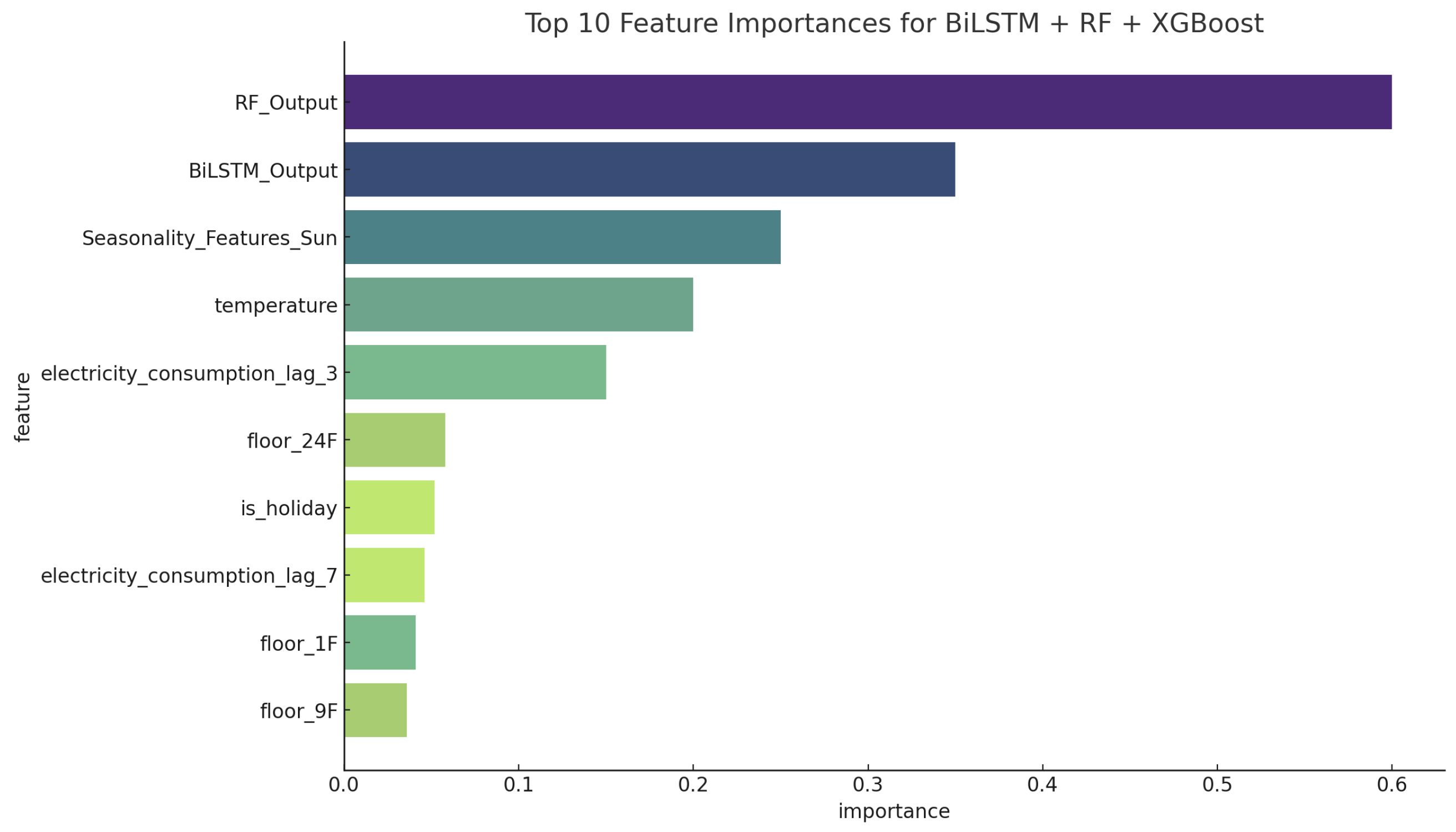
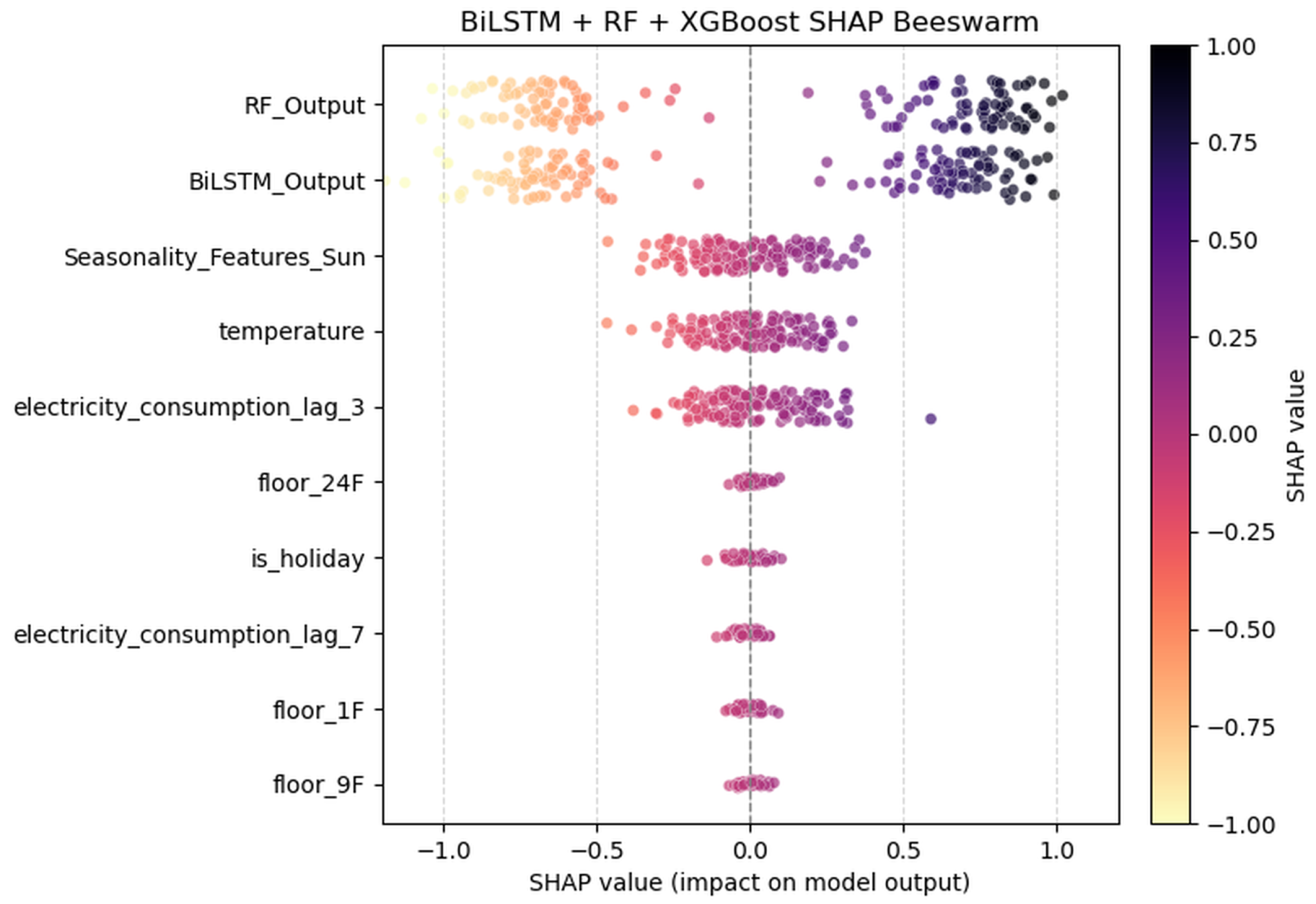
4.4. Feature Importance Analysis
5. Conclusions and Prospect
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ARIMA | Autoregressive Integrated Moving Average Model |
| AR | Autoregressive Model |
| MA | Moving Average |
| UAV | Unmanned Aerial Vehicle |
| RNN | Recurrent Neural Network |
| SVR | Support Vector Regression |
| CNN | Convolutional Neural Networks |
| GRU | Gated Recurrent Unit |
| LSTM | Long Short-Term Memory |
| BILSTM | Bidirectional Long Short-Term Memory |
| XGBOOST/XGB | Extreme Gradient Boosting |
| RF | Random Forest |
| GP | Gaussian Processes |
| EI | Expected Improvement |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| R2 | R-squared |
| TSCV | Time Series Cross-Validation |
References
- Sathishkumar, V.E.; Lee, M.; Lim, J.; Kim, Y.; Shin, C.; Park, J.; Cho, Y. An energy consumption prediction model for smart factory using data mining algorithms. KIPS Trans. Softw. Data Eng. 2020, 9, 153–160. [Google Scholar]
- Bilgili, M.; Pinar, E. Gross electricity consumption forecasting using LSTM and SARIMA approaches: A case study of Türkiye. Energy 2023, 284, 128575. [Google Scholar] [CrossRef]
- Ribeiro, A.M.N.C.; do Carmo, P.R.X.; Rodrigues, I.R.; Sadok, D.; Lynn, T.; Endo, P.T. Short-term firm-level energy-consumption forecasting for energy-intensive manufacturing: A comparison of machine learning and deep learning models. Algorithms 2020, 13, 274. [Google Scholar] [CrossRef]
- Semmelmann, L.; Henni, S.; Weinhardt, C. Load forecasting for energy communities: A novel LSTM-XGBoost hybrid model based on smart meter data. Energy Inform. 2022, 5, 24. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, J.; Wang, L.; Xu, C. Electricity, heat, and gas load forecasting based on deep multitask learning in industrial-park integrated energy system. Entropy 2020, 22, 1355. [Google Scholar] [CrossRef]
- Tang, C.; Zhang, Y.; Wu, F.; Tang, Z. An improved cnn-bilstm model for power load prediction in uncertain power systems. Energies 2024, 17, 2312. [Google Scholar] [CrossRef]
- Peng, B.; Liu, L.; Wang, Y. Monthly electricity consumption forecast of the park based on hybrid forecasting method. In Proceedings of the China International Conference on Electricity Distribution (CICED), Shanghai, China, 7–9 April 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 789–793. [Google Scholar]
- Son, N.; Shin, Y. Short-and medium-term electricity consumption forecasting using Prophet and GRU. Sustainability 2023, 15, 15860. [Google Scholar] [CrossRef]
- Essien, A.; Giannetti, C. A deep learning model for smart manufacturing using convolutional LSTM neural network autoencoders. IEEE Trans. Ind. Inform. 2020, 16, 6069–6078. [Google Scholar] [CrossRef]
- Liu, F.; Liang, C. Short-term power load forecasting based on AC-BiLSTM model. Energy Rep. 2024, 11, 1570–1579. [Google Scholar] [CrossRef]
- Pooniwala, N.; Sutar, R. Forecasting short-term electric load with a hybrid of arima model and lstm network. In Proceedings of the International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 27–29 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Luo, S.; Wang, B.; Gao, Q.; Wang, Y.; Pang, X. Stacking integration algorithm based on CNN-BiLSTM-Attention with XGBoost for short-term electricity load forecasting. Energy Rep. 2024, 12, 2676–2689. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, X.; Zhang, J.; Zhang, A.; Shi, G.; Yang, Q. UAV Trajectory Prediction Based on Flight State Recognition. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2629–2641. [Google Scholar]
- Gustafsson, O.; Villani, M.; Stockhammar, P. Bayesian optimization of hyperparameters from noisy marginal likelihood estimates. J. Appl. Econ. 2023, 38, 577–595. [Google Scholar] [CrossRef]
- Pierre, A.A.; Akim, S.A.; Semenyo, A.K.; Babiga, B. Peak electrical energy consumption prediction by ARIMA, LSTM, GRU, ARIMA-LSTM and ARIMA-GRU approaches. Energies 2023, 16, 4739. [Google Scholar] [CrossRef]
- Shi, Z.; Jia, Y.; Shi, G.; Zhang, K.; Ji, L.; Wang, D.; Wu, Y. Design of Motor Skill Recognition and Hierarchical Evaluation System for Table Tennis Players. IEEE Sens. J. 2024, 24, 5303–5315. [Google Scholar] [CrossRef]
- Shi, Z.; Shi, G.; Zhang, J.; Wang, D.; Xu, T.; Ji, L.; Wu, Y. Design of UAV Flight State Recognition System for Multisensor Data Fusion. IEEE Sens. J. 2024, 24, 21386–21394. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, Z.; Yuan, S.; Lan, G. Short Term Power Load Forecasting Model Based on XGBoost-BiLSTM. In Proceedings of the 9th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 20–22 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1691–1694. [Google Scholar]
- Chen, Y.; Fu, Z. Multi-step ahead forecasting of the energy consumed by the residential and commercial sectors in the United States based on a hybrid CNN-BiLSTM model. Sustainability 2023, 15, 1895. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-sequence LSTM-RNN deep learning and metaheuristics for electric load forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef]
- Al-Jamimi, H.A.; BinMakhashen, G.M.; Worku, M.Y.; Hassan, M.A. Advancements in household load forecasting: Deep learning model with hyperparameter optimization. Electronics 2023, 12, 4909. [Google Scholar] [CrossRef]
- Chang, W.; Chen, X.; He, Z.; Zhou, S. A prediction hybrid framework for air quality integrated with W-BiLSTM (PSO)-GRU and XGBoost methods. Sustainability 2023, 15, 16064. [Google Scholar] [CrossRef]
- Yang, F.; Yan, K.; Jin, N.; Du, Y. Multiple households energy consumption forecasting using consistent modeling with privacy preservation. Adv. Eng. Inform. 2023, 55, 101846. [Google Scholar] [CrossRef]
- Liu, D.; Sun, K. Random forest solar power forecast based on classification optimization. Energy 2019, 187, 115940. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Liu, Y.; Chow, Y.H.; Iu, H.H.-C.; Fernando, T. Long-term energy and peak power demand forecasting based on sequential-XGBoost. IEEE Trans. Power Syst. 2023, 39, 3088–3104. [Google Scholar] [CrossRef]
- Hajj-Hassan, M.; Awada, M.; Khoury, H.; Abou Saleh, Z. A behavioral-based machine learning approach for predicting building energy consumption. In Proceedings of the Construction Research Congress 2020, Tempe, AZ, USA, 8–10 March 2020; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2020; pp. 1029–1037. [Google Scholar]
- Sun, D.; Xu, J.; Wen, H.; Wang, D. Assessment of landslide susceptibility mapping based on Bayesian hyperparameter optimization: A comparison between logistic regression and random forest. Eng. Geol. 2021, 281, 105972. [Google Scholar] [CrossRef]
- Joy, T.T.; Rana, S.; Gupta, S.; Venkatesh, S. Batch Bayesian optimization using multi-scale search. Knowl.-Based Syst. 2020, 187, 104818. [Google Scholar] [CrossRef]



| Model/Component | Hyperparameter | Search Range | Remarks |
|---|---|---|---|
| Base Models (RNN, LSTM, BiLSTM) | |||
| RNN | units | (32, 128) | Number of RNN units |
| dropout_rate | (0.0, 0.5) | Dropout rate | |
| learning_rate | (0.0001, 0.01) | Learning rate | |
| LSTM | units | (32, 128) | Number of LSTM units |
| dropout_rate | (0.0, 0.5) | Dropout rate | |
| learning_rate | (0.0001, 0.01) | Learning rate | |
| BiLSTM | units | (32, 128) | Units per LSTM in BiLSTM |
| dropout_rate | (0.0, 0.5) | Dropout rate | |
| learning_rate | (0.0001, 0.01) | Learning rate | |
| seq_length | (5, 20) | Input sequence length | |
| XGBoost (Base Model and Meta-Learner Component) | |||
| XGBoost | n_estimators | (100, 1000) | Number of trees |
| learning_rate | (0.005, 0.1) | Learning rate | |
| max_depth | (3, 10) | Tree max depth | |
| subsample | (0.6, 1.0) | Subsample ratio of training samples | |
| colsample_bytree | (0.5, 1.0) | Subsample ratio of columns | |
| gamma | (0.0, 0.5) | Minimum loss reduction for split | |
| reg_alpha | (0.0, 0.5) | L1 regularization | |
| reg_lambda | (0.0, 0.5) | L2 regularization | |
| BiLSTM-XGBoost (Hybrid Model) | |||
| BiLSTM component | lstm_units | (32, 128) | BiLSTM units |
| lstm_dropout_rate | (0.0, 0.5) | BiLSTM dropout rate | |
| lstm_learning_rate | (0.0001, 0.01) | BiLSTM learning rate | |
| XGBoost component | n_estimators | (100, 1000) | XGBoost trees |
| learning_rate | (0.005, 0.1) | XGBoost learning rate | |
| max_depth | (3, 10) | XGBoost tree depth | |
| subsample | (0.6, 1.0) | XGBoost subsample | |
| colsample_bytree | (0.5, 1.0) | XGBoost column subsample | |
| gamma | (0.0, 0.5) | XGBoost gamma | |
| reg_alpha | (0.0, 0.5) | XGBoost L1 regularization | |
| reg_lambda | (0.0, 0.5) | XGBoost L2 regularization | |
| BiLSTM-RF-XGBoost (Hybrid Model) | |||
| BiLSTM component | lstm_units | (32, 64) | BiLSTM units |
| lstm_dropout_rate | (0.1, 0.4) | BiLSTM dropout rate | |
| lstm_learning_rate | (0.001, 0.01) | BiLSTM learning rate | |
| RF component | n_estimators_rf | (50, 300) | RF number of trees |
| max_features | (0.6, 0.9) | RF max features ratio | |
| min_samples_leaf | (3, 15) | RF minimum samples per leaf | |
| XGBoost component | n_estimators_xgb | (100, 500) | XGBoost number of trees |
| learning_rate_xgb | (0.01, 0.1) | XGBoost learning rate | |
| max_depth_xgb | (3, 8) | XGBoost tree depth | |
| subsample_xgb | (0.6, 0.9) | XGBoost subsample ratio | |
| colsample_bytree_xgb | (0.5, 0.9) | XGBoost column subsample | |
| gamma_xgb | (0.1, 0.6) | XGBoost gamma | |
| reg_alpha_xgb | (0.1, 0.6) | XGBoost L1 regularization | |
| reg_lambda_xgb | (0.1, 0.6) | XGBoost L2 regularization | |
| Field Name | Data Type | Description |
|---|---|---|
| data | Datetime | Date |
| electricity_consumption | Numerical | Daily total electricity consumption |
| temperature | Numerical | Daily average temperature |
| is_holiday | Boolean | Whether the day is a holiday |
| Seasonality_Features | Categorical | reflecting weekly seasonality |
| Name | RNN | LSTM | BILSTM | XGBOOST | BILSTM-XGB | BILSTM-RF-XGB |
|---|---|---|---|---|---|---|
| units | 68 | 95 | 125 | \ | 64 (BILSTM) | 116 (BILSTM) |
| dropout_rate | 0.024 | 0.001 | 0.030 | \ | 0.094 (BILSTM) | 0.1 (BILSTM) |
| learning_rate | 0.009 | 0.010 | 0.007 | \ | 0.010 (BILSTM) | 0.002 (BILSTM) |
| seq_length | 5 | 5 | 5 | \ | \ | \ |
| n_estimators | \ | \ | \ | 912 | 217 | 114 |
| XGB learning_rate | \ | \ | \ | 0.050 | 0.080 | 0.066 |
| max_depth | \ | \ | \ | 11 | 7 | 4 |
| subsample | \ | \ | \ | 0.864 | 0.618 | 0.936 |
| colsample_bytree | \ | \ | \ | 0.567 | 0.761 | 0.867 |
| gamma | \ | \ | \ | 0.011 | 0.008 | 0.015 |
| reg_alpha | \ | \ | \ | 0.030 | 0.023 | 0.092 |
| reg_lambda | \ | \ | \ | 0.165 | 0.140 | 0.175 |
| RF max_features | \ | \ | \ | \ | \ | 0.855 |
| RF min_samples_leaf | \ | \ | \ | \ | \ | 3 |
| RF n_estimators | \ | \ | \ | \ | \ | 350 |
| Model | TSCV Average R2 | MSE | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| RNN | −101.775 | 0.62131 | 0.78822 | 0.92327 | 184.67% |
| LSTM | −11.628 | 0.08174 | 0.28601 | 0.21754 | 43.51% |
| BILSTM | −7.141 | 0.06817 | 0.26109 | 0.21255 | 42.28% |
| XGBoost | 0.911 | 0.00045 | 0.02121 | 0.01039 | 2.09% |
| BILSTM + XGBoost | 0.953 | 0.00007 | 0.00837 | 0.00431 | 0.86% |
| BILSTM + RF + XGBoost | 0.989 | 0.00003 | 0.00548 | 0.00130 | 0.26% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, B.; Liang, H. Building Electricity Prediction Using BILSTM-RF-XGBOOST Hybrid Model with Improved Hyperparameters Based on Bayesian Algorithm. Electronics 2025, 14, 2287. https://doi.org/10.3390/electronics14112287
Liu Y, Li B, Liang H. Building Electricity Prediction Using BILSTM-RF-XGBOOST Hybrid Model with Improved Hyperparameters Based on Bayesian Algorithm. Electronics. 2025; 14(11):2287. https://doi.org/10.3390/electronics14112287
Chicago/Turabian StyleLiu, Yuqing, Binbin Li, and Hejun Liang. 2025. "Building Electricity Prediction Using BILSTM-RF-XGBOOST Hybrid Model with Improved Hyperparameters Based on Bayesian Algorithm" Electronics 14, no. 11: 2287. https://doi.org/10.3390/electronics14112287
APA StyleLiu, Y., Li, B., & Liang, H. (2025). Building Electricity Prediction Using BILSTM-RF-XGBOOST Hybrid Model with Improved Hyperparameters Based on Bayesian Algorithm. Electronics, 14(11), 2287. https://doi.org/10.3390/electronics14112287







