Abstract
Flocking control in networked agent systems (NASs) has been extensively studied, yet many existing methods overlook two critical issues: the need for fast, predictable convergence, and resilience against false data injection (FDI) attacks. To tackle these challenges, this paper proposes a secure predefined-time quasi-flocking control scheme leveraging neural networks. First, a predefined-time control protocol is formulated via a time-varying scaling function, which ensures that all agents achieve quasi-flocking behavior within a prescribed time, independent of their initial conditions. This design guarantees rapid and predictable convergence. Second, radial basis function (RBF) neural networks are employed to estimate the unknown disturbances induced by FDI attacks. A novel adaptive update law is developed to dynamically compensate for these uncertainties in real-time. Lyapunov-based analysis rigorously proves that the proposed control strategy achieves predefined-time quasi-flocking while preserving robustness against adversarial attacks. Finally, extensive simulation results demonstrate that the proposed approach ensures rapid convergence and robust performance in flocking control.
1. Introduction
1.1. Background
Networked agent systems (NASs) have garnered significant research interest in recent years owing to their capability to accomplish complex cooperative missions, such as collaborative reconnaissance and coordinated strikes, that surpass the operational capacity of individual agents [1,2,3,4,5,6,7,8]. Driven by the continuous advancements in computation, communication, and sensing technologies, the cooperative control of NASs has experienced rapid progress. However, the growing complexity of mission objectives and operational environments imposes increasingly stringent requirements on the design and performance of such control strategies. Among the various collective behaviors exhibited by NASs, flocking represents a fundamental and widely studied phenomenon, inspired by natural aggregations of birds, fish, and other biological agents [9,10,11,12]. A rigorous understanding of flocking dynamics and their intrinsic coordination principles is crucial, as it facilitates the development of scalable and robust distributed control algorithms. These insights find broad applicability in diverse domains such as sensor networks [13] and multi-agent formation control [14].
1.2. Related Works
Inspired by the emergent flocking behaviors observed in biological groups such as birds, fish, and insects, Reynolds [15] pioneered the modeling of such phenomena by formulating three foundational rules, separation, alignment, and cohesion, that collectively govern individual interactions within a group. This seminal work laid the groundwork for subsequent studies in both biological and artificial systems. Building upon this foundation, researchers have extensively investigated flocking behaviors in the context of NASs, leading to the development of a wide range of control strategies tailored for various task requirements and environmental conditions. In particular, constraint-aware flocking has been introduced to account for physical and communication limitations among agents [16]. At the same time, optimization-based approaches aim to enhance performance metrics such as convergence speed, energy efficiency, or robustness against disturbances [11,17]. Moreover, anti-flocking strategies have been proposed to model adversarial or competitive interactions, where agents are designed to avoid cohesion or exhibit divergent behavior under specific scenarios deliberately [18,19]. To provide a comprehensive understanding of the evolution and current state of flocking research, Beaver et al. [20] offer a detailed survey that categorizes and analyzes existing methodologies, highlights emerging trends, and identifies open challenges in this field.
It is well recognized that the convergence speed constitutes a critical performance metric in the design and evaluation of control algorithms, particularly in time-sensitive and mission-critical applications [21,22]. In such scenarios, it is often desirable for the system to accomplish its objective not only reliably, but also within a finite or even prescribed time horizon [23]. However, the majority of existing flocking algorithms in the literature [24,25,26,27] primarily focus on ensuring asymptotic convergence, whereby the desired coordination is achieved only in the limit as time approaches infinity. To address this limitation, finite-time and fixed-time stability have received considerable attention due to their fast convergence advantages in various nonlinear systems [17,23,28]. Since these concepts are now well established, we only briefly summarize the key ideas here to better motivate this paper’s objectives. The finite-time technique enables NASs to complete flocking in a finite time, but it is influenced by the original system conditions and the controller parameters, which have significant limitations. Further, scholars have studied fixed-time flocking. Compared with finite time, the convergence time is only dependent on the controller’s parameters, and the convergence time has stronger flexibility, so it is more applicable in practical applications.
Traditional finite-time and fixed-time flocking strategies typically exhibit convergence times that are influenced by both the system’s initial conditions and the chosen control parameters, thereby limiting their adaptability to predefined temporal objectives [29,30]. This drawback is particularly problematic in time-critical missions, such as coordinated missile operations, where strict synchronization within a designated time window is mandatory. To address this issue, the predefined-time control paradigm has been proposed, allowing systems to complete their tasks within a preassigned time bound that is entirely independent of initial conditions and control parameter tuning [31,32,33,34]. This methodology greatly enhances temporal predictability and design adaptability, making it especially advantageous for mission-critical applications with rigid timing demands. To date, predefined-time control has been extensively applied to problems of consensus [35,36,37] and formation control [38,39,40] in NASs. However, its integration into flocking control remains relatively underexplored and continues to present open challenges in both theoretical analysis and practical implementation.
Moreover, existing studies on flocking control [41,42,43] often rely on idealized NAS models, typically neglecting the influence of false data injection (FDI) attacks. In contrast, real-world applications frequently encounter security threats in networked systems, such as FDI attacks [44,45], highlighting the growing necessity for resilient control strategies with inherent attack resistance. In [46], the authors proposed adaptive control protocols to address the consensus and flocking control problem of second-order nonlinear NASs under FDI attacks, achieving fixed-time consensus and finite-time flocking with derived settling time bounds. While existing research results generally lack a comprehensive consideration of dynamic disturbances and FDI attacks, both of which can notably reduce system performance through the contamination of control inputs. To address this problem, a very straightforward and effective approach is to estimate the attacks and disturbances and then design compensation modules in the controller. However, due to the complexity and variability of external attacks and disturbances, it is very difficult to perform the estimation, and it has been a very challenging task. Nowadays, with the rapid development of computer computing power, neural networks are widely used in more and more fields [47,48,49,50]. In NASs, researchers use neural network techniques to approximate the unknown uncertainty, which enhances the robustness of the control algorithms. In [51], the problem of flocking in NASs in which the leader and the followers have different dynamics was investigated. By designing a neuroadaptive controller and adaptive updating law, flocking is realized while avoiding collisions between agents.
1.3. Motivations
In summary, many real-world applications necessitate that networked agents complete coordination tasks within strict and predictable timeframes. However, conventional flocking strategies, whether based on asymptotic, finite-time, or fixed-time convergence, fail to ensure precise synchronization at a preassigned instant, thereby limiting their effectiveness in mission-critical scenarios. In parallel, the increasing openness and interconnectivity of communication networks in NASs have rendered them particularly vulnerable to cyber threats, among which FDI attacks pose a significant challenge. Such adversarial manipulations can lead to erroneous state estimates and control decisions, thereby compromising system stability, coordination accuracy, and overall safety. To address the pressing challenge of achieving both time-guaranteed flocking and resilience against malicious data interference, this paper addresses the flocking control problem of NASs under FDI attacks. The objective is to design a control strategy that ensures flocking convergence within a strictly predefined time, independent of initial conditions, while maintaining robustness against adversarial disturbances.
1.4. Contributions
The main contributions of this paper are summarized as follows:
- (1)
- A predefined-time control scheme is constructed to ensure that the flocking behavior is achieved within an arbitrarily prescribed time interval, regardless of the initial conditions and control parameter selections. This property distinguishes the proposed approach from conventional finite-time and fixed-time flocking strategies [41,43,52], whose convergence time is typically influenced by system-dependent factors. The ability to explicitly specify the settling time makes the proposed method particularly suitable for time-critical coordination tasks.
- (2)
- A robust quasi-flocking control strategy is developed for networked agent systems subject to FDI attacks, where RBF neural networks are introduced to approximate and compensate for unknown nonlinear disturbances induced by the attacks. An adaptive weight update law is designed in conjunction with the predefined-time stability framework to enable real-time suppression of adversarial influences. In contrast to existing methods such as [53], which do not consider the impact of FDI attacks, the proposed scheme explicitly accounts for adversarial disturbances and thereby substantially enhances the robustness of the controller.
1.5. Organization
The structure of this paper is as follows. Section 2 presents the necessary background and mathematical preliminaries. In Section 3, the predefined-time quasi-flocking control problem is formulated. Section 4 details the main theoretical results on achieving quasi-flocking within a predefined time, along with rigorous analysis. Section 5 provides numerical examples to demonstrate the effectiveness of the proposed control strategy.
2. Preliminaries
2.1. Notations
We denote the set of real numbers by , and the space of real matrices by . The Euclidean norm is written as , and the absolute value of a scalar as . The transpose operation for vectors and matrices is represented by . A diagonal matrix with diagonal entries for is denoted by . The function denotes the standard signum operator.
2.2. Graph Theory
The communication topology among N agents is represented by a weighted directed graph , where is the set of nodes (agents), and denotes the set of directed edges indicating information flow. An edge implies that agent receives information from agent . The adjacency matrix characterizes the interaction weights, where if , and otherwise. The corresponding degree matrix is given by , where represents the total outgoing weight from node . The Laplacian matrix is then defined as , capturing the network’s structural and dynamical connectivity.
2.3. Predefined-Time Stability
Consider the following nonlinear system dynamics:
where denotes the system state, and is the control input associated with the ith agent. The nonlinear function is assumed to be continuous in time t and satisfies a Lipschitz condition with respect to the state variable . Additionally, the origin is an equilibrium point, i.e., for all t.
where is a time-scaling function related to the predefined horizon T and satisfies:
Definition 1
([54]). An equilibrium point of system (1) is said to be predefined-time stable if there exists a constant , independent of the initial state and system parameters, such that for any , the solution remains bounded and satisfies for all .
Lemma 1
([54]). System (1) is said to exhibit input-to-state stability (ISS) within a predefined time T if there exist functions and such that, for all , the following inequality holds:
- (1)
- , where ;
- (2)
- .
It is worth noting that various time-varying functions can satisfy the conditions for . For instance, consider , where is an integer. Consequently, is given by
Lemma 2
([55]). Let be a positive, radially unbounded, and differentiable function, with positive constants , , and , satisfying
Then, it holds that
where .
Lemma 3
([56]). Consider an undirected and connected graph . Its corresponding symmetric Laplacian matrix has N real eigenvalues satisfying
Notably, the second smallest eigenvalue quantifies the algebraic connectivity of the graph.
Lemma 4
([57]). For any two real scalars , the following inequality holds:
2.4. RBF Neural Network
Lemma 5
([58]). Radial basis function (RBF) neural networks are capable of approximating continuous nonlinear functions by tuning their weights. For any continuous function defined over a compact domain Ω, there exists an RBF network of the form such that
where ω denotes the ideal weight vector, is the approximation error, and comprises the basis functions of the network. In particular, is adopted, where x is the input, and c, σ represent the center and width of the kernel, respectively. The optimal weight ω minimizes the worst-case approximation error over Ω, and is given by
3. Problem Formulation
In this paper, each agent follows the dynamics described by
where denote the position and velocity vectors of the ith agent, respectively, and is the corresponding control input at time t. The index is defined as . In this paper, the FDI attacks on the i-th agent are described using and . denotes the unknown actuator attack coefficients, and denotes the unknown uncertainty of the injected agent, a continuous unknown nonlinear function. The overall scheme of the NASs under FDI attack is shown in Figure 1, which presents the architecture of the proposed predefined-time robust control scheme under FDI attacks. Each agent i computes the local error based on the communication topology and generates the control input through the predefined-time controller. However, may be tampered with by adversarial attacks before reaching the actuator. The FDI attack block models such actuator-side disturbances, which are unknown but bounded. Despite these disturbances, the proposed control scheme guarantees that all agent errors converge to zero within a predefined time. This diagram highlights the information flow and the location of potential attacks, illustrating the relevance of the proposed resilient control design.
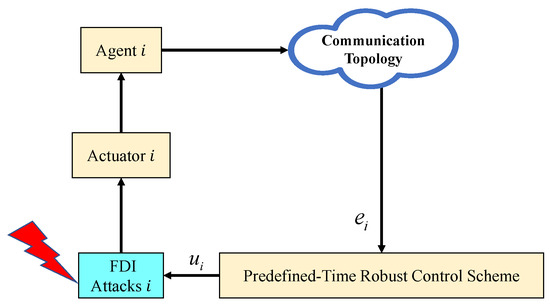
Figure 1.
The overall control scheme diagram of the NASs under FDI attacks.
In this study, agent dynamics are modeled using double integrator systems, which originate from second-order differential equations based on Newtonian mechanics. This modeling choice is motivated by both its physical interpretability and its wide applicability. Double integrator dynamics serve as effective approximations for numerous real-world systems, such as robotic platforms, mechanical manipulators, and aerial vehicles (e.g., quadrotors), when linearized around equilibrium points. Their use facilitates theoretical analysis and simplifies controller synthesis for second-order systems.
Assumption 1.
Assumption 2.
The unknown actuator degradation coefficients satisfy , where represents a known positive lower bound. When , the corresponding agent is unaffected by FDI attacks; whereas indicates that the actuator has failed severely, rendering the system inoperative.
Remark 1.
The assumption that the actuator attack coefficients have a lower bound in Assumption 2 is reasonable and necessary for current robust control methods against FDI attacks. A similar research approach can be found in the existing works [23,59]. Moreover, the lower bound can be obtained by continuously conducting experiments.
To facilitate the subsequent analysis, we introduce the formal definition of predefined-time quasi-flocking for the NAS.
Definition 2.
The NAS governed by (8) is said to achieve predefined-time flocking if the following conditions are met:
- (1)
- Velocity Alignment: The velocity of each agent converges to a common value within a predefined time T, i.e., for all ,where denotes the initial time.
- (2)
- Cohesion: There exists a constant such that the group’s spatial spread remains uniformly bounded:
- (3)
- Collision Avoidance: A constant exists such that the minimum inter-agent distance remains strictly positive:
Condition (9) ensures that all agents achieve velocity consensus within a predefined time, thereby moving in a coordinated direction. Condition (10) guarantees that the overall group remains cohesive. Finally, Condition (11) ensures inter-agent collision avoidance throughout the evolution of the system. Satisfying all three conditions constitutes the emergence of predefined-time flocking behavior.
Remark 2.
Flocking behaviors can be distinguished by the nature of the settling time T as introduced in Definition 2. When T depends on both the initial conditions and control parameters, the behavior is termed finite-time flocking. If T relies solely on controller parameters and is independent of the initial state, it is known as fixed-time flocking. In contrast, predefined-time flocking refers to the case where T is completely independent of both the initial state and controller parameters.
Remark 3.
This paper develops a robust predefined-time flocking control scheme that mitigates the impact of FDI attacks by employing RBF neural networks to approximate and compensate for the induced disturbances after their occurrence. It should be emphasized that the detection of such attacks, although crucial for the broader scope of cyber-physical system security, is beyond the scope of this paper.
However, attaining exact consensus in NASs presents practical challenges, such as FDI attacks and unknown perturbations. The presence of completely unknown system nonlinearities may compromise the effectiveness of the consensus protocol, potentially leading to instability. Therefore, ensuring that the consensus error remains within uniformly ultimate bounds is crucial. This implies that each agent’s consensus error should asymptotically decrease within a specified time, allowing for a minimal residual error. Therefore, the concept of predefined-time quasi-flocking is introduced next.
The primary objective of this paper is to design a control law that ensures quasi-flocking among agents within a predefined time T while maintaining a minimal residual error. Specifically, the proposed protocol guarantees that
Building upon flocking control principles in NASs, we define the velocity consensus error as
For conciseness, the velocity consensus error is rewritten as
where and .
In this section, RBF neural networks are utilized to estimate the unknown nonlinear term associated with the injected agent dynamics in (8). As stated in Lemma 5, the function can be approximated with arbitrary precision over a compact set , yielding the representation
where denotes the ideal weight vector and is the corresponding basis function vector.
4. Flocking Controller Design and Stability Analysis
This section introduces a robust control protocol designed to achieve predefined-time quasi-flocking despite the presence of adversarial disturbances, including FDI attacks. The proposed approach embeds radial basis function (RBF) neural networks within a predefined-time stability framework, facilitating both time-guaranteed coordination and online disturbance compensation. To verify the theoretical soundness and performance of the control strategy, a comprehensive stability analysis is carried out, which is structured into three parts.
4.1. Predefined-Time Flocking Controller Design
In this subsection, we construct the predefined-time flocking controller as follows:
with the weight updating law for given by
where denotes the vector of radial basis functions, and , , and are positive design parameters. The neural network weight estimation error is defined as , where is the estimated weight and denotes its ideal value.
The control protocol for achieving predefined-time flocking consists of three key components. The first term, , acts as a negative proportional gain. The second term, , serves as a time-varying negative feedback regulation function. The third term, , employs neural networks to estimate the system’s unknown nonlinearities. The combined effect of these three components enables uncertain NASs to achieve flocking within the predefined time. Specifically, the RBF neural network is employed as a nonlinear approximator to estimate the unknown disturbance caused by the FDI attacks. By utilizing the error signal through a back-propagation update mechanism, the network adaptively adjusts its parameters to learn the attack-induced discrepancy in real time. The estimated output of the RBF network is then used to construct a feedforward compensation term in the control input.
The following theorem provides a rigorous guarantee of predefined-time quasi-flocking under the developed control scheme.
Theorem 1.
Suppose that Assumption 1 holds. In addition, assume that the initial positions and velocities satisfy the condition
for some and predefined time . Then, the NAS described by (8) achieves predefined-time quasi-flocking under the control scheme proposed in this paper.
Proof of Theorem.
The proof is organized into three main steps. First, we show that the velocities of all agents achieve quasi-consensus within a predefined time, ensuring directional alignment of subgroups. Second, we demonstrate that the positions of agents remain uniformly bounded throughout the evolution of the system, thereby guaranteeing cohesion. Finally, we prove that inter-agent distances are strictly positive, which implies that no collisions occur during the flocking process. These three aspects will be analyzed in detail in the subsequent subsections. □
Remark 4.
The parameter serves as a proportional gain in the control law. While increasing this gain generally accelerates convergence, it may also induce large transient responses in the closed-loop system. Moreover, real-world platforms such as unmanned aerial vehicles (UAVs) are subject to actuation limits, for instance, the maximum rotational speed of propellers. Hence, careful tuning is required to balance control performance with hardware constraints. In fact, time-varying gain functions are often designed to diverge as to ensure convergence at a specified terminal time T. However, this divergence can lead to unbounded control inputs, which are impractical or unsafe for physical systems. To ensure implementability, an upper bound must be imposed on the gain function. The selection of this bound reflects a trade-off: higher values improve robustness against disturbances, whereas lower values help respect actuator limitations and keep control effort within feasible limits.
4.2. Stability Analysis: Velocity Alignment
In this subsection, we first demonstrate that the velocities of all agents in the NAS satisfy Condition (1) of Definition 2, up to a minimal residual error. This establishes predefined-time quasi-consensus in velocity and forms the foundation for subsequent analysis.
Consider the following Lyapunov candidate function:
where captures the kinetic consensus energy, and represents the neural network weight estimation error.
Under Assumption 1, and based on Lemma 3 together with classical matrix theory, it follows that the Laplacian matrix admits an orthogonal decomposition , where is an orthogonal matrix and is a diagonal matrix consisting of the eigenvalues of arranged in ascending order.
Next, the function can be expressed as
where the diagonal matrix be defined as , where is a positive scalar satisfying . Define , which can be verified to be positive definite. Consequently, the term is positive definite with respect to the consensus error .
Furthermore, the derivatives of and with respect to t can be computed along the trajectories of the system (8) over the interval :
Thus, it can be inferred that
Suppose the compact set encompasses the working states of NASs. By substituting the control protocol (14) and the weight updating law (15) into (19), we obtain the following:
Thus, we obtain
According to Lemma 4, we have
Furthermore, it can be obtained from (24) that
where .
According to Equation (18), we have
Then,
Additionally, applying Lemma 2, we obtain
where . Utilizing Lemma 1 and Equation (29), it follows that the errors and remain bounded for all t in the interval . Consequently, we conclude that This guarantees that predefined-time consensus on velocity is achieved with a small residual error . Thus, Theorem 1 is proven. Furthermore, the system remains continuously controlled due to the residual error . Hence, a time exists such that
Remark 5.
From the proof procedure, we conclude that the proposed controller guarantees convergence within a user-defined predefined time T, which is theoretically independent of the initial states and system parameters such as controller gains or the communication topology. This contrasts with existing finite-time or fixed-time flocking control schemes [41,43,52], where the convergence time typically depends on such factors. It should be noted, however, that although T can be arbitrarily prescribed in theory, the actual selection of controller parameters must still be carried out carefully to ensure that the convergence conditions are satisfied within the given time frame in practical implementations.
4.3. Stability Analysis: Cohesion
Next, we analyze the spatial behavior of the agents and show that their positions remain uniformly bounded throughout the evolution of the system. This guarantees that the agents do not disperse arbitrarily and thereby ensures group cohesion. The result corresponds to Condition (2) in Definition 2.
Define the following Lyapunov-like functions:
Based on Theorem 1, it follows that for all , and remains bounded for . In particular, there exists a constant such that .
Differentiating along the time trajectory yields
By integrating the differential inequality (31) over the interval , we obtain
Consequently, it follows that
Therefore, from (33), it follows that
4.4. Stability Analysis: Collision Avoidance
Furthermore, we prove that the minimum inter-agent distance remains strictly positive over the entire time horizon. This confirms that no collisions occur among agents during the flocking process, which is essential for the safe execution of coordinated motion in physical NASs.
In this part, we employ Lyapunov-based analysis to implicitly guarantee collision avoidance by examining velocity alignment and initial position conditions. The approach does not require the interaction graph to be complete. According to the Cauchy–Schwarz inequality, the time derivative of the squared distance between any two agents i and j is
Dividing both sides of (36) by (assuming ) gives
Integrating (37) over the interval yields
As established in Step 1, the relative velocity difference is bounded by
for some constant . Substituting (39) into (38), we obtain
To derive a lower bound, we employ the triangle inequality as follows:
Using (37) and integrating over again, we get
and a similar bound for . These can be collectively bounded using initial velocities and predefined-time stability properties.
This implies that no collisions occur between agents i and j throughout the evolution of the system. Thus, collision avoidance is guaranteed under Condition (42).
Based on the preceding analysis, Theorem 1 rigorously establishes that both conditions in Definition 2 are satisfied under the proposed control protocol. Consequently, the networked agent system described by (8) achieves predefined-time quasi-flocking. The theoretical guarantee is derived through the construction of a Lyapunov function and the application of Lemma 1, which together demonstrate that flocking behavior emerges within a user-specified time interval. This result provides a formal validation of the effectiveness of the proposed control design. Notably, the settling time established in Theorem 1 is a predefined constant that does not depend on the system’s initial state, controller gain selection, or the underlying communication topology. By implementing the control law (14) together with the adaptive weight update rule (15), all agents are guaranteed to achieve flocking within the specified time bound. This property represents a key improvement over prior works [23,41,60], which predominantly focus on finite-time or asymptotic convergence without explicit control over the convergence time.
Remark 6.
Inspired by Reynolds’ foundational work [15], flocking behavior is generally understood to emerge when the three core rules, alignment, cohesion, and separation, are satisfied. While considerable research has focused on enforcing separation to prevent collisions, most existing methods, such as artificial potential fields and barrier functions, increase system nonlinearity and may introduce singularities, which can degrade convergence performance. To circumvent these drawbacks, the present work simplifies the control objective by explicitly focusing on alignment and cohesion, and proposes a predefined-time control protocol designed to achieve these two key behaviors efficiently and reliably. Most existing studies [53,61,62] assume that system dynamics are known or can be predetermined. However, handling uncertain nonlinear NASs remains a critical challenge with broad applicability. This paper focuses on predefined-time flocking control for NASs with unknown nonlinear dynamics. Unlike previous works [53,61,62], our approach integrates an adaptive neural network into the control scheme, significantly enhancing closed-loop system robustness.
5. Numerical Simulation
This section provides numerical simulations to validate the effectiveness and robustness of the proposed predefined-time quasi-flocking control strategy. Specifically, we consider the second-order NAS model described by (8), composed of 9 interacting agents. The nonlinear disturbance acting on each agent, which may stem from actuator faults or adversarial interference, is modeled as
where M denotes the coupling gain that determines the strength of velocity coupling among agents, and represents the intrinsic uncertainty associated with the ith agent. Each is randomly drawn from a uniform distribution over the interval , reflecting heterogeneous and uncertain local dynamics. To evaluate the controller’s resilience against FDI attacks, we simulate degraded actuator effectiveness by introducing unknown attack coefficients . The values are set as follows:
These coefficients simulate varying levels of attack severity across agents, with smaller values representing more significant control degradation. Such a setting enables us to test the control protocol’s ability to ensure predefined-time flocking despite heterogeneous, nonlinear disturbances and actuator anomalies.
The following simulation results are obtained by implementing the proposed control protocol (14), coupled with the adaptive weight updating law (15). The communication topology governing agent interactions is illustrated in Figure 2, where each directed edge represents a unidirectional communication link with unit weight. Accordingly, the weighted adjacency matrix associated with the network is given by
The initial positions and velocities are randomly initialized within the intervals and , respectively. The controller parameters are selected as and , with the flocking convergence time predefined as . Each RBF neural network, represented by , is constructed with 100 nodes. The centers c of the basis functions are uniformly distributed over , and the width parameter is set as .
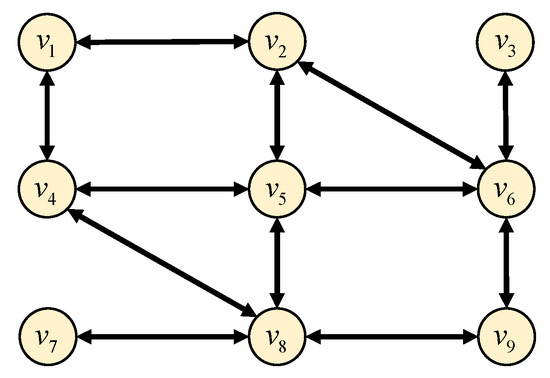

Figure 2.
The communication topology among the NAS with 9 agents.
In simulation experiments, we compare three flocking controllers: the neural network-based robust predefined-time controller (14), the standard neural network-based robust controller, and the standard predefined-time controller, as detailed below.
The state trajectories of and with controller (46) is shown in Figure 3. Moreover, as shown in Figure 4, FDI attacks can significantly affect the velocity consensus error, preventing effective flocking behavior. Unlike the controller (14), the controller (45) excludes the time-scale function term. A comparison of Figure 3 with Figure 5 indicates that the predefined-time flocking controller accelerates system convergence, allowing the settling time to be predefined. Furthermore, compared to the controller (14), the neural network estimation term and actuator attack compensation term are omitted in the controller (46). Moreover, as illustrated in Figure 5, using the robust neural network-based control scheme proposed in this paper can enable the agents to achieve velocity consensus and thus promote effective flocking behavior. Additionally, the simulation results indicate that employing a standard flocking control scheme significantly reduces convergence speed and increases the settling time of the closed-loop error system when the initial values of the networked agents vary substantially. Consequently, the effectiveness and advantages of the neural network-based robust predefined-time flocking control scheme proposed in this paper are validated through the aforementioned simulations and analyses.
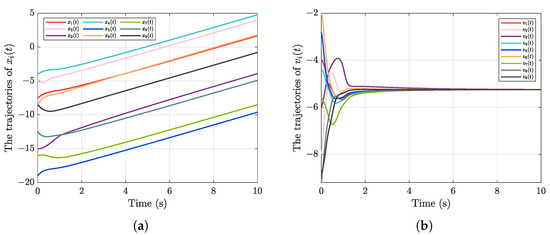
Figure 3.
The state trajectories of (a) ; (b) with controller (45).
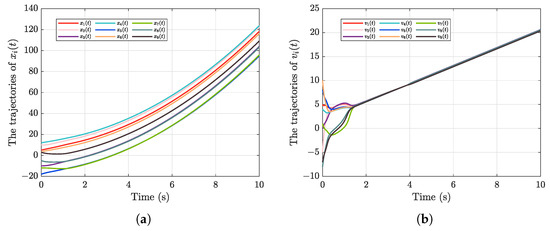
Figure 4.
The state trajectories of (a) ; (b) with controller (46).
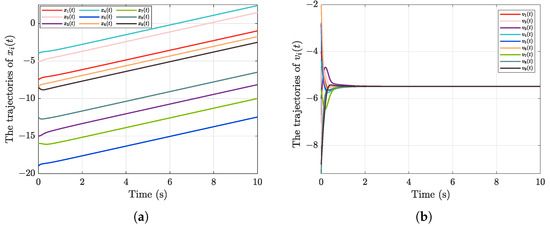
Figure 5.
The state trajectories of (a) ; (b) with controller (14).
To validate the neural approximation mechanism used to compensate for FDI-induced uncertainties, we provide additional simulation results showing the performance of the RBF network estimator. The corresponding approximation error is also shown in Figure 6. As depicted in Figure 6, the RBF estimator accurately tracks the unknown nonlinear attacks within a predefined time.
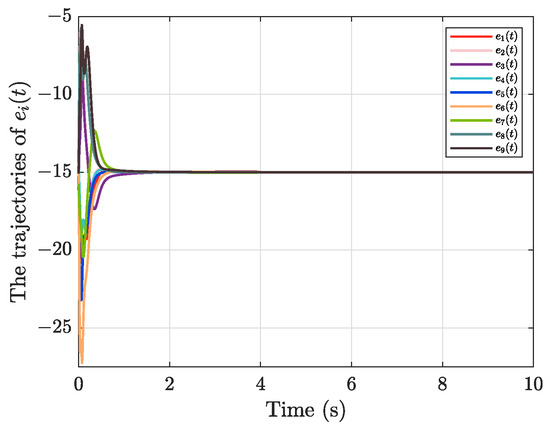
Figure 6.
The trajectories of with unknown FDI attacks .
To further assess the robustness of the proposed control framework under adversarial conditions, a comparative study is conducted against the classical Lyapunov-based control scheme introduced in [53], which does not utilize neural network-based disturbance estimation. This benchmark method represents a widely adopted approach for flocking control, yet it lacks adaptive mechanisms to handle unknown nonlinearities or attack-induced uncertainties. As illustrated in Figure 7, the reference controller fails to effectively mitigate the influence of FDI attacks. Specifically, the agents exhibit large steady-state errors and a noticeable delay in reaching velocity consensus, indicating degraded performance in the presence of actuator compromise. In contrast, the proposed control strategy, which integrates RBF neural networks for real-time approximation of unknown attack effects, successfully guarantees accurate flocking behavior within the predefined time horizon. The comparison highlights the superiority of our method in terms of both convergence accuracy and resilience. Even under severe and heterogeneous attack conditions, the predefined-time control objective is reliably achieved, demonstrating the controller’s robustness and practical applicability.
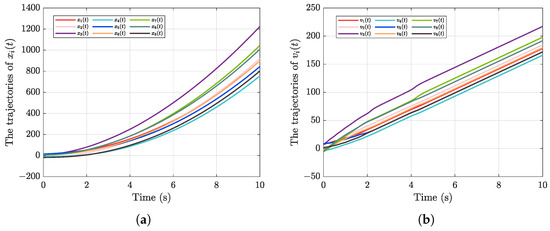
Figure 7.
The state trajectories of (a) ; (b) with controller in [53].
6. Conclusions
This paper has addressed the predefined-time quasi-flocking control problem for NASs operating under FDI attacks. A novel control strategy is developed to achieve coordinated flocking within a user-specified time interval, regardless of initial conditions and control parameters. To improve resilience against adversarial disturbances, RBF neural networks are employed to estimate and counteract the unknown nonlinear effects caused by FDI attacks in real time. Theoretical guarantees are established via a Lyapunov-based analysis, which confirms predefined-time convergence. Numerical simulations are provided to demonstrate the robustness and effectiveness of the proposed approach.
It should be noted that the current study is restricted to fixed, undirected, and delay-free communication topologies. In contrast, practical multi-agent networks often encounter dynamic communication structures, directional interactions, time delays, and channel uncertainties. These aspects have not been addressed in the current framework. As part of future research, we plan to extend the proposed method to accommodate directed and switching topologies, and to incorporate realistic network constraints such as communication delays, packet loss, and bandwidth limitations. These extensions are expected to improve the applicability of the control strategy in more complex and uncertain environments.
Author Contributions
Writing—original draft, B.L.; Writing—review & editing, B.L., M.L., Z.L. and M.S.; Visualization, Y.L.; Supervision, K.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Natural Science Foundation of Sichuan Province under Grant 2024NSFSC0021, the Sichuan Science and Technology Programs under Grant MZGC20240139, and the Fundamental Research Funds for the Central Universities under Grants ZYGX2024K028 and ZYGX2025K028.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, Z.; Li, B.; Shi, L.; Cheng, Y.; Shao, J. Broadcasting-based Cucker–Smale flocking control for multi-agent systems. Neurocomputing 2024, 573, 127266. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Wu, Y.; Liu, Z.; Chen, K.; Chen, C.P. Fixed-time formation control for uncertain nonlinear multi-agent systems with time-varying actuator failures. IEEE Trans. Fuzzy Syst. 2024, 32, 1965–1977. [Google Scholar] [CrossRef]
- Wang, Y.; Han, L.; Li, X.; Ren, Z. Time-varying formation tracking for multi-agent systems with maneuvering leader under DDoS attacks and actuator faults. ISA Trans. 2024, 144, 38–50. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Peng, L.; Xie, L.; Yu, H. Dynamic event-triggered sliding-mode bipartite consensus for multi-agent systems with unknown dynamics. IEEE Trans. Autom. Sci. Eng. 2024, 22, 7170–7180. [Google Scholar] [CrossRef]
- Yang, S.; Liang, H.; Pan, Y.; Li, T. Security control for air-sea heterogeneous multiagent systems with cooperative-antagonistic interactions: An intermittent privacy preservation mechanism. Sci. China Technol. Sci. 2025, 68, 1420402. [Google Scholar] [CrossRef]
- Guo, S.; Pan, Y.; Li, H.; Cao, L. Dynamic event-driven ADP for N-player nonzero-sum games of constrained nonlinear systems. IEEE Trans. Autom. Sci. Eng. 2025, 22, 7657–7669. [Google Scholar] [CrossRef]
- Wang, X.; Pang, N.; Xu, Y.; Huang, T.; Kurths, J. On state-constrained containment control for nonlinear multiagent systems using event-triggered input. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2530–2538. [Google Scholar] [CrossRef]
- Wang, Z.; Mu, C.; Hu, S.; Chu, C.; Li, X. Modelling the Dynamics of Regret Minimization in Large Agent Populations: A Master Equation Approach. In Proceedings of the IJCAI, Vienna, Austria, 23–29 July 2022; pp. 534–540. [Google Scholar]
- Li, C.; Yang, Y.; Huang, T.Y.; Chen, X.B. An improved flocking control algorithm to solve the effect of individual communication barriers on flocking cohesion in multi-agent systems. Eng. Appl. Artif. Intell. 2024, 137, 109110. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X. Hybrid event-triggered impulsive flocking control for multi-agent systems via pinning mechanism. Appl. Math. Model. 2023, 114, 23–43. [Google Scholar] [CrossRef]
- Pei, H.; Hu, X.; Luo, Z. Multi-agent flocking control with complex obstacles and adaptive distributed convex optimization. J. Frankl. Inst. 2024, 361, 107181. [Google Scholar] [CrossRef]
- Dey, S.; Xu, H. Distributed Adaptive Flocking Control for Large-Scale Multiagent Systems. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 3126–3135. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, J.; Wang, G.; Allgöwer, F.; Chen, J. Data-driven control of distributed event-triggered network systems. IEEE/CAA J. Autom. Sin. 2023, 10, 351–364. [Google Scholar] [CrossRef]
- Hung, S.M.; Givigi, S.N. A Q-learning approach to flocking with UAVs in a stochastic environment. IEEE Trans. Cybern. 2016, 47, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, Anaheim, CA, USA, 27–31 July 1987; pp. 25–34. [Google Scholar]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Chen, J.; Yang, Y.; Qin, S. A distributed optimization algorithm for fixed-time flocking of second-order multiagent systems. IEEE Trans. Netw. Sci. Eng. 2024, 11, 152–162. [Google Scholar] [CrossRef]
- Semnani, S.H.; Basir, O.A. Semi-flocking algorithm for motion control of mobile sensors in large-scale surveillance systems. IEEE Trans. Cybern. 2014, 45, 129–137. [Google Scholar] [CrossRef]
- Wang, G.G.; Wei, C.L.; Wang, Y.; Pedrycz, W. Improving distributed anti-flocking algorithm for dynamic coverage of mobile wireless networks with obstacle avoidance. Knowl.-Based Syst. 2021, 225, 107133. [Google Scholar] [CrossRef]
- Beaver, L.E.; Malikopoulos, A.A. An overview on optimal flocking. Annu. Rev. Control 2021, 51, 88–99. [Google Scholar] [CrossRef]
- Wang, H.; Xu, K.; Qiu, J. Event-triggered adaptive fuzzy fixed-time tracking control for a class of nonstrict-feedback nonlinear systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3058–3068. [Google Scholar] [CrossRef]
- Chen, H.; Zong, G.; Shen, M.; Gao, F. Finite-Time Resilient Control of Networked Markov Switched Nonlinear Systems: A Relaxed Design. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 2569–2579. [Google Scholar] [CrossRef]
- Lu, J.; Qin, K.; Li, M.; Lin, B.; Shi, M. Robust finite/fixed-time bipartite flocking control for networked agents under actuator attacks and perturbations. Chaos Solitons Fractals 2024, 180, 114556. [Google Scholar] [CrossRef]
- Shi, L.; Cheng, Y.; Shao, J.; Sheng, H.; Liu, Q. Cucker-Smale flocking over cooperation-competition networks. Automatica 2022, 135, 109988. [Google Scholar] [CrossRef]
- Shi, X.; Shi, L.; Zhou, Q.; Chen, K.; Cheng, Y. Bipartite flocking for Cucker-Smale model on cooperation-competition networks subject to denial-of-service attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 3379–3390. [Google Scholar] [CrossRef]
- Chen, K.; Ma, Z.; Bai, L.; Sheng, H.; Cheng, Y. Emergence of bipartite flocking behavior for Cucker-Smale model on cooperation-competition networks with time-varying delays. Neurocomputing 2022, 507, 325–331. [Google Scholar] [CrossRef]
- Fan, M.C.; Zhang, H.T.; Wang, M. Bipartite flocking for multi-agent systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3313–3322. [Google Scholar] [CrossRef]
- Ahn, H. Finite-time flocking of uncountable agents. Chaos, Solitons Fractals 2024, 185, 115107. [Google Scholar] [CrossRef]
- Guo, W.; Shi, L.; Sun, W.; Jahanshahi, H. Predefined-time average consensus control for heterogeneous nonlinear multi-agent systems. IEEE Trans. Circuits Syst. II: Express Briefs 2023, 70, 2989–2993. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Liang, H.; Ahn, C.K. Neural-network-based predefined-time adaptive consensus in nonlinear multi-agent systems with switching topologies. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 9995–10005. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Q.; Yu, H.; Hao, F. Predefined-time practical consensus for multi-agent systems via event-triggered control. J. Frankl. Inst. 2023, 360, 2116–2132. [Google Scholar] [CrossRef]
- Yang, T.; Dong, J. Practically predefined-time leader-following funnel control for nonlinear multi-agent systems with fuzzy dead-zone. IEEE Trans. Autom. Sci. Eng. 2024, 21, 3886–3895. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, Z.; Gui, W. Multiobjective Distributed Optimization via a Predefined-Time Multiagent Approach. IEEE Trans. Autom. Control 2023, 68, 6998–7005. [Google Scholar] [CrossRef]
- Pan, Y.; Chen, Y.; Liang, H. Event-triggered predefined-time control for full-state constrained nonlinear systems: A novel command filtering error compensation method. Sci. China Technol. Sci. 2024, 67, 2867–2880. [Google Scholar] [CrossRef]
- Li, K.; Hu, Q.; Liu, Q.; Zeng, Z.; Cheng, F. A predefined-time consensus algorithm of multi-agent system for distributed constrained optimization. IEEE Trans. Netw. Sci. Eng. 2024, 11, 957–968. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Tang, Y.; Liu, C. Predefined-time consensus tracking of second-order multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2550–2560. [Google Scholar] [CrossRef]
- Jiang, J.; Chi, J.; Wu, X.; Wang, H.; Jin, X. Adaptive predefined-time consensus control for disturbed multi-agent systems. J. Frankl. Inst. 2024, 361, 110–124. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, Y.; Fu, J. Optimal Formation Control of Second-Order Heterogeneous Multi-Agent Systems Using Adaptive Predefined-Time Strategy. IEEE Trans. Fuzzy Syst. 2024, 32, 2390–2402. [Google Scholar] [CrossRef]
- Ren, D.; Liu, Y.J.; Lan, J. Event-Based Predefined-Time Fuzzy Formation Control for Nonlinear Multi-Agent Systems with Unknown Disturbances. IEEE Trans. Fuzzy Syst. 2024, 32, 3497–3507. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, W.; Lam, H.K.; Cao, L. An improved predefined-time adaptive neural control approach for nonlinear multiagent systems. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6311–6320. [Google Scholar] [CrossRef]
- Xiao, Q.; Liu, H.; Wang, X.; Huang, Y. A note on the fixed-time bipartite flocking for nonlinear multi-agent systems. Appl. Math. Lett. 2020, 99, 105973. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S. An improved fixed-time bipartite flocking protocol for nonlinear multi-agent systems. Int. J. Control 2022, 95, 900–905. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Huang, Y.; Liu, Y. A new class of fixed-time bipartite flocking protocols for multi-agent systems. Appl. Math. Model. 2020, 84, 501–521. [Google Scholar] [CrossRef]
- Yang, Y.; Qian, Y.; Yue, W. A secure dynamic event-triggered mechanism for resilient control of multi-agent systems under sensor and actuator attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 1360–1371. [Google Scholar] [CrossRef]
- Chen, H.; Zong, G.; Liu, X.; Zhao, X.; Niu, B.; Gao, F. A sub-domain-awareness adaptive probabilistic event-triggered policy for attack-compensated output control of Markov jump CPSs with dynamically matching modes. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4419–4431. [Google Scholar] [CrossRef]
- Xia, W.; Xiao, Q.; Luo, Z. Fixed-time consensus and finite-time flocking of second-order nonlinear multi-agent systems under false data injection attacks. Int. J. Control 2024, 1–10. [Google Scholar] [CrossRef]
- Zhang, H.; Gu, M.; Jiang, X.; Thompson, J.; Cai, H.; Paesani, S.; Santagati, R.; Laing, A.; Zhang, Y.; Yung, M.H.; et al. An optical neural chip for implementing complex-valued neural network. Nat. Commun. 2021, 12, 457. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Deng, Q.; Xu, C.; Deng, Z.; Zhou, C. Review on chaotic dynamics of memristive neuron and neural network. Nonlinear Dyn. 2021, 106, 959–973. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Tassi, C.R.N.; Ali, M.; Lee, J.; Humt, M.; Feng, J.; Kruspe, A.; Triebel, R.; Jung, P.; Roscher, R.; et al. A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 2023, 56, 1513–1589. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Q.; Liu, Y. Synchronisation of quaternion-valued neural networks with neutral delay and discrete delay via aperiodic intermittent control. Int. J. Syst. Sci. 2025, 56, 1395–1412. [Google Scholar] [CrossRef]
- Zhang, Q.; Hao, Y.; Yang, Z.; Chen, Z. Adaptive flocking of heterogeneous multi-agents systems with nonlinear dynamics. Neurocomputing 2016, 216, 72–77. [Google Scholar] [CrossRef]
- Li, P.; Xu, S.; Chen, W.; Wei, Y.; Zhang, Z. Adaptive finite-time flocking for uncertain nonlinear multi-agent systems with connectivity preservation. Neurocomputing 2018, 275, 1903–1910. [Google Scholar] [CrossRef]
- Cheng, X.; Yu, J.; Chen, X.; Yu, J.; Cheng, B. Preassigned-Time Bipartite Flocking Consensus Problem in Multi-Agent Systems. Symmetry 2023, 15, 1105. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y.; Holloway, J.; Krstic, M. Time-varying feedback for regulation of normal-form nonlinear systems in prescribed finite time. Automatica 2017, 83, 243–251. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, C.; Shang, Y. Prescribed-time adaptive neural feedback control for a class of nonlinear systems. Neurocomputing 2022, 511, 155–162. [Google Scholar] [CrossRef]
- Wu, C.W. Synchronization in Complex Networks of Nonlinear Dynamical Systems; World Scientific: Singapore, 2007. [Google Scholar]
- Qian, C.; Lin, W. A continuous feedback approach to global strong stabilization of nonlinear systems. IEEE Trans. Autom. Control 2001, 46, 1061–1079. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, S.; Ahn, C.K.; Xie, Y. Adaptive neural consensus for fractional-order multi-agent systems with faults and delays. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7873–7886. [Google Scholar] [CrossRef]
- Meng, M.; Xiao, G.; Li, B. Adaptive consensus for heterogeneous multi-agent systems under sensor and actuator attacks. Automatica 2020, 122, 109242. [Google Scholar] [CrossRef]
- Ma, L.; Zhu, F.; Zhang, J.; Zhao, X. Leader–follower asymptotic consensus control of multiagent systems: An observer-based disturbance reconstruction approach. IEEE Trans. Cybern. 2021, 53, 1311–1323. [Google Scholar] [CrossRef]
- Wei, H.; Chen, X.B. Flocking for multiple subgroups of multi-agents with different social distancing. IEEE Access 2020, 8, 164705–164716. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Li, X.; Liu, Y. Finite-time flocking and collision avoidance for second-order multi-agent systems. Int. J. Syst. Sci. 2020, 51, 102–115. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).