Task-Based Quantizer for CSI Feedback in Multi-User MISO VLC/RF Systems
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Related Works
1.3. Main Contribution
- We propose the TQ-CE scheme, which focuses on optimizing the end-task performance rather than minimizing the raw quantization error. Unlike traditional quantizers, TQ-CE is designed to preserve the features critical for accurate CSI reconstruction rather than the original channel matrix itself.
- To reduce the uplink feedback overhead, we designed a compact vector quantization (VQ)-based codebook. In addition, a closed-form MMSE-based post-processing matrix was derived to refine the quantized representation, thereby enhancing the channel estimation accuracy.
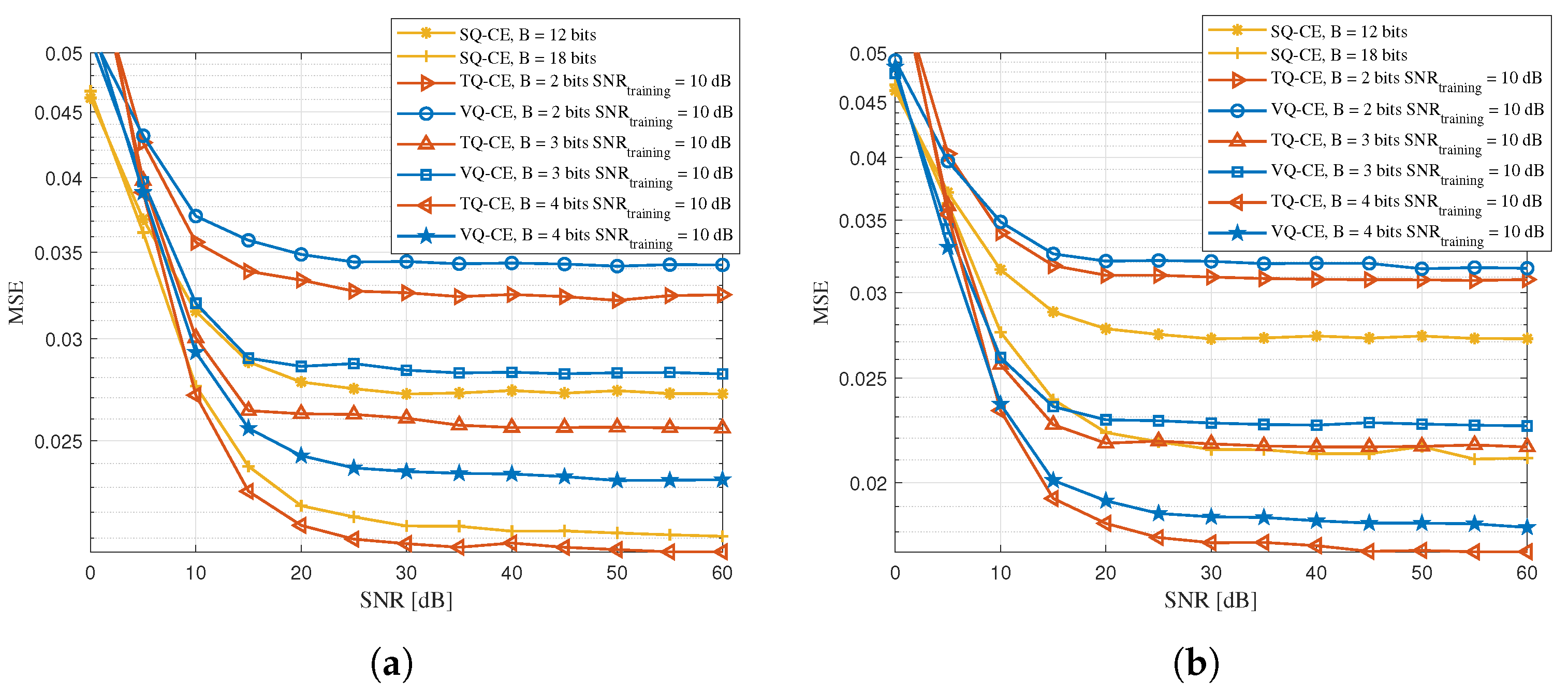
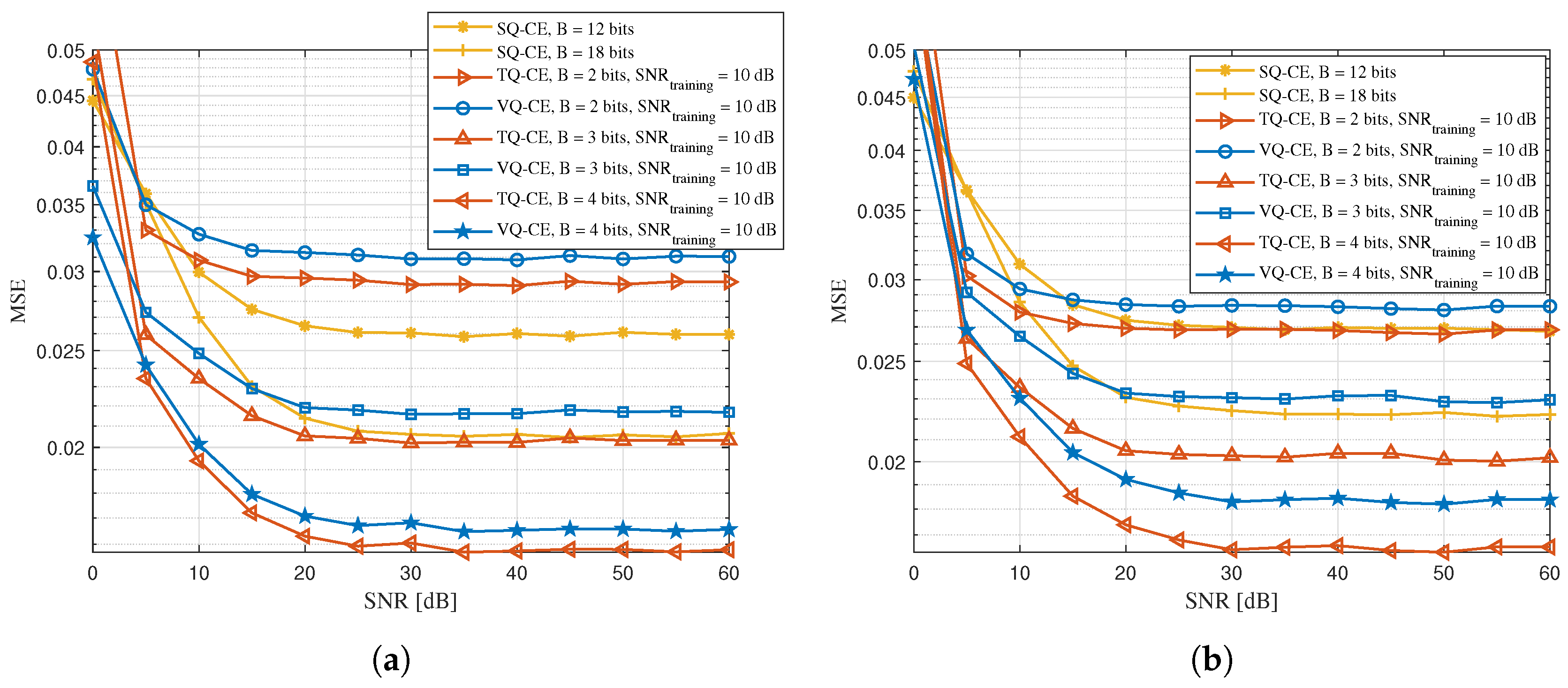
- The simulation results show that the proposed TQ-CE achieved data rate gains of and over the conventional SQ-CE [27] and VQ-CE [25], respectively. Moreover, in terms of the feedback overhead, compared with the 18-bit SQ-CE, the 4-bit TQ-CE achieved a 22.2% reduction in uplink bits. Thus, our proposed TQ-CE can achieve a high data rate with few bits, which makes them ideal for deployment in hybrid RF/VLC-based IoT environments where the uplink bandwidth is scarce and bandwidth-efficient processing is essential.
2. System Model and Problem Formulation
2.1. DL System Model
2.2. UL System Model
2.3. Problem Formulation
3. Task-Based Quantizer for CSI Estimation (TQ-CE)
3.1. VQ-Based Codebook Design
| Algorithm 1 Vector quantization algorithm |
|
3.2. Post-Processing Matrix Optimization
4. Simulation Results
Computational Complexity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSI | Channel state information |
| MISO | Multiple-input single-output |
| VLC | Visible light communication |
| CGI | Channel gain information |
| BS | Base station |
| RF | Radio frequency |
| TQ-CE | Task-based quantization for channel estimation |
| SQ-CE | Scalar quantization-based channel estimation |
| VQ-CE | Vector quantization-based channel estimation |
References
- Abidin, Z.; Mahendra, A.G.R.; Mahendra, D.F.; Imami, M.R.N.; Mehanny, W.M.H. Performance Analysis of LED Driver for Transmitter of Visible Light Communication Using Pulse Width Modulation. In Proceedings of the 2020 10th Electrical Power, Electronics, Communications, Controls and Informatics Seminar (EECCIS), Malang, Indonesia, 26–28 August 2020; pp. 178–182. [Google Scholar]
- Wang, W.; Zhu, Y.; Zhang, Y.; Zhang, J. An Optimal Power Allocation for Multi-LED Phase-Shifted-Based MISO VLC Systems. IEEE Photon. Technol. Lett. 2015, 27, 2391–2394. [Google Scholar] [CrossRef]
- Massive MIMO Systems for 5G and beyond Networks—Overview, Recent Trends, Challenges, and Future Research Direction. Sensors 2020, 20, 2753. [CrossRef] [PubMed]
- Zhang, M.; Gao, J.; Zhong, C. A Deep Learning-Based Framework for Low Complexity Multiuser MIMO Precoding Design. IEEE Trans. Wirel. Commun. 2022, 21, 11193–11206. [Google Scholar] [CrossRef]
- Li, Q.; Wen, M.; Renzo, M.D. Single-RF MIMO: From Spatial Modulation to Metasurface-Based Modulation. IEEE Wirel. Commun. 2021, 28, 88–95. [Google Scholar] [CrossRef]
- Ghasemzadeh, P.; Hempel, M.; Banerjee, S.; Sharif, H. A Spatial-Diversity MIMO Dataset for RF Signal Processing Research. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Lang, O.; Hofbauer, C.; Feger, R.; Huemer, M. Range-Division Multiplexing for MIMO OFDM Joint Radar and Communications. IEEE Trans. Veh. Technol. 2023, 72, 52–65. [Google Scholar] [CrossRef]
- Liang, P.; Fan, J.; Shen, W.; Qin, Z.; Li, G.Y. Deep Learning and Compressive Sensing-Based CSI Feedback in FDD Massive MIMO Systems. IEEE Trans. Veh. Technol. 2020, 69, 9217–9222. [Google Scholar] [CrossRef]
- Wang, F.; Yang, F.; Pan, C.; Song, J.; Han, Z. Joint illumination and communication optimization in indoor VLC for IoT applications. IEEE Internet Things J. 2022, 9, 20788–20800. [Google Scholar] [CrossRef]
- Narmanlioglu, O.; Uysal, M. Limited feedback channel estimation for multi-user massive mimo visible light communications. In Proceedings of the IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar]
- Zargari, S.; Kolivand, M.; Nezamalhosseini, S.A.; Abolhassani, B.; Chen, L.R.; Kahaei, M.H. Resource Allocation of Hybrid VLC/RF Systems with Light Energy Harvesting. IEEE Trans. Green Commun. Netw. 2022, 6, 600–612. [Google Scholar] [CrossRef]
- Wang, F.; Yang, F.; Pan, C.; Song, J.; Han, Z. Hybrid VLC-RF Systems with Multi-Users for Achievable Rate and Energy Efficiency Maximization. IEEE Trans. Wirel. Commun. 2023, 22, 6157–6170. [Google Scholar] [CrossRef]
- Maimaiti, S.; Huang, S.; Zhang, K.; Liu, X.; Xu, Z.; Mi, J. Collaborative Online Learning-Based Distributed Handover Scheme in Hybrid VLC/RF 5G Systems. Electronics 2025, 14, 1142. [Google Scholar] [CrossRef]
- Tolba, B.; Elsabrouty, M.; Abdu-Aguye, M.G.; Gacanin, H.; Kasem, H.M. Massive MIMO CSI Feedback Based on Generative Adversarial Network. IEEE Commun. Lett. 2020, 24, 2805–2808. [Google Scholar] [CrossRef]
- Liang, X.; Chang, H.; Li, H.; Gu, X.; Zhang, L. Changeable Rate and Novel Quantization for CSI Feedback Based on Deep Learning. IEEE Trans. Wirel. Commun. 2022, 21, 10100–10144. [Google Scholar] [CrossRef]
- Zhao, Q.; Fan, J.; Lin, B.; Chen, C. A Quantized CSI Acquisition Strategy Based on Position Information Feedback for Indoor VLC-Based IoT Systems. IEEE Internet Things J. 2025; Early Access. [Google Scholar] [CrossRef]
- Shin, J.; Kang, Y.; Jeon, Y.S. Vector Quantization for Deep-Learning-Based CSI Feedback in Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2024, 13, 2382–2386. [Google Scholar] [CrossRef]
- Baskin, C.; Liss, N.; Schwartz, E.; Zheltonozhskii, E.; Giryes, R.; Bronstein, A.; Mendelson, A. Uniq: Uniform noise injection for non-uniform quantization of neural networks. ACM Trans. Comput. Syst. 2021, 37, 1–15. [Google Scholar] [CrossRef]
- Naderipour, M.; Taherpour, A.; Taherpour, A.; Gazor, S. Design of Optimal Non-Uniform Quantizer in Imperfect Noisy Reporting Channels for Collaborative Spectrum Sensing. IEEE Trans. Veh. Technol. 2020, 69, 12870–12882. [Google Scholar] [CrossRef]
- Lin, J.; Li, L.; Bi, M.; Li, J.; Hu, M.; Hu, W. A study on performance improvement of IMDD-UFMC with modified k-means non-uniform quantization. Opt. Commun. 2020, 476, 126324. [Google Scholar] [CrossRef]
- Mielczarek, B.; Krzymien, W.A. Vector Quantization of Channel Information in Linear Multi-User MIMO Systems. In Proceedings of the 2006 IEEE Ninth International Symposium on Spread Spectrum Techniques and Applications, Manaus, Brazil, 28–31 August 2006; pp. 302–306. [Google Scholar]
- Roh, J.; Rao, B. Vector quantization techniques for multiple-antenna channel information feedback. In Proceedings of the 2004 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 11–14 December 2004; pp. 402–406. [Google Scholar]
- Huang, C.M.; Harris, R. A comparison of several vector quantization codebook generation approaches. IEEE Trans. Image Process. 1993, 2, 108–112. [Google Scholar] [CrossRef]
- Gao, W.; Xie, S.; Wang, H.; Zhang, Y.; Ling, Y. Adaptive Modem Based on LSTM-AutoEncoder with Vector Quantization. Electronics 2024, 13, 3124. [Google Scholar] [CrossRef]
- Muñoz, O.; Pascual-Iserte, A.; San Arranz, G. Robust precoding for multi-user visible light communications with quantized channel information. Sensors 2022, 22, 9238. [Google Scholar] [CrossRef]
- Widrow, B.; Kollar, I.; Liu, M.C. Statistical theory of quantization. IEEE Trans. Instrum. Meas. 1996, 45, 353–361. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, B.; Zou, L. Recursive Fault Estimation with Energy Harvesting Sensors and Uniform Quantization Effects. IEEE/CAA J. Autom. Sin. 2022, 9, 926–929. [Google Scholar] [CrossRef]
- Bernardo, N.I.; Zhu, J.; Eldar, Y.C.; Evans, J. Design and Analysis of Hardware-limited Non-uniform Task-based Quantizers. IEEE Trans. Signal Process. 2023, 71, 1551–1562. [Google Scholar] [CrossRef]
- Sui, Y.; Wu, L.; Gao, H. Channel Prediction Technology Based on Adaptive Reinforced Reservoir Learning Network for Orthogonal Frequency Division Multiplexing Wireless Communication Systems. Electronics 2025, 14, 575. [Google Scholar] [CrossRef]
- Lee, J.H.; Choi, W. Unified Codebook Design for Vector Channel Quantization in MIMO Broadcast Channels. IEEE Trans. Signal Process. 2015, 63, 2509–2519. [Google Scholar] [CrossRef]
- Kang, J.; Choi, W. Novel Codebook Design for Channel State Information Quantization in MIMO Rician Fading Channels with Limited Feedback. IEEE Trans. Signal Process. 2021, 69, 2858–2872. [Google Scholar] [CrossRef]
- Guo, J.; Wen, C.; Chen, M.; Jin, S. Environment Knowledge-Aided Massive MIMO Feedback Codebook Enhancement Using Artificial Intelligence. IEEE Trans. Commun. 2022, 70, 4527–4542. [Google Scholar] [CrossRef]
- Palitharathna, K.W.S.; Suraweera, H.A.; Godaliyadda, R.I.; Herath, V.R.; Thompson, J.S. Neural network-based channel estimation and detection in spatial modulation VLC systems. In Proceedings of the IEEE International Conference on Communications (ICC), Seoul, Republic of Korea, 16–20 May 2022; pp. 1–6. [Google Scholar]
- Şaylı, O.; Doğan, H.; Panayırcı, E. Spline interpolation based channel estimation for ACO-OFDM over visible light channels. In Proceedings of the the 24th Signal Processing and Communications Applications Conference (SIU), Zonguldak, Turkey, 16–19 May 2016; pp. 333–336. [Google Scholar]
- Yaseen, M.; Canbilen, A.E.; Ikki, S. Channel estimation in visible light communication systems: The effect of input signal-dependent noise. IEEE Trans. Veh. Technol. 2023, 72, 14330–14340. [Google Scholar] [CrossRef]
- Yapıcı, Y.; Güvenç, I. NOMA for VLC Downlink Transmission with Random Receiver Orientation. IEEE Trans. Commun. 2019, 67, 5558–5573. [Google Scholar] [CrossRef]
- Mossaad, M.S.A.; Hranilovic, S.; Lampe, L. Visible Light Communications Using OFDM and Multiple LEDs. IEEE Trans. Commun. 2015, 63, 4304–4313. [Google Scholar] [CrossRef]
- Al Hammadi, A.; Sofotasios, P.C.; Muhaidat, S.; Al-Qutayri, M.; Elgala, H. Non-Orthogonal Multiple Access for Hybrid VLC-RF Networks with Imperfect Channel State Information. IEEE Trans. Veh. Technol. 2021, 70, 398–411. [Google Scholar] [CrossRef]
- Hussein, Y.S.; Alias, M.Y.; Abdulkafi, A.A. On performance analysis of LS and MMSE for channel estimation in VLC systems. In Proceedings of the 2016 IEEE 12th International Colloquium on Signal Processing & Its Applications (CSPA), Melaka, Malaysia, 4–6 March 2016; pp. 204–209. [Google Scholar]
- Su, W.; Zhuang, H.; Qiu, X. Moving targets detection and tracking based on improved codebook algorithm and Kalman filtering. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 11494–11498. [Google Scholar]
- Codling, E.A.; Plank, M.J.; Benhamou, S. Random walk models in biology. J. R. Soc. Interface 2008, 5, 813–834. [Google Scholar] [CrossRef] [PubMed]
- Shlezinger, N.; Eldar, Y.C. Task-based quantization with application to MIMO receivers. arXiv 2020, arXiv:2002.04290. [Google Scholar] [CrossRef]
- Radfar, M.; Dansereau, R.; Sayadiyan, A. A novel low complexity VQ-based single channel speech separation technique. In Proceedings of the 2006 IEEE International Symposium on Signal Processing and Information Technology, Vancouver, BC, Canada, 27–30 August 2006; pp. 572–577. [Google Scholar]




| Scheme | Feedback Overhead | CSI Accuracy | Complexity |
|---|---|---|---|
| SQ-CE | High (e.g., 18 bit) | Low | Low |
| VQ-CE | Low (e.g., 4 bit) | Moderate | Medium |
| Environmental-aided VQ | Medium | Higher | High |
| D/A feedback | Very low | Extremely low | Low |
| TQ-CE | Low (e.g., 4 bit) | High | High |
| Name of Parameters | Values |
|---|---|
| Room size (length×width×height) | 4 m × 4 m × 2.5 m |
| PD height | 0.75 m |
| Number of LEDs, | 4 |
| Number of users with single PD, U | 4 |
| LED operating current range, [,] | |
| LED half-power angle, | |
| Receiver half-field-of-view angle, | |
| LED Lambertian coefficient, m | 1 |
| Effective detection area of PD, A | 1 |
| Schemes | SQ-CE (B = 18) | VQ-CE (B = 4) | TQ-CE (B = 4) |
|---|---|---|---|
| Transmission bits | 72 | 16 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, F.; Wang, C.; Nie, Y.; Fan, X.; Zhang, C.; Yang, Y. Task-Based Quantizer for CSI Feedback in Multi-User MISO VLC/RF Systems. Electronics 2025, 14, 2277. https://doi.org/10.3390/electronics14112277
He F, Wang C, Nie Y, Fan X, Zhang C, Yang Y. Task-Based Quantizer for CSI Feedback in Multi-User MISO VLC/RF Systems. Electronics. 2025; 14(11):2277. https://doi.org/10.3390/electronics14112277
Chicago/Turabian StyleHe, Fugui, Congcong Wang, Yao Nie, Xianglin Fan, Chensitian Zhang, and Yang Yang. 2025. "Task-Based Quantizer for CSI Feedback in Multi-User MISO VLC/RF Systems" Electronics 14, no. 11: 2277. https://doi.org/10.3390/electronics14112277
APA StyleHe, F., Wang, C., Nie, Y., Fan, X., Zhang, C., & Yang, Y. (2025). Task-Based Quantizer for CSI Feedback in Multi-User MISO VLC/RF Systems. Electronics, 14(11), 2277. https://doi.org/10.3390/electronics14112277






