Abstract
Hyperparameter Optimization (HPO) is an important and challenging problem in machine learning. Traditional HPO methods require substantial evaluations to search for superior configurations. Recent Large Language Model (LLM)-based approaches leverage domain knowledge and few-shot learning proficiency to discover promising configurations with minimal human effort. However, the repetition issues causes LLMs to generate configurations similar to context examples, which may confine the optimization process to local regions. Moreover, since LLMs rely on the examples they generate for a few-shot learning, a self-reinforcing loop is formed, hindering LLMs from escaping local optima. In this work, we propose EvoContext, which aims to intentionally generate configurations that differ significantly from examples via external interventions and actively breaks the self-reinforcing effect for a more efficient approximation of the global optimum. Our EvoContext method involves two phases: (i) initial example generation through cold or warm starting and (ii) iterative optimization that integrates genetic operations for updating examples to enhance global exploration capabilities. Additionally, it employs LLMs in-context learning to generate configurations based on competitive examples for local refinement. Experiments on several real-world datasets show that EvoContext outperforms traditional and other LLM-driven approaches on HPO.
1. Introduction
Hyperparameter Optimization (HPO) critically impacts model generalization [1,2]. Traditional manual hyperparameter tuning, which relies on expert knowledge, faces significant limitations that drive the development of automated methods. Early approaches, including black-box optimization [3,4] and Automated Machine Learning (AutoML) tools [5,6], are unable to transfer expert knowledge to new tasks, resulting in the need for an excessive number of searches. When faced with large-scale data and complex models, the feasibility of such computationally intensive strategies encounters significant challenges. Therefore, the optimization problem addressed in this paper is “identify the optimal hyperparameter configuration of a machine learning algorithm with as few searches as possible under a limited evaluation budget”.
Large Language Models (LLMs) have acquired rich domain knowledge and emerged with few-shot learning capabilities through pre-training on rich corpora [7,8,9]. The rich knowledge embedded in LLMs resembles the experience of human experts, while their few-shot learning ability enables them to learn from others’ experiences. This allows LLMs to incorporate prior knowledge when handling new HPO tasks, enabling faster convergence from a better initialization and reducing both the number of searches and the overall evaluation budget. However, the repetition issues cause LLM outputs to lack diversity, which limits the variety of explored configurations and increases the risk of the HPO process getting stuck in local optima. The repetition issues refer to the tendency of LLMs to replicate input text patterns and reuse identical phrases during generation, consequently reducing the diversity and creativity of the output [10,11,12]. Figure 1 shows a specific example of the repetition issues in LLMs for a HPO task.

Figure 1.
Examples of the repetition issues in LLMs for a HPO task. LLMs tend to mimic high-performance configurations, resulting in a lack of diversity in the output. The Qwen2.5-72B exhibits a consistent pattern in few-shot learning, with its hyperparameter configurations closely resembling those of high-scoring examples. Notably, the ‘booster’ parameter is invariably set to ‘gblinear’, the ‘learning rate’ hovers between 0.7 and 0.8, and the ‘gamma’ parameter is consistently within the range of [650, 750].
Existing solutions to mitigate repetitions can be categorized into training-based [13,14,15,16], decoding-based [10,17,18], and soft prompt-based [7,8,19,20] methods. Training-based methods reduce repetition by adding duplicate samples to the training data and penalizing repeated tokens during training. However, these methods require retraining LLMs, which is costly and complex. Decoding-based methods avoid retraining. They adjust decoding strategies, such as changing the temperature, to reduce repetition. However, since the input remains the same, the predicted token sequence is also the same. These methods only sample differently from a fixed output distribution and do not change it fundamentally. Soft prompt-based methods rely on a simple fact: different inputs produce different outputs. By dynamically updating the prompts, they directly change the output distribution and generate more diverse results. Few-shot prompt information involves task descriptions and contextual examples. Since the task description is usually immutable, the contextual examples become adjustable during dynamic prompt updates. Existing soft prompt-based methods dynamically update the prompts by letting LLMs continuously generate new examples and add them to the prompt. However, since LLMs tend to mimic the examples in the prompt, the newly generated examples are often very similar to the existing ones. Over time, this leads to minimal changes in the in-context examples. Even with varied prompts, LLMs may fail to generate diverse results due to limited variations in contextual examples, thereby constraining exploration across broader search spaces. Thus, the core research question addressed in this paper is as follows: How to balance the expansion of valid information with sustained exploration toward optimal solutions during dynamic example updates?
This paper proposes an approach to address the repetition issue in LLMs by introducing an external intervention mechanism. By incorporating an alternative example updating method, the examples that LLMs imitate are no longer limited to those generated by the model itself, increasing the chance of discovering novel examples. We notice that the crossover and mutation operators of the genetic algorithms effectively introduce novel examples while preserving excellent example advantages. Inspired by this, we propose EvoContext, which aims to address the limited search space exploration in HPO caused by the repetition issue in LLMs, which enables efficient global exploration and local optimization under a limited evaluation budget. EvoContext uses genetic algorithms as an external intervention mechanism, and integrates genetic algorithms with the in-context learning capability of LLMs to achieve balance exploration: genetic algorithms enable broad solution space exploration through crossover and mutation, while LLMs facilitate refined search by emulating high-quality demonstration patterns for hyperparameter optimization.
Finally, we compare EvoContext with several traditional and state-of-the-art LLM-based HPO methods. Specifically, we select three classical HPO algorithms (random search, Bayesian optimization, and evolutionary algorithm) and two popular AutoML tools (NNI [5] and FLAML [6]). Among LLM-driven innovations, we include advanced techniques like MLCopilot [21], LLAMBO [19], and EvoPrompt [20], along with fundamental prompt engineering methods (Few-Shot [8] and Zero-Shot [7]). On two public datasets HPOB [22] and HPOBench [23], as well as a new dataset we construct, EvoContext shows superior HPO capabilities. Module ablation experiments validate the synergistic enhancement from integrating genetic algorithms with LLMs during iterative optimization phases to improve model performance.
The main contributions of our work can be summarized as follows:
- We propose updating contextual examples in prompts using genetic algorithms to address the limited search space exploration caused by repetition issues in LLMs during HPO, thus enhancing optimization performance.
- We design an iterative optimization method that alternates between genetic algorithms and LLMs, balancing solution space exploration and local refinement.
- The superiority of EvoContext is verified on different datasets, and the experiments show that EvoContext outperforms traditional and LLM-based HPO methods.
- Revealing through ablation studies the indispensable synergistic effects between genetic evolutionary and LLMs reasoning modules, providing new insights for integrating traditional optimization algorithms with LLMs.
The remainder of this paper is organized as follows: Section 2 reviews related work on hyperparameter optimization and the integration of LLMs with traditional optimization algorithms. Section 3 provides a concise introduction to the theoretical context required by the proposal. Section 4 presents our proposed method in detail, including the problem formulation and the EvoContext framework. Section 5 describes comprehensive experiments comparing EvoContext with baseline methods. Section 6 discusses its limitations and future research directions. Section 7 concludes the paper.
2. Related Work
2.1. Hyperparameter Optimization
HPO is critical to the success of machine learning tasks [1,2]. With the advent of LLMs, HPO techniques can be categorized into traditional and LLM-based approaches. Traditional methods mainly include black-box optimization algorithms and AutoML tools. Classic black-box optimization algorithms encompass random search [3], Bayesian optimization [24], and Evolutionary algorithms [4,25], while AutoML frameworks such as NNI [5] and FLAML [6] streamline the tuning process by enabling automated HPO with minimal coding effort. Although traditional methods efficiently identify high-performance hyperparameter configurations, they require substantial evaluation resources when searching through a large number of hyperparameters to determine the optimal configuration [21].
LLM-based HPO methods leverage rich knowledge from LLM pre-training to identify competitive hyperparameter configurations with reduced evaluation budgets. MLCopilot [21] converts historical optimization data into a textual experience and extracts knowledge for LLMs to generate configurations. LLAMBO [19] integrates LLMs into Bayesian optimization workflows. Recent studies further utilize LLMs to autonomously analyze optimization trajectories for dynamic hyperparameter adjustments [26,27]. Existing LLM-based approaches predominantly adopt few-shot prompting techniques [7]. However, current implementations iteratively update contextual examples using exclusively LLM-generated historical configurations, causing the example set to converge toward homogeneous patterns during optimization and thereby severely limiting exploration capabilities.
Our proposed EvoContext method innovatively integrates evolutionary mechanisms from genetic algorithms into LLM-driven HPO. Before hyperparameter generation, EvoContext dynamically updates the demonstration sets through crossover and mutation operations, ensuring the continuous injection of diverse high-performance examples during optimization. This strategy preserves the historical success patterns of LLMs while disrupting their inherent cognitive biases, achieving a balance between global exploration and local exploitation. Consequently, it significantly enhances search space exploration capabilities.
2.2. LLMs and Optimization Algorithms
There is a synergistic interplay between LLMs and optimization algorithms [28]. Current integration strategies predominantly focus on leveraging generative capabilities and domain knowledge in LLMs to enhance the search efficiency of conventional algorithms. For example, OPRO [29] employs natural language prompts to iteratively generate optimization solutions through LLMs, while LLAMBO [19] integrates LLMs into Bayesian optimization. Similarly, FunSearch [30], EvoPrompting [31], and EvoPrompt [20] utilize LLMs to augment evolutionary algorithms for automated discovery of mathematical solvers, neural architectures, and prompts.
EvoPrompting selects the top-k performing examples from a seed pool, then constructs few-shot prompts for guiding LLMs in generating neural architecture code. The generated architectures are trained, evaluated, and added to the seed pool for iterative optimization. FunSearch follows a similar process. It employs an island model to maintain the seed pool and does not rely solely on top-k selection. EvoPrompt adopts a different strategy: it selects two parent prompts via a roulette-wheel algorithm, then requires LLMs to perform crossover and mutation to generate new prompts. Unlike EvoPrompt, FunSearch and EvoPrompting do not enforce strict genetic operations, nor are their prompts limited to two examples.
Overall, all three methods rely solely on LLM-generated examples, which limits seed pool diversity. In contrast, EvoContext enhances diversity by incorporating examples generated with LLMs and genetic algorithms. Existing methods are simplified variants of EvoContext without the genetic module. However, the genetic module cannot be directly applied to EvoPrompt’s prompt optimization or the code generation of EvoPrompting and FunSearch.
3. Background
This work builds on two key capabilities: the in-context learning ability of LLMs and the global search ability of GAs.
In-context learning of LLMs. LLMs acquire extensive knowledge through pretraining. With strong pattern recognition and attention mechanisms, it can infer task rules directly from the given context, e.g., examples, and this allows it to respond effectively to new tasks without additional training. LLMs can adapt to changing examples and use high-quality ones to guide fine-grained searches.
Global search of GAs. GAs simulate biological evolution, e.g., selection, crossover, and mutation. It maintains a population of candidate solutions. Fitter individuals are selected and preserved. Crossover mixes parts of different individuals to explore the search space. Mutation introduces random changes to increase diversity. This process allows GAs to search broadly and escape local optima.
In summary, LLMs focus on local optimization by learning from examples. GAs focus on global exploration.
4. Methodology
This paper addresses the following research question: How can dynamically updating in-context examples mitigate the self-reinforcing loop in LLMs to balance global exploration with local optimization, thereby enhancing HPO performance?
This study focuses on low-dimensional HPO tasks for traditional machine learning models. It is based on two key hypotheses:
- Collaborative Optimization: The genetic algorithm is responsible for global exploration. The LLM performs local optimization using high-quality examples. Their alternating updates help balance exploration and exploitation, leading toward the global optimum.
- Dynamic Example: Adding examples generated by the genetic algorithm into prompts helps break the repetition in LLM outputs. This improves both the diversity and quality of hyperparameter configurations.
EvoContext utilizes a dynamically updated demonstration set to guide hyperparameter optimization, addressing three critical challenges, namely (1) initial example construction, (2) balancing information enrichment with optimization direction preservation during dynamic updates, and (3) LLM-guided generation of high-quality hyperparameter configurations. This section presents the problem formulation and EvoContext workflow, followed by detailed implementation descriptions of its two core components: the genetic algorithm and LLMs for hyperparameter optimization.
4.1. Problem Formulation
For a hyperparameter optimization problem , the objective is to identify the optimal configuration within a limited evaluation budget. This is formulated as follows:
where denotes the search space, with and representing continuous and categorical hyperparameter subspaces; represents the set of hyperparameter configurations explored by the algorithm after N evaluations, which is a subset of the search space ; N is a small predefined maximum evaluation budget; is a computationally expensive black-box evaluation function; Eval evaluates model performance on the test set ; denotes model parameters obtained by training on with hyperparameters , i.e.,
Directly prompting LLMs to generate hyperparameter configurations based on the example set at iteration t suffers from the repetition issues. The repetition issues in LLMs are reflected in their tendency to generate configurations similar to previous examples, resulting in low output diversity. This similarity can be defined in terms of a neighborhood, where the search space is limited to the vicinity of historical examples. Formally, for any , existence of probability constraints:
where denotes the degree of similarity between the configurations generated by the LLM and historical examples. A smaller indicates a high concentration of outputs around prior examples. represents the probability that the LLM generates a configuration outside this neighborhood. A small indicates that the LLM rarely explores beyond the local region. Then, denotes the conditional probability of generating given and defines an -neighborhood around . This implies that predominantly resides near exemplars in the neighborhood.
Since is generated by an LLM, the example set update rule:
for any iteration t, the updated example set is also in the -neighborhood of the example set , i.e.,
therefore, when hyperparameter configurations are generated solely by the LLM, the solution space coverage of the example set exhibits minimal expansion, i.e.,
let diam(·) denote a function that computes the extent of the solution space covered by the example set. In a one-dimensional space, according to Equation (3), the new configuration generated by the LLM always falls within the -neighborhood of some existing example , meaning the distance between them does not exceed . If the current example set has a diameter D, adding a new point extends the range by at most on both the left and right, resulting in a new diameter of . In two-dimensional space, the range extends by in four directions (up, down, left, right), so the diameter becomes . By the same logic, in n-dimensional space, adding restricts expansion to at most .
From Equation (6), we observe that the search can be expanded by increasing and . The size of is usually determined by the characteristics of the LLM itself, and in practice, it is possible to use different LLMs or adjust the temperature parameter to change to expand the search range. However, none of the above means avoids or solves the repetition issues inherent in the LLM itself, thus leading to small values of . If itself is not generated by the LLM, the extent of the solution space it can cover can be changed independently of the LLM itself, that is, it is not limited by the size of .
In this paper, we introduce an external intervention to perturb the generation distribution of the example set, ensuring that the update of the example set is not solely dependent on the LLM. This approach decreases the likelihood of the hyperparameters generated being confined within the -neighborhood of . EvoContext utilizes genetic algorithms to intervene by perturbing example sets through crossover and mutation operations. The example set now combines LLM-generated and GA-generated configurations, i.e., , where and denote configurations from the LLM and the genetic algorithm, respectively.
The genetic algorithm generation process facilitates the expansion of the solution space coverage in the example sets:
since genetic algorithms involve stochastic operators, they are not subject to the probabilistic constraint defined by Equation (3) for the repetition issue in LLMs. Due to the absence of probabilistic constraints in genetic algorithms and their substantial divergence from LLM-based generation mechanisms, the new configuration exhibits an elevated probability of residing out the neighborhood of exemplar configurations, i.e.,
specifically, there is a higher probability that the growth due to the genetic algorithm is greater than the growth due to the LLM itself, i.e.,
4.2. EvoContext
4.2.1. Framework Overview
EvoContext achieves an efficient hyperparameter search under limited evaluation budgets through alternating iterations of evolutionary operations and LLM generation. As shown in Figure 2, the workflow of EvoContext consists of two stages, i.e., (i) Example Initialization that generates seed demonstrations via LLM zero-shot reasoning [7] or extracts from historical optimization data and (ii) Iterative Optimization that dynamically updates demonstrations through alternating genetic operations and in-context reasoning of LLMs. Each iteration first evolves the demonstration set via crossover and mutation, then leverages the enhanced prompt to guide LLMs in generating superior configurations. This synergistic design allows the genetic algorithm to provide a rich contextual semantic foundation for the LLMs, preventing them from over-relying on successful patterns mined by themselves.
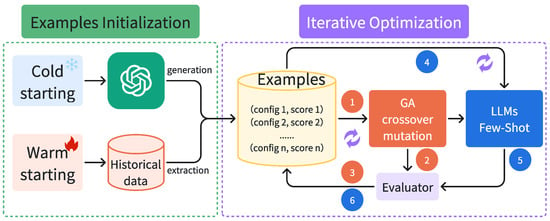
Figure 2.
Overall framework of EvoContext, where genetic algorithms facilitate the LLM escape from local optima in the HPO task by providing examples of different distributions.
The steps of EvoContext are presented in Algorithm 1.
| Algorithm 1 EvoContext |
Input: Evaluation budget N, initialization mode Starting (cold/warm) Output: Optimal configuration index Phase 1: Examples Initialization 1: if Starting is cold then 2: LLM_Generate(Promptzero-shot) 3: Evaluate , update 4: 5: else 6: History_Data 7: end if Phase 2: Iterative Optimization 8: while
do 9: Evolutionary operations 10: RouletteWheelSelection () 11: UniformCrossover() 12: GaussianMutate() 13: RandomCategoryReplace() 14: Evaluate , update 15: 16: LLM operations 17: GreedySelect() 18: LLM_Generate(Textualize()) 19: Evaluate , update 20: 21: end while 22: return |
Examples Initialization (Lines 1–7): EvoContext initializes the exemplar set according to startup modes. Under cold-start conditions (Lines 2–4), the initial configuration set is constructed by prompting the LLM through zero-shot inference, followed by actual performance evaluation. This process updates the remaining evaluation budget to and yields the initial exemplar set . For warm-start scenarios (Line 6), the historical configurations are loaded directly as while maintaining the full evaluation budget .
Iterative Optimization (Lines 8–20): EvoContext alternately executes genetic algorithm operations and LLM generation to optimize hyperparameters through exemplar set updates. Each iteration begins with evolutionary operations (Lines 10–15). The set of parent individuals is selected from the current example set proportionally to fitness by a roulette strategy (Line 10), followed by performing uniform crossover on the parent individuals (Line 11), with each parameter dimension exchanged independently at crossover rate to generate children. Gaussian noise (Line 12) is applied to the numerical hyperparameters at mutation rate to the perturbation to replace the category-based hyperparameters with other candidate values randomly (Line 13). Evolution-generated configurations are evaluated, augmenting the intermediate set while updating remaining evaluations (Lines 14–15).
Configurations with the top-K are selected from the intermediate example set (Line 17), which are converted into structured natural language descriptions to construct a few-shot prompt to drive the LLM generation of new candidates (Line 18). Parsed textual configurations are evaluated and merged into , with , and the remaining evaluations are updated as to complete one round of iteration (Lines 19–20).
Upon exhausting the evaluation budget R, the highest-performing configuration in the final set is selected (Line 22). This synergistic process combines evolutionary boundary expansion via perturbation with LLM contextual learning for local refinement, progressively approximating global optima under finite evaluation constraints.
4.2.2. Genetic Algorithm
The hyperparameter configuration generation via genetic algorithms comprises four steps: parent selection, parent crossover, offspring mutation, and offspring evaluation.
The parent selection strategy in genetic algorithms employs a fitness-proportionate probabilistic mechanism. Each selection probability of an individual is proportional to its fitness, ensuring that high-performance configurations are preferentially chosen while retaining diversity through low-probability participation of suboptimal candidates. For HPO tasks, the selection probability for each configuration is
a cumulative probability distribution is then constructed as
finally, a random probability value p is generated, and the individual that satisfies is selected.
The selected parent configurations undergo a uniform crossover operation to generate offspring configurations. For each parameter dimension, the corresponding values between the parents are exchanged with a crossover probability . Specifically, for the i-th parameter of and , if a uniformly sampled probability p satisfies , the i-th parameter values are swapped; otherwise, they remain unchanged. This process yields two offspring configurations, each comprising a hybrid combination of parental parameters.
Furthermore, we employ distinct mutation strategies for numerical and categorical hyperparameters. For numerical parameters, Gaussian noise perturbation is applied with mutation probability :
using a standard normal distribution with . For categorical parameters, the original value is replaced with a randomly sampled alternative from the candidate set under the same , ensuring that the new value differs from the original.
All mutated offspring are empirically evaluated to obtain configuration-performance pairs . The evaluated results are then merged with the current exemplar set to form an intermediate set .
4.2.3. LLM Operation
The LLM leverages its in-context learning capabilities and pre-trained knowledge of HPO to identify success patterns in the intermediate exemplar set , generating improved candidate configurations. This design is grounded in the hypothesis that the LLM generation process inherently satisfies
where the constraint defines an acceptable threshold for performance loss, which ensures that LLM-generated configurations maintain performance within of the current optimal configuration, i.e., new candidates must either match or closely approach the best-known performance to enable refined exploration.
LLMs, predominantly pre-trained on natural language corpora, exhibit limited proficiency in processing structured data pairs. Textual conversion bridges this gap by aligning exemplar data with the knowledge representation of LLMs. We first sort the exemplars by descending the performance scores, forming an ordered set , where . This ordered set is then encoded into natural language descriptions, constructing contextual exemplars understandable to LLMs through the following formalization:
the textualization function is defined as
the ⊕ denotes string concatenation with fixed-order parameter arrangement to reinforce structural patterns.
We construct a three-component few-shot prompt template: (i) Task Specification: Provide LLM with dataset metadata, hyperparameter definitions, and optimization objectives; (ii) Exemplar Examples: Embeds textualized ordered exemplars into the prompt; and (iii) Generation Instruction: Requires output of new configurations adhering to the exemplar format. Guided by this prompt, the LLM learns the patterns of high-performance configurations to generate new competitive configurations as
5. Experiments
We evaluated EvoContext on three benchmarks to answer the following questions: (i) Does EvoContext outperform traditional and LLM-based HPO methods; (ii) How critical are individual modules of EvoContext to its performance improvement; (iii) What is the impact of parameter settings on optimization performance.
5.1. Experimental Setup
All historical examples were extracted from training logs from the subsequently described benchmark datasets. The random seed in all experiments is fixed at 42. Each task is repeated five times. As the objective is to identify the best configuration under a limited evaluation budget, the number of configurations explored per task is restricted to 15. In EvoContext, the genetic algorithm module was configured with mutation and crossover rates of 0.8 and 0.2, respectively, while the temperature parameter of the LLM was set to 0. To balance computational efficiency and model representativeness, we selected two open-source LLMs, namely Meta-Llama-3-8B-Instruct [32] and Qwen2.5-14B-Instruct [33], as base models. All LLMs were accessed via their official APIs.
Benchmark Datasets. The benchmark data comprises three datasets. Public benchmarks include HPOB [22] (with 82 tasks) and HPOBench [23] (with 40 tasks), while the self-constructed dataset, Uniplore-HPO, consists of 11 real-world HPO tasks derived from an industrial machine learning platform. To ensure reliability, each task was evaluated through five independent trials, with averaged results as statistical results to minimize randomness.
Prompts Structured. The zero-shot and few-shot prompts used in the experiments are shown in Figure 3. Their difference lies in whether the prompt includes examples. Each prompt consists of six components:

Figure 3.
Exemplar prompt. The zero-shot prompt is denoted in blue color. The few-shot prompt constitutes texts in both blue and red colors.
- Role: the role the LLM is expected to play.
- Task: the task to be completed by the LLM.
- Model: the algorithm to be tuned.
- Dataset: the information about the dataset used.
- Examples: the reference examples for the LLM (included only in few-shot prompts).
- Output Format: the required output format.
Evaluation Metrics. We employ a dual-metric combining and to comprehensively assess the effectiveness of hyperparameter search by providing a quantitative assessment of both optimization performance and exploratory capability.
For optimization performance, the metric measures the cumulative over n-evaluated hyperparameter configurations. The is mathematically defined as
quantifies the relative deviation of the current solution from the theoretical extremes, with denoting the best and worst scores, respectively [22]. Each comparative method was required to perform 15 iterations of the hyperparameter search, with the optimization effectiveness dynamically tracked by recording performance peaks per iteration. The is defined as
In solution space, the diversity metric employs a dual-distance measurement to quantify hyperparameter configuration distribution characteristics by simultaneously considering structural dissimilarity and performance discrepancy. Structural dissimilarity is computed through a hybrid distance approach employing Hamming distance for categorical parameters and Manhattan distance for continuous parameters, with subsequent normalization and averaging to derive standardized parameter space distances.
the performance discrepancy is quantified as the absolute difference in objective function values between configuration pairs. The composite distance (sum of structural and performance distance) for all configuration pairs subsequently undergoes global averaging, establishing a quantitative measure for exploration breadth throughout the optimization process, i.e.,
this composite calculation strategy reflects the coverage of the parameter structure space and captures the diversity within the performance space.
5.2. Comparative Study
5.2.1. Baselines
We evaluate traditional HPO methods against LLM-based approaches. For traditional baselines, we include three classical algorithms: random search, Bayesian optimization (implemented via SMAC3 [34]), and evolutionary algorithms (via DEAP [35]), alongside two AutoML tools: NNI [5] (focusing on its integrated TPE-Bayesian optimization and evolutionary modules) and FLAML [6]. For LLM-based approaches, we evaluate LLAMBO [19], which reconstructs Bayesian optimization pipelines via LLM-driven initialization, sampling, and surrogate modeling; MLCopilot [21], embedding historical knowledge into prompts for optimization guidance; and EvoPrompt [20], innovatively employing LLMs as evolutionary crossover or mutation operators for automated prompt optimization. The EvoPrompt, a successful blend of LLM and evolutionary algorithms, is used here as a baseline, echoing the fusion attempt in the paper. Furthermore, basic prompt engineering methods (Zero-Shot [7] and Few Shot [8]) are compared to comprehensively assess LLM potential in HPO.
5.2.2. Results
Based on the experimental results, we summarize the following key conclusions.
As illustrated in Figure 4, EvoContext demonstrates consistent superiority across all experimental settings. In warm-start scenarios, it achieves state-of-the-art results on all benchmarks, outperforming traditional algorithms, AutoML tools, and existing LLM-based methods. Under cold-start conditions without historical data, EvoContext closely matches MLCopilot (which leverages over 10,000 historical data points) on HPOB and HPOBench datasets while surpassing all baselines on Uniplore-HPO datasets except performing comparably to FLAML when using Qwen2.5-14B. Our experiments reveal the unique value of LLMs in HPO. Under cold-start conditions, EvoContext leveraging LLMs outperforms traditional methods in early search phases (less than three configuration evaluations), generating superior hyperparameter configurations. This finding carries critical practical implications: LLM-driven configuration generation achieves viable solutions with minimal computational overhead, providing an innovative resource-efficient optimization strategy.
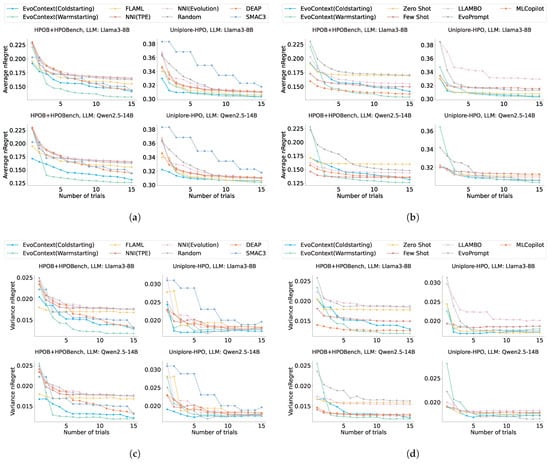
Figure 4.
Results of different HPO methods. (a) Comparison of EvoContext with traditional optimization algorithms and AutoML tools. (b) Comparison of EvoContext with existing LLMs-driven methods. (c) Variance of EvoContext results compared to traditional optimization algorithms and AutoML tools. (d) Variance of EvoContext results compared to existing LLMs-driven methods.
EvoContext demonstrates substantial superiority in solution space exploration compared to contemporary LLM-based HPO techniques. As illustrated in Figure 5, EvoContext maintains comparable diversity levels in parameter configurations across cold-start and warm-start scenarios, revealing minimal dependence on initialization strategies for exploration capability. EvoContext achieves improvements ranging from 13% to 58% in the diversity of hyperparameter configurations compared to existing LLM approaches.
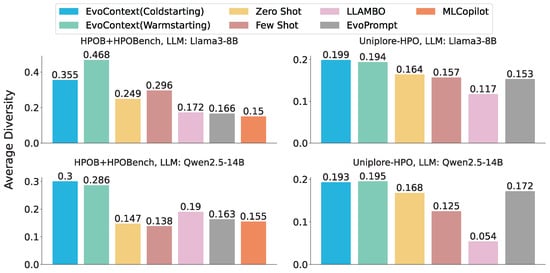
Figure 5.
Results in term of the diversity of LLM-based HPO methods.
We further compare the time consumption of different methods during the hyperparameter search process, measuring the search process duration exclusive of black-box function evaluations. As illustrated in Figure 6, LLM-driven approaches exhibit prolonged search durations compared to conventional methods, primarily attributable to the substantial computational overhead inherent in LLM inference processes. However, LLM-based approaches aim to reduce the number of black-box function evaluations by minimizing the iteration count. In black-box optimization scenarios, the evaluation of the black-box function constitutes the predominant computational burden, and the increase in time expenditure for the hyperparameter search is acceptable.
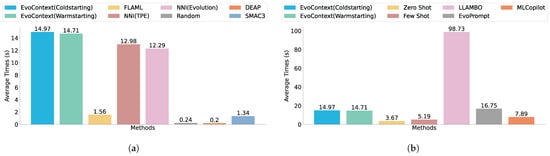
Figure 6.
Time required by traditional (a) and LLM-driven (b) methods to complete a single HPO task. Note that the evaluation time is excluded.
5.2.3. Significance Test
This experiment aims to test whether the performance of the configurations found by EvoContext after 15 hyperparameter searches is statistically significantly better than that of the baseline methods, using significance testing methods. Due to variance differences between EvoContext and the baselines, Welch’s t-test is used.
As shown in Table 1, EvoContext significantly outperforms most baselines in the majority of cases. The only exception is MLCopilot, where the performance difference is not statistically significant under various settings. However, EvoContext has a key advantage: it operates with no historical data in the cold-start setting or with only a few examples in the warm-start setting. In contrast, MLCopilot relies on tens of thousands of historical records to initialize its hyperparameter optimization knowledge.

Table 1.
p-Value of Welch’s t-test for the hypothesis that our methods outperform the baselines. We bolded the p-values above = 0.05, which are the rare cases where the hypothesis does not hold.
5.3. Ablation Study
5.3.1. Module Ablation
The ablation study examines the synergistic mechanism between the LLM and the genetic algorithm modules in the iterative optimization phase. Two baselines were established: (i) genetic algorithm-only optimization (w/o LLM) and (ii) LLM-only optimization (w/o Evolution). The experimental results reveal the following critical insights.
First, the intervention of external evolutionary mechanisms effectively addresses the limitations of LLM self-iteration optimization. As shown in Figure 7, when relying solely on LLM autoregressive generation (w/o Evolution), baseline performance underperforms EvoContext across all models except Qwen2.5-14B. LLM iterations based on initial examples lead to the homogenization of contextual examples, causing generated configurations to converge toward local optima under probabilistic decoding mechanisms. In contrast, EvoContext expands the diversity of contextual examples through genetic crossover and mutation operators, enabling sustained progression toward high-performance regions.
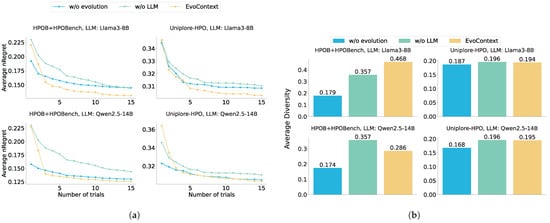
Figure 7.
Results for the module ablation in terms of performance (a) and diversity (b).
Second, the LLM module plays a critical role in the directed exploration of high-performance configurations. As shown in Figure 7, for the genetic algorithm-only baseline (w/o LLM), although global search maintains exploration breadth in the parameter space, its peak performance significantly degrades compared to the full framework. This suggests that random evolutionary mechanisms alone struggle to identify optimal hyperparameters. Implicit reasoning capabilities in LLMs, derived from contextual learning, encode historical high-performance configurations as decision priors, focusing evolutionary search on promising subspaces.
Third, the synergistic optimization mechanism achieves an effective balance between exploration breadth and depth. EvoContext-derived hyperparameter configurations maintain appropriate diversity while ensuring comprehensive coverage of high-performance regions. In contrast, the approach without LLM (w/o LLM), while demonstrating optimal configuration diversity, this approach fails to achieve high performance. Meanwhile, methods without evolutionary algorithms (w/o Evolution) produce concentrated performance distributions (reduced diversity) with clusters predominantly in high-performance zones. Genetic operators, such as crossover and mutation, systematically expand the search landscape. Reasoning in LLMs allows for precise refinement of optimal solutions through contextual pattern recognition. The complementary interaction ensures the simultaneous preservation of exploratory diversity and intensive exploitation of promising regions.
5.3.2. Iteration Order
We investigate the impact of the execution order of the LLM and the genetic algorithm on optimization performance. In Figure 8, experimental results demonstrate that the sequence (LLM-first vs. genetic-first) exerts limited influence on final outcomes: While LLM initialization tends to yield better performance when the number of trials is less than or equal to 3, prioritizing genetic algorithms leads to slightly superior results when the number exceeds 3. Crucially, the synergistic interaction between both modules—rather than their ordering—significantly enhances EvoContext efficacy. The genetic algorithm acts as an enabler, guiding the LLM to discover high-performance configuration regions unattainable through standalone LLM optimization.
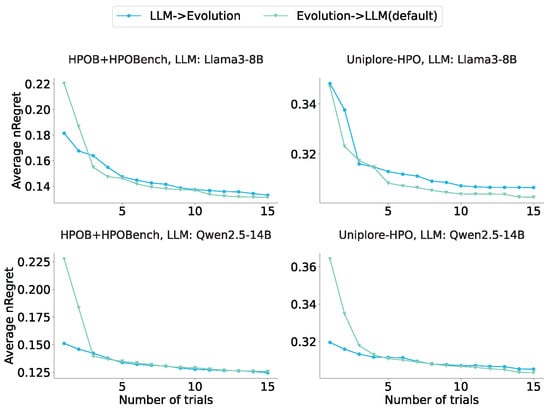
Figure 8.
Results for the iteration order ablation.
5.3.3. Prompt Engineering
We systematically investigate how prompt example construction impacts algorithm performance, focusing on four factors: example ordering strategies, textual representation, selection scope, and performance score annotation. We compare three ordering methods (descending/ascending performance order, random), two presentation formats (JSON data structures vs. natural language descriptions), and three selection scopes (all examples, top-5 performing examples, evolutionarily generated examples). Additionally, we examine whether explicit performance score annotation in prompts enhances model reasoning.
As shown in Figure 9, experimental results demonstrate two key findings. First, non-default prompt construction strategies generally degrade optimization effectiveness. The ordering strategy of examples directionally influences outcomes—descending performance order combined with explicit score annotation enhances recognition efficiency of high-quality configuration patterns. Converting configurations to natural language descriptions and restricting examples to the top 5 performers improves reasoning quality through knowledge alignment and noise reduction. Second, for Llama3-8B on Uniplore-HPO datasets, non-default strategies cause significantly worse performance degradation. This discrepancy is attributable to dual factors: Uniplore-HPO datasets may exceed the coverage of general LLM’s pre-trained knowledge, hindering contextual learning from capturing underlying optimization patterns; meanwhile, differences in model parameter size and architecture directly affect contextual reasoning capabilities, with smaller models exhibiting heightened sensitivity to prompt variations.
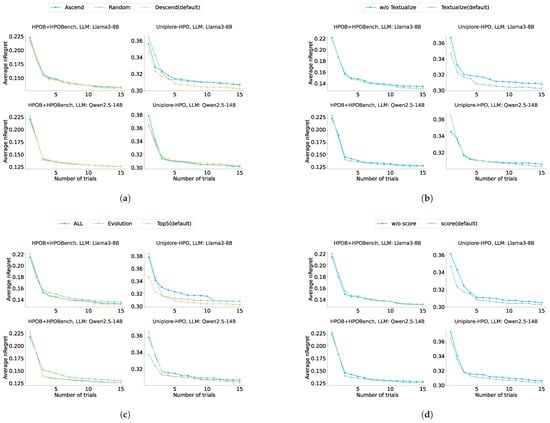
Figure 9.
Results for the ablation on prompt engineering. (a) Ablation on example sort method. (b) Ablation on example textualization. (c) Ablation on example selection method. (d) Ablation on example performance score presentations.
5.4. Effect of Algorithm Parameters
We further investigate the impact of critical algorithm parameters on performance, including the LLM temperature parameter, crossover and mutation rates in the genetic algorithm, and the LLM driving the EvoContext.
5.4.1. Effect of LLM Temperature Parameter
Adjusting the LLM temperature parameter improves text diversity [15,16,36], which is a decoding-based approach to solve repetition issues in LLMs. This experiment examines whether temperature adjustment alone significantly improves LLM hyperparameter optimization. We tested LLMs by varying temperatures (range 0 to 1 in 0.1 intervals) and compared Few-Shot and EvoContext methods.
In Figure 10, the results indicate that temperature tuning moderately increases text diversity, enhancing hyperparameter optimization efficacy. However, the few-shot method does not perform as well as the EvoContext method, despite variations in the temperature parameters. Especially on the HPOB and HPOBench dataset, the few-shot method consistently underperforms the EvoContext method for any temperature setting. This suggests that temperature primarily affects token selection probabilities by amplifying output stochasticity, yet preserves the intrinsic probability distribution governing all generated examples. The findings underscore the necessity of external intervention mechanisms to diversify probability distributions during example generation, which expands search space exploration and improves optimization outcomes.
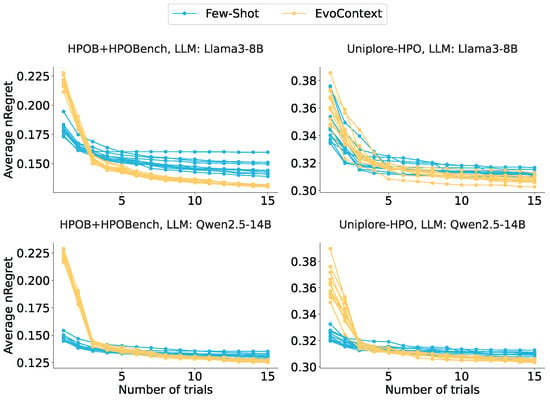
Figure 10.
Impact of the LLM temperature parameter.
5.4.2. Crossover and Mutation Rates
This experiment evaluates how these critical hyperparameters influence the performance of EvoContext. We designed four combinations: low mutation (0.2)/high crossover (0.8), high mutation (0.8)/low crossover (0.2), low mutation/crossover (0.2/0.2), and high mutation/crossover (0.8/0.8), representing varying genetic operation intensities. In Figure 11, the results show that higher mutation rates consistently yield superior performance, confirming genetic algorithms’ capacity to explore hyperparameter configurations beyond LLM-accessible regions. Elevated mutation rates probabilistically enhance the discovery of these configurations.
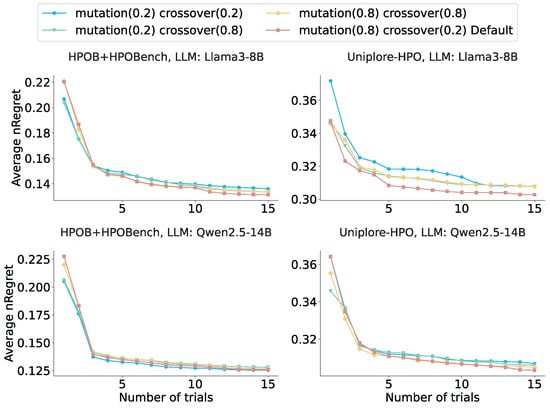
Figure 11.
Impact of crossover and mutation rates in the genetic algorithm.
5.4.3. LLM-Driven Algorithms
We investigates how LLM series and parameter scales affect EvoContext’s performance. In Figure 12, the experimental setup includes smaller open-source models (Llama3-8B, Qwen2.5-3B, Qwen2.5-14B), larger open-source models (Llama3-70B, Qwen2.5-72B), and closed-source models (GPT-4o [37], DeepSeek-v3 [38]). In addition, a proprietary model in programming (Qwen2.5-Coder-14B) is included.
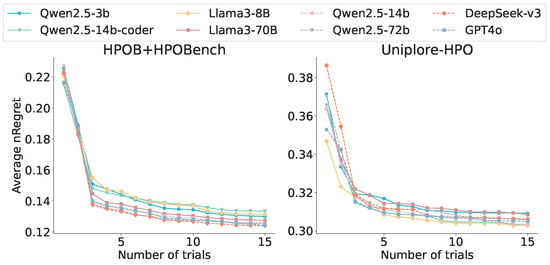
Figure 12.
Impact of the LLM driving the algorithms.
The HPOB and HPOBench results show that GPT-4o and DeepSeek-v3 perform best. Llama3-8B performs worse than Llama3-70B. In Qwen2.5 models, smaller general models show weaker performance. Results prove that stronger models improve EvoContext, which can be attributed to enhanced generalization, knowledge capacity, and pattern recognition in the prompt demonstrated by more powerful models. Notably, Qwen2.5-3B (3B parameters) outperforms Qwen2.5-Coder-14B (14B parameters), and this suggests general models work better for EvoContext than proprietary ones. This might occur because when general models become specialized through fine-tuning, they lose some hyperparameter knowledge while gaining domain-specific knowledge.
6. Discussions
EvoContext still confronts three primary limitations.
First, compared to traditional HPO algorithms, EvoContext relies on LLMs for reasoning, which may result in prolonged configuration search times. Nevertheless, we aim to minimize black-box function evaluations rather than optimize configuration search time. This design makes EvoContext particularly advantageous in scenarios with high-cost black-box function evaluations.
Second, our experimental validation currently addresses only low-dimensional optimization tasks. Future research could explore extending EvoContext to more complex high-dimensional scenarios, such as neural architecture search [31]. EvoContext can be easily extended to high-dimensional scenarios, as they do not introduce additional complexity for the method. The only difference between high- and low-dimensional cases lies in the amount of contextual information about the optimization parameters included in the prompt. EvoContext leverages LLMs to handle both cases in a unified manner. However, we expect high-dimensional tasks to place greater demands on the capabilities of LLMs. If the model lacks sufficient knowledge capacity, it may struggle to provide high-performing hyperparameter configurations. If in-context learning ability is limited, excessive contextual information may hinder the identification of commonalities in outstanding examples, thereby reducing optimization performance. If the context length is limited, and the dimension is very large, making the prompt length too long for the model’s context window, EvoContext will not work.
Third, this study exclusively employs genetic algorithms as external intervention mechanisms to generate diverse examples. Subsequent research should systematically investigate alternative optimization algorithms as external intervention strategies and develop an adaptive intervention framework that dynamically optimizes prompts via evolving contextual examples.
7. Conclusions
This paper addresses the challenge of limited solution space exploration in LLM-based hyperparameter optimization caused by the repetition issues in LLMs. We propose EvoContext, which utilizes the global search for genetic algorithms and the in-context learning of LLMs to perform the optimization process alternatively, balancing exploration and exploitation. The method initializes exemplar sets through cold/warm-start strategies, introduces diversity via crossover-mutation operations, and leverages LLMs to generate superior configurations by learning from high-quality examples. Experiments demonstrate its superiority over existing methods on different datasets, with ablation studies confirming the necessity of module synergy. This research offers a new pathway to overcoming the rigidity of LLM-generated results: When LLMs outputs become repetitive, external interventions can enforce prompt modifications to enhance diversity.
Author Contributions
Conceptualization, Y.X., M.C. and H.L.; methodology, Y.X., M.C. and H.L.; software, Y.X. and G.Q.; validation, Y.X. and G.Q.; formal analysis, Y.X., P.C., X.W., W.Z. and H.L.; investigation, Y.X. and G.Q.; resources, Y.X. and H.L.; data curation, Y.X. and G.Q.; writing—original draft preparation, Y.X.; writing—review and editing, Y.X., Y.W., P.C., X.W., W.Z. and H.L.; visualization, Y.X.; supervision, H.L.; project administration, Y.X., Y.W., P.C., X.W., W.Z. and H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Fund of National Natural Science Foundation of China (No. 61562010), National Key Research and Development Program of China (No. 2023YFC3341205), Guizhou Provincial Major Scientific and Technological Program (No. [2024]003), Guizhou Provincial Program on Commercialization of Scientific and Technological Achievements (No. [2025]008, No. [2023]010), Research Projects of the Science and Technology Plan of Guizhou Province (No. [2023]276, No. [2022]261, No. [2022]271).
Data Availability Statement
The official access links for all publicly available datasets are provided in the manuscript. At the same time, all data and codes related to this study are available at https://github.com/ACMISLab/EvoContext (accessed on 2 April 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Weerts, H.J.P.; Müller, A.C.; Vanschoren, J. Importance of Tuning Hyperparameters of Machine Learning Algorithms. arXiv 2020, arXiv:2007.07588. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Mirjalili, S.; Song Dong, J.; Sadiq, A.S.; Faris, H. Genetic Algorithm: Theory, Literature Review, and Application in Image Reconstruction. In Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer: Cham, Switzerland, 2020; pp. 69–85. [Google Scholar] [CrossRef]
- Microsoft. NNI. Available online: https://github.com/microsoft/nni (accessed on 29 March 2025).
- Wang, C.; Wu, Q.; Weimer, M.; Zhu, E. FLAML: A Fast and Lightweight AutoML Library. In Proceedings of the Fourth Conference on Machine Learning and Systems, Virtual, 5–9 April 2021; pp. 434–447. [Google Scholar]
- Kojima, T.; Gu, S.S.; Reid, M.; Matsuo, Y.; Iwasawa, Y. Large Language Models are Zero-Shot Reasoners. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 22199–22213. [Google Scholar]
- Brown, T.B.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language Models are Few-Shot Learners. In Proceedings of the 34th International Conference on Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 1877–1901. [Google Scholar]
- Ouyang, L.; Wu, J.; Jiang, X.; Almeida, D.; Wainwright, C.L.; Mishkin, P.; Zhang, C.; Agarwal, S.; Slama, K.; Ray, A.; et al. Training language models to follow instructions with human feedback. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 27730–27744. [Google Scholar]
- Xu, J.; Liu, X.; Yan, J.; Cai, D.; Li, H.; Li, J. Learning to Break the Loop: Analyzing and Mitigating Repetitions for Neural Text Generation. In Proceedings of the 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022; pp. 3082–3095. [Google Scholar]
- Wang, W.; Li, Z.; Lian, D.; Ma, C.; Song, L.; Wei, Y. Mitigating the Language Mismatch and Repetition Issues in LLM-based Machine Translation via Model Editing. In Proceedings of the 2024 Conference on Empirical Methods in Natural Language Processing, Miami, FL, USA, 12–16 November 2024; pp. 15681–15700. [Google Scholar] [CrossRef]
- Fu, Z.; Lam, W.; So, A.M.; Shi, B. A Theoretical Analysis of the Repetition Problem in Text Generation. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, Virtual Event, 2–9 February 2021; pp. 12848–12856. [Google Scholar] [CrossRef]
- Freitag, M.; Al-Onaizan, Y. Beam Search Strategies for Neural Machine Translation. In Proceedings of the First Workshop on Neural Machine Translation, Vancouver, BC, Canada, 4 August 2017; pp. 56–60. [Google Scholar] [CrossRef]
- Peeperkorn, M.; Kouwenhoven, T.; Brown, D.; Jordanous, A. Is Temperature the Creativity Parameter of Large Language Models? In Proceedings of the 15th International Conference on Computational Creativity, Jönköping, Sweden, 17–21 June 2024; pp. 226–235. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Awadallah, A.H. Cost-effective hyperparameter optimization for large language model generation inference. In Proceedings of the Second International Conference on Automated Machine Learning, Hasso Plattner Institute, Potsdam, Germany, 12–15 November 2023; pp. 1–17. [Google Scholar]
- Renze, M. The effect of sampling temperature on problem solving in large language models. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP 2024, Miami, FL, USA, 12–16 November 2024; pp. 7346–7356. [Google Scholar] [CrossRef]
- Welleck, S.; Kulikov, I.; Roller, S.; Dinan, E.; Cho, K.; Weston, J. Neural Text Generation with Unlikelihood Training. In Proceedings of the Eighth International Conference on Learning Representations, Virtual, 26 April–1 May 2020. [Google Scholar]
- Lin, X.; Han, S.; Joty, S.R. Straight to the Gradient: Learning to Use Novel Tokens for Neural Text Generation. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 6642–6653. [Google Scholar]
- Liu, T.; Astorga, N.; Seedat, N.; van der Schaar, M. Large Language Models to Enhance Bayesian Optimization. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Guo, Q.; Wang, R.; Guo, J.; Li, B.; Song, K.; Tan, X.; Liu, G.; Bian, J.; Yang, Y. Connecting Large Language Models with Evolutionary Algorithms Yields Powerful Prompt Optimizers. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Zhang, L.; Zhang, Y.; Ren, K.; Li, D.; Yang, Y. MLCopilot: Unleashing the Power of Large Language Models in Solving Machine Learning Tasks. In Proceedings of the 18th Conference of the European Chapter of the Association for Computational Linguistics, St. Julian’s, Malta, 17–22 March 2024; pp. 2931–2959. [Google Scholar]
- Pineda-Arango, S.; Jomaa, H.S.; Wistuba, M.; Grabocka, J. HPO-B: A Large-Scale Reproducible Benchmark for Black-Box HPO based on OpenML. In Proceedings of the Thirty-Fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual, 6–14 December 2021; pp. 1–12. [Google Scholar]
- Eggensperger, K.; Müller, P.; Mallik, N.; Feurer, M.; Sass, R.; Klein, A.; Awad, N.H.; Lindauer, M.; Hutter, F. HPOBench: A Collection of Reproducible Multi-Fidelity Benchmark Problems for HPO. In Proceedings of the Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2), Virtual, 6–14 December 2021; pp. 1–17. [Google Scholar]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Hayes-Roth, F. Review of “Adaptation in Natural and Artificial Systems by John H. Holland”, The U. of Michigan Press, 1975. SIGART Newsl. 1975, 53, 15. [Google Scholar] [CrossRef]
- Zhang, M.R.; Desai, N.; Bae, J.; Lorraine, J.; Ba, J. Using Large Language Models for Hyperparameter Optimization. In Proceedings of the NeurIPS 2023 Foundation Models for Decision Making Workshop, New Orleans, LA, USA, 4–9 December 2023; pp. 1–29. [Google Scholar]
- Zhang, S.; Gong, C.; Wu, L.; Liu, X.; Zhou, M. AutoML-GPT: Automatic Machine Learning with GPT. arXiv 2023, arXiv:2305.02499. [Google Scholar] [CrossRef]
- Huang, S.; Yang, K.; Qi, S.; Wang, R. When large language model meets optimization. Swarm Evol. Comput. 2024, 90, 101663. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.; Lu, Y.; Liu, H.; Le, Q.V.; Zhou, D.; Chen, X. Large Language Models as Optimizers. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Romera-Paredes, B.; Barekatain, M.; Novikov, A.; Balog, M.; Kumar, M.P.; Dupont, E.; Ruiz, F.J.R.; Ellenberg, J.S.; Wang, P.; Fawzi, O.; et al. Mathematical discoveries from program search with large language models. Nat. Commun. 2024, 625, 468–475. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Dohan, D.; So, D.R. EvoPrompting: Language Models for Code-Level Neural Architecture Search. In Proceedings of the 37th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; pp. 7787–7817. [Google Scholar]
- Meta AI. Llama 3. Available online: https://github.com/meta-llama/llama3 (accessed on 29 March 2025).
- Qwen Team. Qwen2 Technical Report. arXiv 2024, arXiv:2407.10671. [Google Scholar] [CrossRef]
- Lindauer, M.; Eggensperger, K.; Feurer, M.; Biedenkapp, A.; Deng, D.; Benjamins, C.; Ruhkopf, T.; Sass, R.; Hutter, F. SMAC3: A versatile Bayesian optimization package for hyperparameter optimization. J. Mach. Learn. Res 2022, 23, 1–9. [Google Scholar]
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.G.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res 2012, 13, 2171–2175. [Google Scholar]
- Caccia, M.; Caccia, L.; Fedus, W.; Larochelle, H.; Pineau, J.; Charlin, L. Language GANs Falling Short. In Proceedings of the 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- OpenAI. GPT-4o. Available online: https://openai.com/index/hello-gpt-4o (accessed on 29 March 2025).
- Liu, A.; Feng, B.; Xue, B.; Wang, B.; Wu, B.; Lu, C.; Zhao, C.; Deng, C.; Zhang, C.; Ruan, C.; et al. Deepseek-v3 technical report. arXiv 2024, arXiv:2412.19437. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).