Abstract
Federated learning (FL) enables privacy-preserving collaborative training by iteratively aggregating locally trained model parameters on a central server while keeping raw data decentralized. However, FL faces critical challenges arising from data heterogeneity, model heterogeneity, and excessive communication costs. To address these issues, we propose a communication-efficient federated learning via knowledge distillation and ternary compression framework (FedDT). First, to mitigate the negative impact of data heterogeneity, we pre-train personalized heterogeneous teacher models for each client and employ knowledge distillation to transfer knowledge from teachers to student models, enhancing convergence speed and generalization capability. Second, to resolve model heterogeneity, we utilize the server-initialized global model as a shared student model across clients, where homogeneous student models mask local architectural variations to align feature representations. Finally, to reduce communication overhead, we introduce a two-level compression strategy that quantizes the distilled student model into ternary weight networks layer by layer, substantially decreasing parameter size. Comprehensive evaluations on both MNIST and Cifar10 datasets confirm that FedDT attains 7.85% higher model accuracy and reduces communication overhead by an average of 78% compared to baseline methods. This approach provides a lightweight solution for FL systems, significantly lowering communication costs while maintaining superior performance.
1. Introduction
In recent years, mobile devices have emerged as the primary computational infrastructure utilized by billions of global users, and the scale of mobile devices is expected to exceed tens of billions in the coming years. In this context, smartphones and wearable devices continue to generate massive amounts of data [1,2], The continuous expansion and dynamic variability of data landscapes empower AI systems to achieve rapid performance gains. Traditional machine learning transfers user data to a centralized server to train models centrally. Still, much of the data are inherently privacy-sensitive, leading to a serious risk of privacy leakage in this process [3]. The sharing of privacy-sensitive data [4,5] across different clients/platforms is increasingly restricted by data protection regulations, including the GDPR, in response to mounting privacy concerns [6]. Achieving a balance between open data ecosystems and individual privacy rights requires innovative approaches, The concept of federated learning (FL) was first put forward by McMahan et al. [7] and has become an effective solution to resolve this conflict and has been widely used in various fields. Among them, FedAvg [8] is the most representative federated averaging algorithm, whose model performance in Google keyboard prediction represents a mere 1.5% deviation from the centralized training baseline. The successful deployment of FedAvg in production applications proves the feasibility of FL in striking a trade-off between privacy preservation and model efficacy. Although FL demonstrates strong capabilities in safeguarding data privacy, it still faces many problems.
The challenge of data heterogeneity, where data are not independently and identically distributed (IID), continues to hinder the performance of FL systems, particularly in real-world applications with diverse data sources. Reference [9] refers to heterogeneity in data distributions across client devices, which usually stems from the fact that the data on each device correspond to a specific user, geographic location, or time window. For example, FedAvg, a simple weighted average approach, needs to be deployed in environments where the data are independently homogeneous and the model is isomorphic. Still, in practice, data are not independently homogeneous across clients. Karimireddy et al. [10] demonstrated that client-side drift occurs when the data are heterogeneous, leading to poor performance, and introduced an algorithmic solution to address client-side drift in local updates through the utilization of control variables to adjust for client-specific variations during the update procedure, which increases the communication cost between devices. Liao et al. [11] proposed a federated uniform representation enhancement framework, which aims to achieve uniform representation generation for federated unsupervised learning on non-independent and/or non-identically distributed (non-IID) data. The client-side flexible uniform regularizer avoids representation collapse by uniformly dispersing samples, and the server-side efficient uniform aggregator promotes global representation consistency by constraining the uniformity of client-side model updates. The above methods mitigate the drift of the model between global and local levels to some extent; nevertheless, this approach is insufficient to completely eradicate the adverse effects of data heterogeneity on convergence behavior and model accuracy. Hence, addressing data heterogeneity is imperative for improving the effectiveness of FL systems.
The presence of model heterogeneity in federated learning leads to barriers to knowledge transfer between participants. In data-heterogeneous federated learning, client data often have different features and distributions [12], different hardware capabilities [13], or different tasks [14], and the suitable model structure and parameter settings will also be different. However, the traditional federated learning algorithm, the FedAvg global model, is aggregated from the average weights of local models, which cannot meet the demand for customized models in various scenarios and tasks, so each client likes to design its local model independently. For example, Makhija et al. [15] proposed Federated Heterogeneous Neural Networks, which allow each client to build personalized models. In real-world scenarios, heterogeneous models [16] do not match in the parameter space during aggregation, and the global gradient drifts, leading to difficulties in transferring knowledge between clients. Li et al. [17] proposed a decentralized federated learning framework leveraging knowledge distillation to tackle the challenge of knowledge transfer on the client side, allowing the application of federated learning across independently designed models; however, this approach relies on a public dataset and lacks a continuous global model update mechanism, restricting its scalability for new participants whose data characteristics may deviate from existing models and potentially degrade overall performance. To address the issue of model heterogeneity, Diao et al. [18] introduced a parameter subset selection strategy based on device parameters to mitigate parameter space mismatch, although this method may cause weight imbalance due to insufficient training of unshared model components in limited data subsets. These limitations highlight the critical need to overcome the constraints of traditional aggregation paradigms and knowledge transfer mechanisms to develop more efficient and robust heterogeneous federated learning frameworks that can accommodate diverse model architectures and data distributions while maintaining computational efficiency across resource-constrained devices.
The substantial communication burden in federated learning frameworks remains a critical issue, leads to reduced efficiency in model training, and becomes a major bottleneck for system scaling. Since federated learning requires frequent exchanges of model parameters [19], when deploying large-scale pre-trained models, the high communication overhead poses a huge pressure on bandwidth-constrained clients, which directly restricts the practical application of large-scale models in federated systems [20,21]. To reduce the communication overhead, current research focuses on two main directions: gradient compression and co-distillation. Gradient compression [22] reduces the amount of transmitted data, but is prone to significant performance degradation at high compression ratios and may weaken the model’s ability to handle data heterogeneity [23]. The co-distillation paradigm [24] reduces communication overhead by sharing local model predictions rather than transmitting model parameters, and the approach is adopted when the local model’s architecture exceeds the representational capacity of the public dataset. However, highly privacy-sensitive data [25] cannot be shared and exchanged in real-world scenarios. Itahara et al. [26] proposed a semi-supervised distillation that reduces communication overhead but still lacks scalability in data-heterogeneous scenarios. The FedKD framework proposed by Wu et al. [27] removes reliance on public data through bidirectional knowledge migration but its performance is limited by the quality of teachers’ models. Therefore, balancing communication overhead and model performance remains a key challenge for federated learning.
In summarize, there are still three major problems with federated learning, although it protects data privacy: (1) data heterogeneity leads to significant model performance degradation; (2) model heterogeneity leads to knowledge transfer obstacles; (3) high communication overhead reduces training efficiency. To address these problems, this paper proposes communication-efficient federated learning via knowledge distillation and ternary compression, named FedDT. This method applies the dynamic combination of knowledge distillation and ternary quantization to federated learning, and the client adopts multiple rounds of local update strategy to compress the model simultaneously in two layers. Firstly, an adaptive knowledge distillation mechanism is employed at the client side to transfer knowledge from the teacher model to a lightweight student model. Secondly, the distilled student model undergoes per-layer quantization and is further trained into a ternary-weight network, effectively reducing the parameter count through structured sparsity induction. Finally, the compressed ternary model is aggregated on the server after multiple rounds of local refinement. This approach not only preserves model performance through iterative optimization but also achieves substantial parameter reduction via progressive compression, demonstrating particular advantages in large-scale distributed learning environments where data heterogeneity poses significant challenges.
This study makes the following key contributions:
(1) Personalized Federated Distillation Framework: We introduce a novel algorithm that enables clients to train customized teacher models tailored to their local data distributions. This personalized approach effectively alleviates the adverse effects of data heterogeneity, which is a critical challenge in federated learning, thereby enhancing both model performance and generalization capability.
(2) This paper addresses the challenge of knowledge transfer across heterogeneous local models by employing a student model as a unified intermediary. Specifically, the global model, initialized by the server, functions as a unified student model shared among all participating clients. During local updates, each client performs knowledge distillation from its personalized teacher model into the homogeneous student model, thereby eliminating cross-client knowledge transfer barriers.
(3) This paper proposes a two-level compression strategy that combines knowledge distillation with ternary quantization to reduce model parameters. In federated distillation, communication costs are fundamentally governed by the magnitude of the student model being transmitted. By leveraging ternary quantization, the continuous weight parameters of the student model are mapped to a discrete space, significantly reducing communication costs while maintaining model performance.
(4) The experimental evaluation indicates that FedDT surpasses three baseline methods by 7.85% in model accuracy under both IID and non-IID conditions on the MNIST and Cifar10 datasets, while simultaneously reducing communication overhead by an average of 78%.
This paper adopts a structured approach to present its contributions as follows: The next section conducts a comprehensive review of prevailing research in the federated learning domain, providing critical context for our work. Section 3 introduces the preliminary definitions and the system architecture of FedDT. Section 4 presents the detailed implementation of the two modules within the FedDT framework, along with the overall implementation of the proposed method. Section 5 conducts comparative experiments between FedDT and three baseline methods, analyzing both model performance and communication overhead. Complementary ablation analyses are further performed to verify the individual contributions of each module. Finally, Section 6 summarizes the key findings and outlines promising avenues for future research.
2. Related Work
This section presents an in-depth analysis of existing research on federated learning, focusing on challenges related to data heterogeneity, model heterogeneity, and communication overhead.
2.1. Data Heterogeneous Federated Learning
Federated learning preserves data confidentiality through localized data storage and processing. The uploaded local parameters are systematically consolidated to derive a unified global model, and this aggregation mechanism may lead to significant deviations between the actual trained global model and the theoretically optimal model [28]. In real-world application scenarios, there are category imbalances both at the global level and in the local dataset of a single client due to industry, geography, culture, and other factors [29,30] that the client is affected by. Unbalanced data bring a double challenge [31]: Initially, the model exhibits a predisposition toward the majority class, and the performance of different classes will be different with an unbalanced number of samples. Second, the lack of minority class data makes it more difficult to learn the features of these classes. Li et al. [32] proposed a solution to FL heterogeneity by modifying local objectives with proximal regularization, improving algorithm stability across heterogeneous clients. Huang et al. [33] developed a personalized FL framework that promotes collaboration between clients with comparable data characteristics. Ruan et al. [34] proposed a federated learning aggregation method that allows more flexible devices to participate in the convergence. Zhang et al. [35] proposed an algorithm to select models with higher frequency. Wang et al. [36] proposed a visual analysis tool, HetVis, to facilitate customers to solve the heterogeneity problem and identified statistical heterogeneity by calculating the predictive behaviors of the global FL model versus the independent models trained using local data. To solve the client model drift problem caused by statistical heterogeneity among different IoT devices, Zhou et al. [37] proposed a federated learning framework incorporating a global–local knowledge fusion mechanism (FedKF). The core concept of FedKF involves the server returning global knowledge for integration with local knowledge during each training iteration, to regularize the local model into a globally optimal one. Casey et al. [38] proposed a collaborative transfer learning (CTL) framework that utilizes representative datasets and adaptive distillation weights to facilitate efficient and privacy-preserving collaboration. Li et al. [39] proposed MOON, which addresses data heterogeneity by constraining the update direction of local models through a model-contrastive loss that anchors on the feature representations of the global model, while reducing communication overhead via a lightweight global architecture. However, MOON does not resolve client-side model heterogeneity and demonstrates sensitivity to hyperparameter configurations, potentially limiting its applicability in practical scenarios.
The above federated learning solutions can solve the vertical federated learning heterogeneity problem but with an overall level of accuracy and loss. For example, the HetVis algorithm for sample analysis is more complex, while the FedKF algorithm is moderately complex, but with less performance improvement. More efficient and robust schemes need to be investigated in the future for the data heterogeneity problem of FL.
2.2. Model Heterogeneous Federated Learning
In practical federated learning settings, the client data’s non-IID and diverse distribution precludes the effectiveness of traditional approaches, necessitating independent local model design by each participant to accommodate unique data characteristics [40]. This idea is more adaptable in non-IID scenarios and has gradually become an important direction to solve the problem of data heterogeneity.
Knowledge distillation (KD), first proposed by Hinton et al. [41], is a knowledge transfer method that takes advantage of the rich representations of features embedded in the probability distributions generated by the softmax function to transfer knowledge from a teacher model to a more compact student model, allowing the student to achieve a performance comparable to the teacher. Due to the network architecture of the student model, KD is well suited for deployment on edge devices. Jeong et al. [42] proposed a novel distributed model training framework called the federated distillation algorithm, which pioneered the collaborative training of heterogeneous models across devices, to enhance the personalization capability of the models. Itahara et al. [26] proved the inevitability of the convergence of the process at the mathematical level, providing theoretical support for the regularized constraint term for distributed distillation. The current distillation-based federated learning methods present two major technical trends: first, a lightweight model architecture, typically represented by FedGTK [43] through the periodic knowledge return mechanism, while maintaining the computational independence of the edge device to continuously optimize the central model; second, integration learning fusion, such as FedBoost [44], which adopts an incremental integration framework through the distribution of the basic model components to achieve distributed integrated learning, taking into account the communication efficiency and model performance. Additionally, Tan et al. [45] proposed FedProto, which addresses data and model heterogeneity by exchanging and aggregating class prototypes (rather than gradients) between clients and the server. However, its limitations primarily stem from the insufficient expressiveness of prototypes to capture complex class features and reduced effectiveness in highly heterogeneous or fine-grained classification tasks.
Knowledge distillation techniques show significant bandwidth optimization advantages in federated learning, especially in coping with device heterogeneity and data distribution bias, which improves the personalization capability of the model. However, as the number of clients and the dimensions of the data continue to increase, the personalization strategy is prone to become a bottleneck in terms of communication and computational resources. How to trade off efficiency and accuracy among knowledge distillation methods will be a long-term research direction.
2.3. Efficient Federal Learning
The client and server need to exchange data, such as model parameters, frequently during the federal learning process. In the present day, the model scale is expanding and the number of parameters is increasing, which is commonly used in computer vision, and has reached 11.69 million. Therefore, model parameters become the main content of federated learning communication. Considering that some of the information in deep learning models is redundant and the non-absolute dependence of most models on numerical accuracy, quantization compression techniques can achieve the efficient use of computational resources with controlled loss of accuracy. However, this means of optimization also poses some challenges, such as the increased complexity of the training process and potential degradation of model accuracy. To address the problem that quantization methods may lead to excessive sparsity, researchers have proposed a ternary quantization strategy to reduce the quantization error by introducing a zero value as the third quantization level. Zhu’s team [46] proposed the trained ternary quantization method (TTQ), which implements asymmetric quantization by introducing two trainable scaling coefficients {}, thereby improving the expressive power of the network. Ternary quantization simplifies computation and storage by mapping weights or activation values to three discrete values. This approach is particularly suitable for deep learning models and can significantly reduce model complexity while preserving as much performance as possible. In federated learning scenarios, quantization compression techniques present two major innovative paths. Fixed quantization-based methods optimize the quantization error through matrix transformation, such as AdaGQ [47]. Dynamically adjusting the quantization bit width and combining the differential allocation of communication capacity can increase the convergence speed by 35%, and the budget-driven EDEN communication strategy [48] can reduce energy consumption by 28%. These methods significantly improve the efficiency of model convergence in heterogeneous environments.
Quantization technology not only reduces the model storage requirement by 50–80% but also reduces the transmission delay by 40–60% by reducing the amount of data per round of communication by 3–5 times, providing key technical support for edge computing scenarios. However, the quantization technique is a lossy compression technique, which restricts the high-precision representation of the model and is not suitable for some applications or tasks that require high precision, so it is necessary to further explore and improve the quantization technique in federated learning to adapt to more complex and wider application scenarios.
In summary, existing federated learning methods suffer from critical limitations including model performance degradation due to data heterogeneity, knowledge transfer barriers caused by model heterogeneity, and excessive communication overhead. These challenges require the development of novel solutions. As shown in Table 1, where × indicates negative impacts, - indicates no improvement, and ✓ indicates positive outcomes, the proposed framework demonstrates comprehensive advantages in addressing data heterogeneity, model heterogeneity, and communication efficiency compared to alternative approaches.

Table 1.
Comparison of representative methods in terms of data heterogeneity, model heterogeneity, and communication overhead.
3. System Architecture
3.1. Preliminary Definitions
Definition 1
(Federated Learning). Let N be the number of participating clients, denoted as , where each client possesses a private local dataset, . In conventional centralized learning, all data are aggregated as , and a global model, , is trained on the combined dataset. In contrast, federated learning enables the training of the collaborative model of without requiring any client to disclose to others. Let and denote the performance metrics of the centralized and federated models respectively, under the condition that
Then, the federated learning algorithm is said to have a loss of δ in accuracy.
Definition 2
(Non-IID Data). Let the local data distribution of user i be and that of user j be , where there is a statistical discrepancy between them. Each user’s data distribution possesses the property of decomposition into the product of a feature distribution, , and a label-conditional distribution, :
The situation of non-IID data labels refers to the case where the conditional probabilities and among different users are the same, but their marginal probabilities and are different. This paper focuses on federated learning algorithms under label-skewed non-IID data conditions.
Definition 3
(Softmax Function). Knowledge distillation employs a generalized softmax function with a temperature parameter:
where T is the hyper-parameterized average temperature, which is used to control the smoothness of knowledge loss. The temperature hyperparameter is utilized to regulate the teacher model’s output, avoiding overly peaked probability distributions. As the temperature value rises, the output probability distribution becomes increasingly smooth. Here, represents the logarithmic output of the teacher model, with i indicating the index of the class, j denoting the total number of classes, and indicating the predicted probability for the class. The term corresponds to the class probability prediction for the class obtained from the softmax outputs of both teacher and student models at the temperature T. This method enhances the student model’s performance by incorporating the teacher model’s predictions as informative soft labels, which function as effective regularization terms during training.
Definition 4
(Cross-Entropy Loss Function). In machine learning, the cross-entropy loss function is employed to quantify the mismatch between a model’s predicted probability distribution and the actual probability distribution. Its mathematical expression is
where ai is the i-th component of the true label (0 or 1); bi is the predicted probability of the model (softmax output) for the i-th class. Here, represents the i-th component of the ground truth label, taking a binary value of either 0 or 1, while denotes the predicted probability of the model for the i-th class, derived from the softmax output.
Definition 5
(Kullback–Leibler Divergence). The Kullback–Leibler (KL) divergence, a measure of dissimilarity between two discrete probability distributions, P and Q, is mathematically defined as
Here, denotes the probability of the i-th element in distribution P, while represents the corresponding probability in distribution Q. A lower KL divergence value reflects a closer alignment between the two probability distributions. The KL divergence possesses important properties including non-negativity, asymmetry, and the non-satisfaction of the triangle inequality. Specifically, it equals zero when P and Q are identical and approaches infinity when they are completely dissimilar. The KL divergence can be interpreted as measuring either information gain (the amount of information obtained when updating from Q to P) or information loss (the amount of information lost when approximating P with Q). As an asymmetric measure, it finds practical applications in comparing similarity/dissimilarity between texts in natural language processing or between images in computer vision tasks.
3.2. System Model of FedDT
The problem of model heterogeneity and communication inefficiency in FL is addressed in this work for data exhibiting non-independent and non-identical distributions; this paper proposes communication-efficient FL via knowledge distillation and ternary compression, named FedDT. A communication-efficient personalized FL model for non-IID scenarios is constructed. The system architecture of FedDT consists of N clients and a server, as shown in Figure 1.
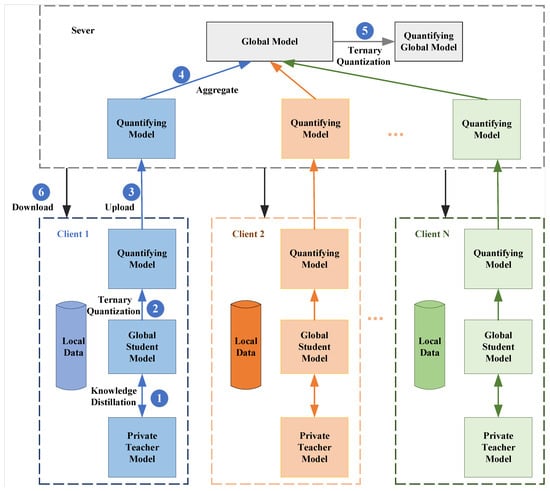
Figure 1.
The overall framework of the proposed method.
(a) Clients: Each client locally stores its private data at . Client data are securely retained within local storage environments. The i-th client’s dataset is designated as , with client possessing-defined computational capacities. Each participant stores a localized version of the comprehensive tutor model (parameters: ) and a localized instance of the efficient student model S with its parameter configuration.
(b) Server: The center server has the characteristics of low latency, high throughput, and high reliability, is capable of handling a large amount of data, and undertakes important tasks such as coordinating the aggregation of client parameters and model updating. Its main tasks are aggregating quantitative models and sending out updated global models.
The main process of FedDT is as follows.
Global model initialization is performed before FL begins. The central server initializes a random global model. Each client downloads the global model as a local student model and pre-trains a personalized teacher model using a local private dataset.
(1) Client-side local model distillation training. The client uses locally labeled data to optimize model parameters through knowledge migration using the self-distillation mechanism to perform local teacher model and student model updates.
(2) Client-side student model quantization. The client compresses the student model using a ternary quantization technique. The student model’s weights are normalized and then quantized.
(3) Client-side uploading of quantization models. The client-side quantitative models participating in the training are uploaded to the server.
(4) The server aggregates the client-uploaded models to derive a global consensus model by utilizing an aggregator to transform each quantized local model into a continuous representation, subsequently synthesizing these into a unified global model.
(5) Quantization of global models on the server. The aggregated global model is quantized and compressed.
(6) Clients download the global model. Each participating training client retrieves the quantized global model to perform local model updates.
The optimization process iterates until both the student and teacher models achieve the convergence criteria, as evidenced by the diminishing gradient updates or the saturation of the validation metric.
4. Method
In this section, we present the implementation of FedDT in the knowledge distillation module and the ternary quantization module on the local side and the overall implementation of the FedDT framework.
4.1. Knowledge Distillation Module
To address the challenges posed by data and model heterogeneity in FL, this study introduces a novel personalized FL approach. Specifically, each client trains a customized heterogeneous teacher model tailored to its unique data distribution, effectively mitigating the adverse effects of data heterogeneity on model optimization. The server maintains a global model that serves as a unified student model across all clients. Through the knowledge distillation process, clients transfer knowledge from their personalized teacher models to this shared student model, thereby obfuscating local model heterogeneity while preserving global consistency. This mechanism leverages the inherent properties of knowledge distillation, where the student model acts as an intermediary to harmonize diverse local models. The detailed local update mechanism is illustrated in Figure 2.
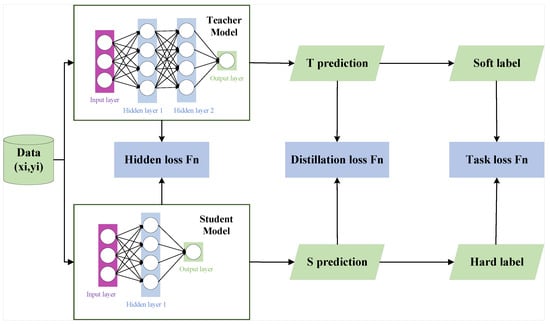
Figure 2.
Knowledge distillation process diagram.
The local knowledge distillation loss function is composed of three distinct components: task loss function, distillation loss function, and adaptive hidden loss.
(1) Task loss function: The discrepancy between the model’s predictions and actual labels is measured by the cross-entropy loss, serving to refine the model’s classification accuracy. When the input sample pair is input, the soft probabilities of the teacher model and the student model after the prediction of the sample are denoted as and , respectively. The task loss is denoted as follows.
(2) Distillation loss function: The training objective combines teacher model soft labels (from its softmax output) with student model hard labels (from its predictions). The distillation loss is computed as the KL divergence between these soft labels, enabling the student to mimic the teacher’s intermediate representations and approximate its output distribution.
In federated knowledge distillation, the teacher–student training dynamics directly influence the loss balance. When models converge effectively, the distillation loss takes precedence, effectively curbing overfitting while possibly impairing the student model’s ability to predict real labels accurately. In contrast, during early training stages or when data noise is pronounced, inadequate prediction reliability causes the task loss to prevail, obstructing efficient knowledge transfer. To overcome these issues, this paper introduces an adaptive distillation mechanism predicated on soft label quality perception as follows.
Adaptive intensity control by dynamically adjusting loss weights based on the predicted correctness of the teacher and student models. In the scenario of a high correct rate, the distillation loss weight is reduced and task learning is focused on. In scenarios with low correct rates, distillation loss weights are increased to enhance knowledge transfer. Distillation loss is balanced with task loss by using temperature and weighting methods to facilitate student model training.
(3) Due to the hidden state of the teacher model and the fact that the attention heat map contains key features of the data with contextual dependencies, additional adaptive hidden loss functions are added on top of traditional knowledge distillation techniques. The student model learns a more robust feature extraction capability by matching these representations. The loss formulas and are as follows.
The mean squared error (MSE) is utilized as the key objective function for optimization in this work. Let , , , and represent the hidden state and the heat of attention map in the ith local teacher and student, respectively. Additionally, let be a parameterized linear transformation matrix. We design an adaptive scaling method for the hidden loss function, dynamically adjusted by the teacher–student prediction accuracy. In summary, the unified loss function for local updates of the teacher and student models for each client is formulated as follows:
The comprehensive loss function is constructed by aggregating the distillation loss, task loss, and adaptive hidden loss. By implementing the backpropagation algorithm, the cumulative loss is reduced to enhance the model’s learning efficiency, and the gradient of the student model on the ith client can be derived from through , where represents the parameter set of the student model. The local teacher model for each client is updated by the local gradient obtained from the loss function . FL, using the knowledge distillation model compression method, has a communication load that depends on the size of the output student model. By capitalizing on the properties of knowledge distillation, the method allows the student model to conceal the heterogeneity of the local model, which helps to mitigate the device heterogeneity and statistical heterogeneity of the data.
4.2. Ternary Quantization Module
To reduce the communication overhead, a two-layer compression strategy is used, and this section is the ternary quantization phase of the local model update, and the local ternary quantization process is shown in Figure 3. For the local client, the distilled student model is trained twice using labeled data, and the student model weights are mapped layer by layer to three discrete values (usually −1, 0, and +1) during the training process to simplify computation and storage. By quantizing the model into a ternary weight network during the training process, this method significantly reduces the model complexity while preserving its performance as much as possible, which is particularly suitable for deep learning.
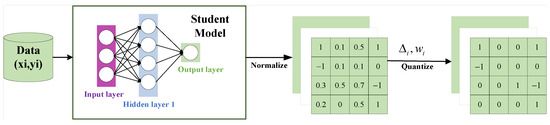
Figure 3.
Ternary quantization process diagram.
First, the weights of the student model are subjected to a normalization operation.
denotes the full-precision weight matrix of the student model, represents the normalized weight matrix, and g signifies the normalization function, which normalizes a vector to a certain random range to make the weight distributions of different layers closer, making the subsequent quantization more stable. Based on normalization, the continuous weights of the student model are discretized into three values (−1, 0, +1) by threshold division, which significantly reduces the storage and computation overhead. Thresholds are determined by generating uniformly distributed random numbers based on the sparsity of the weights used.
where denotes the parameter set of client k, signifies the adaptive optimum value, d indicates the number of layers, and is set to 0.7.
Subsequently, realizing layer-by-layer weight quantization is adopted, in which the quantization accuracy is balanced by adaptive thresholds based on the number of layers and global scaling factors, breaking through the limitations of traditional fixed thresholds.
In this context, denotes a step function, the Hadamard product applies a thresholding operation that sets elements to 1 when their absolute values surpass a certain threshold, is a layer-specific quantization factor that undergoes layer-wise training in conjunction with the local model’s weights, and represents the quantized ternary weights. Therefore, can be expressed as the concatenation of the positive indicator matrix and the negative indicator matrix .
Upon completing the quantization of the entire network, the loss function is calculated, and the error is transmitted backward via backpropagation. and the gradient of the potential full-precision model is computed as follows.
Reducing upstream and downstream communication overhead by quantizing distilled student models also enhances privacy preservation in FL due to the lower weights making it harder to reverse inference sensitive data.
The local model ternary quantization Algorithm 1 is as follows:
| Algorithm 1: Local model ternary quantization . |
 |
4.3. FedDT
The FedDT method uses a multi-round local update strategy, combining two modules, knowledge distillation and ternary quantization. The primary aim is to boost the global model’s accuracy via successive training iterations, while performing model compression during training minimizes storage consumption. The client-side local update process of the FedDT method is illustrated in Figure 4.
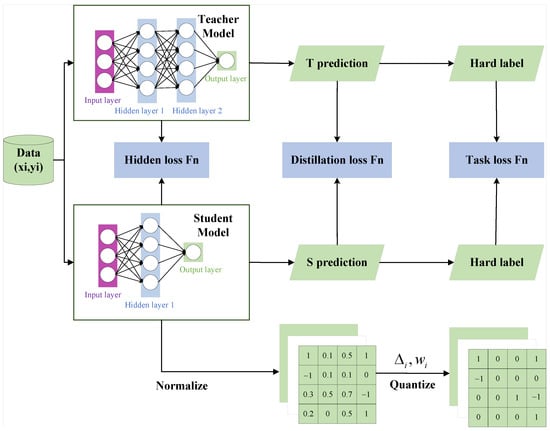
Figure 4.
FL client local update diagram.
The FedDT-specific training process is as follows:
In the context of FL, the server first initializes a global model, , with random weights before the training process begins. Clients subsequently download this model from the server and utilize it as their local student model, . Acknowledging the potential association between client data distributions and model parameters, this study introduces a personalized teacher model, , which is pre-trained for each client using labeled private data to align with the specific patterns of its local data distribution.
(1) Client-Side Local Model Distillation Training. This study employs three distinct loss functions—task loss (Equation (4)), distillation loss (Equation (8)), and hidden loss (Equation (10))—to facilitate reciprocal knowledge transfer between the teacher and student models during training. Dynamic weight allocation is performed throughout the knowledge distillation process, with weights adjusted based on the intensity of either the task loss or distillation loss to enhance student model training. Furthermore, an adaptive hidden loss function is introduced to enable the student model to acquire knowledge from the teacher model’s hidden states (Ht) and attention heatmaps (At).
(2) Local Model Quantization on the Client Side. To further decrease communication overhead and improve model accuracy, the locally labeled data are employed for retraining the student model. Normalization techniques are applied to the student model’s weights during training. On top of normalization, the weights are quantized from full-precision floating-point numbers to a ternary representation (−1, 0, 1) with reduced bit-width, compressing the student model into an adaptive ternary quantized weight network.
(3) Small Model Uploading by the Client. The local quantization model for the clients participating in this training is uploaded to the server.
(4) The central server conducts aggregation of miniature models. During each communication cycle, the server converts the uploaded quantized local models into continuous counterparts and fuses them into the global model.
(5) The server quantizes the global model with the threshold and two quantization factors, and , as defined in Equations (11) and (12). After completing the aggregation process, the server propagates the quantized global model to the client.
(6) Clients obtain the global model. Each participating client in the training phase downloads the quantized global model to perform local model updates. This cycle repeats until the student model and the global model converge.
Algorithm 2 shows the detailed process of knowledge distillation and ternary quantization.
| Algorithm 2: FedDT. |
 |
5. Theoretical Analysis
In this section, we conduct both unbiasedness and convergence proofs for the local knowledge distillation module and the ternary quantization module within the FedDT framework.
5.1. Unbiasedness of FedDT
The unbiasedness proof aims to demonstrate that the output results of the FedDT algorithm, after passing through the knowledge distillation module and the ternary quantization module, are unbiased in the expectation sense. We will separately analyze and prove that the expected outputs of the entire knowledge distillation module and the ternary quantization module are equal to the true unbiased estimates.
Assumption 1.
For all and any , the expectation is taken with respect to the client index k, where w denotes model parameters and B is the heterogeneity bound.
Proposition 1.
In the local knowledge distillation process of federated learning, where the student model optimizes its parameters by learning from the teacher model’s knowledge, we have the following:
Proof of Proposition 1.
According to Equation (4), the task loss function adopts the cross-entropy loss, which is computed based on the true label and the model prediction . Furthermore, during the data sampling process, the samples are independently and identically distributed. Let denote the true label distribution for sample . Since the model training objective is to minimize the cross-entropy loss, the task loss functions and satisfy
The task loss function is unbiased in expectation because the model optimizes towards minimizing the cross-entropy between predictions and true labels.
According to Equation (5), the distillation loss function is based on Kullback–Leibler (KL) divergence, which measures the difference between two probability distributions. During knowledge distillation, the teacher model’s soft labels approximate the true data distribution. As the teacher and student models optimize during training, their predictions converge towards the true data distribution. Thus, the distillation loss satisfies
The distillation loss is unbiased in expectation because the soft labels of teacher model guide the student model to learn a distribution close to the true data distribution.
The adaptive hidden loss function is defined as
where and are the hidden states and attention heatmaps of the teacher model and and are those of the student model. During training, these representations are optimized to approximate the true data features. Thus, the adaptive hidden loss satisfies
The adaptive hidden loss is unbiased in expectation because the hidden states and attention heatmaps are optimized to capture true data features. According to Equations (11) and (12), the total loss function for the knowledge distillation module is
During the knowledge distillation process, the student model optimizes its own parameters by learning from the teacher model’s knowledge. Therefore, the output of knowledge distillation can be regarded as an unbiased estimator of the input.
To theoretically prove the unbiasedness of the ternary quantization module in FedDT, we introduce the following assumption. □
Assumption 2.
The elements of the normalized full-precision parameter Θ are uniformly distributed between −1 and 1, that is,
Based on Assumption 2, we prove Proposition 2:
Proposition 2.
Let Θ be the local scaled network parameters of a certain client in a given federated learning system. If Θ is quantized by the TTQ algorithm, then
Proof of Proposition 2.
According to Equations (21) and (22), is calculated from the elements of the set , where is a fixed number after parameter generation under Assumption 1. Therefore, the elements indexed by I follow a uniform distribution between and 1, that is,
So, the probability density function f of can be expressed as . According to Proposition 2, we can obtain
Let u be a random variable following the distribution in Equation (39), and I represents the number of elements in the set I. We know that
It can be further transformed into
Then, we calculate , and its value is
Under Assumption 2, we have
From this, we can immediately obtain the following:
Therefore, the output of the ternary quantizer can be considered an unbiased estimate of the input. When the weights are uniformly distributed, we can ensure the unbiasedness of FedDT in the federated learning system. □
5.2. Convergence Analysis
We have proven that the unbiasedness of FedDT holds. This section conducts a convergence analysis of FedDT.
Proposition 3.
Let be L-smooth and μ-strongly convex functions.
where are the mini-batch data points uniformly randomly sampled from the data of the k-th client.
In addition, we assume that the smallest eigenvalue of the client loss function is uniformly bounded below by a constant, . For all and any , where the expectation is calculated with respect to the client index k.
Then, for a federated learning system where all N devices fully participate and the data are distributed independently and identically, the convergence rate of the FedDT algorithm is , where R is the total number of iterations of stochastic gradient descent (SGD) performed by each client.
Proof of Proposition 3.
Here, we provide a concise proof that primarily relies on the proof given by Qu et al. [49]. According to Equations (11) and (12), the loss function of the knowledge distillation module consists of three components:
For the task loss function, we adopt the cross-entropy loss, whose gradient is . The distillation loss function is based on KL divergence, with the gradient . The adaptive hidden loss function F (based on the mean squared error) has the gradient .
In each iteration, the parameter update rule is
where is the learning rate.
According to convergence theorem of gradient descent, if the loss function F is convex and the learning rate satisfies certain conditions (e.g., , where L is the Lipschitz constant of F), then where is the optimal parameter.
For the loss function F in the knowledge distillation module, by analyzing its gradient, we obtain
This indicates that the student model’s parameters converge to the optimal solution as the number of iterations r increases. Let
and the corresponding
According to Proposition 2, we have
So, based on Proposition 3, we let , and we set the step size according to [49]. Then, based on Proposition 3, we have
Then, according to Equations (54) and (55), we can obtain the convergence rate of FedDT in the following way:
where is a sufficiently large constant for inequality scaling. Therefore, if we set the local error , then , and the convergence rates of the federated averaging algorithm FedAvg and FedDT are both . □
6. Experiment
In this section, detail how we performed an empirical evaluation of the FedDT framework against leading FL algorithms, examining communication overhead, model performance, and convergence behavior. Moreover, ablation studies were carried out to quantitatively measure the individual contributions of each novel component. Finally, we systematically analyzed the underlying mechanisms driving the observed experimental outcomes.
6.1. Experimental Setup
6.1.1. Datasets
Two benchmark datasets, MNIST and Cifar10, which are widely used in classification tasks, were adopted as FL datasets, as shown in Table 2. These two datasets are widely used in the field of FL and provided us with rich and diverse data resources to train and test the performance of various FL algorithms.

Table 2.
Statistical information of common deep neural network compression and acceleration.
(1) MNIST: The MNIST dataset consists of 10 categories (handwritten numbers 0 to 9); each image is a 28 × 28 pixel grayscale map. Because of its simple feature extraction mechanism, the MNIST dataset is widely adopted for training and validating small neural networks, making it a popular choice for educational purposes and algorithm benchmarking.
(2) Cifar10: The Cifar10 dataset contains 10 distinct object categories represented as 32 × 32 pixel RGB images with three color channels. To address the challenges in feature extraction arising from the dataset’s complexity, we applied data augmentation strategies such as random cropping and horizontal flipping to enrich training data diversity.
6.1.2. Data Distribution
In the real world, data present a non-independent homogeneous distribution in different scenarios. The distribution characteristics, the diversity of the labels, the extent of the dataset critically affect the training performance and the model’s applicability across diverse scenarios. Accordingly, the deliberate construction of data allocation schemes is fundamental for the comprehensive assessment of FL methodologies. To more realistically simulate the randomness of data and the non-independent homogeneous distribution of labels in the real world, this paper designed two data partitioning strategies, independent homogeneous distribution and non-independent homogeneous distribution, for the datasets.
(1) IID data: The entire dataset was first randomly disrupted, and then the same number of samples was uniformly sampled and distributed to 100 clients to maintain congruence between the local data distribution at each client and the global data distribution.
(2) Non-IID data: The aggregated dataset across all clients encompassed the complete dataset, yet the class distribution among clients remained uneven, with each client containing a subset of the total 10 classes. By employing labeling strategies, we could allocate distinct classes to each client, where represents the predetermined number of labeled classes per client.
6.1.3. Basic Configuration
Hardware Configuration: In evaluating the proposed FedDT, each client maintained communication solely with the server, prohibiting any form of information sharing among clients. Usually, 100 clients are used for simulation experiments. The training parameters are listed in Table 3 below.

Table 3.
FL parameter settings.
6.1.4. Baselines
To verify the efficiency of the FedDT method’s communication and the accuracy of model prediction, we chose three advanced FL baseline algorithms for comparison, including the classical FL algorithm FedAvg [7], and four efficient FL algorithms for data heterogeneity, Feddistll [42], FedKD [27], MOON [39], and FedProto [45]. The above three schemes are the best performing studies at present, so in this paper, we compared FedDT with the above three baseline methods.
(1) FedAvg is the first FL algorithm that systematically solves the distributed data training problem and has been applied in practice in production. The core idea is to achieve privacy protection through localized training, where the raw data remain stored locally on client devices, with only model parameter updates transmitted to the server.
(2) The Feddistill method combines two complementary federated augmentation (FAug) and federated distillation (FD) techniques, in which a GAN is used in federated augmentation to locally heterogeneous data augmented into independent and homogeneously distributed data, and federated distillation uploads logit vectors to reduce the communication overhead in FL caused by large-scale model parameters and frequent client–server interactions.
(3) The FedKD algorithm optimizes privacy leakage in the Feddistill method and further improves model performance and decreases communication overhead in heterogeneous FL via the combination of state-of-the-art FL integrating adaptive mutual knowledge distillation and dynamic gradient compression.
(4) MOON is a simple yet effective federated learning framework. Its core concept lies in addressing data heterogeneity by leveraging model-level contrastive learning, which corrects local training processes through the similarity between global model representations and local model representations, thereby mitigating the adverse effects of non-IID data distributions.
(5) FedProto replaces gradient communication with abstract class prototypes. Clients compute class prototypes based on their local data; the server aggregates these client prototypes to generate global prototypes. During training, clients align their local prototypes with global prototypes while minimizing classification loss.
6.2. Performance Analysis on the IID Dataset
6.2.1. Results on Centralized Machine Learning and FL
For a fair assessment of model performance, comparisons were made after 100 training iterations, ensuring that each model was trained on the same number of samples. In the case of MNIST, for example, there were 100 clients in the FL system, each with 600 samples, running 100 rounds of model training. Correspondingly, centralized model training used 60,000 samples to train 100 epochs. As the ratio remained bounded by 1, FL inherently employed a reduced training sample size compared to centralized learning frameworks.
A summary of the accuracy levels achieved by the baseline models in the centralized machine learning and FL paradigms is provided in Table 4.

Table 4.
Accuracy of different models on IID and non-IID Cifar10 datasets.
6.2.2. Results on FedDT and Baseline Algorithms
In this section, a conventional IID FL scenario is analyzed, where all clients participated in training a common global model.
Figure 5 illustrates the convergence of test performance for six federated learning algorithms under IID data distributions over 100 communication rounds. The y-axis represents the model prediction accuracy, while the x-axis denotes communication rounds. As shown in Figure 5a, in the IID MNIST dataset, FedDT achieved an accuracy of 99.09%, comparable to that of FedKD. As training progressed, both FedDT and FedKD significantly outperformed the other four algorithms. In Figure 5b, it can be seen that in the IID Cifar10 dataset, FedDT achieved an accuracy of 87%, second only to MOON, and demonstrated clear superiority over the other four baseline methods.
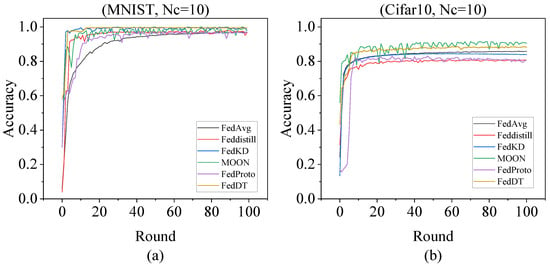
Figure 5.
Convergence performance comparison of six algorithms across communication rounds under IID conditions. (a) Convergence performance comparison of six algorithms on the MNIST dataset under IID conditions. (b) Convergence performance of six algorithms on the Cifar10 dataset under IID conditions.
Table 5 summarizes the performance of various algorithms on MNIST/Cifar10 under standard federated learning settings. Figure 6 provides a visual comparison of the accuracy gaps between FedDT and other algorithms. FedDT achieved high accuracy levels of 99. 09% with MNIST and 87. 04% with Cifar10, underscoring its robustness and generalization capability in IID environments. These results validate that FedDT’s multiround local update strategy enhances model performance through iterative local training.

Table 5.
Comparison of accuracy of different algorithms on various IID datasets in image classification tasks.
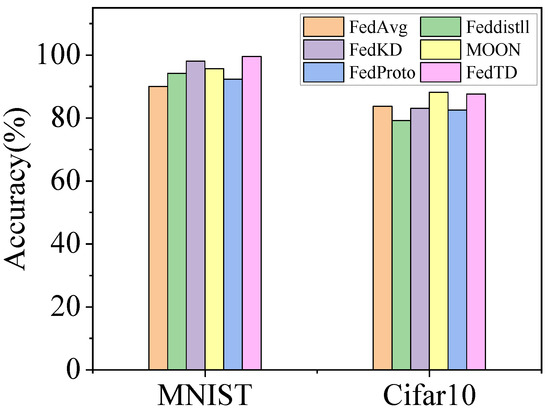
Figure 6.
Comparison of accuracy of six algorithms on MNIST and Cifar10 datasets.
6.2.3. Performance Analysis of Non-IID Data
For the non-independently identically distributed data scenario (non-IID), we proposed a category-controlled data partitioning strategy, as visualized in Figure 7. The vertical axis (y-axis) of the plot represents sample labels ranging from 0 to 9. Under the IID setting ( = 10), each client was randomly allocated an equal share of 10 labeled categories via uniform sampling, maintaining the original IID distribution of both training and testing data. For non-IID scenarios, the data partitioning followed a deliberate stratification approach to generate class-imbalanced distributions across clients. For example, when = 2, each client contained only two types of data labels, and there was no overlap of the data of clients. When = 5, each client had five types of data labels, and at this time, there was some overlap in client data.
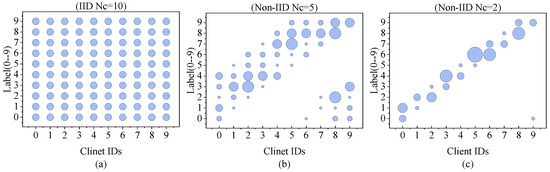
Figure 7.
Data partitioning for clients when = 10; = 5; and = 2. Bubble size indicates the amount of data. (a) Data partitioning scenario with = 10, where client datasets were randomly sampled from the overall distribution. (b) Partitioning configuration with = 5, allocating 5 class labels per client while permitting controlled data overlap. (c) Strict partitioning case with = 2, assigning exactly 2 class labels per client with zero data overlap between clients.
Figure 8 depicts the convergence behavior of six federated learning algorithms on Cifar10 under non-IID settings ( = 2 and = 5) over 100 communication rounds. FedDT consistently outperformed the other five algorithms in both convergence speed and final accuracy. Table 6 details the performance of all algorithms on non-IID Cifar10 ( = 2 and = 5), while Figure 9 highlights the accuracy gap between FedDT and traditional methods. FedDT achieved state-of-the-art accuracy rates of 89.67%, 90.89%, 52.36%, and 74.41% on MNIST and Cifar10, surpassing all competitors.
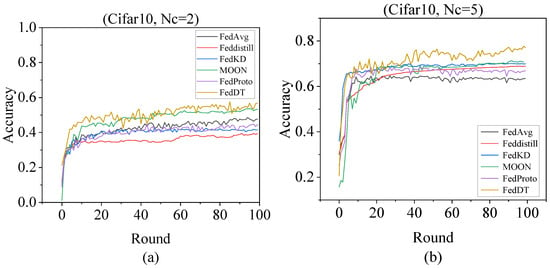
Figure 8.
Convergence curves of test performance for six algorithms in terms of communication rounds under IID conditions. (a) Communication round convergence analysis of six FL algorithms on Cifar10 with = 2 client partitions. (b) Communication round convergence analysis of six FL algorithms on Cifar10 with = 5 client partitions.

Table 6.
Algorithm accuracy under data heterogeneity.
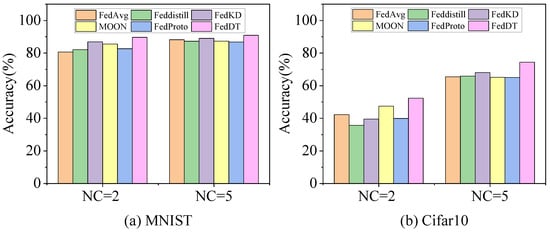
Figure 9.
Algorithm accuracy under data heterogeneity. (a) Comparative convergence analysis of six FL algorithms over 100 communication rounds on non-IID MNIST with = 2 and = 5 client settings. (b) Comparative convergence analysis of six FL algorithms over 100 communication rounds on non-IID Cifar10 with = 2 and = 5 client settings.
The experimental results confirm that FedDT effectively mitigates data shift issues in heterogeneous federated learning while preserving global model diversity. This advantage stems from its dynamic integration of knowledge distillation and ternary quantization within a multi-round local update framework, enabling robust performance under both IID and non-IID conditions.
6.3. Ablation Experiments
Results on Model Accuracy
To assess the performance of the FedDT approach, we performed an ablation analysis. Four experimental strategies were applied to non-IID MNIST and Cifar10 datasets to evaluate the FL model’s prediction performance. None means that neither the knowledge distillation nor ternary quantization method was applied, D means that only the knowledge distillation method was applied, T means that only the ternary quantization method was applied, and Both means that both strategies were applied at the same time.
The precision of the models trained with FL in the ablation experimental study is demonstrated in Table 7, and a more visual comparison of the model performance accuracy gap under the application of each module is presented in Figure 10. On the MNIST/Cifar10 datasets with data independently and identically distributed, the precision was improved by 2.42% and 9.34% using only the knowledge distillation method and by 3.46% and 3.23% using only ternary quantization.

Table 7.
Accuracy using different strategies on non-IID MNIST and Cifar10 datasets.
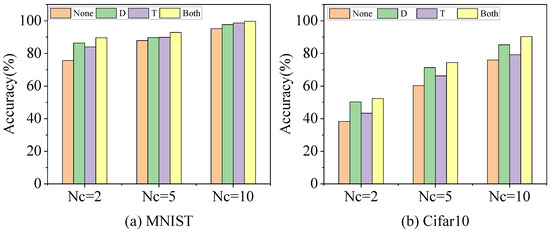
Figure 10.
Accuracy using different strategies on non-IID MNIST and Cifar10 datasets. (a) Model accuracy under four ablation strategies across three distinct data distribution scenarios on MNIST dataset. (b) Model accuracy under four ablation strategies across three distinct data distribution scenarios on Cifar10 dataset.
In heterogeneous FL, on the MNIST/Cifar10 datasets at Nc = 2, the accuracy was improved by 10.82% and 11.91% using only knowledge distillation and by 8.38% and 5.07% using only ternary quantization; on the MNIST/Cifar10 datasets at Nc = 5, the accuracy was improved by 2.81% using only knowledge distillation and 11.11%, and using only ternary quantization improved accuracy by 1.99% and 5.9%.
By comparing the accuracy values of the knowledge distillation and ternary quantization of the boosted models in different scenarios, it is demonstrated that the knowledge distillation strategy contributed more to the model accuracy than the ternary quantization strategy in FL with data heterogeneity, based on the fact that knowledge distillation compensated for the client-side data distribution bias through the property of soft-label delivery.
6.4. Results on Communication Overhead
In this section, we detail how we conducted a comprehensive experimental analysis focusing on communication overhead as a critical performance metric. First, we compared the total communication costs of six federated learning methods over 100 training rounds. Furthermore, an ablation study was performed to quantify the impact of individual system components on communication efficiency.
6.4.1. Communication Efficiency
Figure 5 demonstrates the per-round accuracy evolution during training under IID federated learning settings. FedDT achieved comparable convergence speed to FedAvg in the initial phase, while attaining higher final accuracy (close to FedKD) in later stages. Figure 8 illustrates the per-round accuracy progression in non-IID federated learning scenarios. FedDT exhibited faster convergence than the other five baseline algorithms and ultimately achieved superior accuracy, outperforming all competitors. This advantage stems from FedDT’s multi-round training strategy, which dynamically balances local model updates and global knowledge distillation to mitigate data heterogeneity.
Table 8 compares the number of communication rounds required for FedDistill, FedKD, MOON, FedProto, and the proposed FedDT to achieve the same accuracy as that of the baseline FedAvg after its convergence. The symbol “-” indicates that a method failed to match the baseline accuracy in a specific scenario. The experimental results demonstrate that FedDT achieved comparable communication rounds to those of MOON and significantly fewer than the baseline FedAvg did, markedly outperforming FedDistill, FedKD, and FedProto and thereby substantially reducing communication cycles.

Table 8.
The number of communication rounds required for different approaches to achieve the same accuracy as that of the baseline FedAvg. Speedup ratios were computed relative to those of FedAvg.
Under both IID and Non-IID federated learning scenarios, FedDT achieved speedup ratios of 6.25×, 5×, 4.762×, and 8.889×, closely aligning with MOON while surpassing all other methods by a wide margin. This efficiency improvement is attributed to FedDT’s multi-round training strategy based on knowledge distillation and ternary compression, which dramatically enhances communication efficiency by decoupling knowledge transfer from high-dimensional parameter synchronization.
6.4.2. Communication Overhead Comparison of Federated Learning Algorithms
To evaluate the advantages of FedDT in reducing communication costs, this study conducted a comparative analysis of the communication costs incurred by three FL baseline algorithms and FedDT across fixed communication rounds. Given that the computation methodology for communication costs remained consistent across both IID and non-IID FL scenarios, the communication cost in non-IID scenarios is not analyzed separately in the following. In FL, the numbers of MLP and CNN model parameters exchanged per global iteration were 24,320 and 1,199,648, respectively. In the experimental design, each client configured the CNN model as the local training model, and the global model generated by knowledge distillation uniformly adopted the MLP model. For FedDT, this study considered the ternary quantization part of the local model 2 bits to calculate the upstream communication cost.
As shown in Table 9, the FedDT algorithm demonstrated a remarkable 99% reduction in communication overhead compared to the baseline FedAvg method under identical training rounds. When compared with four other communication-efficient federated learning approaches, FedDT maintained competitive communication efficiency, exhibiting costs only marginally higher than those of the MOON method. These results highlight FedDT’s breakthrough improvements in communication efficiency over conventional federated learning frameworks while remaining comparable to state-of-the-art solutions.

Table 9.
Communication costs of six algorithms using MLP and CNN models.
This significant advancement primarily benefits from FedDT’s two-tier compression mechanism: knowledge distillation-based model compression transfers knowledge from large teacher models to compact student models, effectively reducing communication costs which depend solely on the student model size; and ternary quantization further compresses upstream communication of local student models to 1/32 of their original parameter size.
It should be noted that due to inherent differences in algorithm personalization and the implementation frameworks across methods, the communication costs presented in Table 9 serve as reference values specific to the tested parameter configurations and model architectures. This comparative analysis focuses primarily on quantifying relative efficiency improvements rather than establishing absolute performance benchmarks.
6.4.3. Ablation Study of Communication Overhead
For a particular device, when the personalized teacher model was a global CNN and the student model was an MLP, the total communication cost of FL was calculated after using different strategies, where the numbers of MLP and CNN model parameters exchanged per global iteration were 24,320 bits and 1,199,648 bits, respectively.
Table 10 demonstrates the effect of different strategy modules in the FedDT method on the cost of FL communication. The knowledge distillation strategy achieved a compression rate of 49.3 times by compressing the high-parameter model into a low-parameter model. The ternary quantization achieved a 16-fold compression rate. This two-layer compression strategy allowed FedDT to maintain 99.74% and 90.34% accuracy on the MNIST and Cifar10 datasets, and the FedDT method demonstrated an ultra-low communication cost equivalent to 0.127% of traditional methods. Its communication load is directly related to the output student model’s size, while the ternary quantization mechanism further reduces model parameters, achieving substantial communication overhead reduction via a two-level compression strategy.

Table 10.
Communication costs using different strategies.
7. Conclusions
This paper proposes a communication-efficient FL framework, named FedDT, which synergizes knowledge distillation and ternary compression techniques. Specifically, we design client-specific heterogeneous teacher models to reduce the negative impact of non-IID data, thereby improving both model performance and generalization capability. To facilitate knowledge transfer across diverse local models, we introduce a shared student model initialized by the server, enabling consistent knowledge aggregation. During local updates, each client distills personalized knowledge from its teacher model into the homogeneous student model, effectively eliminating cross-client knowledge transfer barriers. Furthermore, we propose a two-level compression strategy that combines adaptive knowledge distillation with ternary quantization to minimize communication overhead. By replacing continuous weight parameters with discrete ternary values, the student model’s size is significantly reduced, thereby lowering communication costs without sacrificing performance. Experimental results demonstrate that, compared to baseline methods on the MNIST and Cifar10 datasets, FedDT achieved significant performance gains in two critical metrics: model accuracy and communication efficiency. Notably, under high-data-heterogeneity scenarios, the multi-round local update strategy substantially improves overall system performance. The proposed approach effectively reduces communication costs while providing a lightweight solution for FL in distributed large-scale data environments.
Although the FedDT method significantly cuts communication overhead while safeguarding model accuracy, it introduces additional computational demands on client devices. Systems applying FL need to consider the overall performance, and our future work will dynamically adjust the model training strategy according to the client’s data distribution, computational power, and network state. Furthermore, we aim to explore more efficient compression algorithms to enhance the model generalization capability in FL, especially under complex scenarios.
Author Contributions
This manuscript was discussed by all authors. Manuscript design, drafting, and technical implementation were completed by Z.H. and G.Z., who also analyzed the experimental results. Critical revisions were performed by S.Z. Manuscript drafting and revision were jointly completed by S.Z., Z.H., E.L., and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 62272162 and 62172159), the Hunan Provincial Natural Science Foundation of China (Grant No. 2025JJ50398), and the project of the Hunan Provincial Social Science Achievement Review Committee of China (Grant No. XSP25YBZ104).
Data Availability Statement
The datasets generated during this study are accessible upon reasonable request to the corresponding author, as they contain sensitive information restricted by privacy regulations.
Acknowledgments
This work greatly benefits from the insightful contributions of all authors, and we are deeply grateful for the institutional resources and laboratory assistance that enabled its completion.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following notation are used in this manuscript:
| Notation | Description |
| Learning rate of teacher model | |
| Learning rate of student model | |
| Parameters of client’s teacher network | |
| Parameters of client’s student network | |
| Local gradients for clients i, , and | |
| represents input data; represents corresponding target | |
| Global model parameters in round r | |
| Crash threshold for model parameters | |
| r | Current round of algorithm |
| T | Total number of rounds |
| K | Index of set of clients |
| Percentage of client selection | |
| Local dataset for client k | |
| Model parameters for client k in round r | |
| , | Collection of indices for positive and negative values |
| , | Weighting of positive and negative values |
References
- Zhang, S.; Pan, Y.; Liu, Q.; Yan, Z.; Choo, K.K.R.; Wang, G. Backdoor attacks and defenses targeting multi-domain ai models: A comprehensive review. ACM Comput. Surv. 2024, 57, 1–35. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Peng, T.; Liu, Q.; Li, X. VADP: Visitor-attribute-based adaptive differential privacy for IoMT data sharing. Comput. Secur. 2025, 156, 104513. [Google Scholar] [CrossRef]
- Ye, M.; Shen, W.; Du, B.; Snezhko, E.; Kovalev, V.; Yuen, P.C. Vertical federated learning for effectiveness, security, applicability: A survey. ACM Comput. Surv. 2025, 57, 1–32. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Q.; Wang, T.; Liang, W.; Li, K.C.; Wang, G. FSAIR: Fine-grained secure approximate image retrieval for mobile cloud computing. IEEE Internet Things J. 2024, 11, 23297–23308. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Li, X.; Liu, Q.; Wang, G. APBAM: Adversarial perturbation-driven backdoor attack in multimodal learning. Inf. Sci. 2025, 700, 121847. [Google Scholar] [CrossRef]
- Kogut-Czarkowska, M.; Shabani, M. Federated networks and secondary uses of health data: Challenges in ensuring appropriate safeguards for sharing health data under the GDPR and EHDS. In The European Health Data Space; Taylor & Francis: Milton Park, UK, 2025. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Tan, A.Z.; Yu, H.; Cui, L.; Yang, Q. Towards personalized federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9587–9603. [Google Scholar] [CrossRef]
- Karimireddy, S.P.; Kale, S.; Mohri, M.; Reddi, S.; Stich, S.; Suresh, A.T. Scaffold: Stochastic controlled averaging for federated learning. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 5132–5143. [Google Scholar]
- Liao, X.; Liu, W.; Chen, C.; Zhou, P.; Yu, F.; Zhu, H.; Yao, B.; Wang, T.; Zheng, X.; Tan, Y. Rethinking the representation in federated unsupervised learning with non-iid data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 22841–22850. [Google Scholar]
- Yang, Z.; Zhang, Y.; Zheng, Y.; Tian, X.; Peng, H.; Liu, T.; Han, B. Fedfed: Feature distillation against data heterogeneity in federated learning. Adv. Neural Inf. Process. Syst. 2023, 36, 60397–60428. [Google Scholar]
- Zhang, J.; Cheng, X.; Wang, W.; Yang, L.; Hu, J.; Chen, K. {FLASH}: Towards a high-performance hardware acceleration architecture for cross-silo federated learning. In Proceedings of the 20th USENIX Symposium on Networked Systems Design and Implementation (NSDI 23), Boston, MA, USA, 17–19 April 2023; pp. 1057–1079. [Google Scholar]
- Ding, Y.; Ji, Y.; Cai, X.; Xin, X.; Lu, Y.; Huang, S.; Liu, C.; Gao, X.; Murata, T.; Lu, H. Towards personalized federated multi-scenario multi-task recommendation. In Proceedings of the Eighteenth ACM International Conference on Web Search and Data Mining, Hannover, Germany, 10–14 March 2025; pp. 429–438. [Google Scholar]
- Makhija, D.; Han, X.; Ho, N.; Ghosh, J. Architecture agnostic federated learning for neural networks. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 14860–14870. [Google Scholar]
- Bharati, S.; Mondal, M.R.H.; Podder, P.; Prasath, V.S. Federated learning: Applications, challenges and future directions. Int. J. Hybrid Intell. Syst. 2022, 18, 19–35. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. Fedmd: Heterogenous federated learning via model distillation. arXiv 2019, arXiv:1910.03581. [Google Scholar]
- Diao, E.; Ding, J.; Tarokh, V. Heterofl: Computation and communication efficient federated learning for heterogeneous clients. arXiv 2020, arXiv:2010.01264. [Google Scholar]
- Beltrán, E.T.M.; Pérez, M.Q.; Sánchez, P.M.S.; Bernal, S.L.; Bovet, G.; Pérez, M.G.; Pérez, G.M.; Celdrán, A.H. Decentralized federated learning: Fundamentals, state of the art, frameworks, trends, and challenges. IEEE Commun. Surv. Tutor. 2023, 25, 2983–3013. [Google Scholar] [CrossRef]
- Qi, P.; Chiaro, D.; Guzzo, A.; Ianni, M.; Fortino, G.; Piccialli, F. Model aggregation techniques in federated learning: A comprehensive survey. Future Gener. Comput. Syst. 2024, 150, 272–293. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, T.; Liu, Q.; Luo, E.; Choo, K.K.R.; Wang, G. ALPS: Achieving accuracy-aware location privacy service via assisted regions. Future Gener. Comput. Syst. 2023, 145, 189–199. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, Z.; Xu, H.; Wang, Z.; Qian, C.; Qiao, C. Federated learning with client selection and gradient compression in heterogeneous edge systems. IEEE Trans. Mob. Comput. 2023, 23, 5446–5461. [Google Scholar] [CrossRef]
- Yue, K.; Jin, R.; Wong, C.W.; Baron, D.; Dai, H. Gradient obfuscation gives a false sense of security in federated learning. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 6381–6398. [Google Scholar]
- Seo, H.; Park, J.; Oh, S.; Bennis, M.; Kim, S.L. Federated knowledge distillation. In Machine Learning and Wireless Communications; Cambridge University Press: Cambridge, UK, 2022; pp. 457–485. [Google Scholar]
- Peng, T.; You, W.; Guan, K.; Luo, E.; Zhang, S.; Wang, G.; Wang, T.; Wu, Y. Privacy-preserving multiobjective task assignment scheme with differential obfuscation in mobile crowdsensing. J. Netw. Comput. Appl. 2024, 224, 103836. [Google Scholar] [CrossRef]
- Itahara, S.; Nishio, T.; Koda, Y.; Morikura, M.; Yamamoto, K. Distillation-based semi-supervised federated learning for communication-efficient collaborative training with non-iid private data. IEEE Trans. Mob. Comput. 2021, 22, 191–205. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Lyu, L.; Huang, Y.; Xie, X. Communication-efficient federated learning via knowledge distillation. Nat. Commun. 2022, 13, 2032. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, B.; Hooi, B.; Yan, S.; Feng, J. Deep long-tailed learning: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10795–10816. [Google Scholar] [CrossRef]
- Peng, T.; Zhong, W.; Wang, G.; Zhang, S.; Luo, E.; Wang, T. Spatiotemporal-aware privacy-preserving task matching in mobile crowdsensing. IEEE Internet Things J. 2023, 11, 2394–2406. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Luo, E.; Liu, Q.; Gu, K.; Wang, G. A traceable and revocable decentralized multi-authority privacy protection scheme for social metaverse. J. Syst. Archit. 2023, 140, 102899. [Google Scholar] [CrossRef]
- Pei, J.; Liu, W.; Li, J.; Wang, L.; Liu, C. A review of federated learning methods in heterogeneous scenarios. IEEE Trans. Consum. Electron. 2024, 70, 5983–5999. [Google Scholar] [CrossRef]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Huang, Y.; Chu, L.; Zhou, Z.; Wang, L.; Liu, J.; Pei, J.; Zhang, Y. Personalized cross-silo federated learning on non-iid data. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 7865–7873. [Google Scholar]
- Ruan, Y.; Zhang, X.; Liang, S.C.; Joe-Wong, C. Towards flexible device participation in federated learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; pp. 3403–3411. [Google Scholar]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Wang, X.; Chen, W.; Xia, J.; Wen, Z.; Zhu, R.; Schreck, T. HetVis: A visual analysis approach for identifying data heterogeneity in horizontal federated learning. IEEE Trans. Vis. Comput. Graph. 2022, 29, 310–319. [Google Scholar] [CrossRef]
- Zhou, X.; Lei, X.; Yang, C.; Shi, Y.; Zhang, X.; Shi, J. Handling data heterogeneity for iot devices in federated learning: A knowledge fusion approach. IEEE Internet Things J. 2023, 11, 8090–8104. [Google Scholar] [CrossRef]
- Casey, J.; Chen, Q.; Fan, M.; Geng, B.; Shterenberg, R.; Chen, Z.; Li, K. Distributed Collaborative Learning with Representative Knowledge Sharing. Mathematics 2025, 13, 1004. [Google Scholar] [CrossRef]
- Li, Q.; He, B.; Song, D. Model-contrastive federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 10713–10722. [Google Scholar]
- Sabah, F.; Chen, Y.; Yang, Z.; Azam, M.; Ahmad, N.; Sarwar, R. Model optimization techniques in personalized federated learning: A survey. Expert Syst. Appl. 2024, 243, 122874. [Google Scholar] [CrossRef]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Jeong, E.; Oh, S.; Kim, H.; Park, J.; Bennis, M.; Kim, S.L. Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data. arXiv 2018, arXiv:1811.11479. [Google Scholar]
- He, C.; Annavaram, M.; Avestimehr, S. Group knowledge transfer: Federated learning of large cnns at the edge. Adv. Neural Inf. Process. Syst. 2020, 33, 14068–14080. [Google Scholar]
- Hamer, J.; Mohri, M.; Suresh, A.T. Fedboost: A communication-efficient algorithm for federated learning. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 3973–3983. [Google Scholar]
- Tan, Y.; Long, G.; Liu, L.; Zhou, T.; Lu, Q.; Jiang, J.; Zhang, C. Fedproto: Federated prototype learning across heterogeneous clients. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 8432–8440. [Google Scholar]
- Zhu, C.; Han, S.; Mao, H.; Dally, W.J. Trained ternary quantization. arXiv 2016, arXiv:1612.01064. [Google Scholar]
- Liu, H.; He, F.; Cao, G. Communication-efficient federated learning for heterogeneous edge devices based on adaptive gradient quantization. In Proceedings of the IEEE INFOCOM 2023-IEEE Conference on Computer Communications, New York, NY, USA, 17–20 May 2023; pp. 1–10. [Google Scholar]
- Vargaftik, S.; Basat, R.B.; Portnoy, A.; Mendelson, G.; Itzhak, Y.B.; Mitzenmacher, M. Eden: Communication-efficient and robust distributed mean estimation for federated learning. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 21984–22014. [Google Scholar]
- Qu, Z.; Lin, K.; Li, Z.; Zhou, J.; Zhou, Z. A unified linear speedup analysis of federated averaging and nesterov fedavg. J. Artif. Intell. Res. 2023, 78, 1143–1200. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).