ESCI: An End-to-End Spatiotemporal Correlation Integration Framework for Low-Observable Extended UAV Tracking with Cascade MIMO Radar Subject to Mixed Interferences

Abstract

Continuous and robust trajectory tracking of unmanned aerial vehicles (UAVs) plays a crucial role in urban air transportation systems. Accordingly, this article presents an end-to-end spatiotemporal correlation integration (ESCI)-based UAV tracking framework by leveraging a high-resolution cascade multiple input multiple output (MIMO) radar. On this account, a novel joint anti-interference detection and tracking system for weak extended targets is presented in this paper; the proposed method handles them jointly by integrating a continuous detection process into tracking. It not only eliminates the threshold decision-making process to avoid the loss of weak target information, but also significantly reduces the interference from other co-channel radars and strong clutters by exploring the spatiotemporal correlations within a sequence of radar frames, thereby improving the detectability of weak targets. In addition, to accommodate the time-varying number and extended size of radar reflections, with the ellipse spatial probability distribution model, the extended UAV with multiple scattering sources can be treated as an entity to track, and the complex measurement-to-object association procedure can be avoided. Finally, with Texas Instruments AWR2243 (TI AWR2243) we can utilize a cascade frequency-modulated continuous wave–multiple input multiple output (FMCW-MIMO) radar platform. The results show that the proposed method can obtain outstanding anti-interference performance for extended UAV tracking compared with state-of-the-art methods.

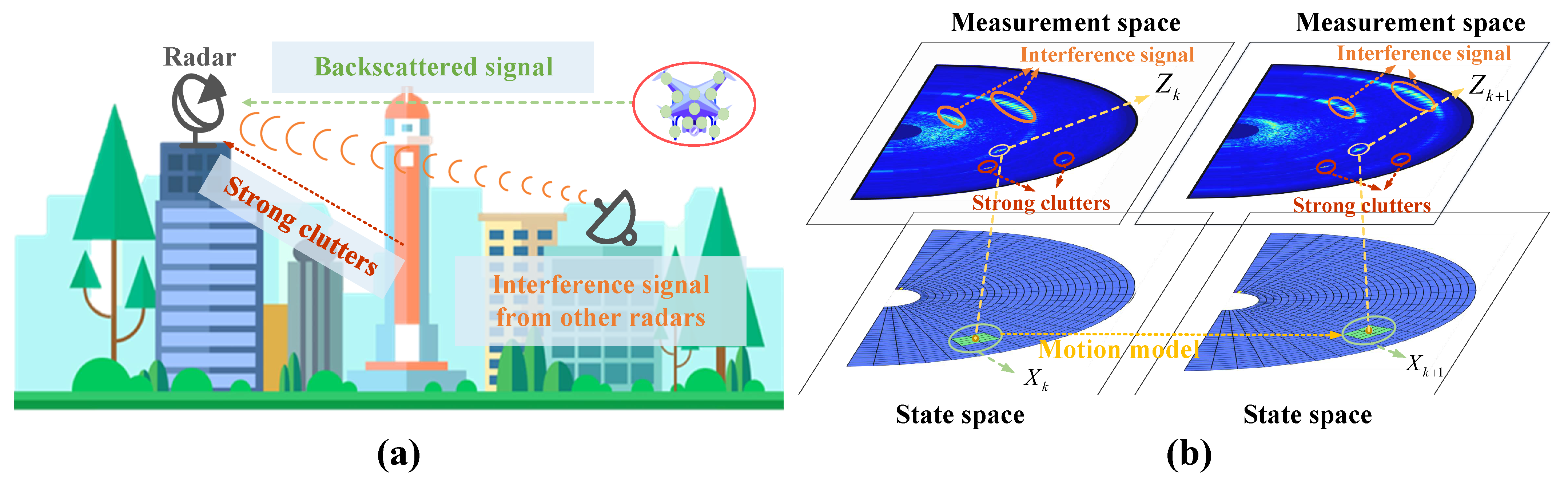
1. Introduction

Thanks to the enormous progress of UAV technology, urban air mobility (UAM) is predicted to be an innovative transportation system that will provide a variety of services, such as the safe and efficient delivery of shipments and passengers, search and rescue missions and medical assistance in low-altitude airspace, which is as important as ground-based transportation systems [1,2]. As a critical component of the bottom-most perception layer in UAM, UAV tracking plays a key role in accurate control decisions, intelligent and safe navigation and malicious vehicle prevention [3,4,5,6]. In addition, in future zero-trust management architecture [7], reliable trajectory tracking is the prerequisite for trust evaluation and safe flight in UAM. However, it is always a popular and challenging issue for UAV tracking because of the small shape and complex interferences in low altitude.

In the past decades, frequency modulated continuous wave (FMCW) radar, which can provide both long detection range and high-range resolution has been widely utilized in moving target tracking [7,8,9,10]. Recently, the advances in cascade multiple input multiple output (MIMO) techniques [11,12] provide increasing resolutions for angle of arrival (AOA). High range and angle resolutions of cascade FMCW-MIMO radar can not only achieve good resistance to interferences from multipath and clutter but also obtain rich extension parameters in addition to conventional locations and kinematic states, such as shape, size and, possibly, directions of motion, which can provide supplemental information for target tracking, as well as next planning and control [13,14]. On this account, we explore the feasibility of implementing low-observable aerial vehicle tracking with high-resolution cascade FMCW-MIMO radar in this article.

In high-resolution cascaded FMCW-MIMO radar systems, there may be multiple spatially distributed measurement sources on the unmanned aerial vehicle (UAV). In each time step, the backscattered signals from different measurement sources will occupy multiple resolution cells of the measurement space, as shown in Figure 1. On this account, the point-target assumption in classical tracking methods, such as particle filter (PF) [15], Kalman filter (KF) and its variants [16,17], will become invalid. Although the spatially distributed measurements can be treated as multiple targets to track by means of data association-based algorithms, such as nearest neighbor data association (NNDA) [18], joint probabilistic data association (JPDA) [19] and multiple hypothesis tracker (MHT) [20], it is difficult to complete accurate measurement-to-source association because the extended measurements highly depend on the properties of the target and the radar-to-object geometry, which often quickly varies with moving targets. Also, the contour tracking algorithm [21] is not appropriate for tracking extended UAV either because it is nearly impossible to correctly extract the contour with the sparse and time-varying radar point cloud. In [22], to achieve extended target tracking, the center point of the multiple spatially distributed measurements was first extracted by density-based spatial clustering of applications with noise (DBSCAN) and then the classic point tracking method was employed to track the cluster center. Unfortunately, the extended features (e.g., the shapes and sizes) hidden in measurements will be lost in the clustering process. By introducing shape parameters in the target state, the random matrix method (RMM) [23,24] and random finite set (RFS) approaches [25,26] can simultaneously track the positions and extensions of a target without considering measurement-to-source association problem. Additionally, the second-order extended Kalman filter (SOEKF) [27] and random hypersurface modeling (RHM) [28] are two other effective extended target tracking methods. Nevertheless, the tracking performance of these approaches highly depend on the accuracy of detections, which may be easily interfered with by interferences in urban air environments, such as mutual intrusion from other co-channel radars and strong clutter interruption from infrastructures.

Aiming at mitigating the impact of interferences in complex electromagnetic environments, several anti-interference techniques have been presented recently. Among these, the moving target indication (MTI) algorithm [29] is a straightforward way to suppress clutter interferences depending on Doppler frequency diversity of clutters and moving targets. In [30], for further mitigating the residual clutters, a subspace tracking algorithm with an H-infinity filter was proposed for robust target tracking. Other algorithms like clutter model [31,32] and multiply-domain joint adaptive processing [33,34] were also utilized for clutter cancellation. Nevertheless, they can only eliminate the clutter interferences.

To address mutual interferences from other radars, in [35,36], the distributed radar networks were presented. By identifying the consistency of real target position and velocity observed by different radars, data correlation testing algorithms were developed to suppress the deception jamming. In [37], Aydogdu et al. indicate that the mutually orthogonal radar waveforms can be employed for high interference suppression. However, they are currently not available for prevalent low-cost hardware architectures. Apart from the radar network and orthogonal waveforms, the advanced signal processing algorithm is a promising alternative for mutual inference suppression. In [38], by employing the low-rank property of target echoes across multiple channels, Wang et al. proposed the tensor decomposition-based interference mitigation method. In [39], the beat-frequencies interpolation, combined with phase matching and reconfigurable linear prediction coefficients estimation, was presented for mutual interference suppression in the short-time Fourier transform (STFT) domain. In [40], the authors exploit the one-way propagation characteristic of mutual interferences to achieve interference detection and suppression. In [41], the convolutional autoencoder deep learning network was given for interference mitigation and multi-person activity sensing. However, the UAV with low radar cross sections (RCS) has weak backscattered signals, which cannot meet the high signal-to-interference-plus-noise ratio (SINR) assumption of the above algorithms [42,43]. Although the long-time coherent integration algorithms [44,45,46,47] can improve SINR by coherently integrating multiple backscattered signals, the integration performance overly relies on the motion model, which is extremely difficult to correctly build in a long-time duration since the movement of UAV is complex and flexible.

In the field of low-observable UAV tracking, the multi-scattering-source characteristics of UAVs lead to spatially distributed backscattered signals spanning multiple resolution cells, rendering classical “point-target” tracking methods ineffective. Data association-based multi-target tracking algorithms face challenges in resolving measurement-to-source association ambiguity, while contour tracking and cluster-center tracking approaches suffer from feature loss or limited applicability, while also being susceptible to mutual interference from co-band radars and strong clutter. Furthermore, current methods encounter bottlenecks in robustness under complex environments, interference suppression capability and adaptability to dynamic motion models. This necessitates further exploration of adaptive tracking techniques and integrated anti-interference technologies tailored for low SINR scenarios.

In this article, we aim to provide a continuous and robust tracking framework for low-observable and extended UAV by employing a high-resolution cascade FMCW-MIMO radar subject to interferences from strong clutters and other radars. In this tracking framework, we first convert the uncertainty of the scattering sources into the randomness of ellipse sizes and intensities in spatially extended resolution cells. The benefits are that the complex measurement-to-source association process is removed and the extended UAV can be treated as an entity to track by means of an ellipse-based spatial probability distribution model. On this basis, for dealing with the low-observable UAV tracking problem in the presence of ghost targets generated from strong clutters or mutual interfering radars in urban low-altitude, we formulate and derive an end-to-end spatiotemporal correlation integration (ESCI)-based tracking framework that can simultaneously capture both the uncertainty regarding the object’s existence as well as the uncertainty of the target’s state. It employs the coherent integration algorithm to sufficiently improve the SINR in one radar frame and then presents the recursive Bayesian estimation-based track-before-detection strategy to complete UAV tracking and interference suppression by directly utilizing the unthresholding radar spectrum, which can avoid weak target information loss caused by the conventional threshold-decision process prior to tracking. The main contributions can be summarized as follows.

(1) We present a two dimension-Keystone transform (2D-KT) to correct the range cell migration (RCM) in the range slow time domain and range-channel plane for coherently integrating the multi-pulse power of the UAV in one radar frame, which can sufficiently improve the SINR in the radar’s raw spectrum.

(2) We regard the occupied resolution cells from time-varying scattering sources spatially structured on the UAV as an entity and further develop an ellipse spatial probability distribution to model the extension of the UAV in the radar spectrum, removing the complex measurement-to-source association process in conventional tracking methods.

(3) By exploring the spatiotemporal correlation characteristics of the backscattered signals from the UAV in a sequence of radar spectra, we propose an ESCI-based UAV tracking framework to recursively estimate the shape parameters and its kinematic variables (position, velocity) of target in the presence of mixed interferences. By means of the ellipse spatial probability distribution model and the point diffusion function, the pseudo-range–Doppler–azimuth spectrum is generated to derive the measurement likelihood ratio for avoiding weak target information loss induced by the threshold-decision process.

(4) Theoretical analysis and experimental results show that the proposed method can obtain outstanding anti-interference performance of UAV tracking in contrast to the state-of-the-art (SOTA) methods, especially under low SINR conditions.

2. System Design

As shown in Figure 2, this section presents the proposed spatioemporal correlation integration-based trajectory tracking framework for low-observable and extended UAV in an urban air transportation system. Firstly, the high-resolution cascade radar platform and the corresponding signal processing algorithm are given in the following subsection, where the power of the received signals from the UAV are maximally accumulated in the range–Doppler–azimuth spectrum to improve the input SINR. Then, with a sequence of range–Doppler–azimuth spectra, an end-to-end spatiotemporal correlation integration-based tracking framework is proposed in the second subsection to recursively track the low-observable and extended UAV.

2.1. Cascade FMCW-MIMO Radar Signal Processing for Intra-Channel and Inter-Channel Coherent Integration

2.1.1. Signal Model of Cascade FMCW-MIMO Radar for Extended UAV

At the transmitter, the FMCW signals are first generated and transmitted to the are of interest, which can be expressed as

$$\mathbf{s}(\widehat{t},t_m)=exp[j2\pi f_0(\widehat{t}+t_m)+j\pi \mu {\widehat{t}}^2]$$

(1)

where $\widehat{t}\in [0,T_p)$ is the fast time variable, $T_p$ is the pulse duration time, $t_m=m{T}_p,$$m=1,2,\dots ,M$ is the slow time variable, M is the number of pulses in one radar frame, $\mu ={\displaystyle \frac{B}{T_p}}$ is the chirp rate, B is the bandwidth and $f_0$ is the carrier frequency.

Then, based on the relationship shown in Figure 3, the backscattered signals of the extended UAV from the $n_T$-th transmitting antenna at the $n_R$-th receiving element can be described as

$$\begin{array}{c}{\mathbf{r}}_u(\widehat{t},t_m,n_T,n_R)={\displaystyle \sum _{i=1}^{I_k}}{\sigma }_{i}exp\left\{j2\pi f_0\right[\widehat{t}+t_m-{\tau }_i^k\left(t_m\right)\hfill \\ -{\tau }_i^k\left(n_T\right)-{\tau }_i^k\left(n_R\right)]+j\pi \mu {[\widehat{t}-{\tau }_i^k\left(t_m\right)-{\tau }_i^k\left(n_T\right)-{\tau }_i^k\left(n_R\right)]}^2\}\hfill \end{array}$$

(2)

where $I_k$ is the number of reflection sources at the k-th radar frame, ${\sigma }_i$ is the backscattered power from the i-th reflection source of extended UAV, ${\tau }_i^k\left(t_m\right)=2(R_i+v_0{t}_m)/c$ is the round-trip time of backscattered signals from the first transmitting antenna at the first receiver, $R_i$ is the initial slant distance between radar and the i-th reflection source, $v_0$ is the initial velocity of UAV, which is assumed as a constant during one radar frame, $c=3\times {10}^8$ m/s is the light speed, ${\tau }_i^k\left(n_T\right)=(n_T-1)d_{T}sin{\theta }_i/c$ and ${\tau }_i^k\left(n_R\right)=(n_R-1)d_{R}sin{\theta }_i/c$ are, respectively, the additional propagation time delays induced by spacing differences of transmitting and receiving antennas, ${\theta }_i$ is the angle of arrival (AOA), which is approximately equal to the angle of departure (AOD), $d_T$ and $d_R$ are, respectively, the spacing distances of transmitting and receiving arrays, $n_T=1,2,\dots ,N_T$ and $n_T=1,2,\dots ,N_R$ are, respectively, the number of transmitting and receiving antennas, $N_T$ is the number of transmitting antennas and $N_R$ is the number of receiving elements.

After demodulation and dechirp processes [48], the beat signal collected by the data capture board can be described as

$$\begin{array}{c}{\mathbf{r}}_{beat}(\widehat{t},t_m,n_T,n_R)={\mathbf{r}}_u(\widehat{t},t_m,n_T,n_R)\times {\mathbf{s}}^{\ast }(\widehat{t},{t^{\prime }}_m)\hfill \\ \approx {\displaystyle \sum _{i=1}^{I_k}}{A}_{i}exp\left(-j{\displaystyle \frac{4\pi \mu \widehat{t}{R}_i}{c}}\right)exp\left[-j{\displaystyle \frac{4\pi (f_0+\mu \widehat{t})v_0{t^{\prime }}_m}{c}}\right]\hfill \\ \times exp\left[-j{\displaystyle \frac{2\pi (f_0+\mu \widehat{t})[(n_T-1)d_{T}sin{\theta }_i+(n_R-1)d_{R}sin{\theta }_i]}{c}}\right]\hfill \end{array}$$

(3)

In this article, as shown in Figure 4, with the time division multiple access-MIMO (TDMA-MIMO) strategy [49], the signals transmitted from different transmitting elements can be separated, and the presented $N_T\times N_R$ MIMO array can be synthesized as a $1\times N_a$ virtual MIMO array, where $N_a=N_T\times N_R$ is the total number of virtual antennas. More specifically, in a single time block, the chirp signals from different transmitting antennas are transmitted to the area of interest at different time slots sequentially. At the receiver, the backscattered signal from the $n_T$-th transmitting element is received at the $n_T$-th time slot. For the signal transmitted by the $n_T$-th antenna and received by the $n_R$-th antenna, the additional propagation path induced by the spacing difference of transmitting and receiving array elements is $(n_T-1)d_{T}sin{\theta }_i+(n_R-1)d_{R}sin{\theta }_i$. Furthermore, by reasonably designing the spacing distances of transmitting arrays (e.g., $d_T=N_R{d}_R$), the additional propagation path can be rewritten as $[(n_T-1)N_R+(n_R-1)]d_{R}sin{\theta }_i$, which is equal to the space difference between the first and $[(n_T-1)N_R+n_R]$-th receiving antennas in a $1\times N_a$ array. Hence, the $N_T\times N_R$ dimensional MIMO array can be restructured as a $1\times N_a$ virtual array. On this condition, the azimuth angle resolution can be increased to $1/(N_T\times N_R)$, which only needs $N_T+N_R$ antennas, far less than $N_T\times N_R$.

Then, the beat signal of the $n_a$-th virtual antenna can be written as

$$\begin{array}{c}{\mathbf{r}}_{beat}(\widehat{t},t_m,n_a)={\displaystyle \sum _{i=1}^{I_k}}{A}_{i}exp\left\{-j{\displaystyle \frac{4\pi \mu \widehat{t}{R}_i}{c}}\right\}\hfill \\ \times exp\left\{-j{\displaystyle \frac{4\pi (f_0+\mu \widehat{t})v_0{t}_m}{c}}\right\}exp\left\{-j{\displaystyle \frac{2\pi (f_0+\mu \widehat{t})n_a{d}_{R}sin{\theta }_i}{c}}\right\}\hfill \end{array}$$

(4)

where $n_a=0,1,\dots ,N_a$ is the virtual antenna number.

Applying 3D Fourier transform (FT) to (4) with respect to $\widehat{t}$, $t_m$ and $n_a$ yields

$$\begin{array}{c}{\mathbf{r}}_{beat}(f_r,f_d,f_a)={\displaystyle \sum _{i=1}^{I_k}}{A^{\prime }}_i\sin \mathrm{c}[f_r-{\displaystyle \frac{2\mu }{c}}(R_i+v_0{t}_m\hfill \\ +{\displaystyle \frac{1}{2}}{n}_a{d}_{R}sin{\theta }_i\left)\right]\sin \mathrm{c}(f_d-{\displaystyle \frac{2v_0}{\lambda }})\sin \mathrm{c}(f_a-{\displaystyle \frac{d_R}{\lambda }}sin{\theta }_i)\hfill \end{array}$$

(5)

where $f_r$, $f_d$ and $f_a$ are the frequency variables in terms of range, Doppler, and azimuth angle, respectively, ${A^{\prime }}_i=A_i{N}_{a}M{T}_c^2$ is a constant, and $\sin \mathrm{c}\left(x\right)={\displaystyle \frac{sinx}{x}}$ is a Sinc function.

From (5), we can observe that for different reflection sources spatially structured on UAV, the differences of $R_i$ and ${\theta }_i$ will cause the extension of the target’s signals where they may occupy several resolution cells in the range–azimuth spectrum, as shown in Figure 3. The rich information, including the extension of target signals, such as shape, size and orientation, can enable the cascade FMCW-MIMO radar to be utilized for UAV control and planning decisions like camera or Lidar. Additionally, due to the coupling of $\widehat{t}$, $t_m$ and $n_a$, we can also see that the peak location of the Sinc function will vary with the target moving when $v_0{t}_m$ or ${\displaystyle \frac{1}{2}}{n}_a{d}_{R}sin{\theta }_i$ is larger than the range resolution, which is well known as range cell migration (RCM). The RCMs in both ranges—the slow time domain and virtual antenna channel plane—would distribute the signal power into different range cells, which may bring about serious integration loss after 3D-FT. Accordingly, inspired by the successful application of keystone transform (KT) in the field of radar imaging, we present a 2D-KT-based coherent integration method to sufficiently accumulate the intra-channel and inter-channel signal power for improving the SINR of raw radar data cube in the following part.

2.1.2. Intra-Channel and Inter-Channel Coherent Integration in the Presence of Interferences

In urban air transportation systems, our cascade MIMO radar system will inevitably be subjected to noise interferences, mutual intrusion from other co-channel radars and strong clutter interruption from infrastructures and high buildings. Consequently, at the receiver, the received signals in (3) can be rewritten as

$$\begin{array}{c}{\mathbf{z}}_{beat}(\widehat{t},t_m,n_a)={\mathbf{r}}_{beat}(\widehat{t},t_m,n_a)\hfill \\ +{\mathbf{r}}_{beat}^{int}(\widehat{t},t_m,n_a)+{\mathbf{c}}_{beat}(\widehat{t},t_m,n_a)+\mathbf{w}(\widehat{t},t_m,n_a)\hfill \end{array}$$

(6)

where

$$\begin{array}{c}{\mathbf{r}}_{beat}^{int}(\widehat{t},t_m,n_a)={\mathbf{r}}^{int}(\widehat{t},t_m)\times {\mathbf{s}}^{\ast }\left(\widehat{t}\right)\hfill \\ \approx {\gamma }^{int}{A}^{int}exp\left\{-j{\displaystyle \frac{2\pi (f_0^{int}-f_0+{\mu }^{int}{R}^{int})}{c}}\widehat{t}\right\}\hfill \\ \times exp\left[-j{\displaystyle \frac{2\pi (f_0^{int}+{\mu }^{int}\widehat{t})v^{int}{t}_m}{c}}\right]\hfill \\ \times exp\left[-j{\displaystyle \frac{2\pi (f_0^{int}+{\mu }^{int}\widehat{t})n_a{d}_{R}sin{\theta }^{int}}{c}}\right]\hfill \end{array}$$

(7)

denotes the received signals from interfering radar, ${\gamma }^{int}\in \left\{0,1\right\}$ denotes the co-channel indicator, which is equal to 1 when the interference signal is in the bandwidth of interest of our radar, ${\mu }^{int}$ denotes the chirp slope of interfering radar, $A^{int}$ denotes the amplitude of the interference signal, $R^{int}$, ${\theta }^{int}$ and $v^{int}$ are, respectively, the relative range, azimuth angle and velocity between victim and interfering radar, ${\mathbf{c}}_{beat}(\widehat{t},t_m,n_a)$ is the backscattered clutters from infrastructures and high buildings and $\mathbf{w}(\widehat{t},t_m,n_a)$ is the noises.

In general, according to the Friis free-space propagation equation and the radar equation, the mutual interference signal is stronger than the desired backscattered signal. As a result, after performing 3D-FT on (6), the ghost target may occur if the carrier frequency of interfering radar is in the bandwidth of interest of our radar. Additionally, the existence of clutters will not only increase the noise floor but also perhaps generate pseudo-targets in radar range–Doppler–azimuth spectrum.

The mutual interference and clutters will sharply decrease the SINR of the raw 3D radar data cube. Accordingly, in this part, we first utilize the 2D-KT to correct the RCM induced by the target moving and spacing differences of the virtual array for sufficiently integrating the intra-channel and inter-channel signal power of the target in a single radar frame, as shown in Figure 5. From (3), we can see that the appearance of RCM is essentially caused by the coupling of $\widehat{t}$ and ${t^{\prime }}_m$ in the second exponential term for a single channel. Additionally, the range drift in different channels is also induced by the coupling of $\widehat{t}$ and ${n^{\prime }}_a$ in the third exponential term. Fortunately, the types of these two couplings are the same and they can be removed through a simple scaling operation, which can be achieved by the interpolation process. Consequently, for removing the couplings of $\widehat{t}$, ${t^{\prime }}_m$ and ${n^{\prime }}_a$, we, respectively, apply $(f_0+\mu \widehat{t})m=f_0{m}^{\prime }$ and $(f_0+\mu \widehat{t})n_a=f_0{n}_a^{\prime }$ to (5) with respect to the slow time ${t^{\prime }}_m$ and channel number ${n^{\prime }}_a$ by means of a Sinc interpolation function and we can obtain

$$\begin{array}{c}{\mathbf{z}}_{beat}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)\hfill \\ ={\displaystyle \sum _0^{M-1}}{\displaystyle \sum _0^{N_a-1}}{\mathbf{z}}_{beat}(\widehat{t},t_m,n_a)\hfill \\ \times \sin \mathrm{c}({\displaystyle \frac{f_0}{f_0+\mu \widehat{t}}}{m}^{\prime }-m)\sin \mathrm{c}({\displaystyle \frac{f_0}{f_0+\mu \widehat{t}}}{n^{\prime }}_a-m)\hfill \\ ={\mathbf{r}}_{beat}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)+{\mathbf{r}}_{beat}^{int}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)\hfill \\ +{\mathbf{c}}_{beat}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)+\mathbf{w}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)\hfill \end{array}$$

(8)

where

$$\begin{array}{c}{\mathbf{r}}_{beat}(\widehat{t},{t^{\prime }}_m,{n^{\prime }}_a)={\displaystyle \sum _{i=1}^{I_k}}{A}_{i}exp\left\{-j{\displaystyle \frac{4\pi \mu \widehat{t}{R}_i}{c}}\right\}\hfill \\ \times exp\left\{-j{\displaystyle \frac{4\pi f_0{v}_0{t^{\prime }}_m}{c}}\right\}exp\left\{-j{\displaystyle \frac{2\pi f_0{n^{\prime }}_a{d}_{R}sin{\theta }_i}{c}}\right\}\hfill \end{array}$$

(9)

${t^{\prime }}_m=m^{\prime }{T}_p,m^{\prime }=0,1,\dots ,M$ and $n_a^{\prime }=1,2,\dots ,N_a$ are, respectively, scaled slow time variable and scaled channel number.

From (8) and (9), we can observe that the couplings of $\widehat{t}$, ${t^{\prime }}_m$ and ${n^{\prime }}_a$ are eliminated in the second and third exponential terms for beat signals of the target, but the couplings still exists in the mutual interference signals. On this account, after performing 3D-FT on (7) along $\widehat{t}$, ${t^{\prime }}_m$ and ${n^{\prime }}_a$, we have

$$\begin{array}{cc}\hfill \mathbf{z}(f_r,f_d,f_a)& ={\mathbf{r}}_{beat}(f_r,f_d,f_a)+{\mathbf{r}}_{beat}^{int}(f_r,f_d,f_a)\hfill \\ \hfill & +{\mathbf{c}}_{beat}(f_r,f_d,f_a)+\mathbf{w}(f_r,f_d,f_a)\hfill \end{array}$$

(10)

where

$$\begin{array}{c}{\mathbf{r}}_{beat}(f_r,f_d,f_a)={\displaystyle \sum _{i=1}^{I_k}}{A^{\prime }}_i\sin \mathrm{c}(f_r-{\displaystyle \frac{2\mu R_i}{c}})\hfill \\ \times \sin \mathrm{c}(f_d-{\displaystyle \frac{2v_0}{\lambda }})\sin \mathrm{c}(f_a-{\displaystyle \frac{d_R}{\lambda }}sin{\theta }_i)\hfill \end{array}$$

(11)

is the range–Doppler–azimuth spectrum of the target, ${\mathbf{z}}_{beat}^{int}(f_r,f_d,f_a)$, ${\mathbf{c}}_{beat}(f_r,f_d,f_a)$ and $\mathbf{w}(f_r,f_d,f_a)$ are the spectra of interference signals, clutters and noises respectively.

In (11), the signal power of the UAV’s i-th reflection source is coherently integrated from multiple diffuse resolution cells into a single resolution unit in the range–Doppler–azimuth spectrum, and the theoretical processing gain is $10lg\left(M{N}_a\right)$[44]. However, due to the residual couplings of $\widehat{t}$, $t_m$ and $n_a$, the signal power of the interfering radar still distributes into different range cells. This accumulation gain can fully improve the SINR in the raw 3D radar data cube and thus improve the trajectory tracking performance for low-observable UAV.

2.1.3. Simulation Results

Figure 6 shows the results of the coherent integration of 2D-KT verified using MATLAB R2023a. In this figure, the radar’s mutual interference was added to the returned signals of the target, and another static object was also presented to simulate the strong clutters. The parameters of the radar system were set as follows: the carrier frequency $f_0=77$ GHz, the bandwidth B = 2.4 GHz, the number of virtual antennas $N_a=128$, the pulse duration $T_p$ = 50 $\mathsf{\mu }$s and the chirp rate $\mu$ = 85.021 MHz/$\mathsf{\mu }$s. In addition, the chirp parameters of the jamming radar are $f_0^{int}=77$ GHz, $T_p^{int}$ = 45 $\mathsf{\mu }$s, ${\mu }^{int}$ = 85.106 MHz/$\mathsf{\mu }$s. The range of the slow plane of the first RX-TX channel before and after KT are given in Figure 6a,b. In Figure 6a, we can clearly see the RCM that the target power of different pulses distributes at different range cells. After KT, the RCM is corrected and the signal power of different pulses from the same reflection source is located at the same range cell. Then, after performing Fourier transform along the pulse number, a peak which integrates the power of all pulses from the same reflection source of the target will occur in the Doppler spectrum range. Figure 6c,d presents the channel plane range of the first chirp before and after KT. Due to the large number of virtual channels, it can be seen from Figure 6c that the spacing distance differences of the virtual antennas also bring about RCM, which will degrade the target detection and tracking performance. Fortunately, this type of RCM can be also removed after a second KT process, as shown in Figure 6d. In addition, due to the difference in chirp rates between interfering and victim radars, from Figure 6a–c, we can observe that the signal power of radar mutual interference distributes at different range cells after KT, which will decrease the final signal power of interference and thus is beneficial to target detection and tracking. The final azimuth spectrum range before and after 2D-KT are depicted in Figure 6e,f. We can observe that, after 2D-KT, the SINR is coherently integrated from 12.84 dB to 31.3 dB, which can effectively improve the low-observable UAV detection and tracking performance.

2.2. End-to-End Spatiotemporal Correlation Integration-Based Tracking Framework with Recursive Bayesian Estimation

2.2.1. State and Existence Indicator Transition Models

In this section, we regard the extended UAV as an entity to track for avoiding the complex measurement-to-source association procedure. In addition, the shape of the extended UAV can be approximatively described by a rectangle which is often modeled as an ellipse in radar spectrum. On this account, we first model the state of extended UAV as ${\mathbf{X}}_k={\left[{\mathbf{x}}_k^c,{\mathbf{s}}_k\right]}^{\mathrm{T}}$, where ${\mathbf{x}}_k^c=\left[x_k^c,y_k^c,v_k^x,v_k^y\right]$ is the kinematic state vector of the scatting center at the k-th time step, ${\mathbf{s}}_k=\left[{\alpha }_k,l_k^a,l_k^b\right]$ is the corresponding elliptic extension state, ${\alpha }_k$, $l_k^a$ and $l_k^b$ is respectively the elliptic heading angle, major axis and minor axis. Generally, due to the short time interval between two adjacent radar frames, the speed of UAV can be nearly treated as a constant. Hence, the state transition model can be formulated as

$${\mathbf{X}}_{k+1}=\mathbf{F}{\mathbf{X}}_k+\mathbf{G}{\mathbf{w}}_k$$

(12)

where $\mathbf{F}=\left[\begin{array}{cc}{\mathbf{F}}_{\mathrm{x}}& {\mathbf{0}}_{4\times 3}\\ {\mathbf{0}}_{3\times 4}& {\mathbf{F}}_{\mathrm{s}}\end{array}\right]$ denotes the state transition matrix, ${\mathbf{F}}_{\mathrm{x}}=\left[\begin{array}{cc}\begin{array}{cc}1& T\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& T\\ 0& 1\end{array}\end{array}\right]$ denotes the kinematic state transition matrix, ${\mathbf{F}}_s=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$ denotes the extension state transition matrix, $T=M{T}_p$ is the time interval between two adjacent radar frames, $\mathbf{G}=\left[\begin{array}{cc}{\mathbf{G}}_{\mathrm{x}}& {\mathbf{0}}_{4\times 5}\\ {\mathbf{0}}_{3\times 4}& {\mathbf{G}}_{\mathrm{s}}\end{array}\right]$ denotes the noise transition matrix, ${\mathbf{G}}_{\mathrm{x}}=\left[\begin{array}{c}\begin{array}{cc}{T}^2/2& 0\\ 0& T\end{array}\\ \begin{array}{cc}{T}^2/2& 0\\ 0& T\end{array}\end{array}\right]$ and ${\mathbf{G}}_s=\left[\begin{array}{ccc}{\epsilon }_{\alpha }& 0& 0\\ 0& {\epsilon }_{la}& 0\\ 0& 0& {\epsilon }_{lb}\end{array}\right]$, ${\epsilon }_{\alpha }$, ${\epsilon }_{la}$ and ${\epsilon }_{lb}$ are the corresponding noise intensities, ${\mathbf{w}}_k={\left[w_x,w_y,w_{vx},w_{vy},w_{\alpha },w_{la},w_{lb}\right]}^T$ denotes the Gaussian white noise vector.

Then, for improving the anti-interference ability, in this article, we introduce an existence indicator $E_k=\{0,1\}$ to describe whether there exists a target in the radar field of view (FOV) at the kth timestamp instead of the threshold-decision detection process. If there exists a target, $E_k=1$; otherwise, $E_k=0$. By introducing the target’s birth and death probabilities, the existence indicator evolution can be modeled as a Markov process which can be described as

$$\left[\begin{array}{c}\mathrm{P}(E_{k+1}=1)\hfill \\ \mathrm{P}(E_{k+1}=0)\hfill \end{array}\right]=\left[\begin{array}{cc}1-P_b& P_b\\ P_d& 1-P_d\end{array}\right]\left[\begin{array}{c}\mathrm{P}(E_k=1)\hfill \\ \mathrm{P}(E_k=0)\hfill \end{array}\right]$$

(13)

where $P_b=P(E_{k+1}=1|E_k=0)$ represents the birth probability, $P_d=P(E_{k+1}=0|E_k=1)$ represents the death probability.

2.2.2. Measurement Model for Cascade MIMO Radar

According to (10), we can obtain a sequence of range–Doppler–azimuth spectra, i.e., ${\mathbf{Z}}_{1:k+1}=\left\{{\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_{k+1}\right\}$, where ${\mathbf{z}}_{k+1}={\left|{\mathbf{z}}_{k+1}(f_r,f_d,f_a)\right|}^2$ denotes the range–Doppler–azimuth power spectrum, which contains $N_r\times N_v\times N_{\theta }$ resolution cells at k + 1th radar frame. In this article, we regard the measurements originating from the extended UAV as two separate processes, including a spatially scattering process and a measurement error process. The former employ an elliptic shape and a spatial probability distribution model to describe how the extended measurement sources are distributed over the UAV. The random scattering sources, following a given spatial probability distribution, are distributed in the ellipse, which must satisfy

$$\begin{array}{c}\left(\left[\begin{array}{cc}{x}_{k+1}^i& y_{k+1}^i\end{array}\right]-\left[\begin{array}{cc}{x}_{k+1}^c& y_{k+1}^c\end{array}\right]\right){\mathbf{D}}_{k+1}\hfill \\ \times {\left(\left[\begin{array}{cc}{x}_{k+1}^i& y_{k+1}^i\end{array}\right]-\left[\begin{array}{cc}{x}_{k+1}^c& y_{k+1}^c\end{array}\right]\right)}^T\le 1\hfill \end{array}$$

(14)

where $\left(x_{k+1}^c,y_{k+1}^c\right)$ and $\left(x_{k+1}^i,y_{k+1}^i\right)$ are, respectively, the position coordinates of the centering and i-th scatting sources, ${\mathbf{D}}_{k+1}=\mathbf{R}\left({\alpha }_{k+1}\right)\left[\begin{array}{cc}{\left(l_{k+1}^a\right)}^2& 0\\ 0& {\left(l_{k+1}^b\right)}^2\end{array}\right]\mathbf{R}{\left({\alpha }_{k+1}\right)}^T$ represents the outline feature information of the ellipse, $\mathbf{R}\left({\alpha }_{k+1}\right)=\left[\begin{array}{cc}cos{\alpha }_{k+1}& -sin{\alpha }_{k+1}\\ sin{\alpha }_{k+1}& cos{\alpha }_{k+1}\end{array}\right]$ represents the rotation matrix.

The measurement error process describes the sensor noise process, which is generally assumed to be a Gaussian white noise vector. In addition, instead of the traditional radar detections, for avoiding the information loss induced by the threshold-decision process, the point diffusion function-based pseudo range–Doppler–azimuth power spectrum is employed to derive the measurement model. On this account, the measurement model for cascade MIMO radar can be derived as

$${\mathbf{z}}_{k+1}=\left\{\begin{array}{c}h\left({\mathbf{X}}_{k+1}\right)+{\mathbf{v}}_{k+1},E_{k+1}\ne 0\hfill \\ {\mathbf{v}}_{k+1},E_{k+1}=0\hfill \end{array}\right.$$

(15)

where

$$\begin{array}{c}h\left({\mathbf{X}}_{k+1}\right)={\displaystyle \sum _{i=1}^{I_{k+1}}}{A}_{k+1}^{i}h\left({\mathbf{x}}_{k+1}^i\right)={\displaystyle \sum _{i=1}^{I_{k+1}}}{A}_{k+1}^{i}exp[{\displaystyle \frac{{(r-r_{k+1}^i)}^2{L}_r}{2N_r}}+{\displaystyle \frac{{(v-v_{k+1}^i)}^2{L}_v}{2N_v}}+{\displaystyle \frac{{(\theta -{\theta }_{k+1}^i)}^2{L}_{\theta }}{2N_{\theta }}}]\hfill \end{array}$$

(16)

is the pseudo-range–Doppler–azimuth power spectrum, $h\left({\mathbf{x}}_k^i\right)$ represents the point diffusion function of the i-th scattering source, ${\mathbf{x}}_{k+1}^i=\left[x_{k+1}^i,y_{k+1}^i,v_{k+1}^x,v_{k+1}^y\right]$ represents the corresponding kinematic state vector, ${\mathbf{v}}_{k+1}$ is the noise matrix, $I_{k+1}$ is the total number of scattering sources of the target at k + 1-th radar frame, $A_{k+1}^i$ is the amplitude of the i-th scattering point, $L_r$, $L_v$ and $L_{\theta }$ represent loss constants, r, v and $\theta$ are, respectively, the range, velocity and azimuth variables, $r_{k+1}^i$, $v_{k+1}^i$ and ${\theta }_{k+1}^i$ are the range, velocity and azimuth of the i-th scattering source, which can be calculated by

$$r_{k+1}^i=\sqrt{{\left(x_{k+1}^i\right)}^2+{\left(y_{k+1}^i\right)}^2}$$

(17)

$$v_{k+1}^i={\displaystyle \frac{x_{k+1}^i{v}_{k+1}^x+y_{k+1}^i{v}_{k+1}^y}{\sqrt{{\left(x_{k+1}^i\right)}^2+{\left(y_{k+1}^i\right)}^2}}}$$

(18)

$${\theta }_{k+1}^i=\arctan {\displaystyle \frac{y_{k+1}^i}{x_{k+1}^i}}$$

(19)

2.2.3. End-to-End Spatiotemporal Correlation Integration-Based State Estimation with Recursive Bayesian Estimation

Since the target information is definitely contained in the radar raw spectrum, in this article, we concentrate on estimating the posterior probability $P({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k+1})$ to achieve UAV tracking by directly utilizing the observed range–Doppler–azimuth spectra, i.e., ${\mathbf{Z}}_{1:k+1}=\left\{{\mathbf{z}}_1,{\mathbf{z}}_2,\dots ,{\mathbf{z}}_{k+1}\right\}$, rather than depending on threshold-decision detections. On this basis, by employing the spatiotemporal correlation of the target trajectory within a sequence of radar frames, the extended low-observable UAV can be detected and tracked simultaneously if the posterior probability $P({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k+1})$ is larger than a given value.

Firstly, in the prediction phase, depending on the state and existence indicator transition models, the prior probability can be described as

$$\begin{array}{c}\mathrm{P}({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k})=\hfill \\ \int \mathrm{P}({\mathbf{X}}_{k+1},E_{k+1}=1,{\mathbf{X}}_k,E_k=1|{\mathbf{Z}}_{1:k})d{\mathbf{X}}_k+\int \mathrm{P}({\mathbf{X}}_{k+1},E_{k+1}=1,{\mathbf{X}}_k,E_k=0|{\mathbf{Z}}_{1:k})d{\mathbf{X}}_k\hfill \\ =(1-P_d)\int \mathrm{P}\left({\mathbf{X}}_{k+1}\right|{\mathbf{X}}_k,E_{k+1}=1,E_k=1)\times \mathrm{P}({\mathbf{X}}_k,E_k=1|{\mathbf{Z}}_{1:k})d{\mathbf{X}}_k+P_b\mathrm{P}\left({\mathbf{X}}_k\right)\hfill \end{array}$$

(20)

where $P\left({\mathbf{X}}_{k+1}\right|{\mathbf{X}}_k,E_{k+1}=1,E_k=1)$ is the state transition probability, which can be calculated by (12), $P({\mathbf{X}}_k,E_k=1|{\mathbf{Z}}_{1:k})$ is the posterior probability at the k-th timestamp and $P\left({\mathbf{X}}_k\right)$ is the initial state probability.

Subsequently, after receiving the latest range–Doppler–azimuth spectrum ${\mathbf{z}}_{k+1}$, the posterior probability at the $k+1$-th timestamp can be derived as

$$\begin{array}{c}\mathrm{P}({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k+1})\propto \mathrm{P}({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k})\mathrm{P}({\mathbf{z}}_{k+1}\left|\right|{\mathbf{X}}_{k+1},E_{k+1}=1)\hfill \end{array}$$

(21)

where $P\left({\mathbf{z}}_{k+1}\right|{\mathbf{X}}_{k+1},E_{k+1}=1)$ is the likelihood probability.

Since the measurements originating from the extended UAV can be separated as a spatial scattering process and a measurement error process, the probability distribution function (PDF) of $P\left({\mathbf{z}}_{k+1}\right|{\mathbf{X}}_{k+1},E_{k+1}=1)$ can be expressed as

$$\begin{array}{c}p\left({\mathbf{z}}_{k+1}\right|{\mathbf{X}}_{k+1},E_{k+1}=1)=\int p({\mathbf{z}}_{k+1},{\mathbf{x}}_{k+1}^i|{\mathbf{X}}_{k+1},E_{k+1}=1)d{\mathbf{x}}_{k+1}^i\hfill \\ =\int p\left({\mathbf{z}}_{k+1}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)\times p\left({\mathbf{x}}_{k+1}^i\right|{\mathbf{X}}_{k+1},E_{k+1}=1)d{\mathbf{x}}_{k+1}^i\hfill \end{array}$$

(22)

where $p\left({\mathbf{x}}_{k+1}^i\right|{\mathbf{X}}_{k+1},E_{k+1}=1)$ is a specific spatial probability distribution model, which is assumed to be a 2D uniform distribution in this article, $p\left({\mathbf{z}}_{k+1}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)$ is the measurement error process.

Assuming each resolution unit is statistically independent in radar spectrum, $p\left({\mathbf{z}}_{k+1}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)$ can be expressed as the product of edge probability PDF of each resolution unit, i.e.,

$$\begin{array}{c}p\left({\mathbf{z}}_{k+1}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)={\displaystyle \prod _{n_r}^{N_r}}{\displaystyle \prod _{n_v}^{N_v}}{\displaystyle \prod _{n_{\theta }}^{N_{\theta }}}p\left(z_{k+1}^{n_r,n_v,n_{\theta }}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)\hfill \end{array}$$

(23)

where $p\left(z_{k+1}^{n_r,n_v,n_{\theta }}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)\sim N(z_{k+1}^{n_r,n_v,n_{\theta }}-A_{k+1}^i{h}^{n_r,n_v,n_{\theta }}\left({\mathbf{x}}_{k+1}^i\right),{\sigma }^2)$ is the edge probability at the resolution cell $(n_r,n_v,n_{\theta })$ and $z_{k+1}^{n_r,n_v,n_{\theta }}$ and ${\sigma }^2$ are, respectively, the corresponding signal power and noise variance.

Then, substituting (23) into (22), we have

$$\begin{array}{c}p\left({\mathbf{z}}_{k+1}\right|{\mathbf{X}}_{k+1},E_{k+1}=1)={\displaystyle \sum _{i=1}^{I_{k+1}}}{\displaystyle \prod _{n_r}^{N_r}}{\displaystyle \prod _{n_v}^{N_v}}{\displaystyle \prod _{n_{\theta }}^{N_{\theta }}}p\left(z_{k+1}^{n_r,n_v,n_{\theta }}\right|{\mathbf{x}}_{k+1}^i,E_{k+1}=1)\hfill \\ ={\displaystyle \sum _{i=1}^{I_{k+1}}}{\displaystyle \prod _{n_r}^{N_r}}{\displaystyle \prod _{n_v}^{N_v}}{\displaystyle \prod _{n_{\theta }}^{N_{\theta }}}{\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp\left\{{\displaystyle \frac{-{[A_{k+1}^i{h}^{n_r,n_v,n_{\theta }}\left({\mathbf{x}}_{k+1}^i\right)-z_{k+1}^{n_r,n_v,n_{\theta }}]}^2}{2{\sigma }^2}}\right\}\hfill \end{array}$$

(24)

In (21), with a sequence of radar frames, the UAV can be detected and tracked simultaneously if the posterior probability $P({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k+1})$ is larger than a given value, where the target detection process is integrated into the tracking procedure. To address the complicated integral problem in (21), in this article, we employ the sequential Monte Carlo sampling to approximately approach the posterior PDF. More specifically, we first uniformly generate a set of independent “samples” with random state vector ${\mathbf{X}}_0^q$. Meanwhile, each sample has its own importance weight $w_0^q$. Then, after obtaining the radar observations ${\mathbf{Z}}_{1:k+1}$ at the $k+1$-th timestamp, the state vector ${\mathbf{X}}_0^q$ and the corresponding importance weight $w_0^q$ are recursively updated as ${\mathbf{X}}_{k+1}^q$ and $w_{k+1}^q$, respectively, which can be mainly divided into prediction and update processes.

In the prediction procedure, with $P_b$ and $P_d$, the samples are randomly classified into three categories, including new born, dead and continuing samples. For the dead samples, the existence indicator is set to 0. For the continuing samples, the predicted state ${\mathbf{X}}_{k+1}^{q-}$ is calculated by (12). For the new born samples, the predicted state ${\mathbf{X}}_{k+1}^{q-}$ is randomly generated.

In the update process, for further enlarging the weight differences between the presence and absence of UAV, we employ the likelihood ratio $L_{k+1}^q\left({\mathbf{z}}_{k+1}|{\mathbf{X}}_{k+1}^{q-}\right)$ to update the importance weight instead of likelihood probability. With (15) and (24), the likelihood ratio can be derived as

$$\begin{array}{c}{L}_{k+1}^q\left({\mathbf{z}}_{k+1}|{\mathbf{X}}_{k+1}^{q-}\right)=\left\{\begin{array}{c}\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^{I_{k+1}}}{\displaystyle \prod _{n_r}^{N_r}}{\displaystyle \prod _{n_v}^{N_v}}{\displaystyle \prod _{n_{\theta }}^{N_{\theta }}}exp\left\{-{\displaystyle \frac{H\left({\mathbf{x}}_{k+1}^i\right)[H\left({\mathbf{x}}_{k+1}^i\right)-2z_{k+1}^{n_r,n_v,n_{\theta }}]}{2{\sigma }^2}}\right\},E_{k+1}^q=1\end{array}\\ 1,E_{k+1}^q=0\end{array}\right.\hfill \end{array}$$

(25)

where $H\left({\mathbf{x}}_{k+1}^i\right)=A_{k+1}^i{h}^{n_r,n_v,n_{\theta }}\left({\mathbf{x}}_{k+1}^i\right)$, $E_{k+1}^q$ denotes the existence indicator of the q-th sample.

With (25), the importance weight $w_{k+1}^q$ can be updated as $w_{k+1}^q\propto L_{k+1}^q\left({\mathbf{z}}_{k+1}|{\mathbf{X}}_{k+1}^{q-}\right)w_k^q$ after receiving the range–Doppler–azimuth power spectrum ${\mathbf{z}}_{k+1}$. In (25), the state ${\mathbf{X}}_{k+1}^{q-}$ of the q-th sample is closer to the true value, and the value of the likelihood ratio $L_{k+1}^q\left({\mathbf{z}}_{k+1}|{\mathbf{X}}_{k+1}^{q-}\right)$ is greater. As a result, the importance weight $w_{k+1}^q$ will also be larger. After normalization and resampling processing, the updated states ${\mathbf{X}}_{k+1}^{q+}$ of most samples will be replaced by the predicted state of samples with large importance weights. Consequently, the optimal state of the extended UAV can be estimated as

$${\widehat{\mathbf{X}}}_{k+1}={\displaystyle \frac{{\displaystyle \sum _{q=1}^{N_q}}{E}_{k+1}^q{\mathbf{X}}_{k+1}^{q+}}{{\displaystyle \sum _{q=1}^{N_q}}{E}_{k+1}^q}}$$

(26)

where $N_q$ is the total number of samples. Finally, after a sequence of consecutive radar frames, the obtained optimal states in (26) can be confirmed as the target’s tracking trajectory when the cumulative existence probability $P_c={\displaystyle \sum _{q=1}^{N_q}}{E}_{k+1}^q/N_q$ is larger than a preset threshold.

2.2.4. Simulation Results

Based on the coherent integration results of 2D-KT in Figure 6, the tracking results of the MATLAB R2023a-implemented ESCI-based framework are presented in Figure 7. In this figure, the flying trajectory of UAV was set as the closed circular loop, as given in Figure 7a. It can be seen that most of the target measurements can be obtained after a threshold-decision process. However, the ghost measurements induced by co-channel radar interferences and static clutters can also be clearly seen in Figure 7a, which causes wrong target-to-measurement association. On this account, the tracking results of RMM, SOEKF and DBSCAN deteriorate seriously. As shown in Figure 7b, although particle filter track-before-detect (PFTBD) also utilizes the non-thresholding spectra, the mismatch of the point-source model decreases the tracking precision of the extended UAV. By maximizing the posterior probability $P({\mathbf{X}}_{k+1},E_{k+1}=1|{\mathbf{Z}}_{1:k+1})$ in a sequence of consecutive radar range–Doppler–azimuth spectra, the proposed method can track the object which satisfies Newtonian dynamic equations and elliptic energy distribution in the presence of radar mutual interferences and strong clutters. As a result, the proposed method can accurately track the low-observable extended UAV. Figure 7c,d present the intersection over union (IoU) between the tracked shape and the true extension and error cumulative distribution functions (CDFs) of the estimated trajectory. We can observe that all estimated IoUs are larger than 0.5 and the errors of the estimated trajectory are within 0.5 m, which means that the proposed method can simultaneously track the shape parameters and kinematic variables of UAV precisely in the presence of radar mutual interferences and strong clutter.

3. Evaluation Metrics and Experimental Results

3.1. Evaluation Metrics

In this article, we employ the error CDF and the IoU to jointly evaluate the tracking performance of the extended UAV. The former can show the error cumulative distribution of the tracked trajectory. The second metric presents the coincidence of the tracked shape and the true extension.

3.2. Comparisons

Comparison method: Firstly, four target tracking methods were proposed as the comparison tools for evaluating the detection and tracking performance of micro unmanned aerial vehicles under FMCW-MIMO radar.

DBSCAN: This method leverages DBSCAN-based density clustering to dynamically configure neighborhood parameters, isolate valid target clusters and compute cluster centroids. Following this, it initializes a Kalman filter to predict target kinematics via state equations and refines the target state using observational updates, enabling robust trajectory tracking.

RMM: By modeling extended targets as a hybrid motion vector and spatial extension matrix, this approach employs random matrix theory to extract dominant eigenvalues for precise signal–noise separation. The integration of Kalman filtering ensures stable tracking of spatially distributed targets.

SOEKF: Utilizing a second-order extended Kalman filter (SOEKF), this framework simultaneously estimates target dynamics and shape parameters. It embeds measurement covariance into likelihood function optimization, dynamically recalibrates model weights through maximum likelihood principles and achieves extended target tracking.

PFTBD: This method improves signal-to-noise ratio (SNR) through multi-frame radar data accumulation. It models target motion via particle filtering, iteratively updates particle weights to approximate posterior distributions and uses the probability ratio test to verify the continuous trajectories, ensuring reliable tracking of extended targets.

3.2.1. Error CDF of Tracked Trajectory

This metric shows the error cumulative distribution of the tracked trajectory, which can be estimated as $F\left(\chi \right)=Prob(d_{error}^k\le \chi )$, where $F\left(\chi \right)$ is the probability when $d_{error}^k\le \chi$, $d_{error}^k=∥{\mathbf{x}}_k^c-{\widehat{\mathbf{x}}}_k^c∥$ is the tracking error at the k-th frame.

3.2.2. Intersection over Union

This coefficient evaluates the similarity between the tracked shape and the true extension, which is defined as $\mathrm{IoU}={\displaystyle \frac{S_{\cap }}{S_{\cup }}}$, where $S_{\cap }$ and $S_{\cup }$ are, respectively, the intersection and union areas of the tracked shape and the true extension.

3.3. Experimental Results

In this section, we verify the tracking effectiveness of the proposed method for low-observable and extended UAV in four different scenarios, including a mutual interference scenario, strong clutter scenario, mixed interferences scenario and rainy scenario. In these experiments, as shown in Figure 8a, a low-cost, high-resolution cascade MIMO radar with four AWR2243 chips was presented to track the flying UAV. In this cascaded radar system, as shown in Figure 8a, with a local-oscillator (LO) signal distributed among all four devices by a single master device, the transmitting and receiving microstrip patch array antennas from different devices can be regarded as an integrated transceiver supporting up to 9 TX and 16 RX antenna elements in azimuth. Meanwhile, the interfering radar presented in our experiments is TI AWR 1642, as shown in Figure 8b. Generally, since the incoherent radar interference that interfering and victim radars have different chirp parameters occurs in most cases and always results in severe performance loss for extended UAV tracking [37,50], we mainly concentrate on incoherent radar interference in this article and the configured parameters of interfering and victim radars are presented in

Table 1. Parameter configuration of victim and interfering radar systems.

Parameters	Victim Radar	Interfering Radar
Carrier frequency	77 GHz	77 GHz
Bandwidth	2.4 GHz	0.87 GHz
Pulse duration	50 $\mathsf{\mu }$s	18.98 $\mathsf{\mu }$s
No. of transmitters	12	2
No. of receivers	16	4
Sweep slope	85.021 MHz/$\mathsf{\mu }$s	85.021 MHz/$\mathsf{\mu }$s
Sample rate	9000 KHz	6250 KHz
Range resolution	0.062 m	0.17 m
Azimuth resolution	1.4062°	14.3°

. It should be pointed out that the dechirp technique [48] is employed in our radar, and thus, the sample rate is significantly smaller than the bandwidth. Figure 8c shows the developed UAV, which was embedded in a high-precision ultra-wideband (UWB) positioning module to obtain the flying trajectories as the ground truth for comparison. In addition, as given in Figure 8d, the DJI Tello Micro-UAV was also employed as the target in a rainy scenario. Three classical extended target tracking methods, i.e., DBSCAN [22], RMM [23,24], SOEKF [27], and the point-target tracking method, i.e., PFTBD [7], are also given for comparison.

3.3.1. Mutual Interference Scenario

In this part, the tracking results of extended UAV in the presence of mutual radar interference (In the same area, multiple radars have overlapping working frequency bands, resulting in the phenomenon that the receiving end receives signals from other radars) are presented in Figure 9. In this experiment, the cascade MIMO radar was located at the coordinate origin and the UAV was controlled to fly a U-shape trajectory in the front of the cascade MIMO radar, as shown in Figure 9a. The start and end position coordinates of the UAV are (−4, 6) and (4, 6), respectively. The radar raw range–azimuth spectra of the 31, 44 and 52 radar frames are presented in Figure 9b–d. We can clearly see the random interfering speckles in the range–azimuth spectrum. In addition, one can also see that the returned signals from UAV also appear in the radar spectrum regularly. On this basis, the proposed method employs this spatiotemporal information to achieve weak UAV tracking and mutual interference suppression. The tracking results of UAV extension and flying trajectory are respectively presented in Figure 9e,f. We can see that both the ghost measurements and the miss detections induced by interfering speckles lead to poor tracking performance of RMM, SOEFK and DBSCAN. The estimated trajectories of RMM, SOEKF and DBSCAN move gradually away from the ground truth, especially in the turn points. Meanwhile, the IoU between the tracked shape and the true extension is also given in Figure 9g. The IoU of the proposed method is larger than 0.3, and the maximum value is approaching 0.6, which means that the proposed method can well track the shape and size of the extended UAV. Figure 9h also presents the error CDF of the tracking trajectory, where we can observe that the proposed method can obtain superior UAV tracking performance than RMM, SOEKF, DBSCAN and PFTBD since it can well mitigate the mutual interferences by jointly addressing a sequence of radar spectra.

3.3.2. Strong Clutter Scenario

In this section, we evaluate the UAV tracking performance of the proposed method in the presence of strong clutter (objects in the environment with high radar cross-section (RCS), such as buildings and large vehicles, cause interference to radar systems). As shown in Figure 10a, two corner reflectors were placed in the radar FOV in advance of the strong clutter interference. Then, the UAV flew a rectangle trajectory in the front of our radar. The radar was also located at the coordinate origin, and the start/end position coordinates of the UAV were (4, 4). The radar raw range–azimuth spectra of the 54-th, 69-th and 79-th radar frames are also shown in Figure 10b–d. We can clearly see the ground clutter and the strong echoes of the two corner reflectors. Figure 10e shows the corresponding tracking results. We can observe that serious ghost measurements induced by the two corner reflectors and ground clutters bring about worse tracking results of RMM and SOEKF in this figure. The estimated trajectories are also presented in Figure 10f. Due to lack of measures to suppress the ghost measurements, SOEKF and DBSCAN cannot complete the weak UAV tracking in the presence of strong clutter in a single radar frame. Although PFTBD employed the non-thresholding radar spectra to track the UAV, the point-target assumption is not appropriate to track the extended object. Instead of the explicit and fixed point-target source model in particle filter-assisted track-before-detection (PFTBD), the proposed method introduces an ellipse shape in addition to a spatial probability distribution as the extent spectrum model to derive the measurement likelihood ratio, achieving robust tracking of the extended UAV, as illustrated in Figure 10g,h. Additionally, we can observe from these images that 100% tracking errors of the proposed method are within 0.5 m and most IoUs are larger than 0.4. Accordingly, the proposed method can track the extended and low-observable UAV in the presence of strong clutter.

3.3.3. Mixed Interference Scenario

For further verifying the effectiveness of the proposed method, we also conduct an experiment in the presence of mutual interference and strong clutters simultaneously. In this scenario, as given in Figure 11a, the UAV was also controlled to fly with a rectangle trajectory that the start/end position coordinate was (−4, 4). The experimental scene and radar raw spectra are presented in Figure 11b–d. The random speckles from the interfering radar and the fixed strong clutters can be clearly seen in radar raw spectra of these images. The tracking results of different methods are presented in Figure 11e–h. It can be seen from Figure 11e,f that RMM, SOEKF, DBSCAN and PFTBD completely obtain wrong trajectories under the mixed interference scenario. Figure 11g depicts the estimated IoUs of RMM, SOEKF and the proposed method, and Figure 11h presents the error CDFs of estimated trajectoies by different methods. It can be seen that the IoUs of RMM and SOEKF are near zero in the whole tracking process, which means that the tracked shape of these two methods have few overlaps with the true extension. We can also notice that in Figure 11g, because the target signals were nearly submerged by interferences around the 28th and 56th frames, the tracking performance of the proposed method decreases quickly around these frames. Fortunately, by deriving an ESCI-based tracking framework, which employs the recursive Bayesian estimation-based track-before-detection strategy to complete UAV tracking and interference suppression by directly utilizing the non-thresholding radar spectra, the positioning errors of the proposed method are within 0.5 m and most IoUs are larger than 0.4. Hence, the proposed method can obtain better tracking performance than RMM, SOEKF, DBSCAN and PFTBD in the presence of ghost targets generated from strong clutters or mutual interfering radars in urban low-altitude.

3.3.4. Rainy Scenario

Robust tracking of UAVs is a fundamental capability for modern radar systems under adverse weather conditions. As a result, we conducted a rainy experiment, where the DJI Tello micro-UAV, which has extremely low RCS, was controlled to fly a rectangle trajectory in the front of our cascade MIMO radar under rainy conditions (in radar echoes, dense precipitation particles will generate dynamic distributed clutter, resulting in attenuation of the target signal), as illustrated in Figure 12a. The start/end position of the DJI Tello micro-UAV was (−2, 6). The range–azimuth spectra of radar echoes at different radar frames are also presented in Figure 12b–d. We can observe that the signal power of the DJI Tello micro-UAV is quite weak, where the UAV is nearly submerged by noises and rain clutter. Additionally, we can also notice that the signal power of raindrops around radar is much stronger than the DJI Tello micro-UAV, and the SINRs in these three frames are all lower than 0 dB, which will cause serious mis-detections and false alarms after a threshold-decision process, as shown in Figure 12e. Since the RMM and the SOEKF highly depend on the radar measurements, they wrongly tracked the rain clutters, as illustrated in this figure. Fortunately, by jointly employing the spatiotemporal correlation information of the target existing in a sequence of radar raw spectra, the proposed method can accurately track the DJI Tello micro-UAV. As shown in Figure 12g, the IoUs of RMM and SOEKF approach zero, but our method is 0.4. The trajectory tracking results and the corresponding error CDF are given in Figure 12f,h. We can see that more than 80% of tracking errors of the proposed method are within 0.6 m, which is much better than other SOTA algorithms. Accordingly, compared with SOTA algorithms, the proposed method can robustly achieve low-observable and extended UAV tracking in the presence of rain clutter.

4. Performance Analysis and Discussion

4.1. Impact of Occlusion

In real applications, the flying UAV may be partially or completely occluded by other objects, which may lead to the failure of target tracking. For evaluating the tracking performance of the proposed method in the occlusion scene (during the radar detection process, due to the intervention of obstructions, the echo signals of the target objects are partially or completely blocked), we continued to conduct an occlusion experiment where the UAV flew as a specific trajectory, and a whiteboard was placed in front of the radar as an occluded object, as shown in Figure 13a. Meanwhile, when tracking the flying UAV, a volunteer also stood on the right front of the radar, which would cause the second occlusion. Figure 13b presents the corresponding radar spectrum, where we can clearly observe the occlusion objects and ground clutters. Figure 13c,d show the UAV tracking results of PFTBD, DBSCAN, SOEKF, RMM and the proposed method. We can observe that although the proposed method failed to continuously track the UAV at the two occlusion cases, it can retrack the UAV quickly after the target reappeared in radar FOV. However, due to the interference of clutter, PFTBD, DBSCAN, SOEKF and RMM cannot complete UAV tracking. The estimated IoUs at different radar frames are presented in Figure 13e. We can see that the estimated IoUs of the proposed method decreases at the two occlusion cases and quickly increases to more than 0.4 after leaving the occlusion area, which implies that the proposed method can robustly track the UAV as long as it occurs in radar FOV. Finally, the error CDF of the estimated trajectory is presented in Figure 13f. We can see that 80% of the tracking errors of the proposed method are within 0.5 m, which is superior than other SOTA algorithms.

4.2. Impact of SINR

Since the weak echoes from extended UAV are easily submerged by noise and interference by means of Monte Carlo simulations, Figure 14 presents the tracking performance of different methods under different SINRs. In this figure, the Gaussian noise was added in the target echoes, and the input SINR varied from −9 dB to 7 dB with a step size of 2 dB. The tracking RMSEs with SINR increasing is first given in Figure 14a. We can see that the proposed method has close tracking performance with RMM, SOEKF, DBSCAN and PFTBD when the SINR is larger than 3 dB. Nevertheless, the tracking RMSEs of RMM, SOEKF and DBSCAN increase quickly when the SINR is less than 3 dB. Thanks to directly utilizing the unthresholding radar spectrum, the RMSE of PFTBD increases until the SINR is less than −3 dB. Figure 14b presents the estimated IoUs with SINR increasing. One can also see that RMM, SOEKF and the proposed method closely estimate IoUs when the SINR is larger than 3 dB, while the IoUs of RMM and SOEKF decrease sharply when the SINR is less than 5 dB. Fortunately, with 2D-KT and the pseudo-spectrum radar measurement model, the RMSE of the proposed method is within 1 m, and the corresponding IoU is about 0.4 when the SINR is reduced to −9 dB, which can get more than a 10 dB improvement of anti-interference ability for extended UAV tracking.

4.3. Computational Complexity Analysis

The main procedure of the proposed method includes range Fast Fourier Transform (FFT), 2D-KD and the ESCI-based tracking algorithm. Assume that $N_r$, $N_v$ and $N_{\theta }$ are, respectively, the number of range samples, the number of integrated pulses in one radar frame and the number of channels. Then, the computational cost of range FFT is $o\left(N_{\theta }{N}_v{N}_r{log}_2{N}_r\right)$. For KT, it can be implemented by means of chirp-z transform (CZT) instead of interpolation with a close computational complexity with FFT [44]. Consequently, the computational complexity of 2D-KT is about $o(N_r{N}_{\theta }{N}_v{log}_2{N}_v+N_v{N}_r{N}_{\theta }{log}_2{N}_{\theta })$. Supposing that $N_q$ is the number of Monte Carlo samples, the computational complexity of the ESCI-based tracking algorithm is about $o\left(N_r{N}_{\theta }{N}_v{N}_p{log}_2{N}_p\right)$. Fortunately, considering that the amplitudes of target echoes attenuate rapidly with the resolution cell away from the target, we employ the impact area, with a size of $M_r\times M_{\theta }\times M_v$, to estimate the likelihood ratio in (25) for avoiding accessing all the resolution cells of the radar spectrum. On this basis, the computational complexity of the ESCI-based tracking algorithm is reduced to $o\left(M_r{M}_{\theta }{M}_v{N}_p{log}_2{N}_p\right)$. Assume $N_r=N_{\theta }=N_v=N_p=N$ and $M_r=M_{\theta }=M_v=M$. Then, the total computational burden of the proposed method can be approximately estimated as $o(3N^3{log}_{2}N+M^{3}N{log}_{2}N)$. For PFTBD, the 3D-FFT operation and the sequential Monte Carlo tracking algorithm are the two main processing parts with a computational complexity of $o(3N^3{log}_{2}N+M^{3}N{log}_{2}N)$. For RMM, SOEKF and DBSCAN, the computational cost is mainly consumed in the 3D-FFT operation and threshold-decision process. Hence, the computational costs of RMM, SOEKF and DBSCAN are $o(3N^3{log}_{2}N+L_w{N}^3)$, where $L_w$ is the length of the sliding window of the threshold-decision algorithm [45]. Since M is far less than N generally, the proposed method has close computational complexity with PFTBD, RMM, SOEKF and DBSCAN. Additionally, we can also observe that the main computational consumption of the proposed method is also concentrated in radar signal processing, which can be implemented on FPGA to meet the real-time requirements in application.

5. Conclusions

In this article, with a high-resolution cascade MIMO radar, we proposed an ESCI-based UAV tracking framework in the presence of strong clutters and radar mutual interference. The major properties of the proposed method can be concluded as follows.

(1) In a single radar frame, we presented a 2D-KT-based coherent integration algorithm to maximally accumulate the target power in different pulses and channels, the SINR is coherently integrated from 12.84 dB to 31.3 dB, which can significantly improve the SINR in radar range–Doppler–azimuth spectrum.

(2) With a sequence of radar range–Doppler–azimuth spectra, we proposed an ESCI-based UAV tracking framework in the presence of radar mutual interferences and strong clutters by maximizing the posterior probability of the target, which satisfies Newtonian dynamic equations and elliptic energy distribution.

(3) Extensive experimental results show that this method can achieve joint positioning and spatial range state estimation and has a high anti-interference ability when facing interference. It performs exceptionally well in complex occlusion, mixed interferences and tracking under adverse weather conditions.

However, in this work, we did not directly remove the interference from radar raw spectrum before tracking, resulting in the performance loss of UAV tracking when the echoes of target and interferences are close to each other in radar range–Doppler–azimuth spectrum. In the future work, we will develop interference identification, localization and elimination algorithms to further improve the UAV tracking performance under harsh environments.