Support Vector Machines with Hyperparameter Optimization Frameworks for Classifying Mobile Phone Prices in Multi-Class
Abstract
1. Introduction
2. Support Vector Machines (SVM) with Hyperparameter Optimization Framework
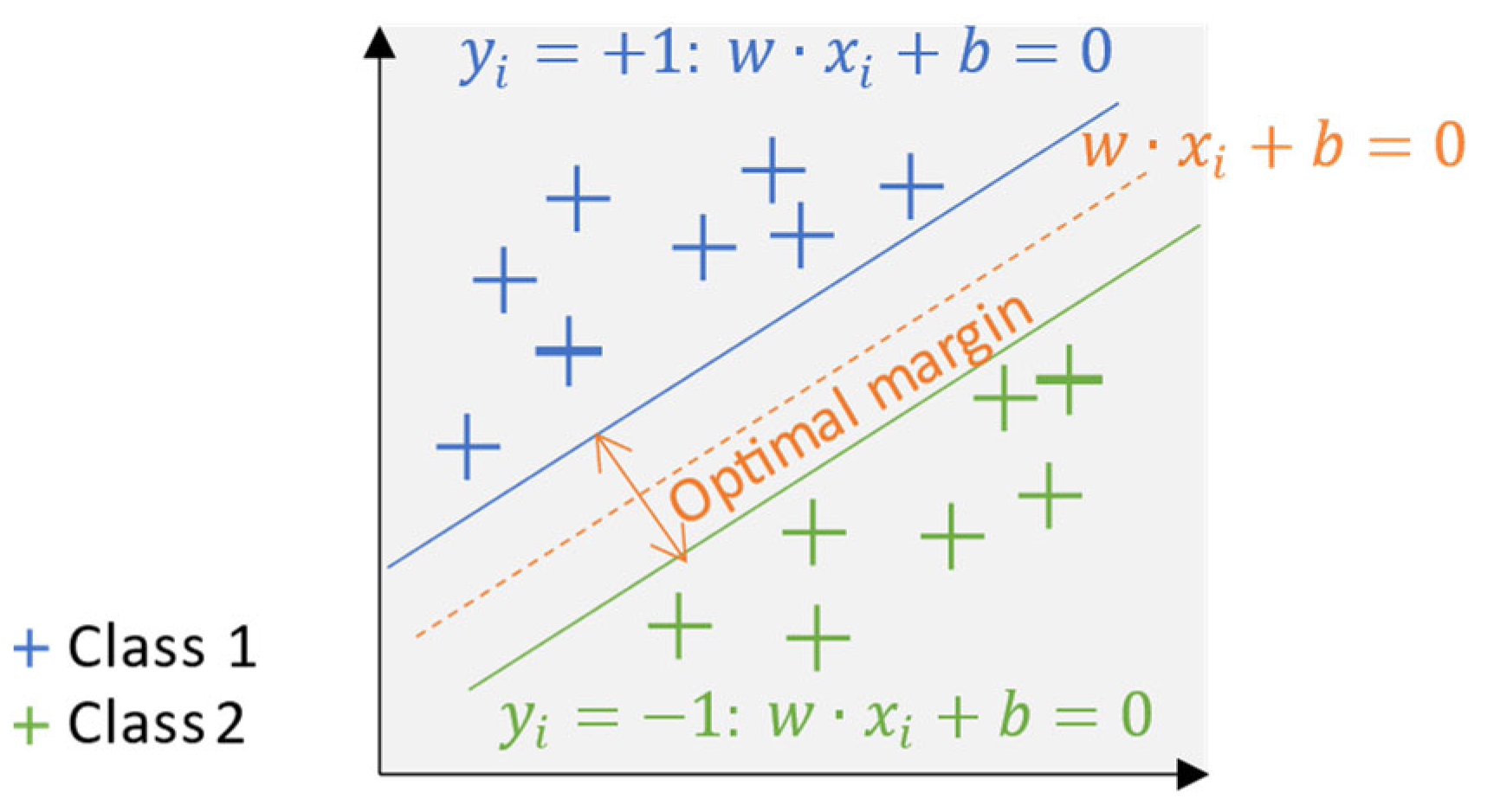
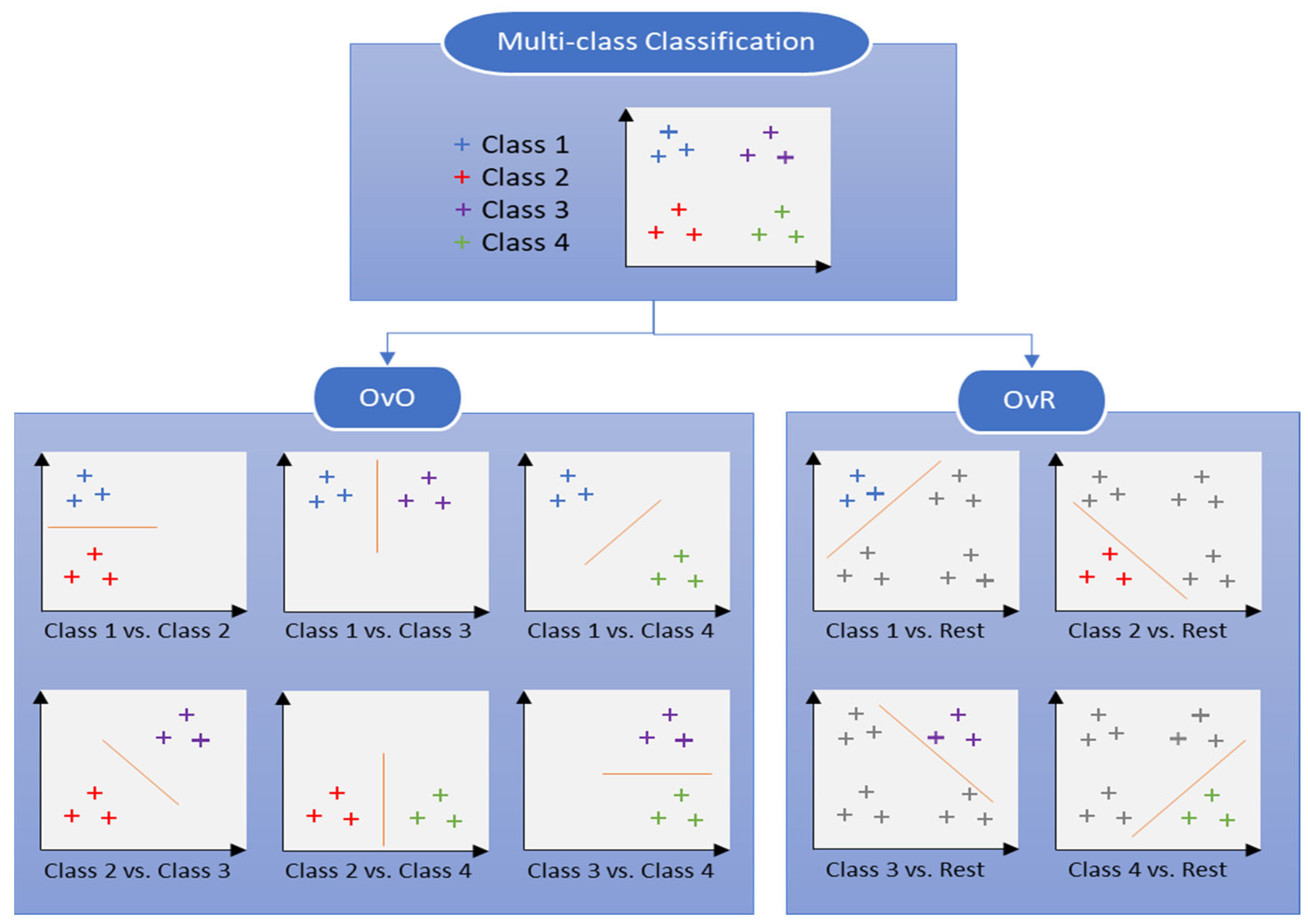
2.1. Support Vector Machines
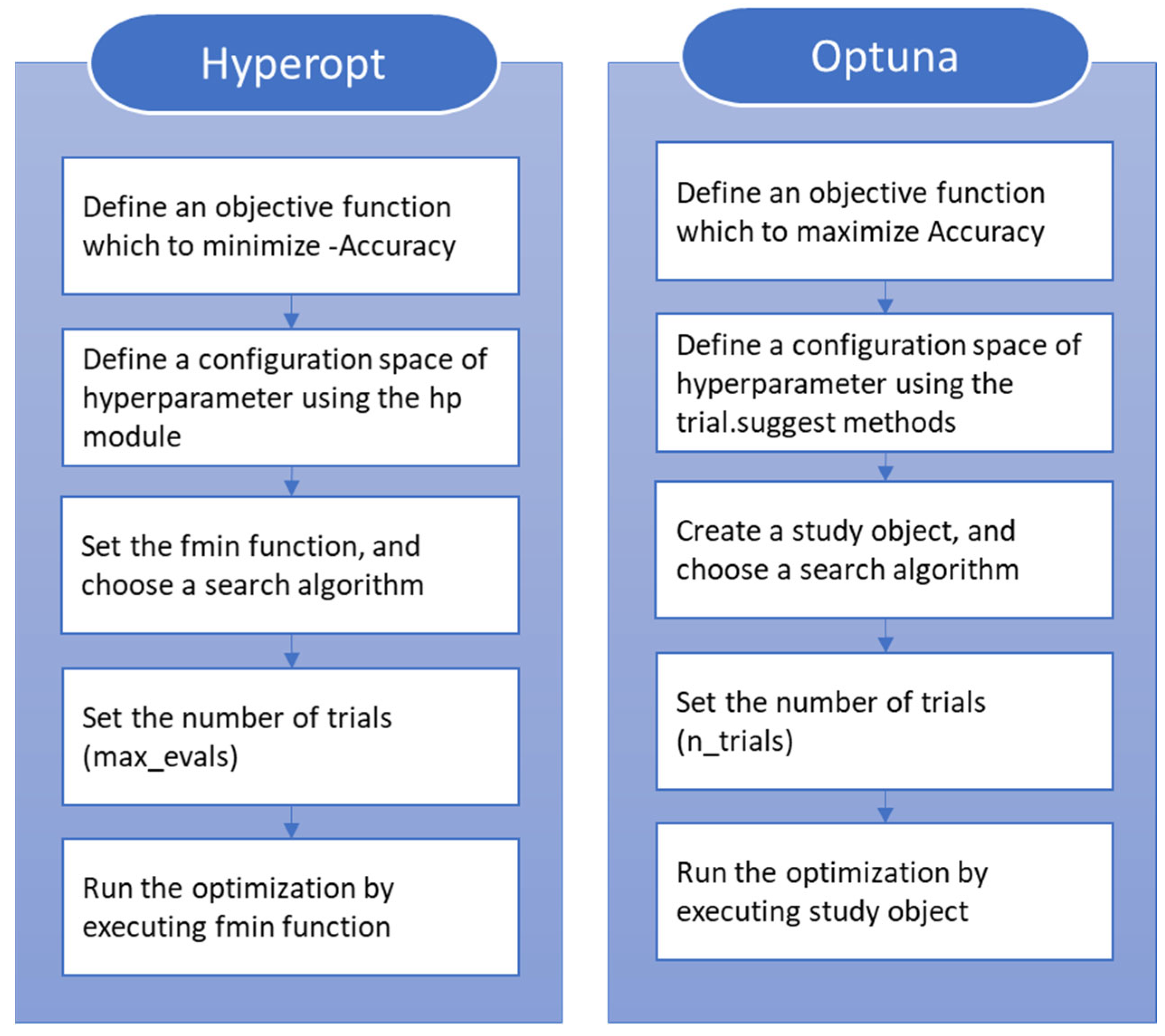
2.2. Hyperparameter Optimization Framework
3. The Proposed Architecture for Predicting Mobile Phone Price
| Algorithm 1. Mobile phone price classification using SVM with HPO |
|
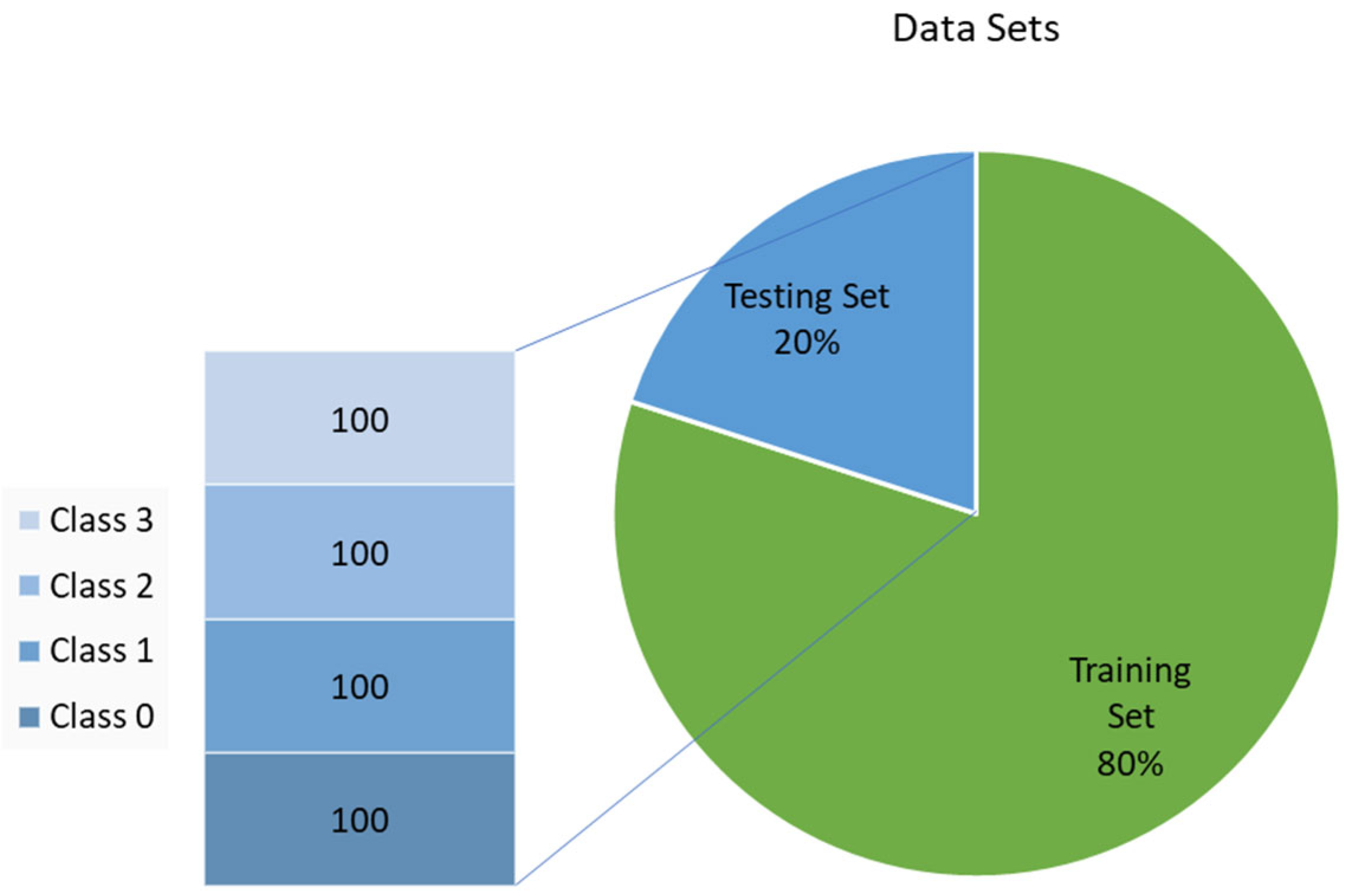
3.1. Data Collection and Splitting
3.2. Model Learning
4. Numerical Results and Discussion
4.1. Numerical Results
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smartphone Market Size & Share Analysis—Growth Trends & Forecasts (2025–2030). Available online: https://www.mordorintelligence.com/industry-reports/smartphones-market (accessed on 17 January 2025).
- Mobile Price Classification. Available online: https://www.kaggle.com/datasets/iabhishekofficial/mobile-price-classification (accessed on 23 October 2024).
- Nasser, I.M.; Al-Shawwa, M.O.; Abu-Naser, S.S. Developing artificial neural network for predicting mobile phone price range. Int. J. Acad. Inf. Syst. Res. 2019, 3, 1–6. [Google Scholar]
- Pipalia, K.; Bhadja, R. Performance evaluation of different supervised learning algorithms for mobile price classification. Int. J. Res. Appl. Sci. Eng. Technol. (IJRASET) 2020, 8, 1841–1848. [Google Scholar] [CrossRef]
- Çetın, M.; Koç, Y. Mobile phone price class prediction using different classification algorithms with feature selection and parameter optimization. In Proceedings of the 2021 5th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 21–23 October 2021; pp. 483–487. [Google Scholar]
- Güvenç, E.; Çetin, G.; Koçak, H. Comparison of KNN and DNN classifiers performance in predicting mobile phone price ranges. Adv. Artif. Intell. Res. 2021, 1, 19–28. [Google Scholar]
- Kalaivani, K.; Priyadharshini, N.; Nivedhashri, S.; Nandhini, R. Predicting the price range of mobile phones using machine learning techniques. In Proceedings of the 4th National Conference On Current And Emerging Process Technologies E-Concept-2021, Erode, India, 20 February 2021. [Google Scholar]
- Pramanik, R.; Agrawal, R.; Gourisaria, M.K.; Singh, P.K. Comparative analysis of mobile price classification using feature engineering techniques. In Proceedings of the 2021 5th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 22–23 October 2021; pp. 1–7. [Google Scholar]
- Kiran, A.V.; Jebakumar, R. Prediction of mobile phone price class using supervised machine learning techniques. Int. J. Innov. Sci. Res. Technol. 2022, 7, 248–251. [Google Scholar]
- Hu, N. Classification of Mobile Phone Price Dataset Using Machine Learning Algorithms. In Proceedings of the 2022 3rd International Conference on Pattern Recognition and Machine Learning (PRML), Chengdu, China, 22–24 July 2022; pp. 438–443. [Google Scholar]
- Chen, M. Mobile Phone Price Prediction with Feature Reduction. Highlights Sci. Eng. Technol. 2023, 34, 155–162. [Google Scholar] [CrossRef]
- Ercan, S.İ.A.; ŞİMŞEK, M. Mobile Phone Price Classification Using Machine Learning. Int. J. Adv. Nat. Sci. Eng. Res. 2023, 7, 458–462. [Google Scholar]
- Zhang, Y.; Ding, Q.; Liu, C. An Enhanced XGBoost Algorithm for Mobile Price Classification. In Proceedings of the 2023 IEEE 6th International Conference on Big Data and Artificial Intelligence (BDAI), Jiaxing, China, 7–9 July 2023; pp. 154–159. [Google Scholar]
- Sunariya, N.; Singh, A.; Alam, M.; Gaur, V. Classification of Mobile Price Using Machine Learning. In Proceedings of the Symposium on Computing & Intelligent Systems, New Delhi, India, 10 May 2024; pp. 55–66. [Google Scholar]
- Chang, Y.-J. A Study of Support Vector Machines and Hyperparameters Selection in Multiclass Classification. Master’s Thesis, National Chi Nan University, Nantou County, Taiwan, 2024. [Google Scholar]
- Jain, T.; Garg, P.; Chalil, N.; Sinha, A.; Verma, V.K.; Gupta, R. SMS spam classification using machine learning techniques. In Proceedings of the 2022 12th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 27–28 January 2022; pp. 273–279. [Google Scholar]
- Gupta, M.; Kumar, R.; Badala, D.; Sharma, R. Optimizing SVM Hyperparameters For Accurate Cancer Cell Classification. In Proceedings of the 2023 International Conference on New Frontiers in Communication, Automation, Management and Security (ICCAMS), Bangalore, India, 27–28 October 2023; pp. 1–5. [Google Scholar]
- Soumaya, Z.; Taoufiq, B.D.; Benayad, N.; Yunus, K.; Abdelkrim, A. The detection of Parkinson disease using the genetic algorithm and SVM classifier. Appl. Acoust. 2021, 171, 107528. [Google Scholar] [CrossRef]
- Wang, J. Optimizing support vector machine (SVM) by social spider optimization (SSO) for edge detection in colored images. Sci. Rep. 2024, 14, 9136. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, Z.; Kong, H.; Yang, J. Learning The Optimal Discriminant SVM with Feature Extraction. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 2897–2911. [Google Scholar] [CrossRef]
- Wei, P.; He, F.; Li, L.; Li, J. Research on sound classification based on SVM. Neural Comput. Appl. 2020, 32, 1593–1607. [Google Scholar] [CrossRef]
- Haile, M.B.; Walle, Y.M.; Belay, A.J. Enhanced Image-Based Malware Multiclass Classification Method with the Ensemble Model and SVM. Open Inf. Sci. 2024, 8, 20240003. [Google Scholar] [CrossRef]
- Suresh Kumar, K.; Radha Mani, A.; Ananth Kumar, T.; Jalili, A.; Gheisari, M.; Malik, Y.; Chen, H.-C.; Jahangir Moshayedi, A. Sentiment Analysis of Short Texts Using SVMs and VSMs-Based Multiclass Semantic Classification. Appl. Artif. Intell. 2024, 38, 2321555. [Google Scholar] [CrossRef]
- Prabhavathy, T.; Elumalai, V.K.; Balaji, E. Hand gesture classification framework leveraging the entropy features from sEMG signals and VMD augmented multi-class SVM. Expert Syst. Appl. 2024, 238, 121972. [Google Scholar]
- Şengül, G.; Ozcelik, E.; Misra, S.; Damaševičius, R.; Maskeliūnas, R. Fusion of smartphone sensor data for classification of daily user activities. Multimed. Tools Appl. 2021, 80, 33527–33546. [Google Scholar] [CrossRef]
- Azhar, M.H.; Jalal, A. Human-Human Interaction Recognition using Mask R-CNN and Multi-class SVM. In Proceedings of the 2024 3rd International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 26–27 November 2024; pp. 1–6. [Google Scholar]
- Thirumala, K.; Pal, S.; Jain, T.; Umarikar, A.C. A classification method for multiple power quality disturbances using EWT based adaptive filtering and multiclass SVM. Neurocomputing 2019, 334, 265–274. [Google Scholar] [CrossRef]
- Dhandhia, A.; Pandya, V.; Bhatt, P. Multi-class support vector machines for static security assessment of power system. Ain Shams Eng. J. 2020, 11, 57–65. [Google Scholar] [CrossRef]
- Liu, F.; Liu, B.; Zhang, J.; Wan, P.; Li, B. Fault mode detection of a hybrid electric vehicle by using support vector machine. Energy Rep. 2023, 9, 137–148. [Google Scholar] [CrossRef]
- Janjarasjitt, S. Investigating the Effect of Vibration Signal Length on Bearing Fault Classification Using Wavelet Scattering Transform. Sensors 2025, 25, 699. [Google Scholar] [CrossRef]
- Phatai, G.; Luangrungruang, T. Improving Multi-Class Classification with Machine Learning and Metaheuristic Algorithm. In Proceedings of the 2025 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 18–21 February 2025; pp. 665–670. [Google Scholar]
- Kamal, S.; Alhasson, H.F.; Alnusayri, M.; Alatiyyah, M.; Aljuaid, H.; Jalal, A.; Liu, H. Vision Sensor for Automatic Recognition of Human Activities via Hybrid Features and Multi-Class Support Vector Machine. Sensors 2025, 25, 200. [Google Scholar] [CrossRef]
- Li, S.; Liu, J.; Xu, W.; Zhang, S.; Zhao, M.; Miao, L.; Hui, M.; Wang, Y.; Hou, Y.; Cong, B. A multi-class support vector machine classification model based on 14 microRNAs for forensic body fluid identification. Forensic Sci. Int. Genet. 2025, 75, 103180. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Advances in Neural Information Processing Systems, Proceedings of the 25th International Conference on Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; Volume 24. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms. SciPy 2013, 13, 20. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Radhika, Y. Resnet-53 for Alzheimer’s Disease Detection from MRI Images and Analysis with SVM Tuning with Hyper Optimization Technique. In Proceedings of the 2024 4th International Conference on Sustainable Expert Systems (ICSES), Kaski, Nepal, 15–17 October 2024; pp. 1065–1072. [Google Scholar]
- Efendi, A.; Fitri, I.; Nurcahyo, G.W. Improvement of Machine Learning Algorithms with Hyperparameter Tuning on Various Datasets. In Proceedings of the 2024 International Conference on Future Technologies for Smart Society (ICFTSS), Kuala Lumpur, Malaysia, 7–8 August 2024; pp. 75–79. [Google Scholar]
- Shin, J.; Matsumoto, M.; Maniruzzaman, M.; Hasan, M.A.M.; Hirooka, K.; Hagihara, Y.; Kotsuki, N.; Inomata-Terada, S.; Terao, Y.; Kobayashi, S. Classification of Hand-Movement Disabilities in Parkinson’s Disease Using a Motion-Capture Device and Machine Learning. IEEE Access 2024, 12, 52466–52479. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J. A user’s guide to support vector machines. Data Min. Tech. Life Sci. 2010, 609, 223–239. [Google Scholar]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Ji, Y.; Song, L.; Yuan, H.; Li, H.; Peng, W.; Sun, J. Prediction of strip section shape for hot-rolled based on mechanism fusion data model. Appl. Soft Comput. 2023, 146, 110670. [Google Scholar] [CrossRef]
- Andhalkar, S.; Momin, B. Multiclass IFROWNN classification algorithm using OVA and OVO strategy. In Proceedings of the 2018 9th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Bengaluru, India, 10–12 July 2018; pp. 1–7. [Google Scholar]
- Pokhrel, P. A Comparison of AutoML Hyperparameter Optimization Tools for Tabular Data. Master’s Thesis, Youngstown State University, Youngstown, OH, USA, 2023. [Google Scholar]
- Shekhar, S.; Bansode, A.; Salim, A. A comparative study of hyper-parameter optimization tools. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Brisbane, Australia, 8–10 December 2021; pp. 1–6. [Google Scholar]
- Shar, L.K.; Duong, T.N.B.; Yeo, Y.C.; Fan, J. Empirical Evaluation of Hyper-parameter Optimization Techniques for Deep Learning-based Malware Detectors. Procedia Comput. Sci. 2024, 246, 2090–2099. [Google Scholar] [CrossRef]
- Woźniacki, A.; Książek, W.; Mrowczyk, P. A novel approach for predicting the survival of colorectal cancer patients using machine learning techniques and advanced parameter optimization methods. Cancers 2024, 16, 3205. [Google Scholar] [CrossRef]
- Khan, S.A.; Khan, M.A.; Amin, M.N.; Ali, M.; Althoey, F.; Alsharari, F. Sustainable alternate binding material for concrete using waste materials: A testing and computational study for the strength evaluation. J. Build. Eng. 2023, 80, 107932. [Google Scholar] [CrossRef]
- Kiraga, S.; Peters, R.T.; Molaei, B.; Evett, S.R.; Marek, G. Reference evapotranspiration estimation using genetic algorithm-optimized machine learning models and standardized Penman–Monteith equation in a highly advective environment. Water 2024, 16, 12. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Mun, S.; Oh, Y.-j.; Lee, S. Data Processing Method for Evaluating Pipe Wall Thinning in Nuclear Secondary Systems using SVM Regression Algorithm. Nucl. Eng. Technol. 2025, 57, 103517. [Google Scholar] [CrossRef]
- Sahoo, R.; Karmakar, S. Comparative analysis of machine learning and deep learning techniques on classification of artificially created partial discharge signal. Measurement 2024, 235, 114947. [Google Scholar] [CrossRef]
- Zhou, B.; Guo, W.; Wang, M.; Zhang, Y.; Zhang, R.; Yin, Y. The spike recognition in strong motion records model based on improved feature extraction method and SVM. Comput. Geosci. 2024, 188, 105603. [Google Scholar] [CrossRef]
- Que, Z.; Lin, C.-J. One-class SVM probabilistic outputs. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 6244–6256. [Google Scholar] [CrossRef]
- Farhadpour, S.; Warner, T.A.; Maxwell, A.E. Selecting and interpreting multiclass loss and accuracy assessment metrics for classifications with class imbalance: Guidance and best practices. Remote Sens. 2024, 16, 533. [Google Scholar] [CrossRef]
- Alsmirat, M.; Kharsa, R.; Alzoubi, R. Supervised Deep Learning for Ideal Identification of Image Retargeting Techniques. IEEE Access 2024, 12, 2169–3536. [Google Scholar] [CrossRef]
- Xie, Y.; Li, S.; Chen, Z.; Du, H.; Jia, X.; Tang, J.; Du, Y. Malware Classification Method Based on Dynamic Features with Sensitive Behaviors. In Proceedings of the 2024 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Kuching, Malaysia, 6–10 October 2024; pp. 4168–4173. [Google Scholar]
- Macsik, P.; Pavlovicova, J.; Kajan, S.; Goga, J.; Kurilova, V. Image preprocessing-based ensemble deep learning classification of diabetic retinopathy. IET Image Process. 2024, 18, 807–828. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems, Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Liaw, R.; Liang, E.; Nishihara, R.; Moritz, P.; Gonzalez, J.E.; Stoica, I. Tune: A research platform for distributed model selection and training. arXiv 2018, arXiv:1807.05118. [Google Scholar]
- Tan, J.M.; Liao, H.; Liu, W.; Fan, C.; Huang, J.; Liu, Z.; Yan, J. Hyperparameter optimization: Classics, acceleration, online, multi-objective, and tools. Math. Biosci. Eng. 2024, 21, 6289–6335. [Google Scholar] [CrossRef] [PubMed]
- Balandat, M.; Karrer, B.; Jiang, D.; Daulton, S.; Letham, B.; Wilson, A.G.; Bakshy, E. BoTorch: A framework for efficient Monte-Carlo Bayesian optimization. In Advances in Neural Information Processing Systems, Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; Curran Associates Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 21524–21538. [Google Scholar]





| Author | Year | Dataset Split | Models Used | HPO Methods | Best Accuracy Result |
|---|---|---|---|---|---|
| Nasser et al. [3] | 2019 | 70% training, 30% testing | ANN * | NS * | ANN: 96.31% |
| Pipalia and Bhadja [4] | 2020 | 70% training, 30% testing | LR, KNN, DT, SVM, GB | NS * | GB: 90% |
| Çetın and Koç [5] | 2021 | 80% training, 20% testing | RF, LR, DT, LDA *, KNN, SVM | Grid Search | SVM: 95.8% |
| Güvenç et al. [6] | 2021 | 80% training, 20% validation | KNN, DNN * | Trial-and-Error | DNN: 94% |
| Kalaivani et al. [7] | 2021 | NS * | SVM, RF, LR | NS * | SVM: 97% |
| Pramanik et al. [8] | 2021 | 80% training, 20% validation | LR, KNN, SVM, NB *, DT, RF, ANN *, XGBoost, LGBM *, CatBoost *, AdaBoost * | NS * | SVM: 96.77% |
| Kiran and Jebakumar [9] | 2022 | 80% training, 20% testing | DT, LDA *, NB *, KNN, RF | NS * | LDA: 95% |
| Hu [10] | 2022 | 70% training, 30% testing | SVM, DT, KNN, NB * | NS * | SVM: 95.5% |
| Chen [11] | 2023 | 80% training, 20% testing | MLP * | Givian | MLP: 95.8% |
| Ercan and Şimşek [12] | 2023 | 70% training, 30% testing | LR, SVM, DT, KNN | NS * | SVM: 96% |
| Zhang et al. [13] | 2023 | 70% training, 15% validation, and 15% testing. | DBO-XGBoost, LR, DT, RF, AdaBoost * | DBO algorithm | DBO-XGBoost: 95.5% |
| Sunariya et al. [14] | 2024 | NS * | SVM, RF, DT, LR, KNN | NS * | SVM: 98% |
| Target and Features | Variable Name | Description | Type | Null Count |
|---|---|---|---|---|
| Target () | price_range | Price range (0: Low, 1: Medium, 2: High, 3: Very High) | int64 | 0 |
| Feature () | battery_power | Battery capacity | int64 | 0 |
| Feature () | blue | Bluetooth (0: No, 1: Yes) | int64 | 0 |
| Feature () | clock_speed | Processor speed (GHz) | float64 | 0 |
| Feature () | dual_sim | Dual SIM (0: No, 1: Yes) | int64 | 0 |
| Feature () | fc | Front camera resolution (MP) | int64 | 0 |
| Feature () | four_g | 4G support (0: No, 1: Yes) | int64 | 0 |
| Feature () | int_memory | Internal memory (GB) | int64 | 0 |
| Feature () | m_dep | Thickness (cm) | float64 | 0 |
| Feature () | mobile_wt | Mobile weight (g) | int64 | 0 |
| Feature () | n_cores | Number of processor cores | int64 | 0 |
| Feature () | pc | Primary camera resolution (MP) | int64 | 0 |
| Feature () | px_height | Pixel resolution height | int64 | 0 |
| Feature () | px_width | Pixel resolution width | int64 | 0 |
| Feature () | ram | RAM (MB) | int64 | 0 |
| Feature () | sc_h | Screen height (cm) | int64 | 0 |
| Feature () | sc_w | Screen width (cm) | int64 | 0 |
| Feature () | talk_time | Maximum time that the battery can last on a single charge (sec) | int64 | 0 |
| Feature () | three_g | 3G support (0: No, 1: Yes) | int64 | 0 |
| Feature () | touch_screen | Touch screen support (0: No, 1: Yes) | int64 | 0 |
| Feature () | wifi | Wi-Fi support (0: No, 1: Yes) | int64 | 0 |
| Hyperparameters | Default Value | Searching Range |
|---|---|---|
| kernel | ‘rbf’ | ‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’ |
| decision_function_shape | ‘ovr’ | ‘ovr’, ‘ovo’ |
| C | 1 | 1 × 10−2, 1 × 102 |
| Gamma | scale | 4.701 × 10−7, 6.701 × 10−7 |
| Predicted Labels | |||||
|---|---|---|---|---|---|
| Class | Class 1 | Class 2 | … | Class n | |
| True Labels | Class 1 | … | |||
| Class 2 | … | ||||
| . | . | . | . | . | |
| . | . | . | . | . | |
| . | . | . | . | . | |
| Class n | … | ||||
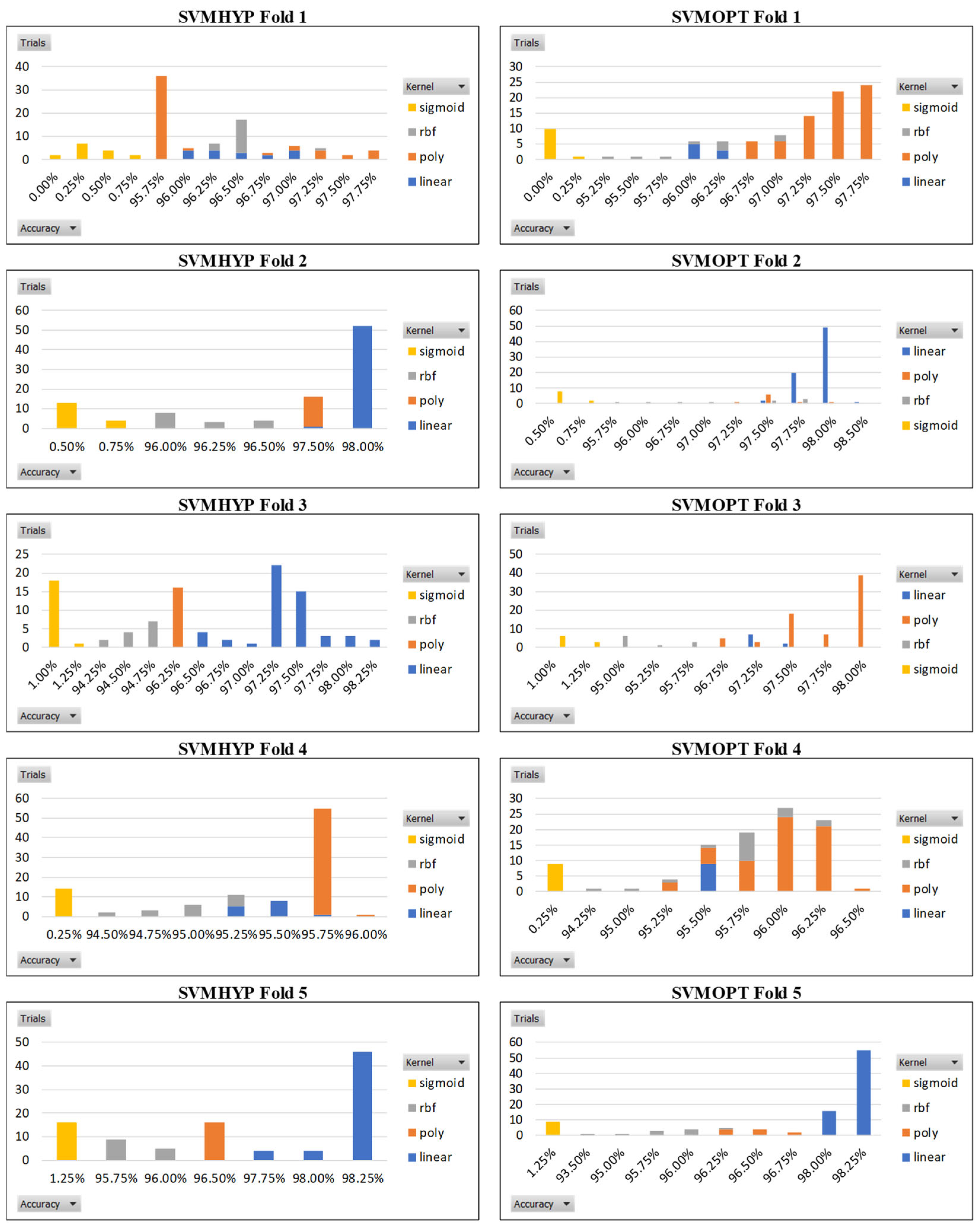
| Fold Number | Best Trail Number | Kernel | C | Gamma | DF_S | Time (s) |
|---|---|---|---|---|---|---|
| Fold 1 | 73 | poly | 24.0911 | 5.7263 × 10−7 | ovr | 181 |
| Fold 2 | 2 | linear | 8.0367 | 6.6103 × 10−7 | ovo | 530 |
| Fold 3 | 34 | linear | 0.0339 | 5.6089 × 10−7 | ovo | 436 |
| Fold 4 | 48 | poly | 5.0618 | 6.0715 × 10−7 | ovo | 66 |
| Fold 5 | 15 | linear | 7.5976 | 6.2982 × 10−7 | ovr | 751 |
| Fold Number | Best Trail Number | Kernel | C | Gamma | DF_S | Time (s) |
|---|---|---|---|---|---|---|
| Fold 1 | 6 | poly | 28.5306 | 5.3762 × 10−7 | ovr | 159 |
| Fold 2 | 93 | linear | 0.0361 | 5.2013 × 10−7 | ovo | 1101 |
| Fold 3 | 0 | poly | 61.8569 | 5.8244 × 10−7 | ovr | 370 |
| Fold 4 | 87 | poly | 86.5157 | 6.5313 × 10−7 | ovr | 63 |
| Fold 5 | 9 | linear | 86.8067 | 5.4853 × 10−7 | ovr | 1505 |
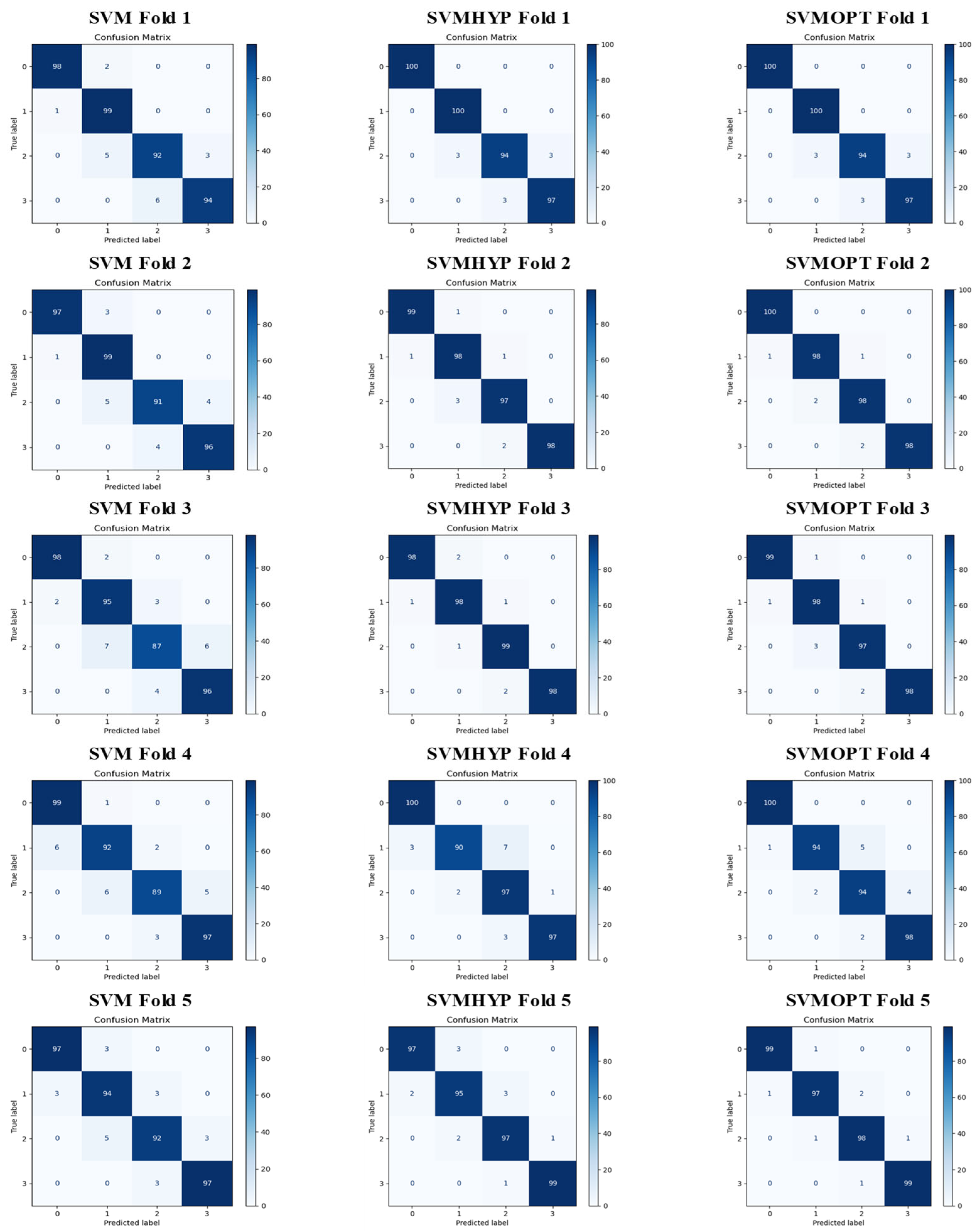
| Fold Number | Accuracy | MA_Precision | MA_Recall | MA_F1-Score |
|---|---|---|---|---|
| Fold 1 | 95.75% | 95.79% | 95.75% | 95.74% |
| Fold 2 | 95.75% | 95.82% | 95.75% | 95.74% |
| Fold 3 | 94.00% | 94.00% | 94.00% | 93.97% |
| Fold 4 | 94.25% | 94.25% | 94.25% | 94.21% |
| Fold 5 | 95.00% | 95.01% | 95.00% | 95.00% |
| Average | 94.95% | 94.97% | 94.95% | 94.93% |
| Fold Number | Accuracy | MA_Precision | MA_Recall | MA_F1-Score |
|---|---|---|---|---|
| Fold 1 | 97.75% | 97.75% | 97.75% | 97.74% |
| Fold 2 | 98.00% | 98.02% | 98.00% | 98.00% |
| Fold 3 | 98.25% | 98.27% | 98.25% | 98.25% |
| Fold 4 | 96.00% | 96.14% | 96.00% | 95.99% |
| Fold 5 | 97.00% | 97.00% | 97.00% | 97.00% |
| Average | 97.40% | 97.44% | 97.40% | 97.40% |
| Fold Number | Accuracy | MA_Precision | MA_Recall | MA_F1-Score |
|---|---|---|---|---|
| Fold 1 | 97.75% | 97.75% | 97.75% | 97.74% |
| Fold 2 | 98.50% | 98.51% | 98.50% | 98.50% |
| Fold 3 | 98.00% | 98.02% | 98.00% | 98.00% |
| Fold 4 | 96.50% | 96.52% | 96.50% | 96.50% |
| Fold 5 | 98.25% | 98.25% | 98.25% | 98.25% |
| Average | 97.80% | 97.81% | 97.80% | 97.80% |
| Fold Number | Models Without PCA | Models with PCA | ||||
|---|---|---|---|---|---|---|
| SVM | SVMHYP | SVMOPT | SVM | SVMHYP | SVMOPT | |
| Fold 1 | 95.75% | 97.75% | 97.75% | 96.25% | 97.50% | 97.50% |
| Fold 2 | 95.75% | 98.00% | 98.50% | 96.25% | 98.00% | 98.50% |
| Fold 3 | 94.00% | 98.25% | 98.00% | 95.00% | 97.25% | 98.50% |
| Fold 4 | 94.25% | 96.00% | 96.50% | 95.25% | 96.75% | 96.75% |
| Fold 5 | 95.00% | 97.00% | 98.25% | 93.00% | 97.75% | 98.25% |
| Average | 94.95% | 97.40% | 97.80% | 95.15% | 97.45% | 97.90% |
| Fold Number | Models Without HPO | Models with Hyperopt | Models with Optuna | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SVM | XGBoost | LGBM | SVMHYP | XGBoostHYP | LGBMHYP | SVMOPT | XGBoostOPT | LGBMOPT | |
| Fold 1 | 95.75% | 89.75% | 89.00% | 97.75% | 92.75% | 92.00% | 97.75% | 92.75% | 91.75% |
| Fold 2 | 95.75% | 93.00% | 92.25% | 98.00% | 94.75% | 94.00% | 98.50% | 95.75% | 94.75% |
| Fold 3 | 94.00% | 92.25% | 92.50% | 98.25% | 92.75% | 92.25% | 98.00% | 93.00% | 92.25% |
| Fold 4 | 94.25% | 91.50% | 91.00% | 96.00% | 93.25% | 93.00% | 96.50% | 93.25% | 93.25% |
| Fold 5 | 95.00% | 89.25% | 88.75% | 97.00% | 93.00% | 92.50% | 98.25% | 93.00% | 92.75% |
| Average | 94.95% | 91.15% | 90.70% | 97.40% | 93.30% | 92.75% | 97.80% | 93.55% | 92.95% |
| Techniques | Accuracy |
|---|---|
| Nasser et al. [3] | 96.31% |
| Pipalia and Bhadja [4] | 90.00% |
| Hu [10] | 95.50% |
| Ercan and Şimşek [12] | 96.00% |
| Proposed (SVMHYP) | 97.50% |
| Proposed (SVMOPT) | 97.67% |
| Techniques | Accuracy |
|---|---|
| Çetın and Koç [5] | 95.80% |
| Güvenç et al. [6] | 94.00% |
| Pramanik et al. [8] | 96.77% |
| Kiran and Jebakumar [9] | 95.00% |
| Chen [11] | 95.80% |
| Proposed (SVMHYP) | 98.25% |
| Proposed (SVMOPT) | 98.50% |
| Techniques | Accuracy |
|---|---|
| Zhang et al. [13] | 95.50% |
| Proposed (SVMHYP) | 99.00% |
| Proposed (SVMOPT) | 99.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.-J.; Lin, Y.-L.; Pai, P.-F. Support Vector Machines with Hyperparameter Optimization Frameworks for Classifying Mobile Phone Prices in Multi-Class. Electronics 2025, 14, 2173. https://doi.org/10.3390/electronics14112173
Chang Y-J, Lin Y-L, Pai P-F. Support Vector Machines with Hyperparameter Optimization Frameworks for Classifying Mobile Phone Prices in Multi-Class. Electronics. 2025; 14(11):2173. https://doi.org/10.3390/electronics14112173
Chicago/Turabian StyleChang, You-Jeng, Ying-Lei Lin, and Ping-Feng Pai. 2025. "Support Vector Machines with Hyperparameter Optimization Frameworks for Classifying Mobile Phone Prices in Multi-Class" Electronics 14, no. 11: 2173. https://doi.org/10.3390/electronics14112173
APA StyleChang, Y.-J., Lin, Y.-L., & Pai, P.-F. (2025). Support Vector Machines with Hyperparameter Optimization Frameworks for Classifying Mobile Phone Prices in Multi-Class. Electronics, 14(11), 2173. https://doi.org/10.3390/electronics14112173








