A Dual-Region MEMS Thermal Flow Sensor with Obstacle-Enhanced Sensitivity and Linearity Across Wide Velocity Ranges

Abstract

This paper introduces a novel MEMS-based thermal flow sensor designed for high sensitivity and linearity across a wide range of gas flow velocities. The sensor incorporates a single microheater and two pairs of thermistors symmetrically arranged around the heater, with strategically placed obstacles to enhance performance. To ensure accuracy under varying flow conditions, the sensor is divided into two functional regions: one optimized for low flow velocities (0–1 m/s) and the other for high flow velocities (1–6 m/s). Simulations conducted using COMSOL Multiphysics reveal that including obstacles improves heat transfer and increases the interaction time between the heated surface and the flow, particularly in the high-flow region. In the low-flow regime, the sensor achieves a sensitivity of 2.5 SK/m with 91% linearity. In contrast, in the high-flow regime, the sensitivity increases to 6.5 SK/m with similarly high linearity. This dual-region design highlights the sensor’s versatility in handling a broad range of flow velocities, making it suitable for applications in medical, industrial, and environmental monitoring. These findings underscore the advantages of the dual-region design and obstacle integration, providing a robust solution for accurate flow measurement under diverse operating conditions.

1. Introduction

In recent years, the evaluation of microelectromechanical systems (MEMSs) has become increasingly significant due to their widespread applications in industrial, medical, and environmental monitoring [1,2,3,4,5]. Known for their high sensitivity and compact size, MEMS sensors have proven to be effective tools in various contexts. However, their delicate structures necessitate rigorous reliability assessments, particularly when operating in complex environments and under fluctuating temperatures. To ensure accurate performance, advancements in sensor design, such as the integration of dual thermistors and precise temperature control circuits, have significantly improved their sensitivity and accuracy in measurement [6]. This enables these sensors to deliver precise results even at low current levels.

Despite these advancements, MEMS sensors remain susceptible to thermal fluctuations and mechanical stresses, which can adversely affect their lifespan and performance [6,7]. Recent innovations have focused on reducing thermal nonlinearity to enhance sensitivity, temperature stability, and overall performance.

These attributes make them particularly well suited for applications such as respiratory monitoring and operation in complex environments [8].

Previous studies have explored various methods to enhance the performance of calorimetric microflow sensors, focusing on optimizing the design of their thermal sensing components. A novel microflow sensor based on thermal feedback was introduced to improve sensitivity and signal stability. This sensor employs digital power distribution to dynamically adjust power consumption within microheaters, effectively mitigating thermal gradients caused by convective flow [9]. Numerical simulations have shown that reducing the distance between the sensors and the heater mitigates the negative effects of flow separation, thereby improving accuracy. Additionally, replacing a cantilever structure with a bridge structure reduces vibrations and increases sensitivity at high flow rates [10]. Key advancements include designing sensors with reduced spacing between the detector and heater, utilizing novel materials to enhance sensitivity, and optimizing packaging and structural designs to improve robustness and minimize vibrations.

Despite these advancements, challenges such as limited measurement range, reduced sensitivity at high flow rates, and structural vibrations remain. Proposed solutions include optimizing the spacing between the detector and heater and reducing resonance through innovative structural designs. A comparative analysis of initial and improved models demonstrates significant improvements in measurement range, sensitivity, and robustness [11].

The sensitivity of thermal flow sensors has also been investigated using numerical models to analyze heat transfer. These models, validated with experimental data, have proposed correlations for predicting sensor sensitivity. Results indicate that factors such as heat loss, the positions of temperature sensors, input power, and heater length significantly influence sensitivity [12]. Other studies have introduced miniaturized flow sensors utilizing thermal feedback and digitized power distribution, achieving high sensitivity and accuracy along with long-term stability and reliable performance under low-amplification conditions. This innovation supports the development of robust flow sensors [13].

Durability and robustness in conductive environments have been enhanced using three different coating materials, with nanocoating offering superior longevity while maintaining sensor performance. This approach has improved the reliability of thermal flow sensors under harsh conditions [14]. Additionally, recent advancements in thermal flow sensors based on time-of-flight technology have addressed the limitations of the calorimetric approach. These sensors enable novel applications through features such as multi-parameter measurement, fluid-independent data acquisition, and self-calibration capabilities [15]. Other studies have developed a multi-gas detection system based on a silicon micro-resonator and machine learning, capable of identifying He, Ar, and CO₂ gases with 100% accuracy without requiring specialized coatings. This system demonstrates potential for compact and intelligent gas sensors [16].

While previous studies have primarily focused on enhancing sensitivity, reducing vibration effects, and optimizing structural designs, persistent limitations include reduced sensitivity at high flow rates, nonlinearity in the sensor response, and diminished accuracy across varying flow ranges. This study introduces a novel approach to address these challenges by integrating digital power control techniques, optimizing thermal structures, and incorporating a flow obstacle to enhance performance at high velocities.

In the design of calorimetric microflow sensors, the incorporation of a flow obstruction has been recognized as an effective approach to enhance sensor performance. Previous studies have demonstrated that placing a barrier upstream of the sensing element can reduce viscous losses, thereby improving measurement accuracy and extending the dynamic range. This method plays a critical role in enhancing the thermal response of the sensor by promoting more directed flow and minimizing disturbances in the sensitive region of the device [17].

In this study, a flow obstruction is employed to enhance the linearity, sensitivity, and accuracy of the microflow sensor. Based on simulation results, the obstacle is strategically designed to optimize both the linear response and sensitivity of the sensor structure. The presence of the obstruction increases the interaction time between the gas flow and the heated surface, thereby improving heat transfer and enhancing sensor sensitivity across a wide range of flow velocities. A key distinction of this work compared to previous studies lies in the primary objective of the obstruction design. While earlier approaches mainly focused on reducing flow separation and improving measurement accuracy under varying flow conditions, the current study emphasizes enhancing thermal performance and maintaining linearity over a broader velocity spectrum. As a result, this approach offers a more optimized design that significantly improves sensor performance under diverse flow conditions.

The incorporation of a flow obstacle ensures a more uniform heat distribution, reduces thermal gradients, and significantly improves sensitivity and response linearity at high flow rates. Additionally, precise thermal distribution adjustments and optimized heat transfer mechanisms minimize output deviations and enhance measurement accuracy. The proposed model mitigates nonlinear thermal effects, enables better temperature control, and refines signal processing, resulting in improved sensor performance under diverse operational conditions. These advancements enhance the accuracy, reliability, and efficiency of MEMS thermal flow sensors, particularly in complex environments

2. Materials and Methods

In the design of MEMS-based thermal flow sensors, achieving high sensitivity and a linear response remains a significant challenge. One effective solution involves introducing an obstacle in the gas flow path. This approach reduces the gas velocity near the sensor, thereby increasing the interaction time between the gas and the heated surface, which enhances heat transfer. As a result, the sensor’s sensitivity to small variations in gas flow is significantly improved.

Additionally, optimizing key design parameters, such as adjusting the distance between the heater and sensors, shortening the heater length, and refining the geometric structure of the sensor, plays a crucial role in improving response linearity. These innovative design strategies enable more accurate and consistent performance across a wide range of gas flow velocities. Figure 1 illustrates the structure of the proposed MEMS thermal flow sensor used in this study.

The materials used in the structure of the thermal flow sensor were selected as outlined in

Table 1. Material properties and components of the thermal flow sensor structure.

Structure Component	Material	Properties
Obstacle	Highly doped polysilicon	High thermal conductivity; mechanical strength
Substrate	Silicon	Thermal stability; electrical insulation
Sensors	Highly doped polysilicon	Compatibility with micromechanical processes
Heater	Platinum	High temperature coefficient of resistance; excellent thermal conductivity
Gas Flow Channel	Air	Natural flow conditions; realistic simulation

. In this design, the obstacle is made of highly doped polysilicon due to its suitable thermal and mechanical properties. The substrate is composed of silicon, which provides excellent thermal stability and electrical insulation. The sensors are made of highly doped polysilicon, which is highly compatible with micromechanical fabrication processes. For the heater, platinum is used because of its high temperature coefficient of resistance and excellent thermal conductivity, ensuring precise performance and stability. Additionally, the gas channel is formed from air, enabling natural flow conditions and a realistic simulation.

2.1. Geometric Model

In the proposed structure, as shown in Figure 1, the sensors, heater, and obstacles are integrated on a single substrate, each designed with precise dimensions and characteristics to enhance performance and increase sensitivity. The sensors are arranged in a two-pair array around the heater, with each sensor measuring 240 µm in length and 150 µm in width and maintaining equal spacing from each other and the heater. One pair of sensors is positioned on the left side of the heater, and another pair is placed on the right side of the heater. The sensors are placed 10 µm away from the heater to enable a faster response to temperature changes caused by gas flow.

The heater, located at the centre, serves as the thermal source, generating the necessary heat via electrical current to establish the required temperature gradient for gas flow detection. It is designed with dimensions of 500 µm in length and 100 µm in width, ensuring uniform heat generation and optimal thermal power distribution spatially. Adjacent to the heater, along the gas flow path, an obstacle with a length of 240 µm and a width of 50 µm is implemented. The dimensions and parameters of this structure were determined based on simulation results from COMSOL to ensure optimal sensor performance.

The obstacle is designed to reduce flow velocity near the sensors, increasing the interaction time between the gas and the heated surface. This improves heat transfer and enhances the sensor’s sensitivity to subtle gas flow variations. In this MEMS thermal flow sensor, all the components are mounted on a silicon substrate, which provides structural support and maintains stable temperatures. The substrate’s thermal conductivity helps prevent temperature fluctuations, ensuring stable operation. This design improves the sensitivity to gas flow changes and provides a more linear response across various flow ranges.

In Figure 1, the dimensions of the various sections of the thermal flow sensor are precisely shown, and these dimensions are provided in

Table 2. Geometrical parameters of the sensor.

Parameter	Term	Value
sensor length	$L_s$	240 μm
sensor width	$W_s$	150 μm
heater length	$L_h$	500 μm
heater width	$W_h$	100 μm
obstacle length	$L_o$	50 μm
obstacle width	$W_o$	240 μm
obstacle height	$H_o$	1 μm
channel width	$W_c$	500 μm
channel length	$L_c$	7000 μm
distance between the sensor and the heater	$L_a$	10 μm
distance between the sensor and the obstacle	$L_b$	10 μm

. In this design, the section with an obstacle is used for high flow velocities, while the unobstructed section is designated for low flow velocities. The thickness of both the heater and sensors is designed to be 1 µm, providing an optimal balance between sensitivity, thermal stability, and long-term durability. This thickness enhances the overall performance of the sensor.

The parameters presented in Table 2, such as the dimensions of the heater, sensor sizes, the spacing between the sensors and heater, and the dimensions of the thermal obstacles, were determined through simulation results obtained using COMSOL Multiphysics version 6.0. These parameters were precisely optimized to improve sensitivity and enhance the linearity of the sensor’s response.

In thermal flow sensors without an obstacle, gas flow can disrupt the temperature profile and reduce sensitivity, as high velocity and shear stress lead to a decrease in the temperature difference between the upstream and downstream sensors. The incorporation of an obstacle in the sensor design creates a region with low velocity and shear stress, which reduces viscous dissipation and stabilizes the thermal gradient. This results in increased sensitivity, an extended flow measurement range, and improved performance at high flow rates. In this paper, a thermal obstacle with dimensions of 50 × 240 × 1 μm is used in front of the sensor. This obstacle stabilizes the thermal gradient by reducing the gas velocity and shear stress in the upstream region of the sensor. Its thin dimensions increase the interaction time of the gas with the heated surface, which, in turn, enhances the sensitivity and measurement range at higher flow rates. This precise design optimizes the impact on the sensor’s performance and minimizes measurement errors under varying flow conditions.

Optimizing the heater dimensions ensures more uniform heat distribution, while the ideal spacing between the sensors and heater increases sensitivity and measurement accuracy. Additionally, carefully designed thermal obstacles reduce gas flow velocity and extend the interaction time with the heated surface. These design improvements significantly enhance sensor performance across a velocity range of 0 to 6 m/s, while minimizing measurement errors.

By minimizing energy loss, polysilicon extends the lifespan of sensor components and ensures reliable operation. Polysilicon plays a crucial role in constructing the sensors and obstacles within the system.

Its compatibility with MEMS fabrication processes and high micro-machinability make it an ideal material for these applications. Highly doped polysilicon, with its appropriate thermal conductivity, aids sensors in accurately receiving heat from the environment while limiting excessive heat transfer. Moreover, it allows the creation of precise obstacles for regulating and controlling gas flow, significantly enhancing the sensitivity and accuracy of measurements.

Air is used as the working gas in this system. Its low thermal conductivity enables a significant temperature gradient between the heater and the sensors, which is essential for proper sensor functionality. Additionally, the low density of air facilitates better observation of the thermal behaviour at low gas flow velocities. Air is a practical choice due to its availability, low cost, and non-corrosive nature, eliminating the need for specialized handling equipment.

2.2. Thermal Flow Sensitivity

These sensors operate on the principle of heat transfer, where the flow rate influences heat dissipation from the heater, and the sensor detects the resulting temperature changes. As the gas flow increases, more heat is carried away through convection, causing a decrease in the sensor’s temperature [8]. The sensitivity of a thermal flow sensor is typically expressed as the rate of change in the measured temperature difference (ΔT) with respect to changes in the flow rate (Q), as calculated using Equation (1).

$$S={\displaystyle \frac{\Delta T}{Q}}$$

(1)

The correlation between the volumetric flow rate (Q) and the flow velocity (u) within a given cross-sectional area depends on the flow type and the geometry of the passage through which the gas flows. Under laminar flow conditions, the sensor exhibits higher sensitivity. However, as the flow rate increases and turbulence develops, the sensitivity decreases.

To ensure accurate measurements across the desired operational range, an optimized sensor design must account for both temperature variations and flow characteristics. This relationship is typically expressed by the following Equation (2):

$$Q=u.A$$

(2)

Since the derivative of Q with respect to u equals A, the sensitivity in relation to flow velocity is expressed by Equation (3).

$$S_u=A.{\displaystyle \frac{\partial \left(\Delta T\right)}{\partial Q}}$$

(3)

This equation demonstrates that the sensitivity to flow velocity is directly proportional to the cross-sectional area A and the derivative of the temperature difference ΔT with respect to the flow rate Q. In other words, increasing the cross-sectional area or enhancing sensitivity to flow rate variations results in a greater sensitivity to flow velocity.

During this process, the heating power regulates the heater temperature, and the resulting temperature variations are directly correlated with the gas flow velocity. The output voltage serves as the final signal for measuring the gas flow rate. Additionally, feedback mechanisms between heating power, heater temperature, and the temperature difference play a critical role in ensuring the sensor’s stability and calibration.

To calculate the temperature difference ΔT in a thermal flow sensor, two key temperatures are measured: the gas temperature before passing over the heat source (upstream sensor) and the gas temperature after passing over the heat source (downstream sensor) [18]. The temperature difference between these two points is calculated using Equation (4).

$$\Delta T=T_d-T_u$$

(4)

Figure 2 illustrates the operating principle of the MEMS-based gas flow sensor. In the absence of flow, the heating element serves as the sole heat source, and due to the lack of gas to facilitate heat transfer, the generated heat is evenly dispersed into the surrounding environment. Under these conditions, no significant temperature difference is detected between the temperature sensors, and the output voltage remains at its minimum level, indicating the absence of gas flow.

Conversely, when gas flow is present, the passage of gas over the heater enhances convective heat transfer, leading to a decrease in the heater’s temperature. As the flow velocity increases, a greater amount of heat is carried away, resulting in a noticeable temperature difference between the upstream and downstream sensors. This temperature difference is converted into an electrical signal and manifests as an output voltage that is proportional to the gas flow rate. This mechanism forms the foundation of the sensor’s operation, whereby variations in output voltage are directly correlated with gas velocity, enabling the accurate measurement of flow rates.

The downstream temperature (T_d) becomes higher than the upstream temperature (T_u) because the gas absorbs heat as it flows over the heat source. The temperature difference (ΔT) increases with higher flow rates [10].

In thermal flow sensors, the mechanism of heat transfer from the heating element to the surrounding gas is governed by Fourier’s Law of Heat Conduction. As the gas flow rate increases, convection enhances heat transfer, resulting in a change in the temperature difference (ΔT). The rate of heat transfer is described by Equation (5).

$$q=-{\displaystyle \frac{dT}{dx}} .A.K$$

(5)

Here, q represents the heat transfer rate (in watts) or heat flux per unit area, k is the thermal conductivity coefficient, A is the cross-sectional area, and dT/dx is the temperature gradient along the material. The symbol k denotes the thermal conductivity, a material property that indicates how efficiently a substance conducts heat.

To evaluate the impact of obstacles on the performance of thermal flow sensors, a set of equations has been developed to model the primary influencing factors, such as the gas flow rate, obstacle size and shape, and the sensor’s response [18]. Equation (6) specifically defines the effective reduction in gas flow velocity (Q_eff) caused by the obstacle:

$$Q_{eff}=Q.\left(1-\alpha S{C}_{shape}\right)$$

(6)

This coefficient quantifies a material’s ability to transfer heat through conduction. The relationships influencing the sensitivity of the thermal flow sensor, including the effects of temperature sensor positioning, heater length, and heat loss, were analyzed in the study conducted by Kim et al. [18]. In this research, a simple numerical model was developed and validated using experimental data. Using this model, a predictive correlation for sensitivity was derived as follows:

$$S_i={\displaystyle \frac{q.L^3.C}{{\left(K.A\right)}^2}}exp\left[D_1+D_2{\left({\displaystyle \frac{L^2}{K_{2}A{R}_r}}\right)}^{D_3}\right]$$

(7)

where

$$D_1=\left[-4.62+\left\{2.04+15.8\left({\displaystyle \frac{L_h}{L_s}}\right)\right\}\left({\displaystyle \frac{L_h}{L}}\right)-1.2{\left({\displaystyle \frac{L_s}{L}}\right)}^2\right]$$

(8)

$$D_2=\left[-2.66+7.54\left({\displaystyle \frac{L_s}{L}}\right)-15.08{\left({\displaystyle \frac{L_s}{L}}\right)}^2+9.59{\left({\displaystyle \frac{L_s}{L}}\right)}^3\right]$$

(9)

$$D_3=\left[0.14+0.72\left({\displaystyle \frac{L_s}{L}}\right)-0.52{\left({\displaystyle \frac{L_s}{L}}\right)}^2\right]$$

(10)

If an array of N sensor pairs is positioned around the heater, the overall sensitivity of the sensor array can be expressed using Equation (11) as follows:

$$S_{total}={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N{S_i}^2}{{{\displaystyle \sum }}_{i=1}^N{S}_i}}$$

(11)

Equation (11) represents an optimized weighted average that accounts for the influence of sensor position, structure, and performance, including blocked, unblocked, and slotted-blocked sensors, in response to flow variations. Unlike the arithmetic mean, this formula assigns greater weight to sensors with higher sensitivity, providing a more accurate estimation of the overall system sensitivity.

In Equation (7), the sensor sensitivity parameters include q (heater heat flux), L (channel length), C (gas heat capacity), K (thermal conductivity), A (sensor channel cross-sectional area), and R_r (radial thermal resistance). Additionally, the empirical coefficients D₁, D₂, and D₃ are related to the geometric ratios of the sensor design, such as the sensor’s temperature position (L_s) and the heater length (L_h). These parameters collectively describe the thermal, geometric, and gas flow characteristics, which determine the sensor’s overall performance [12].

Figure 3 illustrates the operating principle of a MEMS-based gas flow sensor. The inclusion of an obstacle in the MEMS thermal flow sensor structure significantly alters the gas flow behaviour near the sensor. When high-velocity airflow passes over the sensor, the obstacle effectively reduces the airflow speed. This reduction allows the air to remain in contact with the heater for a longer duration, thereby facilitating improved heat transfer to the sensors.

At higher flow velocities, as the gas moves faster, more heat is transferred from the heater to the gas. The presence of the obstacle enhances this heat transfer, resulting in improved sensor sensitivity at higher velocities. Conversely, in regions without obstacles, the sensor exhibits better sensitivity at lower velocities compared to configurations with obstacles. This design—offering high sensitivity at higher flow velocities while maintaining adequate accuracy at lower velocities—ensures reliable sensor performance across a wide range of gas flow speeds.

The integration of obstacles into the structure of MEMS thermal flow sensors reduces the gas flow velocity near the sensor. This reduction enhances heat transfer from the sensor to the gas, ensuring that the sensor’s sensitivity remains consistent even at higher flow velocities. As a result, the sensor maintains optimal performance under varying flow conditions.

Previous studies have shown that the distance between the sensor and the heater is a critical parameter for optimizing the performance of MEMS-based thermal flow sensors. In this study, the distance between the sensor and the heater was 10 µm in both cases, with and without the obstacle. This distance directly affects heat transfer efficiency, sensor sensitivity, and measurement accuracy. Research conducted by Xue, D. [19] demonstrated that a sensor-to-heater distance in the range of 10 to 30 µm yields optimal performance [19]. However, more recent findings, such as those from Valizadeh [9], identified a 10 µm distance as the optimal value for achieving maximum sensor sensitivity. At this distance, heat is transferred more efficiently from the heater to the gas and subsequently to the sensor, leading to improved responsiveness and reduced thermal delay.

Additionally, maintaining a 10 µm distance prevents excessive thermal dissipation, further enhancing sensor sensitivity. Xue, D. [19] also noted that reducing the sensor-to-heater distance below 10 µm increases noise in the sensor signals and negatively affects the linearity of the thermal response.

In addition to the sensor-to-heater distance, the spacing between the sensor and the obstacle is another key factor influencing sensor performance. Studies by Wang, R. (2021) [20] revealed that maintaining a 10 µm gap between the sensor and the obstacle significantly improves sensitivity. This configuration regulates gas flow behaviour and increases thermal interaction between the gas and the sensor surface, thereby enhancing measurement accuracy. Furthermore, maintaining this gap minimizes turbulence around the sensor, ensuring a more stable response to sudden flow variations. Reducing this distance below 10 µm, as confirmed by Xue, D., Wang, J., and Li, X. (2020) [19], leads to increased flow disturbances that adversely affect sensor performance.

The proper selection of these key distances can significantly enhance the performance of MEMS-based thermal flow sensors under varying flow conditions. Based on existing research, a 10 µm sensor-to-heater distance and a 10 µm sensor-to-obstacle distance represent the most effective configuration for achieving maximum sensitivity, stability, and measurement accuracy.

At higher flow velocities (1 to 6 m/s), this optimized 10 µm sensor-to-heater gap ensures efficient heat transfer while minimizing thermal dissipation, resulting in improved response linearity and greater measurement accuracy. Similarly, maintaining a 10 µm gap between the sensor and the obstacle significantly enhances sensitivity by regulating flow behaviour and optimizing heat exchange. This design ensures maximum sensitivity, stability, and precise performance across a wide range of flow conditions.

2.3. Readout Circuit

The proposed MEMS thermal flow sensor is designed using the Wheatstone bridge readout method, as illustrated in Figure 4a. R_u and R_d represent the upstream and downstream resistors, respectively, with additional resistors R₁ and R₂ completing the thermistor bridge. Without gas flow, the temperature profile is symmetrically distributed around the microheater, resulting in a zero-temperature difference between the upstream and downstream detectors. In the presence of gas flow, the values of the R_u and R_d resistors change. Since the voltage across the bridge is weak, it is fed into a low-noise amplifier (LNA), as shown in Figure 4a. The heater can operate in either constant current (CC) mode or constant temperature difference (CTD) mode, with the CTD mode offering superior performance compared to the CC mode. To operate the sensor in CTD mode, the heater must be equipped with a feedback control circuit, as illustrated in Figure 4b. The value of R_c can be calculated using Equation (12).

$${\displaystyle \frac{R_r+R_c}{5}}=R_h\left(1+\alpha \Delta T\right)$$

(12)

3. Results and Discussion

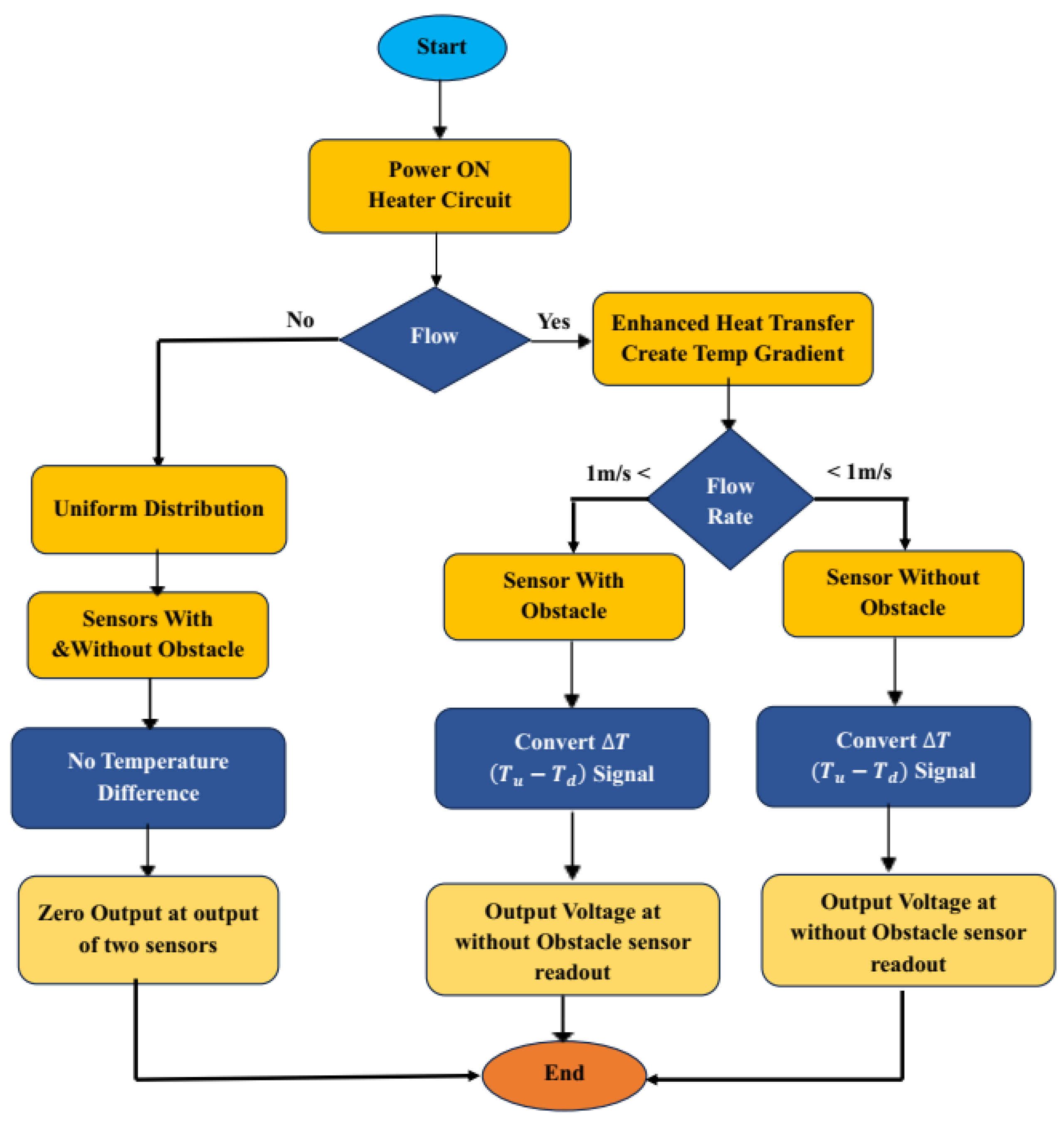
In this section, several criteria for improving the performance of the sensor are simulated based on the initial model. Additionally, the effectiveness of the proposed enhancements is evaluated and discussed in terms of sensitivity, linearity, accuracy, and the range of applied gas flow velocities. The performance of the proposed MEMS thermal flow sensor was analyzed through simulations, focusing on key parameters, such as sensitivity, linearity, accuracy, and flow velocity range. The results highlight the significant impact of thermal obstacles and sensor positioning on optimizing heat transfer and improving measurement accuracy.

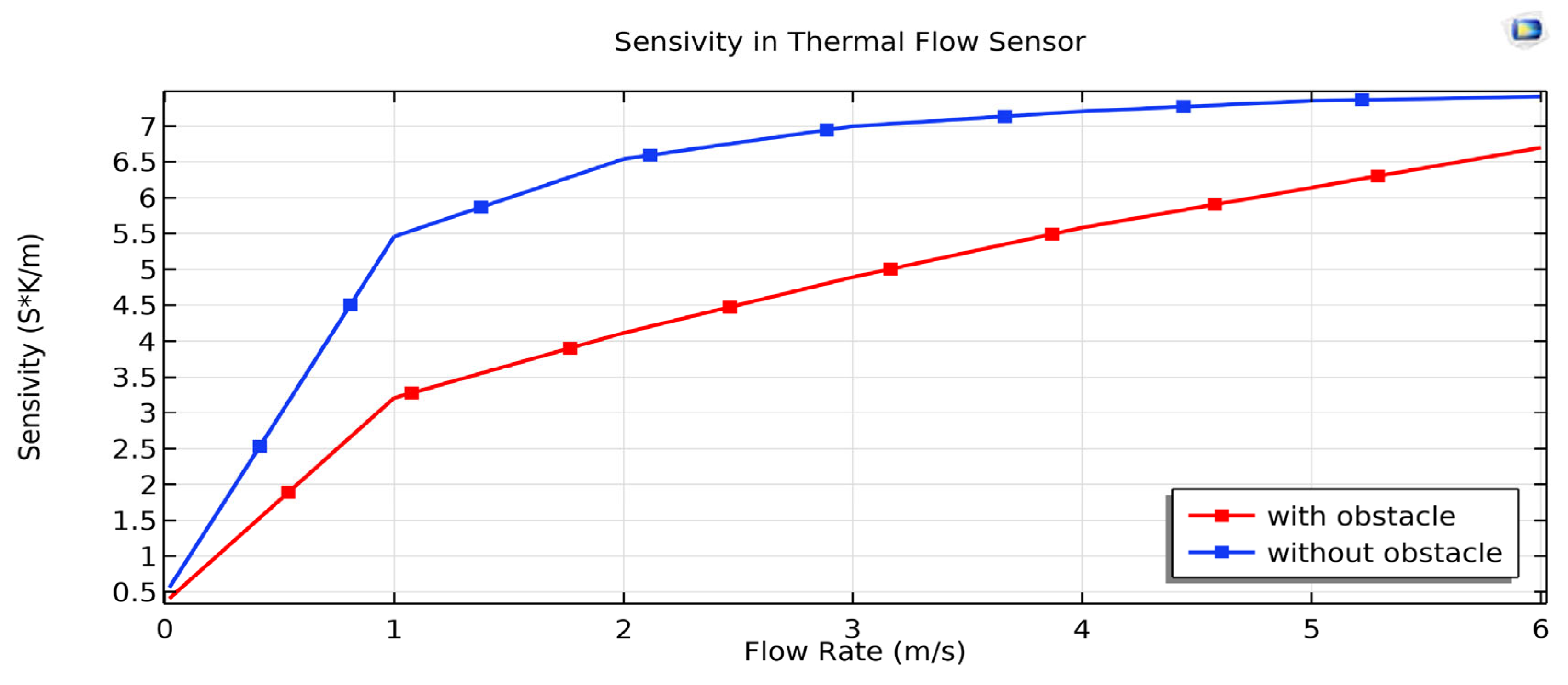
The sensor’s sensitivity was determined by measuring the temperature difference (ΔT) between the upstream and downstream thermistors. Simulation results indicate that the presence of thermal obstacles enhances heat transfer, resulting in increased sensitivity at higher flow rates. Specifically, in the low-flow region (0–1 m/s), the sensor achieved a sensitivity of 2.5 SK/m, while in the high-flow region (1–6 m/s), sensitivity increased to 6.5 SK/m. Furthermore, the sensor exhibited an exceptionally high linearity of approximately 91%, ensuring accurate and repeatable flow measurements. Under high-velocity conditions, the obstacle effectively reduced flow speed near the heater, increasing the interaction time between the gas and the heated surface, thereby enhancing heat transfer efficiency. In low-velocity conditions, the presence of obstacles induced flow disturbances that reduced the thermal boundary layer thickness, improving the sensor’s sensitivity to minor flow variations. Additionally, temperature distribution analysis provided valuable insights into sensor performance. The results reveal that at higher flow velocities, the temperature difference (ΔT) between the upstream and downstream sensors increases, confirming the sensor’s ability to accurately estimate flow rates.

Comparative results demonstrate that the proposed design outperforms previous MEMS flow sensors, particularly in terms of sensitivity, accuracy, and adaptability across a wider range of flow conditions. These findings establish the proposed MEMS thermal flow sensor as a reliable and robust solution for high-precision flow measurement applications.

3.1. Fabrication Process

The proposed fabrication process for the sensor is designed in such a way that it is a simple and feasible approach, as shown in Figure 5. The steps outlined in the fabrication process are based on well-established and widely used microfabrication techniques, such as Piranha cleaning, thermal oxidation, LPCVD polysilicon deposition and patterning, Pt sputtering, and lift off. Although the sensor has not been fabricated yet, its fabrication process is designed to be straightforward and reproducible, as it relies on standard processes commonly employed in MEMS fabrication. The fabrication of the sensor, along with a detailed comparison between the simulation results and the experimental measurement results, will be reported in our future work. We believe this approach ensures the feasibility of the proposed design and provides a clear path for experimental validation.

3.2. The Effects of an Obstacle on Sensor Performance

In the proposed structure, the sensors, heater, and obstacle are integrated on a single substrate, each designed with specific dimensions and characteristics to enhance performance and increase sensitivity. Two sensors are positioned on either side of the heater, with each sensor measuring 240 µm in length and 150 µm in width. The sensors are placed 10 µm away from the heater to enable a rapid response to temperature changes caused by gas flow.

Since temperature is influenced by changes in flow rate, the relationship between temperature and flow velocity can be expressed as shown in Equation (13). Based on Equation (5), the temperature difference (ΔT) can be written as a function of flow velocity (u):

$$\Delta T=-{\displaystyle \frac{q.L}{K.A}}$$

(13)

Here, q is indirectly dependent on the flow velocity, as changes in flow velocity influence the convective heat transfer coefficient (h). Based on gas dynamics principles, it can be assumed that

$$h \propto u^n$$

(14)

Therefore, the relationship for temperature variations can be expressed as Equation (15):

$$\Delta T={\displaystyle \frac{u^n.A.\left(T_u-T_d\right)}{K}}$$

(15)

According to Equation (15), which represents temperature variations, the parameters are defined as follows: A, which represents the surface area of contact between the gas flow and the heated surface, directly affecting heat transfer; K, the thermal conductivity coefficient of the heated surface material, indicating the material’s ability to conduct heat; and L, the length of the heat transfer path, typically the distance the gas flow travels over the heated surface. These parameters combine to influence the temperature changes and the system’s sensitivity to changes in flow velocity.

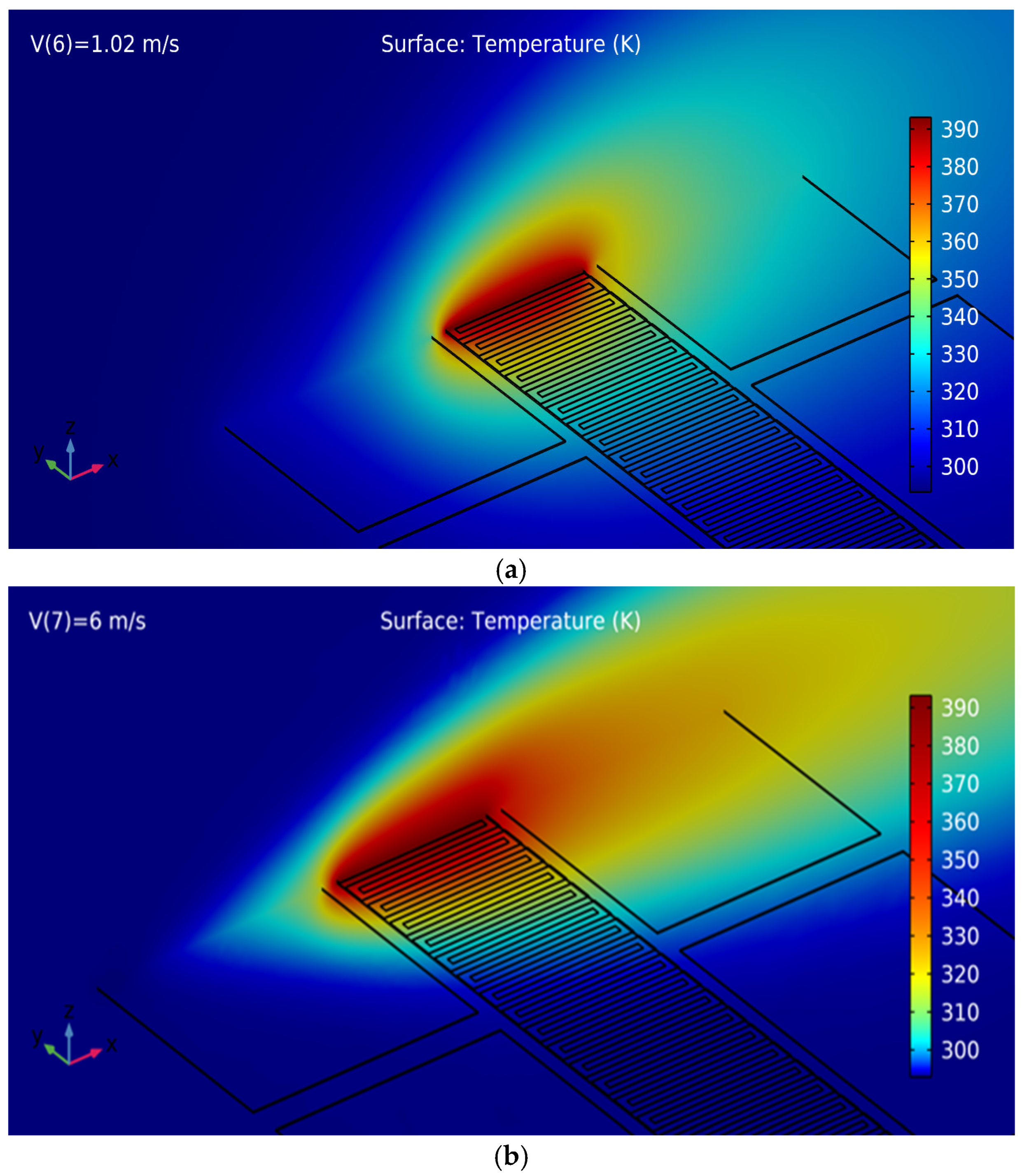
Figure 6 illustrates the temperature distribution as a function of flow velocity and demonstrates the heat transfer from the heater to the sensors. In this configuration, air is selected as the working gas due to its low viscosity, low density, and appropriate heat capacity, which directly influence heat transfer and sensor performance. Air’s ability to generate a significant temperature gradient between the heater and the passing flow is critical for enhancing the measurement accuracy of MEMS thermal flow sensors. Additionally, its thermal stability, widespread availability, and non-corrosive nature make it an ideal choice for precise flow rate sensing applications. At low flow velocities (0–1 m/s), air moves more slowly, resulting in a longer contact time with the heater surface. This leads to a greater temperature difference between the upstream and downstream sensors, thereby enhancing the sensor’s sensitivity. In this range, heat transfer is primarily governed by natural convection, allowing the airflow to absorb sufficient thermal energy from the sensor surface. At higher flow velocities (1–6 m/s), the air passes over the heater more rapidly, reducing its contact time with the heated surface. Under these conditions, forced convection becomes dominant, leading to an increased heat transfer rate. The use of thermal obstacles in this configuration significantly impacts sensor performance. At high flow velocities, obstacles reduce the local flow velocity near the heater, prolonging the interaction time between the gas and the heated surface. This mechanism enhances sensor sensitivity at higher flow rates and improves the linearity of the sensor’s response, as shown in Figure 6b. At low flow velocities, obstacles induce flow complexity by creating static or low-flow regions, which reduce the thermal boundary layer thickness. This improves heat exchange and enhances sensitivity to small changes in flow velocity, as depicted in Figure 6a. In this figure, a lower obstacle is used for high flow velocities, while an upper obstacle is employed for low flow velocities.

Thermal obstacles play a crucial role in optimizing the sensitivity and linearity of thermal flow sensors. In the absence of obstacles, gas flows at higher velocities, reducing heat transfer and consequently lowering sensitivity. By introducing an obstacle, the flow velocity decreases, increasing the gas’s contact time with the sensor surface and enhancing sensitivity. Additionally, obstacles optimize the flow pattern, ensuring more uniform heat distribution, which further improves sensitivity and enhances the linearity of the sensor’s response. At low flow velocities, obstacles create flow disturbances and reduce the thermal boundary layer thickness, resulting in increased sensitivity to small variations in flow velocity. At higher flow velocities, obstacles slow down the flow and improve heat transfer, preventing thermal saturation effects and making the temperature–velocity relationship more linear. However, optimal obstacle design is essential to avoid excessive flow disturbances while maintaining both sensitivity and linearity in the sensor’s response. Overall, the use of air as the working gas, combined with an optimized geometric design incorporating thermal obstacles, significantly improves heat transfer efficiency, sensor sensitivity, and measurement accuracy across a broad range of flow velocities. The careful placement and design of obstacles enhance sensor performance, ensuring high accuracy and sensitivity for diverse flow conditions.

The temperature variations in the upstream and downstream detectors of the sensor show that as the gas flow velocity increases, the temperature difference between the detectors becomes more pronounced. Specifically, at higher flow velocities, the temperature at the downstream detector exceeds that at the upstream detector. This occurs because the gas passing over the heater absorbs heat and transfers it downstream, creating a measurable thermal gradient. These temperature differences are crucial for assessing the sensor’s sensitivity to gas flow variations and optimizing its performance, particularly in applications requiring precise flow measurements, such as environmental monitoring and industrial process control. Additionally, as shown in Figure 3, which illustrates the sensitivity curve, the variations in temperature and sensitivity with respect to flow velocity follow a similar pattern. This alignment indicates the direct dependence of these two parameters on the heat transfer rate and the interaction time between the gas flow and the heated surface.

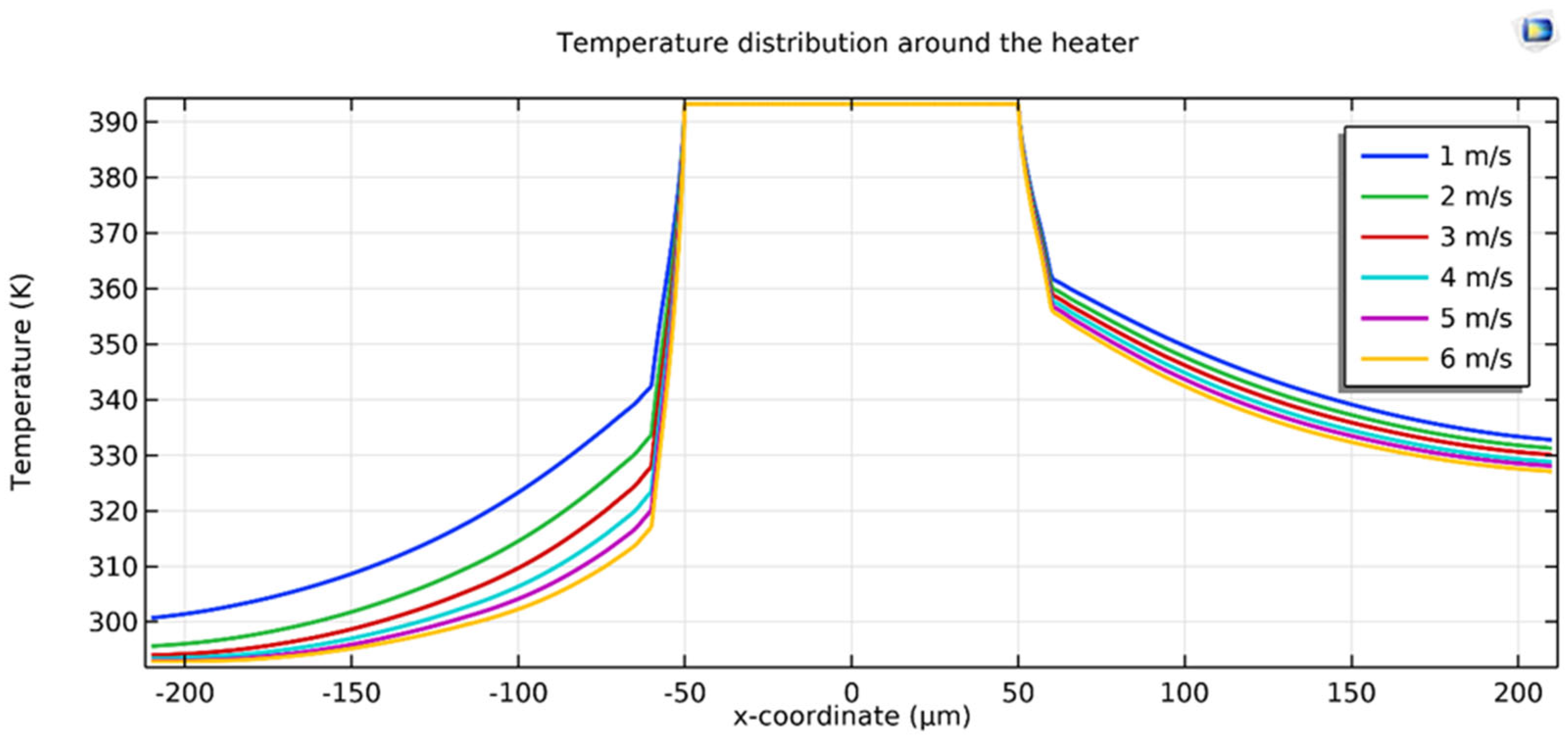
Figure 7 presents the temperature distribution around the heater for flow velocities ranging from 1 to 6 m/s. The diagram highlights how temperature patterns evolve across different regions surrounding the heater under varying flow conditions. This visualization provides valuable insights into the heat transfer dynamics and the sensor’s performance under different flow rates.

The observed temperature differences between the upstream and downstream detectors result from the interaction between the convective heat transfer caused by the gas flow and the thermal energy generated by the heater. The uniformity or asymmetry in the temperature distribution provides valuable insights into the effects of flow dynamics, such as turbulence and boundary layer formation, on sensor behaviour. Additionally, key material properties, including the thermal conductivity and heat capacity of the detector elements, significantly influence the sensor’s sensitivity and response time. The heater design, including its geometry and power input, also plays a crucial role in defining the temperature field and determining the overall performance of the sensor. Furthermore, the flow regime—laminar or turbulent—affects heat transfer efficiency and the accuracy of flow detection. These results provide a deeper understanding of the sensor’s thermal behaviour and serve as a foundation for optimizing its design.

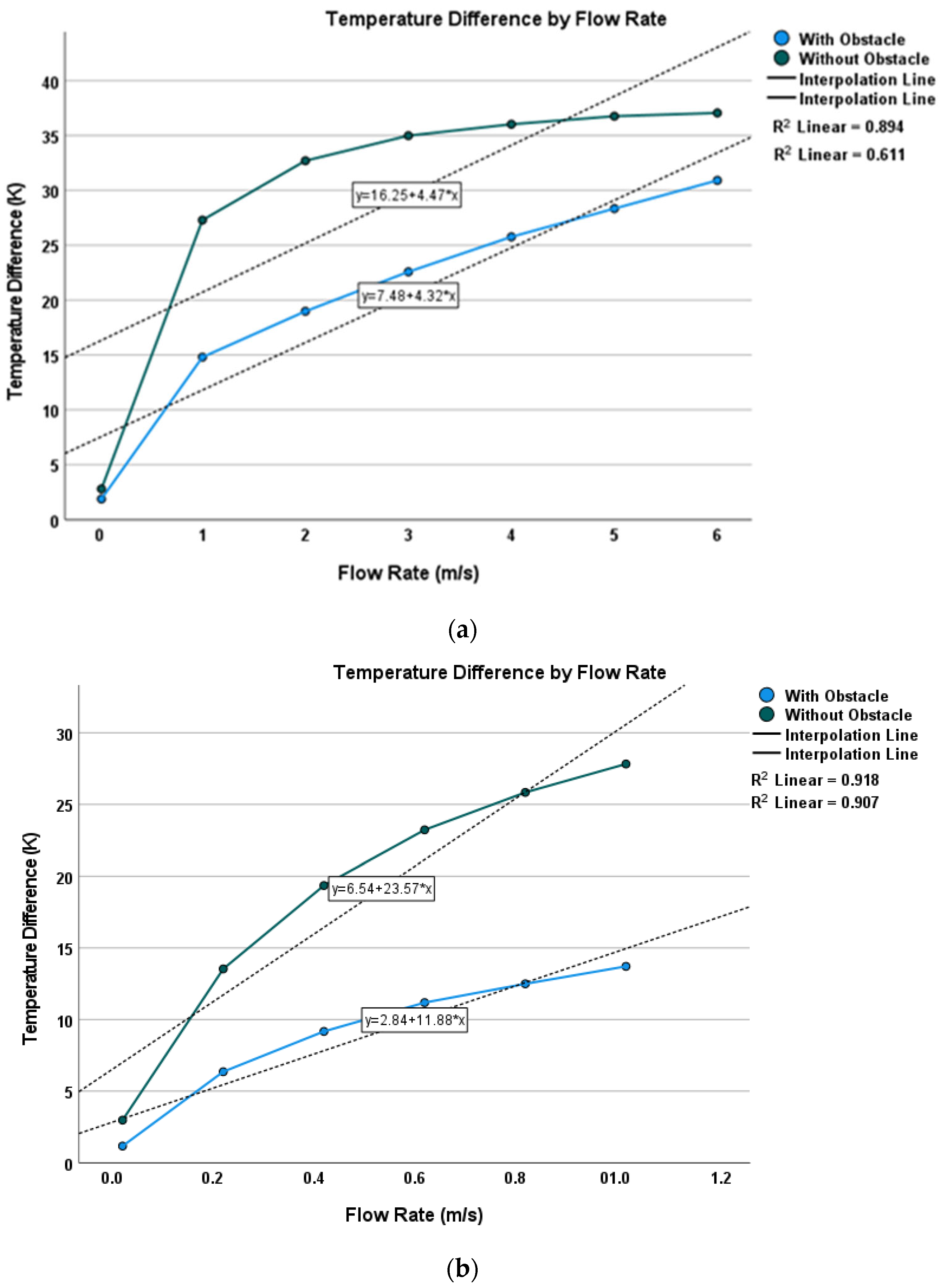
Figure 7 also illustrates the temperature distribution around the heater, under conditions with and without obstacles. The obstacle used in this structure has a length of 240 µm, a width of 50 µm, and a height of 1 µm. In the presence of obstacles, the reduction in gas flow velocity near the sensor increases the interaction time between the gas and the heater, resulting in enhanced heat transfer. This improvement leads to greater sensitivity and better linearity in the sensor’s response. The inclusion of obstacles in the sensor structure demonstrates that, compared to the structure without obstacles, linearity is significantly improved at higher flow velocities, while sensitivity is enhanced at lower flow velocities.

In contrast, under conditions without obstacles, the gas flow velocity is higher, but the interaction time between the gas and the sensor is reduced. This reduction in interaction time limits heat transfer, leading to decreased sensitivity and reduced linearity in the sensor’s response, particularly at higher flow velocities. These findings underscore the positive impact of incorporating obstacles into the sensor design to improve its performance across various gas flow velocity conditions.

In Figure 8, the simulation results indicate that the obstacle is designed in such a way that it does not induce turbulence or flow disturbance in the sensor’s operating region. The gas flow remains smooth and stable, while the obstacle primarily enhances the thermal interaction between the gas and the heated surface. This design improves the sensor’s sensitivity in measuring flow rates without compromising its accuracy.

As the distance between the obstacle and the sensor increases, both the temperature variation and the sensitivity of the sensor typically decrease. This is because a greater distance reduces the interaction time between the gas flow and the heated surface of the sensor. The shorter interaction time results in decreased convective heat transfer between the sensor surface and the gas, leading to smaller temperature changes at the sensor. Consequently, the sensitivity of the sensor, which strongly depends on temperature variations, is also reduced. Therefore, when the obstacle is placed closer to the sensor, the interaction time between the gas and the heated surface increases. This leads to enhanced heat transfer and, ultimately, the improved sensitivity of the sensor. Additionally, in this closer configuration, the linearity of the sensor’s response is also better maintained, which is crucial for ensuring accurate and stable performance in various applications.

Additionally, the length of the obstacle is adjusted to match the length of the sensor, ensuring optimal alignment. The width of the obstacle is determined based on the characteristics of the gas flow and the need for maximum thermal interaction between the flow and the heated surface, ensuring efficient heat transfer and an optimal system response.

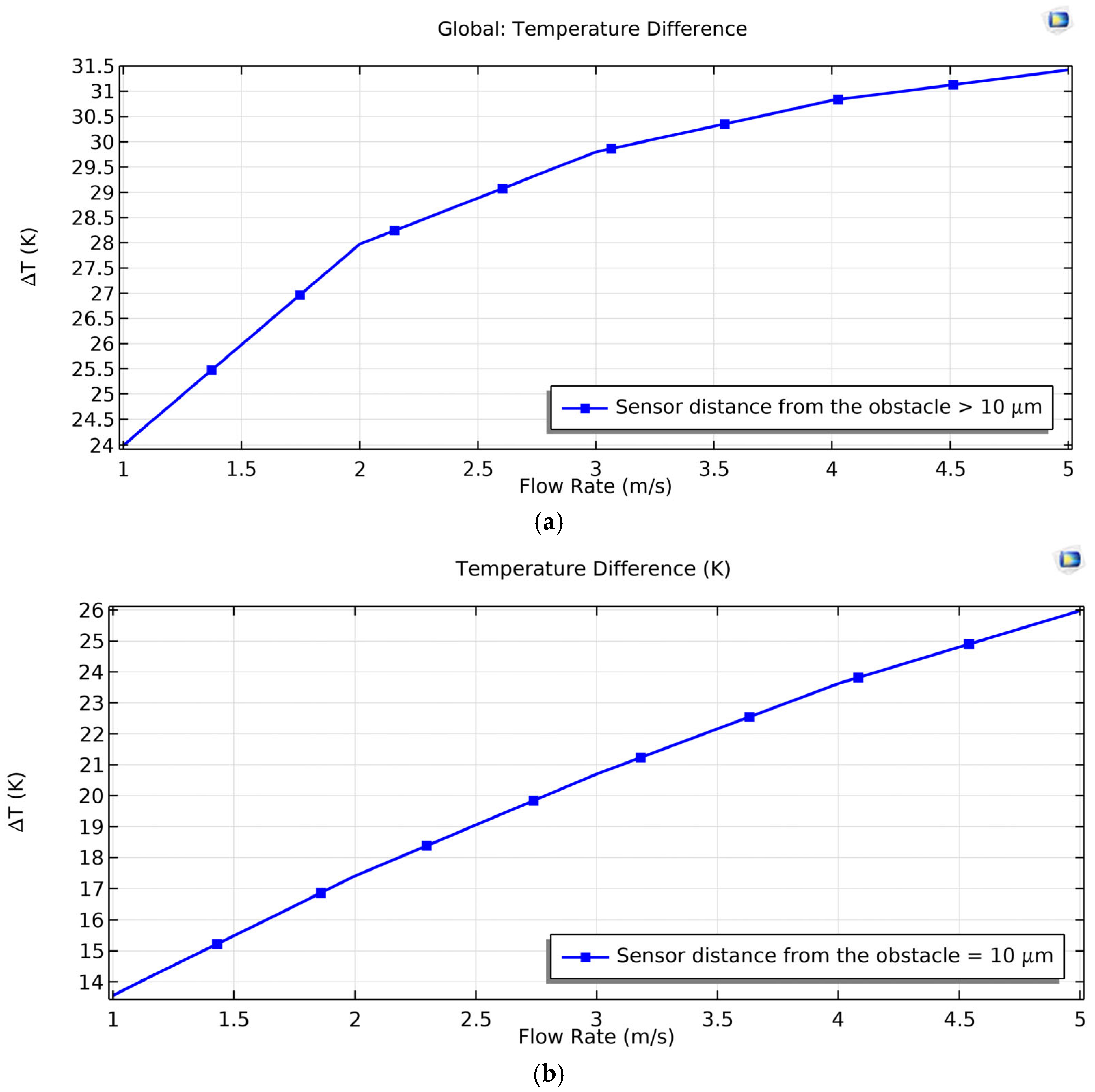
According to the simulation results, Figure 9a illustrates the temperature changes with respect to flow velocity when the sensor–obstacle distance is greater than 10 μm. In this case, the temperature variation is noticeably smaller, resulting in reduced sensitivity. In contrast, Figure 9b shows the temperature distribution at a 10-micrometre distance, where the proximity of the obstacle enhances heat transfer and temperature variation, thus improving the sensor’s sensitivity.

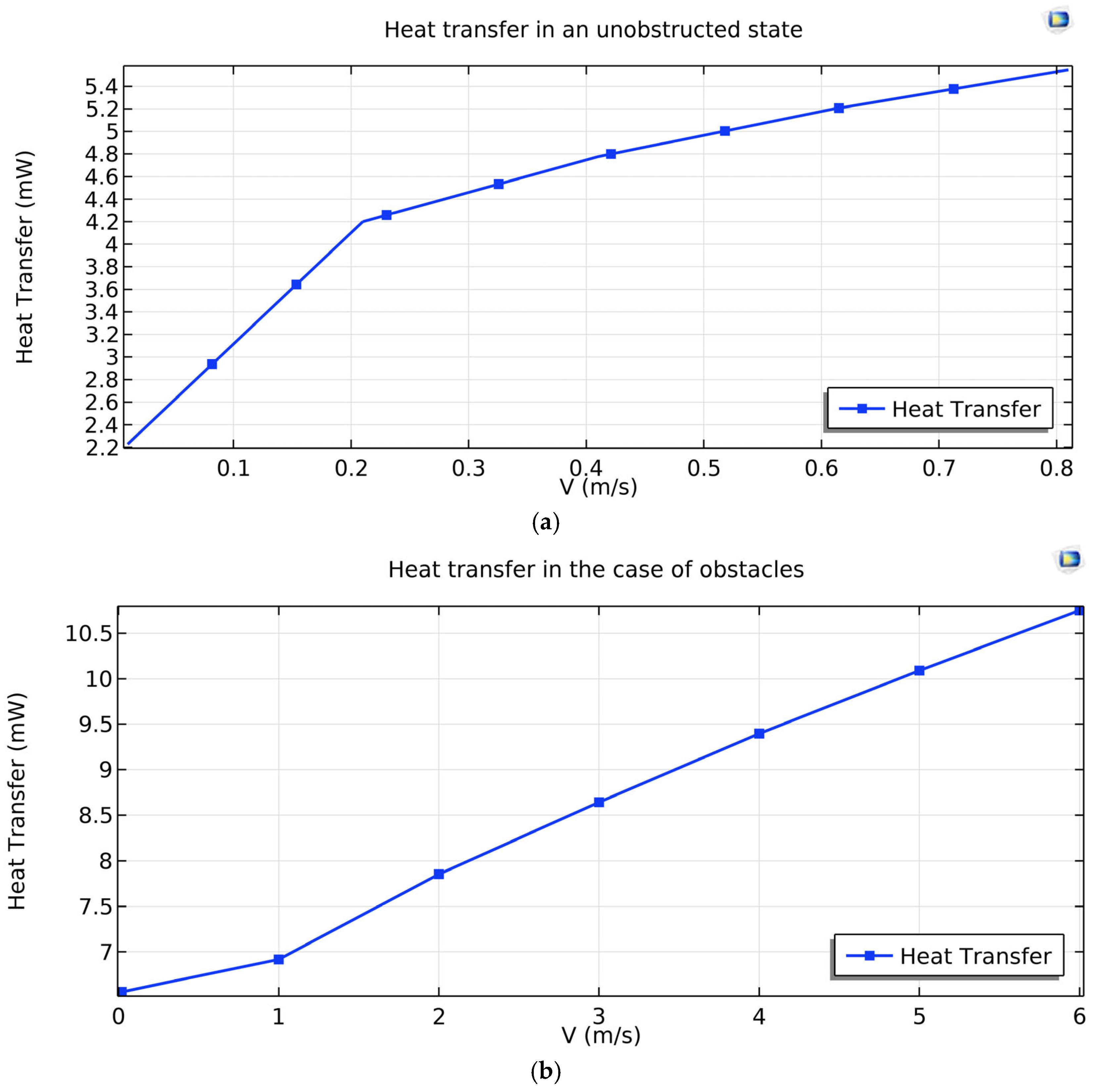
In Figure 10, the heat transfer versus flow velocity for different cases with and without an obstacle is examined. In Figure 10a, in the case with an obstacle, especially at higher velocities, it is observed that heat transfer increases significantly due to the increased interaction time of the gas flow with the heated surface. This improvement in heat transfer results in enhanced sensor sensitivity and accuracy in flow measurement at higher speeds. In contrast, in Figure 10b, in the case without an obstacle and at lower velocities, the heat transfer to the gas flow is lower because the interaction time between the flow and the heated surface is reduced, resulting in smaller temperature variations at the sensor. These differences clearly demonstrate the impact of the obstacle on improving the sensor’s performance, particularly at higher flow velocities.

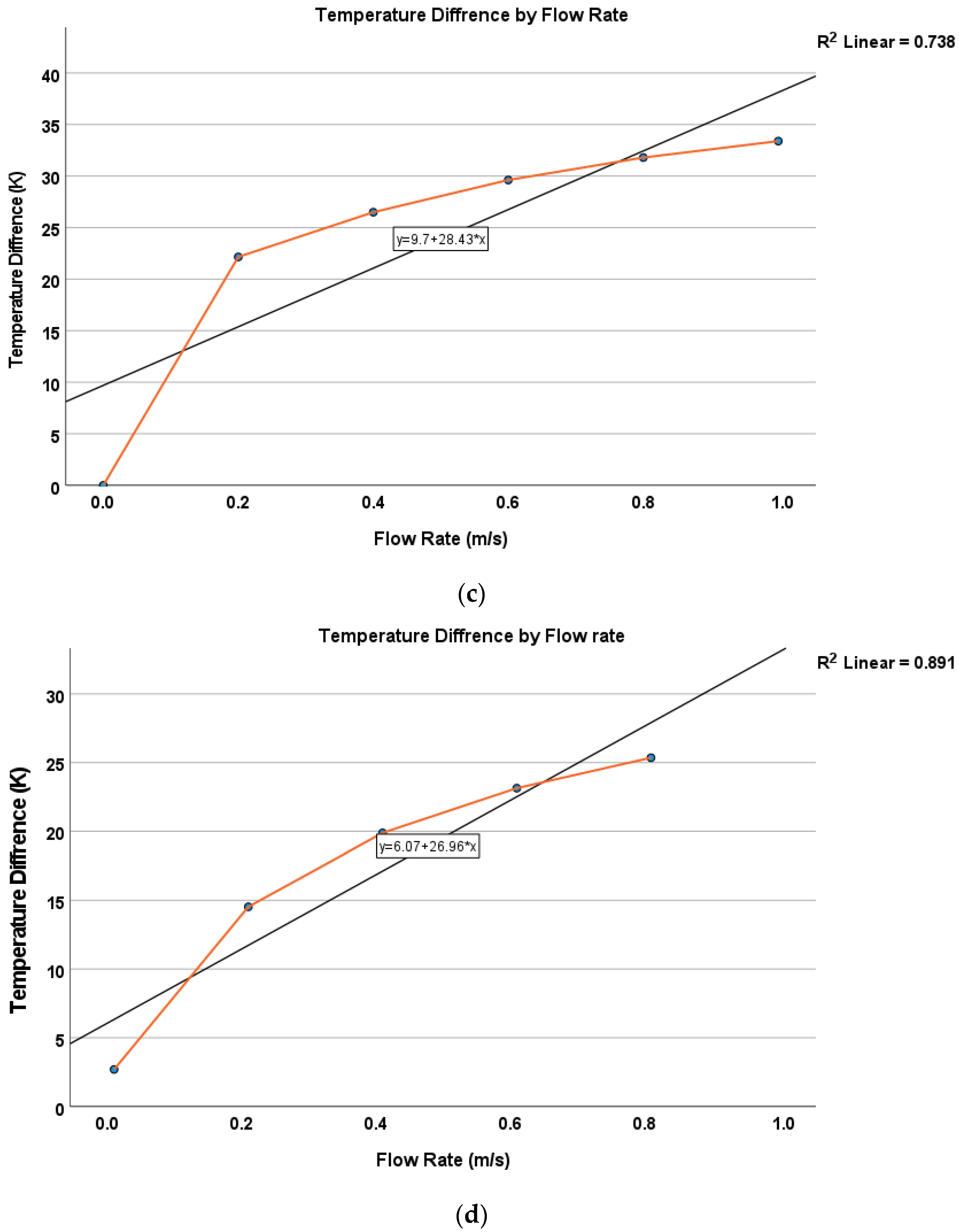
Figure 11 presents the simulated temperature variations for the proposed structure compared to prior designs. Chart (a) demonstrates the improved linearity and sensitivity of the proposed structure in response to changes in flow velocity. In contrast, chart (b) shows the temperature variations for the Valizadeh (2016) [9] structure, which exhibits lower linearity compared to the proposed design. Similarly, chart (c) illustrates the temperature variations for the Takashi Kasai (2021) [8] structure, further highlighting the performance advantages of the proposed design over previous approaches.

The comparisons indicate that the proposed structure outperforms previous designs in maintaining accuracy and sensitivity over a broader range of flow velocities [8,9]. In earlier structures, the sensitivity of the sensor was constrained by the design of its components, and the temperature–flow velocity relationship often exhibited nonlinearity, particularly at high speeds or under uneven flow conditions. In contrast, the proposed structure demonstrates significant improvements in both sensitivity and linearity, primarily due to the incorporation of obstacles in the sensor design. These obstacles reduce the gas velocity near the sensor, increasing the interaction time between the gas and the sensor, which enhances heat transfer and improves sensitivity.

The inclusion of obstacles has a positive impact on heat transfer and helps maintain the linearity of the sensor’s response even at higher flow velocities. These features enable the sensor to operate more accurately and linearly across a wide range of flow velocities, representing a substantial advancement over previous designs. Higher sensitivity allows the sensor to detect smaller changes in flow velocity, while improved accuracy ensures consistent and reliable measurements. Unlike earlier designs, the proposed structure maintains both sensitivity and linearity across a wide range of low and high flow velocities.

As shown in

Table 3. Performance comparison of previously reported flow sensor.

	[20]	[8]	[9]	This Work
Sensor Principle	CMOS MEMS	Mems Thermal	Mems Thermal	Mems Thermal
Fluids	Air	Air	Air	Air
Flow Range (m/s)	0~1	0~1	0~1	0~6
Sensitivity (SK/m)	70%	74%	80%	92%
Linearity (J/kg.K)	0.77	0.73	0.89	0.91
Accuracy (m/SK)	0.05	0.07	0.06	0.03

, the sensitivity and linearity of the proposed structure are significantly improved compared to the three most recent studies. This demonstrates the sensor’s ability to operate effectively over a broader range of flow velocities with high accuracy and repeatability. These advancements underline the sensor’s applicability in more complex environments, such as HVAC systems and various industrial applications, where precise and reliable flow measurements are critical.

4. Conclusions

A novel MEMS flow sensor has been proposed, designed to achieve high sensitivity, high linearity, and low power consumption. The linearity of the sensor plays a crucial role in its overall performance, significantly influencing both sensitivity and accuracy. Most previously reported sensors were optimized for low gas velocities, as maintaining linearity at higher velocities posed challenges. The inclusion of obstacles in the proposed design has a remarkable effect on improving linearity. Specifically, the sensor incorporates distinct regions: one optimized for low-velocity sensing and the other for high-velocity sensing.

The sensitivity, linearity, temperature differences between the upstream and downstream thermistors, and the temperature distribution around the heater were simulated and compared with recently published works. These comparisons demonstrate the superior performance of the proposed sensor.

The maximum sensitivity of the sensor is 2.5 (SK/m) for velocities below 1 m/s and 6.5 (SK/m) for velocities above 1 m/s, with a linearity of 91%. Furthermore, the readout circuits for sensing and controlling the heater temperature were discussed in detail in this paper. These advancements make the proposed sensor a highly effective solution for applications requiring precise flow measurement across a wide range of velocities.