Path-Planning and Navigation for Robots Considering Human–Robot–Environment Interactions in Supermarket Environments
Abstract
1. Introduction
- Developed a unified guidance and navigation framework for ground robotic platforms operated in grocery store environments, incorporating stakeholder requirements to improve operational efficiency and enhance the customer shopping experience.
- Integrated a real-time, collision-free navigation algorithm into a global planning framework with low computational overhead, enabling robust and safe robotic operations in complex, dynamic environments.
2. Preliminary
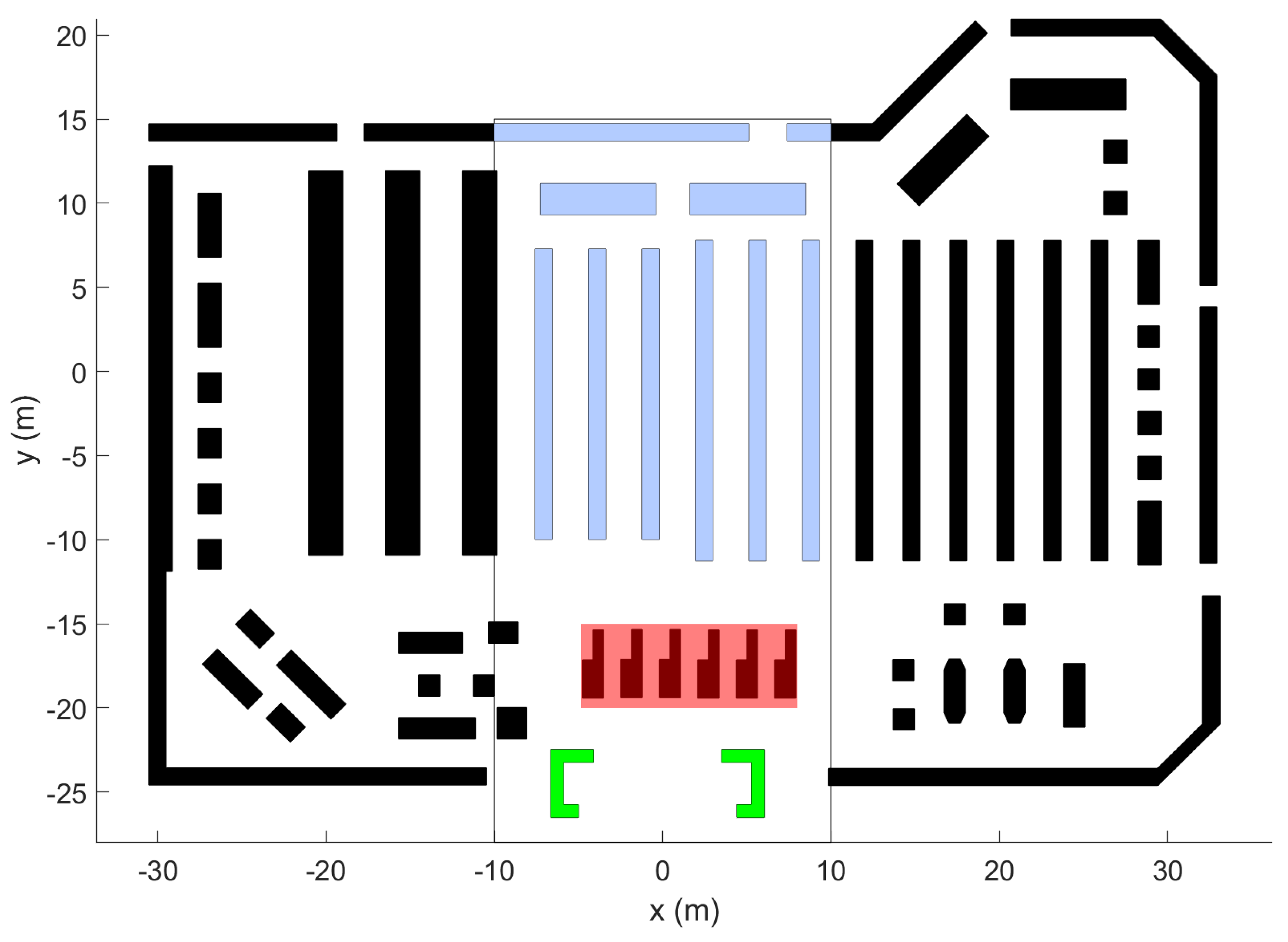
2.1. Environment
2.2. Stakeholders
2.2.1. Cart-Type Robot for Shopping Assistant
2.2.2. Store Employees
2.2.3. Human Shopper
2.3. Dijkstra’s Algorithm
2.4. Genetic Algorithm
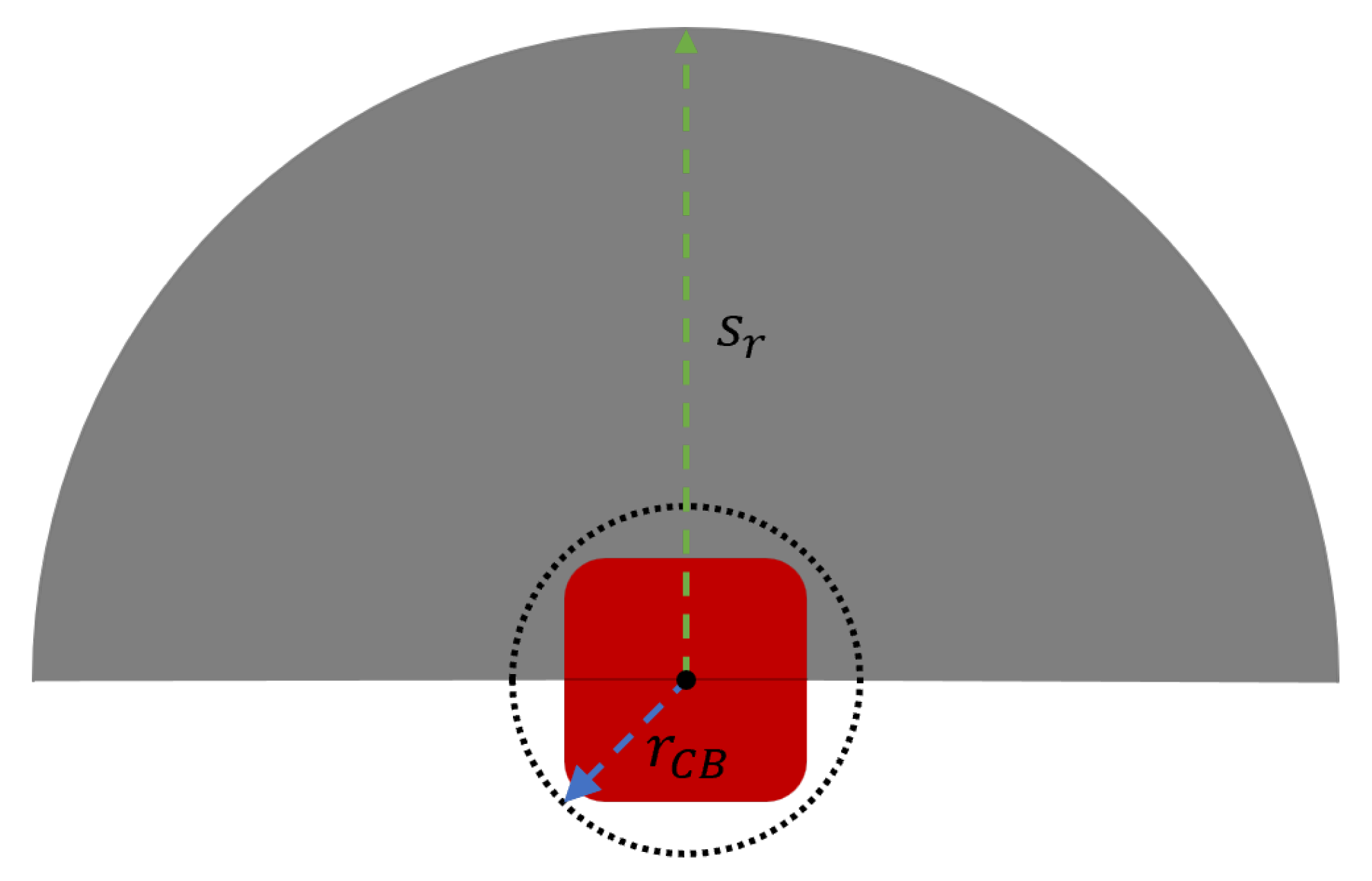
2.5. Enhanced Potential Field Algorithm
| Algorithm 1: EPF direction determination |
 |
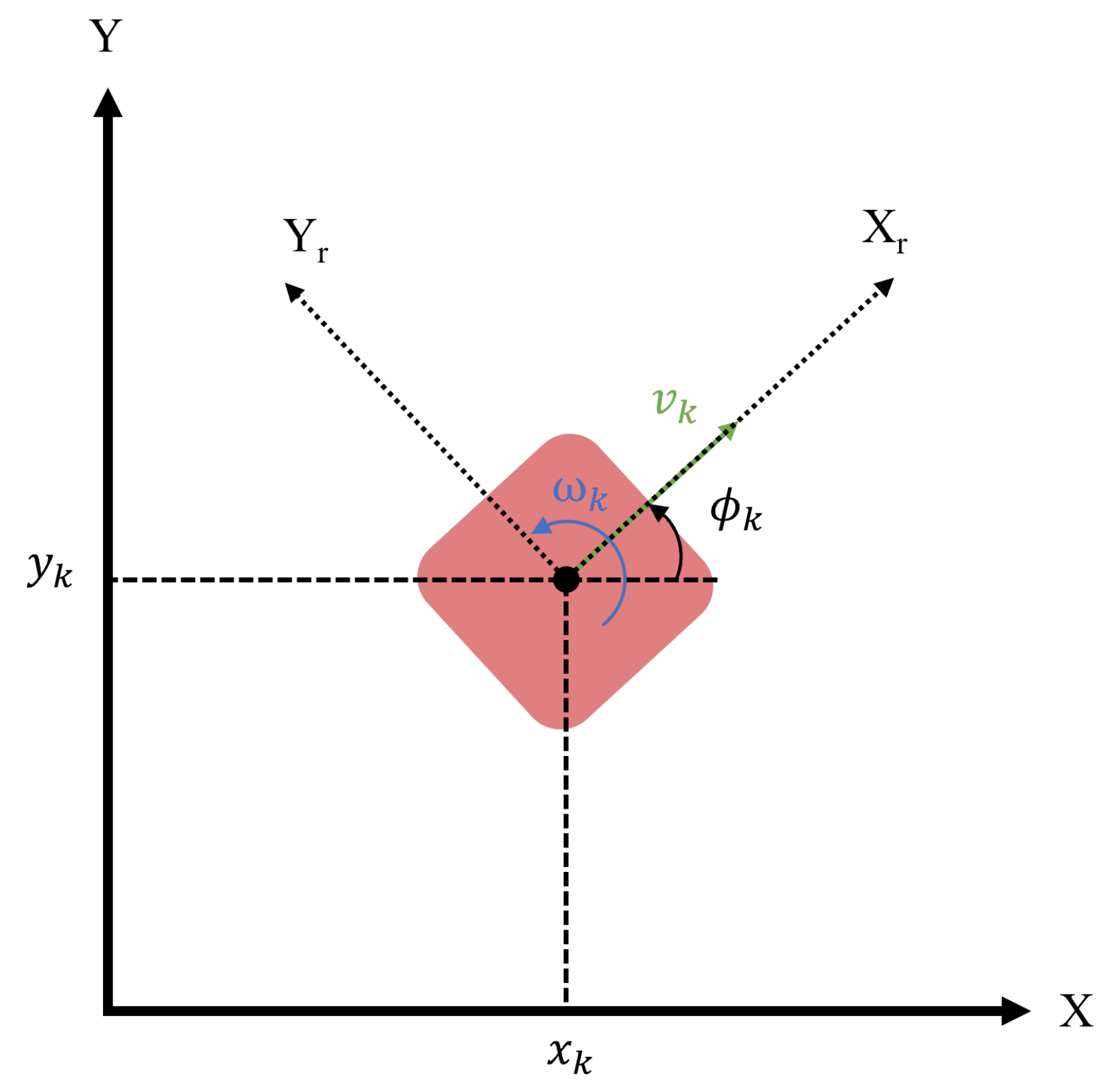
2.6. Robot Model
3. Methodology
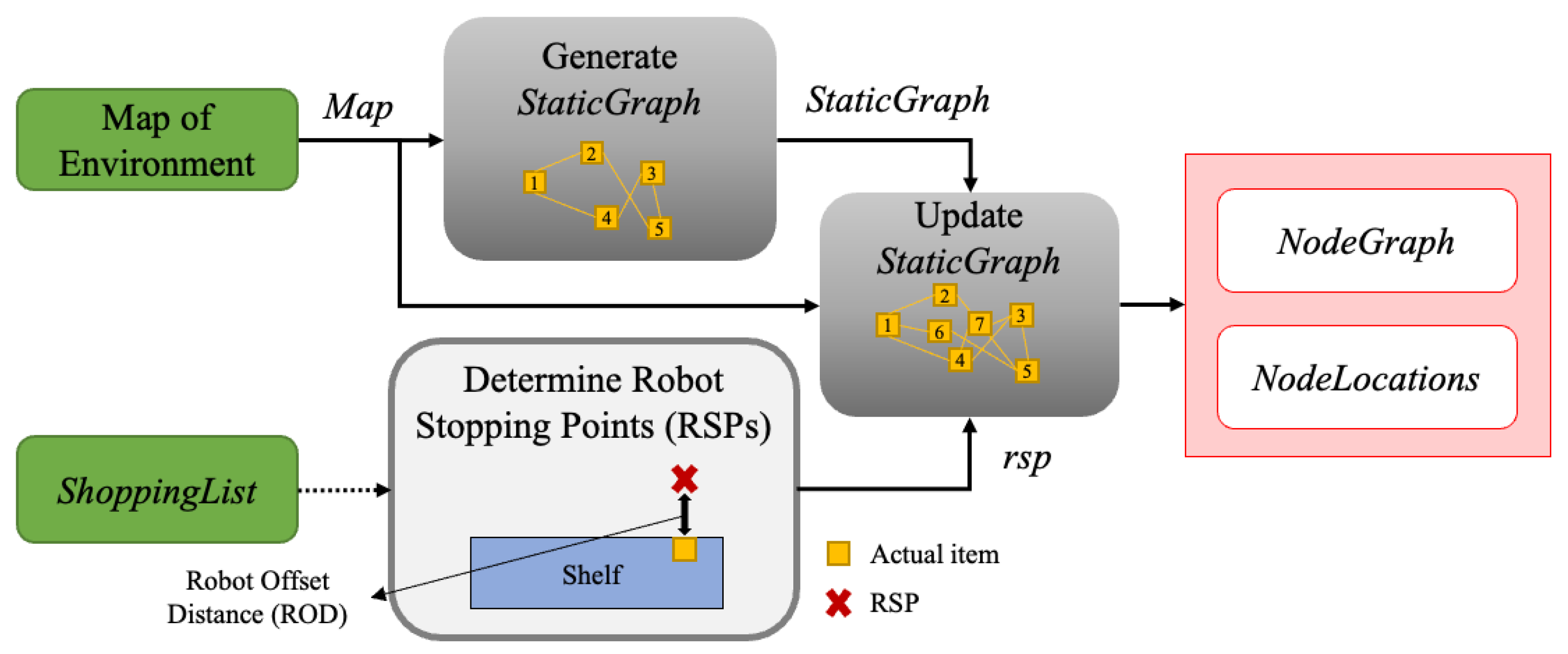
3.1. Process Overview/Framework
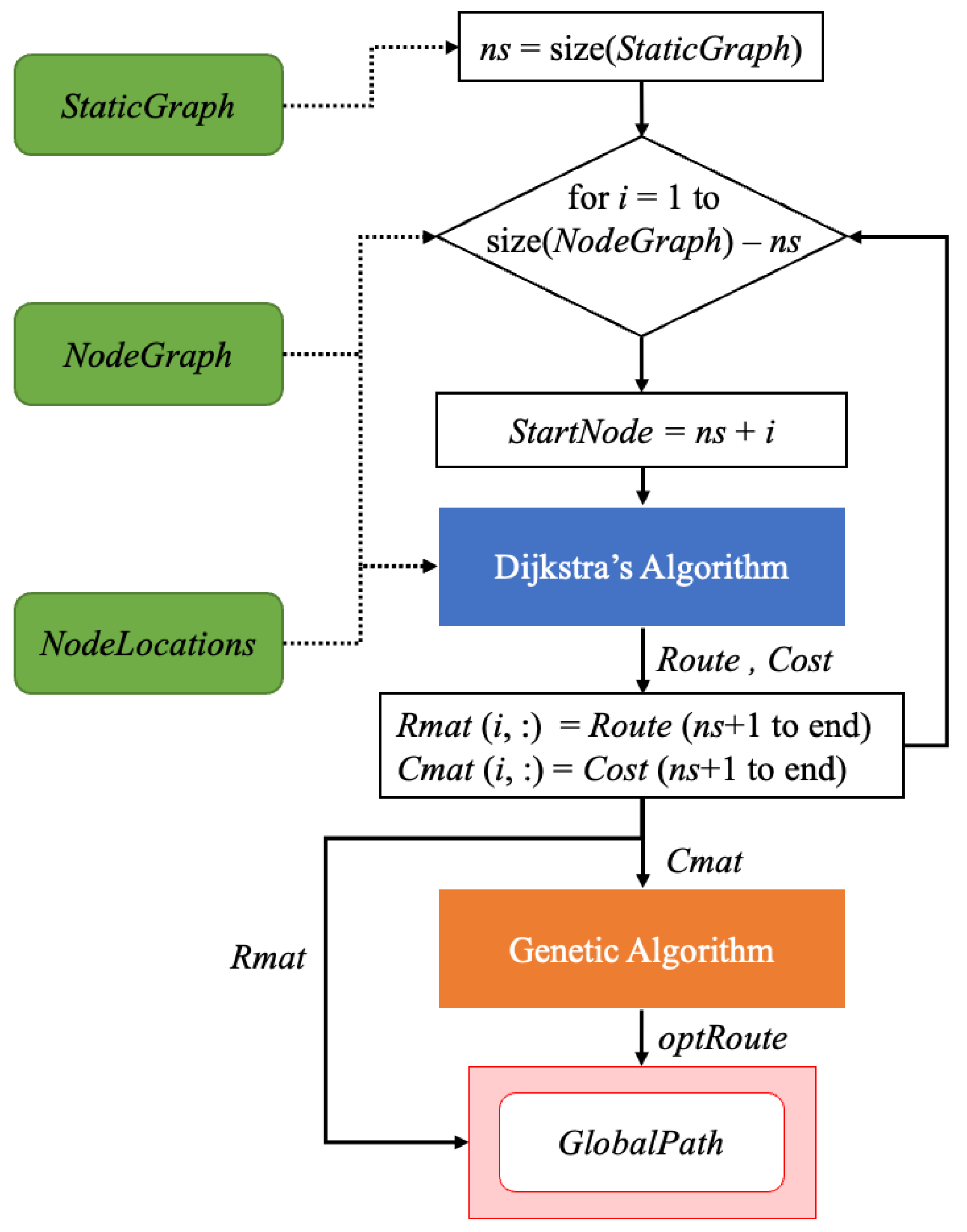
3.2. Global Planner
3.2.1. Undirected Graph Generation
3.2.2. Global Path Calculation
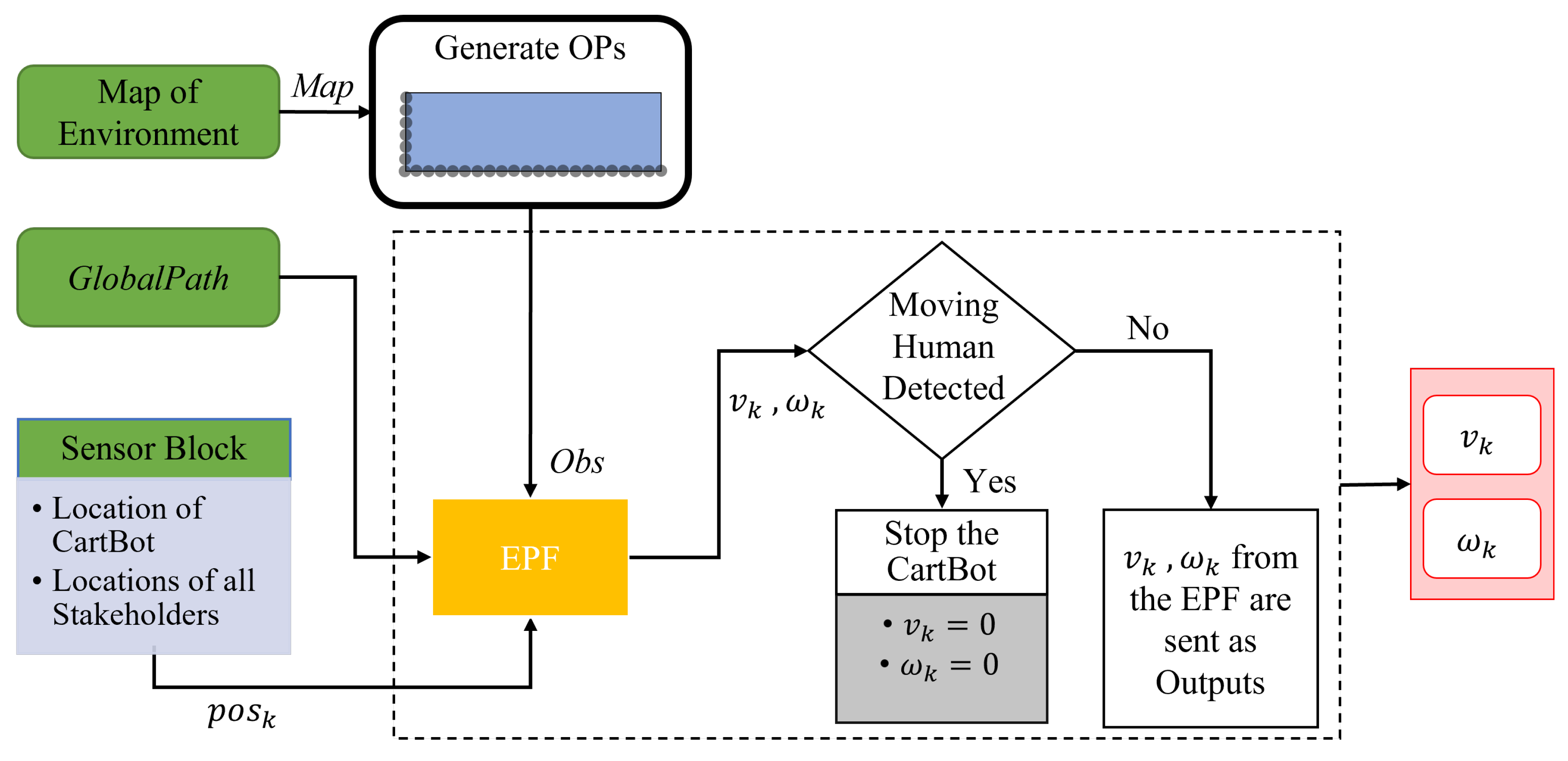
3.3. Local Planner
3.3.1. Robot–Environment Interaction (Static Obstacles)
3.3.2. Robot–Robot or Robot–Human Interaction (Dynamic Obstacles)
4. Simulation Study
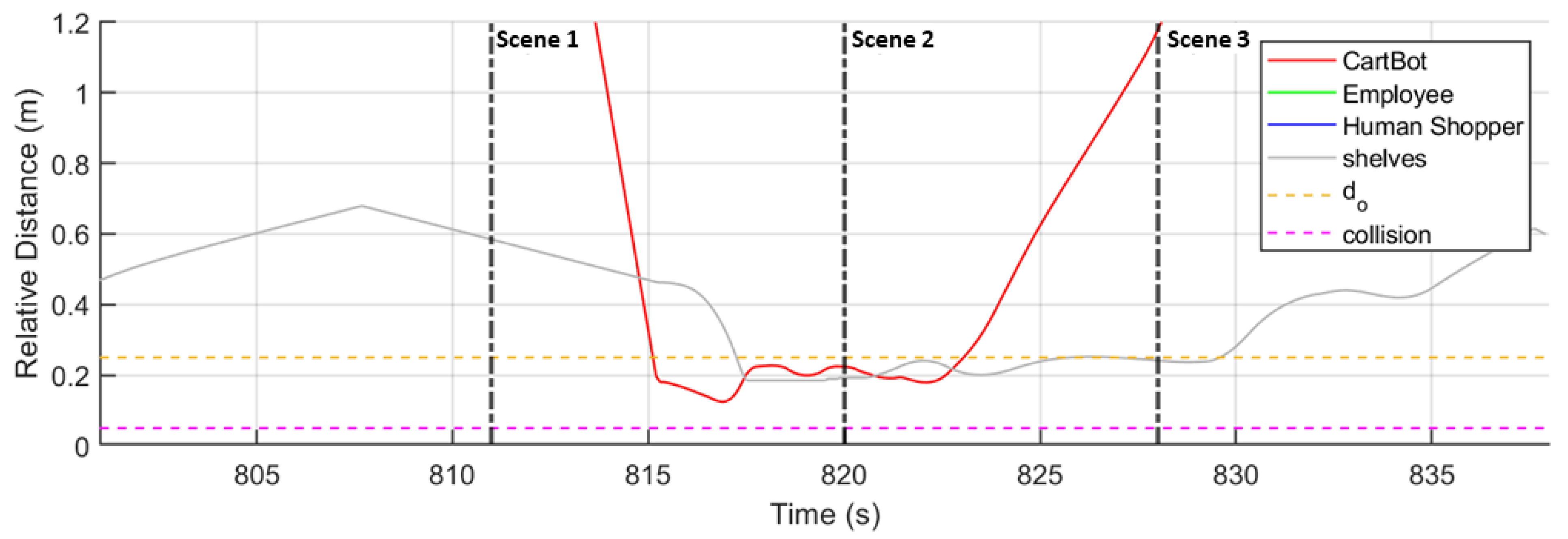
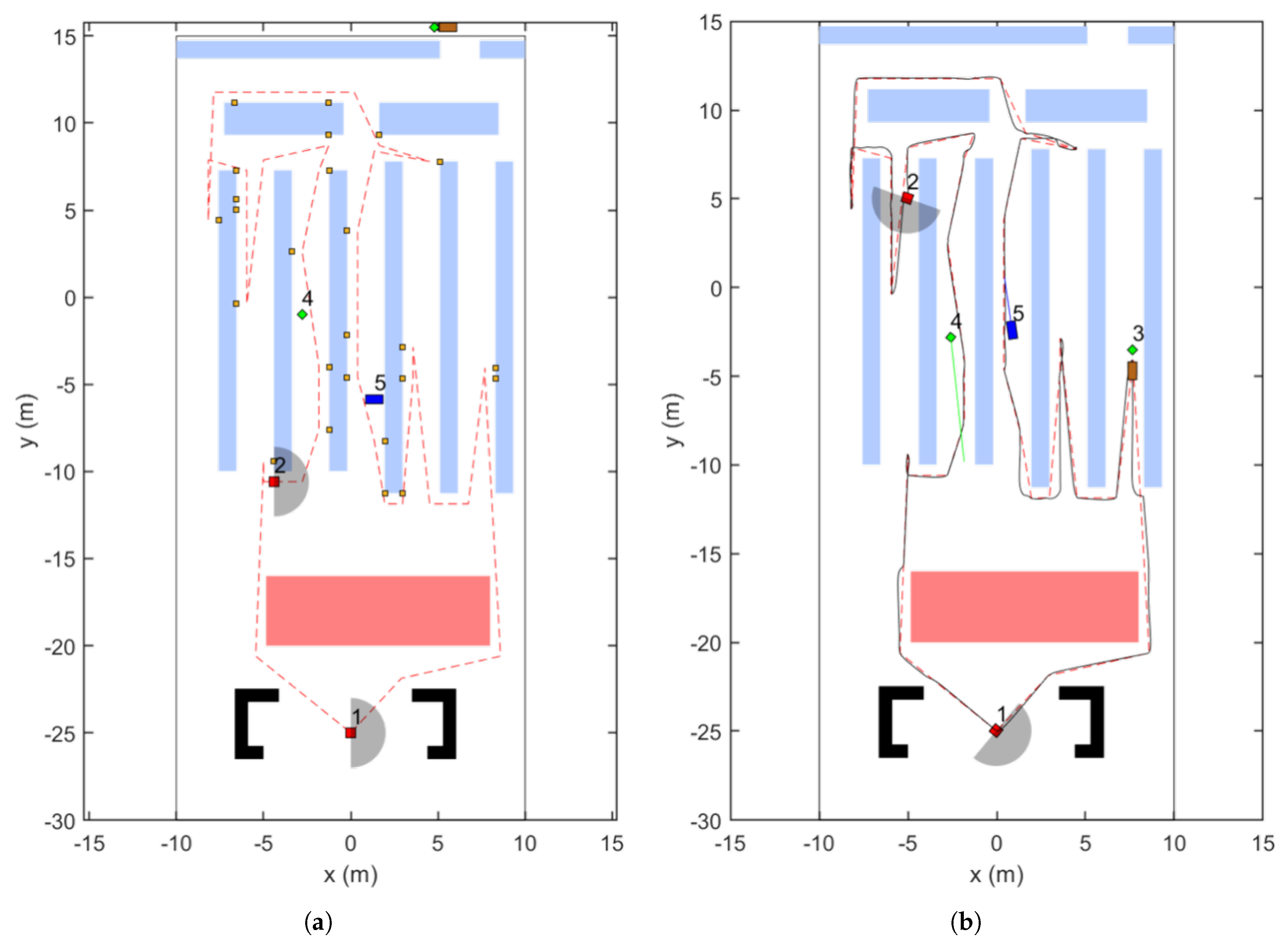
4.1. Single Agent: Robot–Environment Interaction
4.2. Multiple Agent: Human–Robot–Environment Interaction
4.3. Multiple Agent: Monte Carlo Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krzykowska-Piotrowska, K.; Rosiński, A.; Paś, J.; Piotrowski, M.; Siergiejczyk, M. Optimizing the Operational Process of a Social Robot for Elderly Assistance: Enhancing Reliability and Readiness. Electronics 2025, 14, 1630. [Google Scholar] [CrossRef]
- Bock, S.; Bomsdorf, S.; Boysen, N.; Schneider, M. A survey on the Traveling Salesman Problem and its variants in a warehousing context. Eur. J. Oper. Res. 2025, 322, 1–14. [Google Scholar] [CrossRef]
- Jungnickel, D. A Hard Problem: The TSP. In Graphs, Networks and Algorithms; Springer: Berlin/Heidelberg, Germany, 1999; pp. 423–469. [Google Scholar] [CrossRef]
- Burgard, W.; Cremers, A.B.; Fox, D.; Hähnel, D.; Lakemeyer, G.; Schulz, D.; Steiner, W.; Thrun, S. Experiences with an interactive museum tour-guide robot. Artif. Intell. 1999, 114, 3–55. [Google Scholar] [CrossRef]
- Thrun, S.; Bennewitz, M.; Burgard, W.; Cremers, A.B.; Dellaert, F.; Fox, D.; Hahnel, D.; Rosenberg, C.; Roy, N.; Schulte, J.; et al. MINERVA: A second-generation museum tour-guide robot. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C), Detroit, MI, USA, 10–15 May 1999; Volume 3. [Google Scholar]
- Vongbunyong, S.; Teerabundit, T.; Khantee, N.; Thamrongaphichartkul, K. Development of Autonomous Mobile Service Robot as A Reception in Department Stores. In Proceedings of the 2024 21st International Joint Conference on Computer Science and Software Engineering (JCSSE), Phuket, Thailand, 19–22 June 2024; pp. 232–238. [Google Scholar] [CrossRef]
- Relay Delivers Everywhere. Available online: https://www.relayrobotics.com (accessed on 24 April 2025).
- Techmetics family of Autonomous Mobile Robots. Available online: https://www.techmetics-group.com (accessed on 24 April 2025).
- Roomba Robot Vacuums. Available online: https://www.irobot.com (accessed on 24 April 2025).
- LoweBot: A Helping Hand for Our Associates. Available online: https://www.lowesinnovationlabs.com/projects/lowebot (accessed on 24 April 2025).
- Meet Tally 3.0, The Most Advanced Autonomous Inventory Robot. Available online: https://www.simberobotics.com/platform/tally (accessed on 24 April 2025).
- Galdelli, A.; Pietrini, R.; Mancini, A.; Zingaretti, P. Retail Robot Navigation: A Shopper Behavior-Centric Approach to Path Planning. IEEE Access 2024, 12, 50154–50164. [Google Scholar] [CrossRef]
- Su, C.Y.; Wang, H.C.; Ko, C.H.; Young, K.Y. Development of an Autonomous Robot Replenishment System for Convenience Stores. Electronics 2023, 12, 1940. [Google Scholar] [CrossRef]
- Cleveland, J.; Thakur, D.; Dames, P.; Phillips, C.; Kientz, T.; Daniilidis, K.; Bergstrom, J.; Kumar, V. Automated system for semantic object labeling with soft-object recognition and dynamic programming segmentation. IEEE Trans. Autom. Sci. Eng. 2016, 14, 820–833. [Google Scholar] [CrossRef]
- Sales, J.; Martí, J.V.; Marín, R.; Cervera, E.; Sanz, P.J. CompaRob: The shopping cart assistance robot. Int. J. Distrib. Sens. Netw. 2016, 12, 4781280. [Google Scholar] [CrossRef]
- Matsuhira, N.; Ozaki, F.; Tokura, S.; Sonoura, T.; Tasaki, T.; Ogawa, H.; Sano, M.; Numata, A.; Hashimoto, N.; Komoriya, K. Development of robotic transportation system-Shopping support system collaborating with environmental cameras and mobile robots. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; pp. 1–6. [Google Scholar]
- Gross, H.M.; Boehme, H.; Schroeter, C.; Müller, S.; König, A.; Einhorn, E.; Martin, C.; Merten, M.; Bley, A. TOOMAS: Interactive shopping guide robots in everyday use-final implementation and experiences from long-term field trials. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 11–15 October 2009; pp. 2005–2012. [Google Scholar]
- Chen, Y.; Wu, F.; Shuai, W.; Wang, N.; Chen, R.; Chen, X. Kejia robot—An attractive shopping mall guider. In Proceedings of the International Conference on Social Robotics, Paris, France, 26–30 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 145–154. [Google Scholar]
- Thompson, C.; Khan, H.; Dworakowski, D.; Harrigan, K.; Nejat, G. An autonomous shopping assistance robot for grocery stores. In Proceedings of the Workshop on Robotic Co-Workers, Madrid, Spain, 1–5 October 2018; Volume 4. [Google Scholar]
- Alves, R.; Linhares, B.A.; Souza, J.R. Autonomous shopping cart: A new concept of service robot for assisting customers. In Proceedings of the 2018 Latin American Robotic Symposium, 2018 Brazilian Symposium on Robotics (SBR) and 2018 Workshop on Robotics in Education (WRE), Joao Pessoa, Brazil, 6–10 November 2018; pp. 451–456. [Google Scholar]
- Choi, D.; Lee, K.; Kim, D. Enhanced potential field-based collision avoidance for unmanned aerial vehicles in a dynamic environment. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 487. [Google Scholar]
- 60 Percent of the Time We Spend in the Supermarket Is Spent Walking Through the Aisles and We Only Need 25 Seconds to Select a Food Product. Available online: https://www.ucm.es/catedra-shopperlab-complutense (accessed on 24 April 2025).
- Masory, O. Safety Issues Regarding Motorized Shopping Carts. In Proceedings of the 17th LACCEI International Multi-Conference for Engineering, Education, and Technology, Montego Bay, Jamaica, 24–26 July 2019. [Google Scholar]
- Electrical Supermarket Trolley Lightens Your Grocery Load. Available online: https://newatlas.com/electrical-super-trolley-shopping-cart/37664 (accessed on 24 April 2025).
- Here’s the Average Walking Speed. Available online: https://www.thehealthy.com/exercise/walking/average-walking-speed (accessed on 24 April 2025).
- Standing—Male (Plan). Available online: https://www.dimensions.com/element/standing-male-plan (accessed on 24 April 2025).
- Curbside Pick Cart. Available online: https://nationalcart.com/products/curbside-pick-cart (accessed on 24 April 2025).
- Regency Supermarket Grocery Cart 6.3 Cu. Ft. Available online: https://www.webstaurantstore.com/regency-supermarket-grocery-cart-3-5-cu-ft/460SHPCRT35.html (accessed on 24 April 2025).
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Khoa, V.; Takayama, S. Effect of Landslide on Energy Efficiency Chain Based Routing Protocol for Wireless Sensor Network. Wirel. Sens. Netw. 2020, 12, 13–36. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: Berlin/Heidelberg, Germany, 1986; pp. 396–404. [Google Scholar]
- Rezaee, H.; Abdollahi, F. Adaptive artificial potential field approach for obstacle avoidance of unmanned aircrafts. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 1–6. [Google Scholar]
- Choi, D.; Chhabra, A.; Kim, D. Intelligent cooperative collision avoidance via fuzzy potential fields. Robotica 2022, 40, 1919–1938. [Google Scholar] [CrossRef]
- Kruse, T.; Pandey, A.K.; Alami, R.; Kirsch, A. Human-aware robot navigation: A survey. Robot. Auton. Syst. 2013, 61, 1726–1743. [Google Scholar] [CrossRef]
- Rodgers, E. State of Grocery Shopping; Technical Report; Drive Research: Syracuse, NY, USA, 2024. [Google Scholar]









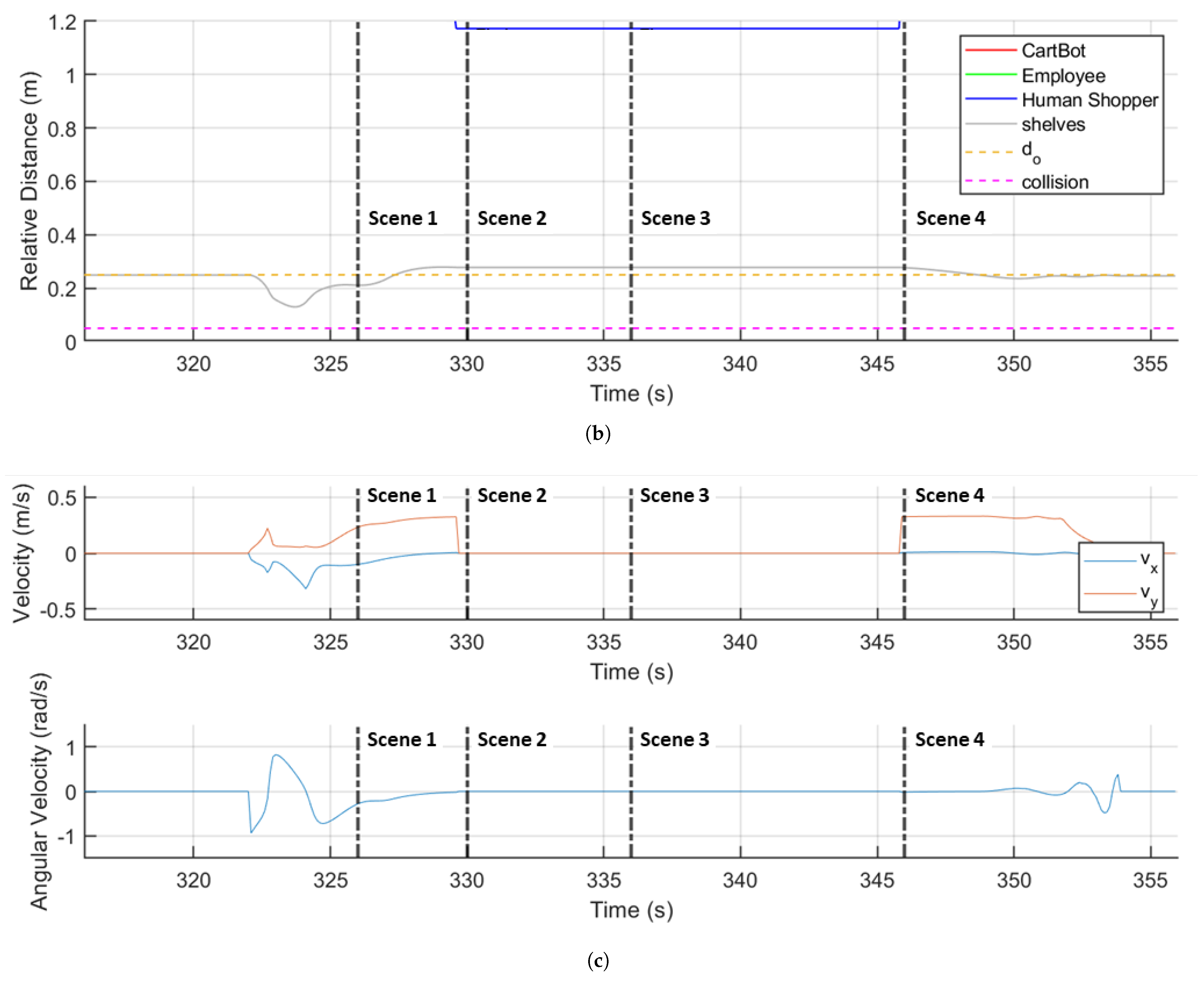
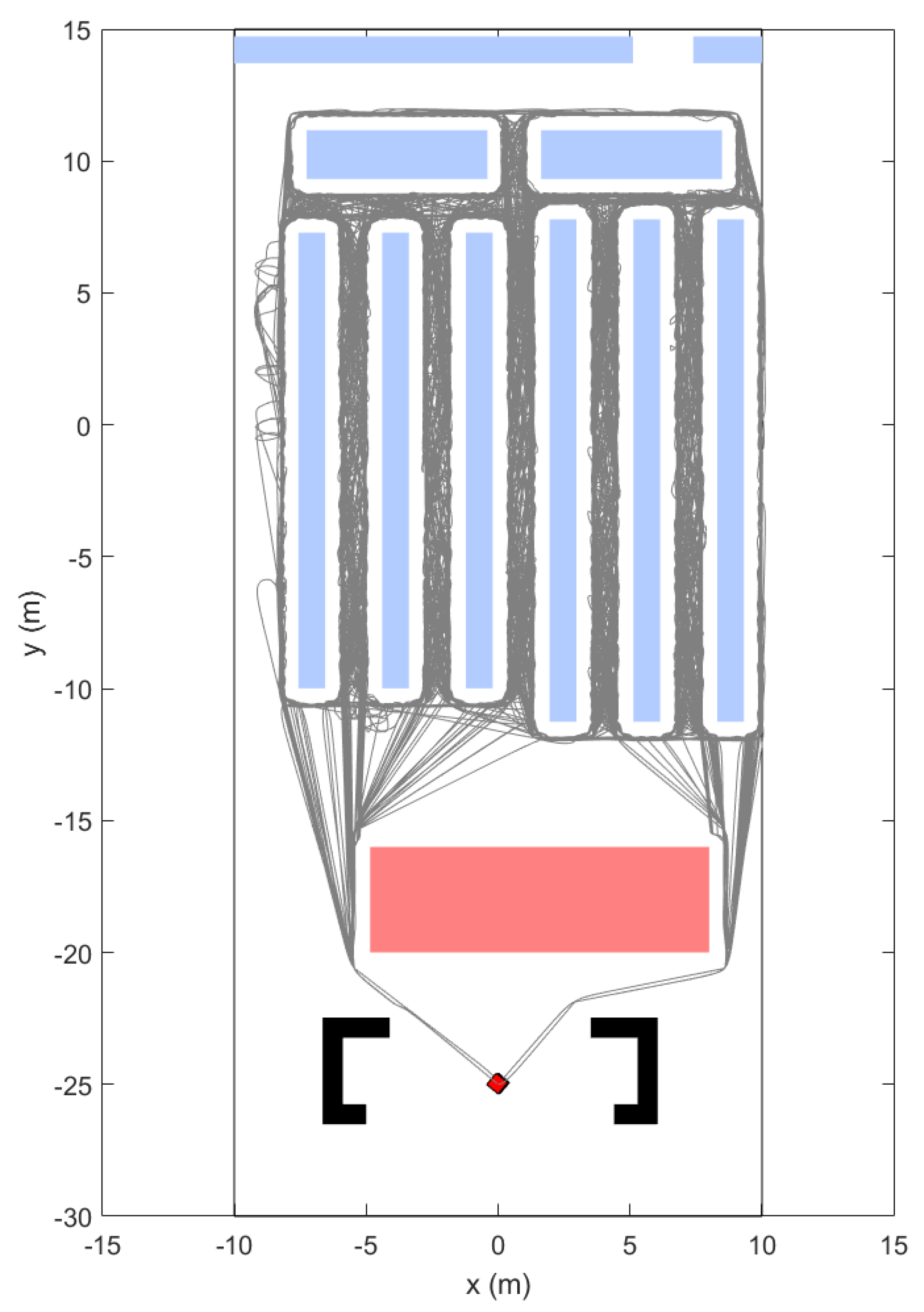
| Description | Variable | Value |
|---|---|---|
| Obstacle influence distance | 0.25 m | |
| Attractive gain coefficient | 100 | |
| Degree of attractive field | 3 | |
| Repulsive gain coefficient | 1 | |
| Degree of repulsive field | 3 | |
| Rotation angle for the rotation matrix | 60° |
| Item | Mean | Standard Deviation |
|---|---|---|
| Global path length (m) | 178.837 | 13.261 |
| Total travel path (m) | 183.229 | 13.476 |
| Global path computation (s) | 0.451 | 0.022 |
| Local planner’s computation at each time step (s) | 2.611 × | 4.798 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, D.; Venepally, J.R.; Kim, D. Path-Planning and Navigation for Robots Considering Human–Robot–Environment Interactions in Supermarket Environments. Electronics 2025, 14, 2111. https://doi.org/10.3390/electronics14112111
Choi D, Venepally JR, Kim D. Path-Planning and Navigation for Robots Considering Human–Robot–Environment Interactions in Supermarket Environments. Electronics. 2025; 14(11):2111. https://doi.org/10.3390/electronics14112111
Chicago/Turabian StyleChoi, Daegyun, Jashwanth Rao Venepally, and Donghoon Kim. 2025. "Path-Planning and Navigation for Robots Considering Human–Robot–Environment Interactions in Supermarket Environments" Electronics 14, no. 11: 2111. https://doi.org/10.3390/electronics14112111
APA StyleChoi, D., Venepally, J. R., & Kim, D. (2025). Path-Planning and Navigation for Robots Considering Human–Robot–Environment Interactions in Supermarket Environments. Electronics, 14(11), 2111. https://doi.org/10.3390/electronics14112111







