Abstract
This paper investigates the outage probability of a hybrid Radio Frequency–Underwater Wireless Optical Communication (RF-UWOC) system that employs the Decode-and-Forward protocol under composite fading channels. It is assumed that the RF link experiences Generalized K distribution fading along with atmospheric path loss, while the UWOC link endures generalized Gamma distribution turbulent fading, accounting for underwater path loss and pointing errors. Based on these assumptions, when intensity modulation with direct detection (IM/DD) and heterodyne detection (HD) are, respectively, utilized at the receiver, the average outage probability and its corresponding asymptotic expression for the considered hybrid dual-hop systems under high signal-to-noise ratios are derived. Subsequently, Monte Carlo simulations are conducted to validate the accuracy of the theoretical analysis results and to explore the influence of various key system parameters on the dual-hop systems.
1. Introduction
Underwater Wireless Optical Communication (UWOC) has received extensive attention from a large number of scientific researchers due to its many advantages such as high signal bandwidth, low transmission delay, strong confidentiality, and exemption from spectrum authorization [1]. In recent years, to meet the practical need of realizing the mutual transmission of observation information between airborne/space/ground nodes on land and underwater targets over long distances, cross-media hybrid relay transmission architectures of Radio-Frequency (RF)-UWOC [2] or Free Space Optical (FSO)-UWOC have emerged [3].
Reference [3] proposed a multi-hop Free Space Optical (FSO) and Underwater Wireless Optical Communication (UWOC) relay communication system that can be used for the tracking of Autonomous Underwater Vehicles (AUVs). In a fading environment, the expressions of the system’s end-to-end average bit error rate (BER) and outage probability were analyzed and derived. For the FSO link, the influences of Gamma–Gamma (GG) turbulence fading and pointing error were considered, while for the UWOC link, the Lognormal distribution was adopted to model the effect of ocean turbulence. Both links used the Beer–Lambert exponential law to model the atmospheric and oceanic path losses.
Reference [4] studied the outage probability, bit error rate, and channel capacity of a hybrid two-hop communication system composed of FSO-UWOC links under the Amplify-and-Forward (AF) mechanism. Among them, the GG atmospheric turbulence model was used for the FSO link, and the Exponential-Generalized Gamma distribution was used to model the underwater turbulence channel for the UWOC link. The impacts of atmospheric and underwater path losses on the system performance were not considered.
Reference [5] studied the outage probability and bit error rate of a two-hop communication system composed of FSO-UWOC hybrid links under the assistance mechanism of Reconfigurable Intelligent Surface (RIS). For the FSO link, the GG atmospheric turbulence fading and pointing error were considered. For the UWOC link, only the Lognormal distribution was selected to simulate the ocean turbulence without considering the influence of pointing error. Also, the path loss factors were not considered for both links. It is obvious that all the above-mentioned studies modeled and analyzed the communication links between airborne/ground and sea surface relay nodes using FSO.
However, in terms of RF-UWOC, which is the focus of this paper’s research, Reference [6] analyzed the outage probability, bit error rate, and ergodic capacity of a RIS-assisted RF-UWOC hybrid two-hop system. Among them, the RF link was modeled as Nakagami-m and Rayleigh small-scale fading, and the UWOC link was modeled as EGG turbulence fading. The path losses encountered by the two links and the adverse effects of the pointing error on the UWOC link were not considered.
Reference [7] derived the outage probability and bit error rate of a UAV-based RF-UWOC hybrid two-hop system in a fading environment and accordingly analyzed and solved the hovering height of the UAV that minimizes the system outage probability. Among them, the RF link was modeled as a hybrid model of Nakagami-m small-scale fading and atmospheric path loss, and the UWOC was modeled as only having EGG turbulence fading. Similarly, the effects of the pointing error and underwater path loss were not considered.
Reference [8] studied the outage probability and ergodic capacity of a hybrid two-hop RF-UWOC system when using power-domain non-orthogonal multiple access technology to address two different underwater users and modeled and solved the optimal power allocation strategy for underwater users with the optimization goal of minimizing the system outage probability. Among them, the RF link was modeled as a small-scale Rayleigh fading channel, and the UWOC only considered the influence of the EGG turbulence fading factor.
Reference [9] proposed an uplink fusion system of multi-hop UWOC and RF assisted by RIS carried by an AUV. Under the conditions of considering ocean turbulence and pointing error, the outage probability and average bit error rate of the system were analyzed. Among them, the UWOC link was modeled as underwater path loss described by the Beer–Lambert law, pointing error, and EGG turbulence effect; the RF link used the complex Fisher–Snedecor F distribution to model the influence of small-scale fading and shadowing effects, and the effect of path loss was not considered. In addition, this paper also did not consider the comparison of the system performance of the UWOC link under different receiving and detection schemes such as heterodyne detection (HD) and intensity modulation with direct detection (IM/DD).
Synthesizing the above research status of the cross-media FSO/RF-UWOC hybrid two-hop relay system, it can be seen that due to the different communication mechanisms, the channel modeling of the FSO and RF links above the water surface is not comparable. However, just in terms of the operation of the RF link, generally only the influence of small-scale fading is considered while the effects of large-scale shadowing or path loss are ignored. Obviously, the channel modeling of the RF link is far from perfect. On the other hand, for the UWOC link, the Lognormal distribution model directly transplanted from the atmospheric FSO environment or the EGG distribution model, which is not transplanted but relatively complex, is generally used to model the ocean turbulence fading. At the same time, the two unfavorable factors of pointing error and underwater path loss are often ignored. Or, although the influence of path loss is considered, the adopted path loss model is the unreasonable single-exponential Beer–Lambert model [10]. That is to say, there are imperfections or irrationalities in the existing channel modeling of the RF-UWOC system, and it is necessary to conduct special research on the performance of this hybrid two-hop system under a novel and complete channel model.
Based on the above background, this paper proposes to model the composite channel fading of the RF link using the Generalized K distribution and atmospheric path loss. Among them, the Generalized K distribution includes Nakagami-m small-scale fading and Lognormal shadowing effects, so that this composite model can comprehensively reflect the complete effects of small-scale fading, large-scale fading, and path loss. The UWOC link is modeled as a novel composite channel fading of the Simple Generalized Gamma Distribution (GGD), zero line-of-sight pointing error(negligible jitter), and Elamassie underwater path loss. Among them, the GGD model, through experimental testing, is an effective model that is simpler in mathematical expression than the EGG model but can perfectly describe the weak–medium–strong, three kinds of turbulence effects [11]. The Elamassie path loss model is also a path loss model that can more accurately describe the path loss including the effects of seawater absorption and scattering, as well as geometric loss than the traditional single-exponential Beer–Lambert law, which has been verified by simulation experiments [10]. Many studies only consider turbulence using the EGG model, but it is too complex and unreasonable, either only considering the pointing error or not considering the path loss, or incomplete consideration. In the system HD (coherent detection), modulation mode (BPSK) was used with devices to realize the underwater complexity less than IM/DD or the OOK complex, but its system performance from the principle is achievable, so the focus of this thesis is to consider the performance of the probability of interruption, and not consider the complexity of its implementation.
Based on this novel and complete composite fading channel model of the two links, the theoretical closed-form expression of the average outage probability of the RF-UWOC hybrid two-hop relay transmission system using the Decode-and-Forward (DF) mechanism and its asymptotic expression under high signal-to-noise ratio are derived. The performance differences in the receiver under different detection schemes of IM/DD and HD are systematically compared and analyzed. Finally, the Monte Carlo numerical simulation is used to verify the correctness of the above theoretical derivation results and to investigate the influence of different core parameters on the system performance. The major contributions of this study are summarized as follows:
- (1)
- Propose a novel composite channel fading environment that models an RF link experiencing Generalized K distribution and atmospheric path loss fading under the “decode-and-forward” mechanism, while the UWOC system undergoes GGD ocean turbulence, zero-axis pointing error loss, and Elamassie underwater path loss.
- (2)
- This paper analyzes the performance of a novel and complete double-link composite fading channel model. First, using advanced transcendental Meijer-G functions and Fox-H functions, we derive detailed theoretical closed-form expressions for the average outage probability of a RF-UWOC hybrid two-hop relay transmission system using the Decode-and-Forward (DF) mechanism. We also provide asymptotic expressions under high signal-to-noise ratios and systematically compare the performance differences in the receiver using different detection schemes of IM/DD and HD. Subsequently, we validate the correctness of the above theoretical derivations through Monte Carlo numerical simulations and examine the impact of key parameters such as oceanic fading index and jitter deviation on system performance.
Table 1 summarizes key differences between the proposed model and related works.

Table 1.
Key differences between the proposed model and related works.
2. System and Channel Model
Consider a Radio Frequency–Underwater Wireless Optical Communication (RF-UWOC) hybrid two-hop relay transmission system as shown in Figure 1. It is assumed that there is an Unmanned Aerial Vehicle (UAV) hovering base station in the air on land, which serves as the signal source (S). It communicates with the underwater destination node (D) through a buoy relay node (R) with the Decode-and-Forward (DF) capability.
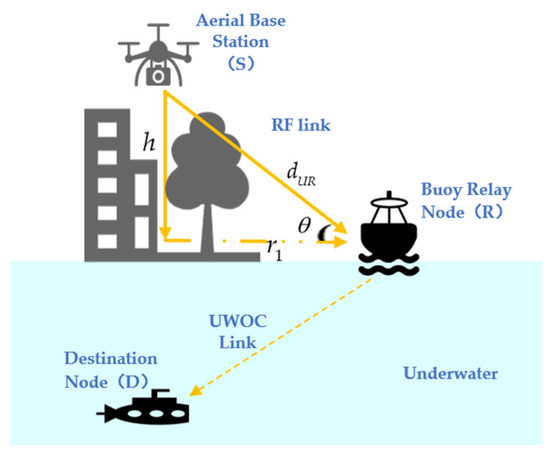
Figure 1.
RF-UWOC hybrid two-hop transmission system model.
The Radio Frequency signal S is first sent to R through the Radio Frequency (RF) link. After photoelectric conversion, the optical signal is then transmitted to D through the Underwater Wireless Optical Communication(UWOC) link. It is assumed that the RF link experiences Generalized K fading and atmospheric path loss, and the UWOC link is modeled as a complex mixed fading that includes the turbulence effect of the Generalized Gamma Distribution (GGD), zero line-of-sight pointing error, and underwater path loss.
As can be seen from Figure 1 above, the distance between the UAV and the relay R can be expressed as , where is the height of the UAV above the horizontal plane, and is the horizontal distance between the UAV and the relay R. is pitch (angle of view).
2.1. Derivation of the Probability Density Function of the Instantaneous Received SNR of the S-R Composite Fading Link
In the RF link, the baseband Radio Frequency signal received at the relay node R can be expressed as follows [12]:
in the above formula, is the unit-amplitude On-off Keying (OOK) signal transmitted from S; is the signal transmission power; is the channel fading coefficient between the UAV and R, which follows a Generalized K distribution (including the comprehensive influence of small-scale Nakagami fading and Lognormal shadowing effect); is the path loss, where is a constant related to the signal frequency and the transmission environment, is the transmission distance between the UAV and R, and is the path loss exponent; is the Additive White Gaussian Noise (AWGN) with a mean of zero and a noise power of .
The path loss exponent is a function of and can be expressed as [13], where and are parameters related to the environment and the signal frequency. represents the probability that the transmission path between the source S and the relay R can be regarded as a Line of Sight (LOS) transmission. Obviously, the larger is, the larger the probability value should be reasonably. There is , so the coefficients and are determined by empirical values. Without loss of generality, , .
It can be seen from Equation (1) that the instantaneous received signal-to-noise ratio (SNR) of the Radio Frequency link is as follows:
in the formula, corresponds to the average SNR of the RF link. Given that the channel fading of the RF link follows a Generalized K distribution, the Probability Density Function (PDF) of the instantaneous SNR is (The exact derivation of (3) can be found in Appendix A):
In the above formula, is the Meijer-G function [14] (Equation 9.301).
2.2. Derivation of the Cumulative Distribution Function of the Instantaneous Received SNR for the S-R Composite Fading Link
Substitute the above Formula (3) into the definition formula of the Cumulative Density Function (CDF) of the instantaneous received SNR , and we have the following:
By using Formula (2.24.2.2) in Reference [15] and making relevant parameter comparisons, Formula (4) can be transformed into the following:
2.3. Derivation of the Probability Density Function of the Instantaneous Received SNR of the R-D Composite Fading Link
Assume that the R-D link adopts the DF (Decode-and-Forward) relay protocol, and the expression of the received signal is as follows:
in the above formula, is the photoelectric conversion coefficient of the UWOC link, represents the decoded signal at the relay node R, and is the transmission power of the reconstructed signal; is a Gaussian random variable with a mean of 0 and a variance of . The underwater channel gain is a mixed fading that includes the underwater path loss , the zero line-of-sight pointing error , and the GGD (Generalized Gamma Distribution) ocean turbulence fading .
Now, first derive the PDF (Probability Density Function) of the mixed fading coefficient . The PDF of the GGD is known as follows [16]:
In the formula, is the scale parameter; and are the shape parameters. In addition, the zero line-of-sight pointing error with a vertical distance of from the transmitting point and a radial error of can be approximately expressed as follows [17]:
In the equation, represents the power ratio of the laser beam collected by the receiver at the center of the detector , where represents the ratio of , the receiver aperture to the beam width , and is the error function. represents the equivalent beam width. Without loss of generality, under zero visual axis jitter error, the radial error of the received beam follows a Rayleigh distribution, and the Probability Density Function (PDF) of pointing error can be expressed as follows [17]:
In Equation (9), , represents the jitter variance of the receiver.
The UWOC link path loss can be expressed using the Elamassie continuous path loss closed form formula as follows [10]:
Equation (10) is a function of the receiver aperture diameter , beam divergence angle , link transmission distance , and extinction coefficient . It may seem simple, but it has the ability to fit both absorption scattering effects and geometric errors through the correction factor and full width beam divergence angle. It actually makes sense, after Monte Carlo simulation, and has been used in many papers. Obviously, when these variables are fixed, they become a constant . Furthermore, assuming that turbulent fading is also known, there is a conditional PDF:
The Probability Density Function of mixed channel can be obtained as follows:
Using Equation (8.4.3.1) from Reference [15], , is available:
Comparing the parameters using Equation (2.24.2.3) from Reference [15]:
Medium dimensional vector in the formula ; .
The equivalent transformation of Formula (8.2.2.15) in Reference [15] and the reduction operation using Formula (8.2.2.9), when taking integers as values (non-integers can be rounded to approximate integers), the final simplified expression of Formula (14) is as follows:
On the basis of the PDF derived above, derive the PDF of instantaneous received SNR given the expression of the received signal in the UWOC link.
- (1)
- In heterodyne detection (HD) [12], the instantaneous received SNR of the R-D link is , and the average received SNR is . Therefore, , the PDF of the instantaneous SNR :
- (2)
- In intensity modulation/direct detection (IM/DD Detection) [12], the instantaneous received SNR is , and the average received SNR is . Therefore, , the PDF of instantaneous SNR :
By combining Equations (16) and (17), the two equations can be combined into a general formula:
in the above equation, represents HD; represents IM/DD detection. , .
2.4. Deduction of Cumulative Distribution Function of Instantaneous Received SNR for R-D Composite Fading Link
Substituting Equation (18) into its CDF definition , there is the following:
According to Formula (9.301) in Reference [14], the Meijer-G function is expanded in the form of a first-order Mellin Barnes integral, resulting in the following:
In the above equation is the Gamma function operator . To enclose the complex integral line by utilizing the properties of the Gamma function , it can be concluded that
The definition formula of the Meijer-G function expressed by Formula (9.301) in Reference [14], after observation and comparison of parameters, can be obtained as follows:
3. Outage Probability and Asymptotic Analysis of the RF-UWOC Dual-Hop System
3.1. Deduction of End-to-End SNR Cumulative Distribution Function and Its Asymptotic Value
For the DF relay scheme, since decoding and reconstruction of the transmission signal are required at the relay node R, the instantaneous SNR of the RF link and UWOC link are independent of each other. Therefore, the equivalent instantaneous SNR of the end-to-end link can be determined by the minimum value between the instantaneous SNR of the S-R link and the R-D link, that is,
Modeling the reliability of the double jump system as a series of independent link reliabilities for easier research.
For the DF relay protocol, the CDF can be written as follows:
Substituting Equations (5) and (22) into Equation (24), the CDF can be expressed as follows:
In the channel fading model studied by us, no one has yet derived the average outage probability of the system using the Meijer-G function.
For the convenience of analyzing the problem, it is assumed that the average SNR of the RF link and the UWOC link are the same, that is, .
When , it can be asymptotically represented as
The exact derivation of (26) can be found in Appendix B.
Similarly, currently no one has derived the asymptotic average interruption probability of the system under our novel model.
3.2. System Average Outage Probability and Its Asymptotic Value
When the signal-to-noise ratio of the end-to-end link in the RF-UWOC hybrid dual-hop system is below a given threshold , the system signal transmission is interrupted, and the probability of this event is calculated as the average outage probability of the system. Therefore, assuming Equation (25) , the outage probability of the RF-UWOC hybrid dual-hop system considering the DF relay protocol can be obtained as
Approach
When the average SNR is high, the asymptotic value of outage probability can be easily expressed by Equation (28) as
4. Simulation Results and Analysis
This section uses Monte Carlo (MC) simulation to verify the accuracy of the theoretical analysis results and examines the impact of core parameter selection on system performance. Assuming that the UWOC link operates in the water quality of the nearshore coast, its extinction coefficient satisfies the require . The typical values of other important parameters required for system simulation are shown in Table 2 Further assuming that the average signal-to-noise ratio of the two-hop links is equal, that is, , the threshold noise is set .

Table 2.
Main parameters of RF-UWOC system performance simulation RF-UWOC.
Figure 2 shows the theoretical calculation values and MC simulation values of the average outage probability of the RF-UWOC hybrid double hop relay transmission system under different RF link parameter values as a function of the average SNR . The solid line in the figure represents IM/DD detection, while the dotted line represents heterodyne detection (HD), the dashed line represents the corresponding asymptotic value curve, and the asterisk represents the MC simulation value. At this point, the coefficient values for the Generalized K distribution channel fading of the first hop RF link are set as follows : [21] (Correspond to the pink, blue, and red curves in the figure respectively). where the horizontal and vertical distances between UAV and R: , and the weak pointing error of the second hop UWOC link (corresponding to jitter deviation , receiver radius , and beam width ); underwater transmission distance ; ocean turbulence scintillation index . From the simulation results in Figure 2, it can be seen that under the condition of fixed parameters of the UWOC link (underwater transmission distance , ocean turbulence intensity , and pointing error ), whether the system adopts IM/DD detection or heterodyne detection receiving schemes, the performance of outage probability will continue to improve due to the increase in coefficient values in the RF link. This is due to the value of m that reflects the intensity of small-scale Nakagami fading in the RF link, and the smaller the value of m, the closer the small-scale fading is to the weak. Rician fading of the direct path signal. The value is inversely proportional to the average power of the random variable that characterizes large-scale shadow fading, and the larger the value, the weaker the shadow effect. All of these indicate that generalized K-fading has a significant impact on the outage probability performance in RF links. In terms of receiving detection schemes, as heterodyne detection belongs to coherent detection, and under the same system average signal-to-noise ratio conditions, heterodyne detection will obtain lower system outage probability values than incoherent IM/DD detection because coherent detection mechanism can effectively suppress noise and fading effects by utilizing the phase and frequency information of the signal, particularly showing stronger performance in composite fading channels (such as strong turbulence and large pointing errors).
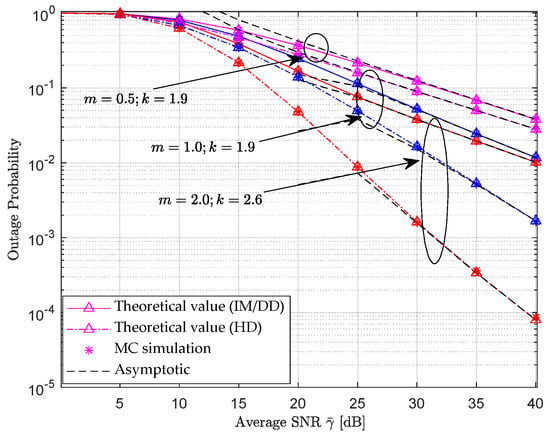
Figure 2.
The variation curve of outage probability of RF-UWOC hybrid double hop system with average SNR under different Generalized K distribution parameters.
In addition, the theoretical calculation values of the system are in good agreement with the MC simulation values, and the asymptotic value of the outage probability at high SNR also basically coincides with the theoretical value at the corresponding signal-to-noise ratio. This indicates the correctness of the closed form formula derivation results related to the theoretical and asymptotic values of the system outage probability mentioned above.
Figure 3 shows the theoretical and MC simulation values of the outage probability of the hybrid dual-hop RF-UWOC relay communication system under different UAV hovering heights and horizontal distances, as a function of the average SNR . Similarly, the solid line in the figure represents IM/DD detection, the dotted line represents heterodyne detection, the dashed line represents asymptotic value curve, and the asterisk represents MC simulation value. Set the horizontal and vertical distances between UAV and R in the RF link as follows : (Correspond to the red, blue, and pink curves in the figure respectively.) corresponding to the linear distance between UAV and R (generalized K-fading coefficient: ), pointing error of the second hop UWOC link, underwater transmission distance , and turbulence scintillation index . From the simulation results in Figure 3, it can be seen that under the condition of fixed UWOC link simulation parameters, the outage probability of the hybrid double hop system will show a downward trend in performance due to the increase in the hovering height of the UAV as a floating base station in the RF link and the horizontal distance from the relay node R. This is mainly due to the increase in the straight-line distance from UAV to R, which leads to an increase in road loss . However, under the same road loss conditions, outage probability still decreases with the increase in the average signal-to-noise ratio, indicating that increasing the received signal-to-noise ratio is still beneficial for improving system performance. Similarly, in terms of receiving detection schemes, as heterodyne detection belongs to coherent detection, under the same system average signal-to-noise ratio conditions, heterodyne detection will obtain lower system outage probability values than incoherent IM/DD detection.
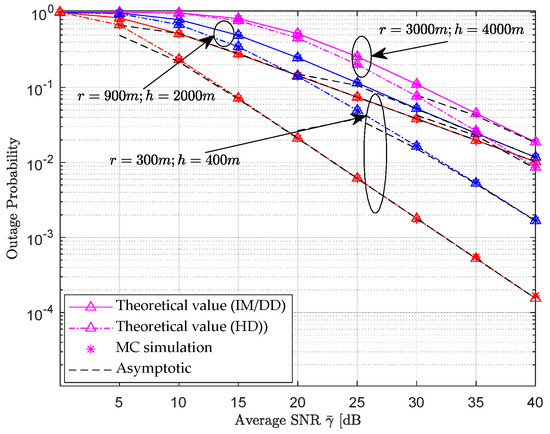
Figure 3.
The outage probability of RF-UWOC hybrid double hop system varies with the average SNR at different UAV heights and horizontal distances.
Figure 4 shows the theoretical outage probability and MC simulation values of a hybrid dual-hop RF-UWOC relay communication system under different intensities of ocean turbulence (turbulence scintillation index = 0.1074/0.2066/0.4548, Correspond to the pink, blue, and red curves in the figure respectively) experienced by the second hop UWOC link with fixed channel parameters of the first hop RF link, as a function of the average signal-to-noise ratio. At this point, the horizontal and vertical distances between UAV and R in the first hop RF link are set as follows :; the coefficient values that obey generalized K-fading are , weak pointing error of the second hop UWOC link; underwater transmission distance . From the simulation results in Figure 4, it can be seen that when the scintillation index, which characterizes the intensity of ocean turbulence, initially increases, the system performance does not deteriorate significantly. For example, , and when the scintillation index increases, the corresponding two performance curves are basically close, while when , the performance gap between the scintillation index and the scintillation index increases, and the performance decreases significantly. The reason for this is that the asymptote formula for system outage probability represented by Equation (29) shows that its asymptote is related to several system attenuation parameters that characterize the intensity of small-scale Nakagami fading in RF links, large-scale shadow fading parameters, ocean turbulence intensity, and UWOC link pointing error. When setting the ocean turbulence scintillation index , it can be observed that compared to other parameter values , , the asymptotic value of the system average bit error rate in high SNR areas is basically determined by the fading parameter of the RF link, which is independent of the intensity of ocean turbulence. When the intensity of ocean turbulence increases , it is less than the values of the other three parameters, so the asymptotic value of this curve will be determined by the ocean turbulence coefficient . Obviously, the performance of the outage probability curve corresponding to ocean turbulence will be even worse than the performance of these two curves. Under the same conditions of ocean turbulence, the probability of system outage decreases with the increase in the average signal-to-noise ratio, and there is also performance improvement with the introduction of coherent HD. All of these indicate that increasing the received signal-to-noise ratio and using coherent reception are beneficial for improving system performance.
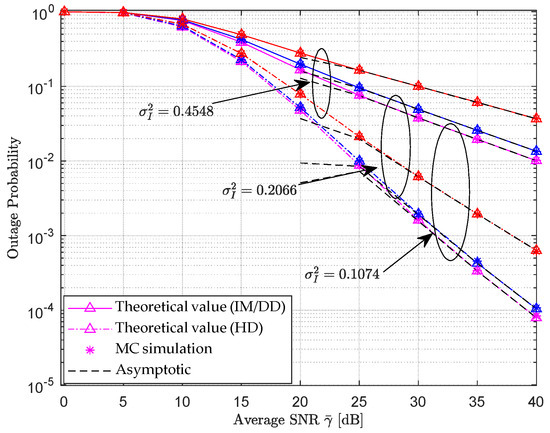
Figure 4.
The variation curve of outage probability of RF-UWOC hybrid double hop system with average signal-to-noise ratio under different ocean turbulence intensities.
Figure 5 shows the theoretical outage probability and MC simulation values of the hybrid dual-hop RF-UWOC relay communication system as a function of the average signal-to-noise ratio when the channel parameters of the first hop RF link are fixed but the jitter dispersion of the second hop UWOC link is changed, Correspond to the pink, blue, and red curves in the figure respectively. At this point, the horizontal and vertical distances between UAV and R in the first hop RF link are set to: , and the coefficients that follow generalized K-fading are set to: . The pointing error of the second hop UWOC link varies with jitter deviation (at this point, the receiver radius and beam width ); underwater transmission distance , ocean turbulence scintillation index . From the simulation results in Figure 5, it can be seen that as the jitter deviation value representing pointing error gradually increases, the overall curve of the system outage probability changing with the average signal-to-noise ratio gradually rises, that is, the outage probability performance shows a downward trend. The reason for this is that the value represents the amplitude of random jitter between the received light intensity at the receiver and the center of the receiving aperture. Obviously, the larger the jitter amplitude, that is, the larger the value, the less signal energy will fall into the receiving aperture, the lower the received signal-to-noise ratio (SNR), and the probability of outage will inevitably decrease. However, the simulation results in Figure 5 also reveal that increasing the average signal-to-noise ratio and changing the detection method can effectively improve the outage probability performance of the system under the same system parameter conditions.
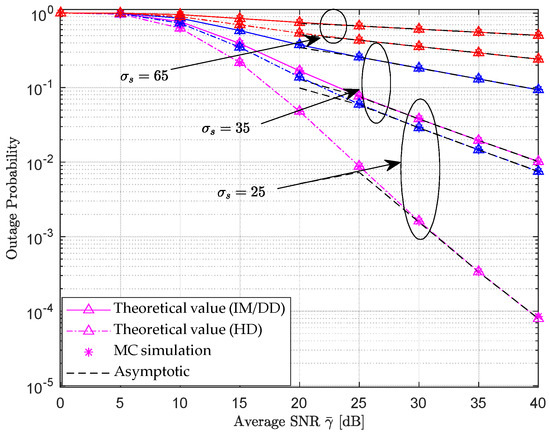
Figure 5.
The variation curve of outage probability of RF-UWOC hybrid double hop system with average signal-to-noise ratio under different jitter deviations.
Figure 6 shows the theoretical outage probability and MC simulation values of a hybrid dual-hop RF-UWOC relay communication system with fixed channel parameters for the first hop RF link but varying transmission distance (Correspond to the pink, blue, and red curves in the figure respectively.) for the second hop UWOC link, as a function of the average signal-to-noise ratio. At this point, the horizontal and vertical distances between UAV and R in the first hop RF link are set to ; the coefficients that follow generalized K-fading are set to , the strong pointing error (receiver radius , beam width ) of the second hop UWOC link, and the ocean turbulence scintillation index . From the simulation results in Figure 6, it can be seen that as the underwater transmission distance decreases, the outage probability performance of the corresponding hybrid double hop system improves. This is due to the significant attenuation of the Elamassie underwater path loss represented by Equation (10) after the transmission path is reduced. Similarly to the simulation results of other figures, under the same system parameter settings, the HD scheme belonging to coherent detection is significantly more effective than the IM/DD scheme belonging to non-correlated detection. Moreover, both the MC simulation values and asymptotes can perfectly match the theoretical values, indicating that the derivation of the outage probability theory formula and asymptote formula mentioned above is correct and reasonable.
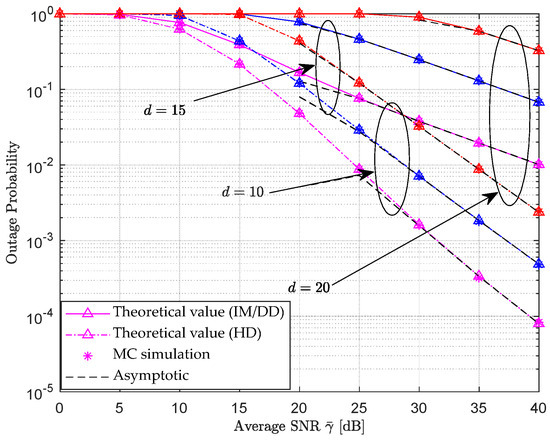
Figure 6.
The variation curve of outage probability of RF-UWOC hybrid double hop system with average SNR under different transmission distances of UWOC links.
5. Conclusions
This paper mainly studies the performance of the average outage probability of an RF-UWOC hybrid two-hop relay transmission system that adopts the “Decode-and-Forward” mechanism in a complex fading transmission environment, when the receiving end selects two detection technologies, namely intensity modulation with direct detection (IM/DD) and heterodyne detection (HD), respectively. Firstly, by using the advanced transcendental Meijer-G function, the theoretical closed-form expression of the end-to-end outage probability of the hybrid two-hop system is derived. Subsequently, based on the power series expansion characteristics of the Meijer-G function near zero, the asymptotic expression of the outage probability under the condition of high average SNR is obtained. Theoretical analysis and numerical simulation results show that the transmission distance of the RF link, the parameters of the Generalized K distribution that can characterize the small-scale fading and large-scale shadowing effect of the RF link, as well as the parameters in the UWOC link that represent ocean turbulence, pointing error, underwater path loss, etc., will all have a significant impact on the system performance of the hybrid two-hop RF-UWOC. Specifically, as revealed by the laws of the asymptotic expression of the outage probability, the system outage probability will be jointly determined by the comprehensive influence of the parameters characterizing ocean turbulence and pointing error, the detection scheme, and the values of the parameters of the Generalized K distribution of the RF link. Under the same parameter configuration conditions, the outage probability of the system still decreases with the increase in the average SNR. Under the same average signal-to-noise ratio conditions, the heterodyne detection, which represents coherent detection, is far superior in performance to the IM/DD scheme of non-coherent detection. This indicates that increasing the received SNR and adopting coherent detection are both beneficial for improving the system performance. Finally, the Monte Carlo numerical simulation results provided in this paper are in good agreement with the theoretical calculation results, indicating that the derived theoretical closed-form expression and asymptotic expression of the outage probability of the hybrid two-hop RF-UWOC system are very accurate. They can provide rapid calculation support for the comprehensive performance analysis of the hybrid RF-UWOC system from a theoretical perspective in the future.
Author Contributions
Conceptualization, M.J.; methodology, Y.L. (Yueheng Li) and Y.L. (Yong Lv); validation, M.G. and Y.L. (Yueheng Li); formal analysis, Y.L. (Yueheng Li); writing—original draft preparation, M.G.; writing—review and editing, Y.L. (Yueheng Li); supervision, Y.L. (Yong Lv). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. U23B20144).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Proofs of Equation (3)
The known channel gain fading coefficient follows the Generalized K distribution, whose Probability Density Function (PDF) [20] is as follows:
In the formula, . Among them, the small-scale Nakagami fading number is , and the shape parameter representing the log-normal shadow; the kind of modified Bessel function is . In addition, is the average power of fading, and without loss of generality , we can set .
By using Formulas (8.4.23.1) and (8.2.2.15) in Reference [14], (A1) can be transformed into
From Equation (2), we know the relationship between the instantaneous signal-to-noise ratio and the channel fading coefficient , which is ; furthermore, , from the PDF solving method of random variable functions [21], we can obtain the PDF of the instantaneous signal-to-noise ratio as
Appendix B. Proofs of Equation (26)
Below is the asymptotic expression for high SNR.
For the convenience of analyzing the problem, it is assumed that the average SNR of the RF link and the UWOC link are the same, that is, . According to the formula (07.34.06.0006.01) in reference [22], that is,
Obviously, . By comparing Equation (A4), the following approximate expression can be obtained:
By utilizing the properties of the Gamma function, it can be concluded that
Ordering , , that is,
Similarly, the asymptotic expression can be obtained:
where , .
Therefore, when , it can be asymptotically expressed as
References
- You, X.; Wang, C.-X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Huang, Y.; Zhang, C.; Jiang, Y.; Wang, J.; et al. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 1–74. [Google Scholar] [CrossRef]
- Deng, H.; Fu, Z.; Miao, X.; Wang, S.; Pan, G.; An, J. Secure uplink transmissions in hybrid RF-UWOC space-ocean systems. IEEE Trans. Wirel. Commun. 2024, 23, 7816–7832. [Google Scholar] [CrossRef]
- Kumar, L.B.; Ramavath, P.N.; Krishnan, P. Performance analysis of multi-hop FSO convergent with UWOC system for security and tracking in navy applications. Opt. Quantum Electron. 2022, 54, 1–26. [Google Scholar] [CrossRef]
- Yang, L.; Zhu, Q.; Li, S.; Ansari, I.S.; Yu, S. On the performance of mixed FSO-UWOC dual-hop transmission systems. IEEE Wirel. Commun. Lett. 2021, 10, 2041–2045. [Google Scholar] [CrossRef]
- Ramavath, P.N.; Chung, W.Y. Performance evaluation of re-configurable intelligent surface-assisted underwater and free-space wireless optical communication in the skip-zones. ICT Express 2024, 10, 320–329. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; da Costa, D.B.; Di Renzo, M.; Alouini, M.-S. On the performance of RIS-assisted dual-hop mixed RF-UWOC systems. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 340–353. [Google Scholar] [CrossRef]
- Yadav, S.; Vats, A.; Aggarwal, M.; Ahuja, S. Performance analysis and altitude optimization of UAV-enabled dual-hop mixed RF-UWOC system. IEEE Trans. Veh. Technol. 2021, 70, 12651–12660. [Google Scholar] [CrossRef]
- Samir, A.; Elsayed, M.; El-Banna, A.A.A.; Ansari, I.S.; Rabie, K.; ElHalawany, B.M. Performance analysis of dual-hop hybrid RF-UOWC NOMA systems. Sensors 2022, 22, 4521. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Wang, P.; Cao, T.; Li, G.; Li, S.; Yang, P. Performance analysis of AUV-carried RISs-aided multihop UWOC convergent with RF MRC systems over WGG oceanic turbulence. Veh. Commun. 2024, 45, 100722. [Google Scholar] [CrossRef]
- Elamassie, M.; Miramirkhani, F.; Uysal, M. Performance characterization of underwater visible light communication. IEEE Trans. Commun. 2019, 67, 543–552. [Google Scholar] [CrossRef]
- Jamali, M.V.; Mirani, A.; Parsay, A.; Abolhassani, B.; Nabavi, P.; Chizari, A.; Khorramshahi, P.; Abdollahramezani, S.; Salehi, J.A. Statistical studies of fading in underwater wireless optical channels in the presence of air bubble, temperature, and salinity random variations. IEEE Trans. Commun. 2018, 66, 4706–4723. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; da Costa, D.B.; Yu, S. Performance analysis of UAV-based mixed RF-UWOC transmission systems. IEEE Trans. Commun. 2021, 69, 5559–5572. [Google Scholar] [CrossRef]
- Azari, M.M.; Rosas, F.; Chen, K.-C.; Pollin, S. Ultra reliable UAV communication using altitude and cooperation diversity. IEEE Trans. Commun. 2018, 66, 330–344. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press: Boston, MA, USA, 2007. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series: Volume 3: More Special Functions; Revista De Ciencias Farmaceuticas: Moscow, Russia, 1989. [Google Scholar]
- Oubei, H.M.; Zedini, E.; Elafandy, R.T.; Kammoun, A.; Abdallah, M.; Ng, T.K.; Hamdi, M.; Alouini, M.-S.; Ooi, B.S. Simple statistical channel model for weak temperature-induced turbulence in underwater wireless optical communication systems. Opt. Lett. 2017, 42, 2455–2458. [Google Scholar] [CrossRef] [PubMed]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Lin, Z.; Xu, G.; Zhang, Q.; Song, Z. Average symbol error probability and channel capacity of the underwater wireless optical communication systems over oceanic turbulence with pointing error impairments. Opt. Express 2022, 30, 15327–15343. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.-Y.; Ma, Y.; Lu, R.-R.; Wang, J.-B.; Lin, M.; Cheng, J. Hovering UAV-based FSO communications: Channel modelling, performance analysis, and parameter optimization. IEEE J. Sel. Areas Commun. 2021, 39, 2946–2959. [Google Scholar] [CrossRef]
- Bithas, P.S.; Sagias, N.C.; Mathiopoulos, P.T.; Karagiannidis, G.K.; Rontogiannis, A.A. On the performance analysis of digital communications over generalized-K fading channels. IEEE Commun. Lett. 2006, 10, 353–355. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications, 5th ed.; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- The Wolfram Functions Website. Available online: http://functions.wolfram.com/ (accessed on 21 May 2017).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).