Enhanced Graph Diffusion Learning with Transformable Patching via Curriculum Contrastive Learning for Session Recommendation

Abstract

The fusion modeling of intra-session item information representation and inter-session item transition pattern for session recommendation has shown performance advantages. However, existing research still suffers from the following challenges: (1) the time-varying effects of complex relationships between item transitions within sessions need to be deeply explored; and (2) the lack of effective representation for inter-session item transition patterns. To address these challenges, we propose a new session recommendation, named EGDLTP-CCL. Specifically, we first design a patch-enhanced gated neural network representation of session item transition patterns, which accurately captures the time-dynamically varying impacts of the complex relationships within sessions of item transitions through a designed transformer patching strategy. Then, we develop an energy-constraint-based graph diffusion model to capture the inter-session item transition patterns, which mitigates the problem of poor simulation of real inter-session item transition patterns by the introduction of an energy-constraint strategy for the graph diffusion model. In addition, patch-enhanced gated neural networks and energy-constrained graph diffusion models are treated as two different views in the contrastive learning framework. By introducing a curriculum learning strategy that explores how to effectively select and train negative samples in a contrastive learning framework, thereby deeply improving performance in contrastive learning task. Finally, we combine and jointly train the recommendation task and the curriculum learning contrastive learning task for optimization based on a multi-task learning strategy to further improve the recommendation performance. Experiments on real-world datasets show that EGDLTP-CCL significantly outperforms state-of-the-art methods.

1. Introduction

Session recommendation models a series of items interacted by a user as a pattern of several session sequences, which can generate efficient personalized recommendations for the user relying only on a limited sequence of items interacted by an anonymous user. Therefore, in recent years, session recommendation has attracted the attention of more and more research scholars [1,2].

Traditional approaches focus on using Markov chains to generate recommendations, but are limited by strong independence assumptions [3]. Recently, deep learning has provided effective solutions to these problems. While these approaches [4,5] have been successful in some ways, they ignore the potentially complex transformation information between items. Encouraged by the great success of graph neural networks in the field of artificial intelligence, several recent studies have focused on graph structures, which aggregate much richer information about the current session. GCE-GNN [6] learns global representations of items outside the session using a graph attention mechanism on a global item set. SR-HGNN [7] proposes a higher-order hybrid gated network for session recommendation. All these approaches using graph neural network architecture have achieved very good performance, but they still face several challenges as follows:

(1)

Several research works [2,6,8] explore information transformation patterns between sessions to further improve recommendation performance through graph neural network techniques. Although these approaches have achieved very good performance, there may be isolated nodes or redundant structures in the graph structure that construct the inter-session global item transformation patterns [9]. As a result, it is difficult for convolutional operations based on graph structures to accurately capture the true item transition relationships between sessions [10]. Several studies have introduced the idea of diffusion [11] into the learning process of graph structures [12]. However, in the diffusion modeling process based on graph structure, due to the influence of noise and other factors, it may lead to a deviation between the graph structure diffusion learning representation and the real value, which cannot accurately characterize the real item transition pattern between sessions.

(2)

The dynamic change characteristics based on time evolution between sequences of items in a session lack in-depth mining. In recent years, some researchers have proposed different temporal encoding functions [13,14] to learn specific temporal change patterns between items. Although these approaches have achieved some success, they essentially default to sessions consisting of items that users interact with based on their temporal ordering properties, ignoring the effect of asynchronous timestamps and future timestamp in the sequential data on the pattern of inter-session item transformations, and lacking in-depth mining of temporal influence patterns [15].

To address these issues, inspired by the literature [16,17], we propose a novel recommendation model for session recommendation (EGDLTP-CCL). First, we construct a global item co-graph based on all the sessions, and then use an energy-constrained graph diffusion-based algorithm to learn the global representation of item transition patterns. The energy-constraint-based L2-weighted diffusion function is used to guide the direction of diffusion information transfer for layer-by-layer regularization, which mitigates the information loss in multiple iterative aggregations of the first-order neighbors of a node, achieving the integration of the information from multi-hop neighboring nodes and accurately characterizing the item transition patterns between sessions. Meanwhile, we design a patch-enhanced gated neural network consisting of GGNN and an LSTM neural network to characterize the dynamic change patterns of items within sessions. Inspired by the literature [17], we innovatively introduce the transformer patch strategy to model the time-varying characteristics of item change patterns in a session. By splitting the time series into sub-sequence-level patches and then aggregating them into item sequence-level patches based on the time step, which focuses more on the local semantics and captures the global semantics. In addition, by using the energy-constrained graph diffusion model and the patch-enhanced hybrid neural network model as two different views, the mutual information between these two view representations is maximized. At the same time, the appropriate negative samples of the curriculum contrastive learning framework are accurately selected through curriculum learning, which achieves the purpose of further improving the performance of the contrastive learning task. Finally, the performance of the recommendation model is improved by integrating and jointly training the recommendation task and the contrastive learning task through a multitasking strategy. Comprehensive experiments demonstrate the superior performance of EGDLTP-CCL.

In summary, the contributions of this paper can be summarized as follows:

1.

The EGDLTP-CCL model employs an energy-constrained graph diffusion technique to learn inter-session item transition patterns. The energy-constraint function guides the global graph diffusion process and alleviates the bias between the graph structure diffusion learning representation and the actual value.

2.

The EGDLTP-CCL model employs a patch-enhanced gated graph neural network to learn intra-session item transition patterns. In particular, the model emphasizes the potential of the patch strategy to capture temporally varying properties of intra-session item transition patterns, enhancing the local semantic features of temporal items and capturing the full semantics through a time-step-based aggregation operation.

3.

The EGDLTP-CCL model employs a contrastive learning framework based on curriculum learning, in which the proposed novel negative sampling method based on curriculum learning enhances the model’s performance and generalization capability.

4.

The performance of the EGDLTP-CCL model is tested on three real-world datasets, and the experimental results show the significant superiority of the proposed model when compared to the state-of-the-art works.

2. Related Work

Our work covers two areas of literature. We review recent advances in the following aspect.

2.1. Deep Learning Based Session Recommendation

Deep learning has achieved great success in the field of recommendation, especially in the field of session recommendation. Hidasi et al. [18] first proposed a new session recommendation model-GRU4REC, which utilizes gated recurrent units to model sequential behaviors in a session. Li et al. [19] proposed integrated attention mechanisms to enhance RNNs to represent item transition patterns in sessions. Wu et al. [20] utilized an MLP with an attention mechanism to fuse different session context representations for learning a more comprehensive session representation.

In recent years, with the successful results achieved by graph neural networks in the field of AI. The seminal work is SR-GNN [21], which constructs session sequences as graph structures and uses gated graph neural networks to learn item representations. Feng et al. [22] pay more attention to the impact of the transition model on the target items. Qiu et al. [23] propose a weighted-attention GNN feature encoder to mine the user’s latent intent, while Wang et al. [24] propose a hypergraph attention network to model the contextual information of items at different granularity levels. Chen et al. [25] introduce a search algorithm to find the optimal graph structure during the composition process, while Zhuo et al. [26] propose a multi-hop memory transformer from a multi-view perspective to comprehensively capture the potential user intent. In contrast, our approach incorporates graph diffusion to model inter-session item transition patterns, and designs a patch-enhanced gating network to strengthen temporal influence modeling to further capture intra-session item transition patterns accurately.

2.2. Application of Contrastive Learning in Recommendation

Contrastive learning (CL) has received widespread attention as an emerging learning paradigm that supports training on large amounts of unlabeled data, alleviates data sparsity, and reduces the model’s dependence on labeled data. Xu et al. [27] employs a novel contrastive learning framework in graph structure to improve recommendation performance based on comprehensive consideration of local and global information during feature representation. Zhang et al. [28] design a hypergraph contrastive learning framework based on multiple granularity compositing strategies for learning different representations of user-user interactions in group recommendations. Wei et al. [29] combine information bottlenecks with contrastive learning to optimize mutual information maximization to improve recommendation performance. Zhao et al. [30] use a contrastive learning approach with disentangled causal embeddings to mitigate data sparsity and long-tailed items in recommendation. Yang et al. [31] propose a spectral domain-based spectral cueing guided by combining cueing learning with contrastive learning to focus on spatial domains with different frequencies of information at different views in a contrastive learning framework. In contrast, our approach employs a curriculum learning strategy to explore how to select better negative samples.

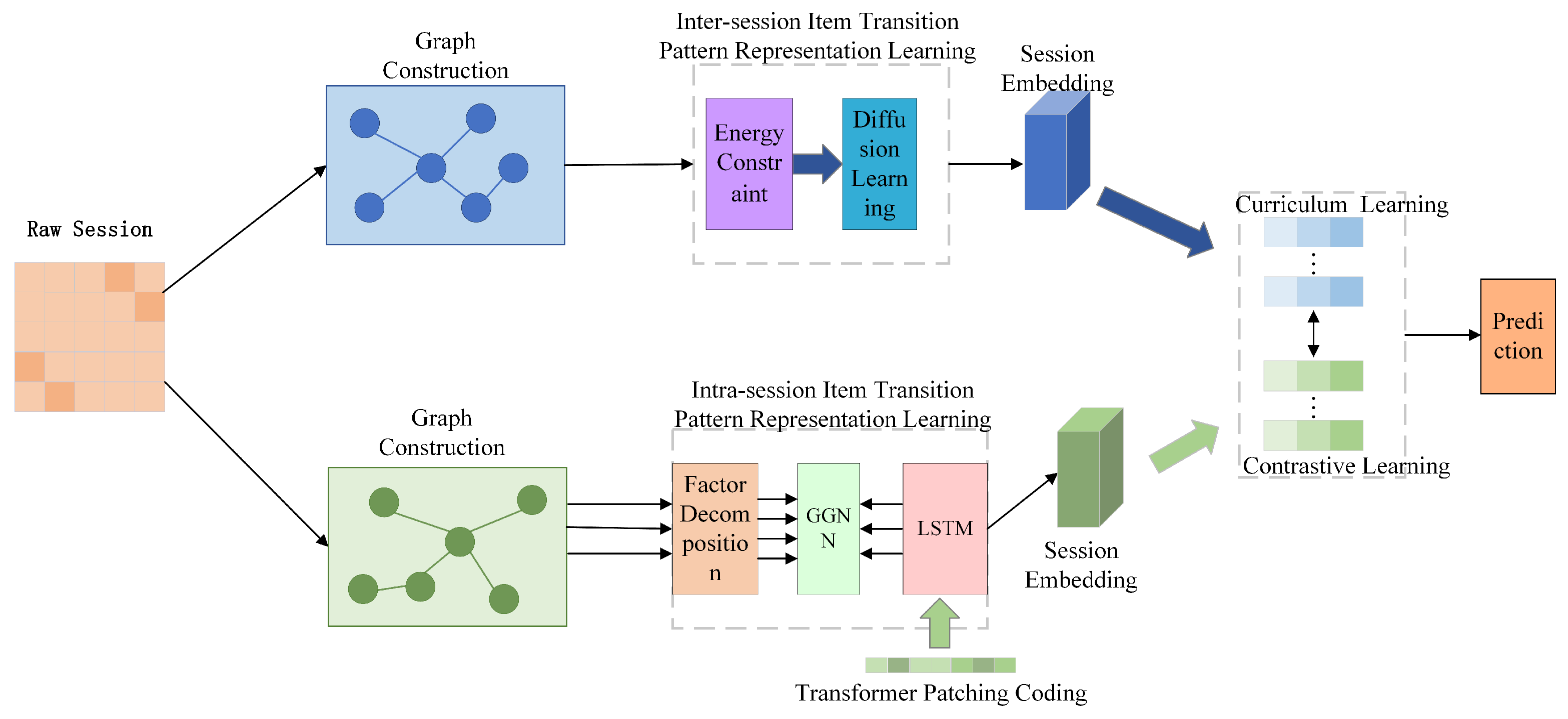
3. EGDLTP-CCL Model

The overall framework of the EGDLTP-CCL model is shown in Figure 1. The model is mainly composed of 4 main parts. (1) Inter-session item transition pattern representation learning. In this module, all session data are first utilized to construct a global synergy graph, and then energy-constraint-based graph diffusion is executed on the global synergy graph to efficiently learn global inter-session item transition patterns. (2) In-session item transition pattern representation learning. In this module, first, consistent with the literature [32], we utilize the disentangle technique for factor-based item initialization. Then, we design a patch-enhanced gated neural network to accurately model the complex transition relations between items in the current session, focusing on local semantics in the time series and comprehensively capturing the global semantics through the introduction of a transformer patch strategy. (3) Curriculum contrastive learning framework. First, intra-session item representation learning and inter-session item representation learning are used as two views of the contrast learning framework. The objective is to maximize the mutual information between the above two views, and select more optimal negative samples based on curriculum learning to further enhance the performance of the contrast task. (4) Fusion representation learning based on a multi-task strategy. In this module, the recommendation task and the contrastive learning task are unified based on a multi-task strategy by utilizing a joint training strategy.

3.1. Formulation

Assume that $V=\{v_1,v_2,\dots ,v_m\}$ is itemset, and m denotes the number of items. The set of sessions is denoted as $S=\{s_1,s_2,\dots ,s_n\}$, and n denotes the number of session. For any session in the session dataset denoted as $s=\{v_{s,1},v_{s,2},\dots ,v_{s,N}\}$, N denotes the number of items in session s, and $v_{s,\zeta }\in V$ ($1\le \zeta \le m$) denotes the item of the $\zeta \mathrm{th}$ interaction in session s. All items are embedded in the same space, denoted as $x\in {\mathbb{R}}^d$.

Given a session, the goal of EGDLTP-CCL is to output a probability distribution for each candidate item, where each element of the distribution represents the probability that the item will be recommended to the user, and finally, the recommended items are output based on the above.

3.2. Inter-Session Item Transition Pattern Representation Learning

Existing works on the inter-session item transition model prefer the traditional encoding approach of stacked multilayer graph convolution. Considering that there are many challenges in the coding approach of multilayer graph convolution [33], we propose an energy-constrained graph diffusion to learn inter-session item transition patterns using the graph diffusion learning approach in the session recommendation scenario. The steps are as follows:

$$D_{e_{n_1},e_{n_2}}=Dis(x_{e_{n_1}},x_{e_{n_2}})e_{n_1},e_{n_2}\in \{1,2,\dots ,m\}$$

(1)

$$A_{e_{n_1},e_{n_2}}=1\{D_{e_{n_1},e_{n_2}}\in \mathrm{top}-k\}{e}_{n_1},e_{n_2}\in \{1,2,\dots ,m\}$$

(2)

$$\overline{A}=\mathrm{Norm}\left(\sum _{n=1}^N\sum _{n=1}^N{A}_{e_{n_1},e_{n_2}}\right)e_{n_1},e_{n_2}\in \{1,2,\dots ,m\}$$

(3)

where F denotes the Euclidean distance function, $Dis(·)$ denotes the distance between the global graph nodes $e_{n_1},e_{n_2}$. The embedding vector $x_{e_{n_1}},\dots ,x_{e_{n_2}}\in {\mathbb{R}}^{m\times D}$, realizes the feature embedding for all m item nodes. The top k nodes are selected and connected to obtain the initial sparse adjacency matrix A. The adjacency matrix A is normalized to obtain the final initial adjacency matrix $\overline{A}$.

Next, the L2 regularized weighted dot product diffusion function with energy constraints guides the information interactions between nodes in the diffusion process, and the results are as follows:

$$K^{k,h}=W_K^{k,h}{x}^k,U^{k,h}=W_U^{k,h}{x}^k,V^{k,h}=W_V^{k,h}{x}^k$$

(4)

$$K_L^{k,h}={\left[{\displaystyle \frac{K_n^{k,h}}{\Vert K_n^{k,h}{\Vert }_2}}\right]}_{n=1}^m,U_L^{k,h}={\left[{\displaystyle \frac{U_n^{k,h}}{\Vert U_n^{k,h}{\Vert }_2}}\right]}_{n=1}^m$$

(5)

$$E(x,k;g)=\parallel x-x^k{\parallel }_F^2+\nu \sum _{e_n,e_m}g\left(\parallel x_{e_{n_1}}-x_{e_{n_2}}{\parallel }_2^2\right)e_{n_1},e_{n_2}\in \{1,2,\dots ,m\}$$

(6)

where $W_K^{k,h}\in {\mathbb{R}}^{D\times D}$, $W_U^{k,h}\in {\mathbb{R}}^{D\times D}$, $W_V^{k,h}\in {\mathbb{R}}^{D\times D}$ denote the parameters of the $h\mathrm{th}$ head of the $k\mathrm{th}$ layer. $K_n^{k,h}$ denotes the $n\mathrm{th}$ row vector of $K_L^{k,h}\in {\mathbb{R}}^{N\times D}$ that realizes the global propagation of the $h\mathrm{th}$ head. $\nu$ represents the weight parameter. Function g is a monotonically increasing concave function. Thus, the diffusivity $P^k$ is expressed as follows:

$$P^k={\displaystyle \frac{1}{h}}\sum _{h=1}^h\left\{dia{g}^{-1}\left(Norm\left(U_L^{k,h}\left({\left(K_L^{k,h}\right)}^T\omega \right)\right)\right)\left[\omega \left({\omega }^T{V}^{k,h}\right)+U_L^{k,h}\left({\left(K_L^{k,h}\right)}^T{V}^{k,h}\right)\right]\right\}$$

(7)

where $\omega$ is an all-1 ${\omega }_{N\times 1}$ vector, $diag(·)$ denotes diagonalization, and $Norm(·)$ denotes regularization constraint. $P^k$ denotes the diffusion probability between different item nodes.

Thus, the diffusion process, as follows:

$${\Delta }^k=\sum _n^N\sum _m^N{P}^k{\overline{A}}_{n,m}^k,x^{k+1}=(1-\delta {\Delta }^k)x^k+\delta {\Delta }^k{x}^k,E(x^{k+1},k;g)\le E(x^k,k-1;g)k\ge 1$$

(8)

$x^{k+1}$ denotes the updating process of the item embedding. $\delta$ is a hyperparameter indicating the probability that the previous layer’s features are retained in this layer’s features. E denotes the energy constraint. $x^{k+1}$ is the global representation of all items between sessions after learning the output variable $X_t^g$ through k-layer diffusion graph. The inter-session item transition pattern representation $s_g={\displaystyle \frac{1}{m}}{\sum }_{t=1}^m{X}_t^g$ is obtained by performing a mean pooling operation on the item embeddings of the whole session.

3.3. Intra-Session Item Transition Pattern Representation Learning

The existing works prefer a simple temporal encoding approach when learning to generate in-session item transition pattern representations, which does not adequately consider the extent to which time-series variations affect users’ behavioral intentions [34]. Meanwhile, asynchronous timestamps can generate noise by incorporating irrelevant user intentions, leading to poor robustness of the session representation and degrading recommendation performance. Consequently, we propose a patch-enhanced gated neural network to learn intra-session item transition pattern representations. This approach aims to learn the exact user’s intention by comprehensively and accurately capturing intra-session temporal sequence dependencies through a transformer patch strategy.

First, consistent with the literature [32], a factor-based initialization of the items of the current session is performed to achieve a better fine-grained characterization of the items using factor features. The session sequence $s=\{v_{s,1},\dots ,v_{s,\tau },\dots ,v_{s,n}\}$ is constructed as a session graph $G_s=(V_s,{\Lambda }_s)$, where $V_s$ and ${\Lambda }_s$ denote the set of nodes and the set of edges of the corresponding session s, respectively. $V_s$ consists of the items that the user has clicked within the current session s. The initial embedding $s_x=\{x_{s,1}^{\left(0\right)},x_{s,2}^{\left(0\right)},\dots ,x_{s,n}^{\left(0\right)}\}$ of the current session, where the initial embedding of the $\tau \mathrm{th}$ item in the session s is denoted as ${\overline{x}}_{s,\tau }^{\left(0\right)}\in {\mathbb{R}}^d$. Each item embedding representation is projected into $\Omega$ different subspaces, where each subspace contains a potential factor feature of the item, utilizing the factor feature $h_{v_{\tau },\Omega }$ to better characterize the item at a finer granularity, as follows:

$$h_{{\nu }_{\tau },\Omega }=\sigma \left(W_k^T{\overline{x}}_{s,\tau }^{\left(0\right)}\right)+b_k$$

(9)

where $W_k\in {\mathbb{R}}^{d\times {\displaystyle \frac{d}{\Omega }}}$ and $b_k\in {\mathbb{R}}^{{\displaystyle \frac{d}{\Omega }}}$ are learnable parameters and $\sigma (·)$ is sigmoid activation function. The factor embeddings use the $L_2$ regularization and dropout strategy. Therefore, the initialized embedding representation of the $\tau \mathrm{th}$ item $v_{\tau }$ is: $x_{s,\tau }^{\left(0\right)}=[h_{{\nu }_{\tau },1}^{\left(0\right)},...,h_{{\nu }_{\tau },k}^{\left(0\right)},...,h_{{\nu }_{\tau },\Omega }^{\left(0\right)}]\in {\mathbb{R}}^d$ and the representation of the session denoted by this item can be updated to $s_x=\{x_{s,1},...,x_{s,\tau },...,x_{s,n}\}$.

Patch-enhanced gating neural network. We designed a patch-enhanced gating neural network aimed at capturing the temporal relationships between different items after completing the initialization of item factor embedding, and further accurately learning the inter-item responsible for the transition relationships. The patch-enhanced gating neural network consists of a GGNN and a patch-enhanced LSTM.

Gated graph neural networks. First, we utilize the GGNN model to learn complex transformations between different item embeddings. Specifically, item factor embeddings are first utilized for message propagation on the intra-session item graph. The item factors are considered to be the smallest representation units in the message propagation process, and then the GGNN is used to learn the embedding representation of the item representations on a factor-by-factor level, as follows:

$${\rho }_{{\nu }_t,k}^i=Concat(A_{s,k,{\nu }_t}^{in}{x}_{s,\tau }^{i-1}{W}^{in}+b^{in},A_{s,k,{\nu }_t}^{out}{x}_{s,\tau }^{i-1}{W}^{out}+b^{out})$$

(10)

$$\begin{array}{cc}\hfill & {\theta }_{{\nu }_t,k}^i=\sigma (W_z{\rho }_{{\nu }_t,k}^i+U_z{h}_{{\nu }_t,k}^{i-1}),\hfill \\ \hfill & r_{{\nu }_t,k}^i=\sigma (W_r{\rho }_{{\nu }_t,k}^i+U_r{h}_{{\nu }_t,k}^{i-1}),\hfill \\ \hfill & {\tilde{h}}_{{\nu }_t,k}^i=tanh(W_o{\rho }_{{\nu }_t,k}^i+U_o(\theta \odot h_{{\nu }_t,k}^{i-1})),\hfill \\ \hfill & h_{{\nu }_t,k}^i=(1-z_{{\nu }_t,k}^i)\odot h_{{\nu }_t,k}^{i-1}+{\theta }_{{\nu }_t,k}^i\odot {\tilde{h}}_{{\nu }_t,k}^i\hfill \end{array}$$

(11)

where $h_{v_t,k}^{i-1}$ denotes the embedded representation of item $v_t$ in the k-th factor in the $i-1\mathrm{th}$ layer of the GGNN, $A_{s,k,v_t}^{\mathrm{in}}$ and $A_{s,k,v_t}^{\mathrm{out}}$ denote the $t\mathrm{th}$ row in matrices $A_{s,k}^{\mathrm{in}}$ and $A_{s,k}^{\mathrm{out}}$, respectively, and $b^{\mathrm{in}},b^{\mathrm{out}}\in {\mathbb{R}}^{{\displaystyle \frac{d}{K}}}$ is a learnable parameter. Then, by combining the representation of item factor $h_{v_t,k}^{i-1}$ in $i-1\mathrm{th}$ layer and its neighbors in $i\mathrm{th}$ layer for representing the transformation information of different neighboring items in the session to the target item.

Patch-enhanced LSTM: We propose a patch-enhanced LSTM network to capture the temporal behavior of the item transition pattern. We first generate a patch-based temporal coding function and then fuse it with LSTM to obtain a patch-enhanced LSTM network that reflects the monotonic change in user intention as it evolves over time.

First, we propose a patch transformer-based temporal encoding function into a low-dimensional embedding representation. Initially, the time series are segmented to obtain multiple patches based on the temporal dimension of the timestamps. Next, the obtained patches are independently fed into the transformer framework. Then, the transformer framework is used to concatenate and integrate the patches’ outputs to yield the final temporal coding function: $\Gamma \left(t\right)={\widehat{t}}^{\left(i\right)}\in R^{1\times t}$.

The $i\mathrm{th}$ univariate time series of length L is represented as follows:

$$t_{1:L}^{\left(i\right)}=\left(t_1^{\left(i\right)},...,t_L^{\left(i\right)}\right)$$

(12)

where $i=1,...,\gamma$. Thus, $t_1,...,t_L$ is split to $\gamma$ univariate series $t^{\left(i\right)}\in {\mathbb{R}}^{1\times L}$. The patch length is denoted as $\xi$, and the stride, the non-overlapping region between two consecutive patches, is denoted as $\varphi$. Then, the patch sequence $t_{\xi }^{\left(i\right)}\in {\mathbb{R}}^{\xi \times \varphi }$,${\lambda }_t$ is generated based on the patches and ${\lambda }_t$ is the number of time patches, denoted as follows:

$${\lambda }_t=⌊{\displaystyle \frac{L-\xi }{\varphi }}⌋+2$$

(13)

By using patches, the number of input tokens dropped to a relatively low level. The $\varphi$ repeated numbers of the last value $t_L^{\left(i\right)}$ are padded to the end of the original sequence before splitting. The nuisance caused by asynchronous timestamps on sequences was also mitigated by the patch being re-partitioned for aggregation.

Then, we use the vanilla transformer framework [35], and the positional encoding represented based on enter patch $t_d^{\left(i\right)}$, as follows:

$$t_d^{\left(i\right)}=W_{\xi }{t}_{\xi }^{\left(i\right)}+W_{position}$$

(14)

Then, the transformer framework is represented as follows, with the final output $O_h^{\left(i\right)}\in {\mathbb{R}}^{D\times N}$:

$$Q_h^{\left(i\right)}={\left(t_d^{\left(i\right)}\right)}^T{W}_h^Q,K_h^{\left(i\right)}={\left(t_d^{\left(i\right)}\right)}^T{W}_h^K,V_h^{\left(i\right)}={\left(t_d^{\left(i\right)}\right)}^T{W}_h^V$$

(15)

$${\left(O_h^{\left(i\right)}\right)}^T=Attention\left(Q_h^{\left(i\right)},K_h^{\left(i\right)},V_h^{\left(i\right)}\right)=\mathrm{Softmax}\left({\displaystyle \frac{Q_h^{\left(i\right)}{K}_h^{{\left(i\right)}^T}}{\sqrt{d_k}}}\right)V_h^{\left(i\right)}$$

(16)

where d is the time dimension of the patch and each header $h=1,...,H$ in the transformer framework. ${\mathcal{Q}}_h^{\left(i\right)}$ denotes the query matrix, $K_h^{\left(i\right)}$ denotes the keyword matrix, and $V_h^{\left(i\right)}$ denotes the value matrix. $W_h^K,W_h^Q\in {\mathbb{R}}^{D\times d_k},W_h^V\in {\mathbb{R}}^{D\times D}$.

Then, the above temporal coding function is fused into the LSTM network:

$$\begin{array}{cc}\hfill & f=\sigma (W_f{h}_{{\nu }_t,k}^i+U_f(h_{{\nu }_t,k}^{i-1}+\Gamma \left(t\right))),\hfill \\ \hfill & {\mu }_f=\sigma (W_i{h}_{{\nu }_t,k}^i+U_i(h_{{\nu }_t,k}^{i-1}+\Gamma \left(t\right))),\hfill \\ \hfill & {\widehat{h}}_{{\nu }_t,k}^i=tanh(W_t{h}_{{\nu }_t,k}^i+U_t(h_{{\nu }_t,k}^{i-1}+\Gamma \left(t\right))),\hfill \\ \hfill & h_{{\nu }_t,k}^{\prime }=f\odot h_{{\nu }_{t,k}}^{i-1}+{\mu }_f\odot {\widehat{h}}_{{\nu }_t,k}^i\hfill \end{array}$$

(17)

where $W_f,W_i,U_f,U_i,U_t\in R^{{\displaystyle \frac{d}{k}}\times {\displaystyle \frac{d}{k}}}$ are all learnable parameters, $\Gamma (·)$ is a time-encoded function describing the temporal ordering relationship, and $\Gamma \left(t\right)$ denotes the $t\mathrm{th}$ value of the timestamp embedding. The item representation $x_{s,\epsilon }^{\prime }=[h_{{\nu }_t,1}^{\prime },...,h_{{\nu }_t,k}^{\prime },...,h_{{\nu }_t,N}^{\prime }]$ is obtained, where $x_{s,\epsilon }^{\prime }$ denotes the $\epsilon \mathrm{th}$ item embedding representation in the current session s.

We learn the embedded representations of all items in each session through the self-attention mechanism and pooling operations to obtain a fine-grained session representation as follows:

$${\eta }_t=\mathrm{softmax}\left[{\displaystyle \frac{Q_{\eta }{K}_{\eta }^t}{\sqrt{d_k}}}\right]V_{\eta }+x_{s,\epsilon }^{\prime }$$

(18)

where ${\eta }_t$ is the output of the self-attention computation and $x_{s,\epsilon }^{\prime }$ is the input item embedding required to generate the final session embedding. $Q_{\eta }=x_{s,\epsilon }^{\prime }{W}_{\eta }^Q$ is the query matrix, $K_{\eta }^t=x_{s,\epsilon }^{\prime }{W}_{\eta }^K$ is the key matrix, $V_{\eta }=x_{s,\epsilon }^{\prime }{W}_{\eta }^V$ is the value matrix, $W_{\eta }^Q,W_{\eta }^K,W_{\eta }^V$ is the weight matrix, $softmax(·)$ is the activation function.

Eventually, the item embedding within the entire session are subjected to the above score-weighted mean pooling operation $s_l={\displaystyle \frac{1}{m}}{\sum }_{t=1}^m{\eta }_t{x}_{s,\epsilon }^{\prime }$ to obtain an intra-session item transformation pattern representation $s_l=\left[{\tilde{x}}_{s,1},...,{\tilde{x}}_{s,t},...,{\tilde{x}}_{s,n}\right]$, where the factor embedding of each item can be represented as ${\tilde{x}}_{s,t}=[h_{v_t,1}^{"},...,h_{v_t,k}^{"},...,h_{v_t,K}^{"}]$.

3.4. Curriculum Contrastive Representation Learning

3.4.1. Sampling of Curriculum Learning

First, ${\tilde{z}}_l$ (or ${\tilde{z}}_g$) is a negative sample obtained by performing a column transformation on $s_l$ (or $s_g$). The different negative sample embeddings ${\tilde{z}}_l$ (or ${\tilde{z}}_g$) are mapped to the $Score(·)$ function. For the scoring function $Score(·)$, we use similarity $sim(s_l,{\tilde{z}}_l)$ to measure the difficulty of the negative samples, thus obtaining an accurate negative sample ranking for the positive samples, where the similarity $sim(·)$ is calculated using the cosine similarity method, as follows:

$$Score\left({\tilde{z}}_l\right)=sim(s_l,{\tilde{z}}_l)={\displaystyle \frac{\left|s_l·{\sum }_{m=1}^m{\tilde{z}}_l\right|}{\left|s_l\right|·\left|{\sum }_{m=1}^m{\tilde{z}}_l\right|}}$$

(19)

where $s_l$ is the ${\tilde{z}}_l$’s corresponding representation of the positive sampling embedding.

Next, after obtaining the scores of individual negatively sampled embeddings ${\tilde{z}}_l$ throughout the contrastive learning process, the pacing function ${\rm Y}\left(\psi \right)$ is used to sequentially feed negative samples into the training process. The pacing function ${\rm Y}\left(\psi \right)$ specifies the sample size of the negative samples in each step $\psi$. The first step consists of the lowest-scoring negative samples. Step $\psi$ consists of the negative samples with the lowest ${\rm Y}\left(\psi \right)$ scores. The batch of negative samples is sampled uniformly from this set, and $\Delta$ denotes the total number of the above training steps.

$${\rm Y}\left(\psi \right)={\left(\psi /\Delta \right)}^{\iota }·\varpi$$

(20)

where l is a smoothing parameter that controls the speed at which the pacing function guides the training process. $\varpi$ denotes the total number of negative samples. During the contrastive learning process, the negative samples are sorted from the lowest score to the highest score according to the scoring function, thus facilitating the introduction of training, which makes the contrastive framework training converge faster and perform better.

3.4.2. The Loss of Contrastive Learning Framework

Consistent with the literature [2], we utilize the InfoNCE to construct the loss function of the proposed model based on the binary cross-entropy loss between positive and corrupted (negative) samples, defined as:

$$L_{cl}=-log\sigma \left(f_{cl}(s_l,s_g)\right)-log\sigma (1-f_{cl}({\tilde{z}}_l,s_g))$$

(21)

$$f_{cl}(s_l,s_g)=\sigma \left(S_l·S_g^T\right)$$

(22)

where ${\tilde{z}}_l$ (or ${\tilde{z}}_g$) is the negative sample obtained after row and column shuffling based on the corrupted $s_l$ ($s_g$). Meanwhile, we design $f_{cl}\left(\right)$ in Equation (22) as a dot product function between two vectors to better learn the score between two input vectors. The learning objective of the loss function in Equation (21) is to maximize the mutual information between the learned session embeddings in different views and to enhance the maximization of the consistency between the positive samples.

3.5. Prediction and Optimization Based on Fusion Representation of Multi-Task Strategies

3.5.1. Prediction

Consistent with the literature [2], we construct the recommendation task loss function based on the intra-session item transition model. After obtaining the intra-session representation and item representation, a factor-by-factor dot product operation on the target session s and candidate items $x_{s,\epsilon }^{\prime }$ is required to compute the scores ${\widehat{z}}_{s,\epsilon }$ of all candidate items.

$${\widehat{z}}_{s,\epsilon }=\sum _{k=1}^{K}s·x_{s,\epsilon }^{\prime }$$

(23)

$${\widehat{y}}_t=Softmax\left({\widehat{z}}_{s,\epsilon }\right)$$

(24)

where ${\widehat{y}}_{\epsilon }$ denotes the probability of predicting the $\epsilon$th candidate item in the session s.

3.5.2. Optimization

Next, for each session, we use cross-entropy to estimate the loss function for the recommendation task as follows:

$$L_{rec}=-\sum _{\epsilon =1}^n{y}_{\epsilon }log\left({\widehat{y}}_{\epsilon }\right)+(1-y_{\epsilon })log(1-{\widehat{y}}_{\epsilon })$$

(25)

where $y_{\epsilon }$ is the one-hot vector of true value items. Then the recommendation task and the contrastive learning task are combined based on the multitasking strategy, and the final loss function of EGDLTP-CCL is defined as:

$$L_t=L_{rec}+{\lambda }_L{L}_{cl}$$

(26)

where ${\lambda }_L$ is the multitasking policy parameter. The pseudocode for the training process of EGDLTP-CCL model is shown as Algorithm 1.

Algorithm 1 The learning algorithm for the EGDLTP-CCL model

Input: Item data V, session data S.

Output: Recommendation list.

for each epoch do:

for the Inter-session item transition pattern representation learning each epoch do:

Calculate the adjacency matrix by Equations (1)–(3).

Calculate the diffusion rate by Equations (4)–(6).

Perform diffusion map data embedding and updating by Equations (7) and (8).

end

for the intra-session item transition pattern representation learning each epoch do:

Fine-grained item feature representation by Equation (9).

Learning complex transitions between different item embeddings based on a gated graph neural network by Equations (10) and (11).

Capturing time behavior of item transition patterns based on patch-enhanced LSTM network by Equations (12)–(17).

end

for each session do:

Sampling and training based on curriculum learning by Equations (18)–(20).

Calculation of the contrastive learning loss for both inter-session and intra-session representations by Equations (21) and (22).

Predicting the probability of the next item by Equations (23) and (24).

Obtain the next predicted loss by Equation (25).

end

Joint optimization of the overall objective in Equation (26).

end

3.5.3. Time Complexity

The time complexity of graph diffusion mainly comes from graph construction and the diffusion rate. The computational complexity of graph construction is consistent with GCN, which can be optimized to $O\left(n^2\right)$, where n is the number of nodes. The diffusion rate is based on the spatial feature embedding and the attention mechanism, which generates ${\lambda }_{\varpi }$ queries, and the time complexity of the diffusion rate is $O\left({\lambda }_{\varpi }·\tau ·{\zeta }_n^2\right)$, while denotes the dimension of the attention mechanism and ${\zeta }_n$ is the dimension of the feature vector. Then, updating the information between nodes and performing multilayer diffusion, where $\varsigma$ denotes the number of layers of graph diffusion. Therefore, the total time complexity of graph diffusion is $O\left(n^2+{\lambda }_{\varpi }·\varsigma ·\tau ·{\zeta }_n^2\right)$.

4. Experiment

4.1. Datasets

We use three real-world datasets for performance evaluation, as follows:

• The Yoochoose dataset is from the 2015 RecSys Challenge and contains data on user clicks to e-commerce websites.
• The RetailRocket dataset is user activity data recorded by a personalized e-commerce company over a six-month period.
• Tmall dataset containing anonymized behavioral logs of Tmall users over a six-month period, which is published in the IJCAI 2015 competition.
• Diginetica dataset is from the CIKM Cup 2016, containing over 6 months of click-through data about users.

Specifically, for each dataset, we remove sessions with only one item and infrequent users and items that appear less than five times in each dataset. Then, the data from the last week of the dataset are used as the test set, and the rest of the data are used as the training set. Subsequently, if the interval between two consecutive items in a user’s interaction history was less than 6 h, they were placed into a session. On the contrary, if the interval is greater than 6 h, they are put into two different sessions, thus exploiting better segmentation. In addition, we enrich the data by segmenting the sequences and generating the corresponding labels, training dataset, and test dataset for augmentation and labeling. In this regard, we are similar to the literature [36,37] in that we use data augmentation for sequence data. The method generates multiple labeled sequences with corresponding labels, each of which is labeled with the last clicked item in it.

Table 1. Statistical of datasets.

Datasets	# Number of Items	# Number of Hits	# Number of Training Sessions	# Number of Test Sessions	Average Length
Yoochoose	16,766	557,248	369,859	55,898	6.16
Retailrocket	36,968	710,586	433,648	15,132	5.43
Diginetica	43,097	982,961	719,470	60,858	5.12
Tmall	40,728	818,479	351,268	25,898	6.69

shows the statistics of each preprocessed dataset.

4.2. Metric

Two evaluation metrics are chosen for the experiment.

• $p@k$ is the percentage of real items in the top items that generate recommendations, which measures the accuracy of the model’s predictions:

  $$p@k={\displaystyle \frac{n_{hit}}{N_p}}$$

  (27)

  where $N_p$ denotes the number of sessions and $n_{hit}$ is the number of ground-truth items in the generated recommendation list.
• $MRR@k$ (Mean Reciprocal Rank) represents the inverse of the rank of the $top-k$ items in the generated recommendation list, which measures the positional relationship between the items. The larger value indicates that the real items are ranked more important, which also means that the model performs better, as shown below:

  $$MRR@k={\displaystyle \frac{1}{N_p}}\sum _{i=1}^{N_p}{\displaystyle \frac{1}{ran{k}_i}}$$

  (28)

  where $ran{k}_i$ is the sorted position of the ground-truth in the list predicted by the i-th session.

4.3. Experimental Setup

Baselines. We selected seven state-of-the-art session recommendations and compared the proposed model with these methods, which are described below:

• GRU4REC [18] is an RNN-based session recommendation that aims to capture sequential dependency patterns between items in a session.
• NARM [19] is a recommendation model that integrates an attention mechanism on an RNN-based approach to enhance the sequence representation capability of RNN models.
• STAMP [20] is a recommendation model that integrates attention mechanisms in MLP to fuse users’ long and short-term interests.
• SR-GNN [21] is a GNN-based session recommendation method and effectively combines users’ general interests and short-term preferences.
• TAGNN [22] proposed a target-aware attention network to model the dynamic process of user interest with different target items in order to generate recommendations for users.
• DHCN [2] is a hypergraph-based approach to capture higher-order information between items, and it also introduces contrastive learning to integrate information between different sessions.
• Disen-GNN [32] is a session recommendation method for disentangled GNNs, where the aim of disentanglement learning is to model factor-level features of items.
• HIDE [36] introduces hypergraphs into session recommendations that comprehensively capture user preferences from different perspectives.
• MSGAT [37] brings two-channel sparse attention networks into session recommendation to mitigate in-session noise, which models user preferences based on two parallel channels integrating intra- and inter-session information.

Table 2. Comparisons of the performance.

Methods		Tmall			Diginetica			Yoochoose			RetailRocket
		P@20	MRR@20		P@20	MRR@20		P@20	MRR@20		P@20	MRR@20
GRU4REC		10.98	5.92		29.98	8.92		60.64	22.89		44.01	23.67
NARM		23.35	10.68		44.35	15.68		68.32	28.63		50.22	24.59
STAMP		26.44	13.35		45.44	14.32		68.74	29.67		50.96	25.17
SR-GNN		27.65	13.76		50.26	17.26		70.57	30.94		50.32	26.57
TAGNN		29.26	13.56		51.33	17.90		71.02	31.12		52.06	18.22
DHCN		31.51	15.08		53.18	18.44		70.39	29.92		53.66	27.30
Disen-GNN		31.56	15.31		53.79	18.99		71.46	31.36		47.44	29.32
HIDE		37.12	18.69		53.68	18.36		70.33	30.66		51.33	28.89
MSGAT		40.14	23.35		55.68	19.22		71.66	31.46		53.88	29.76
EGDLTP-CCL		43.27	26.10		56.27	19.89		71.78	31.56		55.65	30.12

shows the parameter settings of EGDLTP-CCL in the experiments. For baselines, all parameters are initialized to a Gaussian distribution with 0 and a standard deviation of 0.1. Then the batch size is set to 100, L2 regularization to ${10}^{-5}$, and the Adam optimization algorithm with the initial learning rate of 0.005 is chosen, and the learning rate is set to 0.001. The parameter ${\lambda }_L$ in the multitasking strategy is selected from $\{0.1,0.01,0.001,0.0001\}$.

4.4. Analysis of Experimental Results

4.4.1. Overall Comparison

The experimental results of the full comparison in Table 2 show that the EGDLTP-CCL model achieves superior recommendation performance, and the following conclusions are analyzed and obtained:

GRU4REC uses a gated loop unit to capture sequential information in session sequences and achieves good results. However, the poorer performance of GRU4REC on the Tmall dataset may be due to the inability of gating recurrent units alone to handle the dynamic drift of user preferences. Therefore, it is necessary to provide additional time-signal modeling to strengthen the ability to model user preferences. NRAM performs much better than GRU4REC because it inherits the advantage of GRU4REC in capturing sequential information and integrates an attention mechanism on top of it, which enables the model to distinguish that different items in the session contribute differently to the user’s overall preference. STAMP replaces the RNN structure with an MLP and, at the same time, takes into account the varying importance of the user’s long- and short-term interests, thus achieving more advanced recommendation performance.

All the GNN-based models achieve better performance. Unlike SR-GNN, TA-GNN proposes a target-aware attention mechanism that considers the impact of the predicted target candidate items on all items within the session. Whereas DHCN can outperform TA-GNN and SR-GNN, it further introduces hypergraphs into session recommendation, which not only captures higher-order information between items, but also integrates inter-session information in combination with self-supervised contrastive learning. While Disen-GNN considers multiple blending factors influencing the user’s preferences and comprehensively models the user’s latent intent through the disentanglement technique. HIDE explores more complex transformational relationships using hypergraphs to model higher-order relationships, which ignore the importance of inter-session information. MSGAT employs a two-channel sparse attention network to model intra- and inter-session information that is further integrated for capturing user preferences with effective noise reduction.

EGDLTP-CCL significantly outperforms baselines on all datasets. For the above experimental results, we analyze them from the following aspects:

First, EGDLTP-CCL models session sequences at the global and local levels, respectively. From the perspective of global modeling, we first consider the different effects that exist between different sessions. Then, in the process of learning global-level item representations using an energy-constraint-based graph diffusion technique, the structure of real item transition patterns between global sessions can be modeled more accurately by the newly designed energy-constraint diffusion. On the other hand, for intra-session learning of item transition mode representations, the patch-enhanced gating network designed in this paper can do a good job of capturing the sequential information of the items in a session, which demonstrates the importance of modeling the effect of temporal variations of the items in session recommendation, because the session sequences are inherently tightly correlated with temporal signals. Third, the proposed curriculum learning optimization strategy for session learning can select better negative samples.

Meanwhile, EGDLTP-CCL achieves leading performance on all three datasets, but its performance on the Yoochoose dataset is relatively lower than that on the Tmall and RetailRocket datasets. The possible reason is that both Tmall and RetailRocket datasets are collected in real e-commerce environments, which have higher data consistency compared to the other datasets, suggesting that our model is more adapted to real-world e-commerce environments. For the Diginetica dataset, the data are from the 2016 CIKM Cup, where the data sources have changed. But the length of the sessions in the dataset is similar to the RetailRocket dataset. Thus, the final result of EGDLTP-CCL is also still excellent. It also indicates that the robustness of EGDLTP-CCL is still very good.

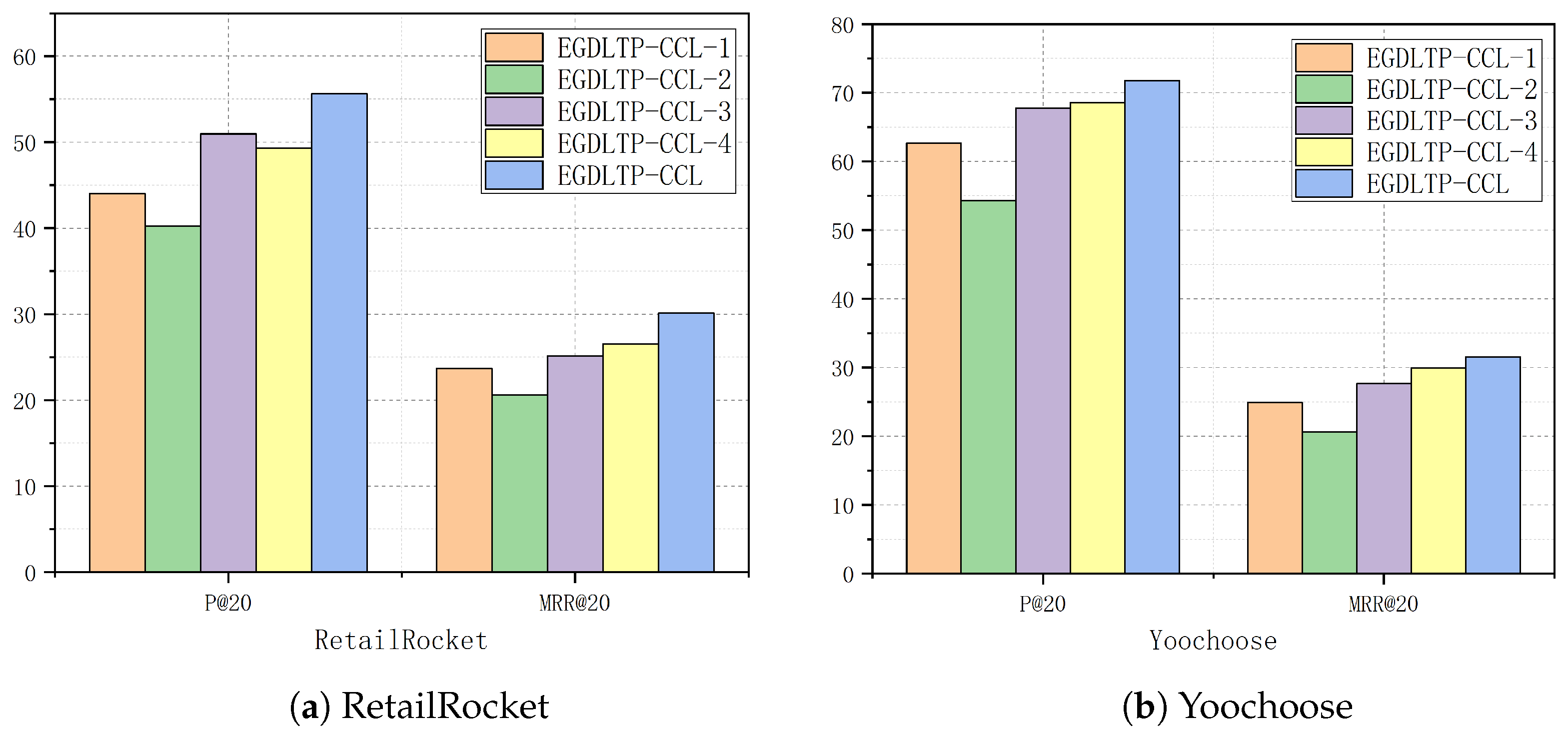
4.4.2. Ablation Analysis

In order to verify the validity of each module of EGDLTP-CCL, we conduct an analysis of ablation experiments, the results are shown in Figure 2. EGDLTP-CCL-1 indicates the removal of the energy-constrained graph diffusion learning module, EGDLTP-CCL-2 indicates the removal of the patch-enhanced gating network module, EGDLTP-CCL-3 indicates the removal of the curriculum contrastive learning task module, EGDLTP-CCL-4 indicates the removal of the curriculum learning strategy of the contrastive learning framework.

The results are shown in Figure 2. The following conclusions are obtained:

1.

EGDLTP-CCL-2 has the worst performance. When the patch-enhanced gated network module is removed, a large amount of important item information is hidden within the session, and contextual temporal information is ignored. Meanwhile, it is shown that accurately obtaining the impact of time-varying correlations in the transition patterns between items within a session is also important for session recommendation performance enhancement.

2.

EGDLTP-CCL-1 ranks fourth among the five models. When the energy-constrained graph diffusion learning module is removed and the intra-session item switching patterns are learned only by patch augmented gated neural networks, it is not able to fit the inter-session item transition patterns adequately, resulting in a degradation of the overall performance of EGDLTP-CCL.

3.

EGDLTP-CCL-3 is the third among the five models, which justifies the fact that the curriculum contrastive learning task integrates the learned intents into the session based on the curriculum learning recommendation model to further improve the performance and robustness.

4.

EGDLTP-CCL-4 is the second among the five models, which shows that the negative sample selection strategy based on curriculum learning can further improve the performance of the contrastive learning task.

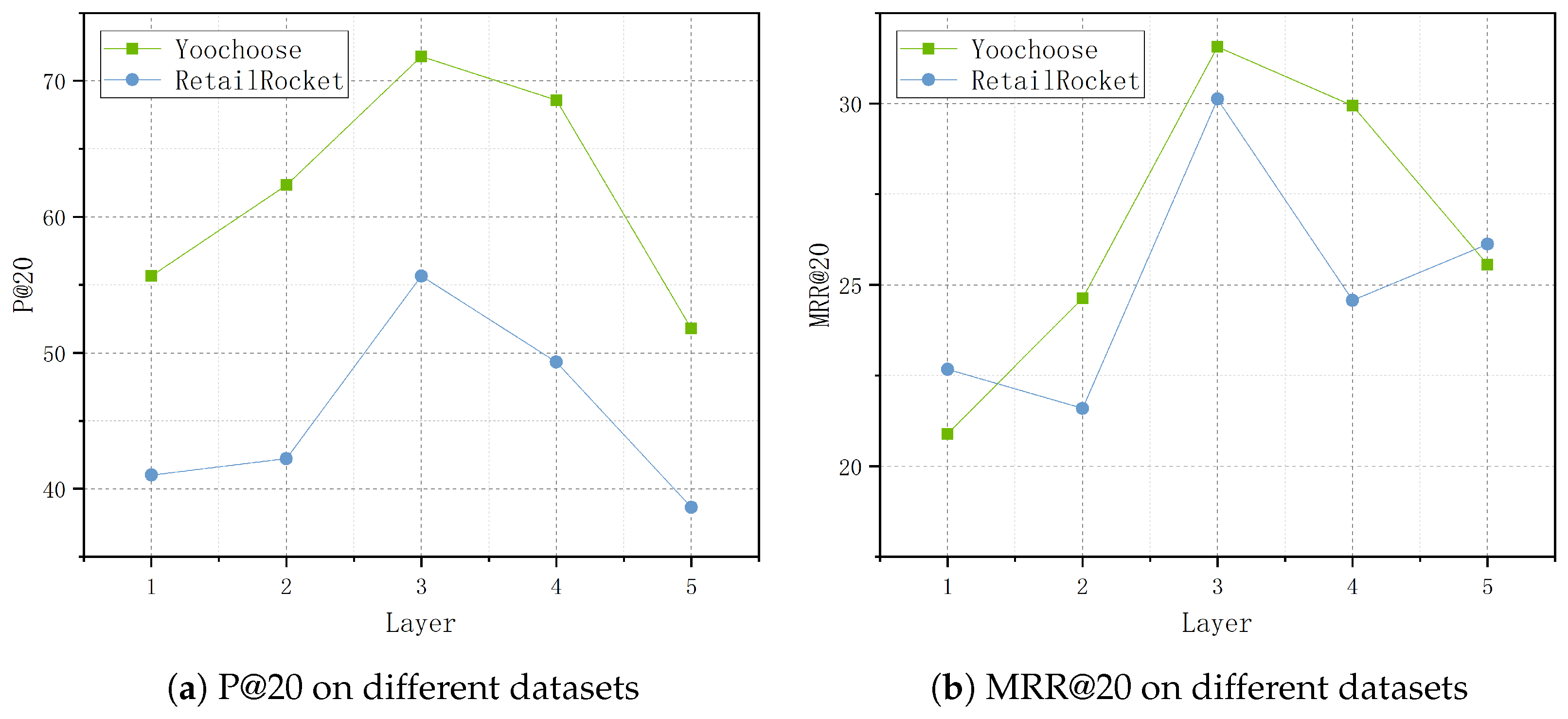
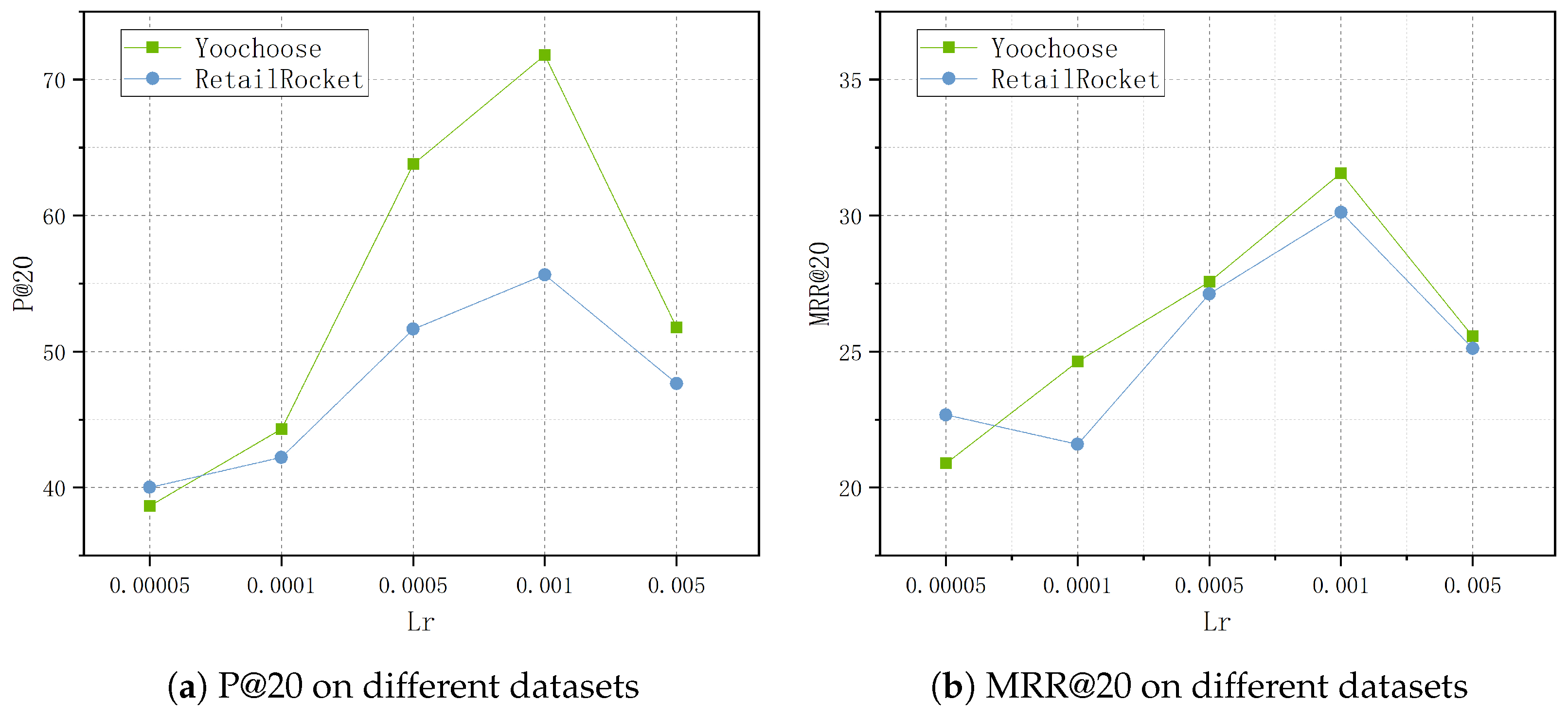
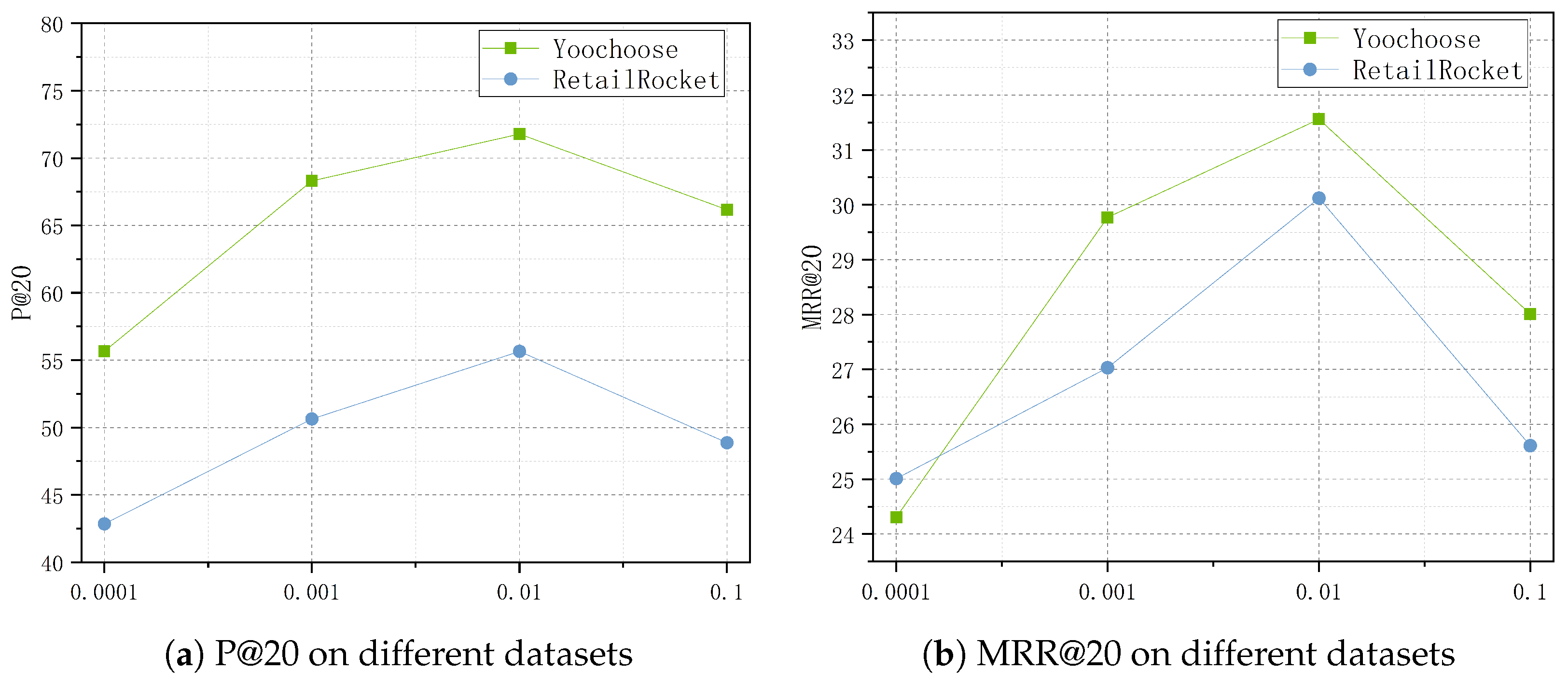
4.4.3. Parameter Sensitivity Analysis

In this section, we evaluate the impact on the performance of EGDLTP-CCL by setting different hyperparameters. Specifically, we explore the different effects that the number of layers of the graph diffusion network in graph diffusion representation learning and the model learning rate on EGDLTP-CCL.

Figure 3 shows the results for different numbers of graph diffusion layers. The Yoochoose dataset and the RetailRocket dataset obtain optimal results when the number of graph diffusion layers is two. This is due to its ability to fully capture the complex relationships of the graph structure. The number of layers in the graph diffusion is important to accurately capture the hidden key information in the item transition pattern.

Figure 4 shows the results for different learning rates. The Yoochoose dataset and RetailRocket dataset have better results when the learning rate is 0.001. The possible reasons for this are: if the learning rate is too large, EGDLTP-CCL will not converge, and if the learning rate is too small, EGDLTP-CCL will converge slowly.

Figure 5 shows the results based on different datasets. Clearly, the impact ${\lambda }_L$ on model performance is obvious. When ${\lambda }_L=0.01$, the model performance reaches its best. A possible reason is the gradient conflict between the contrastive learning task and the recommendation task.

In Figure 6, we show the results of MRR@20 and P@20 based on the Yoochoose dataset and RetailRocket set. The curves in the figure demonstrate that the values of MRR@20 and P@20 stabilize with the gradual change in epoch. The values corresponding to different datasets reaching the stabilized epoch are different, which is also caused by different data characteristics of the two datasets.

5. Conclusions

We propose a new session recommendation model (EGDLTP-CCL) that fuses both inter-session and intra-session representation to learn item transition pattern representations, and then further improves recommendation performance based on curriculum contrastive learning. Specifically, first, an energy-constrained graph diffusion method is utilized to capture inter-session item transition patterns, which improves the diffusion efficiency through the introduction of energy-constrained strategies. Meanwhile, we also develop a patch-enhanced gating network to capture intra-session item transition patterns, which further focuses on the temporal impact of transition patterns between items in a session through a well-designed network of patch transformer strategies. In addition, a curriculum contrastive learning task is designed to maximize the mutual information of item transition pattern representations intra-session and inter-session, and the curriculum learning strategy helps the contrastive learning framework to select more optimal negative samples, which further enhances the performance of the contrastive task. The effectiveness of the EGDLTP-CCL is validated through extensive experiments on three datasets.

EGDLTP-CCL does not take into account the dynamic changes in the diffusion boundary during the graph diffusion process, which limits the range of the model’s receptive field and affects the further improvement of the model’s performance. Meanwhile, for the patch method, EGDLTP-CCL mainly emphasizes capturing the long-term dependencies of long-term time series and pays little attention to the short-term correlations within the patches, which fails to accurately focus on the local semantic representations and affects the further improvement of the model performance. In the future, we consider adaptively changing graph diffusion models that can adapt to the dynamic changes in diffusion boundaries to a greater extent. At the same time, we develop patch-based spatio-temporal models capable of capturing features at different time scales, thus capturing the global and local semantics of the model at a fine-grained level.

The graph diffusion approach indeed has a great potential to be explored in a wider range of application scenarios and complex graph structures. The core advantage of the proposed method lies in its ability to model the “local interaction → global propagation” law, which is highly compatible with the operation mechanism of a large number of complex application scenarios in the real world. For application scenarios, the proposed method has a wide range of applications in the direction of personalized diffusion enhancement in recommender systems, urban computing-transportation network, and resource scheduling, and biomedical-molecular and disease association analysis. For different types of graph-structured data, the proposed method can achieve a breakthrough in combining heterogeneity, dynamics, higher-order relationships, and other complex graph-structured features for hypergraph-based higher-order diffusion models, dynamic graph-based time-aware diffusion models, and multimodal data diffusion.