Horizontal Attack Against EC kP Accelerator Under Laser Illumination

Abstract

Devices employing cryptographic approaches have to be resistant to physical attacks. Side-Channel Analysis (SCA) and Fault Injection (FI) attacks are frequently used to reveal cryptographic keys. In this paper, we present a combined SCA and laser illumination attack against an Elliptic Curve Scalar Multiplication accelerator, while using different equipment for the measurement of its power traces, i.e., we performed the measurements using a current probe from Riscure and a differential probe from Teledyne LeCroy, with an attack success of 70% and 90%, respectively. Our experiments showed that laser illumination increased the power consumption of the chip, especially its static power consumption, but the success of the horizontal power analysis attacks changed insignificantly. After applying 100% of the laser beam output power and illuminating the smallest area of 143 µm², we observed an offset of 17 mV in the measured trace. We assume that using a laser with a high laser beam power, as well as concentrating on measuring and analysing only static current, can significantly improve the attack’s success. The attacks exploiting the Static Current under Laser Illumination (SCuLI attacks) are novel, and their potential has not yet been fully investigated. These attacks can be especially dangerous against cryptographic chips manufactured in downscaling technologies. If such attacks are feasible, appropriate countermeasures have to be proposed in the future.

1. Introduction

Physical attacks pose a great threat to today’s semiconductor devices, in which cryptographic approaches are frequently used to ensure security requirements such as confidentiality, data integrity, service availability, and authentication. The strength of cryptographic approaches is based on the secrecy of the key(s) used, where their lengths depend on the applied algorithm and security requirements. The state-of-the-art approaches provide a proven level of security using keys of recommended lengths, i.e., the algorithms cannot be compromised by cryptanalysis nor brute-force attacks in a reasonable time. The issue is that, in real-world scenarios, the devices are usually physically accessible, thus they can be stolen or attacked in a lab. Side-Channel Analysis (SCA) and Fault Injection (FI) attacks are frequently used to breach the devices’ protection. SCA is based on the analysis of a device’s physical emissions. An analysis of the measured emissions can be performed using either many traces or a single measured trace. The first approach involves vertical attacks while the second employs horizontal attacks [1]. In the past, the analysis of a single trace was performed mostly against asymmetric cryptographic approaches such as RSA [2] or the Elliptic Curve Cryptosystem (ECC) [3,4], often only via the visual observation of differences in the measured trace. Due to the simplicity of this analysis, this approach was denoted as Simple Power Analysis (SPA) or Simple Electromagnetic Analysis (SEMA) [5,6]. Single-trace attacks were often associated with simple analysis. For this reason, in the past, simple SCA attacks were even defined as attacks requiring only a single measured trace for the analysis. But different statistical analysis methods, such as the difference-of-means or correlation analysis, have also been applied for the analysis of a single measured trace [7,8,9,10]. Applying statistical analysis methods contradicts the intuitive understanding of a simple (i.e., visual) analysis of a single trace. Thus, the definition of horizontal attacks as single-trace attacks [1] has clarified the attack classification that will be applied in the rest of this work.

FI attacks aim to manipulate the device’s normal operation by inducing a fault while it is in operation. Faults can be injected by perturbing different environmental and operating parameters using different external sources of perturbation. Attacks using lasers were introduced by Skorobogatov [11]. Although they are expensive due the attack’s preparation phase, they open up the possibility to inject a fault precisely in a selected logic cell(s) during a specified time frame. The minimal laser spot size is limited due to diffraction, so laser-based attacks are frequently performed against chips manufactured in “old” technologies, i.e., technologies with a large node size. For example, in [11], it was feasible to manipulate a single transistor, because the illuminated microcontroller was manufactured with 1.2 μm technology, while the laser beam spot size was 1 μm, i.e., the length of the transistor gate was comparable to the laser beam spot size. In this work, we investigated our own cryptographic accelerator manufactured in our in-house 250 nm technology containing logic and memory cells, whose sensitivity to optical FI attacks were investigated in [12]. For scaled technologies, logic cells are significantly smaller than the smallest diffraction-limited laser beam spot, i.e., a single laser beam illuminates many cells simultaneously. This makes FI into a single selected logic cell more difficult. However, modern chips are more sensitive to laser illumination, i.e., not only transient but also permanent faults can be injected using relatively low laser beam power. Thus, precise single-bit transient faults are expected to be impracticable in the future.

The main focus of optical attacks will be shifted to illumination of security-critical blocks without any fault injections, measuring a power or electromagnetic trace(s) under laser illumination. Such a combination of power analysis and laser illumination attack was described in [13], where a hardware implementation of the symmetric cipher DES was attacked. For the analysis, the current through an FPGA was measured and analysed, i.e., the attack exploited the influence of the laser illumination on the (mostly) dynamic power consumption of the cryptographic chip. Please note that laser illumination influences not only the dynamic power consumption but also the static leakage current of the chip, as shown in the simulations of the AES S-Box in [14]. The static power consumption of the illuminated blocks increased significantly, making their contribution in the measured (static) power trace “more visible”. This can be beneficial for the key extraction process, accelerating the power analysis attack.

In the past, static leakage current has already been successfully exploited as a side-channel to reveal the cryptographic secrets attacking different symmetric cyphers [15,16,17,18,19] and ECC [20]. The static current was measured and analysed, but these attacks were performed without laser illumination.

In this paper, we present a horizontal attack against IHP’s Elliptic Curve Scalar Multiplication accelerator, measuring its dynamic and static power consumption under laser illumination. The attacked chip is a hardware implementation of the kP operation, manufactured using IHP’s 250 nm technology. Power traces of a kP execution are measured with and without laser illumination of a selected area of the chip. In contrast with the usual laser fault injection attacks, a big area of the chip has to be illuminated with a high-power laser beam during the whole execution of a kP operation, precisely measuring the alternating and direct currents through the illuminated chip. In addition, our attack does not require knowledge about the placement of a certain—previously selected—logic or memory cell to be precisely illuminated in space and time. The knowledge of the placement of a security-critical block(s), for example, an S-Box in symmetric ciphers or a controller, bus, or register(s) in ECC hardware designs, is enough. The proposed attacks against asymmetric cryptographic hardware implementations require a powerful laser that is able to work in continuous wave (CW) mode, illuminating a large area, and equipment enabling the precise measurement of the dynamic and/or static power components consumed by the attacked chip. We experiment with two commercially available measurement probes to determine the most suitable one. Our goal is to estimate the impact of laser illumination on the measured traces, as well as on the success of the attack. In real-world scenarios, such attacks can be targeted at critical infrastructure systems, where the costs of implementing the attack are negligible compared to the losses caused in case of a successful attack.

This paper is structured as follows: Section 2 gives a brief introduction on SCA and FI attacks, as well as an overview of works applying laser illumination to improve SCA attacks. Section 3 describes our Elliptic Curve Scalar Multiplication accelerator, our experimental setup, and its configuration and settings. Section 4 discusses the attack results, and Section 5 concludes this work.

2. Combining SCA with Laser Illumination

2.1. SCA and Laser Illumination Attacks

SCA attacks are feasible due to changes in physical parameters while the device performs its operations, e.g. power consumption, electromagnetic emanation, time taken to perform an operation, etc. Analysing measured parameters using, for example, statistical analysis methods can reveal a secret/private key processed during the observed cryptographic operation. To counter SCA attacks many algorithmic approaches are known. Additionally, noise can hide the power consumption of the security-critical block(s). For example, block(s) functioning in parallel to the security-critical block produce noise, making the extraction of the cryptographic key more difficult.

Laser illumination attacks are feasible due to the known interaction between light and semiconductors. Using laser illumination, it is feasible to perform the following:

• to inject a fault in a logic cell via switching one of the illuminated transistors, or
• to increase the power consumption of the illuminated logic cells without switching transistor(s) of the attacked circuit.

Increasing the contribution of the power consumption of a security-critical block via its illumination allows us to increase the success of the key extraction, i.e., attacks can be improved combining SCA and laser illumination without fault injections.

2.2. State-of-the-Art

Attacks exploiting the measurements of a side-channel parameter under laser illumination, without introducing any faults, are rare in the literature. In the past, only a few works have reported SCA attacks with laser illumination. Authors in [13] used a laser beam to increase the power consumption of a circuit by illuminating an SBOX block during the last round of DES implemented in an FPGA. SBOX blocks are the security-critical blocks used in symmetric cryptographic approaches. As a result, the authors were able to perform successful differential power analysis attacks with a reduced number of power traces as well as to recover a sub-key, which was unfeasible without laser illumination. In [13], the dynamic power consumption was measured and analysed. In [21], the author used laser illumination to detect access events in SRAM memory. In [22], the authors used laser illumination to extract data stored in EEPROM. While illuminating the EEPROM sense amplifiers, it was possible to retrieve the program stored in the memory. In [23], the static power consumption of the chip was measured under laser illumination without injecting a fault. According to the results obtained, the laser illumination increased the static power consumption significantly. Moreover, the increased static current is data dependent, i.e., the static power consumption of an illuminated logic cell depends on its inputs. In [24], the vulnerability of specific circuits to laser illumination attacks was simulated at an electrical level using Simulation Program with Integrated Circuit Emphasis (SPICE) models. In [25], the authors simulated the influence of laser illumination on data leakage of a complex circuit, realizing AES rounds using a mechanistic gate-level model. It was shown that laser illumination allowed for the disclosure of processed data. In this work, we focus on the measuring both the dynamic and static power consumption of a hardware accelerator for an asymmetric cryptographic approach illuminating its multiplier block with a laser.

3. Cryptographic Accelerator and Attack Setup

3.1. IHP’s Elliptic Curve Scalar Multiplication Accelerator

The attacked accelerator was manufactured at IHP [26] using its 250 nm technology. It was designed to perform Elliptic Curve (EC) point multiplication with a scalar, i.e., kP operation, where P is a point on an EC and k is a secret binary number, for example, a private key. In this section, we describe the structure of our kP design, focusing on the details necessary to understand the changes in the attack success rate when selected blocks were illuminated during the measurement of a power trace of a kP execution.

The structure of the attacked IHP kP accelerator is shown in Figure 1.

The attacked kP design contains 10 registers, and only two blocks calculating field operations, as follows:

• The field multiplier block (further denoted also as Multiplier) calculates a field product of two different operands (A · B) mod f(t).
• The block denoted as ALU performs a field addition of two operands (A + B) mod f(t) or a field squaring operation A² mod f(t).

The operands A and B are polynomials from the binary extended field GF(2²³³), with the irreducible polynomial f(t) = t²³³ + t⁷⁴ + 1, i.e., the IHP kP design accelerates the Elliptic Curve Point Multiplication for the NIST EC B-233 [27]. In binary extended fields, the addition of polynomials is performed as a bitwise XOR, and the squaring operation can be performed easily as follows:

$$A^2={(a_{n-1}{a}_{n-2}\dots a_2{a}_1{a}_0)}^2 \mathrm{m}\mathrm{o}\mathrm{d} f\left(t\right)=a_{n-1}{ 0 a}_{n-2} 0 \dots {0 a}_2 0 a_1 0 a_0 \mathrm{m}\mathrm{o}\mathrm{d} f\left(t\right)$$

(1)

The product of the two n-bit long polynomials before the reduction step is a (2n − 1)-bit long number. After the reduction, the product is an up to n-bit long number representing a polynomial from the GF(2ⁿ). Of course, the squaring operation can be performed as a field multiplication of two identical operands, but calculations corresponding to (1) are fast (only one clock cycle long) and require much less energy than a multiplication. Due to these reasons, this kind of the calculations was selected for the implementation. The field multiplication of two different polynomials A and B is implemented corresponding to the iterative 4-segment Karatsuba multiplication formula and requires the calculation of nine partial products, one per clock cycle, accumulating the field product step-by-step. Applying the 4-segment Karatsuba multiplication formula, or other multi-segment Karatsuba multiplication methods, reduces the execution time and energy consumption for product calculation and increases the resistance to horizontal collision correlation attacks [10]. The partial multiplier for 59-bit long operands is implemented using the classical or school-book multiplication formula. This results in a relatively big area and higher energy consumption in comparison to other multiplication methods but serves as an additional noise source hiding security-critical processes.

Each field arithmetic block, i.e., ALU and Multiplier, consists of different logic gates and flip-flops (more details about the logic cells of the Multiplier can be found in Appendix B), and contains a functional unit performing the field reduction in each clock cycle if the block is active. This not only increases the energy consumption of the blocks but also serves as noise, increasing the resistance of the kP accelerator to SCA attacks, as the field multiplier is resistant against SCA attacks. The blocks have to exchange their values. Intermediate values are stored in six registers. All field and register operations are managed via a block denoted as the Controller, corresponding to the Montgomery kP algorithm (based on Montgomery’s idea [28]) using projective Lopez–Dahab coordinates [29,30]. The implemented algorithm is described in detail in [31].

Here, it is important to know that all blocks work in parallel to the field multiplier, which is the biggest block of the design, consuming most of the energy. The activity of the field multipliers hides (at least partially) other processes that are also SCA leakage sources. Despite the hiding role of the Multiplier, the design is vulnerable to horizontal address-bit SCA attacks, due to the inherent vulnerability of the Montgomery ladder to these types of attacks and missing algorithmic countermeasures. Please note that well-known countermeasures, such as key randomization, EC point blinding, and the randomization of the projective coordinates of an EC point P, as proposed by Coron [32], as well as many other masking and randomization countermeasures, for example [33,34,35], are not effective against horizontal, i.e., single-trace, address-bit vulnerability. The reason of this vulnerability is the fact that the data storing/reading operations to/from different registers are key-dependent and not equivalent from the SCA point of view, i.e., the assumption that operations with different registers are identical [36] is not true, at least not for hardware implementations of cryptographic algorithms. The address-bit phenomenon for a hardware accelerator of the kP operation was observed and published by [37] in 2002. The address-bit vulnerability, as well as possible countermeasures for cryptographic ASICs, are discussed in [31] in detail.

Since the major goal of our research is to investigate whether illuminating an ASIC under attack improves the attack’s success, we decided to use our own design as the Device Under Test (DUT) due to the following facts: In our earlier works, we analysed simulated power traces and the traces measured on FPGAs and ASICs manufactured using different technologies, as well as versions in which we had applied different synthesis options, environmental, and working parameters [38]. In summary, the attacked kP design is well investigated; its vulnerability to horizontal address-bit SCA attacks and SCA leakage sources are known to us. Knowledge about the placement of the security-critical blocks and the well-understood design vulnerability was decisive. This reduced the effort needed to mount a successful attack. Our cryptographic ASIC was manufactured using IHP’s 250 nm technology. We are aware of the fact that a chip manufactured with a scaled technology, such as an FPGA in 22 nm, it would be likely to achieve better attack results due to the following two reasons: First, its leakage current would be higher than that of a chip manufactured with 250 nm technology. Second, more gates will be illuminated by a laser beam spot of the same size. But in this work, we are not interested in achieving a near-optimal attack result; instead, our goal is to demonstrate the feasibility of our new attack approach.

The field multiplier is a kind of countermeasure, partially hiding the key-dependent power consumption caused by addressing different registers. Thus, we expect that the increased power consumption of the Multiplier block under laser illumination would provide better hiding for the security-critical activity of the block Controller, as well as for the communication of the registers via the Bus.

3.2. Attack Setup

To perform an SCA under laser illumination, the equipment available at IHP was used. The setup is shown schematically in Figure 2.

The applied measurement setup consists of the following: a PC used to communicate with the EC cryptographic accelerator (denoted as the attacked chip in Figure 1); two different commercially available probes connected to V_core—a current probe [39] from Riscure (Riscure BV, Delft, The Netherlands) and a differential probe [40] from Teledyne LeCroy (Teledyne LeCroy GmbH, Heidelberg, Germany)—an oscilloscope [41] used to measure the power consumption during the execution of the kP operation; a stable power supply [42] used to power the EC cryptographic accelerator and to track its power consumption (coarse); a modified laser station from Riscure [43], with a red (808 nm) single-mode Pulse-on-Demand Module from ALPhANOV [44] (ALPhANOV Optical and Laser Technology Center, Talence, France; the Module shipped from Riscure BV, Delft, The Netherlands), connected to the station via optical fibre, further denoted as laser; and a high-precision X-Y stage [45] used to precisely select the area for laser illumination. Details about the laser station and the single-mode laser, as well as the evaluation of its parameters, can be found in [46].

3.3. Setup Configuration and Initial Parameters

In this work, we describe in detail the configuration of the setup, as well as the parameters used to perform the experiments, with the goal of enabling reproducibility of the experiments. The issue of experimental reproducibility was covered in [47].

To perform the attacks, the chip was bonded to a printed circuit board (PCB) without any packaging. The PCB was fixed onto a metal board that was placed onto the X-Y stage. The X-Y stage was controlled using the Riscure Inspector FI (software release 4.12.3). The PCB with the attacked chip, a photo of the chip, and its layout with the illuminated area are shown in Figure 3. The middle area of the Multiplier block was selected for laser illumination.

During our experiments, we tracked the correctness of the calculations performed by the accelerator with and without laser illumination, i.e., if there were no disruptions (no injected faults), while the chip performed the kP operation. The chip operating frequency was set to 4 MHz. The execution time of the kP operation was only a few msec. To start measurements at the correct time, one of the chip’s pins was used as a trigger, since the signal at the pin was in a high logic state during the execution of the kP operation. All oscilloscope measurements in this work were performed with a sampling rate of 5 GS/s resulting in 1250 samples per clock cycle.

Figure 3. EC cryptographic accelerator: (a) PCB with ECC accelerator; (b) photo of attacked chip, zoomed in; (c) placement of design blocks: Multiplier is highlighted (white); (d) PCB with attacked chip placed on X-Y stage for laser experiments. Diameter of laser beam spot is in range of 13 µm to 75 µm; more details can be found in Section 4.2, see Figure 6.

Figure 3. EC cryptographic accelerator: (a) PCB with ECC accelerator; (b) photo of attacked chip, zoomed in; (c) placement of design blocks: Multiplier is highlighted (white); (d) PCB with attacked chip placed on X-Y stage for laser experiments. Diameter of laser beam spot is in range of 13 µm to 75 µm; more details can be found in Section 4.2, see Figure 6.

The kP accelerator was illuminated through the front. No decapsulation of the chip was required. We used a single-mode laser due to the known power distribution (Gaussian) and its ability to operate in a continuous wave (CW) mode. The last prerequisite is important, as the kP operation typically takes ~3.2 ms, and the laser should be able to generate a uniform beam with a constant output power during the operation. The lasers used to perform the optical FI attacks were designed to operate in a pulsed mode, i.e., in a range up to hundreds of µs [48]. The single-mode laser was controlled using the ALPhANOV control software (software release 1.6.8). The laser beam output power was controlled by the current. The control current in the ALPhANOV control software was denoted as the DC or Offset parameter [49] and was expressed in mA. The maximum current per channel is limited to 450.0 mA, which corresponded to 100% of the laser beam power in the CW mode. The laser had two channels (PDM 2+) that each generated a beam. Each channel could be activated separately or simultaneously, combining to form a single laser beam. In our experiments, we used both a single channel and both channels simultaneously. We illuminated the central part of the field multiplier of the kP accelerator, as shown in Figure 3. In all the experiments, we visually ensured that the laser beam centre remained fixed. It was illuminated for ~5 s before we started the execution of the kP operation under laser illumination. In our attacks, we used a long working distance NIR 5× magnification objective [50] from Mitutoyo (Mitutoyo Corporation, Kanagawa, Japan), with the goal of achieving the biggest laser beam spot at focus in the setup. To further increase the illuminated area, in some experiments, we moved away from the focus to a point where the area illuminated by the laser was ~30 times larger than the one in the focus.

4. Performed Attacks and Their Results

4.1. SCA Without Laser Illumination

First, we measured two reference traces, i.e., traces without laser illumination, the first trace using the current probe from Riscure [39] and the second trace using the differential probe from Teledyne LeCroy [40].

4.1.1. Power Trace Analysis

After implementation, designers test the resistance of their cryptographic designs using different statistical and/or machine learning analysis methods. One popular test is, for example, the difference-of-means test, as shown in [51]. The analysis exploits the following basic statistical assumption: if a set consists of two subsets that can be distinguished from each other, the average values of both subsets are significantly different. Designers use their knowledge of the scalar k to separate all slots of the trace into the following two subsets: the slots corresponding to the processing of key bit values ‘0’, and the slots corresponding to the processing of key bit values ‘1’. The mean trace is calculated for each subset, and the significance of their distinguishability is analysed.

Attackers perform the analysis of the trace without knowledge of the scalar k, assuming the following:

• Each slot has its own shape due to the processing of different values during slot execution, i.e., shapes of all the slots are (at least) slightly different.
• The shapes of the slots from the same subset differ less than the shapes of the slots from different subsets, i.e., two ‘0’ slots are more similar to each other than a ‘0’ slot and a ‘1’ slot.

Please note that the attackers’ assumptions, based on a simple (visual) analysis of the trace, are the same as described above, i.e., the attackers attempt to separate the trace into slots and classify each slot into a ‘0’ or ‘1’ subset based on the observable similarities or distinguishabilities. If the differences are fine and cannot be easily seen with the eyes, attackers can use statistical methods. For example, attackers can calculate the mean slot and use it as a kind of threshold, sample-wise, as follows:

$$\mathit{m}\mathit{e}\mathit{a}\mathit{n}=\left\{m^1,\dots ,m^S\right\},\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} m^j={\displaystyle \frac{1}{l}}{\sum }_{i=0}^{l-1}{v}_i^j, \mathrm{f}\mathrm{o}\mathrm{r} \forall j\in \{\mathrm{1,2},\dots ,S\}$$

(2)

where j is the current number of the sample within each slot; l is the number of the slots, i.e., it is the number of key bits processed in the main loop of the implemented kP algorithm; and $v_i^j$ is the value of the sample number j from the slot with number i, whereby i refers to the bit number of the scalar k processed in the main loop of the algorithm.

The i^th bit of the key candidate $k^{candidate\_ j}$ is ‘1’ if, in the slot with number i, the sample value with number j is smaller than the sample value with the same number j in the mean slot. Otherwise, the i^th bit of the j^th key candidate is equal to ‘0’, as follows:

$$k_i^{candidate\_j}=\left\{\begin{array}{c}1, \mathrm{i}\mathrm{f} v_i^j<m^j\\ 0, \mathrm{i}\mathrm{f} v_i^j\ge m^j\end{array}\right.$$

(3)

Thus, each sample of the mean slot results in a key candidate, i.e., assumption (3) allows us to obtain S key candidates. If assumption (3) is not correct, the opposite assumption would be correct. Thus, the attacker obtains additional S key candidates through bitwise inversion of the key candidates obtained by applying assumption (3).

This method was applied in our early works and denoted as comparison to the mean. Using this simple method, we were able to observe the distinguishability caused by the address-bit phenomenon analysing only a single trace. To evaluate the correctness of obtained key candidates, we applied a simple bitwise comparison of each $k_i^{candidate\_ j}$, with the scalar k processed during the kP execution as follows:

$$\begin{array}{c}{\delta }_1^j={\displaystyle \frac{NumberOfCorrectRevealedBits\left(k^{candidate\_j}\right)}{l}}·100\%,\hspace{1em}\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\\ NumberOfCorrectRevealedBits\left(k^{candidat{e}_j}\right)=l-{\displaystyle \sum _{i=0}^{l-1}}\left(k_i^{candidate\_j}\mathrm{X}\mathrm{O}\mathrm{R}{k}_i\right)\end{array}$$

(4)

The result of the comparison of $k^{candidate\_ j}$ with the scalar k corresponding to (4) is the relative correctness ${\delta }_1^j$. This value is the number of the correctly revealed bits in the key candidate divided by the number of all revealed bits. For example, if 200 bits of a key candidate were revealed correctly and 230 bits of the scalar k were processed in the main loop, the correctness ${\delta }_1$ = (200/230)·100% ≈ 87%. Thus, the designer’s knowledge of the scalar k is applied only at this step of the analysis, i.e., the comparison-to-the-mean method reveals an unknown processed scalar that can be used by either the attackers or the designers to evaluate the success of an attack or the resistance of the design, respectively.

The relative correctness ${\delta }_1^j$ is a value between 0% and 100%. If a key candidate $k^{candidate\_ j}$ has a correctness ${\delta }_1^j=100\%$, it means that the key candidate is equal to the scalar k processed in the main loop. A correctness equal to 0% means that all the extracted bits of the key candidate are wrong. This also means that assumption (3), which is used for the extraction of the key candidate, is wrong and the opposite assumption needs to be correct. In this case, we can easily obtain the new key candidates by performing a bitwise inversion of the key candidates obtained. Considering this fact, we can calculate the relative correctness as a value between 50 and 100%, as follows:

$${\delta }^j=50\%+|50\%-{\delta }_1^j|$$

(5)

Thus, (5) takes into account both assumptions used to obtain key candidates, i.e., assumption (3) and its opposite. Please note that an attack resulting in key candidates with a correctness of 50% is the worst-case scenario from an attacker’s point of view. This means that the statistical method used for the analysis cannot even provide a slight hint as to whether the key bit being processed is more likely a ‘1’ or a ‘0’, i.e., this means that the attack is not successful at all. The worst-case scenario from the attacker’s point of view is an ideal case from the designer’s point of view.

To simplify the analysis, each clock cycle can be represented using only one value calculated, for example, as the sum of the squared values of all samples within the clock cycle period. Other compression methods—for example, the sum of raw or absolute values [52], or a sample with the maximum (or minimum) value—can be successfully applied. Please note that compression can significantly influence the attack’s success, and the reasonability or selection of the compression method must be tested in practice. In our case, the sum of the squared values resulted in better attack success and allowed us to reduce the size of the processed trace. After compression, each slot contains S = 54 values only instead of 67,500 samples.

The analysis method described here was automated [31] and applied for key extraction by analysing the traces measured during our laser illumination experiments.

4.1.2. Measurements with the Current Probe from Riscure

We performed the attacks using a Riscure probe since Riscure is a world-renowned company that performs security testing and certification for many companies, as well as provides equipment for SCA and FI attacks; Riscure is now part of Keysight (Keysight Technologies, Santa Rosa, CA, USA) [53]. The trace measured using the Riscure probe is shown in Figure 4a, and the results of its analysis are shown in Figure 4b.

Please note that processing a key bit requires only 54 clock cycles and is always performed using the same operation sequence [31].

According to our analysis, the correctness of the four best key candidates is only 64%, 70%, 68%, and 69% at clock cycles 14, 39, 41, and 44, respectively. For the best key candidate with a correctness of 70%, 30% of the key bits are revealed incorrectly (30% of a 233-bit-long key are 70 key bits). Even if the attackers know the positions of each incorrectly revealed key bit—which is a really strong assumption and, usually, this information is unknown to attackers—approximately ~2⁷⁰ kP operations have to be executed to reveal these 70 key bits, as expressed in the following equation:

2⁷⁰ = (2¹⁰)⁷ = 1024⁷ ≈ (10³)⁷ = 10²¹ kP operations

Even if the duration of a kP is 1 ps using a hypothetical accelerator, which is 3 billion times faster than our accelerator, brute-forcing would require 10²¹ · 10⁻¹² s = 10⁹ s ≈ 32 years.

Such a low correctness of the key candidates indicates that the accelerator is resistant to the horizontal SCA attack performed.

4.1.3. Measurements with the Differential Probe from Teledyne LeCroy

Next, we performed the same attacks as described above but using the differential probe from Teledyne LeCroy to measure the trace. The trace is shown in Figure 5a, and the results of its analysis are shown in Figure 5b.

According to the analysis, the correctness of the best key candidates have the same index numbers of 14, 39, 41, and 44, and are 82%, 90%, 83% and 80%, respectively. Additionally, the correctness of key candidate 53 increased from 53% to 72%. Using the assumption described above, it is necessary to reveal 232 bits · 10% ≈ 23 bits only using the best key candidate (39) with a correctness of 90%. Brute-forcing requires the calculation of 2²³ = (2¹⁰)² · 8 = 1024² · 8 ≈ 10⁷ kP operations. Using our accelerator with a kP duration of about 3 ms, only 10⁷ · 3 ms = 30,000 s ≈ 8 h are required to reveal these 23 key bits. Using the same hypothetical accelerator as above, which is 3 billion times faster than our accelerator, brute-forcing requires only 0.00001 s. These calculations demonstrate that the attacked accelerator is vulnerable to SCA attacks.

Figure 5. Results of SCA attack using the differential probe from Teledyne LeCroy: (a) oscilloscope waveform of measured power trace (60 mV/div, −70 mV offset; 500 µs/div); (b) result of trace analysis representing correctness of 54 key candidates.

Figure 5. Results of SCA attack using the differential probe from Teledyne LeCroy: (a) oscilloscope waveform of measured power trace (60 mV/div, −70 mV offset; 500 µs/div); (b) result of trace analysis representing correctness of 54 key candidates.

Please note that the difference between the attacks is only the measurement probe. The same cryptographic chip was attacked, and all the other components of the measurement setup, as well as the analysis method, were unchanged.

The quality of the trace measured using the LeCroy in comparison to the trace measured using the Riscure current probe differed significantly. The signal-to-noise ratio (SNR) was 1.3 for the trace measured with the Riscure probe (see Figure 4a), and 5.6 with the Teledyne LeCroy probe (see Figure 5a). SNR is calculated as the ratio between peak-to-peak values of signal and noise, i.e., SNR = Vsignal_peak-to-peak/Vnoise_peak-to-peak. The peak values were selected from 1 million samples for the signal and the noise part in the measured data. These experiments clearly demonstrate that the quality of the measured traces significantly influence the security test results, i.e., the success of the attack depends directly on the measurement equipment.

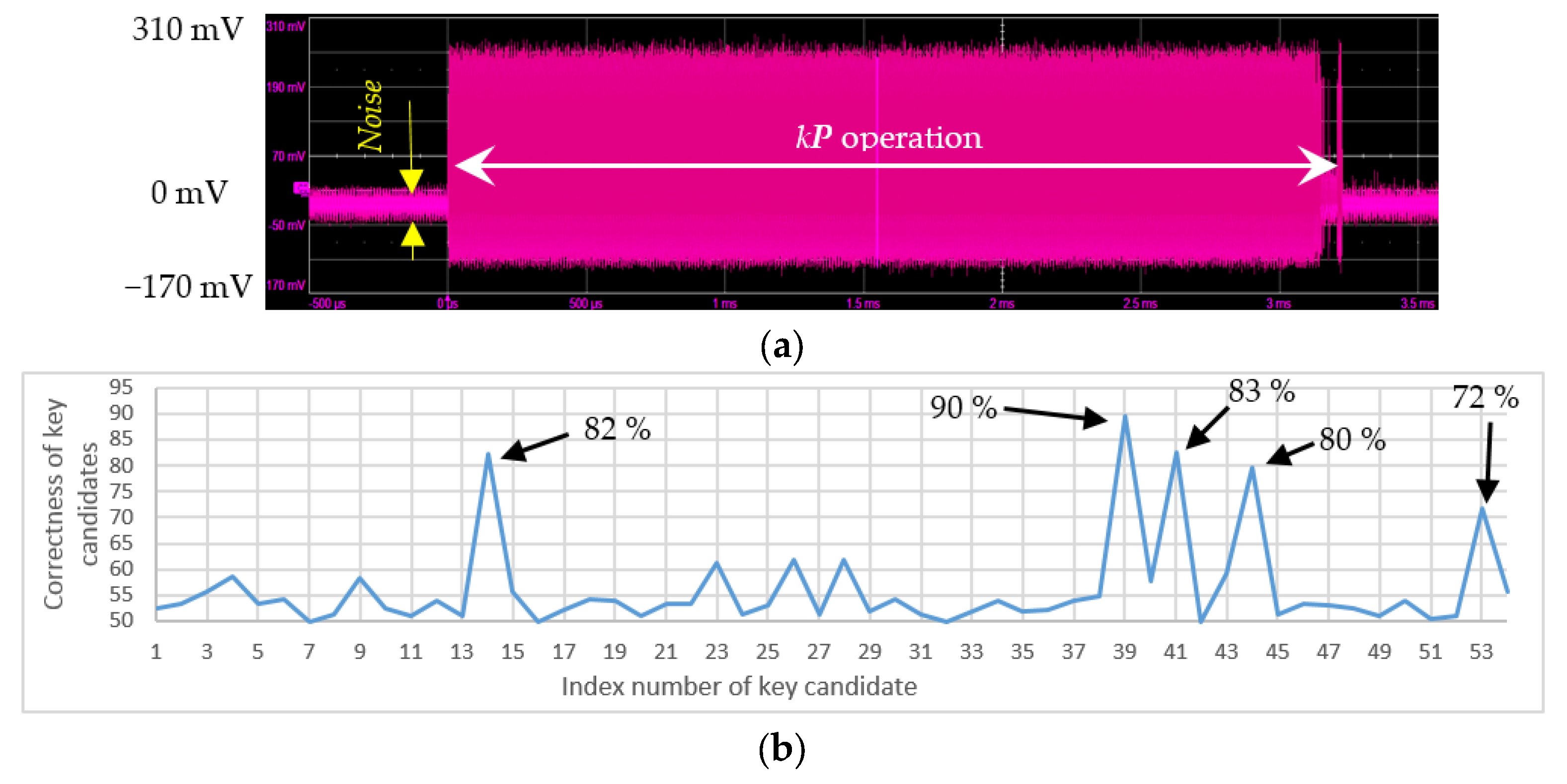
4.2. SCA Under Laser Illumination

We illuminated IHP’s EC cryptographic accelerator with a laser during the kP operation, varying the laser beam parameters. Our goal was to demonstrate the influence of laser illumination on power consumption and to investigate the influence of the illumination on the success of an attack.

The attacked chip had different blocks—field multiplier, field adder, registers, and controller—that managed the sequence of the operations, as well as a multiplexer organizing the data transfer between the blocks. It was expected that illuminating the field multiplier would deteriorate the key extraction because this block was not an SCA leakage source, but rather a source of noise. So, if the power consumption of the Multiplier increased via laser illumination, its contribution to the total power consumption would hide the contribution of the other design blocks. Thus, we expected that by illuminating the Multiplier, the success of the attack would decrease.

All our experiments described in this sub-section were performed with the laser at a fixed position over the chip surface, illuminating an area of the field multiplier. The precise position of the laser beam spots above the Multiplier block is given in Appendix B, see Figure A1. Please note that the chip surface was partially covered with metal fillers, i.e., small metal rectangles that act as obstacles for the laser beam. According to the IHP technological process requirements, the 250 nm technologies have to comply with a predefined metal density, which is defined for each metal layer as the percentage of metal area in a layer to the whole area of the layer. Metal fillers are applied as standard means to reduce layout sensitivity in metal etch and chemical–mechanical polishing process steps during manufacturing. The placement of the metal fillers is a mandatory step of the layout process that is performed automatically using computer-aided design tools. As a result, only a small portion of the laser light can reach the transistor level through the gaps between the metal fillers. All power traces were measured with the differential probe from Teledyne LeCroy due to the better signal/noise ratio compared to the current probe from Riscure, see Section 4.1. Please note that the differential probe measured not only the alternating current but also the direct current, i.e., the measured traces demonstrated the influence of laser illumination on both the dynamic and static power consumption of the attacked chip. In our experiments, we captured a total of 15 power traces—3 without laser illumination and 12 under laser illumination. We experimented with different laser beam powers and spot sizes to evaluate their influence on the shape of the traces and on the success of the attack.

Table 1 shows the settings and parameters applied in our experiments.

Due to the fact that the laser beam power was set via the control current, we provide these values as a part of the settings in our experiments to guarantee the reproducibility of the experiments. We assumed that the relationship between the laser beam power and the control current was linear. The last column of the table shows the success of each attack, represented by the relative correctness of the best key candidates extracted by analysing each of the traces; see Section 4.1. for more details about the analysis and the evaluation of the attack’s success. Attacks were performed by applying two different private keys, k₁ and k₂, and two points on the EC, P₁ and P₂, in the following combinations: k₁P₁, k₂P₁, k₁P₂ (detailed hexadecimal values of k and P are given in Appendix A). In all experiments with the laser, we used the 5× magnification objective. To illuminate a relatively big area, we unfocused the laser beam. We used both channels of the single-mode laser to control the laser beam power; see Section 3.3. for further details on controlling the laser beam power. The traces analysed in Table 1 were measured on the same day.

In the following section, we describe the results in detail. In the initial experiments, we evaluated laser beam spot sizes and the distribution of the energy in the laser beam using a laser beam profiler [54] from Kokyo (Kokyo, Inc.; Kyoto, Japan) to understand what area could be illuminated using our setup, as well as to achieve high reproducibility of the experiments. Figure 6 shows the measured laser beam spots.

The laser beam spot sizes were measured by applying the Full Width at Half Maximum (FWHM) measurement standard, as the laser beam spot sizes, starting from a distance of 2520 ± 12 µm from the focus, were larger than the field of view of the laser beam profiler used, i.e., the laser beam spots could not be (fully) captured by the laser beam profiler.

Table 1. Overview of our experiments.

Performed kP	Nr. of Experiment	Laser Beam Power, %	Control Current, mA	Laser Beam Spot Area (in Comparison to the Chip’s Area *)	Offset **, mV	Correctness of the Best Key Candidate δ, %
k1P1	1	Reference trace (i.e., without laser illumination)			-	91 ***
	2	3	13.5	143 µm2 (0.005% of the chip area)	−0.13 ± 3.92	89
	3	5	22.5		−0.29 ± 4.29	92
	4	20	90.0		−0.36 ± 4.08	89
	5	50	225.0		5.93 ± 4.27	91
	6	100	450.0		17.06 ± 4.60	92
	7	13	60.0	509 µm2 (0.017% of the chip area)	−0.19 ± 4.21	92
	8	59	265.5	2050 µm2 (0.068% of the chip area)	7.49 ± 4.05	90
	9	100	450.0	3004 µm2 (0.1% of the chip area)	16.10 ± 4.32	90
k1P2	10	Reference trace (i.e., without laser illumination)			-	89
	11	5	22.5	143 µm2 (0.005% of the chip area)	0.23 ± 4.51	89
	12	100	450.0	3004 µm2 (0.1% of the chip area)	15.29 ± 4.43	90
k2P1	13	Reference trace (i.e., without laser illumination)			-	90
	14	5	22.5	143 µm2 (0.005% of the chip area)	−0.20 ± 4.62	89
	15	100	450.0	3004 µm2 (0.1% of the chip area)	14.98 ± 4.27	89

* area of EC accelerator is 2,996,127 µm² ≈ 3 mm². ** average offset and standard deviation (±σ) of measured and reference traces: traces were aligned (i.e., synchronised), all samples of traces were processed, including noise parts (25 Mio. samples). *** reference trace shown in Figure 5 and reference trace used to evaluate influence of laser illumination were measured on different days.

Table 1. Overview of our experiments.

Performed kP	Nr. of Experiment	Laser Beam Power, %	Control Current, mA	Laser Beam Spot Area (in Comparison to the Chip’s Area *)	Offset **, mV	Correctness of the Best Key Candidate δ, %
k1P1	1	Reference trace (i.e., without laser illumination)			-	91 ***
	2	3	13.5	143 µm2 (0.005% of the chip area)	−0.13 ± 3.92	89
	3	5	22.5		−0.29 ± 4.29	92
	4	20	90.0		−0.36 ± 4.08	89
	5	50	225.0		5.93 ± 4.27	91
	6	100	450.0		17.06 ± 4.60	92
	7	13	60.0	509 µm2 (0.017% of the chip area)	−0.19 ± 4.21	92
	8	59	265.5	2050 µm2 (0.068% of the chip area)	7.49 ± 4.05	90
	9	100	450.0	3004 µm2 (0.1% of the chip area)	16.10 ± 4.32	90
k1P2	10	Reference trace (i.e., without laser illumination)			-	89
	11	5	22.5	143 µm2 (0.005% of the chip area)	0.23 ± 4.51	89
	12	100	450.0	3004 µm2 (0.1% of the chip area)	15.29 ± 4.43	90
k2P1	13	Reference trace (i.e., without laser illumination)			-	90
	14	5	22.5	143 µm2 (0.005% of the chip area)	−0.20 ± 4.62	89
	15	100	450.0	3004 µm2 (0.1% of the chip area)	14.98 ± 4.27	89

* area of EC accelerator is 2,996,127 µm² ≈ 3 mm². ** average offset and standard deviation (±σ) of measured and reference traces: traces were aligned (i.e., synchronised), all samples of traces were processed, including noise parts (25 Mio. samples). *** reference trace shown in Figure 5 and reference trace used to evaluate influence of laser illumination were measured on different days.

Please note that the laser beam spots measured were not completely circular due to the imperfect quality of the laser beam. Beam quality factor (M²) is a measure of how tightly a laser beam can be focused under certain conditions. M² = 1 is the highest quality for a diffraction-limited Gaussian beam. According to [55], the beam quality of the similar single-mode 1064 nm laser from ALPhANOV is M² = 1.3. Please note that the energy in the laser beam spot was normally distributed (Gaussian distribution). Most of the energy was concentrated in the centre of the spot.

To evaluate the influence of laser beam spot size on the success of the attack, we increased the illuminated area while keeping a similar laser beam output power per unit area (i.e., the same intensity). For example, we set the laser beam power to 5% and laser beam spot of 143 µm² in experiment 3. In experiment 7, we increased both the power and area by about three times. The relationship between the power in experiments 8 and 7 was about four times, and the same applied to the areas.

To compare the traces measured with and without laser illumination, we calculated the difference between the trace measured under laser illumination and the reference trace, as well as the standard deviation (σ). According to these calculations, the influence of the laser was observable in experiments 5, 6, 8, 9, 12, and 15, where the mean offset was greater than σ.

Figure 6. Laser beam spot sizes used in our experiments: (a) spot area A = 143 µm² (distance from focus 0 ± 12 µm, applied in exp.: 2–6, 11, 14); (b) spot area A = 509 µm² (distance from focus 720 ± 12 µm, applied in exp.: 7); (c) spot area A = 2050 µm² (distance from focus 1800 ± 12 µm, applied in exp.: 8); (d) spot area A = 3004 µm² (distance from focus 2520 ± 12 µm, applied in exp.: 9, 12, 15). To measure spot sizes, we set the offset current of the single-mode laser in the control software to 100 mA, see Section 3.3.

Figure 6. Laser beam spot sizes used in our experiments: (a) spot area A = 143 µm² (distance from focus 0 ± 12 µm, applied in exp.: 2–6, 11, 14); (b) spot area A = 509 µm² (distance from focus 720 ± 12 µm, applied in exp.: 7); (c) spot area A = 2050 µm² (distance from focus 1800 ± 12 µm, applied in exp.: 8); (d) spot area A = 3004 µm² (distance from focus 2520 ± 12 µm, applied in exp.: 9, 12, 15). To measure spot sizes, we set the offset current of the single-mode laser in the control software to 100 mA, see Section 3.3.

Figure 7 shows a part of the measured power traces captured during experiments 3, 7, 8, and 9. Increasing the area illuminated by the laser caused an increased offset—the bigger the area, the higher the offset—while applying almost the same laser beam output power per area unit. The highest offset of about 16 mV was observed in experiment 9, illuminating the biggest area, i.e., 3004 µm².

Figure 8 shows the results of an analysis of the measured traces shown in Figure 7.

In order to evaluate the influence of laser beam output power on the success of the attack, we changed the output power while keeping the same area of illumination, i.e., a constant laser beam spot size in focus while using the 5× magnification objective; see experiments 2–6 in Table 1. Figure 9 shows a part of the measured power traces, demonstrating an increasing offset under laser illumination with increasing laser beam power.

Our measurements also show that laser beam power is the parameter that significantly influences the power consumption of the attacked chip; 100% of the laser beam output power illuminating the smallest area (laser beam spot in focus) and the same power illuminating an area 30 times larger caused a similar increase in the power consumption of the illuminated chip, i.e., 17 mV and 16 mV, respectively; see Table 1. Figure 10 shows a part of the measured power traces, demonstrating the offset achieved by applying 100% of the laser beam output power with a 143 µm² spot size (in focus), as well as by applying 100% of the laser beam output power with a 3004 µm² spot size.

This means that an attacker can illuminate either a critical block—or even a small part of it—precisely by trying to amplify the contribution of the selected part of the chip to the total power consumption of the cryptographic chip. In both cases, the power consumption of the attacked chip depends significantly on the laser beam power applied.

The results of our attacks show that laser illumination has an insignificant impact on the success of the attack, within a range of about ±1%, compared to the reference traces. To ensure that these changes were caused by laser illumination and not by measurement tolerance, we analysed three reference traces for k₁P₁. The first one is shown in Figure 5, the second one is from experiment 1—see Table 1—and the last one is an additional measurement. The traces were captured on different days using the same measurement equipment, inputs, etc. The offsets differed within a range of ±1.05 mV compared to the measured trace shown in Figure 5, while the success of the attack was 90 ± 1%, based on the correctness of the best key candidate (index number 39 in Figure 5 and Figure 8). These results differ within a similar range to those observed in our experiments with laser illumination. Hence, we selected the four next best key candidates with indices 14, 39, 41, and 44 for additional comparison; see

Table 2. Overview of Correctness of the Key Candidates.

	Correctness of Selected Key Candidates δ, %
Index nr. of Key Cand.	14	39	41	44
Exp. Nr.
1	85.65	90.87	88.70	86.52
5	84.35	90.87	87.39	90.43
6	78.26	91.74	87.83	83.91
8	81.74	90.43	85.65	85.65
9	81.30	90.00	90.00	83.48
10	81.30	89.13	83.91	75.65
12	76.09	90.43	85.65	74.78
13	80.87	88.70	90.43	77.83
15	85.22	86.96	89.13	83.04

. For the comparison, we only used the traces with an explicitly observable laser influence, i.e., experiments 5, 6, 8, 9, 12 and 15.

In our attacks, we expected that laser illumination would decrease the success of the attack, since we illuminated the field multiplier block, which was not an SCA leakage source, and increasing its power consumption could hide the contributions of other design blocks. The correctness of the majority of the key candidates in experiments 5, 6, 8, and 9 with k₁P₁ decreased; see the cells marked in green in Table 2. In the experiments with k₂P₁ and those with k₁P₂, we observed a decrease as well as an increase in the correctness of key candidates with equal likelihood.

Thus, we did not observe a significant impact of laser illumination on the success of the attacks in our experiments. But it is crucial to note that laser illumination noticeably influences power traces, especially the static component, even when illuminating a very small area of a big cryptographic chip using a relatively low-power laser. We assumed that using a laser in Continuous Wave mode with high laser beam power, combined with focusing solely on measuring and analysing the static current, can significantly improve the attack’s success, based on the fact that the static power consumption of the chip under laser illumination markedly increases [23]. Attacks exploiting the Static Current under Laser Illumination (SCuLI attacks) are novel and have not yet been investigated. The feasibility and potential of SCuLI attacks have to be evaluated. If they are feasible, the appropriate countermeasures have to be researched. We also plan to perform SCuLI attacks against chips manufactured using a smaller technology. Please note that different aspects have to be considered when measuring power traces under laser illumination, e.g., operational parameters such as the temperature of the environment and of the chip (time between measurements for its cooling). In the early stages of the design phase, accurate simulation models of logic and memory cells under laser illumination—applicable for the simulating the behaviour of large cryptographic circuits—enable vulnerability evaluation and can pave the way for the development of appropriate countermeasures. While the behaviour of individual cells can be simulated using TCAD, this approach is not applicable to large illuminated areas containing many different cells operating over an extended execution time. Previous studies by Sarafianos [56,57] modelled the behaviour of individual NMOS and PMOS transistors under infrared laser illumination, taking into account the Gaussian power distribution of the beam, with experiments conducted using their own manufacturing technology. However, there are currently no practical methodologies available for simulating the behaviour of logic or memory cells under laser illumination—particularly when accounting for specific laser types, target technologies, beam intensity distribution, distance to the device, lens characteristics, and so on. It is important to note that theoretical models must be validated experimentally. The development of such models is a complex and time-consuming process that requires suitable measurement equipment. These practical and theoretical aspects need to be investigated in the future.

5. Conclusions

In this work, we performed horizontal SCA attacks against an Elliptic Curve Scalar Multiplication hardware accelerator, measuring its power traces with and without laser illumination of selected blocks of a chip. We experimented with different probes in our measurement setup, namely with the current probe from Riscure, which is a world-renowned company that performs security testing, and with the differential probe from Teledyne Lecroy. Our experiments clearly demonstrated the improved quality of the traces measured with the differential probe. Without laser illumination, the correctness of the best key candidate was 70% when analysing the trace measured using the Riscure probe and 90% when using the differential probe from Teledyne Lecroy. These measurements were taken under the same conditions while processing the same input data. Analysis of the traces measured under laser illumination showed only a small impact of the laser beam spot size and output power on the attack’s success. However, our measurements demonstrated that laser illumination influenced the power consumption of the illuminated chip, especially of the static “component”. The potential of attacks exploiting the Static Current under Laser Illumination (SCuLI attacks) remains unexplored. These attacks can be especially dangerous against cryptographic chips manufactured in scaled technologies. If such attacks are feasible, the appropriate countermeasures have to be investigated in the future.