Abstract
K-means, as a commonly used clustering method, has been widely applied in data analysis for smart meters. However, this method requires repeatedly computing the similarity between all data points and cluster centers in each iteration, which leads to high computational overhead. Moreover, the process of analyzing electricity consumption data by K-means can cause the leakage of users’ privacy, and the current differential privacy technique adopts a uniform privacy budget allocation for data, which reduces the availability of the data. In order to reduce the computational overhead of smart meter data analysis and improve data availability while protecting data privacy, this paper proposes an adaptive differential privacy-based CK-means clustering scheme, named DPCK. Firstly, we propose a CK-means method by improving K-means, which not only reduces the computation between data and centers but also avoids repeated computation by calculating the adjacent cluster center set and stability region for each cluster, thus effectively reducing the computational overhead of data analysis. Secondly, we design an adaptive differential privacy mechanism to add Laplace noise by calculating a different privacy budget for each cluster, which improves data availability while protecting data privacy. Finally, theoretical analysis demonstrates that DPCK provides differential privacy protection. Experimental results show that, compared to baseline methods, DPCK effectively reduces the computational overhead of data analysis and improves data availability by 11.3% while protecting user privacy.
1. Introduction
Smart meters can collect real-time electricity consumption data from users, providing decision support for electric companies in areas such as load forecasting, energy optimization, and demand response [1]. How to efficiently and accurately analyze these electricity consumption data to extract valuable information has become a key challenge [2,3]. Clustering analysis, as a key method in data analysis, can group electricity consumption data based on specific similarity metrics, helping electric companies classify user groups and provide personalized services and energy-saving recommendations [4,5]. Therefore, clustering analysis has become an essential tool for smart meter data analysis.
Among various clustering methods, K-means has been widely applied in smart meter data analysis due to its simple computational principle and easy realization [6,7]. For example, Choksi et al. [8] proposed a feature-based clustering method that integrates K-means with feature selection techniques to analyze smart meter data, aiding electric companies in making decisions more effectively. Rafiq et al. [9] employed K-means to measure the similarity between electricity consumption data and classify users, enabling electric companies to offer differentiated services. However, these methods incur high computational overhead when calculating data similarity. They show that K-means is widely used in smart meter data analysis, but it often incurs significant computational overhead.
Some researchers have reduced the computational overhead of K-means by decreasing computational workloads [10]. For example, Alguliyev et al. [11] introduced a novel parallel batch clustering method based on K-means, which partitions the dataset into blocks for computation, thereby improving computational efficiency. This method still requires calculating the data similarity between all data points and cluster centers in each iteration, leading to significant repeated computations. Nie et al. [12] proposed an optimized K-means algorithm (IK-means), which eliminates the need to compute cluster centers in each iteration and requires only a small number of additional intermediate variables during optimization. This algorithm still does not resolve the issue of repeated computation in K-means. Therefore, reducing both the computational workload and repeated computation is crucial for improving the efficiency of K-means in data analysis.
In addition, the process of analyzing electricity consumption data using K-means can lead to the leakage of users’ privacy, such as lifestyle patterns, electricity consumption habits, and economic status [13,14,15,16]. The exposure of such sensitive information can threaten users’ safety [17,18,19]. To protect user privacy during K-means-based electricity consumption data analysis, many researchers have applied differential privacy by adding noise to the data [20,21]. For example, Gough et al. [22] proposed an optimized differential privacy method that protects electricity consumption data through a random noise sampling technique. Similarly, Zheng et al. [23] introduced a distributed privacy-preserving mechanism for smart grids, which injects Laplace noise in a distributed manner to prevent attacks on electricity consumption data. However, these methods apply a uniform privacy budget allocation for data, resulting in low data availability. Therefore, applying a uniform differential privacy mechanism for electricity consumption data can reduce data availability.
In summary, current research mainly faces two challenges: (1) When analyzing electricity consumption data, K-means requires computing the similarity between all data points and cluster centers in each iteration, leading to a lot of repeated computations and significantly increasing the computational overhead of data analysis. (2) Although differential privacy is used to protect data during K-means-based electricity consumption data analysis, applying a uniform privacy budget allocation reduces data availability.
To address the above issues, this paper proposes an adaptive differential privacy-based CK-means clustering scheme, named DPCK. It adopts the CK-means method to reduce the computational overhead of data analysis and employs an adaptive differential privacy mechanism to enhance data availability while preserving the privacy of smart meter data. The main contributions are as follows:
- We propose a CK-means clustering method by improving the K-means algorithm. This method only computes data similarity between data points and the adjacent cluster center set, effectively reducing the computational workload. In addition, during iterations, data that do not require repeated computation are placed into a stability area, avoiding repeated computation. This method significantly decreases the computational overhead of data analysis.
- We design an adaptive differential privacy mechanism to protect smart meter data. During the CK-means analysis of electricity consumption data, this mechanism calculates an appropriate privacy budget for each cluster based on its distribution and adds Laplace noise. It protects data privacy while enhancing data availability in the clustering process.
- Theoretical analysis demonstrates that DPCK provides differential privacy protection and effectively protects user privacy. Experimental results show that, compared to baseline methods, DPCK effectively reduces the computational overhead of data analysis and improves data availability by 11.3% while preserving data privacy.
The rest of this paper is structured as follows. We review related work on K-means and differential privacy methods in Section 2. After introducing the system model and relevant definitions in Section 3, we provide a detailed introduction and theoretical analysis of the proposed DPCK scheme in Section 4 and Section 5, respectively. We verify its performance in Section 6. Finally, we conclude this paper in Section 7.
2. Related Work
In this section, we briefly introduce related work on the K-means method for data analysis. We divide it into two parts: K-means clustering and differential privacy-based K-means.
2.1. K-Means Clustering
K-means algorithm was first proposed by Mac [24] and has been widely used in data analysis. However, K-means incurs high computational overhead in practical applications. For example, Yue et al. [25] proposed a clustering method based on the segmental slope of the load curve, which improves the efficiency of the K-means method by capturing the shape features of smart metering load curves. This method does not consider the high computational workload caused by K-means. Similarly, Khan et al. [26] proposed an ensemble clustering algorithm that extends the standard fuzzy K-means algorithm by introducing two additional steps into the objective function to improve clustering accuracy. However, these methods increase the computational overhead of clustering.
To reduce the computational overhead of K-means, Hu et al. [27] proposed a K-means clustering method based on Lévy flight trajectories, using Lévy flight to search for new centers, to mitigate the issue of non-uniform distributed cluster centers and enhance clustering efficiency. Based on a nearest-neighbor density matrix, Chen et al. [28] proposed a K-means clustering method, which combines the advantages of both density-based and partition-based clustering algorithms to improve the clustering speed of K-means. Although these methods reduce computational overhead to some extent, they do not consider the extensive repeated computations involved in the K-means iterative process, which directly leads to high computational costs.
In summary, existing K-means methods have the issue of high computational overhead in practical applications. Repeated computation during clustering iterations is a significant factor contributing to this issue. Therefore, reducing the amount of repeated computations during the clustering process is crucial.
2.2. Differential Privacy-Based K-Means
Due to privacy leakage in the K-means data analysis process, many researchers have adopted differential privacy techniques to protect data [29,30]. For example, Gupta et al. [31] proposed a K-means method based on differential privacy, which effectively avoided the risk of privacy leakage by adopting differential privacy to protect data when using K-means for data analysis. Yu et al. [32] proposed a differential privacy K-means clustering scheme, which protects privacy by adding noise to the initial centers based on the density of data distribution. A density-based differential privacy clustering method was proposed by Wu et al. [33]. It uses the Laplace mechanism to inject noise into data during density estimation to preserve users’ privacy. Since these methods introduce excessive noise to protect data privacy, they significantly reduce data availability. To enhance data availability, some researchers have explored improved clustering techniques. For instance, Xiong et al. [34] proposed a clustering mechanism, named PADC, which enhances data availability by refining the distance calculation method between data points and cluster centers. However, these methods employ a uniform differential privacy mechanism, which significantly degrades data availability.
To address this issue, many researchers have applied personalized differential privacy to protect data [35,36]. For example, Balcan et al. [37] proposed a K-means privacy protection algorithm that combines local search techniques and the exponential mechanism, providing personalized privacy protection for individual users by generating locally learned prototypes. Through adaptive clipping, weight compression, and parameter reorganization techniques, He et al. [38] proposed a localized differential privacy clustering scheme, which achieves personalized privacy protection during the clustering process. Although personalized differential privacy enhances data availability, its high computational overhead makes it impractical for relatively larger datasets, such as smart meter data.
In summary, existing differential privacy-based K-means clustering methods protect data privacy using a uniform privacy budget allocation, which reduces data availability. Personalized differential privacy methods suffer from high computational overhead, limiting their practicality. Therefore, improving data availability and controlling computational overhead while preserving data privacy is a key challenge in current privacy-preserving clustering methods. In order to clearly compare the characteristics of different methods, we summarize the methods mentioned in related work and DPCK from the three dimensions of computational overhead, privacy protection, and data availability, as shown in Table 1.

Table 1.
Comparison of representative methods in terms of computational overhead, privacy mechanisms, and data utility.
3. System Model and Related Definitions
This section introduces the system model and some definitions relevant to the DPCK scheme.
3.1. System Model
The system model of DPCK is shown in Figure 1. The model consists of three main entities: smart meters, a data clusterer, and control centers, which are described as follows:
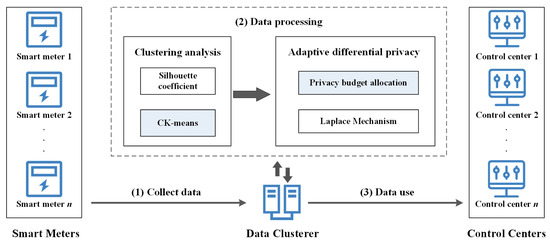
Figure 1.
System model of DPCK.
- Smart Meters: Responsible for collecting users’ electricity consumption data and transmitting them to the data clusterer.
- Data Clusterer: Responsible for performing clustering analysis on the collected electricity consumption data, applying adaptive differential privacy to protect the data, and finally sending the noise-added clustering results to the control centers.
- Control Centers: Responsible for analyzing the received clustering results statistically and classifying users based on these data, facilitating operations such as service provision by the electric company.
In this paper, smart meters transmit users’ electricity consumption data to the electric company’s control centers periodically or in real-time. The data clusterer collects the electricity consumption data transmitted from the smart meters, performs clustering analysis and privacy protection, and then sends the noise-added clustering results to the control centers. The control centers can use the clustering results for billing, optimizing power services, and other value-added services, enhancing the intelligence level of smart meter applications in urban settings.
3.2. Definitions
3.2.1. K-Means Clustering
The basic idea of K-means is to partition a dataset into clusters based on the similarity between data points, where the similarity in this paper is measured using Euclidean distance. It is a commonly used measure for evaluating the similarity between data points, where similarity is inversely proportional to the distance between data objects. In other words, the smaller the distance is, the higher the similarity is. The formula for calculating the Euclidean distance is as follows:
where x and y are two data points in an n-dimensional space.
K-means randomly selects k center points from the dataset. First, it calculates the Euclidean distance between each data point and the k center points, assigning each data point to the cluster of its nearest center. Then, the algorithm recalculates the center of each cluster by taking the mean of all data points within the cluster as the new center. K-means repeats these two steps until the data points in each cluster remain stable.
3.2.2. Differential Privacy
Definition 1
(Differential Privacy). For any algorithm M, let be the set of all possible outputs of M. If for any pair of adjacent datasets D and , and for any subset of , M satisfies the Equation (2), then it is shown that M provides differential privacy:
The parameter ε is the privacy budget, and the smaller its value is, the stronger the privacy protection is and the lower the data availability is.
Definition 2
(Laplace Mechanism). Let be a query function, where D is the dataset. is protected for data privacy using the Laplace mechanism, and the perturbed result is obtained as follows:
where is random noise following the Laplace distribution with the scale parameter , and is the sensitivity of the query function , representing the maximum possible change in output between adjacent datasets. ε is the privacy budget parameter that controls the strength of the privacy protection. Compared with other noise-adding mechanisms of differential privacy (such as geometric mechanisms), the Laplace mechanism does not require a complex probabilistic selection process and is more suitable for scenarios in this scheme that require frequent updates of cluster centers and privacy budgets, thereby effectively reducing computational overhead and improving data availability while ensuring privacy.
4. Our Proposed DPCK Scheme
We will detail the proposed DPCK scheme in this section, which consists of the following three steps: initialization, CK-means, and adaptive differential privacy. The architecture of DPCK is shown in Figure 2, and the descriptions of the notations used in this paper are shown in Table 2.
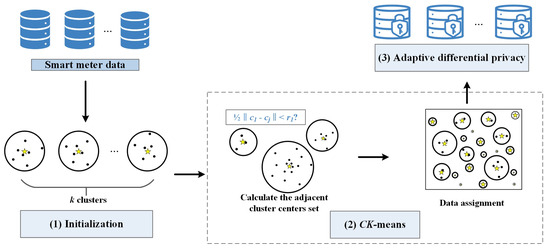
Figure 2.
Architecture of DPCK.

Table 2.
A description of the notations.
4.1. Initialization
We use Max-Min normalization [39] to standardize the electricity consumption data. It is a linear normalization that linearly maps the original data to the range ; the dataset x is normalized to obtain as follows:
The core idea of the silhouette coefficient method [40] is to calculate the silhouette coefficient for all clusters and identify the peak as the optimal number of clusters k. The silhouette coefficient is as follows:
where is the average distance between the data point x and all other points within the same cluster. And is the minimum average distance from the data point x to all points in any other cluster.
We determine the optimal number of clusters k by comparing the average silhouette coefficients under different k values and selecting the k corresponding to the highest coefficient. For the query cluster, when the data points within the cluster do not move and no new data points are added, we mark the flag of the query cluster as TRUE. Conversely, it is marked as FALSE.
4.2. CK-Means Clustering
After completing the initialization, and if the is FALSE, DPCK reduces the computational workload during cluster analysis by the CK-means algorithm. A circle is the set of all points consisting of a fixed point as the center of mass and a fixed distance as the radius. The CK-means algorithm uses this structure to improve the traditional K-means algorithm, where circles are used to describe clusters. The specific definition of a circular cluster is as follows.
Definition 3
(Circular Cluster). A cluster C with the center c and the radius r is defined as a circular cluster, where x represents a data point in the cluster. The center c and radius r are defined as
where is the amount of data in the cluster C. Furthermore, we propose the concept of adjacent clusters to reduce the computation between clusters that are far away from each other. The definition of adjacent clusters is as follows.
Definition 4
(Adjacent Cluster). Let represent the center of the query cluster and stand for the center of . If satisfies Equation (8), then is the adjacent cluster of the queried cluster .
We will introduce the CK-means algorithm in detail, which consists of two steps: calculating the adjacent cluster center set and data assignment.
4.2.1. Calculating the Adjacent Cluster Centers Set
DPCK calculates the movement of the center point of the cluster between the t-th and -th iterations and the distance between and its adjacent cluster center in the t-th iteration. and are defined as
Subsequently, the adjacent cluster of the query cluster is identified using Equation (8), and its center is added to the adjacent center set of . As illustrated in Figure 3, if half the distance between and is less than the radius , then is considered an adjacent cluster of . In contrast, if half the distance between and another cluster, C, exceeds , then C is not regarded as adjacent.
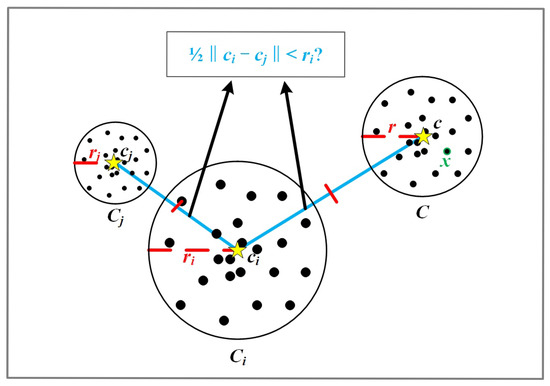
Figure 3.
Comparison of the distance between the centers of the query cluster and other clusters with the radius of the query cluster.
When computing distances between data points in the query cluster and other cluster centers, only the centers in the adjacent set are considered. This adjacency-based filtering helps eliminate unnecessary comparisons with distant clusters, significantly reducing the overall computational burden during clustering. The adjacent center set is initialized as , and all cluster centers satisfying the distance condition are added to it.
When performing distance calculations, it is only necessary to compute the distance between each cluster’s data points and adjacent cluster centers. Therefore, this step reduces the computational workload of clustering analysis, and it is detailed in Algorithm 1.
| Algorithm 1 Calculating the adjacent cluster center set. |
Input: Dataset X, k, initial centers c. Output: , . 1: for to k do 2: if then 3: Calculate the movement of the center of cluster ; 4: Calculate the radius ; 5: end if 6: end for 7: if
then 8: Calculate the distance ; 9: else 10: for to k do 11: for to k do 12: if then 13: ; 14: end if 15: end for 16: end for 17: end if 18: for
do 19: if then 20: Append to ; 21: end if 22: end for 23: return , . |
4.2.2. Data Assignment
After calculating the adjacent cluster center set, we assign data by dividing each cluster into stability areas and circular areas. Specifically, DPCK calculates the distance between data points of circular areas and the adjacent centers and assigns the data points to the closer clusters.
Let be the query cluster and be the set of centers of adjacent clusters of . If is the center of and , then the stability area of is defined as a area with the clustering center and radius . The rest of the area is the moving area. The points within the stability area do not participate in data assignment, meaning that they are excluded from distance calculations and do not move. Let ; if , then has no adjacent cluster, and the data points in the cluster of do not need to be involved in the calculation.
Then, DPCK divides the moving area of C into i circular areas. Let C be a query cluster with c and r, and let be the set of centers of clusters adjacent to C, where and . Let and be the center of the i-th and -th nearest adjacent clusters of C. The i-th circular area of cluster C is
Figure 4 shows the stability area and the circular areas of the cluster C. From Equation (11) and Figure 4, it can be seen that data points in the i-th circular area of C are closer to the center c than to the center of the -th nearest cluster. Therefore, they can only be assigned within the query cluster C and its i nearest adjacent clusters.
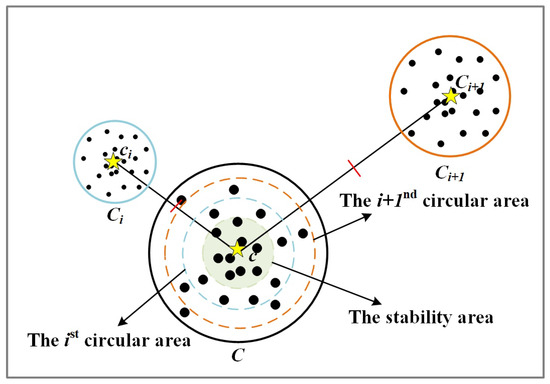
Figure 4.
The stability area and the circular area of the query cluster C.
For data points in the circular area, the distances to the centers in the adjacent center set are calculated, and these data points are assigned to the nearest cluster, completing the data assignment. This process is detailed in Algorithm 2.
| Algorithm 2 Data assignment. |
Input: Dataset X, k, , . Output: The set of centers c, the set of clusters C. 1: for to k do 2: if and and then 3: continue 4: else 5: Sort by distance in ascending order; 6: for each x in do 7: if then 8: continue 9: else 10: if x in the i-th circular area then 11: Compute the distance from x to its first i closest centers; 12: Assign x to the nearest cluster; 13: end if 14: end if 15: end for 16: end if 17: end for 18: for to k do 19: if is stable then 20: = TRUE 21: else 22: = FALSE 23: end if 24: end for 25: ; 26: return c, C. |
4.3. Adaptive Differential Privacy
After the current iteration of CK-means, DPCK assigns an appropriate privacy budget to each cluster and adds Laplace noise to achieve adaptive differential privacy protection. In the context of smart meter data, potential privacy threats include membership inference, where an adversary attempts to determine whether a specific user’s data were used in the dataset, and linkage attacks, where external information is used to associate anonymous records with individuals. Our adaptive differential privacy mechanism is designed to mitigate such risks by ensuring that the inclusion or exclusion of any individual user data does not significantly affect the output, thereby preserving plausible deniability and robustness against these inference-based threats. The within-cluster variance for the cluster , represented as the sum of the Euclidean distances between data points in and the center , is defined as
The between-cluster variance for the cluster , represented as the Euclidean distance between the center and the mean of the k centers, is defined as
where is the mean center of all clusters. The clustering effectiveness of the cluster , denoted as , is defined as
A higher value in the current iteration indicates the tighter clustering of data points within the cluster and greater separation from other clusters, implying better clustering performance. However, it should be noted that the definition of implicitly assumes that the cluster structure remains relatively stable over time. In practice, household energy consumption behaviors may vary significantly due to seasonal, behavioral, or external factors. This temporal variability may lead to a lag between the metric and the actual clustering effectiveness. To address this limitation, a practical solution is to re-evaluate cluster stability and recompute at regular intervals or upon detecting significant changes in consumption patterns.
DPCK evaluates clustering performance using the value and calculates appropriate privacy budgets for each cluster:
A lower implies poorer clustering quality or greater instability in cluster structure, suggesting a higher risk of distortion under noise. To compensate, DPCK allocates a larger privacy budget, , to such clusters to improve utility.
Based on clustering performance, we calculate the privacy budget and inject Laplace noise, , into each cluster to achieve adaptive differential privacy protection. This noise perturbs the data points’ values and affects their distribution, requiring the recalculation of the cluster centers. To ensure numerical stability, especially when the denominator becomes very small due to noise, we introduce a safeguard by setting a lower bound, . The updated cluster center is computed as
where is the sensitivity of the query function, and is a small positive constant to prevent instability without compromising privacy guarantees.
After computing the noisy cluster centers, we compare them with those from the previous iteration. If the centers remain consistent, DPCK terminates and outputs the final clustering results. Otherwise, the procedure in Section 4.2 and Section 4.3 is repeated until convergence.
5. Theoretical Analysis
In this section, we analyze the time complexity of DPCK and prove that it provides differential privacy protection for electricity consumption data through privacy analysis.
5.1. Complexity Analysis
Let N and k represent the number of data points in the dataset and the number of clusters, respectively. The time complexity of DPCK mainly consists of three parts: initialization, calculation of the adjacent cluster centers set, and data assignment.
(1) In the initialization phase, the silhouette method is used to calculate the optimal number of clusters k, and it costs .
(2) To search for the adjacent clusters of the query cluster, the distances between the query cluster center and the centers of the other clusters need to be calculated in the worst case, which costs . In Algorithm 2, the quicksort algorithm is used to sort the adjacent cluster center set in ascending order based on the distance to the query cluster center (line 5). The time complexity of this process is . In the worst case, multiplying this by all k centers gives a time complexity of . Since the adjacent clusters of the query cluster have a specific stability between successive iterations, and for many sorting algorithms, the existence of some pre-existing order in the set to be sorted can reduce the cost. Therefore, the time complexity of sorting the m distances from the center of the cluster C to the center of its m adjacent clusters is generally less than .
(3) Let and represent the number of data points in the moving area and the average number of adjacent clusters of the query cluster, respectively. The data points in the stability area remain unchanged in the current iteration and do not participate in the calculations. Therefore, during the clustering process, it is only necessary to calculate the distances from all data points in the moving area to the adjacent cluster centers, which costs . In addition, the distances from all data points in all clusters to their respective cluster centers must be calculated, which costs .
Overall, considering the worst-case scenario and all other evident loops in the algorithm, the total time complexity per iteration of DPCK is . However, an increasing number of spherical clusters become stable in the practical application, and the data points within these stable spherical clusters are not be included in any distance calculations. Consequently, in subsequent iterations, the time complexity per iteration decreases to a sublinear level.
5.2. Privacy Analysis
The DPCK scheme ensures -differential privacy for the clustering results by adding appropriate noise, satisfying the Laplace distribution of the centers during the clustering process. Let and be adjacent datasets, and let and represent the outputs of executing DPCK on these datasets, respectively. Let S denote any possible output set. If DPCK satisfies -differential privacy, then the following holds:
Assume that the query function f returns and as the true query results for the adjacent datasets and . Let denote a specific output result. According to the probability formula of the Laplace distribution, we have
Similarly, we can obtain
According to the above equations, we have
We can also have
According to the above formula, we can obtain
Therefore, DPCK can provide -differential privacy protection for data. In real-world scenarios, it is impossible to access users’ sensitive information.
6. Experiments
In this section, we will detail how we verified the performance of DPCK by conducting experiments with other comparative methods.
6.1. Exprimental Settings
All experiments were conducted using Microsoft Windows 11 using the Python 3.9 programming language. The hardware environment used was AMD Ryzen 7 5800HS Creator Edition 3.20 GHz CPU, 16GB RAM.
The datasets used in experiments include data with different dimensions, sample sizes, and categories. They were sourced from the UCI Machine Learning Repository [41]. The specific descriptions are as follows:
- Iris: This dataset includes three classes, with 50 instances per class, totaling 150 instances, and four attributes. Each class represents a type of iris plant. Notably, the 35th sample needs to be manually modified to 4.9, 3.1, 1.5, 0.2, ‘Iris-setosa’; the 38th sample needs to be manually modified to 4.9, 3.6, 1.4, 0.1, ‘Iris-setosa’.
- Wine: This dataset includes 178 instances, divided into three classes, each containing 13 attribute, with no missing values.
- Electrical Grid data: This dataset includes 10,000 instances, 12 attributes, and no missing values. It is a simulated dataset designed for studying the stability of electrical grid systems.
- Gamma: This dataset includes 19,020 instances, 10 attributes, and no missing values.
- Eco dataset: The Eco dataset provides total electricity consumption data at 1 Hz, collected as part of the smart meter service project at ETH Zurich [42]. Each file contains 86,400 rows (i.e., one row per second), with rows with missing measurements represented by “−1”.
6.2. Evaluation Criteria Metrics
In this section, we introduce the indicators for evaluating the experiments: the F-measure, objective function value, and silhouette coefficient.
We used the F-measure to evaluate data availability, which is the harmonic mean of Precision (Pre) and Recall (Re). Pre refers to the proportion of correctly classified instances among all instances classified as a certain category. Re refers to the proportion of correctly classified instances among all instances that actually belong to that category. The F-measure is the weighted harmonic mean of Pre and Re, and the formula is as follows:
where is the balance coefficient for Pre and Re, which we set to 1 by default. A higher F-measure value indicates that the noise has less impact on the results, the availability of the data is higher, and the experimental outcome is better.
We analyzed the convergence of the DPCK scheme by comparing the objective function values of DPCK and other algorithms with different numbers of iterations. The objective of the K-means clustering algorithm is to minimize the Sum of Squared Errors (SSE) between each data point and the center of its assigned cluster. The SSE is used as the objective function value and is
where is the set of k cluster centers, and represents the center of the i-th cluster . The smaller the objective function value is, the smaller the convergence value of the scheme is. If the initial convergence value of the scheme is closer to the final convergence value, it means that the convergence of the scheme is better, which means that the clustering performance of the scheme is better.
We used the silhouette coefficient to evaluate the clustering performance of the DPCK scheme under different privacy budgets. The silhouette coefficient was adopted to evaluate the performance of clustering results without relying on ground truth labels. It reflected both the cohesion within clusters and the separation between different clusters. For a given data point, its silhouette coefficient was calculated as follows: Let denote the average distance between the point and all other points in the same cluster (intra-cluster distance) and denote the minimum average distance from the point to all points in the nearest neighboring cluster (inter-cluster distance). The silhouette coefficient of the point is then
The overall silhouette coefficient was obtained by averaging the values of all data points. A higher silhouette coefficient indicates that data points are more tightly grouped within their clusters and well separated from other clusters, implying better clustering performance.
6.3. Discussion of Experiments
We conducted experiments on computational overhead, convergence, and data availability and discuss the results. To ensure statistical reliability, each experiment was independently repeated 20 times under the same conditions. The results represent the mean values across these 20 runs.
6.3.1. Computational Overhead
In this subsection, we will analyze the computational overhead of the DPCK scheme during clustering analysis by comparing the running times for different methods. The comparison methods include the K-means++ algorithm [43], the IK-means algorithm proposed by Nie et al. [12], and the PADC mechanism proposed by Xiong et al. [34]. Specifically, the K-means++ algorithm improves upon standard K-means by introducing a probabilistic initialization method that selects distant points as initial centers with higher probability, thereby reducing sensitivity to initialization and improving convergence speed. IK-means does not require computing the cluster centers in each iteration and needs only a few additional intermediate variables during the optimization process, demonstrating both effectiveness and efficiency. The PADC mechanism improves the selection of initial centers and the distance calculation from other points to the centers. In the experimental analysis of this section, we removed the adaptive differential privacy module and only retained the CK-means method in DPCK for comparison with other methods.
Figure 5 shows the running time of methods under different values of k. The running time of the DPCK scheme was significantly lower than that of other methods, and its increase in running time was minimal as k grew, where the advantages of DPCK became more evident on relatively larger datasets. To further clarify the computational overhead of the DPCK scheme, we roughly divided its overall running time into two parts: the CK-means and the adaptive differential privacy. Empirically, we observed that CK-means accounted for approximately 75–85% of the overall running time, while the adaptive differential privacy constituted the remaining 15–25%. The main reason is that the DPCK scheme reduced the computation workload by calculating the adjacent clusters. It also avoided repeated computation by assigning the data points that did not need to be involved in the calculation into the stability region. These factors enabled DPCK to incur lower computational overhead compared to other methods.
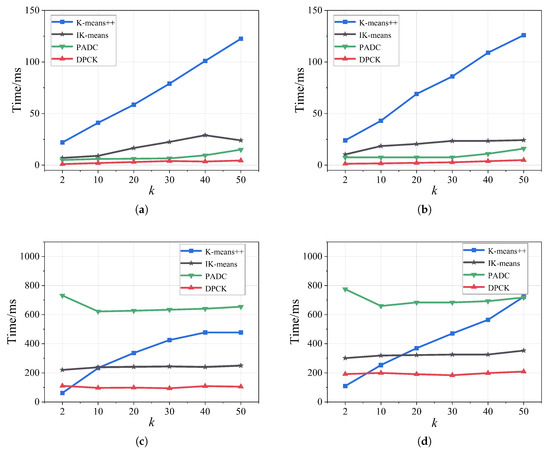
Figure 5.
Comparison of the running time under different k. (a) Iris. (b) Wine. (c) Electrical Grid data. (d) Gamma.
Therefore, compared to other methods, DPCK effectively reduced the computational overhead during clustering analysis, with its advantages becoming more pronounced as the number of clusters increased.
6.3.2. Convergence
In this subsection, we will analyze the convergence of the DPCK scheme by the calculated objective function values in different iterations for the IK-means algorithm, Lloyd’s K-means algorithm, and the K-means++ algorithm.
Figure 6 demonstrates the objective function values of methods in different iterations. The results of Figure 6a,b show that the convergence values of methods had small differences. The main reason is that the small-scale dataset involved fewer distance calculations, so the differences between the methods were subtle. However, the results of Figure 6c,d show that the initial convergence value of DPCK was significantly smaller than that of the other methods, and its convergence curve was more stable in relatively larger datasets. This is because our method no longer needed to compute the distance between all data points and the center points in subsequent iterations, which significantly improved the convergence speed and ensured more stable convergence.
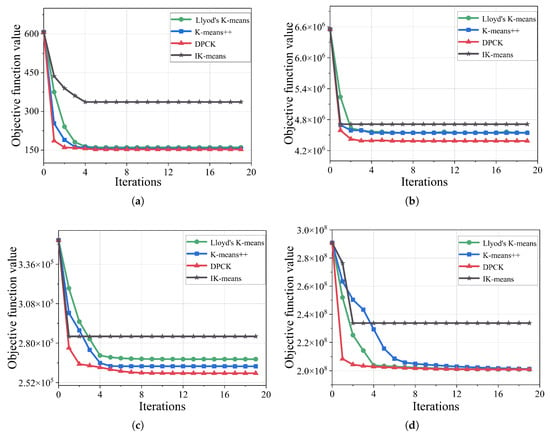
Figure 6.
Comparison of convergence curves under different iterations. (a) Iris. (b) Wine. (c) Electrical Grid data. (d) Gamma. Note: variance was near zero across repeated runs, so error bars are omitted for clarity.
Therefore, CK-means proposed in DPCK achieved a faster convergence rate and a lower initial objective function value, indicating that DPCK has better clustering performance.
6.3.3. Data Availability
In this section, we will analyze the data availability by the calculated F-measure for the PADC mechanism, Differentially Private K-means (DP K-means), and the DPCK scheme on different datasets. Where the DP K-means is an algorithm that combines the K-means clustering algorithm with differential privacy techniques, it is used as a baseline method for DPCK to compare data availability. The privacy budget value gradually increased from 0.1 to 1.0. The larger the value was, the less the noise added was, resulting in lower data privacy and clustering results closer to the true results.
Figure 7 shows the F-measure of methods under different privacy budgets. As shown in Figure 7a,b, the DPCK scheme averaged 8.0% higher than the other schemes. The results in Figure 7c,d show that the DPCK scheme outperformed other methods by an average of 12%, and the advantage was more pronounced as increased in relatively larger datasets. Overall, under the same privacy protection conditions, DPCK achieved an average F-measure improvement of 11.3% over the baseline methods. The main reason for this is that in the DPCK scheme, the necessary privacy budget was calculated based on the distribution of data points in each cluster after each clustering iteration, allowing Laplace noise to be adaptively added. It prevented either insufficient or excessive privacy protection, maximally protecting user privacy while enhancing data availability.
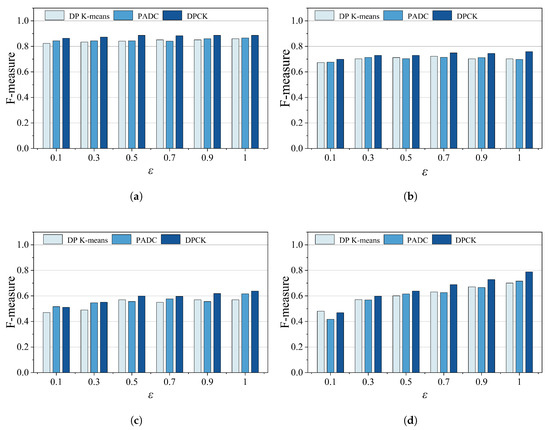
Figure 7.
Comparison of F-measure under different privacy budgets. (a) Iris. (b) Wine. (c) Electrical Grid data. (d) Gamma.
Furthermore, we evaluated the precision of DPCK by calculating the values of Pre and Re. With = 0.1 and = 0.9, the results for different methods are presented in Table 3 and Table 4. We can conclude from the tables that as the privacy budget increased, the amount of noise added to the data decreased, resulting in clustering outcomes that more closely approximated the actual data. For instance, in Table 4, it is shown that when = 0.9, the higher privacy budget yielded clustering results nearly identical to the real data, thereby leading to relatively small differences in the experimental results between different methods. Therefore, in the case of the same privacy budget, the Pre and Re values of DPCK were better than those of the other methods.

Table 3.
The values of P and R for datasets while = 0.1.

Table 4.
The values of P and R for datasets while = 0.9.
Therefore, DPCK enhances data availability compared to other methods while effectively protecting user privacy.
6.3.4. Clustering Performance
In this section, we evaluate the clustering performance of the PADC mechanism, DP K-means, and the DPCK scheme by the silhouette coefficient calculated with different datasets. The higher the silhouette coefficient was, the better the clustering performance of the method was. The privacy budget ranged from 0.1 to 1.0.
Figure 8 shows the silhouette coefficient values obtained by each method under different privacy budgets. We can see from the figure that the silhouette coefficient of DPCK was significantly higher than that of the other two comparison methods, and its fluctuation was relatively stable as the privacy budget increased. These results indicate that the DPCK scheme provided better clustering cohesion and separation across all tested datasets and privacy levels. The primary reason for this is that DPCK adaptively allocated the privacy budget based on the clustering distribution after each iteration, ensuring that an appropriate level of Laplace noise was injected. This mechanism preserved meaningful cluster boundaries and internal consistency, thus yielding a better clustering performance under differential privacy constraints.
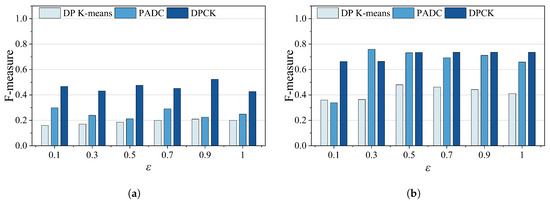
Figure 8.
Comparison of silhouette coefficient under different privacy budgets. (a) Electrical Grid data. (b) Eco dataset.
7. Conclusions
In this paper, we propose a CK-means clustering scheme based on adaptive differential privacy, named DPCK. It introduces a CK-means clustering algorithm, effectively avoiding repeated computation and thereby reducing the computational overhead of clustering analysis. Furthermore, DPCK incorporates an adaptive differential privacy mechanism that mitigates the impact of excessive or insufficient noise caused by uniform privacy budget allocation, thereby significantly enhancing data availability. The experimental results show that the DPCK scheme effectively reduced the computational overhead during clustering analysis, with more pronounced advantages in relatively larger datasets. And compared to baseline methods, it improved the data availability by 11.3%.
In future work, we aim to improve CK-means to mitigate the impact of outliers and enhance clustering robustness. Outliers (such as meters exhibiting sudden spikes or flatlines) may significantly skew cluster centroids. We plan to investigate simple pre-filtering or localized-noise strategies to reduce their influence. We will also explore strategies to optimize the computational efficiency of the DPCK algorithm to enable faster processing on relatively large-scale energy datasets. Based on the current complexity of the DPCK scheme, we estimate that it could handle a dataset with around one million records within a few minutes on standard computing infrastructure, due to the efficiency gains from the reduction in repeated calculations and the filtering of stable regions. In addition, we plan to conduct a fine-grained runtime analysis by decomposing the overall execution time into key components—such as the CK-means loop and differential privacy adjustment—to better understand performance bottlenecks, especially in high-dimensional spaces. In terms of privacy, we plan to investigate localized differential privacy mechanisms to protect user data on the client side, including strategies to reduce the influence of extreme behaviors such as consumption spikes or flatlines. These efforts will collectively help strengthen the trade-off between computational overhead and data availability in practical deployments and will help advance the development of data analysis and privacy protection.
Author Contributions
Conceptualization, S.Z. and J.Z.; methodology, J.Z.; software, E.L.; validation, X.Z.; data curation, Q.Y.; writing—original draft preparation, J.Z.; writing—review and editing, S.Z.; supervision, E.L. and Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant Numbers 62272162, 62302062, and 62172159, the Hunan Provincial Natural Science Foundation of China under Grant Number 2025JJ50398 and 2023JJ40081, the project of Hunan Provincial Social Science Achievement Review Committee of China under Grant Number XSP25YBZ104, and the Scientific Research Fund of Hunan Provincial Education Department under Grant Number 23B0797.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mari, A.; Remlinger, C.; Castello, R.; Obozinski, G.; Quarteroni, S.; Heymann, F.; Galus, M. Real-time estimates of Swiss electricity savings using streamed smart meter data. Appl. Energy 2025, 377, 124537. [Google Scholar] [CrossRef]
- Athanasiadis, C.L.; Papadopoulos, T.A.; Kryonidis, G.C.; Doukas, D.I. A review of distribution network applications based on smart meter data analytics. Renew. Sustain. Energy Rev. 2024, 191, 114151. [Google Scholar] [CrossRef]
- Gumz, J.; Fettermann, D.C. User’s perspective in smart meter research: State-of-the-art and future trends. Energy Build. 2024, 308, 114025. [Google Scholar] [CrossRef]
- Zhang, S.; Mao, X.; Choo, K.-K.R.; Peng, T.; Wang, G. A trajectory privacy-preserving scheme based on a dual-K mechanism for continuous location-based services. Inf. Sci. 2020, 527, 406–419. [Google Scholar] [CrossRef]
- Xiong, A.; Zhou, H.; Song, Y.; Wang, D.; Wei, X.; Li, D.; Gao, B. A multi-task based clustering personalized federated learning method. Big Data Min. Anal. 2024, 7, 1017–1030. [Google Scholar] [CrossRef]
- Wang, S.; Song, A.; Qian, Y. Predicting smart cities’ electricity demands using k-means clustering algorithm in smart grid. Comput. Sci. Inf. Syst. 2023, 20, 657–678. [Google Scholar] [CrossRef]
- Yuan, L.; Zhang, S.; Zhu, G.; Alinani, K. Privacy-preserving mechanism for mixed data clustering with local differential privacy. Concurr. Comput. Pract. Exp. 2023, 35, e6503. [Google Scholar] [CrossRef]
- Choksi, K.A.; Jain, S.; Pindoriya, N.M. Feature based clustering technique for investigation of domestic load profiles and probabilistic variation assessment: Smart meter dataset. Sustain. Energy Grids Netw. 2020, 22, 100346. [Google Scholar] [CrossRef]
- Rafiq, H.; Manandhar, P.; Rodriguez-Ubinas, E.; Barbosa, J.D.; Qureshi, O.A. Analysis of residential electricity consumption patterns utilizing smart-meter data: Dubai as a case study. Energy Build. 2023, 291, 113103. [Google Scholar] [CrossRef]
- Xu, H.; Yao, S.; Li, Q.; Ye, Z. An improved k-means clustering algorithm. In Proceedings of the 2020 IEEE 5th International Symposium on Smart and Wireless Systems within the Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Dortmund, Germany, 17–18 September 2020; pp. 1–5. [Google Scholar]
- Alguliyev, R.M.; Aliguliyev, R.M.; Sukhostat, L.V. Parallel batch k-means for Big data clustering. Comput. Ind. Eng. 2021, 152, 107023. [Google Scholar] [CrossRef]
- Nie, F.; Li, Z.; Wang, R.; Li, X. An effective and efficient algorithm for K-means clustering with new formulation. IEEE Trans. Knowl. Data Eng. 2022, 35, 3433–3443. [Google Scholar] [CrossRef]
- Zhang, S.; Pan, Y.; Liu, Q.; Yan, Z.; Choo, K.-K.R.; Wang, G. Backdoor attacks and defenses targeting multi-domain AI models: A comprehensive review. ACM Comput. Surv. 2024, 57, 1–35. [Google Scholar] [CrossRef]
- Parker, K.; Hale, M.; Barooah, P. Spectral differential privacy: Application to smart meter data. IEEE Internet Things J. 2021, 9, 4987–4996. [Google Scholar] [CrossRef]
- Zhu, P.; Hu, J.; Li, X.; Zhu, Q. Using blockchain technology to enhance the traceability of original achievements. IEEE Trans. Eng. Manag. 2023, 70, 1693–1707. [Google Scholar] [CrossRef]
- Wang, J.; Wu, L.; Zeadally, S.; Khan, M.K.; He, D. Privacy-preserving data aggregation against malicious data mining attack for IoT-enabled smart grid. ACM Trans. Sens. Netw. (TOSN) 2021, 17, 1–25. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, W.; Li, X.; Liu, Q.; Wang, G. APBAM: Adversarial perturbation-driven backdoor attack in multimodal learning. Inf. Sci. 2025, 700, 121847. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, P.; Li, J.; Qi, Y.; Xia, Y.; Wang, F.-Y. A secure medical information storage and sharing method based on multiblockchain architecture. IEEE Trans. Comput. Soc. Syst. 2024, 11, 6392–6406. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Tan, Z.; Peng, T.; Wang, G. A caching and spatial K-anonymity driven privacy enhancement scheme in continuous location-based services. Future Gener. Comput. Syst. 2019, 94, 40–50. [Google Scholar] [CrossRef]
- Zhang, S.; Choo, K.-K.R.; Liu, Q.; Wang, G. Enhancing privacy through uniform grid and caching in location-based services. Future Gener. Comput. Syst. 2018, 86, 881–892. [Google Scholar] [CrossRef]
- He, J.; Wang, N.; Xiang, T.; Wei, Y.; Zhang, Z.; Li, M.; Zhu, L. ABDP: Accurate Billing on Differentially Private Data Reporting for Smart Grids. IEEE Trans. Serv. Comput. 2024, 17, 1938–1954. [Google Scholar] [CrossRef]
- Gough, M.B.; Santos, S.F.; AlSkaif, T.; Javadi, M.S.; Castro, R.; Catalão, J.P.S. Preserving privacy of smart meter data in a smart grid environment. IEEE Trans. Ind. Inform. 2021, 18, 707–718. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, T.; Bashir, A.K.; Alazab, M.; Mumtaz, S.; Wang, X. A decentralized mechanism based on differential privacy for privacy-preserving computation in smart grid. IEEE Trans. Comput. 2021, 71, 2915–2926. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; University of California Press/University of California: Berkeley, CA, USA, 1967; pp. 281–298. [Google Scholar]
- Xiang, Y.; Hong, J.; Yang, Z.; Wang, Y.; Huang, Y.; Zhang, X.; Chai, Y.; Yao, H. Slope-Based Shape Cluster Method for Smart Metering Load Profiles. IEEE Trans. Smart Grid 2020, 11, 1809–1811. [Google Scholar] [CrossRef]
- Khan, I.; Luo, Z.; Shaikh, A.K.; Hedjam, R. Ensemble clustering using extended fuzzy k-means for cancer data analysis. Expert Syst. Appl. 2021, 172, 114622. [Google Scholar] [CrossRef]
- Hu, H.; Liu, J.; Zhang, X.; Fang, M. An effective and adaptable K-means algorithm for big data cluster analysis. Pattern Recognit. 2023, 139, 109404. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, P.; Li, M.; Yin, H.; Tang, R. K-means clustering method based on nearest-neighbor density matrix for customer electricity behavior analysis. Int. J. Electr. Power Energy Syst. 2024, 161, 110165. [Google Scholar] [CrossRef]
- Yang, M.; Huang, L.; Tang, C. K-means clustering with local distance privacy. Big Data Min. Anal. 2023, 6, 433–442. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Q.; Wang, T.; Liang, W.; Li, K.-C.; Wang, G. FSAIR: Fine-grained secure approximate image retrieval for mobile cloud computing. IEEE Internet Things J. 2024, 11, 23297–23308. [Google Scholar] [CrossRef]
- Gupta, A.; Ligett, K.; McSherry, F.; Roth, A.; Talwar, K. Differentially private combinatorial optimization. In Proceedings of the Twenty-First Annual ACM-SIAM Symposium on Discrete Algorithms, Austin, TX, USA, 17–19 January 2010; pp. 1106–1125. [Google Scholar]
- Yu, Q.; Luo, Y.; Chen, C.; Ding, X. Outlier-eliminated k-means clustering algorithm based on differential privacy preservation. Appl. Intell. 2016, 45, 1179–1191. [Google Scholar] [CrossRef]
- Wu, F.; Du, M.; Zhi, Q. Density-based clustering with differential privacy. Inf. Sci. 2024, 681, 121211. [Google Scholar] [CrossRef]
- Xiong, J.; Ren, J.; Chen, L.; Yao, Z.; Lin, M.; Wu, D.; Niu, B. Enhancing privacy and availability for data clustering in intelligent electrical service of IoT. IEEE Internet Things J. 2018, 6, 1530–1540. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, J.; Zhang, G.; Cui, L.; Gao, T.; Yu, S. APDP: Attribute-based personalized differential privacy data publishing scheme for social networks. IEEE Trans. Netw. Sci. Eng. 2022, 10, 922–933. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.; Peng, T.; Liu, Q.; Li, X. VADP: Visitor-attribute-based adaptive differential privacy for IoMT data sharing. Comput. Secur. 2025, 156, 104513. [Google Scholar] [CrossRef]
- Balcan, M.F.; Dick, T.; Liang, Y.; Mou, W.; Zhang, H. Differentially private clustering in high-dimensional Euclidean spaces. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 322–331. [Google Scholar]
- He, Z.; Wang, L.; Cai, Z. Clustered federated learning with adaptive local differential privacy on heterogeneous IoT data. IEEE Internet Things J. 2023, 11, 137–146. [Google Scholar] [CrossRef]
- Al Shalabi, L.; Shaaban, Z. Normalization as a preprocessing engine for data mining and the approach of preference matrix. In Proceedings of the 2006 International Conference on Dependability of Computer Systems, Szklarska Poreba, Poland, 25–27 May 2006; pp. 207–214. [Google Scholar]
- Zhou, H.B.; Gao, J.T. Automatic method for determining cluster number based on silhouette coefficient. Adv. Mater. Res. 2014, 951, 227–230. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository; School of Information and Computer Sciences, University of California: Irvine, CA, USA, 2007; Available online: https://archive.ics.uci.edu (accessed on 22 April 2025).
- Kleiminger, W.; Beckel, C.; Santini, S. Household Occupancy Monitoring Using Electricity Meters. In Proceedings of the 2015 ACM International Joint Conference on Pervasive and Ubiquitous Computing (UbiComp 2015), Osaka, Japan, 9–11 September 2015. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-Means++: The Advantages of Careful Seeding; Technical Report 2006-13; Stanford InfoLab: Stanford, CA, USA, 2006; Available online: http://ilpubs.stanford.edu:8090/778/ (accessed on 13 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).