Low-Profile Omnidirectional and Wide-Angle Beam Scanning Antenna Array Based on Epsilon-Near-Zero and Fabry–Perot Co-Resonance
Abstract
1. Introduction
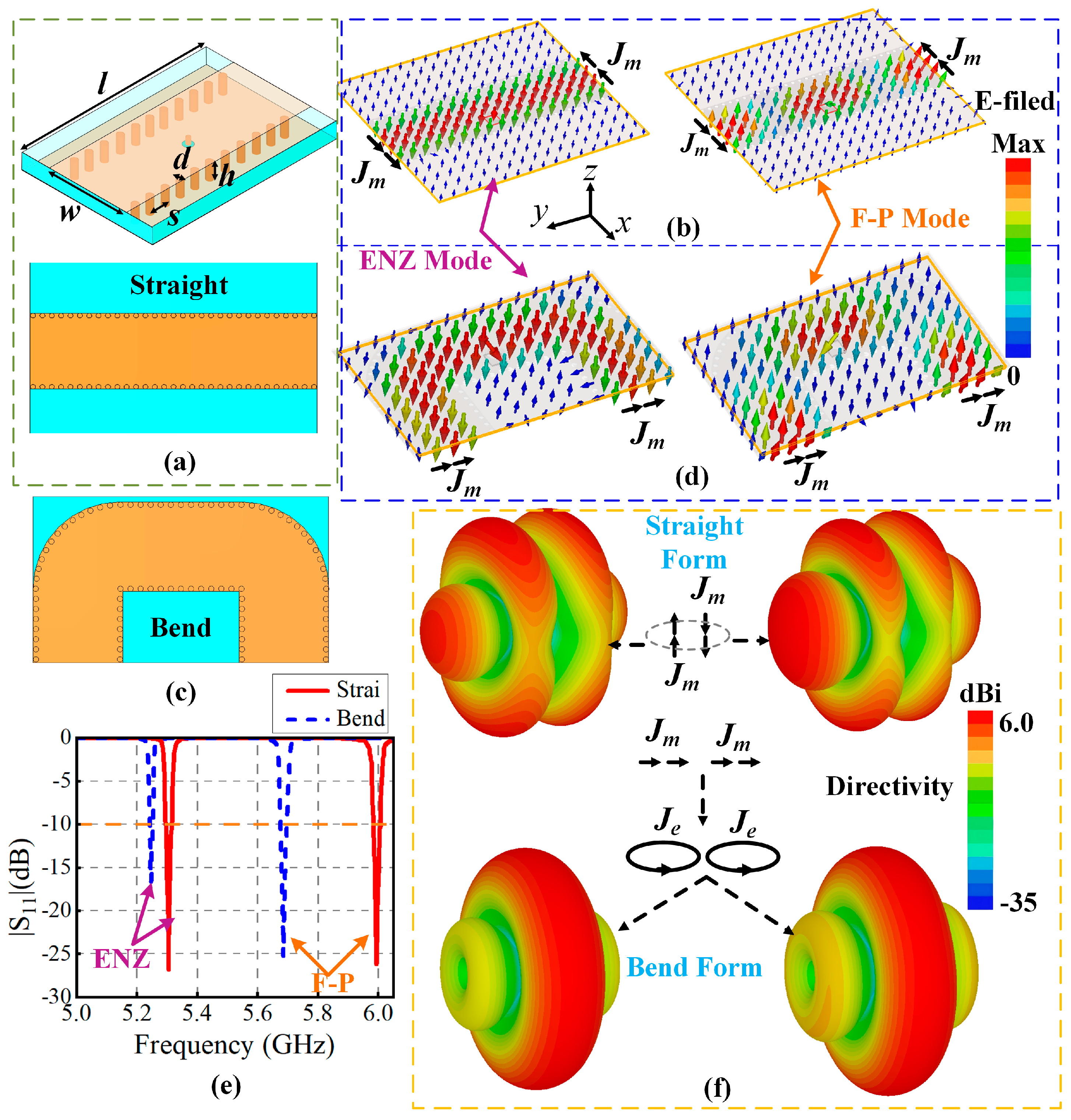
2. Omnidirectional Antenna Array
2.1. Theoretical Analysis
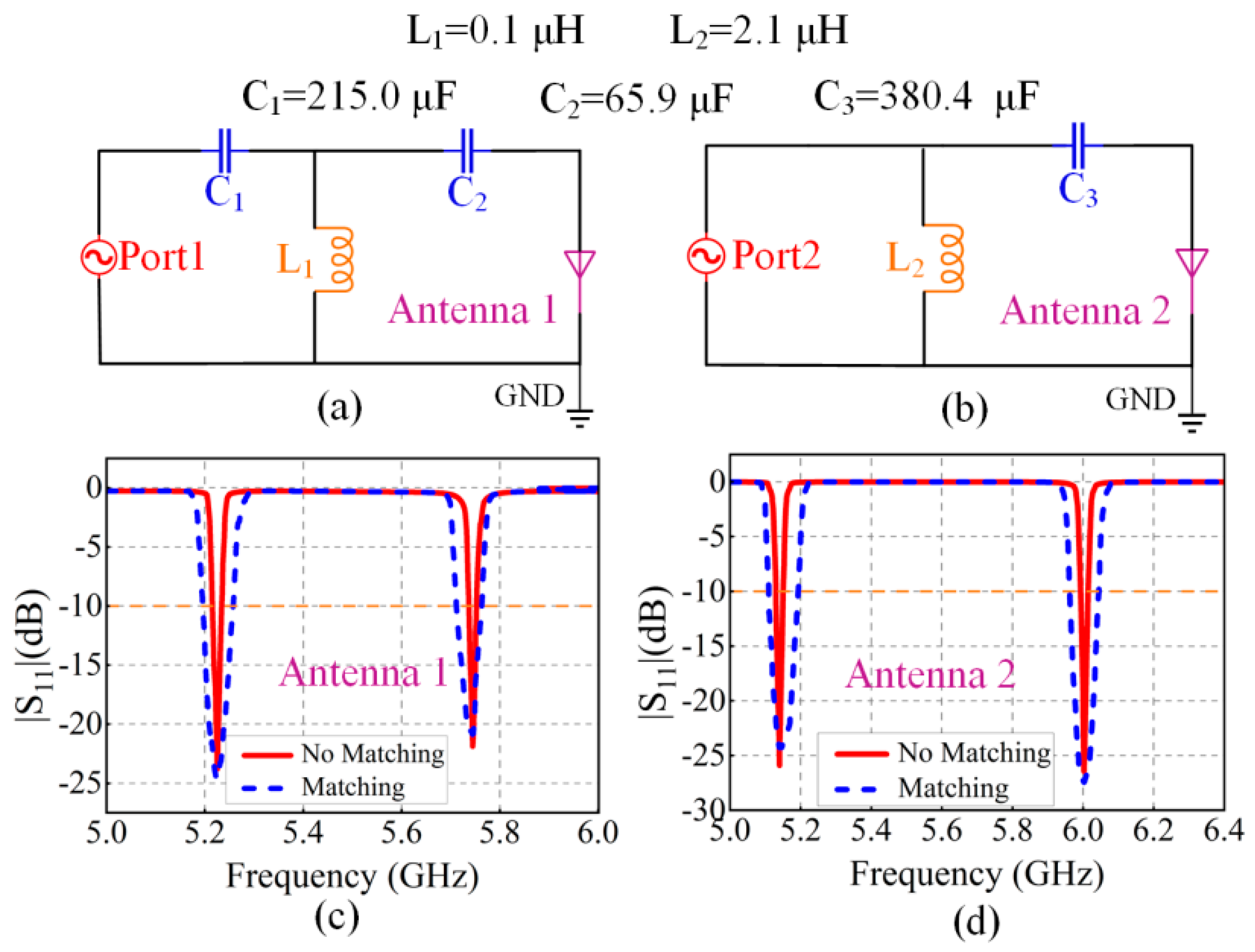
2.2. Antenna Design and Simulation
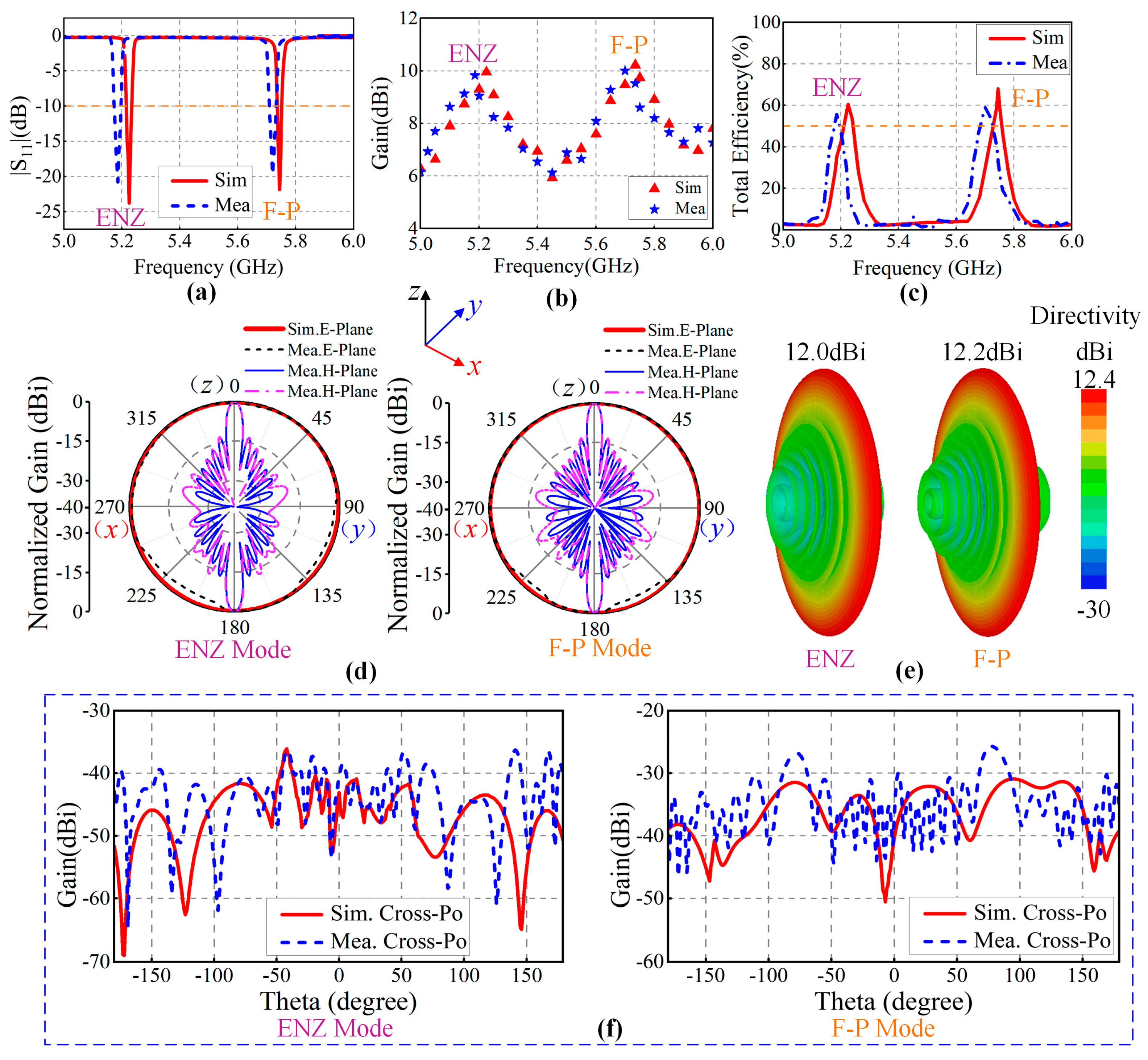
2.3. Experimental Validation
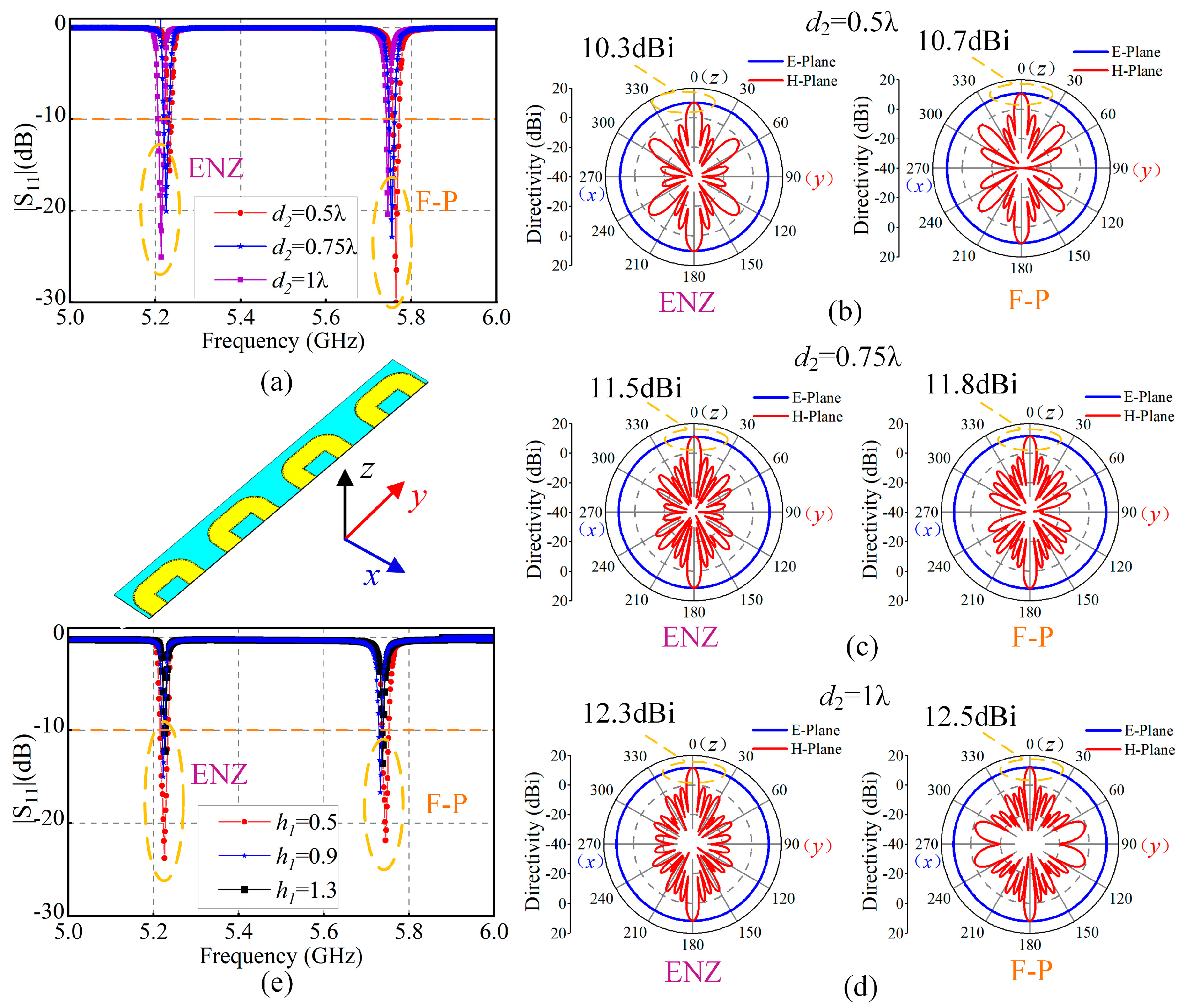
3. Beam Scanning Antenna Array
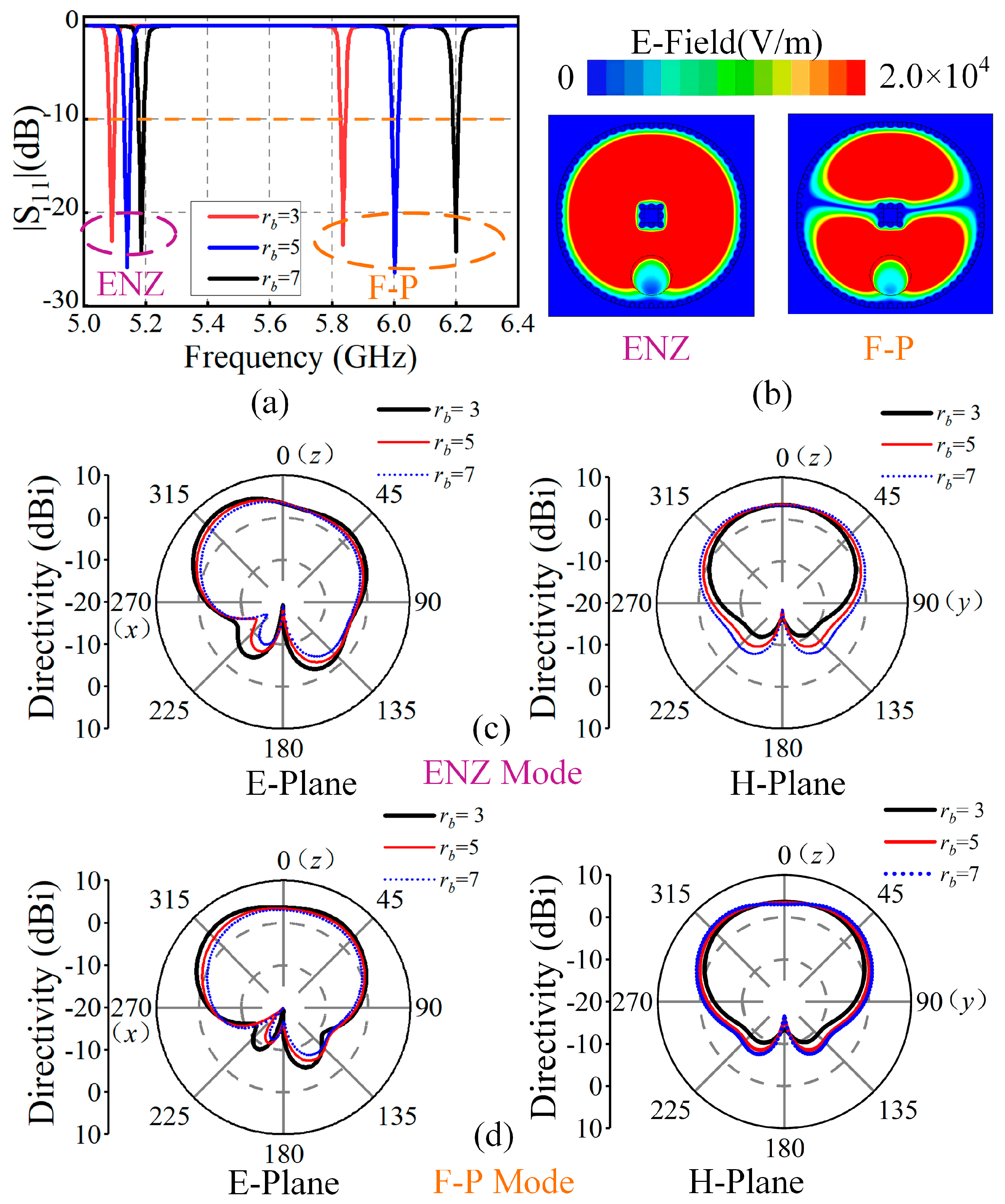
3.1. Antenna Design and Analysis
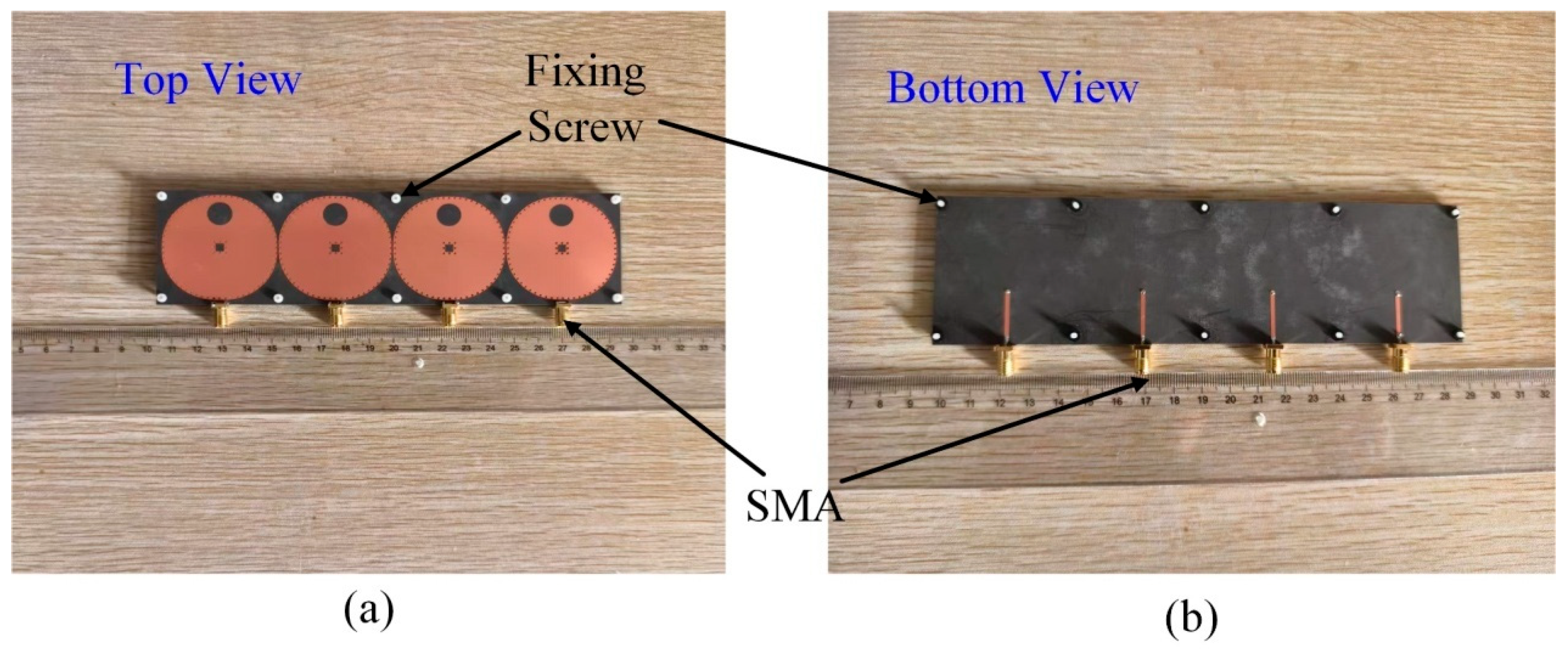
3.2. Simulation and Experimental Test
4. Discussion and Conclusions
4.1. Discussion of Bandwidth Broadening
4.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ENZ | Epsilon-Near-Zero |
| F−P | Fabry–Perot |
| SIW | Substrate Integrated Waveguide |
| PCB | Printed circuit board |
| UAV | Unmanned Aerial Vehicle |
| OFDM | Orthogonal Frequency Division Multiplexing |
| CFAR | Constant False Alarm Rate Detector |
References
- Qin, Y.; Han, M.; Zhang, L.; Mao, C.X.; Zhu, H. A Compact Dual-Band Omnidirectional Circularly Polarized Filtering Antenna for UAV Communications. IEEE Trans. Veh. Technol. 2023, 72, 16742–16747. [Google Scholar] [CrossRef]
- Ye, K.; Lu, Y.; You, Q.; Wang, K.; Xu, J.; Huang, J. Compact Dual-Band Shared-Aperture Omnidirectional Biconical Antenna for Microwave and Millimeter-Wave Applications. IEEE Trans. Antennas Propag. 2024, 72, 4594–4599. [Google Scholar] [CrossRef]
- Zhou, J.; Ke, Y.H.; Chen, J.X. A Dual-Polarized Omnidirectional Antenna with Small Plane Size for Indoor Distribution Applications. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1878–1882. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, Y.; Yang, X.; Guo, R.Y.; Li, Y.; Ge, L. High-Gain Omnidirectional Transmitarray Antenna. IEEE Trans. Antennas Propag. 2023, 71, 8441–8449. [Google Scholar] [CrossRef]
- Chen, D.; Xue, Q.; Yang, W.; Chin, K.S.; Jin, H.; Che, W. A Compact Wideband Low-Profile Metasurface Antenna Loaded with Patch-Via-Wall Structure. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 179–183. [Google Scholar] [CrossRef]
- Abdulkarim, Y.I.; Awl, H.N.; Muhammadsharif, F.F.; Karaaslan, M.; Mahmud, R.H.; Hasan, S.O.; Işık, Ö.; Luo, H.; Huang, S. A Low-Profile Antenna Based on Single-Layer Metasurface for Ku-Band Applications. Int. J. Antennas Propag. 2020, 2020, 8813951. [Google Scholar] [CrossRef]
- Ta, S.X.; Park, I. Low-Profile Broadband Circularly Polarized Patch Antenna Using Metasurface. IEEE Trans. Antennas Propag. 2015, 63, 5929–5934. [Google Scholar] [CrossRef]
- Liberal, I.; Engheta, N. The rise of near-zero-index technologies. Science 2017, 358, 1540–1541. [Google Scholar] [CrossRef]
- Liberal, I.; Engheta, N. Near-zero refractive index photonics. Nat. Photonics 2017, 11, 149–158. [Google Scholar] [CrossRef]
- Liberal, I.; Mahmoud, A.M.; Engheta, N. Geometry-invariant resonant cavities. Nat. Commun. 2016, 7, 10989. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Qin, X.; Liang, P.; Wei, K.; Li, Y. Dual-Polarized Microstrip Antenna with Single-Dimension-Constraint Resonant Frequency. IEEE Trans. Antennas Propag. 2024, 72, 8365–8374. [Google Scholar] [CrossRef]
- Wang, Z.; Dong, Y. Novel Pattern Reconfigurable Epsilon-Near-Zero (ENZ) Antenna for Intelligent IoT Communication Applications. IEEE Internet Things J. 2024, 11, 22364–22375. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Sun, W.; Li, Y. Low-Profile Epsilon-Near-Zero (ENZ) Cavity Antenna Array for Wide-Angle Beam Scanning. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 2115–2119. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Z.; He, Y.; Sun, W.; Li, Y.; Liberal, I.; Engheta, N. Geometry-independent antenna based on Epsilon-near-zero medium. Nat. Commun. 2022, 13, 3568. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, H.; Zhao, Y.; Li, Y. 2-D Epsilon-Near-Zero (ENZ) Feeding Network for High-Gain Millimeter-Wave Slot Antenna Array using Bulk Silicon MEMS Technology. IEEE Trans. Antennas Propag. 2024, 72, 3055–3063. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Z.; Zhao, Y.; Li, Y. Low-loss beam synthesizing network based on epsilon-near-zero (ENZ) medium for on-chip antenna array. Chip 2023, 2, 100049. [Google Scholar] [CrossRef]
- George, D.M.; Chandroth, A. 5 GHz high gain slotted SIW epsilon near zero antenna array for wireless communications. Eng. Res. Express 2020, 2, 045014. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Y. Effective epsilon-near-zero (ENZ) antenna based on transverse cutoff mode. IEEE Trans. Antennas Propag. 2019, 67, 2289–2297. [Google Scholar] [CrossRef]
- Li, H.; Zhou, Z.; Li, Y. Length-irrelevant dual-polarized antenna based on antiphase epsilon-near-zero mode. IEEE Trans. Antennas Propag. 2021, 70, 720–725. [Google Scholar] [CrossRef]
- Forati, E.; Hanson, G.W.; Sievenpiper, D.F. An epsilon-near-zero total-internal-reflection metamaterial antenna. IEEE Trans. Antennas Propag. 2015, 63, 1909–1916. [Google Scholar] [CrossRef]
- Zhiming, L.; Jens, B.; Shaobin, L.; Xiangkun, K. Investigations and prospects of Fabry-Perot antennas: A review. J. Syst. Eng. Electron. 2021, 32, 731–747. [Google Scholar] [CrossRef]
- Zhou, L.; Duan, X.; Luo, Z.; Zhou, Y.; Chen, X. High Directivity Fabry–Perot Antenna with a Nonuniform Partially Reflective Surface and a Phase Correcting Structure. IEEE Trans. Antennas Propag. 2020, 68, 7601–7606. [Google Scholar] [CrossRef]
- Jeon, Y.G.; Yun, G.R.; Kim, J.; Kim, D. Polarization Reconfigurable High-Gain Fabry–Perot Cavity Antenna. IEEE Trans. Antennas Propag. 2022, 70, 7727–7734. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Y.; He, Y.; Zhang, Z.; Chen, P.Y. A Slender Fabry–Perot Antenna for High-Gain Horizontally Polarized Omnidirectional Radiation. IEEE Trans. Antennas Propag. 2021, 69, 526–531. [Google Scholar] [CrossRef]
- Hussain, N.; Jeong, M.J.; Park, J.; Kim, N. A Broadband Circularly Polarized Fabry-Perot Resonant Antenna Using A Single-Layered PRS for 5G MIMO Applications. IEEE Access 2019, 7, 42897–42907. [Google Scholar] [CrossRef]
- Sadeghzadeh, R.A.; Zarrabi, F.B. Metamaterial Fabry–Perot cavity implementation for gain and bandwidth enhancement of THz dipole antenna. Optik 2016, 127, 5181–5185. [Google Scholar] [CrossRef]
- Syrytsin, I.; Zhang, S.; Pedersen, G.F.; Morris, A.S. Compact Quad-Mode Planar Phased Array with Wideband for 5G Mobile Terminals. IEEE Trans. Antennas Propag. 2018, 66, 4648–4657. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, S.; Dong, Y. Metamaterial-Based Wide-Beam Dielectric Resonator Antenna for Broadband Wide-Angle Beam-Scanning Phased Array Applications. IEEE Trans. Antennas Propag. 2022, 70, 9061–9072. [Google Scholar] [CrossRef]
- Yang, G.; Li, J.; Zhou, S.G.; Qi, Y. A Wide-Angle E-Plane Scanning Linear Array Antenna with Wide Beam Elements. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2923–2926. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, S. Dual-Polarized Wide-Angle Scanning Phased Array Antenna for 5G Communication Systems. IEEE Trans. Antennas Propag. 2022, 70, 7427–7438. [Google Scholar] [CrossRef]
- Feng, X.; Wu, K. Guided-wave and leakage characteristics of substrate integrated waveguide. IEEE Trans. Microw. Theory Tech. 2005, 53, 66–73. [Google Scholar] [CrossRef]
- Rotman, W. Plasma simulation by artificial dielectrics and parallel-plate media. IRE Trans. Anntenas Propag. 1962, 10, 82–95. [Google Scholar] [CrossRef]
- Chang, L.; Li, Y.; Zhang, Z.; Feng, Z. Horizontally Polarized Omnidirectional Antenna Array Using Cascaded Cavities. IEEE Trans. Antennas Propag. 2016, 64, 5454–5459. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Li, P.; Yan, W.; Wang, S.; Fu, P.; Zhang, Y.; Li, Y. Engineering Epsilon-Near-Zero Media with Waveguides. Adv. Phys. Res. 2024, 3, 2400070. [Google Scholar] [CrossRef]
- Rao, R.S. Microwave Engineering; PHI Learning Pvt. Ltd.: New Delhi, India, 2015. [Google Scholar]
- Li, J.; Zhao, L.; Wu, H. A Novel Highly Directional Antenna Array Based on Epsilon-Mu-Near-Zero (EMNZ) with Air Gap Structure. IEEE Trans. Antennas Propag. 2024, 73, 2357–2368. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Z.; Li, Y.; Li, Y. Integrated epsilon-near-zero antenna for omnidirectional radiation. Appl. Phys. Lett. 2021, 119, 151904. [Google Scholar] [CrossRef]

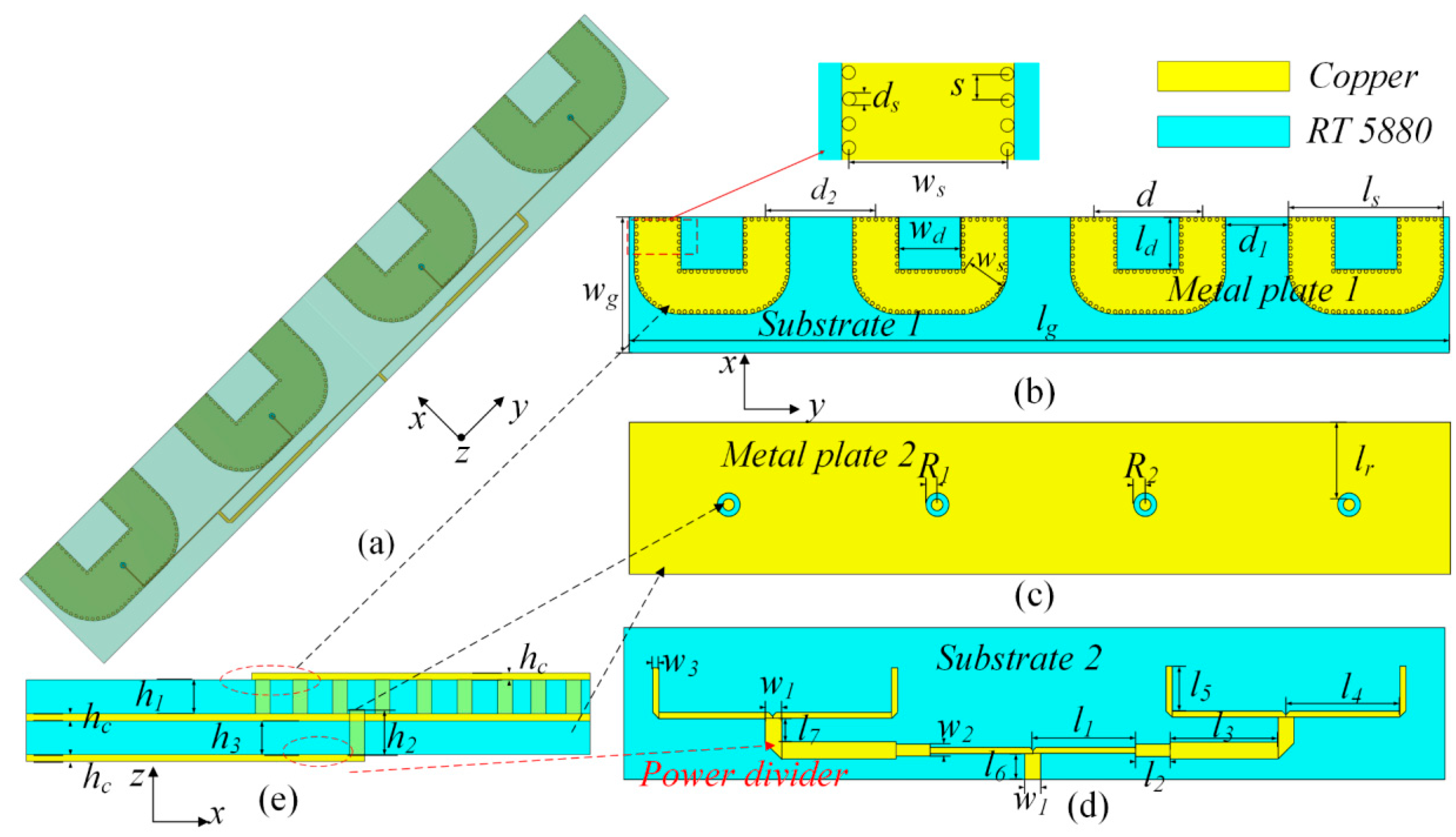

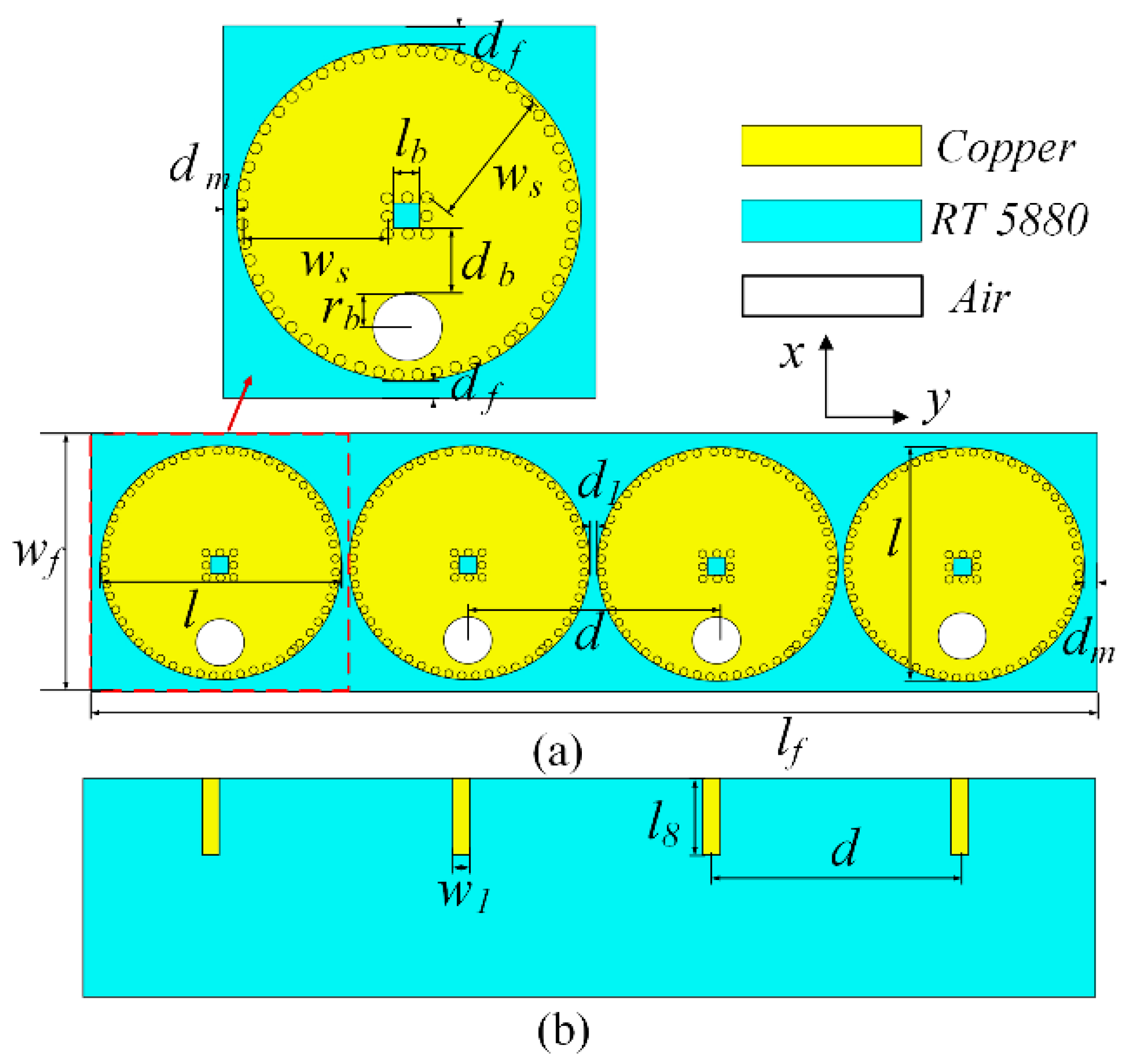
| Parameter | Value (mm) | Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|---|---|
| lg | 370 | l1 | 33.7 | l2 | 10.3 |
| l3 | 52.5 | l4 | 48.05 | ls | 70.3 |
| l5 | 12.4 | l6 | 4.1 | lr | 25.2 |
| ld | 17 | wg | 48.5 | w1 | 1.5 |
| w2 | 0.82 | w3 | 0.4 | ws | 20 |
| wd | 27.7 | s | 2.4 | ds | 1.3 |
| hc | 0.035 | h1 | 0.508 | h2 | 0.635 |
| h3 | 0.508 | R1 | 0.6 | R2 | 1.3 |
| l7 | 5.5 | d2 = d | 27.7 | d1 | 49 |
| Parameter | Value (mm) | Parameter | Value (mm) | Parameter | Value (mm) |
|---|---|---|---|---|---|
| lf | 189 | lb | 3.5 | l | 45.9 |
| d | 1 | d1 | 46.9 | lr | 25.2 |
| ld | 17 | wf | 49.9 | l8 | 18.3 |
| df | 2 | dm | 1.2 | rb | 5 |
| db | 8.2 | w1 | 1.5 |
| Reference | Antenna Type | Size (mm) | Element Number | CF (GHz) | Gain (dBi) | Profile (λ) | Radiation Mode | Bandwidth |
|---|---|---|---|---|---|---|---|---|
| [1] | Patch | 25 × 25 | 1 | 2.4\5.8 | 0\1.5 | 0.042 | Omni | 4.1% |
| [15] | ENZ | 22 × 51 | 6 × 10 | 63.5 | 21.8 | 0.3 | Dir. | 0.1% |
| [24] | F−P | 360 × 18 | 5 | 2.5 | 8.52 | 0.032 | Omni. | 3.6% |
| [33] | PLs | 168 × 18 | 5 | 5.95 | 8.67 | 0.04 | Omni. | 2.0% |
| [29] | Microstrip | 350 × 40 | 9 | 4.0 | 12.8 | 0.23 | B-S(±70°) | 15% |
| [30] | Microstrip | 300 × 60 | 8 | 5 | 13.2 | 0.71 | B-S(±60°) | 12% |
| [37] | EMNZ | 300 | 10 | 5 | 13.75 | 0.5 | Dir. | 0.1% |
| [38] | ENZ | 214 × 24 | 4 | 7.75 | No Given | 0.06 | Omni. | 0.4% |
| Ant.1 | ENZ−FP | 370 × 48.5 | 4 | 5.18\5.72 | 9.8\10.1 | 0.018 | Omni. | 2.4% |
| Ant.2 | ENZ−FP | 189 × 49.9 | 4 | 5.14\6.0 | 9.3\9.4 | 0.018 | B-S(±63°\±67°) | 2.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhao, L.; Long, D.; Xie, H. Low-Profile Omnidirectional and Wide-Angle Beam Scanning Antenna Array Based on Epsilon-Near-Zero and Fabry–Perot Co-Resonance. Electronics 2025, 14, 2012. https://doi.org/10.3390/electronics14102012
Li J, Zhao L, Long D, Xie H. Low-Profile Omnidirectional and Wide-Angle Beam Scanning Antenna Array Based on Epsilon-Near-Zero and Fabry–Perot Co-Resonance. Electronics. 2025; 14(10):2012. https://doi.org/10.3390/electronics14102012
Chicago/Turabian StyleLi, Jiaxin, Lin Zhao, Dan Long, and Hui Xie. 2025. "Low-Profile Omnidirectional and Wide-Angle Beam Scanning Antenna Array Based on Epsilon-Near-Zero and Fabry–Perot Co-Resonance" Electronics 14, no. 10: 2012. https://doi.org/10.3390/electronics14102012
APA StyleLi, J., Zhao, L., Long, D., & Xie, H. (2025). Low-Profile Omnidirectional and Wide-Angle Beam Scanning Antenna Array Based on Epsilon-Near-Zero and Fabry–Perot Co-Resonance. Electronics, 14(10), 2012. https://doi.org/10.3390/electronics14102012





