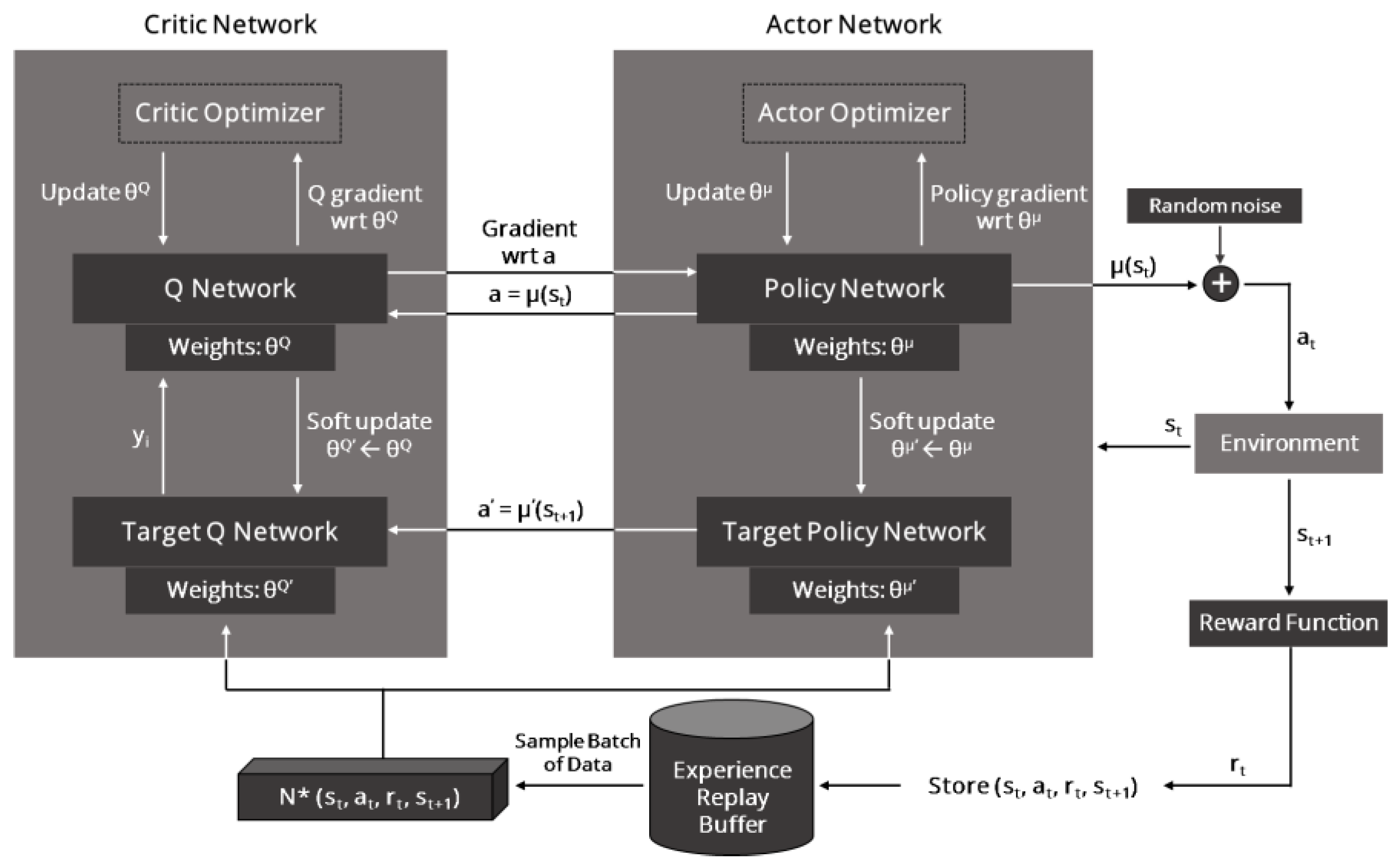
To ensure a fair comparison among the three developed approaches, a standardized framework has been devised wherein the same parking scenario is applied to each approach. In this controlled setting, the three approaches undergo testing across 100 identical parking scenarios in the CARLA Simulator, and their respective performances are meticulously collected for in-depth analysis. The comparison primarily centers on three key aspects: success rate, average steps per successful episode, and average reward per successful episode.
5.1. Success Rate
The first aspect examines the success rate, quantifying the frequency with which each approach achieves successful parking outcomes. This metric serves as a pivotal indicator of the overall efficacy and reliability of the approaches under consideration. To further strengthen the results, 95% confidence intervals for the success rates are calculated based on 10 separate trials, each consisting of 100 identical parking scenarios. Each set of tests was conducted independently, providing a robust estimate of the variability and reliability of the success rates across multiple testing repetitions.
Figure 10 illustrates a bar plot representing both the success rates and their corresponding 95% confidence intervals for the three approaches. The plot reveals that the DDPG-IL approach boasts the highest success rate (98%), with a 95% confidence interval of (97.17%, 98.83%). The DDPG approach follows closely with a success rate of 92% and a confidence interval of (90.74%, 93.26%). As anticipated, the IL approach exhibits the lowest success rate of 63%, with a confidence interval of (60.54%, 65.46%).
In comparing these findings with those from other studies, Piao et al. [
11] tested their multi-sensor self-adaptive trajectory generation method across ten parallel parking scenarios, achieving a success rate of 90%. While this demonstrates the effectiveness of their method within specific spatial constraints, as the parking space was 1.38 times the vehicle length, the limited scope of testing in only ten scenarios raises concerns about the applicability of their findings to varied real-world parking situations. Additionally, Sousa et al. [
26] found that successful parallel parking was only achievable when the parking spot length was at least twice the vehicle’s length. Although specific success rates were not reported, the requirement for larger parking spaces significantly limits the applicability of this approach in real-world scenarios.
Furthermore, Zhang et al. [
25] evaluated their method in five scenarios for both standalone NNs and those combined with the MCTS, using parking spot lengths of 1.28. 1.4, and 1.54 times the vehicle length. While all scenarios were completed successfully, the limited number of test scenarios suggests potential issues regarding the robustness of the findings across diverse parking environments. Song et al. [
24] tested their approach in 25 real parallel parking scenarios, where the parking space was 1.54 times the vehicle length. The DERL method achieved a 100% success rate, while the baseline MCTS approach with a refined vehicle model recorded a success rate of 84%, both under conditions where the initial vehicle positions were the same as those used during training. To further test the generalization capability, the second set of experiments involved varying the initial orientation of the vehicle across 20 tests. In these tests, the DERL method maintained a 100% success rate, while the MCTS approach’s success rate dropped to 70%, highlighting the DERL method’s superior adaptability to unseen initial parking poses.
Notably, in the present work, the ratio of parking space length to vehicle length is 1.2, which is the smallest compared to all other studies discussed. This tighter constraint enhances the relevance of our findings to real-world scenarios where space limitations are more pronounced. Finally, Du et al. [
27] evaluated their DQN and DRQN based on the performance of the latest 5000 training parking scenarios over 105,000 episodes, yielding average success rates of 98.4% for DQN and 94.3% for DRQN using discrete action spaces with 42, 62, 82, and 102 actions. While these results are commendable, there are notable concerns when addressing the complexities of autonomous parking tasks with discrete action spaces.
It is worth mentioning that research on conventional APS approaches [
10,
13,
14] does not focus on evaluating success rates. Instead, these studies primarily utilize metrics such as the length of the parking path, the time taken to park, and the computation time associated with path planning.
5.4. Discussion
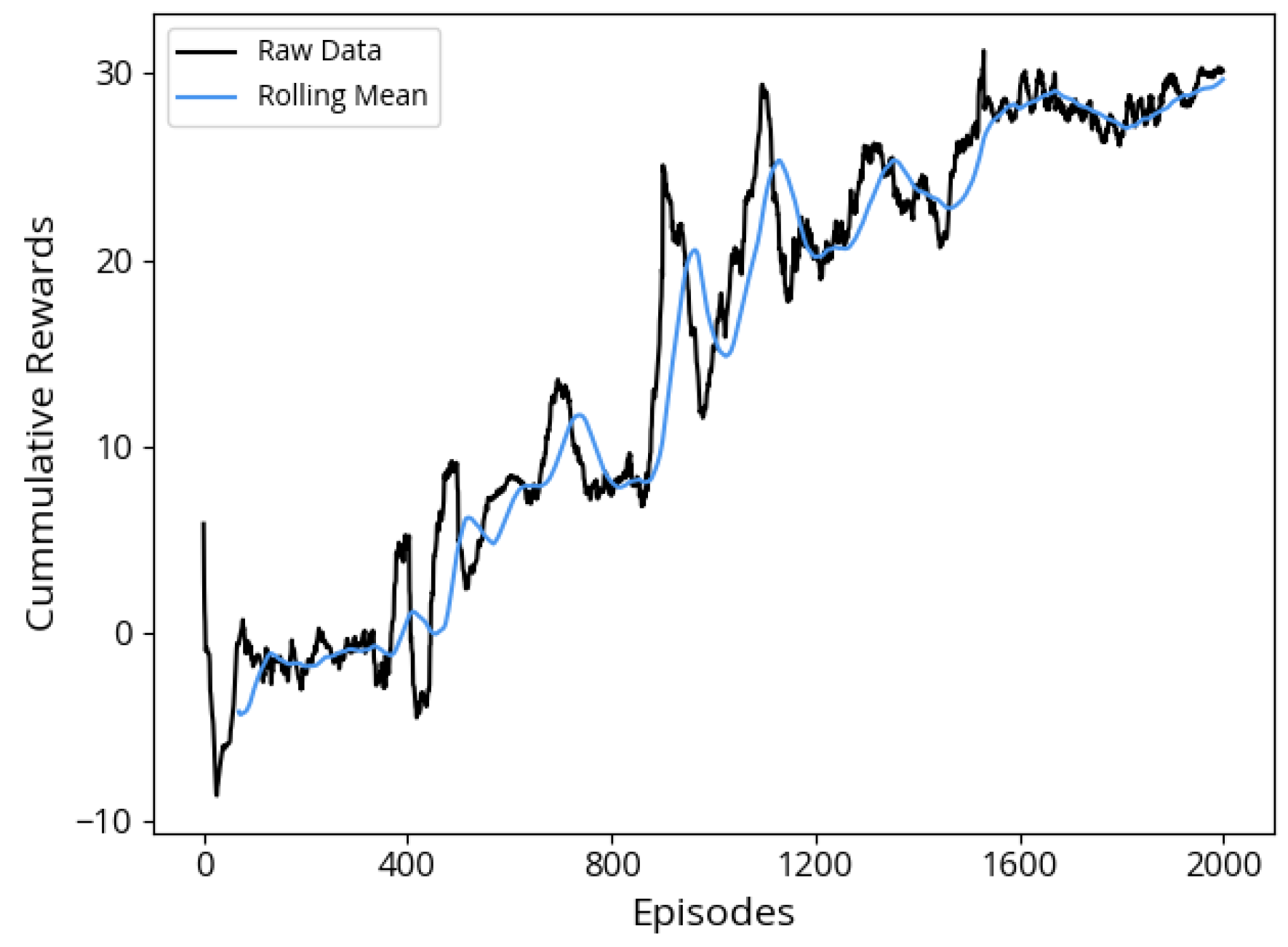
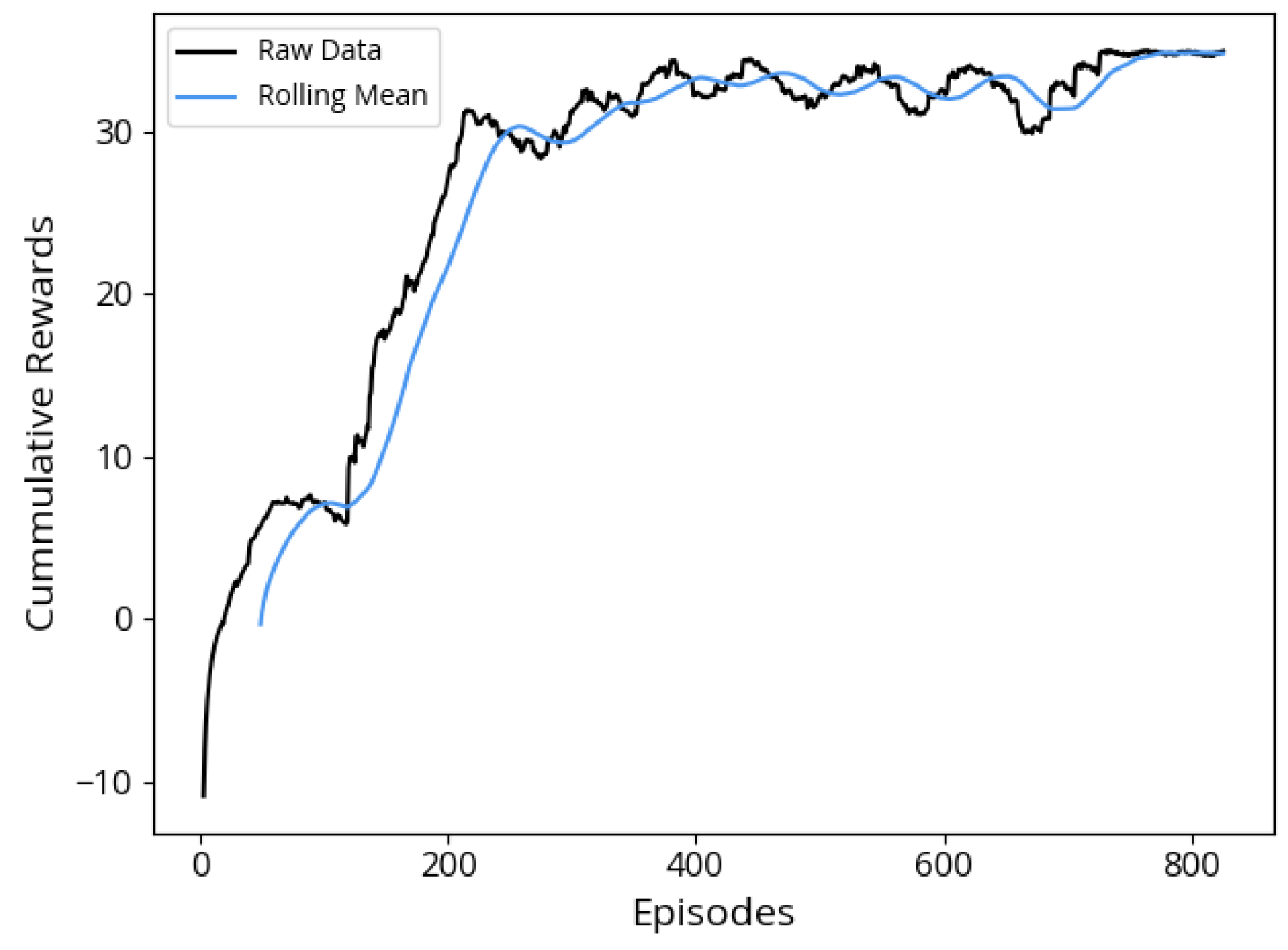
Overall, in the IL approach, the ego vehicle demonstrates a proficient start to its parking maneuver, effectively replicating behaviors learned from the training scenarios. However, it exhibits a notable challenge when confronted with novel and unanticipated situations, causing uncertainties in decision making. The success of parking attempts correlates significantly with scenarios closely mirroring those encountered during the training phase. Despite showcasing better efficiency in terms of average steps per successful parking attempt compared to the other two algorithms, its success rate of 63%, combined with the fact that in the remaining attempts, episodes terminated due to the ego vehicle colliding with obstacles, diminishes its overall effectiveness and renders this approach unsafe.
In the DDPG algorithm, successful parking attempts occur, but a limitation of this approach is the relatively high number of steps required for the vehicle to successfully execute parallel parking, and a notable observation is that the vehicle does not strictly adhere to real-world rules of parallel parking. Another limitation was observed in 8% of the attempts, where 3% of these resulted in collisions with obstacles, either minor or severe. These collisions were primarily with motorbikes or bicycles, which are smaller and harder for radar sensors to detect, that were parked in front or below the parking space. Other obstacles, such as objects on the sidewalk, also contributed to some of the collisions. In the remaining 5% of the failed attempts, the vehicle failed to complete the parking within the 100-step limit, but without any collisions. Despite this factor, the overall success rate makes the approach effective and acceptable.
Remarkably, the DDPG-IL algorithm exhibits superior performance, achieving a 98% success rate. It excels in both successful attempts and average rewards, with the addition of Imitation Learning data significantly improving the vehicle’s ability to handle a wider range of scenarios. This improvement makes the agent more adept at avoiding obstacles, including motorbikes, bicycles, and other unexpected objects. Notably, all of the 2% unsuccessful attempts in the DDPG-IL approach were due to timeouts, with no collisions observed. Although unsuccessful episodes did not result in collisions, the vehicle required more steps to complete the parking maneuver, demonstrating room for improvement in efficiency. Importantly, the DDPG-IL approach closely mimics the parking maneuvers commonly executed by human drivers in real-life scenarios. It is also important to highlight that the experiments were conducted in a simulated environment. Therefore, real-world implementation would necessitate further adaptation to account for environmental variability, perception uncertainty, and integration challenges with onboard systems. Furthermore, given that most commercial Autonomous Parking Systems are deployed under human supervision, the presence of a driver can provide an additional safety layer by allowing manual intervention in rare cases of failure.
Additionally, the effect of increasing the amount of imitation data in the DDPG-IL approach was examined. Contrary to expectations, performance declined when 30 or 40 demonstrations were used instead of the original 20. This degradation is likely due to overfitting, where the agent learns a narrower behavioral pattern that does not generalize well to new situations, and to replay buffer imbalance, where imitation data disproportionately influenced the training due to their relatively large share. These findings underscore the need for careful calibration of demonstration volume to avoid compromising generalization capabilities.
Ultimately, the DDPG-IL hybrid approach stands out as the most robust and effective solution for autonomous parallel parking in this study. The integration of IL data with DDPG training not only enhances overall performance but also contributes to safer and more efficient parking maneuvers. Notably, unsuccessful parking episodes in the DDPG-IL approach did not involve collisions but required more steps from the ego vehicle.
To further illustrate the performance of the developed approaches,
Figure 13 and
Figure 14a,b show snapshots of the ego vehicle’s movement at different stages in three identical scenarios for the IL, DDPG, and DDPG-IL algorithms, respectively.
In this scenario, both the DDPG-IL and DDPG approaches successfully complete the parking attempt, whereas the IL approach results in the vehicle deviating from the parking space and ending up on the sidewalk. The observed behavior highlights a critical limitation of the IL approach: its inability to navigate challenging situations effectively. In contrast, the DDPG-IL approach achieves the parking task within 26 steps, while the DDPG approach requires 33 steps. Importantly, the DDPG-IL approach closely mimics human-like parking maneuvers due to leveraging data designed to replicate human behavior, whereas the DDPG approach adopts a distinct, less efficient maneuvering strategy.