Hash-Based Message Authentication Code with a Reverse Fuzzy Extractor for a CMOS Image Sensor †
Abstract
1. Introduction
- A CMOS Image Sensor with a Message Authentication Code (CIS-MAC) is proposed.
- The evaluation results of the responses of the physically Unclonable Function (PUF) and the random numbers used to generate cryptographic keys and MAC tags are presented.
- The integrity and authenticity of image protection technology are discussed.
- Feasibility study for a small area implementation of CIS-MAC is performed.
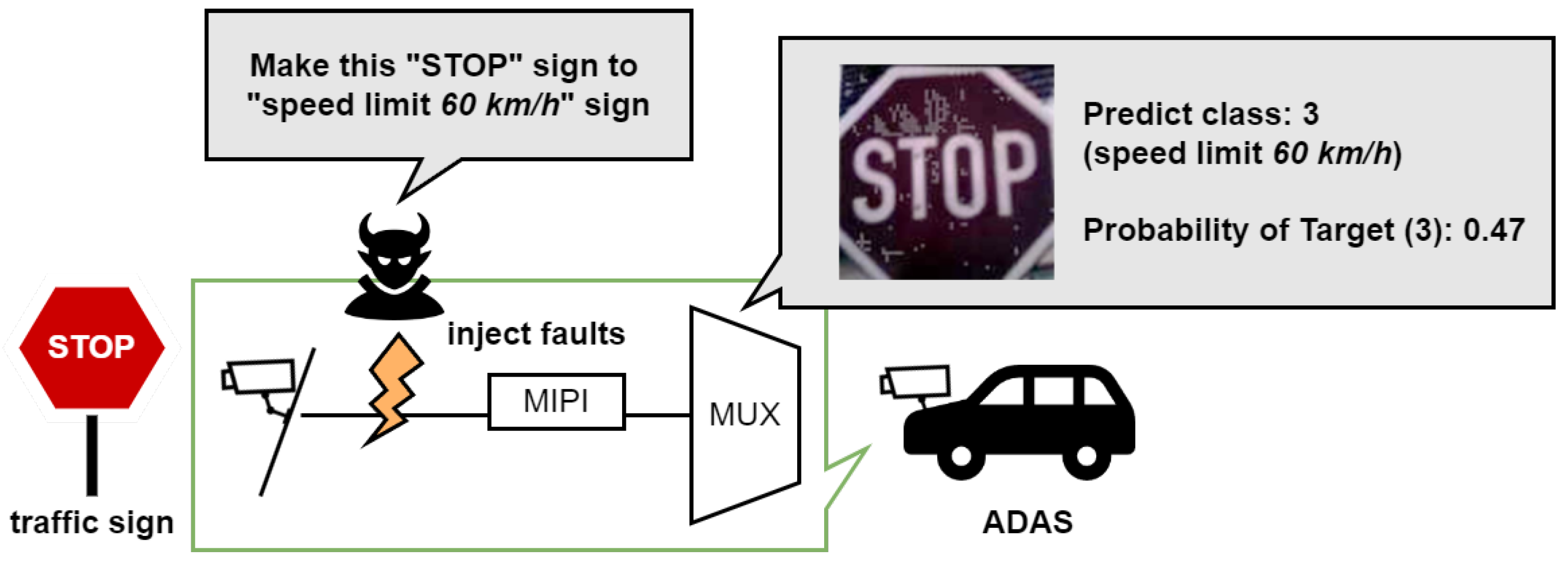
2. Security Risks for Image Sensor Data
- The attacker first pre-obtains a target image (e.g., a traffic sign) from the victim system. This image is used to pre-compute the perturbations used in the AE.
- The attacker then connects an attack device to the victim system, which is capable of generating the pre-computed perturbations to implement a fault injection attack.
- The AE is triggered only when the target traffic sign is captured, at which time the attack device continuously adds perturbations to the captured image by injecting fault signals into the image sensor interface.
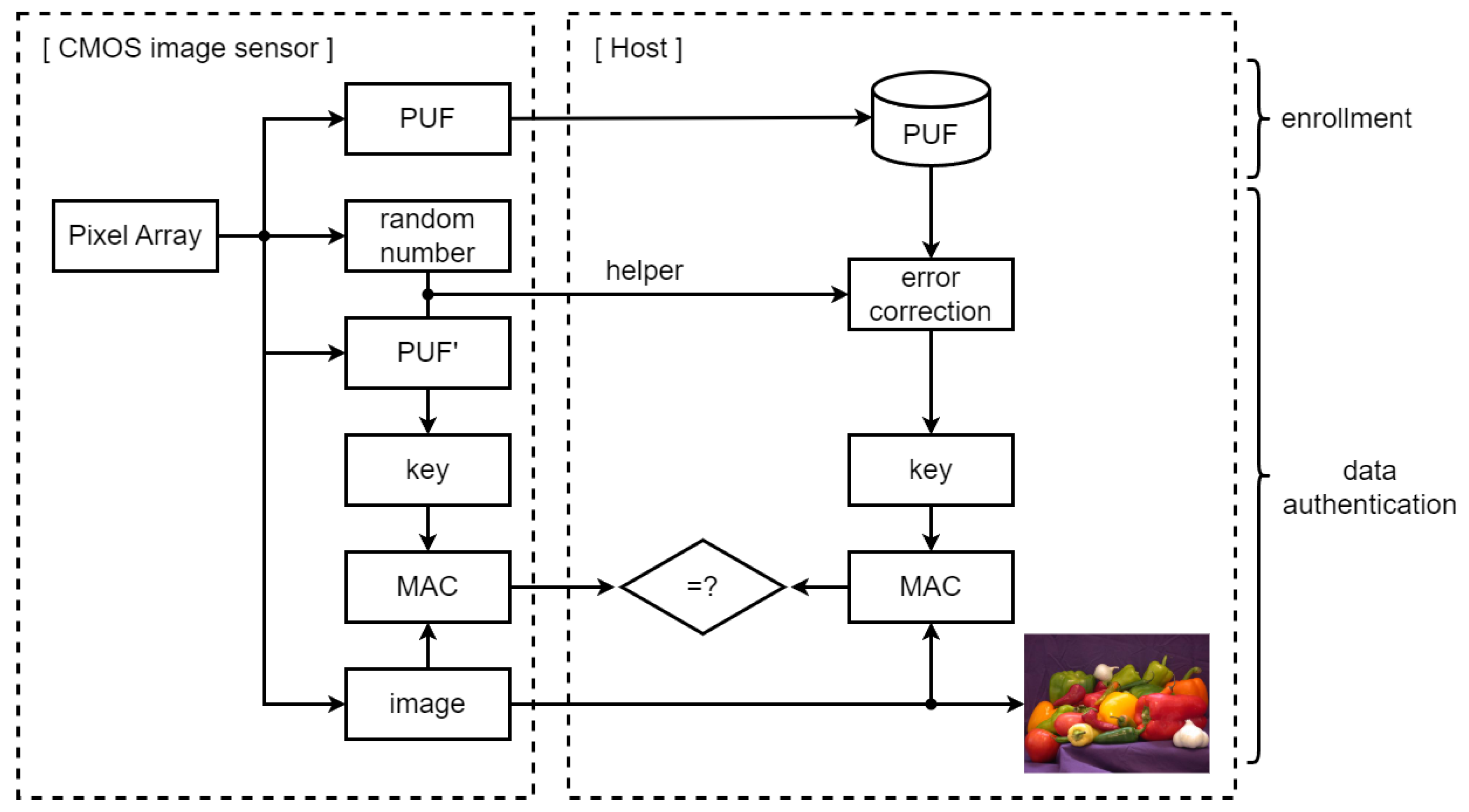
3. Overview of Message Authentication from CMOS Image Sensor to Host Device
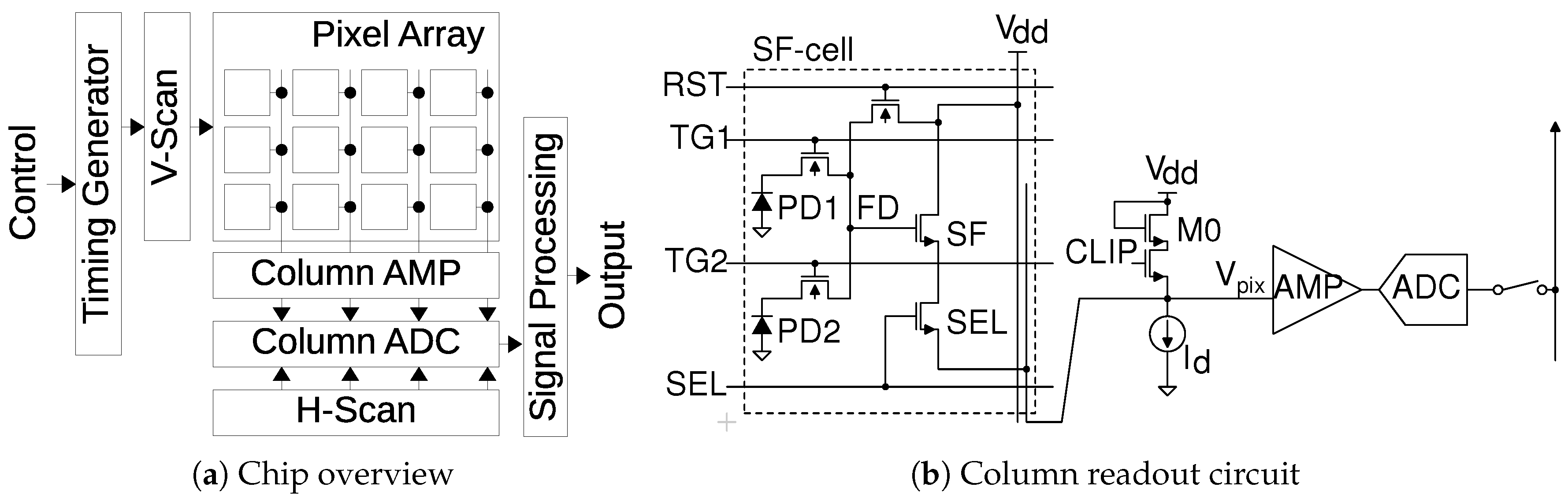
3.1. PUF Response and Random Number
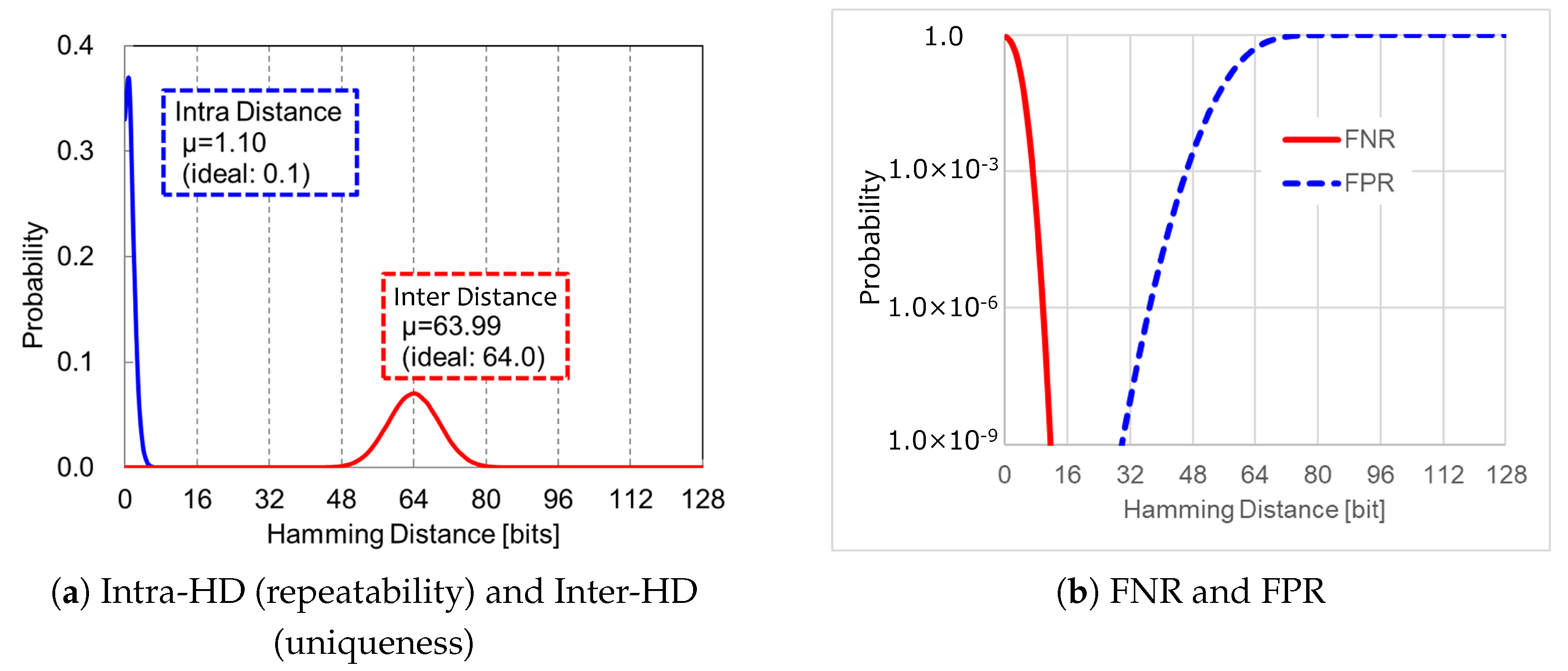
3.1.1. Evaluation of PUF Response
3.1.2. Evaluation of Random Number
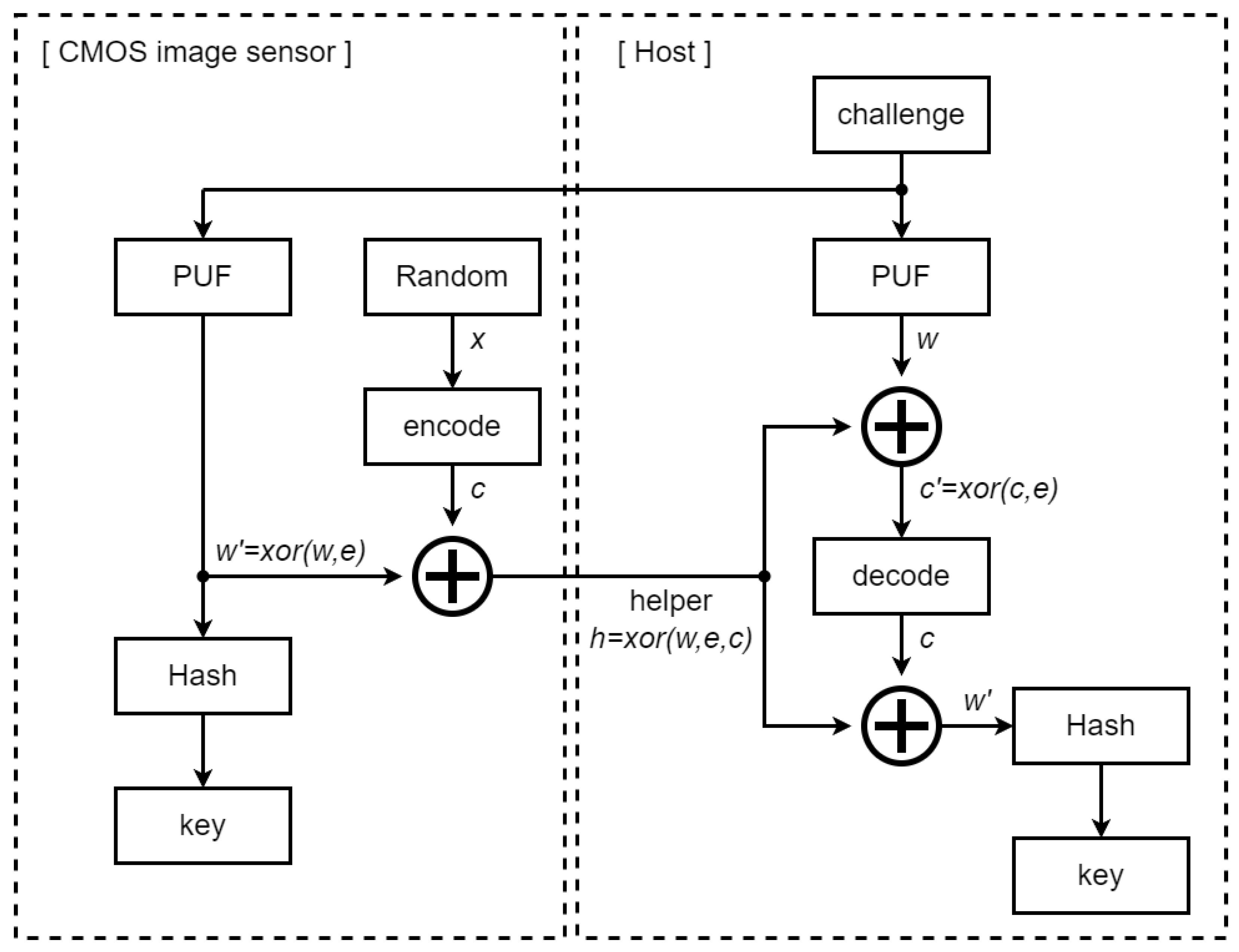
3.2. Key Generation Circuit
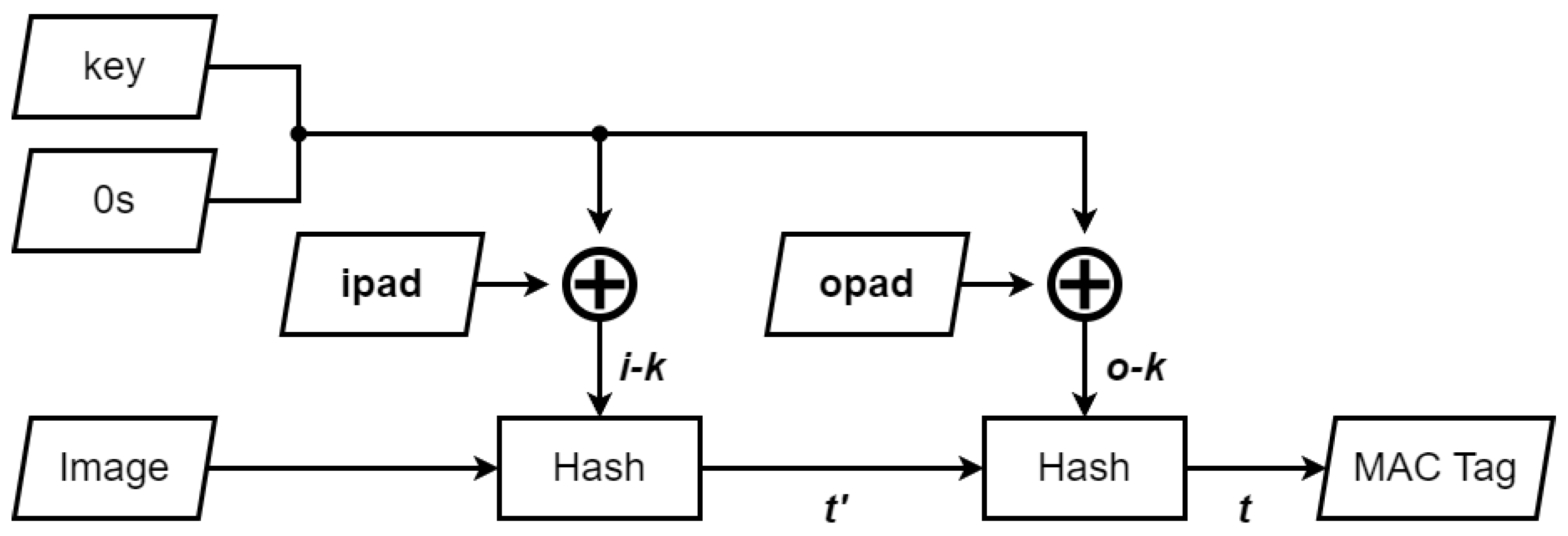
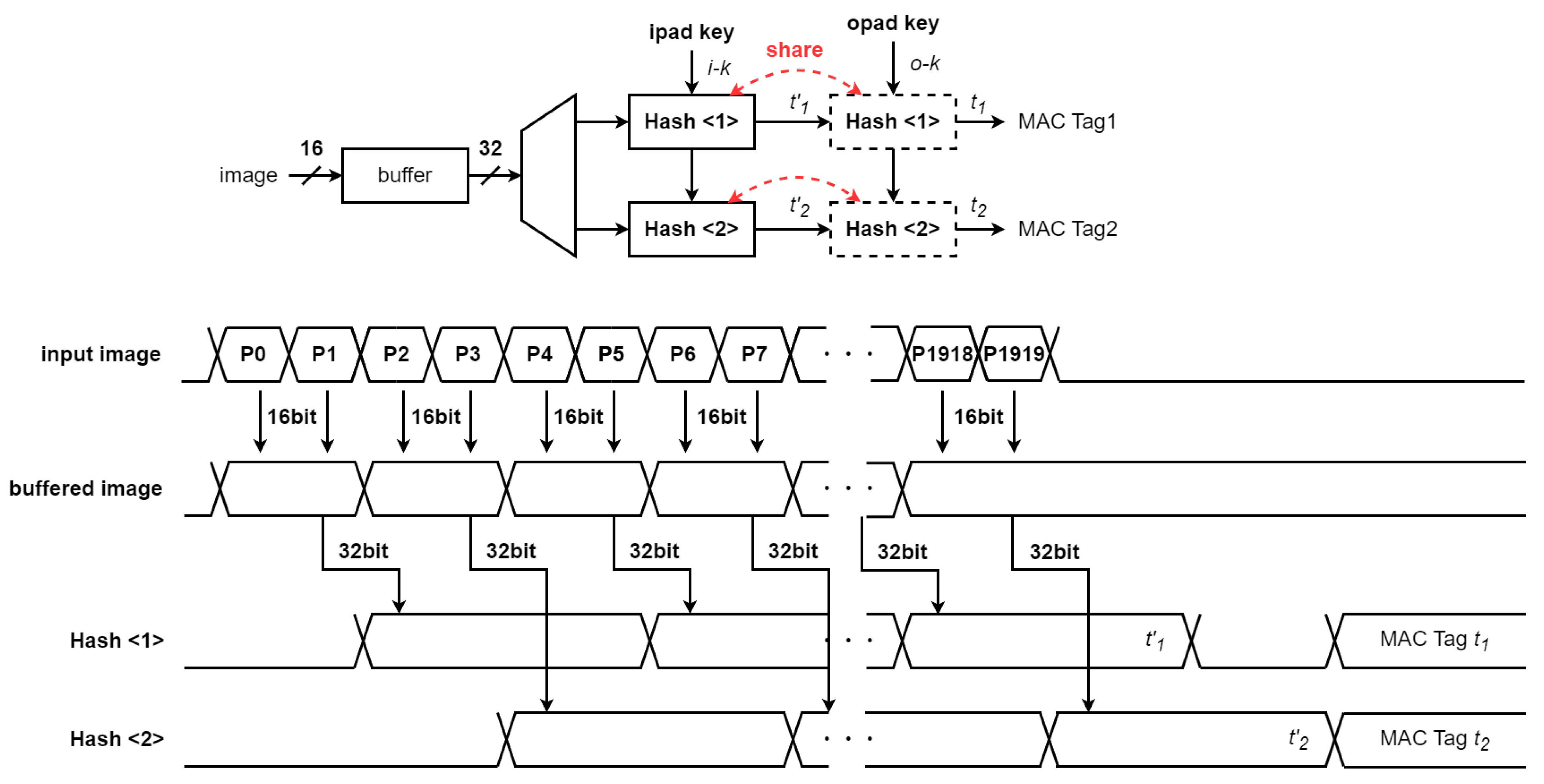
3.3. MAC Tag Generation Module
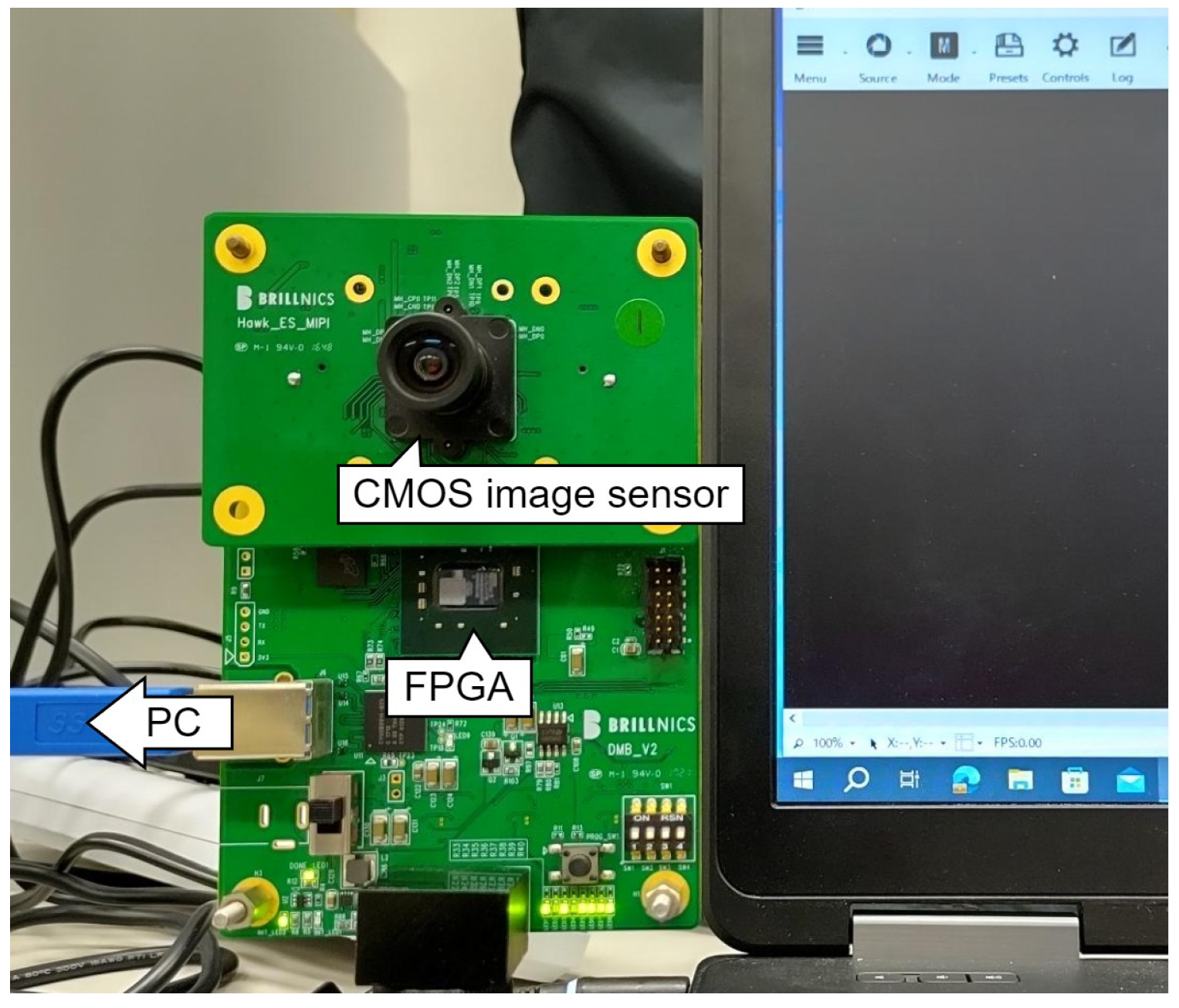
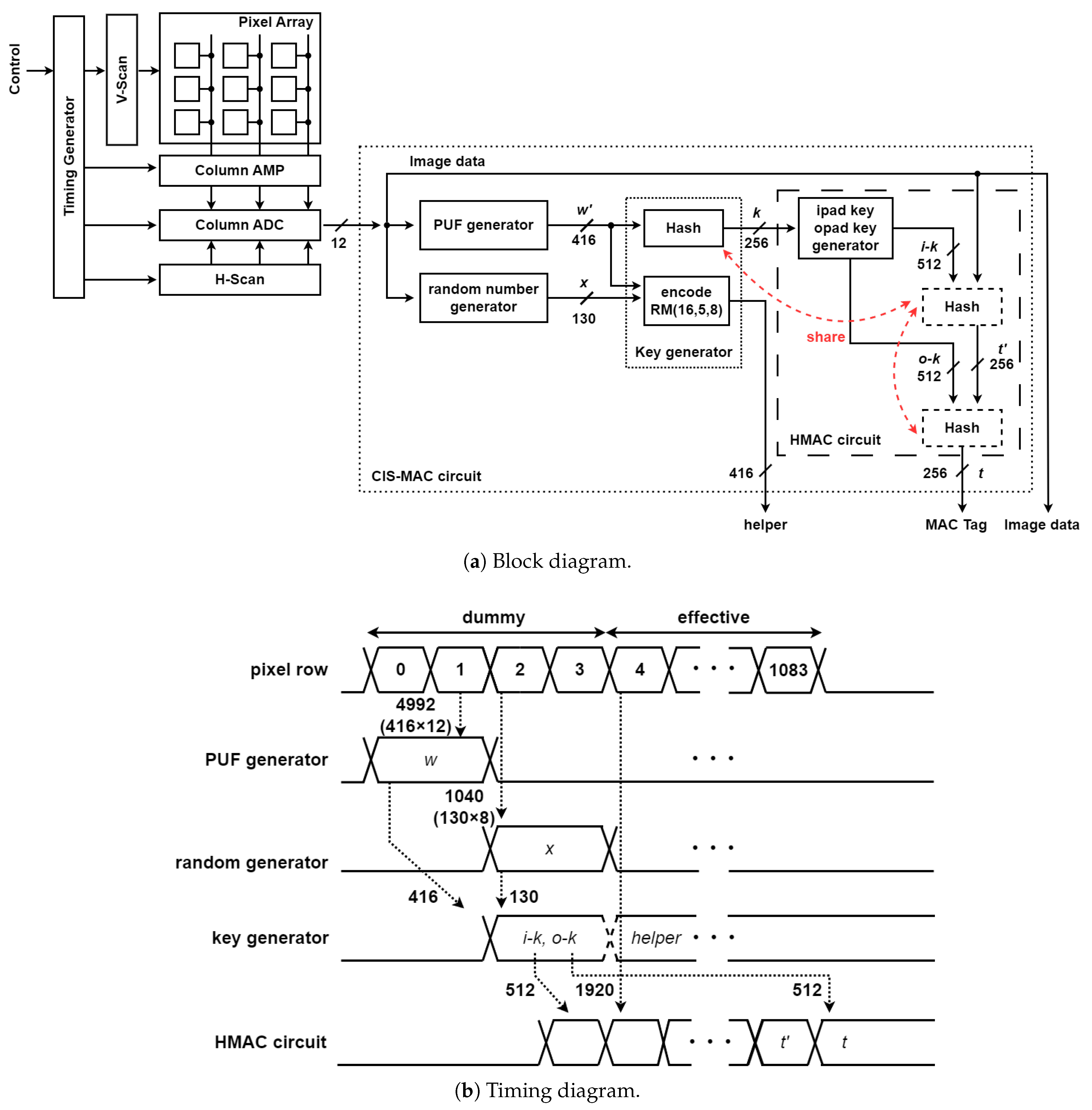
4. Design of the CIS–MAC Circuit
4.1. Proposed CMOS Image Sensor with Message Authentication
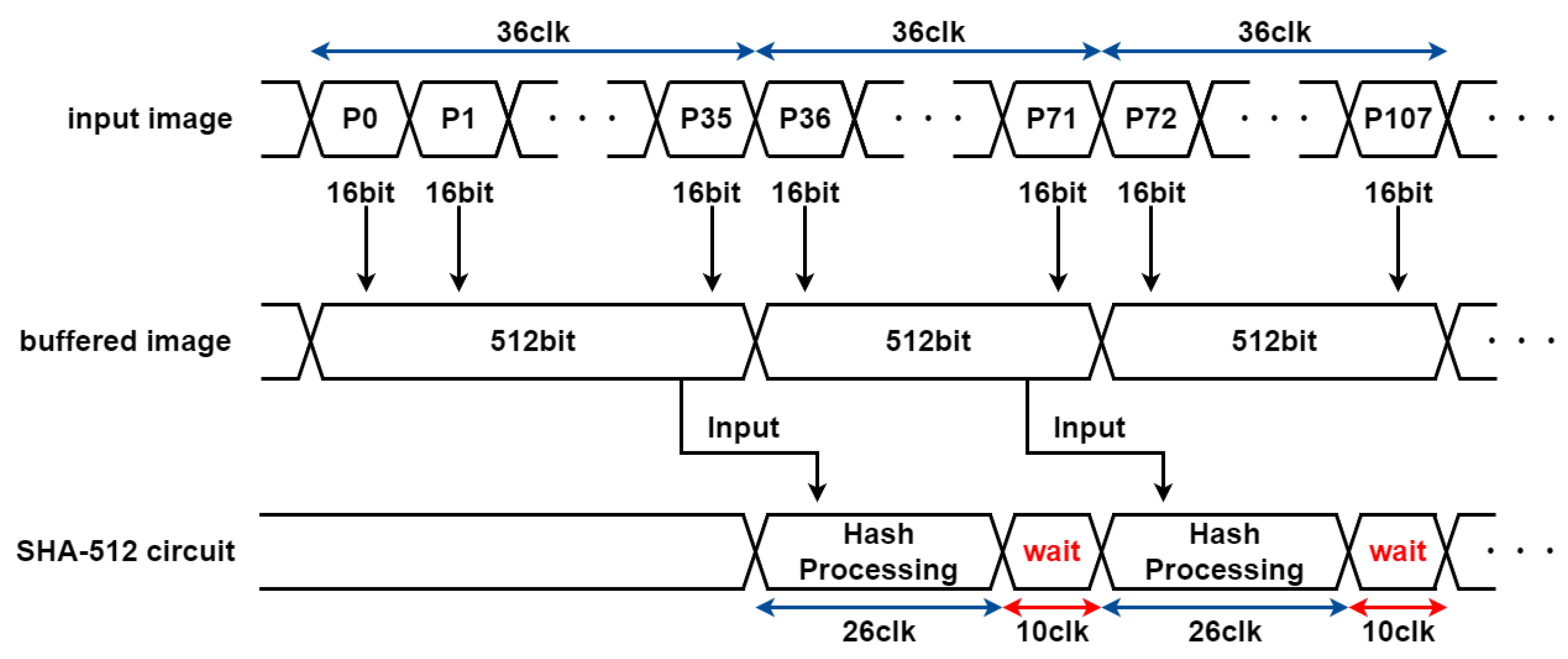
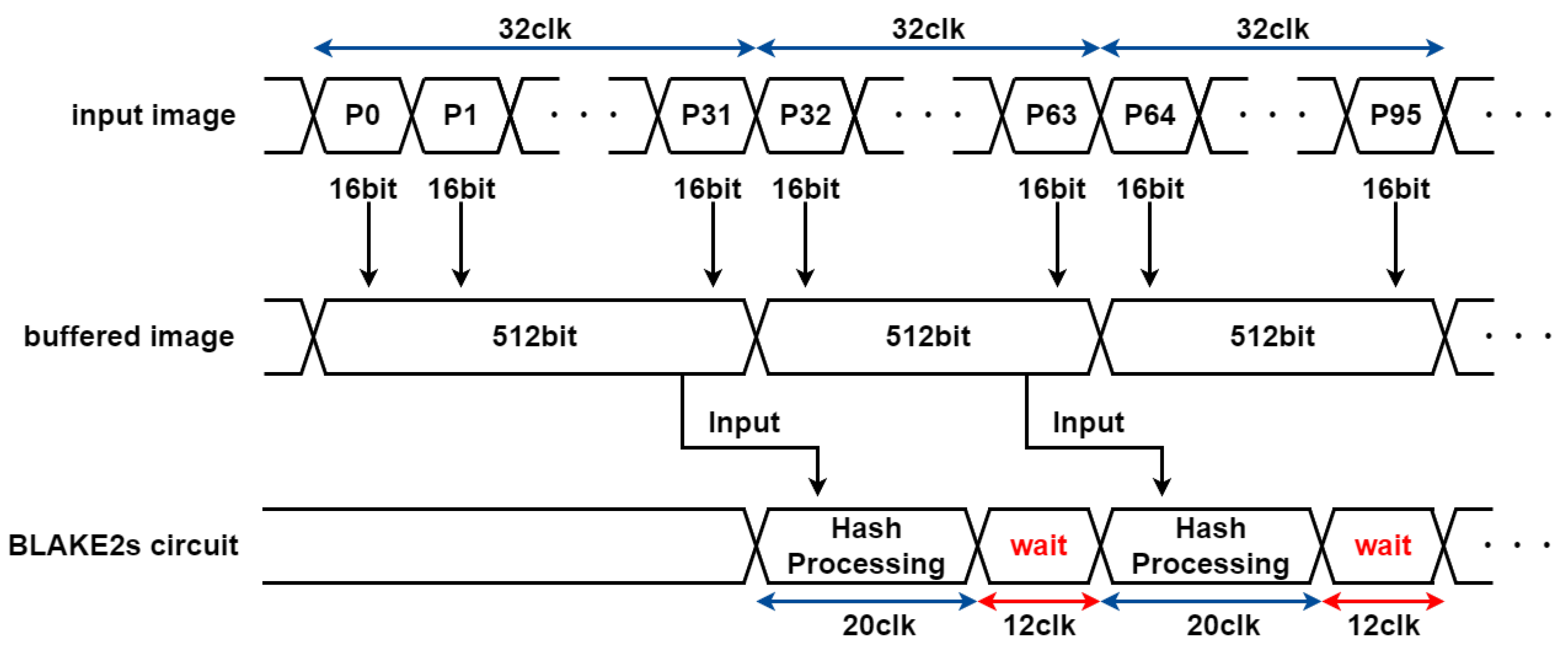
4.2. Evaluation of Hash Functions for the CIS–MAC
4.3. Timing Design of the HMAC Circuit
4.4. Simulation Results
4.5. Circuit Area Estimation via Logic Synthesis
5. Conclusions and Future Work
6. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Seok, M. A 3.07 μm2/bitcell physically unclonable function with 3.5% and 1% bit-instability across 0 to 80 ∘C and 0.6 to 1.2 V in a 65 nm CMOS. In Proceedings of the Symposia on VLSI Technology and Circuits, Kyoto, Japan, 16–19 June 2015; pp. C250–C251. [Google Scholar] [CrossRef]
- Yoshimoto, Y.; Katoh, Y.; Ogasahara, S.; Wei, Z.; Kouno, K. A ReRAM-based physically unclonable function with bit error rate <0.5% after 10 years at 125 ∘C for 40 nm embedded application. In Proceedings of the Symposia on VLSI Technology and Circuits, Honolulu, HI, USA, 13–17 June 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Willers, O.; Huth, C.; Guajardo, J.; Seidel, H. MEMS-Based Gyroscopes as Physical Unclonable Functions; IEICE Technical Committee on CCS Computer and Communications Security: Vienna, Austria, 24–28 October 2016. [Google Scholar]
- Chen, J.; Tanamoto, T.; Noguchi, H.; Mitani, Y. Further investigations on traps stabilities in random telegraph signal noise and the application to a novel concept physical unclonable function (PUF) with robust reliabilities. In Proceedings of the Symposia on VLSI Technology and Circuits, Kyoto, Japan, 16–19 June 2015; pp. T40–T41. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, L.; Zalivaka, S.S.; Chang, C.H.; Chen, S. CMOS Image Sensor Based Physical Unclonable Function for Coherent Sensor-Level Authentication. IEEE TCAS-I 2015, 62, 2629–2640. [Google Scholar] [CrossRef]
- Lu, L.; Kim, T.T.H. A High Reliable SRAM-Based PUF With Enhanced Challenge-Response Space. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 589–593. [Google Scholar] [CrossRef]
- Lin, B.; Pang, Y.; Gao, B.; Tang, J.; Wu, D.; Chang, T.W.; Lin, W.E.; Sun, X.; Yu, S.; Chang, M.F.; et al. A Highly Reliable RRAM Physically Unclonable Function Utilizing Post-Process Randomness Source. IEEE J. Solid-State Circuits 2021, 56, 1641–1650. [Google Scholar] [CrossRef]
- Okura, S.; Nakura, Y.; Shirahata, M.; Shiozaki, M.; Kubota, T.; Ishikawa, K.; Takayanagi, I.; Fujino, T. A Proposal of PUF Utilizing Pixel Variations in the CMOS Image Sensor. In Proceedings of the International Image Sensor Workshop, Hiroshima, Japan, 30 May–2 June 2017; pp. 66–69. [Google Scholar]
- Okura, S.; Ishiki, R.; Shirahata, M.; Kubota, T.; Shiozaki, M.; Ishikawa, K.; Takayanagi, I.; Fujino, T. A Dynamic Soft-Decision Fuzzy Extractor for a CMOS Image Sensor PUF. In Proceedings of the 2018 ISPACS, Ishigaki, Japan, 27–30 November 2018. [Google Scholar]
- Turay, T.; Vladimirova, T. Toward Performing Image Classification and Object Detection with Convolutional Neural Networks in Autonomous Driving Systems: A Survey. IEEE Access 2022, 10, 14076–14119. [Google Scholar] [CrossRef]
- Fujiyoshi, H.; Hirakawa, T.; Yamashita, T. Deep learning-based image recognition for autonomous driving. IATSS Res. 2019, 43, 244–252. [Google Scholar] [CrossRef]
- Badjie, B.; Cecílio, J.; Casimiro, A. Adversarial Attacks and Countermeasures on Image Classification-based Deep Learning Models in Autonomous Driving Systems: A Systematic Review. ACM Comput. Surv. 2024, 57, 1–52. [Google Scholar] [CrossRef]
- Suman, S.; Kumar, D.; Kumar, A. Fuzzy Based Convolutional Noise Clustering Classifier to Handle the Noise and Heterogeneity in Image Classification. Mathematics 2022, 10, 4056. [Google Scholar] [CrossRef]
- Oyama, T.; Okura, S.; Yoshida, K.; Fujino, T. Backdoor attack on deep neural networks triggered by fault injection attack on image sensor interface. In Proceedings of the 5th Workshop on Attacks and Solutions in Hardware Security, Virtual, 19 November 2021; pp. 63–72. [Google Scholar]
- Liu, W.; He, W.; Hu, B.; Chang, C.H. A practical man-in-the-middle attack on deep learning edge device by sparse light strip injection into camera data lane. In Proceedings of the 2022 IEEE 35th International System-on-Chip Conference (SOCC), Belfast, UK, 5–8 September 2022; pp. 1–6. [Google Scholar]
- Jiang, Q.; Ji, X.; Yan, C.; Xie, Z.; Lou, H.; Xu, W. GlitchHiker: Uncovering vulnerabilities of image signal transmission with IEMI. In Proceedings of the 32nd USENIX Security Symposium (USENIX Security 23), Anaheim, CA, USA, 9–11 August 2023; pp. 7249–7266. [Google Scholar]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Gu, T.; Dolan-Gavitt, B.; Garg, S. Badnets: Identifying vulnerabilities in the machine learning model supply chain. arXiv 2017, arXiv:1708.06733. [Google Scholar]
- Gu, T.; Liu, K.; Dolan-Gavitt, B.; Garg, S. Badnets: Evaluating backdooring attacks on deep neural networks. IEEE Access 2019, 7, 47230–47244. [Google Scholar] [CrossRef]
- Oyama, T.; Yoshida, K.; Okura, S.; Fujino, T. Fundamental study of adversarial examples created by fault injection attack on image sensor interface. In Proceedings of the 2022 Asian Hardware Oriented Security and Trust Symposium (AsianHOST), Singapore, 14–16 December 2022; pp. 1–6. [Google Scholar]
- Versaci, M.; Angiulli, G.; La Foresta, F.; Laganà, F.; Palumbo, A. Intuitionistic fuzzy divergence for evaluating the mechanical stress state of steel plates subject to bi-axial loads. Integr. Comput.-Aided Eng. 2024, 31, 1–17. [Google Scholar] [CrossRef]
- Stallkamp, J.; Schlipsing, M.; Salmen, J.; Igel, C. Man vs. computer: Benchmarking machine learning algorithms for traffic sign recognition. Neural Netw. 2012, 32, 323–332. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Maes, R.; Peeters, R.; Herrewege, A.; Wachsmann, C.; Katzenbeisser, S.; Sadeghi, A.R.; Verbauwhede, I. Reverse Fuzzy Extractors: Enabling Lightweight Mutual Authentication for PUF-enabled RFIDs. In Proceedings of the Financial Cryptography and Data Security: 16th International Conference, FC 2012, Kralendijk, Bonaire, 27 Februray–2 March 2012; Revised Selected Papers 16. pp. 374–389. [Google Scholar] [CrossRef]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Proceedings of the Advances In Cryptology-EUROCRYPT 2004: International Conference On The Theory And Applications Of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Proceedings 23. Springer: Berlin/Heidelberg, Germany, 2004; pp. 523–540. [Google Scholar]
- Okura, S.; Ishiki, R.; Takano, S.; Shirahata, M.; Kubota, T.; Shiozaki, M.; Ishikawa, K.; Takayanagi, I.; Fujino, T. A 2-Mpixel CMOS Image Sensor with Device Authentication and Encryption Key Generation based on Physically Unclonable Function. In Proceedings of the International Image Sensor Workshop, Snowbird Resort, UT, USA, 24–27 June 2019; pp. 119–122. [Google Scholar]
- Shiozaki, M.; Hori, Y.; Fujino, T. Entropy Estimation of Physically Unclonable Functions with Offset Error. Cryptology ePrint Archive, Paper 2020/1284. 2020. Available online: https://eprint.iacr.org/2020/1284 (accessed on 31 December 2024).
- Zhang, R.; Wang, X.; Liu, K.; Shinohara, H. A 0.186-pJ per Bit Latch-Based True Random Number Generator Featuring Mismatch Compensation and Random Noise Enhancement. IEEE J. Solid-State Circuits 2022, 57, 2498–2508. [Google Scholar] [CrossRef]
- Turan, M.S.; Barker, E.; Kelsey, J.; McKay, K.; Baish, M.; Boyle, M. NIST, SP 800–90B: Recommendation for the Entropy Sources Used for Random Bit Generation; Technical Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Clavier, C.; Gaj, K. Cryptographic Hardware and Embedded Systems-CHES 2009: 11th International Workshop Lausanne, Switzerland, 6–9 September 2009; Proceedings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 5747. [Google Scholar]
- Maes, R.; Tuyls, P.; Verbauwhede, I. A soft decision helper data algorithm for SRAM PUFs. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Republic of Korea, 28 June–3 July 2009; pp. 2101–2105. [Google Scholar] [CrossRef]
- Turner, J.M. The keyed-hash message authentication code (hmac). Fed. Inf. Process. Stand. Publ. 2008, 198, 1–13. [Google Scholar]
- Abed, S.; Jaffal, R.; Mohd, B.J.; Al-Shayeji, M. An analysis and evaluation of lightweight hash functions for blockchain-based IoT devices. Clust. Comput. 2021, 24, 3065–3084. [Google Scholar] [CrossRef]
- Rao, V.; Prema, K.V. Light-weight hashing method for user authentication in Internet-of-Things. Ad Hoc Netw. 2019, 89, 97–106. [Google Scholar] [CrossRef]
- Dobraunig, C.; Eichlseder, M.; Mendel, F. Security Evaluation of sha-224, sha-512/224, and sha-512/256; Institute for Applied Information Processing and Communications, Graz University of Technology: Graz, Austria, 2015. [Google Scholar]
- Turan, M.S.; Perlner, R.; Bassham, L.E.; Burr, W.; Chang, D.; jen Chang, S.; Dworkin, M.J.; Kelsey, J.M.; Paul, S.; Peralta, R. Status Report on the Second Round of the SHA-3 Cryptographic Hash Algorithm Competition; NIST Interagency Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011; Volume 7764. [Google Scholar]
- Sekioka, Y.; Oyama, T.; Tatsuno, H.; Yoshida, K.; Okura, S.; Fujino, T. A Study on Small Area HMAC-SHA256 Circuit Suitable for CMOS Image Sensor; Technical Report; HWS Technical Committee on Hardware Security; Institute of Electronics, Information and Communication Engineers: Tokyo, Japan, 7–8 March 2022; Volume 122. [Google Scholar]
- Guo, J.; Peyrin, T.; Poschmann, A. The PHOTON Family of Lightweight Hash Functions. Cryptology ePrint Archive, Paper 2011/609. 2011. Available online: https://eprint.iacr.org/2011/609.pdf (accessed on 31 December 2024).
- Aumasson, J.P.; Henzen, L.; Meier, W.; Naya-Plasencia, M. Quark: A Lightweight Hash. J. Cryptol. 2013, 26, 313–339. [Google Scholar] [CrossRef]
- Bogdanov, A.; Knezevic, M.; Leander, G.; Toz, D.; Varici, K.; Verbauwhede, I. SPONGENT: The Design Space of Lightweight Cryptographic Hashing. Cryptology ePrint Archive, Paper 2011/697. 2011. Available online: https://eprint.iacr.org/2011/697.pdf (accessed on 31 December 2024).
- Nannipieri, P.; Bertolucci, M.; Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Falaschi, F.; Fanucci, L.; Saponara, S. SHA2 and SHA-3 accelerator design in a 7 nm technology within the European Processor Initiative. Microprocess. Microsystems 2021, 87, 103444. [Google Scholar] [CrossRef]
- Aumasson, J.P.; Neves, S.; Wilcox-O’Hearn, Z.; Winnerlein, C. BLAKE2: Simpler, smaller, fast as MD5. Cryptology ePrint Archive, Paper 2013/322. 2013. Available online: https://eprint.iacr.org/2013/322 (accessed on 31 December 2024).
- Saarinen, M.J.O.; Aumasson, J.P. The BLAKE2 Cryptographic Hash and Message Authentication Code (MAC); RFC 7693; Internet Engineering Task Force: Fremont, CA, USA, 2015. [Google Scholar] [CrossRef]
- Onodera, H.; Hirata, A.; Kitamura, T.; Kobayashi, K.; Tamaru, K. P2Lib: Process Portable Library and Its Generation System. Trans. Inf. Process. Soc. Jpn. 1999, 40, 1660–1669. [Google Scholar]
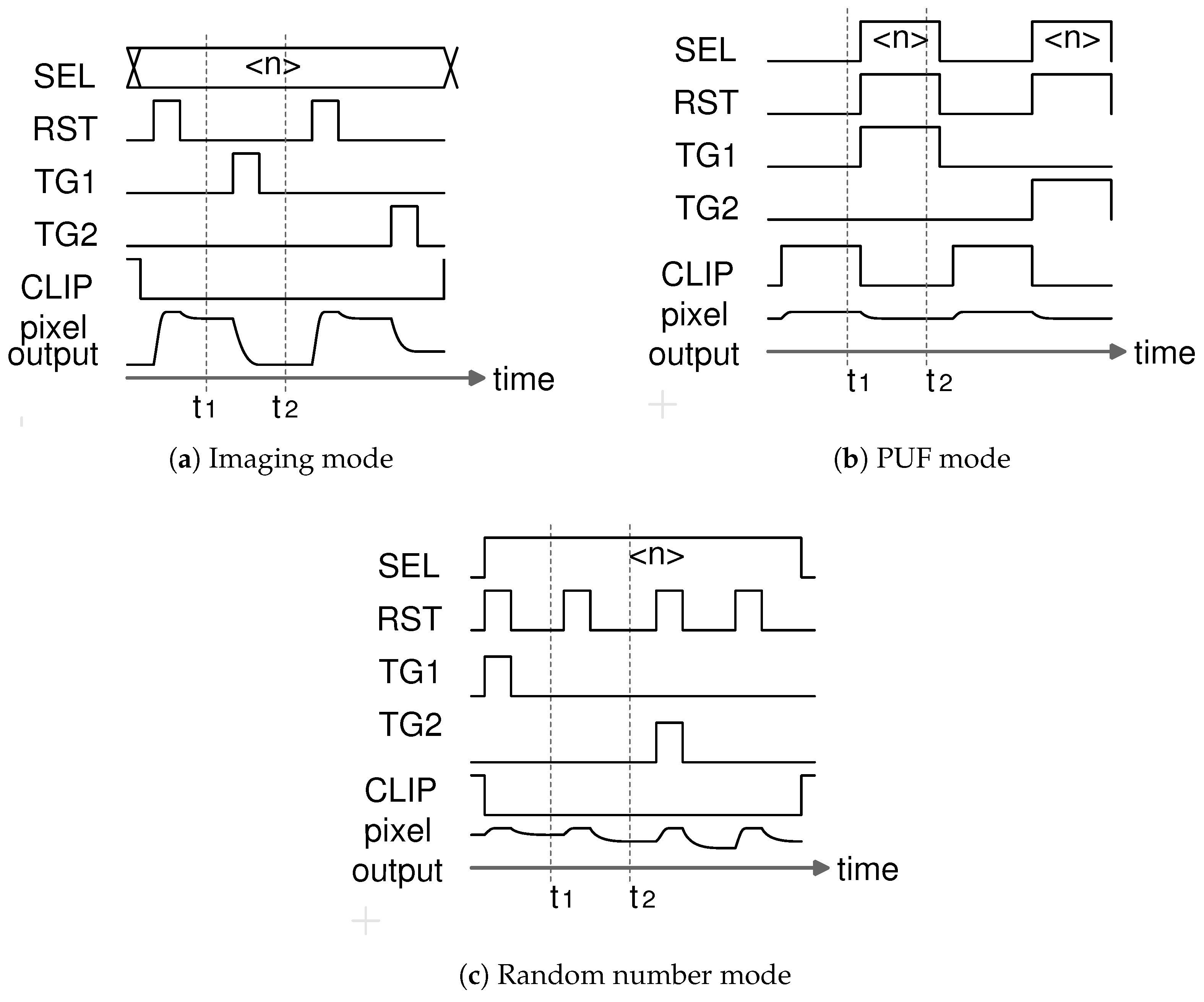
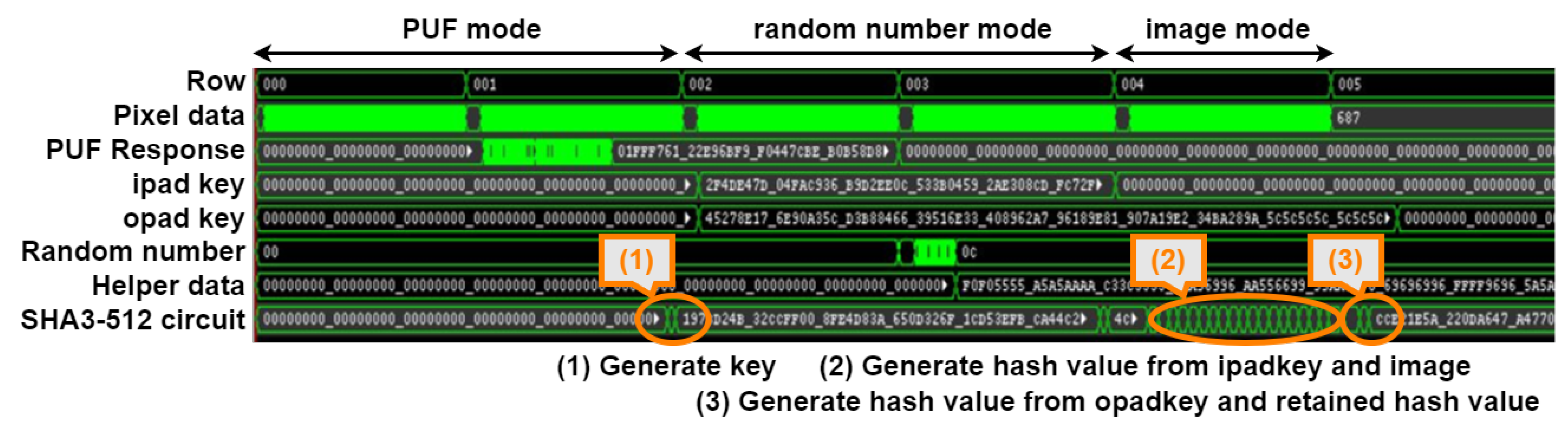
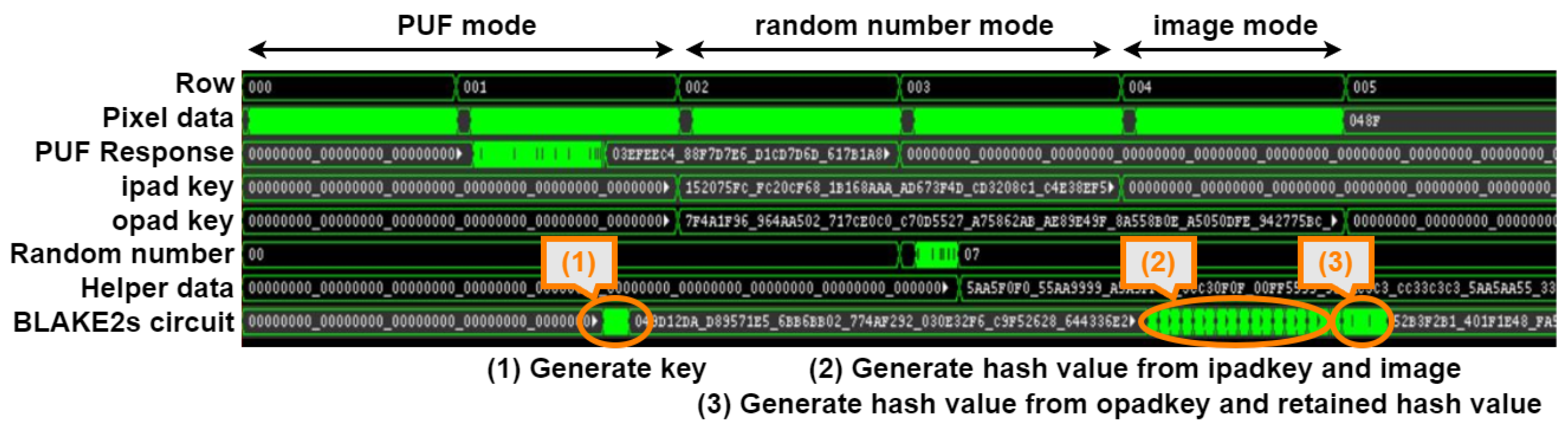
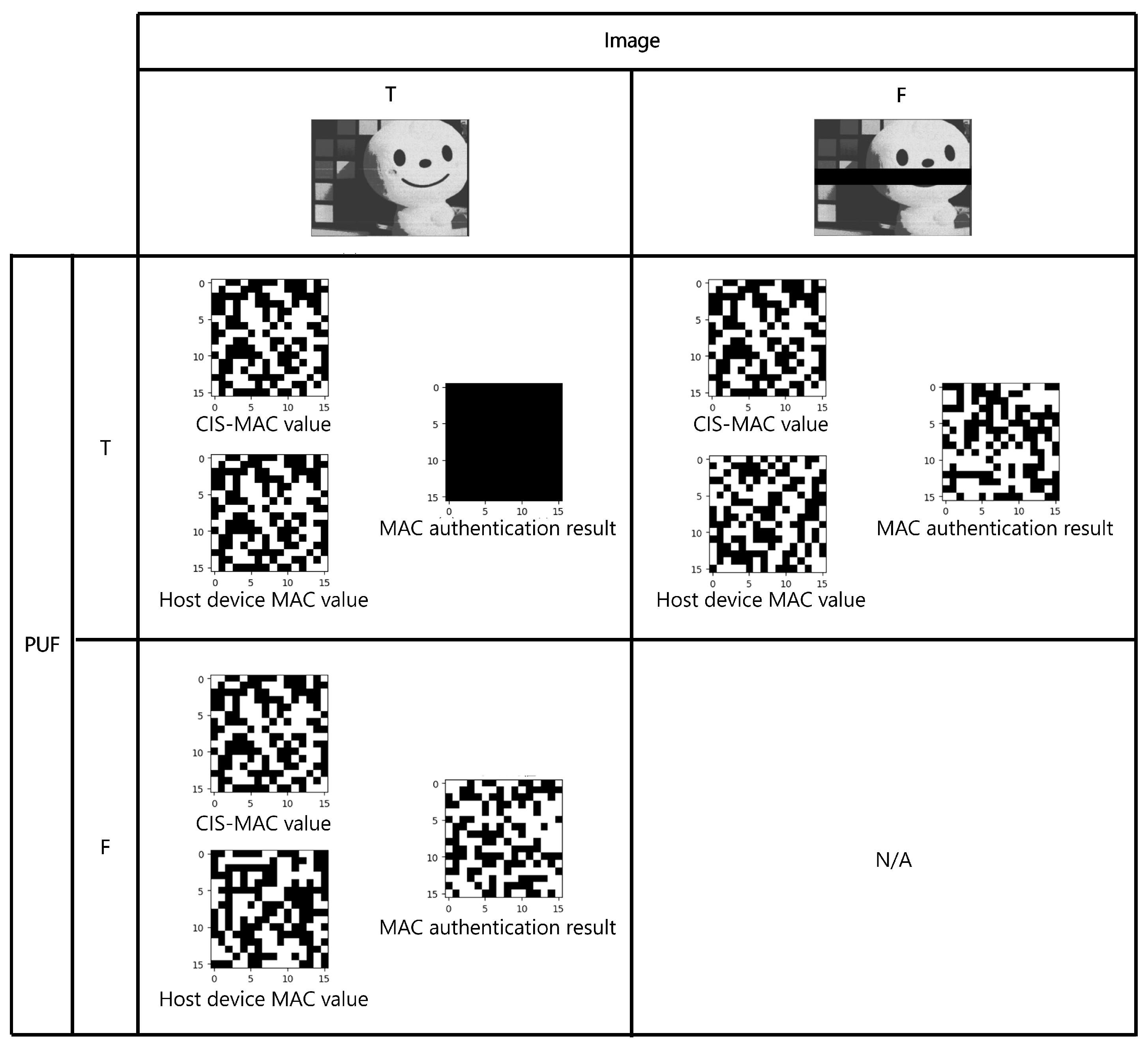
| Mode | Imaging | PUF | Random Number |
|---|---|---|---|
| Optical Signal | readout | removed | canceled |
| Vth variation | canceled | readout () | canceled |
| kTC noise | canceled | readout () | readout |
| #XOR | Min. Entropy |
|---|---|
| XOR ×0 | 0.780533 |
| XOR ×1 | 0.907243 |
| XOR ×2 | 0.923184 |
| XOR ×3 | 0.932590 |
| (A) Ave. p-Value | (A) Passed | (B) Ave. p-Value | (B) Passed | |
|---|---|---|---|---|
| Frequency | 0.000000 | 0/60 | 0.275709 | 59/60 |
| BlockFrequency | 0.000000 | 0/60 | 0.468595 | 59/60 |
| CumulativeSums | 0.000000 | 0/60 | 0.949602 | 59/60 |
| Runs | 0.000000 | 0/60 | 0.931952 | 58/60 |
| LongestRun | 0.000000 | 0/60 | 0.888137 | 59/60 |
| Rank | 0.437274 | 59/60 | 0.931952 | 58/60 |
| FFT | 0.000000 | 0/60 | 0.299251 | 57/60 |
| NonOverlappingTemplate | 0.000296 | 55/60 | 0.976060 | 60/60 |
| OverlappingTemplate | 0.000000 | 0/60 | 0.804337 | 59/60 |
| Universal | 0.000000 | 0/60 | 0.671779 | 59/60 |
| ApproximateEntropy | 0.000000 | 0/60 | 0.568055 | 58/60 |
| RandomExcursions | — | — | 0.804337 | 38/38 |
| RandomExcursionsVariant | — | — | 0.739918 | 37/38 |
| Serial | 0.000000 | 8/60 | 0.568055 | 59/60 |
| LinearComplexity | 0.834308 | 59/60 | 0.964295 | 60/60 |
| Hash Circuit | Input Bits [bit] | Cycle [clk] | Number of Interleaved Circuits | Circuit Area [kGE/Unit] | Area of the Entire Interleaved Circuit [kGE] |
|---|---|---|---|---|---|
| SHA–256 | 512 | 68 | 3 | 13 | 39 |
| SHA–512 | 1024 | 88 | 2 | 28.4 | 56.8 |
| PHOTON 80/20/16 | 20 | 132 | 106 | 1.2 | 123.8 |
| PHOTON 128/16/16 | 16 | 156 | 156 | 1.7 | 266.5 |
| PHOTON 160/36/36 | 36 | 180 | 80 | 2.1 | 169.4 |
| PHOTON 224/32/32 | 32 | 204 | 102 | 2.8 | 284.2 |
| PHOTON 256/32/32 | 32 | 156 | 78 | 4.4 | 340.2 |
| U–Quark | 8 | 68 | 136 | 2.4 | 325.3 |
| D–Quark | 16 | 88 | 88 | 2.8 | 248.1 |
| S–Quark | 32 | 64 | 32 | 4.6 | 148.5 |
| SPONGENT–88 | 8 | 45 | 90 | 1.1 | 101.4 |
| SPONGENT–128 | 8 | 70 | 140 | 1.7 | 236.2 |
| SPONGENT–160 | 16 | 90 | 90 | 2.2 | 197.1 |
| SPONGENT–224 | 16 | 120 | 120 | 2.9 | 348.4 |
| SPONGENT–256 | 16 | 140 | 140 | 3.3 | 459.3 |
| SHA3–224 | 1152 | 25 | 1 | 31.3 | 31.3 |
| SHA3–256 | 1088 | 25 | 1 | 31.6 | 31.6 |
| SHA3–384 | 832 | 25 | 1 | 31.4 | 31.4 |
| SHA3–512 | 576 | 25 | 1 | 30.7 | 30.7 |
| BLAKE2b | 1024 | 29 | 1 | 41.5 | 41.5 |
| BLAKE2s | 512 | 20 | 1 | 20.8 | 20.8 |
| Hash Circuit | Circuit Area [GE] |
|---|---|
| SHA–256 | 113k (Hash circuit: 13k) |
| SHA3–512 | 71k (Hash circuit: 26k) |
| BLAKE2s | 67k (Hash circuit: 21k) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogi, Y.; Hagizaki, M.; Oyama, T.; Ogawa, H.; Yoshida, K.; Fujino, T.; Okura, S. Hash-Based Message Authentication Code with a Reverse Fuzzy Extractor for a CMOS Image Sensor. Electronics 2025, 14, 1971. https://doi.org/10.3390/electronics14101971
Rogi Y, Hagizaki M, Oyama T, Ogawa H, Yoshida K, Fujino T, Okura S. Hash-Based Message Authentication Code with a Reverse Fuzzy Extractor for a CMOS Image Sensor. Electronics. 2025; 14(10):1971. https://doi.org/10.3390/electronics14101971
Chicago/Turabian StyleRogi, Yuki, Manami Hagizaki, Tatsuya Oyama, Hiroaki Ogawa, Kota Yoshida, Takeshi Fujino, and Shunsuke Okura. 2025. "Hash-Based Message Authentication Code with a Reverse Fuzzy Extractor for a CMOS Image Sensor" Electronics 14, no. 10: 1971. https://doi.org/10.3390/electronics14101971
APA StyleRogi, Y., Hagizaki, M., Oyama, T., Ogawa, H., Yoshida, K., Fujino, T., & Okura, S. (2025). Hash-Based Message Authentication Code with a Reverse Fuzzy Extractor for a CMOS Image Sensor. Electronics, 14(10), 1971. https://doi.org/10.3390/electronics14101971






