Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts
Abstract
1. Introduction
2. System Description
2.1. Sytstem Setup
2.1.1. Power Supply System
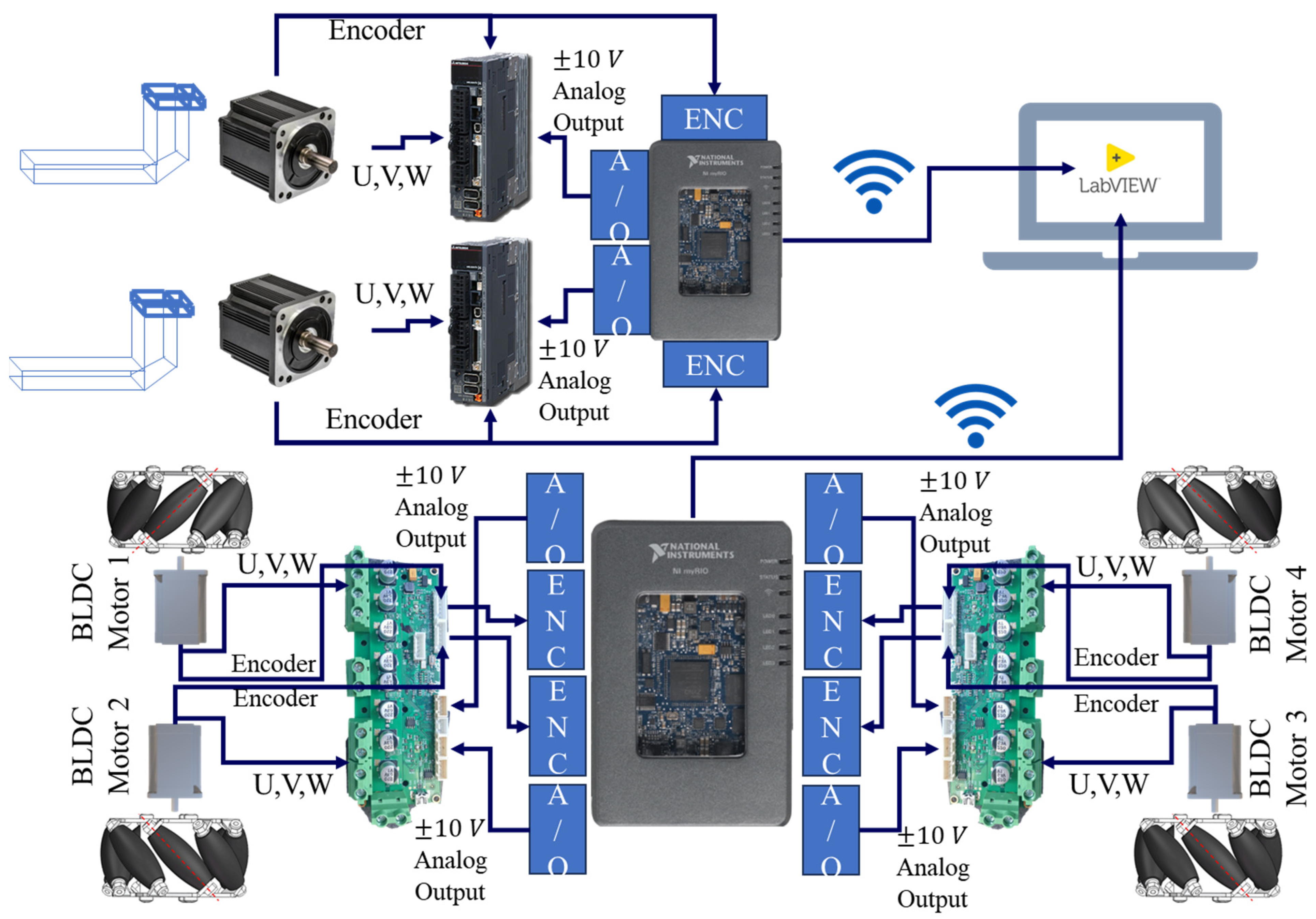
2.1.2. Connection Diagram
2.1.3. Control Components
3. Mecanum-Wheeled Mobile Robot System Modeling
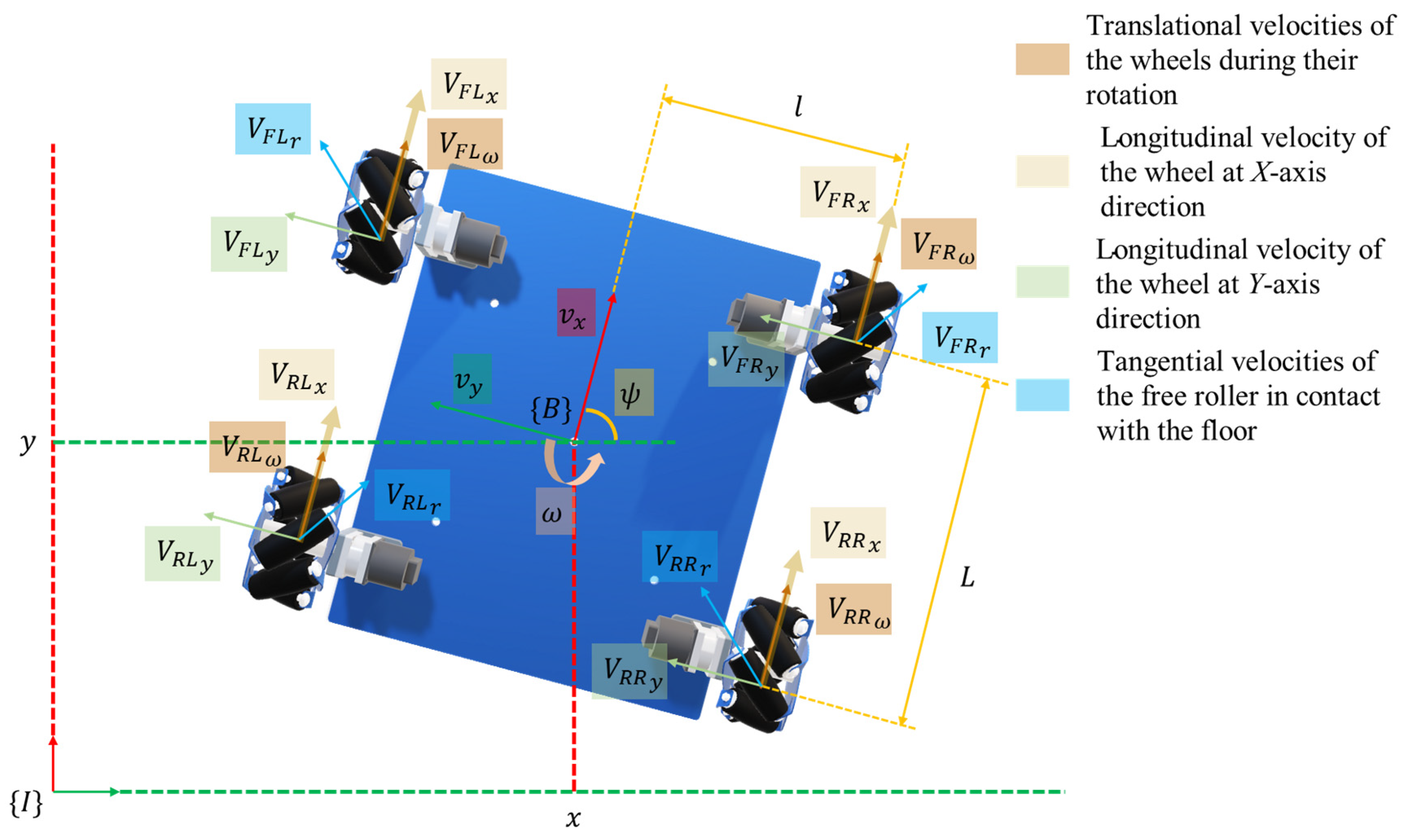
3.1. Vehicle Kinematics
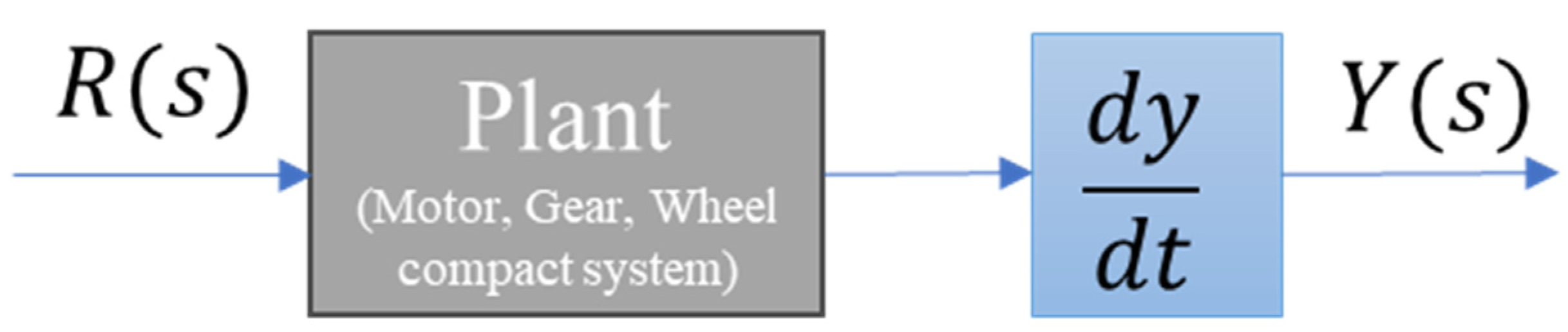
3.2. System Identification of Mecanum-Wheeled Mobile Robot System
3.3. Control Design of Mecanum-Wheeled Mobile Robot System
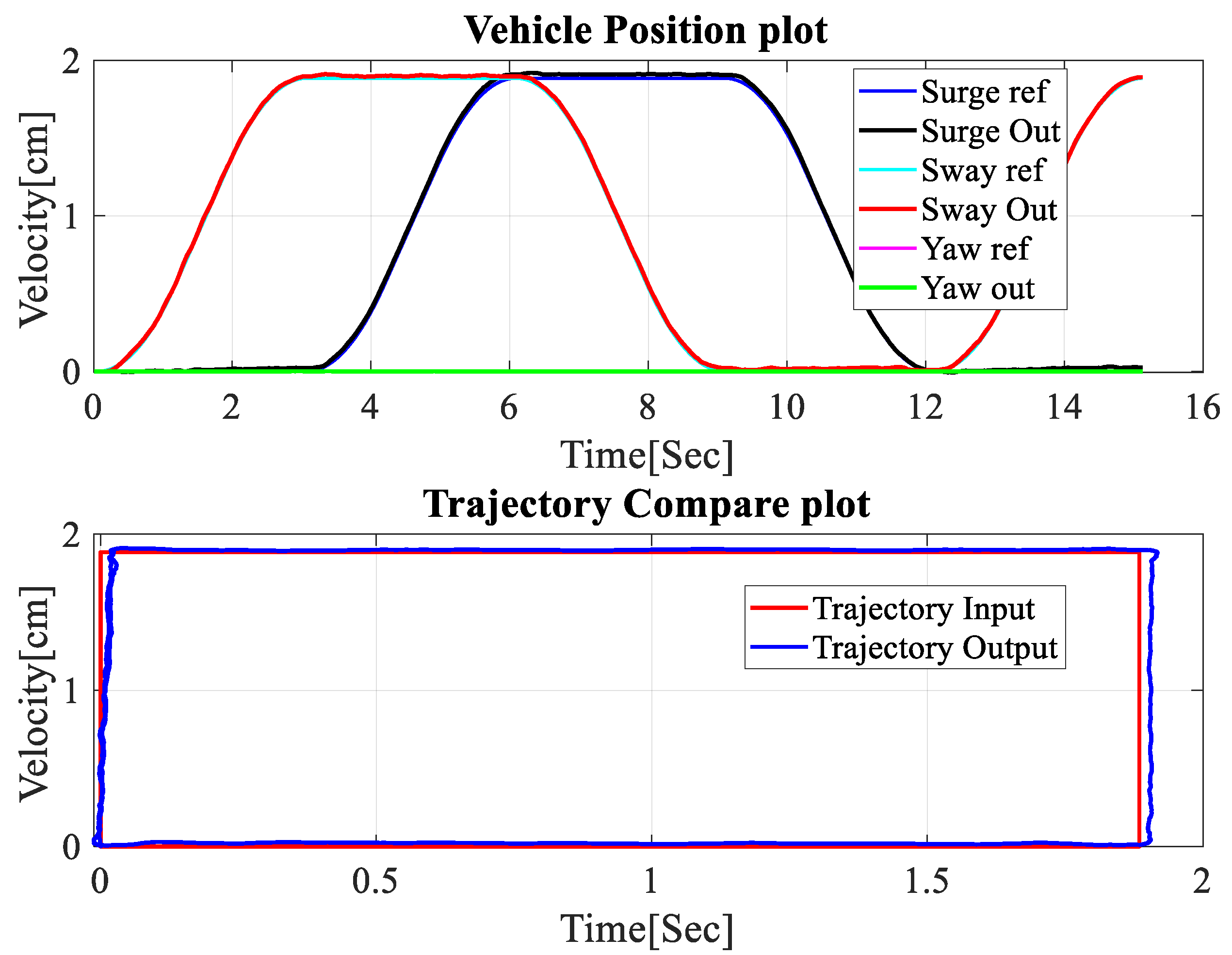
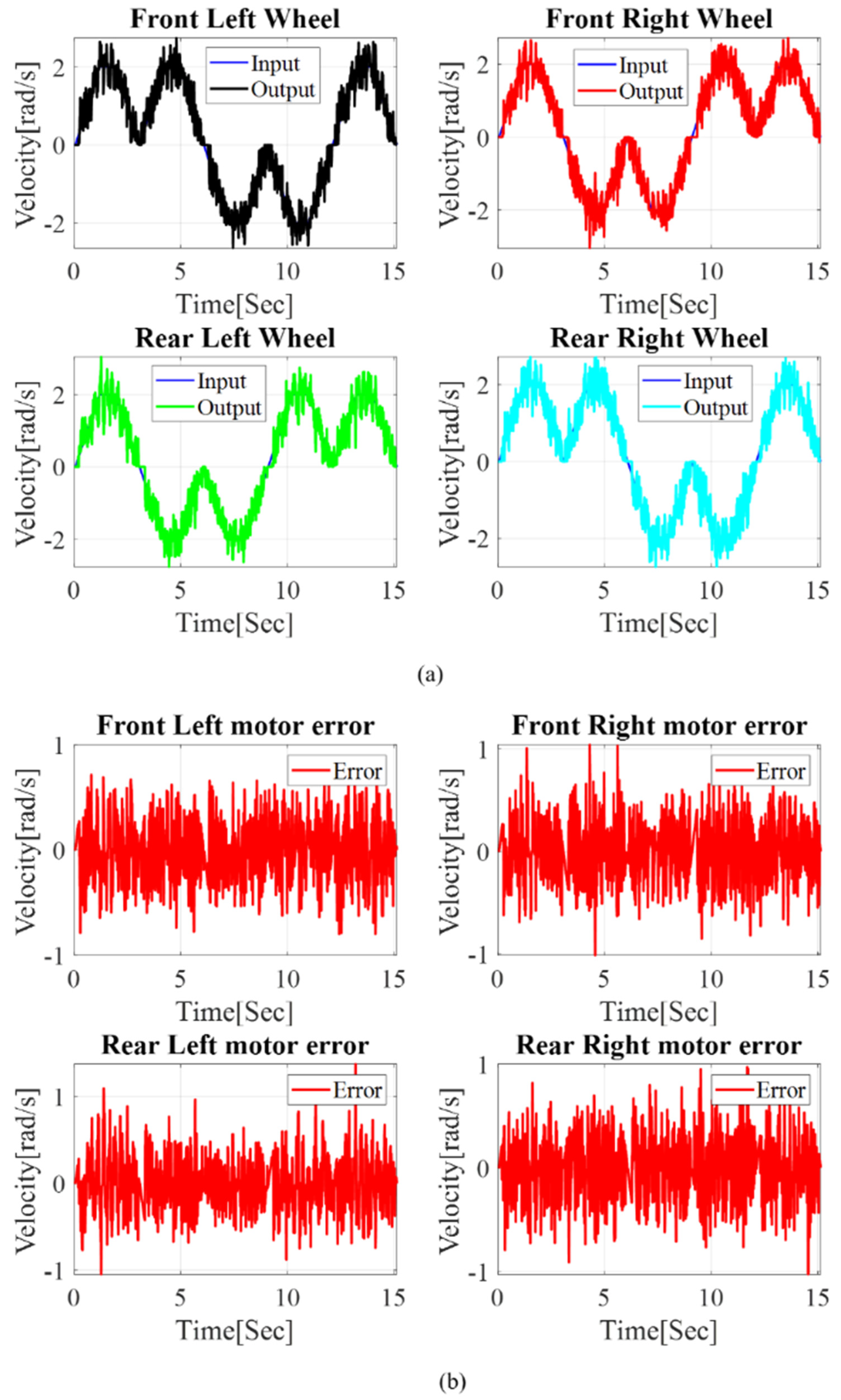
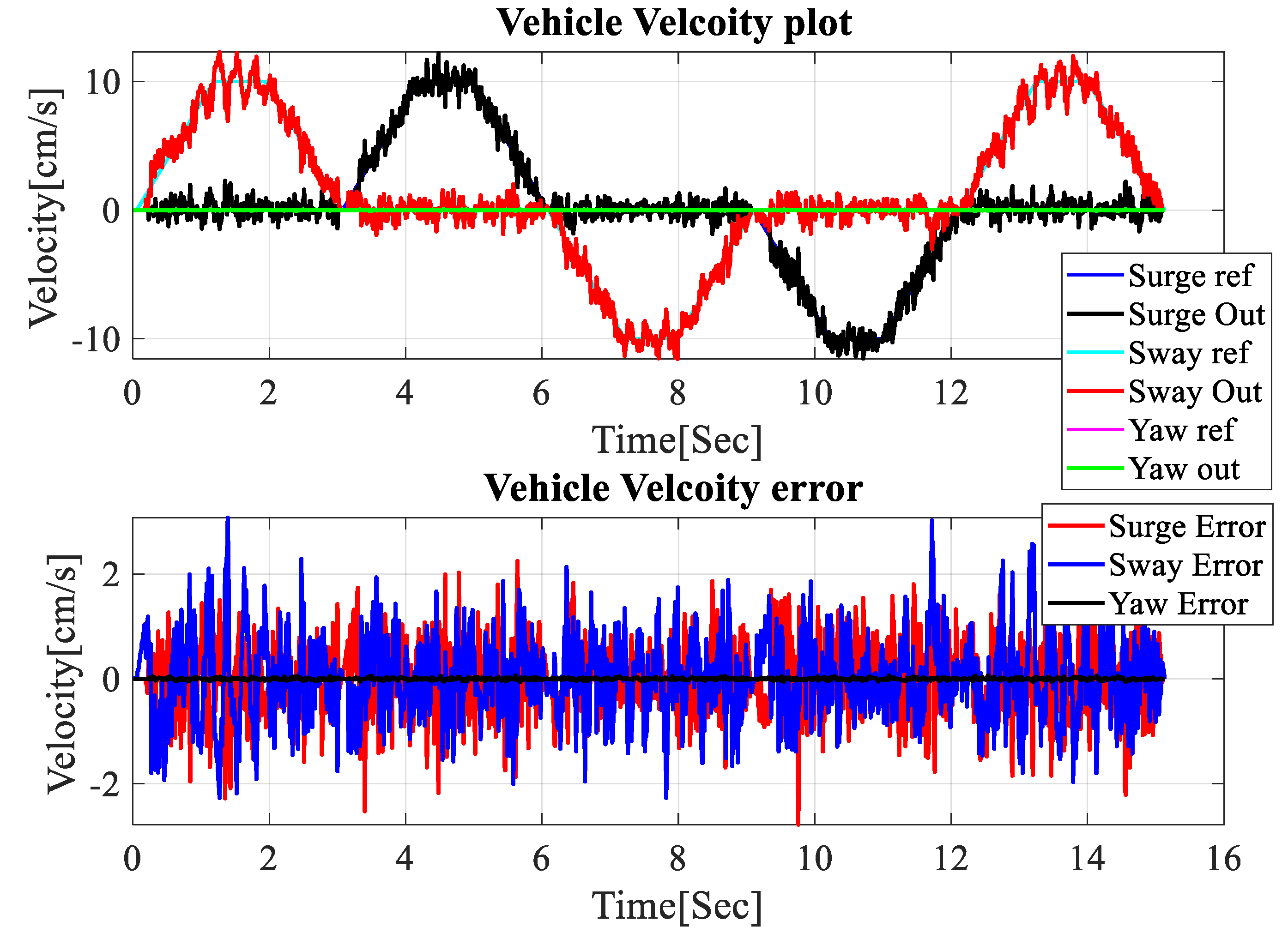
3.4. Control Performance Test of Mecanum-Wheeled Mobile Robot System
4. Forklift System Modeling
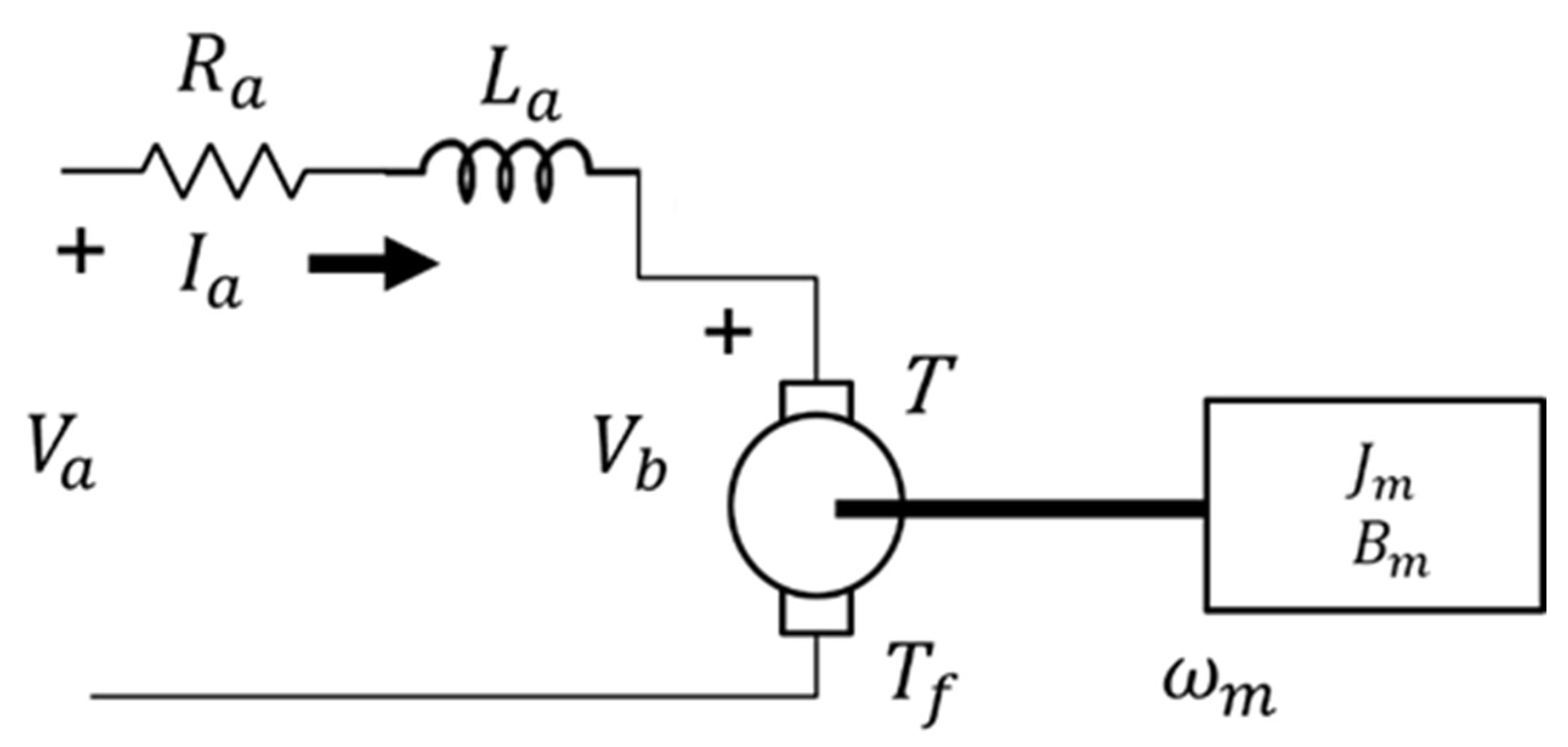
4.1. System Dynamics of Servo AC Motor
4.2. System Identification of the Servo AC Motor
5. Position Controller Design
5.1. Synchronization Methods for Pallet Carrier Motors
5.1.1. Independent Control Method
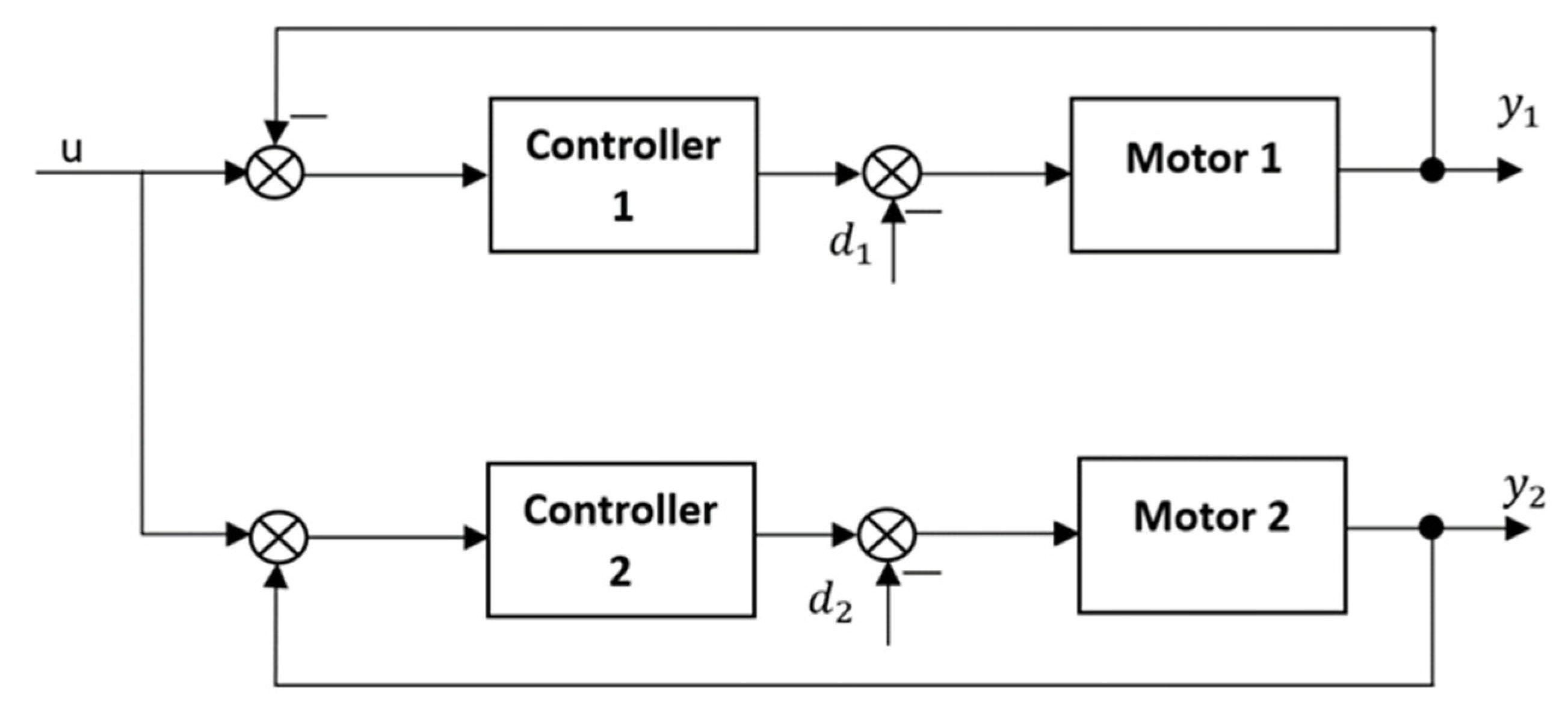
5.1.2. Master–Slave Control Method
5.1.3. Proposed Control Method
6. Experiments of Synchronization Performance
6.1. Experimental Setup
6.2. Experiments
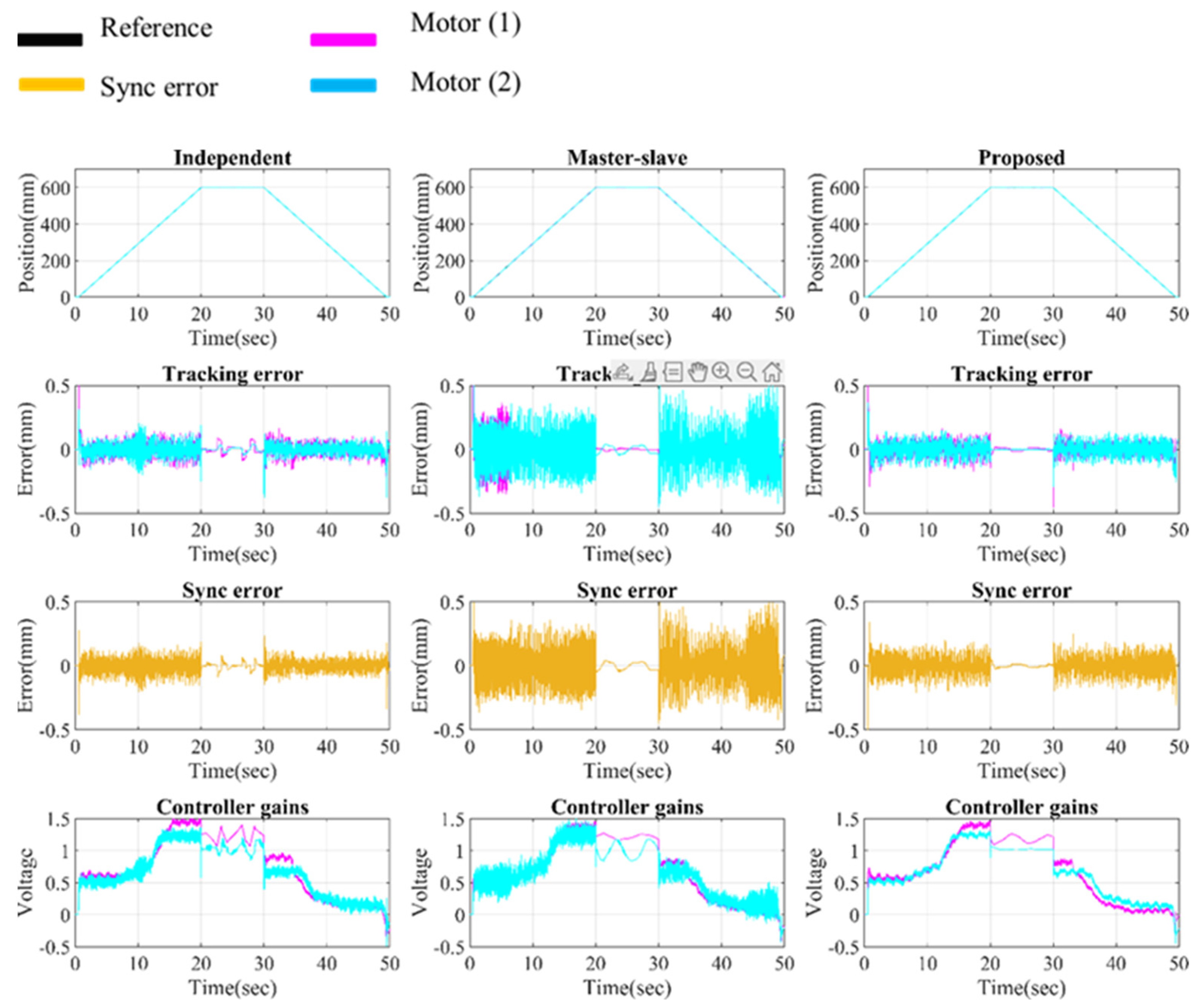
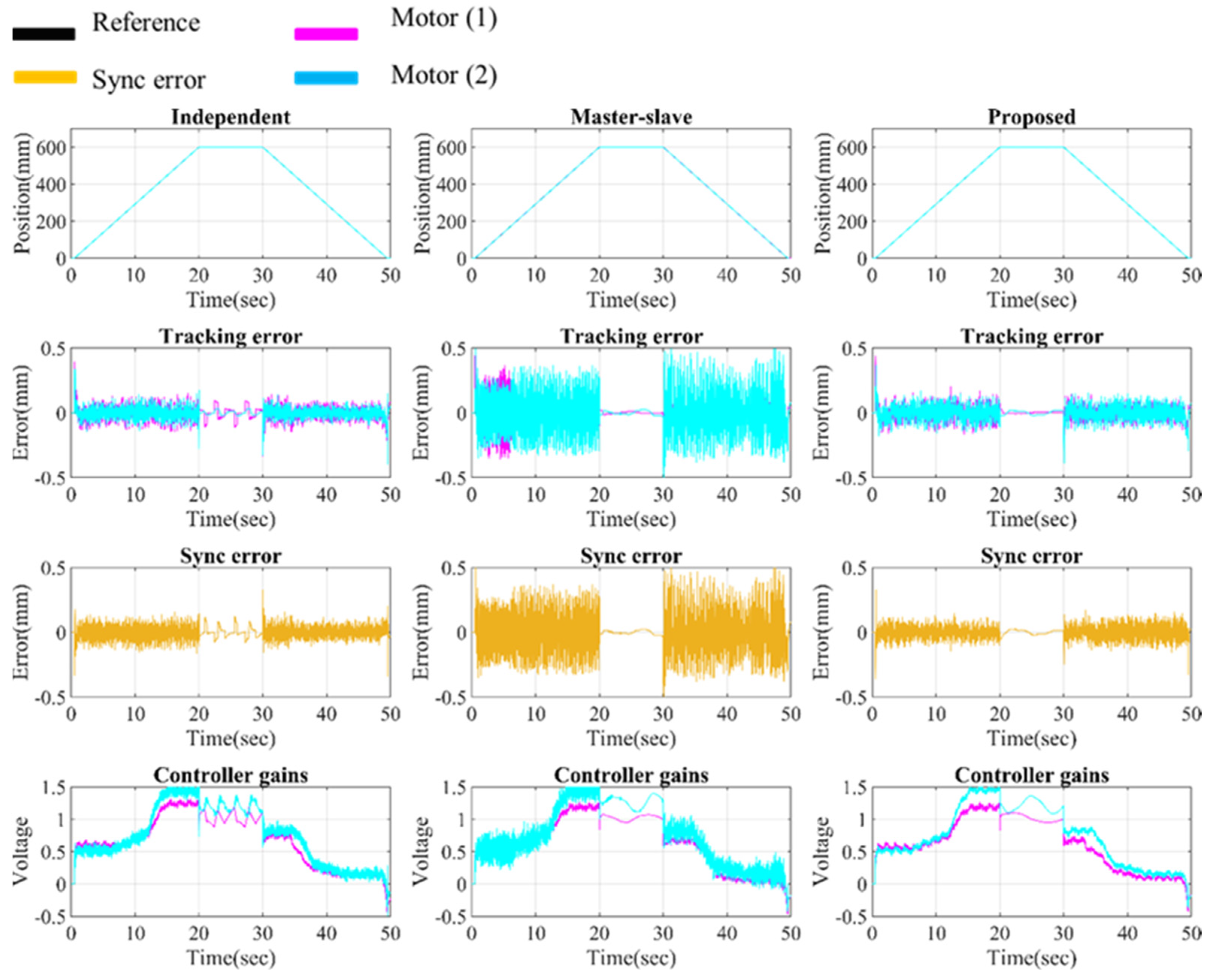
6.2.1. No Load Condition
6.2.2. Equal Load Condition
6.2.3. Unequal Load Condition
7. Results and Analysis
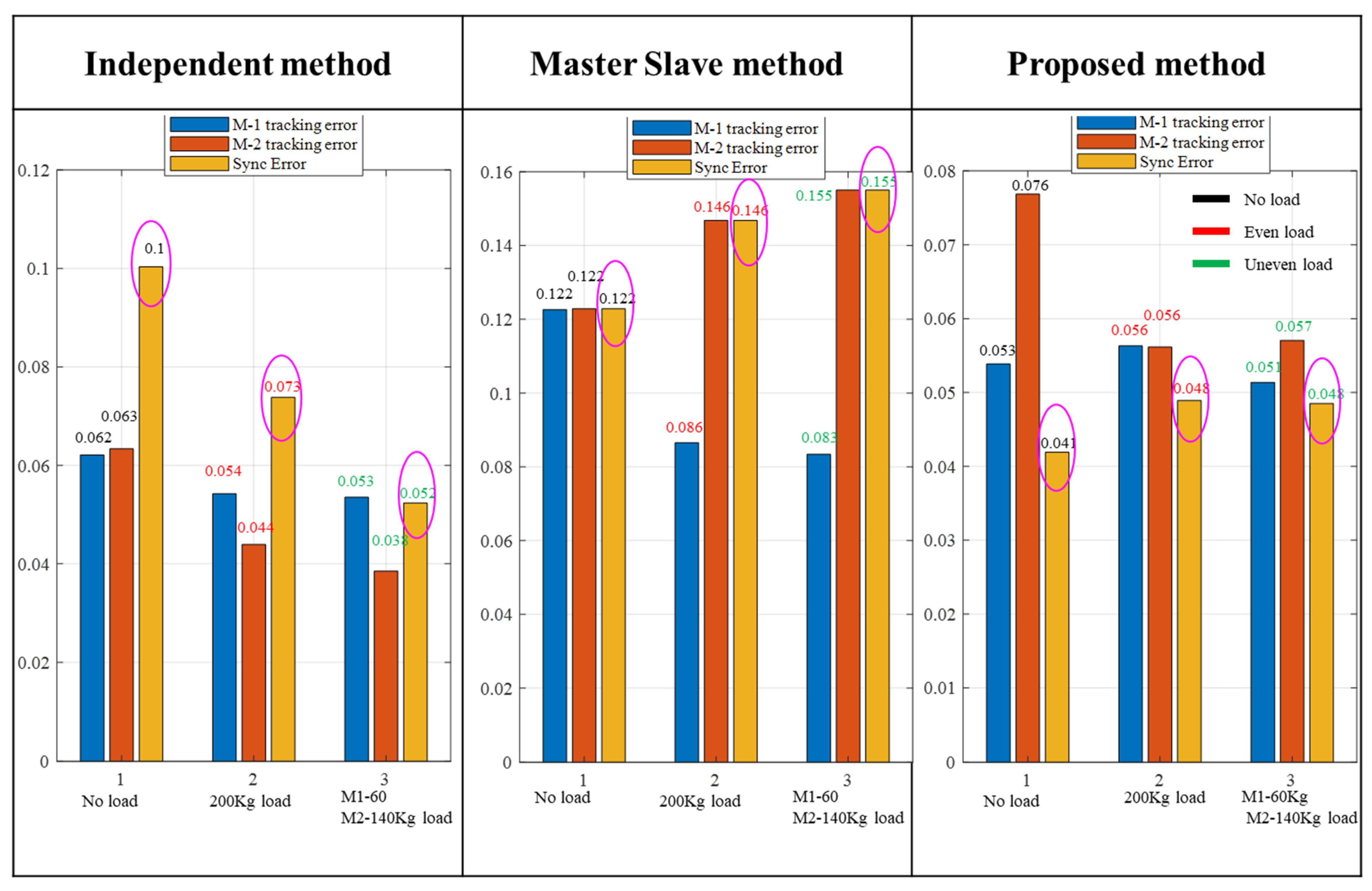
7.1. RMS Analysis of Errors
7.1.1. RMS Error during No Load
7.1.2. RMS Error during Equal Load
7.1.3. RMS Error during Unequal Load
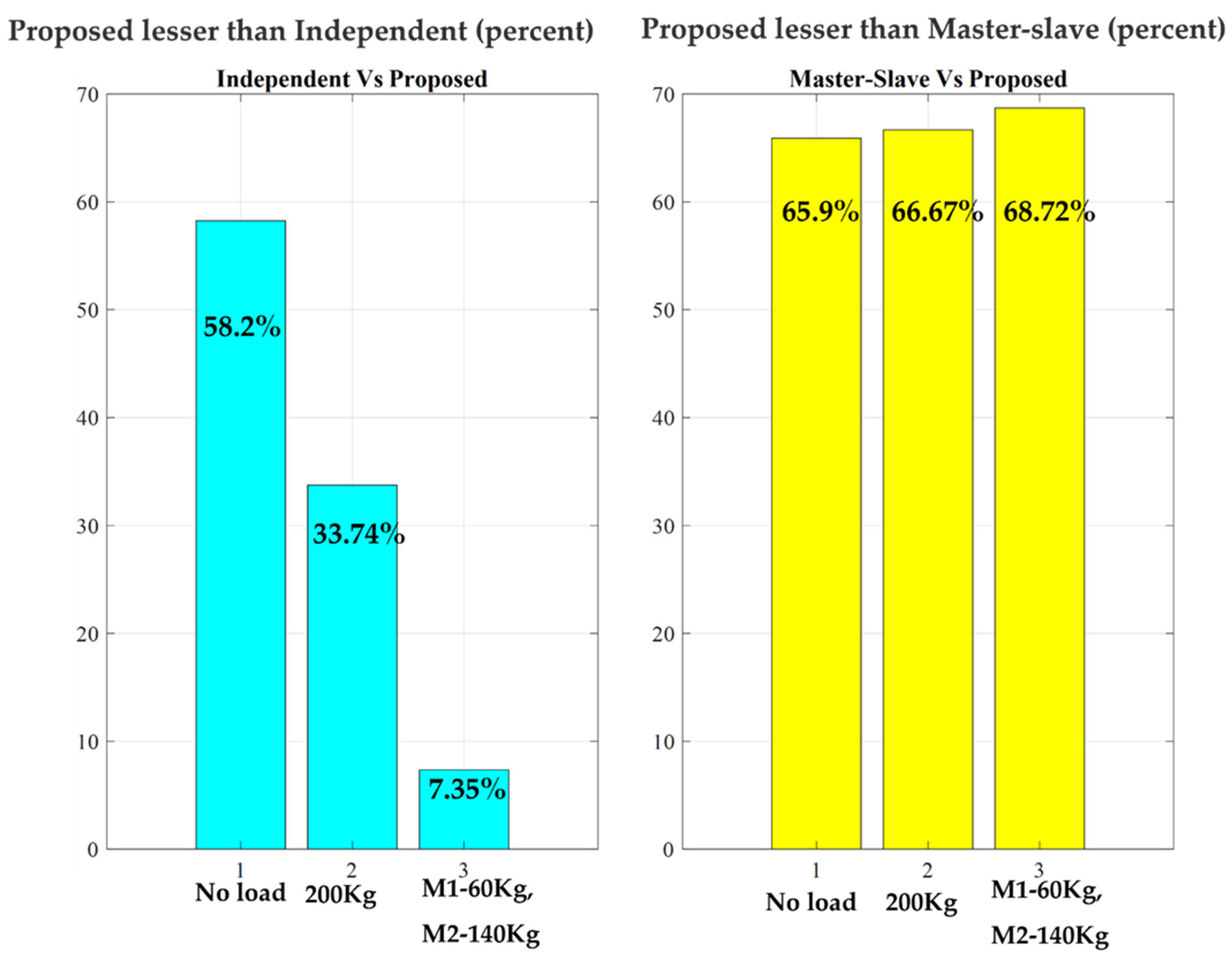
7.2. Percentage Analysis of Errors
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pradnya, T.C.; Ganesh, R. An Autonomous Industrial Load Carrying Vehicle. Adv. Electron. Electr. Eng. 2014, 4, 169–178. Available online: http://www.ripublication.com/aeee.htm (accessed on 1 May 2023).
- Garibott, G.; Ilic, M.; Bassino, P.; Masciangelo, S. ROBOLIFT: A Vision Guided Autonomous Fork-Lift for Pallet Handling. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. IROS ’96, Osaka, Japan, 8 November 1996; Volume 2, pp. 656–663. [Google Scholar]
- Automatic Visual Guidance of a Forklift Engaging a Pallet—ScienceDirect. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0921889006001023 (accessed on 8 November 2023).
- Lecking, D.; Wulf, O.; Wagner, B. Variable Pallet Pick-Up for Automatic Guided Vehicles in Industrial Environments. In Proceedings of the 2006 IEEE Conference on Emerging Technologies and Factory Automation, Prague, Czech Republic, 20–22 September 2006; pp. 1169–1174. [Google Scholar]
- Hamilton-Baillie, B.; Jones, P. Improving Traffic Behaviour and Safety through Urban Design. Proc. ICE-Civ. Eng. 2005, 158, 39–47. [Google Scholar] [CrossRef]
- Chang, H.J.; Yi, K.M.; Yin, S.; Kim, S.W.; Baek, Y.M.; Ahn, H.S.; Choi, J.Y. PIL-EYE: Integrated System for Sustainable Development of Intelligent Visual Surveillance Algorithms. In Proceedings of the 2011 International Conference on Digital Image Computing: Techniques and Applications, Noosa, QLD, Australia, 6–8 December 2011; pp. 231–236. [Google Scholar]
- Tutunji, T.A. DC Motor Identification Using Impulse Response Data. In Proceedings of the EUROCON 2005—The International Conference on “Computer as a Tool”, Belgrade, Serbia, 21–24 November 2005; IEEE: Belgrade, Serbia, 2005; pp. 1734–1736. [Google Scholar]
- Ljung, L.; Glover, K. Frequency Domain versus Time Domain Methods in System Identification. Automatica 1981, 17, 71–86. [Google Scholar] [CrossRef]
- Lozoya, C.; Marti, P.; Velasco, M.; Fuertes, J.M. Effective Real-Time Wireless Control of an Autonomous Guided Vehicle. In Proceedings of the 2007 IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; IEEE: Vigo, Spain, 2007; pp. 2876–2881. [Google Scholar]
- You, S.H.; Bonn, K.; Kim, D.S.; Kim, S.-K. Cascade-Type Pole-Zero Cancellation Output Voltage Regulator for DC/DC Boost Converters. Energies 2021, 14, 3824. [Google Scholar] [CrossRef]
- Burke, J.L.; Murphy, R.R. Human-Robot Interaction in USAR Technical Search: Two Heads Are Better than One. In Proceedings of the RO-MAN 2004. 13th IEEE International Workshop on Robot and Human Interactive Communication (IEEE Catalog No.04TH8759), Kurashiki, Japan, 22 September 2004; IEEE: Kurashiki, Japan, 2004; pp. 307–312. [Google Scholar]
- Fahmizal; Kuo, C.-H. Trajectory and Heading Tracking of a Mecanum Wheeled Robot Using Fuzzy Logic Control. In Proceedings of the 2016 International Conference on Instrumentation, Control and Automation (ICA), Bandung, Indonesia, 29–31 August 2016; pp. 54–59. [Google Scholar]
- Chevallereau, C.; Khalil, W. A New Method for the Solution of the Inverse Kinematics of Redundant Robots. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation Proceedings, Philadelphia, PA, USA, 24–29 April 1988; Volume 1, pp. 37–42. [Google Scholar]
- Abdul Ali, A.; Alquhali, A. Improved Internal Model Control Technique for Position Control of AC Servo Motors. Elektr.-J. Electr. Eng. 2020, 19, 33–40. [Google Scholar] [CrossRef]
- Vonkomer, J.; Béai, I.; Huba, M. Disturbance Observer Control for AC Speed Servo with Improved Noise Attenuation. IFAC-Pap. 2017, 50, 4300–4305. [Google Scholar] [CrossRef]
- Perez-Pinal, F.J.; Nunez, C.; Alvarez, R.; Cervantes, I. Comparison of Multi-Motor Synchronization Techniques. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society, 2004. IECON 2004, Busan, Republic of Korea, 2–6 November 2004; IEEE: Busan, Republic of Korea, 2004; Volume 2, pp. 1670–1675. [Google Scholar]
- Huang, H.; Tu, Q.; Jiang, C.; Ma, L.; Li, P.; Zhang, H. Dual Motor Drive Vehicle Speed Synchronization and Coordination Control Strategy. AIP Conf. Proc. 2018, 1955, 040005. [Google Scholar]
- Li, C.; Li, C.; Chen, Z.; Yao, B. Advanced Synchronization Control of a Dual-Linear-Motor-Driven Gantry with Rotational Dynamics. IEEE Trans. Ind. Electron. 2018, 65, 7526–7535. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, M.; Zhang, R.; Zhu, X.; Yang, L.; Guo, X.; Cai, B. A New Synchronous Control Method for Dual Motor Electric Vehicle Based on Cognitive-Inspired and Intelligent Interaction. Future Gener. Comput. Syst. 2019, 94, 536–548. [Google Scholar] [CrossRef]
- Zeng, F.; Piao, C.; Liang, K.; Dang, J. Research on Synchronous Control Method of Dual Motor Based on ADRC Speed Compensation. In Advances in Computer Science and Ubiquitous Computing; Park, J.S., Yang, L.T., Pan, Y., Park, J.H., Eds.; Springer Nature: Singapore, 2023; pp. 27–35. [Google Scholar]







| Part | Specification | |
|---|---|---|
| Robot | Model | HR200-L70-W6B-0100R05 |
| Type | Ball screw | |
| Length, Stroke | 200 mm, 100 mm | |
| Max load | 150 kgf (Horizontal), 50 kgf (Vertical) | |
| Max speed | 250 mm/s | |
| Forklift | Capacity | 300 Kg |
| Speed | 2.5 m/s. Max | |
| Size | 1050 × 850 × 650 (mm) | |
| Battery | Nominal Voltage and capacity | 12 V, 120 Ah |
| Pallet carrier motor | Model, Type | Mitsubishi HG-KR 73(B), PMSM |
| Rated speed | 3000 rpm | |
| Permissible load | Radial-392N, Thrust-147N | |
| Rated Torque | 2.4 Nm | |
| Rated voltage and current | 109 V, 4.8 A | |
| Pallet carrier motor driver | Model | Mitsubishi MR-J4-70A |
| Control method | Sinewave PWM control, current control | |
| Torque limit | External analog input (0 V DC to +10 V DC/maximum torque) | |
| Rated Output | Voltage 3-phase 170 V AC, current 5.8 A | |
| Communication | RS-422: 1: n communication (up to 32 axes) | |
| Encoder | Rotary incremental type, (A/B/Z-phase pulse) | |
| Variable | Definition |
|---|---|
| Instantaneous longitudinal velocity of the wheel at X-axis direction [i = FL, FR, RL, RR, and these suffixes are pointed towards front left, front right, rear left, rear right wheel accordingly] | |
| Instantaneous longitudinal velocity of the wheel at Y-axis direction [i = FL, FR, RL, RR] | |
| Translational velocities of the wheels during their rotation [i = FL, FR, RL, RR] | |
| Tangential velocities of the free roller in contact with the floor [i = FL, FR, RL, RR] | |
| angular velocity of the wheels [i = FL, FR, RL, RR] | |
| axis (sway motion) | |
| axis (surge motion) | |
| axis (yaw motion) | |
| Wheel radius | |
| Angular displacement of the rollers of the mecanum wheels | |
| Lateral gap of the wheels to the center of mass | |
| Longitudinal gap of the wheels to the center of mass | |
| Position and orientation of the platform in relation to the inertial frame |
| Variable | Definition |
|---|---|
| [Related to nominal plant] | |
| [Related to nominal plant] | |
| s | Output variable for Laplace transform |
| Feedback band width [Related to designed control system] | |
| Feedback control [Related to designed control system] | |
| Feedforward control [Related to designed control system] | |
| Feedback band width [Related to designed control system] | |
| Damping ratio [Related to designed control system] | |
| Q filter band width [Related to designed control system] |
| Variable | Definition | Units |
|---|---|---|
| armature current | Amperes (A) | |
| armature resistance | ) | |
| armature inductance | Henrys (H) | |
| terminal voltage | Volts (V) | |
| back emf | Volts (V) | |
| angular position | Radians (rad) | |
| angular velocity | (rad/s) | |
| angular acceleration | 2) | |
| T | motor torque | Newton meters (Nm) |
| load torque | Newton meters (Nm) | |
| frictional torque | Newton meters (Nm) | |
| motor inertia | ||
| motor friction co-efficient | Nm/s |
| Variable | Definition | Unit |
|---|---|---|
| Nm/s | ||
| Feedback band width | Hz | |
| Feedback control | - | |
| Feedforward control | - | |
| Feedback band width | Hz | |
| Damping ratio | - | |
| Q filter band width | Hz | |
| Target position input | rad | |
| forklift motor-1 (master) position output | rad | |
| forklift motor-2 (slave) position output | rad | |
| Position feedback for contact force | Nm | |
| Sync error gain | rad | |
| Tracking error gain | rad | |
| Tracking error of master motor | rad | |
| Sync error between master and slave | rad | |
| Tracking error of slave motor | rad |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amio, F.F.; Ahmed, N.; Jeong, S.; Jung, I.; Nam, K. Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts. Electronics 2024, 13, 1732. https://doi.org/10.3390/electronics13091732
Amio FF, Ahmed N, Jeong S, Jung I, Nam K. Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts. Electronics. 2024; 13(9):1732. https://doi.org/10.3390/electronics13091732
Chicago/Turabian StyleAmio, Fahim Faisal, Neaz Ahmed, Soonyong Jeong, Insoo Jung, and Kanghyun Nam. 2024. "Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts" Electronics 13, no. 9: 1732. https://doi.org/10.3390/electronics13091732
APA StyleAmio, F. F., Ahmed, N., Jeong, S., Jung, I., & Nam, K. (2024). Optimizing Precision Material Handling: Elevating Performance and Safety through Enhanced Motion Control in Industrial Forklifts. Electronics, 13(9), 1732. https://doi.org/10.3390/electronics13091732






