Magnetic Characterization of MR Fluid by Means of Neural Networks
Abstract
1. Introduction
- A measurement device is designed and realized for the characterization of MR fluids.
- The MR device exhibits a magnetic response to electrical stimuli. Measurements of the magnetic permeability () and magnetic field intensity (B) have been conducted in the complex configuration of the MR fluid device.
- An advanced radial basis function neural network (RBF) with a Gaussian activation function is developed to relate the relative magnetic permeability and magnetic field intensity of MR fluids.
2. Related Works
3. Theoretical Background
3.1. Radial Basis Function
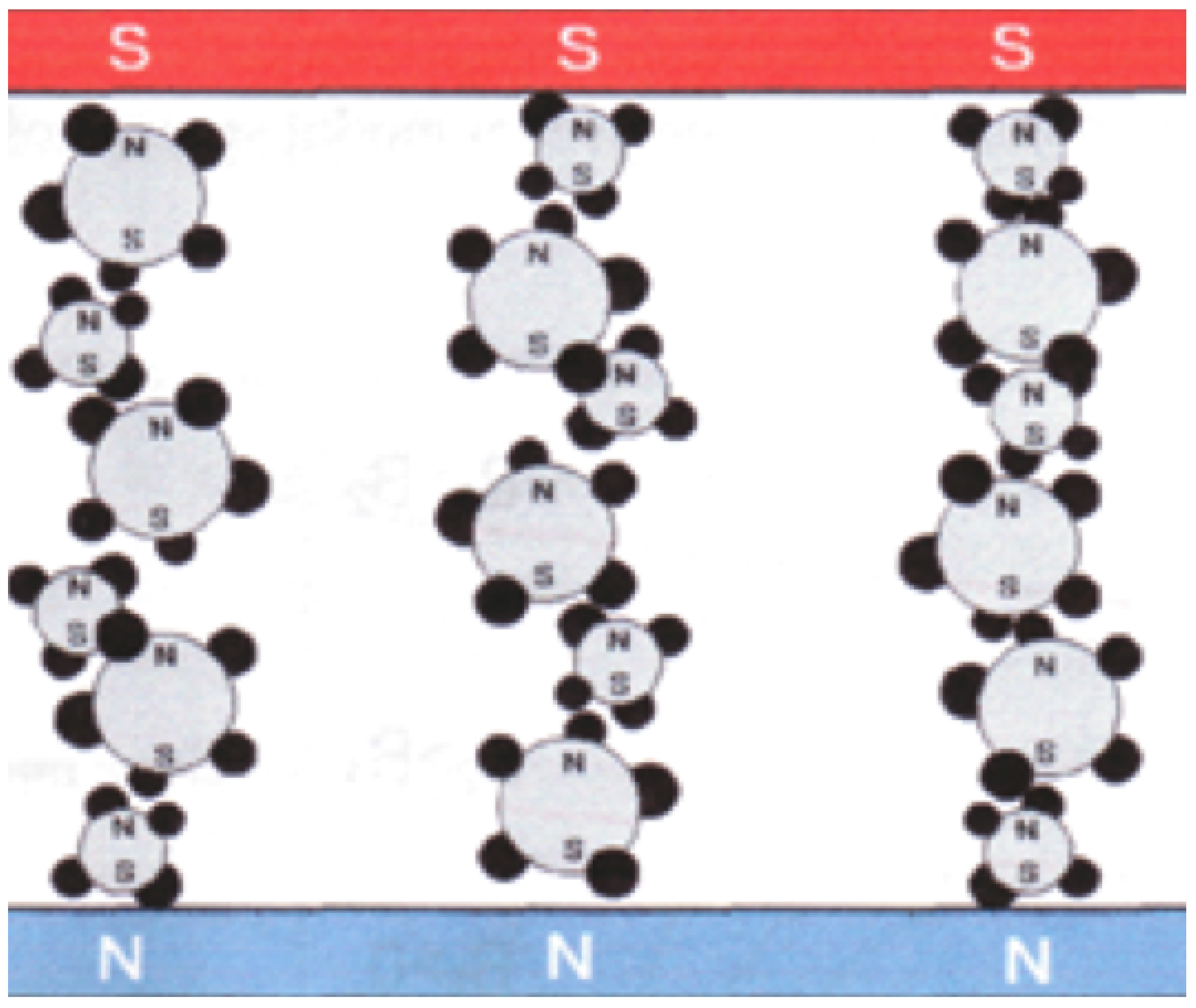
3.2. Magnetorheological Fluids
- A liquid carrier;
- Ferromagnetic particles;
- A non-magnetic surface coating (surface-active agent).
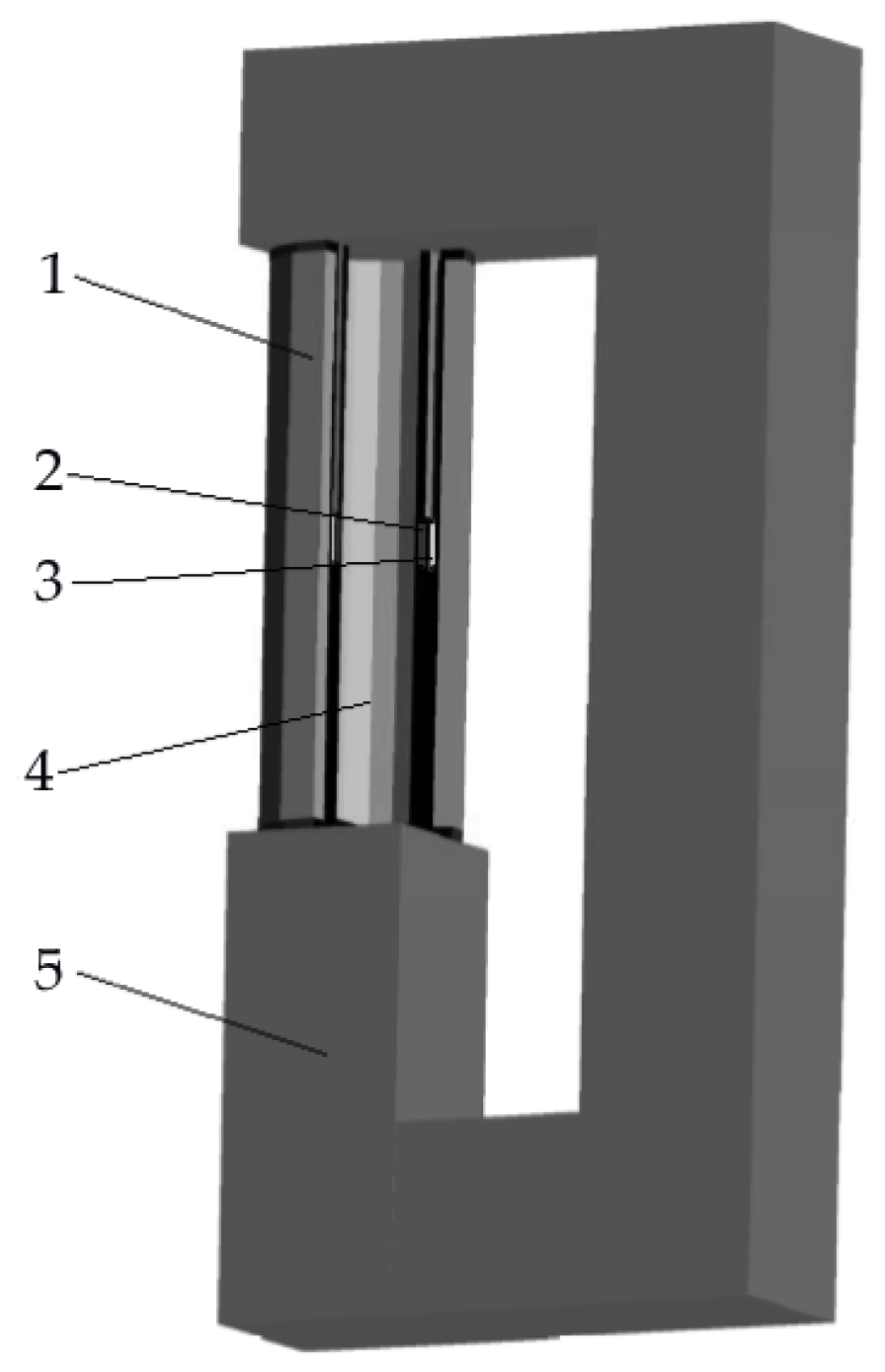
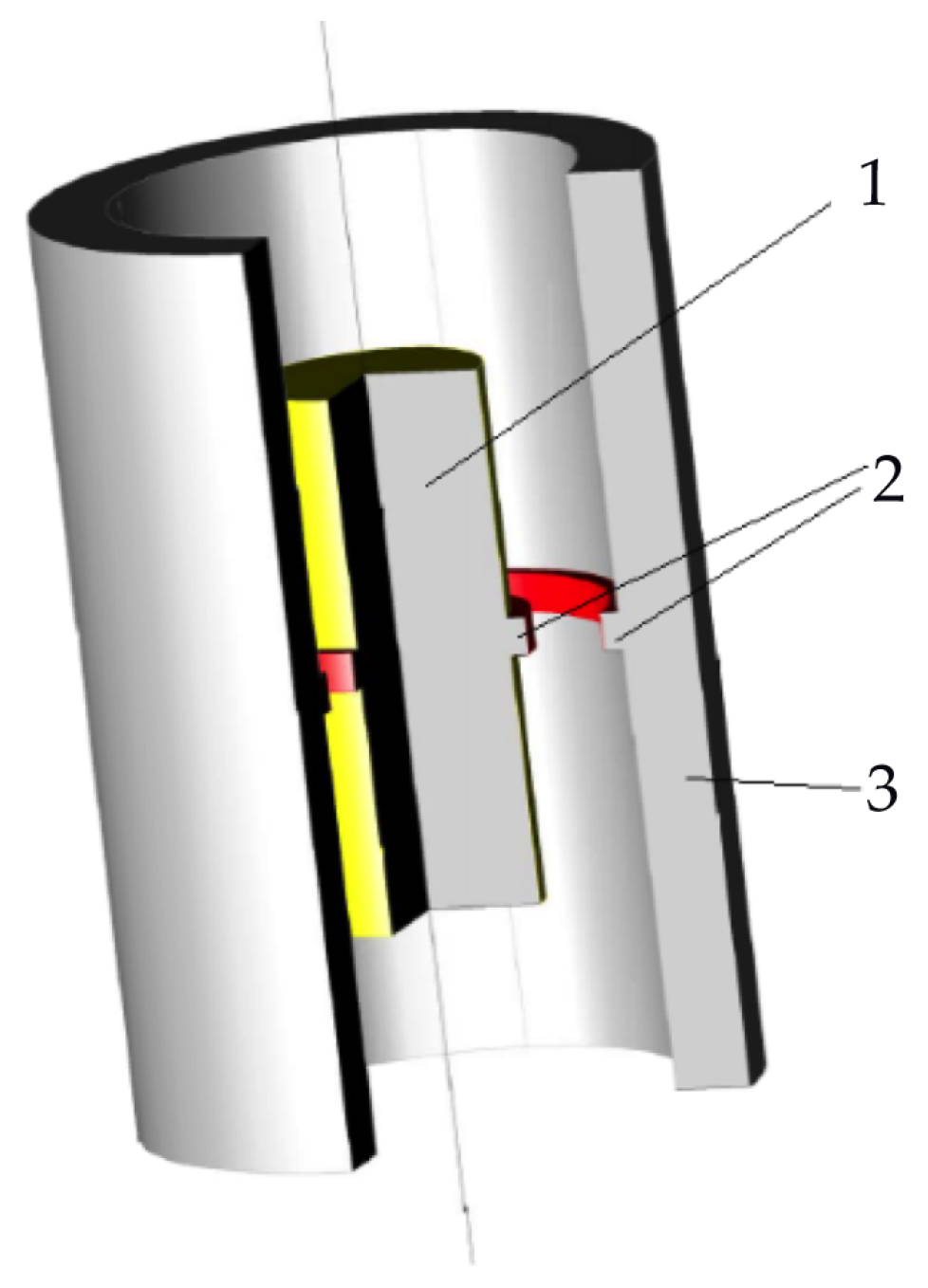
4. Experimental Set-Up
4.1. Experimental Tests
- measuring equipment;
- a variable AC transformer;
- an ammeter and a voltmeter;
- a two-channel oscilloscope.
4.2. Devices and Materials
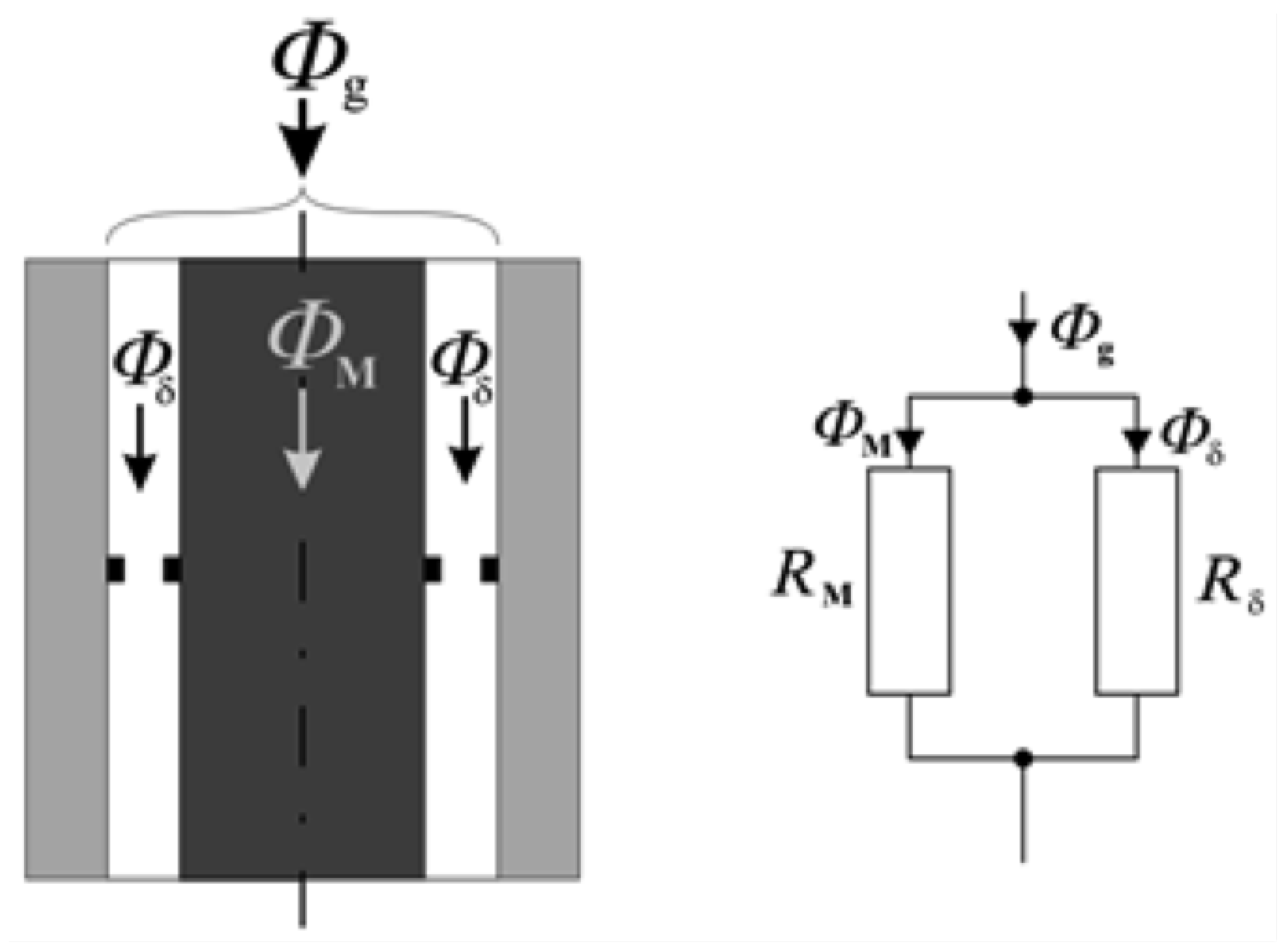
4.3. Mathematical Model of Measuring Device
4.4. MR Fluid Permeability and MR Fluid Permeability
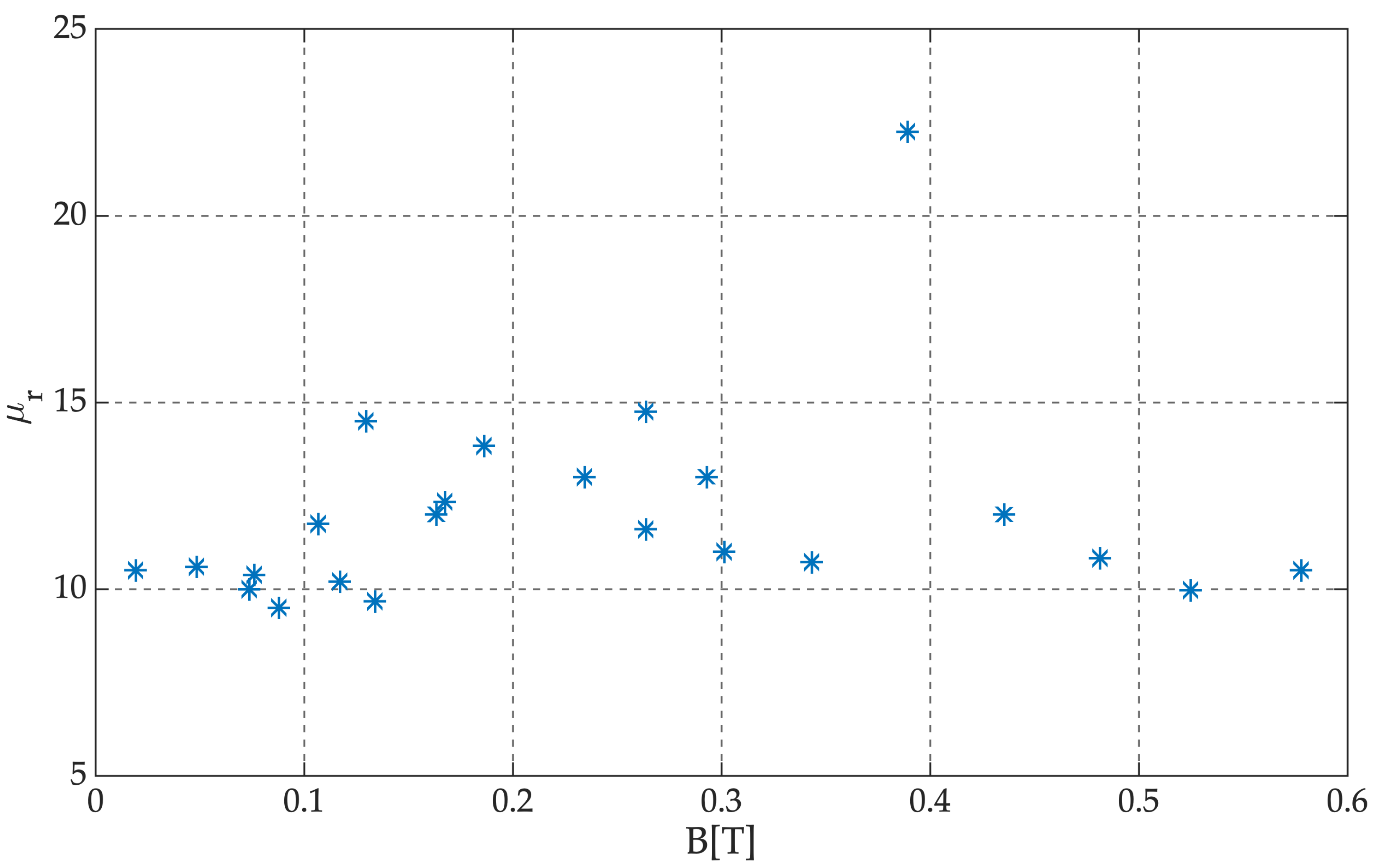
5. Results
Experimental Results and Neural Modeling
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kowalewska, A.; Majewska-Smolarek, K. Synergistic Self-Healing Enhancement in Multifunctional Silicone Elastomers and Their Application in Smart Materials. Polymers 2024, 16, 487. [Google Scholar] [CrossRef]
- De Schryver, R.; Jiao, D.; Yardimci, M.Y.; Lesage, K.; De Schutter, G. A conceptual model for numerical simulation of Active Rheology Control validated for cementitious pumping. Cem. Concr. Res. 2024, 179, 107471. [Google Scholar] [CrossRef]
- Le, C.V.; Yoon, H. Advances in the Use of Conducting Polymers for Healthcare Monitoring. Int. J. Mol. Sci. 2024, 25, 1564. [Google Scholar] [CrossRef]
- Caushaj, S.; Imberti, G.; de Carvalho Pinheiro, H.; Carello, M. Electromagnetic Interaction Model between an Electric Motor and a Magnetorheological Brake. Designs 2024, 8, 25. [Google Scholar] [CrossRef]
- Ciulli, E. Vastness of Tribology Research Fields and Their Contribution to Sustainable Development. Lubricants 2024, 12, 33. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, H.; Zhao, W.; Yang, J.; Ouyang, Q. Design and Control of Upper Limb Rehabilitation Training Robot Based on a Magnetorheological Joint Damper. Micromachines 2024, 15, 301. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Tan, X.; Huang, Y.; Tao, Y.; Yang, N.; Yuan, R.; Liu, L.; Ge, L. Transformable Magnetic Liquid-Metal Nanoplatform for Intracellular Drug Delivery and MR Imaging-Guided Microwave Thermochemotherapy. ACS Appl. Mater. Interfaces 2024, 16, 9826–9838. [Google Scholar] [CrossRef]
- Hu, G.; Yi, F.; Tong, W.; Yu, L. Development and Evaluation of a MR Damper With Enhanced Effective Gap Lengths. IEEE Access 2020, 8, 156347–156361. [Google Scholar] [CrossRef]
- Nordin, N.H.D.; Muthalif, A.G.A.; Razali, M.K.M.; Ali, A.; Salem, A.M. Development and Implementation of Energy-Efficient Magnetorheological Fluid Bypass Damper for Prosthetics Limbs Using a Fuzzy-Logic Controller. IEEE Access 2022, 10, 18978–18987. [Google Scholar] [CrossRef]
- Hu, G.; Wu, L.; Li, L.; Yu, L. Performance Analysis of Rotary Magnetorheological Brake With Multiple Fluid Flow Channels. IEEE Access 2020, 8, 173323–173335. [Google Scholar] [CrossRef]
- Dutra, R.M.A.; de Andrade, R.M.; Soares, A.B.; Thakor, N.V.; Vimieiro, C.B.S. Magnetorheological fluid in prostheses: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2024, 35, 1045389X231213126. [Google Scholar] [CrossRef]
- Rajput, A.S.; Das, M.; Kapil, S. A Hybrid Electrochemical Magnetorheological Finishing Process for Surface Enhancement of Biomedical Implants. J. Manuf. Sci. Eng. 2024, 146, 051004. [Google Scholar] [CrossRef]
- Chauhan, V.; Kumar, A.; Sham, R. Magnetorheological fluids: A comprehensive review. Manuf. Rev. 2024, 11, 6. [Google Scholar] [CrossRef]
- Bai, X.X.; Chen, P. On the hysteresis mechanism of magnetorheological fluids. Front. Mater. 2019, 6, 36. [Google Scholar] [CrossRef]
- Behera, S.K.; Sarangi, S. Constitutive modeling of electro-magneto-rheological fluids before yielding. Mech. Res. Commun. 2024, 136, 104253. [Google Scholar] [CrossRef]
- Khajehsaeid, H.; Alaghehband, N.; Bavil, P. On the yield stress of magnetorheological fluids. Chem. Eng. Sci. 2022, 256, 117699. [Google Scholar] [CrossRef]
- Wang, H.; Bi, C.; Liu, W.; Zhou, F. Squeeze behaviors of magnetorheological fluids under different compressive speeds. Materials 2023, 16, 3109. [Google Scholar] [CrossRef]
- Kumar, J.S.; Paul, P.S.; Raghunathan, G.; Alex, D.G. A review of challenges and solutions in the preparation and use of magnetorheological fluids. Int. J. Mech. Mater. Eng. 2019, 14, 1–18. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Q.; Fan, X.; Song, Y.; Zheng, Q. Smart magnetorheological elastomer peristaltic pump. J. Intell. Mater. Syst. Struct. 2019, 30, 1084–1093. [Google Scholar] [CrossRef]
- Hafez, A.; Liu, Q.; Santamarina, J.C. Magneto-rheological fluids: Tele-manipulation of ferromagnetic particles with external magnetic field for flow control and zonal isolation. Geoenergy Sci. Eng. 2023, 228, 212029. [Google Scholar] [CrossRef]
- Upadhyay, R.V.; Choi, S.B. Modeling, measurements and validation of magnetic field dependent flow behavior of magnetorheological fluids; static and dynamic yield stress. Smart Mater. Struct. 2021, 30, 117002. [Google Scholar] [CrossRef]
- Dai, X.R.; Zhu, M. Frame set for Gabor systems with Haar window. Appl. Comput. Harmon. Anal. 2024, 71, 101655. [Google Scholar] [CrossRef]
- Yarali, E.; Mohammadi, A.; Mafakheri, S.; Baghani, M.; Adibi, H. Mathematical modeling and experimental evaluation of a prototype double-tube Magnetorheological damper. SN Appl. Sci. 2019, 1, 1–10. [Google Scholar] [CrossRef]
- Lin, H.; Dai, H.; Mao, Y.; Wang, L. An optimized radial basis function neural network with modulation-window activation function. Soft Comput. 2024, 28, 4631–4648. [Google Scholar] [CrossRef]
- Lo Sciuto, G.; Capizzi, G.; Shikler, R.; Napoli, C. Organic solar cells defects classification by using a new feature extraction algorithm and an EBNN with an innovative pruning algorithm. Int. J. Intell. Syst. 2021, 36, 2443–2464. [Google Scholar] [CrossRef]
- Lo Sciuto, G.; Napoli, C.; Capizzi, G.; Shikler, R. Organic solar cells defects detection by means of an elliptical basis neural network and a new feature extraction technique. Optik 2019, 194, 163038. [Google Scholar] [CrossRef]
- Liu, S.; Yu, G.; Kim, Y. Supplier Evaluation in Supply Chain Environment Based on Radial Basis Function Neural Network. Int. J. Inf. Technol. Web Eng. (IJITWE) 2024, 19, 1–18. [Google Scholar] [CrossRef]
- Singh, R.; Srivastava, A.; Kant, R.; Maurya, S.; Mahadasu, P.; Verma, N.; Hema, G.; Kushwaha, P.; Richa; Singh, K.; et al. Integrated thin layer classification and reservoir characterization using sparse layer reflectivity inversion and radial basis function neural network: A case study. Mar. Geophys. Res. 2024, 45, 3. [Google Scholar] [CrossRef]
- Taoufyq, E.; Mohammed, O.; Hamid, B. Multi-objective optimization of radial basis function neural network training using genetic algorithm. AIP Conf. Proc. 2024, 3034, 020001. [Google Scholar]
- Stanišić, D.; Mejić, L.; Jorgovanović, B.; Ilić, V.; Jorgovanović, N. An Algorithm for Soft Sensor Development for a Class of Processes with Distinct Operating Conditions. Sensors 2024, 24, 1948. [Google Scholar] [CrossRef]
- Zahir, H.; Gul, J.; Inc, M.; Alqahtani, R.T. Impact of fractional magnetohydrodynamic and hall current on ree-eyring fluid flow by using radial basis function method. Alex. Eng. J. 2024, 88, 210–215. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Yin, C.; Cheng, Q. Fractional-Order Sliding-Mode Control and Radial Basis Function Neural Network Adaptive Damping Passivity-Based Control with Application to Modular Multilevel Converters. Energies 2024, 17, 580. [Google Scholar] [CrossRef]
- Moezi, S.A.; Sedaghati, R.; Rakheja, S. Nonlinear dynamic modeling and model-based AI-driven control of a magnetoactive soft continuum robot in a fluidic environment. ISA Trans. 2024, 144, 245–259. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, S.; Xiao, Y. Effective permeability model of magnetorheological fluids and its experimental verification. J. Magn. Magn. Mater. 2022, 562, 169774. [Google Scholar] [CrossRef]
- Bi, C.; Bi, E.; Wang, H.; Deng, C.; Chen, H.; Wang, Y. Magnetic circuit design for the performance experiment of shear yield stress enhanced by compression of magnetorheological fluids. Sci. Rep. 2024, 14, 741. [Google Scholar] [CrossRef]
- Li, Z.; Fu, B.; Liao, C. Impact behavior of a novel magnetorheological energy absorber based on wedge-shaped squeeze flow model. J. Intell. Mater. Syst. Struct. 2024, 35, 1045389X231220796. [Google Scholar] [CrossRef]
- Kubík, M.; Žáček, J.; Gołdasz, J.; Nečas, D.; Sedlačík, M.; Blahuta, J.; Bańkosz, W.; Sapiński, B. Grasping the behavior of magnetorheological fluids in gradient pinch mode via microscopic imaging. Phys. Fluids 2024, 36, 042004. [Google Scholar] [CrossRef]
- Yu, B.; Ma, J.; Zhao, X.; Chen, Y. Numerical simulation for microstructure evolution of magnetorheological fluid based on combined disk DDA-LBM approach. Powder Technol. 2024, 437, 119585. [Google Scholar] [CrossRef]
- Alimisis, V.; Dimas, C.; Sotiriadis, P.P. A Low-Power Analog Integrated Euclidean Distance Radial Basis Function Classifier. Electronics 2024, 13, 921. [Google Scholar] [CrossRef]
- Stenkin, D.; Gorbachenko, V. Mathematical Modeling on a Physics-Informed Radial Basis Function Network. Mathematics 2024, 12, 241. [Google Scholar] [CrossRef]
- Lang, Q.; Lu, J. Learning Memory Kernels in Generalized Langevin Equations. arXiv 2024, arXiv:2402.11705. [Google Scholar]
- Galushkin, A.I. Neural Networks Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Fedorowicz, K.; Prosser, R. The elastic perfectly plastic constitutive equation for yield stress fluids. J. Non-Newton. Fluid Mech. 2024, 352, 105201. [Google Scholar] [CrossRef]
- Feng, Z.; Zhang, Z.; Yang, J.; Yu, J.; Feng, J.; Zhou, H.; Shi, C.; Meng, F. Advanced nonlinear rheology magnetorheological finishing: A review. Chin. J. Aeronaut. 2023, 37, 54–92. [Google Scholar]
- Kowol, P.; Pilśniak, A.; Zioło, G.; Lo Sciuto, G. Stanowisko do badania przenikalności magnetycznej cieczy magnetoreologicznej. Pomiary Autom. Robot. 2020, 24, 11–17. [Google Scholar]
- Dong, X.; Rudelson, M. Approximately Hadamard matrices and Riesz bases in random frames. Int. Math. Res. Not. 2024, 2024, 2044–2065. [Google Scholar] [CrossRef]
- Loh, C.H.; Chen, Y.C.; Su, C.T. Using Transfer Learning and Radial Basis Function Deep Neural Network Feature Extraction to Upgrade Existing Product Fault Detection Systems for Industry 4.0: A Case Study of a Spring Factory. Appl. Sci. 2024, 14, 2913. [Google Scholar] [CrossRef]
- Song, S.; Wang, P.; Heidari, A.A.; Zhao, X.; Chen, H. Adaptive Harris hawks optimization with persistent trigonometric differences for photovoltaic model parameter extraction. Eng. Appl. Artif. Intell. 2022, 109, 104608. [Google Scholar] [CrossRef]
- Fernández, J.; Chiachío, M.; Chiachío, J.; Muñoz, R.; Herrera, F. Uncertainty quantification in Neural Networks by Approximate Bayesian Computation: Application to fatigue in composite materials. Eng. Appl. Artif. Intell. 2022, 107, 104511. [Google Scholar] [CrossRef]
- Tan, Y.; Liu, H. How does a kernel based on gradients of infinite-width neural networks come to be widely used: A review of the neural tangent kernel. Int. J. Multimed. Inf. Retr. 2024, 13, 8. [Google Scholar] [CrossRef]
- Lazovskiy, N.V. Neural Network System for Monitoring the Condition of Equipment and Predicting Malfunctions. In Proceedings of the 2024 Conference of Young Researchers in Electrical and Electronic Engineering (ElCon), St. Petersburg, Russia, 29–31 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 421–423. [Google Scholar]





| Typical Properties | MRF-132DG |
|---|---|
| Appearance | dark gray liquid |
| Viscosity | |
| Pa-s@40 C (104 F) calculated | |
| as slope 800–1200 | |
| Density g/ | 2.98–3.18 |
| Operating Temperature C | to |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kowol, P.; Lo Sciuto, G.; Brociek, R.; Capizzi, G. Magnetic Characterization of MR Fluid by Means of Neural Networks. Electronics 2024, 13, 1723. https://doi.org/10.3390/electronics13091723
Kowol P, Lo Sciuto G, Brociek R, Capizzi G. Magnetic Characterization of MR Fluid by Means of Neural Networks. Electronics. 2024; 13(9):1723. https://doi.org/10.3390/electronics13091723
Chicago/Turabian StyleKowol, Paweł, Grazia Lo Sciuto, Rafał Brociek, and Giacomo Capizzi. 2024. "Magnetic Characterization of MR Fluid by Means of Neural Networks" Electronics 13, no. 9: 1723. https://doi.org/10.3390/electronics13091723
APA StyleKowol, P., Lo Sciuto, G., Brociek, R., & Capizzi, G. (2024). Magnetic Characterization of MR Fluid by Means of Neural Networks. Electronics, 13(9), 1723. https://doi.org/10.3390/electronics13091723








