Abstract
The pursuit of energy-efficient solutions in the context of reconfigurable intelligent surface (RIS)-assisted wireless networks has become imperative and transformative. This paper investigates the integration of RIS into an orthogonal frequency-division multiple access (OFDMA) framework for multi-user downlink communication systems. We address the challenge of jointly optimizing RIS reflection coefficients alongside OFDMA frequency and power allocations, with the aim of maximizing energy efficiency. This optimization is subject to specific quality-of-service (QoS) requirements for each user equipment (UE) and a constraint on transmission power and the RIS phase shift matrix. To address this complex optimization problem, we propose a novel practical and low-complexity approach that is based on optimizing a computationally efficient and numerically tractable lower bound on energy efficiency. The numerical results highlight the effectiveness of our approach, demonstrating a substantial increase in energy efficiency compared to scenarios without RIS, with random RIS integration, and with the scheme using the Genetic Algorithm (GA).
1. Introduction
Energy efficiency (EE) has become a crucial topic in the research and development of next-generation wireless networks, particularly in sixth generation (6G). However, the deployment of 6G in the industry is quite challenging. Due to non-line of sight (NLOS), the energy efficiency and throughput of the network decrease. NLOS also gives rise to multi-path fading, attenuation, and interference due to reflection and refraction. To overcome this problem, reconfigurable intelligent surface (RIS) is the primary solution. RIS reduces attenuation and improves network performance [1].
A RIS is a meta-surface made up of numerous inexpensive passive antennas that may effectively reflect the electromagnetic waves impinging on it to improve performance [2]. In wireless communication networks with RIS assistance, a base station (BS) communicates control signals to a RIS controller to enhance incident wave characteristics and user communication quality. As a reflector, the RIS does not engage in any digitization processes. Therefore, if implemented properly, a RIS promises to use substantially less energy than conventional amplify-and-forward (AF) relays [2,3].
When using a RIS in wireless communications, radio resource allocation to optimize the network performance is a prime concern [4]. Effective resource allocation can aid to further enhance a RIS-assisted wireless network’s energy efficiency.
1.1. Related Works
The design of reflection coefficients (or passive beamforming) for narrowband transmission over frequency-flat channels was the main focus of earlier studies on RIS-enhanced wireless communication [3,5]. However, more recent studies in [6,7,8,9,10,11,12,13,14] have looked at the more general broadband transmission over frequency-selective channels for the case of a single-user setup.
In [6], the authors proposed a majorization–minimization (MM)-based iterative approach for optimizing RIS passive beamforming in an OFDM system, achieving near-optimal performance with lower computational complexity compared to the existing sine cosine algorithm (SCA). The work in [7] introduces a scalable framework for channel estimation and reflection optimization in RIS-enhanced OFDM systems, achieving improved rate performance with reduced training overhead and computational complexity. The authors in [8] proposed a practical transmission protocol for RIS-enhanced OFDM systems under frequency-selective channels, optimizing the achievable rate through a joint optimization of transmit power allocation and RIS passive array reflection coefficients while reducing training overhead. The work in [9] addresses the ergodic achievable rate optimization in RIS-assisted mmWave MIMO-OFDM systems with statistical CSI, utilizing majorization theory and alternating optimization for the joint design of the transmit covariance matrix and RIS reflection coefficients. The work in [10] proposed a framework for integrating RIS technology into wireless networks by leveraging localization information for robust user multiplexing, minimizing the overhead of channel estimation and phase shift optimization in OFDM systems. The authors in [11] suggested an intelligent resource allocation scheme utilizing reinforcement learning (RL) for maximizing the sum-rate in RIS-enhanced OFDM systems, considering both primary and secondary user scenarios, and demonstrated significant transmission rate improvements compared to benchmark schemes. The work in [12] investigates spectral efficiency improvement in an OFDM system with a 1-bit resolution RIS, utilizing a deep RL algorithm for optimizing reflection phase shifts, leading to significant performance gains and reduced calculation delay. The work in [13] addresses the optimization of RIS-enhanced two-way D2D OFDM systems, maximizing the bidirectional sum-rate via sub-band, power, and discrete phase shift optimization. In [14], the authors presented joint optimization of the UAV trajectory, RIS scheduling, and resource allocation in OFDMA systems to maximize the sum-rate while considering heterogeneous QoS requirements, showing promising performance gains with RIS deployment in UAV-based communication.
To the best of our knowledge, very few articles have examined a passive beamforming design and resource allocation for multi-user broadband communication. The multi-user system design is more complex than the single-user case because the RIS reflection coefficients must be concurrently optimized with the multi-user transmission scheduling and resource allocation. The use of RIS in orthogonal frequency-division multiple access (OFDMA) systems, a multi-user variant of the well-known orthogonal frequency-division multiplexing (OFDM) digital modulation method, has been the subject of an expanding body of study. The fundamental benefit of OFDMA is that it enables variable resource allocation, which is essential for enhancing wireless networks’ energy efficiency. Designing efficient resource allocation algorithms that can effectively use the available resources is one of the major issues in putting RIS-assisted OFDMA systems into practice. To tackle this problem, many scholars have suggested numerous optimization strategies, including machine learning, convex optimization, and game theory. These techniques have the potential to increase the system’s energy efficiency by allocating resources as efficiently as possible.
Recent publications [15,16,17,18,19,20], among others, have looked at the usage of RISs in OFDMA systems, as listed in Table 1. The works in [15,16,17,18,19,20] have focused on maximizing the sum-rate in an OFDMA network. The work in [15] proposes a RIS-aided multi-user THz MIMO system with OFDM access, aiming to maximize the weighted sum-rate via joint analog/digital beamforming at the base station and reflection matrix optimization at the RIS. In [16], the authors propose a novel uplink communication system with a transmissive RIS transceiver, employing OFDMA for multiple users, and utilize alternating optimization to maximize the system sum-rate while meeting QoS constraints. The work in [17] investigates the joint design of MU beamformers and RIS’s programmable reflecting elements (PREs) for quality-of-service in RIS-aided OFDM networks. In [18], the authors propose a resource allocation algorithm for RIS-aided MISO OFDMA multicell networks targeting URLLC users, ensuring QoS while maximizing system throughput through a sub-optimal iterative approach. The authors in [19] propose the optimal beam reflection based on the the federated learning (OBR-FL) algorithm for RIS-assisted communications, utilizing federated learning to optimize beam reflection based on sparse CSI while preserving user privacy. The work in [20] proposes dynamic passive beamforming for RIS-integrated OFDMA systems, optimizing reflection coefficients and resource allocations to maximize users’ common rate while flexibly adapting to channel variations and outperforming fixed passive beamforming approaches. On the other hand, the authors in [21] delve into the investigation of maximizing energy efficiency fairness in an active RIS-aided cell-free network. In contrast to the studies mentioned, recent research is oriented towards formulating an energy-efficient problem in the DL direction of a RIS-aided single input single output (SISO) OFDMA system, taking passive RIS into account. The consideration of a single-antenna BS and users allows for a more straightforward simplification of our proposed problem. The presented problem is intricate, involving high-dimensional discrete and continuous variables. Given the complexity, suggesting a model-based optimal solution proves impractical. Additionally, the unavailability of accessible data for training hinders the utilization of machine learning methods. Consequently, in comparison to other solutions outlined in the literature and presented in Table 1, a sub-optimal solution is advocated by us through the lower-bound optimization of the EE problem.

Table 1.
Literature review.
1.2. Contributions
The key contributions of this work are outlined below:
- The EE problem in the SISO-OFDMA communication system for the DL direction is formulated by us. This formulation takes into account THE subchannel and power allocation within the OFDMA network, as well as the phase shift of the RIS. The intricate relationship among the optimization variables renders the problem non-convex, posing a significant challenge to finding an optimal solution directly.
- Within the framework of AO, a highly efficient sub-optimal solution strategy is introduced by us. This approach capitalizes on the lower bound of the EE problem by introducing a novel parameter into the EE formula. The integration of this new parameter allows for the dissection of the intricate objective function of EE into individual components for each user. Subsequently, a resourceful greedy method called the maximizing-EE-lower-bound-based downlink subcarrier assignment (MDSA) is proposed by us for subcarrier allocation, ensuring the effective utilization of available subchannels. Simultaneously, the approach employs the sequential quadratic programming method (SQP) for power allocation, a versatile optimization technique. Furthermore, the RIS phase shift is optimized using the particle swarm optimization (PSO) algorithm, recognized for its adaptability in finding optimal solutions within complex optimization spaces.
- The simulation results demonstrate that the proposed low-complexity sub-optimal method, employing MDSA and PSO, enhances the performance of RIS-enabled SISO-OFDMA communication systems compared to benchmark methods.
Notation: In this paper, vectors and matrices are denoted by bold-face lower-case and upper-case letters, respectively. Sets are designated by upper-case calligraphic letters. Additionally, the functions , , , , and indicate distinct properties of a complex number, namely, its real part, imaginary part, modulus, complex conjugate, and angle, in that order. denotes the identity matrix of size , and denotes the column of . denotes a square diagonal matrix with the elements of on the main diagonal. denotes the norm. The distribution of a circularly symmetric complex Gaussian (CSCG) random variable with mean and variance is denoted by . Some other notations used in the paper are defined in Table 2.

Table 2.
Notations used.
2. System Model and Problem Formulation
2.1. System Model
The depicted system model can be observed in Figure 1, illustrating the interaction between a single-antenna base station and K single-antenna users. These entities establish communication through the intermediary of a RIS comprising M elements.
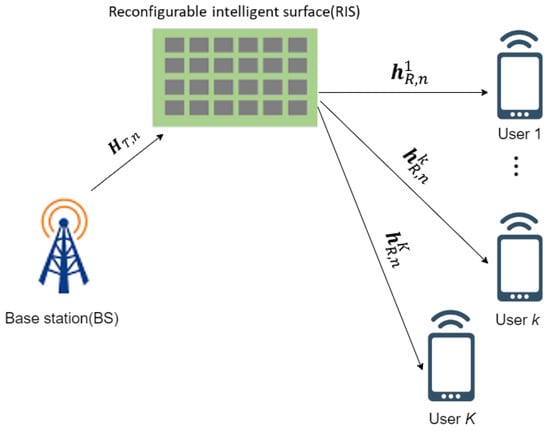
Figure 1.
The considered RIS-based multi-user SISO-OFDMA system.
The channel model is based on an OFDM with N subcarriers. The channels from the transmitter and the kth user to the RIS are defined as and , respectively, where and . is denoted as the transmitting signal from the transmitter to the kth user over the nth subcarrier.
In particular, the direct line-of-sight (LOS) link between the transmitter and the receiver is blocked (i.e., occlusion due to buildings). Thus, the received signal at the kth receiver is given as
where is the RIS configuration matrix describing the phase shift effect of the RIS on the incident signal. Note that the amplitude of the incident signal does not change, which means for any and . Furthermore, denotes the additive white Gaussian noise (AWGN) at the receivers.
The signal-to-noise ratio (SNR) perceived by the user on the subcarrier is formulated as follows:
In this context, represents the variance of the AWGN noise. The total bandwidth, B, is divided into N subcarriers, each with a bandwidth of .
Next, the maximum achievable data rate of the kth user on the nth subcarrier, , and the overall rate of the system, R, can be expressed as:
Also, indicates whether or not the subcarrier is assigned to the user. A feasible subcarrier assignment indictor matrix, , should satisfy:
where and represent the sets of all subcarriers and all UEs, respectively. To minimize interference between users, each subcarrier is assigned exclusively to one user at a time. Also, the total power consumption of the system is represented as:
where , and denotes any possible power allocation matrix and should be subject to:
In this context, , , and , respectively, represent the circuit power of the base station, the power consumption of users, and the power consumption of the m-th element of RIS. In addition, , and the parameter is used to describe the drain efficiency of the power amplifier at the side of the transmitter.
2.2. Problem Formulation
The expression for the generalized EE in downlink transmission is given as the ratio of the total delivered bits to the total consumed energy, represented mathematically as:
To ensure quality-of-service (QoS) for each user equipment (UE), we consider the generalized EE while incorporating minimum rate requirements and the peak transmit power . To simplify the problem, we assume an infinite resolution for the reflectors’ phase shifting (). Furthermore, we assume perfect knowledge of all communication channels ( and ) by the BS for all .
Therefore, we can express the optimization problem for maximizing the EE in downlink transmission through the following formula:
where denotes the individual QoS constraint of the user. Also, constraint (8b) accounts for the fact that each RIS reflecting element can only provide a phase shift, without amplifying the incoming signal.
3. Proposal Method and Discussion
The EE optimization problem presented in (8) poses a significant computational challenge due to its NP-hard nature. This difficulty arises from the discrete variable and the unit modulus constraint imposed on . Finding optimal solutions for such problems is generally infeasible within reasonable time frames. To address these complexities, we propose a sub-optimal solution strategy using an AO framework.
In our AO-based approach, we iteratively optimize two sets of variables: the OFDMA resources and and the RIS reflection coefficients . Crucially, we keep one set of variables fixed while optimizing the other. This alternating optimization scheme allows us to tackle the intricate EE problem more effectively.
In the initial stages of our approach, we employ sub-optimal solutions. This choice is motivated by the computational expense associated with obtaining closed-form optimal solutions for all variables simultaneously. Instead, by initially focusing on one set of variables, we streamline the optimization process. Subsequently, in the following step of our AO framework, we introduce the PSO algorithm to further enhance the optimization process.
3.1. Optimization Respect to Subcarrier and Power Allocations
It is difficult to optimize the original objective function in (8) directly, but it may be possible to optimize a surrogate objective function that is easier to handle. In this case, the lower bound of the objective function can be used as a surrogate objective function to facilitate the optimization process. The surrogate objective function is then optimized instead of the original objective function, and the solution obtained using the surrogate objective function is used as a lower bound on the optimal value of the objective function.
Based on the insights from the work conducted in [22], the following theorem and corollary are established.
Theorem 1.
By considering a fixed value for the RIS phase shifts and introducing a new parameter into Equation (8), the optimal EE is given by:
where and . The structure of the optimal solution, as demonstrated in Theorem 1 presented in Appendix A, can be depicted in a split form. This split form provides valuable insights that enable the derivation of Corollary 1.
Corollary 1.
For any fixed , the optimal energy efficiency () in (9) is bounded from below by:
Assuming that corresponds to the optimal energy efficiency () in Equations (8) and (9), can be interpreted as the portion of static circuit power individually allocated to the UE and the RIS element when aiming for maximum EE.
This decomposition allows us to split the complex optimization objective in Equation (8) into a set of relatively independent and simpler objectives in Equation (10). Consequently, we can employ sub-optimal methods for efficient problem-solving.
3.1.1. Subcarrier Allocations
Utilizing a heuristic algorithm is advantageous in this scenario since the maximum achievable energy efficiency of the UE, , depends solely on its own parameters and the subcarriers it occupies, without being influenced by the power adaptation strategies of other users. To simplify, we assume there is no difference in the RIS configuration matrix between subcarriers of the same user, meaning .
Additionally, constant values for are considered for further simplification. Negative values of may arise due to the nature of , representing the hypothetical static circuit power allocated to the UE and RIS element. It is important to note that this value serves as a conceptual representation rather than a concrete physical reality. In practice, the total static circuit power remains constant at .
To solve the optimization problem in Equation (10), we employ a heuristic algorithm called MDSA [22]. The power allocation is optimized using the SQP method, which is integrated into the MDSA algorithm.
The central concept behind the MDSA algorithm is to iteratively assign subcarriers, with the aim of maximizing the minimum individual EE, denoted as , while ensuring that QoS requirements are met. Initially, each UE virtually receives its worst subcarrier, a conservative starting point. In this scenario, an individual EE is optimized under the QoS constraint using the algorithm employed for the power allocation, as described in Lines 2 to 5.
In each iteration, the UE with the lowest individual EE selects its preferred subcarrier from the pool of unassigned subcarriers. The UE then optimizes its individual EE under the QoS requirements using the SQP method. This iterative process continues until all subcarriers have been assigned, as outlined in lines 7 to 12 of Algorithm 1.
| Algorithm 1: MDSA Maximizing-EE-lower-bound-based downlink subcarrier assignment. |
1. Input: ; , ; 2. Output: 3. For each UE 4. Find the subcarrier 5. Calculate 6. End 7. While 8. Find the UE such that 9. Find the UE such that 10. Set ; ; 11. 12. End |
Notably, the MDSA algorithm does not impose a total transmit power constraint explicitly. However, this constraint is likely to be automatically satisfied during subcarrier allocation for several reasons:
By appropriately choosing the parameter , the eventually optimized individual EEs tend to converge to similar values. If a UE initially requires excessive power to meet its QoS, it likely has a lower individual EE and will request more subcarriers later. This allows the UE to reduce its transmit power and increase its EE. In this work, a fixed set of parameters is employed for more simplification.
When the EE improvement achieved by the energy-efficient design compared to the spectral-efficient design is substantial, the actual transmit power used for the energy-efficient design should be significantly lower than the maximum transmit power, ensuring efficient power utilization.
In the following, we delve into the SQP method employed to optimize power allocations.
3.1.2. Power Allocations
The sequential quadratic programming method is an iterative optimization technique used to solve constrained optimization problems, often encountered in mathematical modeling and engineering applications. SQP combines principles from both Newton’s method and Lagrange multipliers to find the optimal solution within a feasible region defined by constraints.
In the context of SQP, the following subproblems should be defined:
where
and
The primary idea behind the SQP method is to use a second-order subproblem at the current point and minimize this subproblem to determine the new point .
In its simplest form, the SQP method defines the second-order subproblem in the iteration as follows:
Here, is the Hessian matrix (second-order partial derivatives matrix) of the Lagrange function for the problem (11), denotes the gradient of the objective function at point , represents the gradient of the constraints, and d is the direction of motion.
Solving this second-order subproblem yields the solution , which, under Karush–Kuhn–Tucker (KKT) conditions, is valid for the problem. A merit function is designed to assess solution suitability and balance the decrease rate of the objective function with respect to the established problem constraints.
The iterations continue until an acceptable answer is acquired [11]. The SQP algorithm is presented in Algorithm 2.
3.2. Optimization with Respect to RIS Phase Shift Matrix
Consider the optimized values for the vectors and obtained in the first step of the AO algorithm. The EE optimization problem with respect to RIS phase shifts is formulated as follows:
In this problem, represents Energy Efficiency, is the RIS phase shift matrix, and the constraints in (16a) ensure that the phase shifts have unit magnitude. This EE maximization problem can be transformed into a rate maximization problem with respect to the RIS phase shift variables.
To tackle this optimization problem, we employ the PSO algorithm, renowned for its versatility in solving complex optimization tasks. PSO maintains a population of particles, each associated with a phase shift vector, and efficiently explores the solution space to find optimal solutions. Here is a more detailed breakdown of the key operations and parameters in the PSO algorithm.
| Algorithm 2: Sequential fractional programming algorithm. |
1. Choose parameters , and an initial pair ; 2. Evaluate ; 3. If a quasi-Newton approximation is used, choose an initial symmetric positive definite Hessian approximation , otherwise compute ; 4. repeat until a convergence test is satisfied 5. Compute by solving (14); let be the corresponding multiplier; 6. Set ; 7. Choose to satisfy with ; 8. Set ; 9. while 10. Reset and ; 11. end(while) 12. and ; 13. Evaluate (and possibly ); 14. If a quasi-Newton approximation is used, set 15. and , 16. and obtain by updating using a quasi-Newton formula; 17. repeat |
The PSO algorithm, outlined in Algorithm 3, efficiently explores the solution space by maintaining a population of particles with associated phase shift vectors. The algorithm’s complexity is proportional to the product of the population size L and the maximum number of iterations T.
For each particle at time t, it is associated with a phase shift vector , where each component is limited within . The fitness value of each particle is evaluated using the fitness function , which can be defined as follows:
Finding the maximum value of in Equation (17) is equivalent to finding the minimum value of . and are defined as the optimal position of particle i and the optimal position of the entire population after t iterations. The following equations update, at each current iteration , the velocity and position of of each particle i as:
In the context of our optimization process, we denote as the velocity vector, and is employed as the inertia weight to carefully balance between local exploitation and global exploration. To introduce stochasticity, we utilize and as random vectors uniformly distributed within the interval [0, 1] for each dimension of the search space (where D represents the dimensionality or size of the problem). Additionally, we incorporate and , which we refer to as acceleration coefficients, as positive constants [23,24,25].
| Algorithm 3: Particle swarm optimization algorithm. |
1. Initialize 2. for do 3. Initialize 4. end for 5. Find , and set ; 6. while do 7. for do 8. Update the velocity and position of particles using Equations (19) and (20): 9. Evaluate fitness value; 10. Calculate the historical optimal position of particle i: 11. 12. Find 13. end for 14. Calculate the historical optimal position of the population: 15. 16. Adjust adaptive parameter shown in Algorithm 4; 17. Set . 18. end while |
The PSO algorithm proceeds through the outlined stages as detailed in Algorithm 3.
- In lines 2–4, we initialize each particle’s position, velocity, and historical best position.
- In line 5, we find the best position among all particles and update the historical best position of the entire population, denoted as . This is the position with the best fitness value.
- The iterative optimization process starts in line 6 and continues until the maximum number of iterations T is reached.
- –
- Within each iteration:- In lines 7–17, we perform operations for each particle i in the population.- Lines 7–8 update the velocity and position of the particle based on its previous position, the best position it has encountered (), and the best position in the entire swarm (). This helps particles explore the solution space.- Line 9 evaluates the fitness value of the particle’s current position.- Lines 10–11 update the historical best position of the particle based on whether the current position or the previous best position is better. This helps particles remember their best-performing positions.- After evaluating and updating each particle, we find the best position among all particles in line 12 and update the historical best position of the entire population () in line 15.- The adaptive parameter is adjusted in lines 16 based on the performance of the swarm according to Algorithm 4.- The dynamic adjustment of aims to strike a balance between exploration and exploitation during the PSO algorithm’s execution. It helps fine-tune the search process to improve convergence and find optimal solutions effectively.
The AO algorithm is presented in Algorithm 5.
| Algorithm 4: Adjust adaptive parameter. |
1. Initialize ; 2. if 3. ; 4. else 5. ; 6. end if 7. if 8. ; 9. else 10. ; 11. if 12. ; 13. else if 14. ; 15. end if 16. end if |
| Algorithm 5: Alternating optimization algorithm. |
1. Input: ; 2. Output: and 3. repeat 4. Fixing the RIS coefficients 5. Find the according to MDSA Algorithm and SQP Algorithm 6. Fixing the power allocation , given initial , update the RIS coefficients via PSO Algorithm 7. Until the objective value of (P1) with the obtained and reaches convergence. 8. and |
4. Simulation Results
In this section, we present the results of our proposed algorithm’s performance evaluation through numerical simulations for downlink communications. All simulations were conducted using MATLAB 2019b. The simulation setup is based on an OFDM system with subcarriers. The multiple single-antenna mobile users are considered to be randomly and uniformly distributed within the 100 m × 100 m rectangular region on the right-hand side of the RIS in the x–y plane. All the provided illustrations represent averaged outcomes obtained from independent scenarios involving variations in users’ positions and channel characteristics. These scenarios were generated following the 3GPP propagation environment detailed in [26], and the relevant parameters are outlined in Table 1. The performance of our proposed joint resource allocation was compared with two benchmark schemes, random passive beamforming and without RIS, where the first scheme considers the BS-user direct link and performs the OFDMA resource allocation. The results also compared with the optimization approach using the genetic algorithm (GA) for phase shift optimization [27]. However, detailed information regarding these schemes are omitted in this context. The specific simulation parameters are outlined in Table 3.

Table 3.
Simulation parameters.
It is noteworthy to point out that a majority of the papers listed in Table 1 primarily concentrate on optimizing the sum-rate. This poses a challenge when attempting to compare our results with the aforementioned papers. Moreover, the study in [21] focuses on maximizing EE and incorporates an active RIS in the system model, presenting a distinction from the system model considered in our work.
The graph in Figure 2 illustrates the performance of achievable EE with respect to variations in in dBm. In this depiction, we have set the minimum QoS constraint as bps/Hz and fixed to for all K users. Our study considers system parameters , , and . As depicted in Figure 2, an increase in correlates with an increase in EE. Nevertheless, around dBm, there is an underutilization of excess transmit power, resulting in a decline in energy efficiency. This can be attributed to the fact that the EE function does not exhibit a strictly increasing trend with the maximum BS transmit power, . Instead, it reaches a finite maximizer. It is essential to emphasize that the proposed algorithm for passive beamforming optimization using PSO outperforms the one using GA, random passive beamforming optimization, as well as the scenario without RIS in terms of EE. Moreover, Figure 3 illustrates the average SE versus for different schemes. It can be observed that with an increase in , there is an enhancement in the achievable SE for all the schemes. It also underscores that for low values of , the problem is frequently infeasible. This is expected since the BS lacks adequate transmit power to meet the rate requirements of the users, leading to significantly low SE values. Nevertheless, as increases, the attainable SE starts to rise. Additionally, similar to the trend in Figure 2, the proposed algorithm for passive beamforming optimization using PSO outperforms other schemes. Besides, Figure 4 portrays the performance of EE concerning the number of RIS elements, denoted as M. As observed, when M is relatively small, i.e., , all designs except for the without-RIS scheme, exhibit the same trend. Particularly, EE performance increases as M increases. However, as M assumes moderate to intermediate values and beyond, EE undergoes a reduction, substantiating the existence of an optimal M for the maximization of EE objectives [28]. The proposed scheme exhibits a significant improvement when contrasted with a random passive beamforming mechanism. Conversely, the performance of the without-RIS scheme remains unaffected by the number of RIS elements in the system, implying the enhancement achievable through RIS in the wireless communication environment.
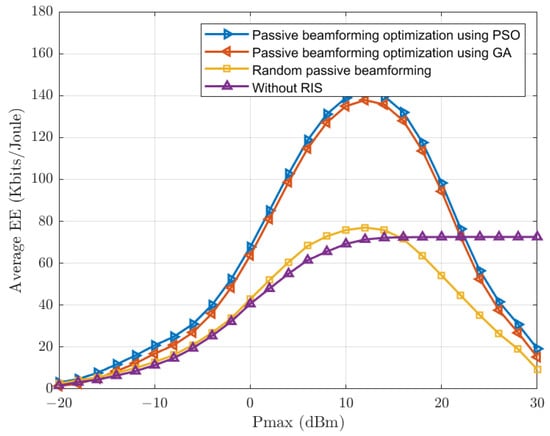
Figure 2.
Average EE versus for bps/Hz, , and .
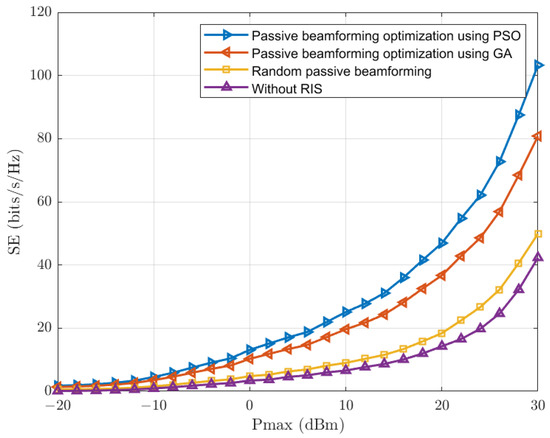
Figure 3.
Average SE versus for bps/Hz, , and .
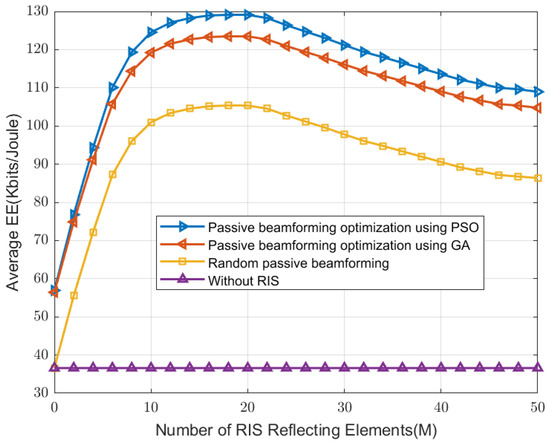
Figure 4.
Average EE versus number of RIS elements, M for bps/Hz, , , and .
Remark
- ComplexitySecuring the optimal solution for problem (P1) requires the application of a power allocation algorithm to each feasible subcarrier assignment that meets the constraint in Equation (4) and subsequently selecting the assignment with the highest EE. Its computational complexity depends on the number of optimizing variables, which can be large if the number of subcarriers and/or the number of UEs is large. Nevertheless, the associated complexity proves excessively high, rendering it impractical for real-world scenarios.In contrast, the proposed sub-optimal solution, facilitated by the MDSA algorithm, eliminates the need to optimize a joint and intricate objective in each step. Subcarrier assignment becomes more manageable with this pragmatic approach. This is because, for each UE, the maximum of its individual EE is contingent solely upon its parameters and the subcarriers it will occupy, without reliance on the power adaptation strategies of other UEs. The complexity of the MDSA algorithm for a given is roughly times that of the SQP method, where is the number of iterations in the outer layer, and N is the total number of subcarriers.The complexity of the SQP algorithm is dependent on the QP subproblem. By using modern interior-point (IP) methods for solving subproblems, a polynomial bound of computational complexity results [29]. Additionally, it is observed that the computational complexity of the PSO algorithm mainly involves the computation of fitness values of L passive beamformers for K users. Thus, the computational complexity is . It is clear that the complexity of the PSO algorithm is only linearly increasing with the number of particles L.
- ConvergenceThe iterative alternating algorithm for solving the EE maximization problem (P3) is given in Algorithm 5. Since the updates through SQP and PSO all maximize the objective function at each iteration, the iterations in Algorithm 5 lead to a monotone increase of the objective function of problem (P3). Since the objective function under the power and amplitude reflection coefficient constraints are bounded, the convergence of the alternating maximization algorithm can be guaranteed with the monotonic convergence theorem [30].
5. Conclusions and Future Work
This study seamlessly integrates RIS technology into multi-user downlink OFDMA communication systems, optimizing RIS reflection coefficients, OFDMA frequency allocations, and power distributions. Guided by stringent QoS requirements and transmission power constraints, as well as unit modulus constraint on the RIS phase shifts, the efficiency-focused methodology systematically address these multifaceted optimizations. These strategies redefine the original problem, deriving computationally accessible lower bounds on energy efficiency while striking a harmonious balance between performance enhancement and real-world feasibility. At its core, the AO algorithm, featuring the MDSA, SQP, and PSO approaches, effectively addresses complex challenges in energy-efficient wireless networks. Robust numerical results confirm substantial energy efficiency improvements compared to non-RIS scenarios. Our current work focuses on the simplicity of the SISO system, avoiding the complexities introduced by MISO and MIMO systems. For future research, we propose the exploration of the application of multiple antennas at both transmitter and receiver ends, anticipating a deeper understanding and a broader scope of findings.
Author Contributions
Conceptualization, S.B. and M.A.O.; methodology, S.B.; software, S.B.; validation, S.B., M.A.O., M.B. and D.M.; formal analysis, S.B.; investigation, S.B.; resources, S.B.; data Creation, S.B.; writing—original draft preparation, S.B.; writing—review and editing, S.B., M.A.O., M.B. and D.M; visualization, S.B.; supervision, M.A.O. and M.B.; project administration, S.B.; funding acquisition, S.B., M.A.O. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This study received no external funding.
Data Availability Statement
Please contact the corresponding author at samaneh.bidabadi@uqtr.ca.
Conflicts of Interest
The authors declare no conflicts of interest.
Acronyms
| RF | Radio Frequency |
| EE | Energy Efficiency |
| SE | Spectral Efficiency |
| RB | Resource block |
| GA | Gradient decent algorithm |
| RL | Reinforcement Learning |
| QoS | quality-of-service |
| ZF | Zero-Forcing |
| RIS | Reconfigurable Intelligent Surface |
| OFDM | Orthogonal Frequency Division Multiplexing |
| OFDMA | Orthogonal Frequency Division Multiple Access |
| SISO | Single Input Single Output |
| MISO | Multiple Input Single Output |
| MIMO | Multiple Input Multiple Output |
| APs | access points |
| MU | Multiple User |
| SNR | Signal to Noise Ratio |
| SINR | Signal to Interference Plus Noise Ratio |
| AWGN | Additive White Gussian Noise |
| CSI | Channel State Information |
| SCA | sine cosine algorithm |
| MM | Majorization–Minimization |
| OBR-FL | optimal beam reflection based on federated learning |
| MC | Monte Carlo |
| AO | Alternating Optimization |
| KKT | Karush Kuhn Tucker |
| SQP | Sequential Programming Method |
| PSO | Particle Swarm Optimization |
Appendix A. Proof of Theorem 1
Proof.
Consider the optimal subcarrier and power allocation matrices, denoted as and , respectively, for (8). In this context, represents the energy efficiency defined as .
For any fixed values of and , we can express the energy efficiency, denoted as EE, as follows:
Here, , and equality holds if and only if:
This equality condition implies that can be expressed as .
Furthermore, it is evident that:
In this equation, . Therefore, the right-hand side (RHS) cannot exceed the left-hand side (LHS) for any . Additionally, equality always holds if the RHS uses the same and as and that achieve the LHS. This requires setting such that . It becomes apparent that through a straightforward substitution of in the expression for , ; we can draw the conclusion that the sum of the optimized values for all k in equals 1.
This concludes the proof. □
References
- Jamil, S.; Rahman, M.; Abbas, M.S.; Fawad. Resource Allocation Using Reconfigurable Intelligent Surface (RIS)-Assisted Wireless Networks in Industry 5.0 Scenario. Telecom 2022, 3, 163–173. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, S.; Zhang, R. IRS-enhanced OFDM: Power allacation and passive array optimization. In Proceedings of the IEEE Global Commun. Conf. (Globecom), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. Available online: https://arxiv.org/abs/1905.00604 (accessed on 9 December 2019).
- Bidabadi, S.; Ouameur, M.A.; Bagaa, M.; Massicotte, D. Energy efficient resource allocation for re-configurable intelligent surface-assisted wireless networks. EURASIP J. Wirel. Commun. Netw. 2023, 2023, 89. [Google Scholar] [CrossRef]
- Lee, G.; Jung, M.; Kasgari, A.T.; Saad, W.; Bennis, M. Deep reinforcement learning for energy-efficient networking with reconfigurable intelligent surfaces. In Proceedings of the IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Tan, F.; Xu, X.; Chen, H.; Li, S. Energy-efficient beamforming optimization for MISO communication based on reconfigurable intelligent surface. Phys. Commun. 2023, 3, 101996. [Google Scholar] [CrossRef]
- He, Z.; Shen, H.; Xu, W.; Zhao, C. Low-cost passive beamforming for ris-aided wideband ofdm systems. IEEE Wirel. Commun. 2022, 11, 318–322. [Google Scholar] [CrossRef]
- An, J.; Wu, Q.; Yuen, C. Scalable channel estimation and reflec- tion optimization for reconfigurable intelligent surface-enhanced ofdm systems. IEEE Wirel. Commun. Lett. 2022, 11, 796–800. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, B.; Zhang, S.; Zhang, R. Intelligent Reflecting Surface Meets OFDM: Protocol Design and Rate Maximization. June 2019. Available online: https://arxiv.org/pdf/1906.09956 (accessed on 9 December 2019).
- Li, R.; Sun, S.; Tao, M. Ergodic achievable rate maximization of RIS-assisted millimeter-wave MIMO-OFDM communication systems. IEEE Trans. Wirel. Commun. 2022, 22, 2171–2184. [Google Scholar] [CrossRef]
- Saggese, F.; Kansanen, K.; Popovski, P. Localization-based OFDM framework for RIS-aided systems. arXiv 2023, arXiv:2303.12763. [Google Scholar]
- Wu, W.; Yang, F.; Zhou, F.; Wu, Q.; Hu, R.Q. Intelligent Resource Allocation for IRS-Enhanced OFDM Communication Systems: A Hybrid Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2023, 22, 4028–4042. [Google Scholar] [CrossRef]
- Chen, P.; Li, X.; Matthaiou, M.; Jin, S. DRL-Based RIS Phase Shift Design for OFDM Communication Systems. IEEE Wirel. Commun. Lett. 2023, 12, 733–737. [Google Scholar] [CrossRef]
- Pradhan, C.; Li, A.; Song, L.; Li, J.; Vucetic, B.; Li, Y. Reconfigurable Intelligent Surface (RIS)-Enhanced Two-Way OFDM Communications. IEEE Trans. Veh. Technol. 2020, 69, 16270–16275. [Google Scholar] [CrossRef]
- Wei, Z.; Cai, Y.; Sun, Z.; Ng, D.W.K.; Yuan, J.; Zhou, M.; Sun, L. Sum-Rate Maximization for IRS-Assisted UAV OFDMA Communication Systems. arXiv 2020, arXiv:2008.09939. [Google Scholar]
- Hao, W.; Sun, G.; Zeng, M.; Chu, Z.; Zhu, Z.; Dobre, O.A.; Xiao, P. Robust Design for Intelligent Reflecting Surface-Assisted MIMO-OFDMA Terahertz IoT Networks. IEEE Internet Things J. 2021, 8, 13052–13064. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Wu, Q.; Zhu, X.; Qin, H.; Wang, K.; Li, J. Towards Transmissive RIS Transceiver Enabled Uplink Communication Systems: Design and Optimization. IEEE Internet Things J. 2023, 11, 6788–6801. [Google Scholar] [CrossRef]
- Yu, H.; Tuan, H.D.; Nasir, A.A.; Dutkiewicz, E.; Hanzo, L. Rate-Fairness-Aware Low Resolution RIS-Aided Multi-User OFDM Beamforming. IEEE Trans. Veh. Technol. 2024, 73, 2401–2415. [Google Scholar] [CrossRef]
- Ghanem, W.R.; Jamali, V.; Schober, R. Joint Beamforming and Phase Shift Optimization for Multicell IRS-aided OFDMA-URLLC Systems. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Ma, D.; Li, L.; Ren, H.; Wang, D.; Li, X.; Han, Z. Distributed Rate Optimization for Intelligent Reflecting Surface with Federated Learning. In Proceedings of the 2020 IEEE International Conference on Communications Workshops (ICC Workshops), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, S.; Zhang, R. IRS-enhanced OFDMA: Joint resource allocation and passive beamforming optimization. IEEE Wireless Commun. Lett. 2020, 9, 760–764. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J. Energy Efficiency Fairness of Active Reconfigurable Intelligent Surfaces-Aided Cell-Free Network. IEEE Access 2023, 11, 5884–5893. [Google Scholar] [CrossRef]
- Xiong, C.; Li, G.Y.; Zhang, S.; Chen, Y.; Xu, S. Energy-Efficient Resource Allocation in OFDMA Networks. IEEE Trans. Commun. 2012, 60, 3767–3778. [Google Scholar] [CrossRef]
- Gad, A.G. Particle swarm optimization algorithm and its applications: A systematic review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Dai, J.; Wang, Y.; Pan, C.; Zhi, K.; Ren, H.; Wang, K. Reconfigurable intelligent surface aided massive MIMO systems with low-resolution DACs. IEEE Commun. Lett. 2021, 25, 3124–3128. [Google Scholar] [CrossRef]
- Pedersen, M.E. Good Parameters for Particle Swarm Optimization; Hvass Laboratories: Luxembourg, 2010. [Google Scholar]
- Björnson, E.; Sanguinetti, L.; Hoydis, J.; Debbah, M. Optimal design of energy-efficient multi-user MIMO systems: Is massive MIMO the answer? IEEE Trans. Wireless Commun. 2015, 14, 3059–3075. [Google Scholar] [CrossRef]
- Peng, Z.; Li, T.; Pan, C.; Ren, H.; Xu, W.; Renzo, M.D. Analysis and optimization for RIS-aided multi-pair communications relying on statistical CSI. IEEE Trans. Veh. Technol. 2021, 70, 3897–3901. [Google Scholar] [CrossRef]
- Zappone, A.; Renzo, M.D.; Xi, X.; Debbah, M. On the optimal number of reflecting elements for reconfigurable intelligent surfaces. IEEE Wireless Commun. Lett. 2021, 10, 464–468. [Google Scholar] [CrossRef]
- Błaszczyk, J.; Karbowski, A.; Malinowski, K. Object Library of Algorithms for Dynamic Optimization Problems: Benchmarking SQP and Nonlinear Interior Point Methods. Int. J. Appl. Math. Comput. Sci. 2007, 17, 515–537. [Google Scholar] [CrossRef]
- Grippo, L.; Sciandrone, M. On the convergence of the block nonlinear Gauss–Seidel method under convex constraints. Oper. Res. Lett. 2000, 26, 127–136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).