Abstract
Since Mars is far away from Earth, the propagation delay between Mars and Earth is very large. To ensure the effective use of the link transmission bandwidth, China’s first Mars exploration mission has put forward a demand for data compression for all scientific payloads. The on-board mature algorithms for data compression are mainly focused on optical images and microwave imaging radar applications. No articles have been published on data compression methods that are applied to subsurface-penetrating radar. Based on the background of this application, this paper proposes a logarithmic lossy compression algorithm which can meet the mission requirements for high compression ratios of 4:1 and 2.5:1. Its compression error is less than that of the block adaptive quantization (BAQ) algorithm. The algorithm is not only easy to implement on field-programmable gate array (FPGA) platforms, but also offers simple ground decompression and fast imaging. The experimental results show that high compression ratios of 4:1 and 2.5:1 can be realized, even if the data in and between traces do not have a strong correlation. And its relative error is less than 2%, which is a new type of high-efficiency data compression method that can be implemented on-board to meet with the demand of subsurface penetrating radar.
1. Introduction
China’s first Mars exploration mission (Tianwen-1) was officially established in 2016. Tianwen-1 was designed to carry out orbiting, landing, and roving in one mission [1]. Tianwen-1 was successfully launched on 23 July 2020 and approached Mars in February 2021. The lander carrying the rover touched down on the southern part of Utopia Planitia, a vast plain in the northern hemisphere of Mars, on 15 May 2021 and successfully detached. TheMars rover on the Tianwen 1 named ZhuRong carried six payloads. The Mars rover subsurface-penetrating radar (RoSPR) is an important payload, which is used to detect the thickness of the upper Martian soil and the structure of potentially buried water ice or dry ice and to determine the depth distribution of the subsurface stratigraphy. Since Mars is far from Earth, the propagation delay in the communication link is very large (more than 20 min). In order to reduce the pressure on the transmission link and ensure the effective use of the link transmission bandwidth, China’s first Mars exploration mission has put forward a demand for data compression for all scientific payload data. Compression algorithms are widely used to reduce data storage requirements in computers. A high-speed CPU and memory can easily solve the resource problems of compression algorithms. Therefore, various algorithms, such as text compression, image compression, and encoding compression, have been proposed and successfully applied in different fields. On the contrary, the compression algorithms required for embedded systems, especially in FPGA applications, cannot directly employ the algorithms mentioned above. With the increasing application of satellites, optical equipment data compression algorithms are becoming increasingly mature. After long-term development, good results have been achieved. The spaceborne mature algorithms of data compression are mainly focused on optical images [2] and microwave radar imaging [3,4]. No articles have been published on data compression methods that are applied to subsurface-penetrating radar. The RoSPR data, taken from underground soil, are far from optical image data, and their characteristics are very different, so the compression algorithm for optical images cannot be used directly. At the same time, microwave imaging radar detects data from the reflection of electromagnetic waves on the surface of ground objects, and the data have normal distribution characteristics, so the block adaptive quantization (BAQ) algorithm is suitable for data compression. The BAQ algorithm has characteristics such as good real-time performance, low difficulty, and easy implementation and is widely used in radar imaging satellites.
In 1987, Joo and Held proposed the block floating point quantization (BFPQ) algorithm [5] for raw echo data compression in synthetic aperture radar (SAR). The SIR-C system launched by the United States in 1993 successfully quantized the original SAR echo data from 8 bits to 4 bits using this algorithm. Considering both resources and compression performance, the BAQ algorithm proposed by Kwok and Johnson is relatively easy to implement in hardware [6]. It has been applied in the SAR system for Magellan aircraft and A-SAR for ENVISAT [7]. Up to now, only the BAQ and BFPQ algorithms have been applied to spaceborne data compression in practical engineering. The BFPQ algorithm was optimized by Israel and India in 2008 and 2009, respectively. The Israeli technical synthetic aperture radar “TecSAR” and Indian imaging satellite “RISAT-2” both used modified block floating point quantization (MBFPQ). In 2016, the European Sentinel series [6,7] adopted two algorithms: the BAQ and flexible dynamic block adaptive quantization (FDBAQ) algorithms [8], which can achieve the optimal quantization output results for different types of target data. In addition to the scalar quantization algorithm, the vector quantization (VQ) algorithm has also appeared [9]. But the dynamic range of the data from the RoSPR is very large (more than 90 dB), and the efficiency of using the VQ algorithm to compress echo data is low [10]. Later, block adaptive vector quantization (BAVQ) [11] and block gain adaptive vector quantization (BGAVQ) were developed. The Institute of Electronics, Chinese Academy of Sciences, has carried out in-depth research on the data compression algorithm and hardware implementation of spaceborne radar [12]. Based on the research on existing algorithms, one-dimensional and two-dimensional nonlinear quantization algorithms and amplitude–phase (AP) compression algorithms that compress the amplitude and phase of the original data were proposed successively. Compared with SAR data, RoSPR data are targeted toward the stratified detection results for the Martian medium below the surface, its signal dynamic range is larger (more than 90 dB usually), data correlation is weak and has low redundancy. After a comparative analysis, it is found that the BAQ algorithm is not as applicable as the method proposed in this article.
In response to the above problem, a logarithmic lossy compression algorithm based on an FPGA is proposed in this paper, and it is easy to implement and has good real-time performance and a lower compression error than the BAQ algorithm. According to mission requirements, RoSPR’s data compression ratios need to meet 2.5:1 and 4:1 [13]. The algorithm model is proposed according to the characteristics of the RoSPR data, and the high compression ratio results of 2.5:1 and 4:1 are verified using actual loopback data. We compare compression data and decompression data measured in glaciers and volcanic vents, and the results show that the data compression error is acceptable and the FPGA resources are less occupied with this method. The proposed algorithm can meet the requirements of the RoSPR data compression, which is a high-efficiency data compression method for subsurface-penetrating radar.
The remaining sections are arranged as follows: Section 2 provides an overview of the RoSPR system. Section 3 introduces the data characteristics of the RoSPR, the algorithm model, and the processing flow. In Section 4, the BAQ and logarithmic compression algorithms are compared in terms of the processing of measured data, and this further shows that the logarithmic compression algorithm is more suitable for the RoSPR. Section 5 describes the implementation of the logarithmic compression algorithm in detail. Section 6 introduces the compression processing results of field test data from glaciers and volcanoes, which demonstrates that the algorithm can meet the application requirements. Finally, a summary and acknowledgements are provided for this article.
2. RoSPR Overview
The subsurface-penetrating radar of the ZhuRong rover is a frequency-domain radar with an FM continuous wave signal, whose block diagram is shown in Figure 1. The RoSPR is equipped with two channels. One is a low-frequency channel, and the other is a high-frequency channel, both of which realize corresponding scientific objects. The low-frequency channel is 15~95 MHz, and the other is 450~2150 MHz. The controller of the radar is composed of a Xilinx Virtex 5 aerospace FPGA, XQR5VFX130T. The main functions of the FPGA are as follows: (1) to generate the two channels’ baseband signals; (2) to fulfill the low-frequency channel functions: echo sampling, digital down-conversion and pulse compression, and data compression; (3) to control the RF frontend; (4) to achieve the high-frequency channel functions: echo sampling and data compression; (5) to acquire telemetry signals; and (6) to perform parameter injection, format and send scientific data [13], and so on.
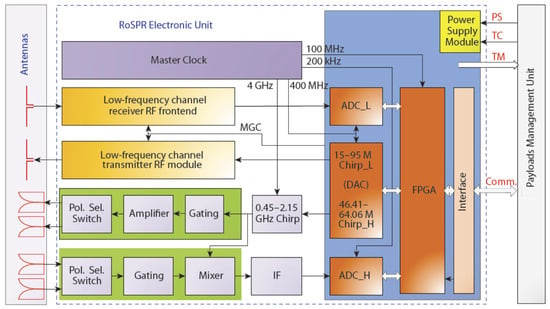
Figure 1.
The RoSPR block diagram.
A block diagram of the RoSPR FPGA is given in Figure 2. The low-frequency channel functions are achieved in the digital domain, which is colored in orange in the block diagram. Meanwhile, a superheterodyne receiver is employed in the hardware for the high-frequency channel, and its function is shown in blue in the block diagram. As for the high-frequency channel, the FPGA only needs to complete its echo sampling and data compression. Moreover, the two channels’ data compression is the same. We use the low-frequency channel as an example to introduce the algorithm in detail in the following sections.
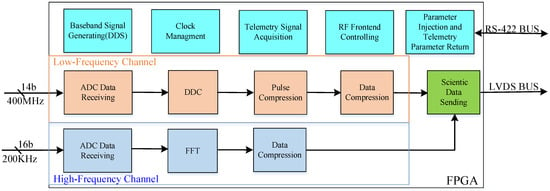
Figure 2.
The RoSPR FPGA block diagram.
3. BAQ and Logarithmic Compression Algorithms
Compression algorithms are generally divided into three categories: (1) scalar quantization compression algorithms; (2) vector compression algorithms; and (3) transform-domain compression algorithms. Transform-domain methods have a high degree of complexity and have not been practically applied in spaceborne SAR systems. Vector compression algorithms, as mentioned above, are not suitable for subsurface-penetrating radar. Therefore, the RoSPR uses a scalar quantization method to achieve lossy compression. Scalar quantization methods include uniform quantization, adaptive quantization, and non-uniform quantization. After pulse compression in the FPGA, the radar data roughly obey the Gaussian distribution. Subsequently, the quantization method needs to employ adaptive quantization or non-uniform quantization instead of uniform quantization. The BAQ algorithm is selected as the adaptive quantization method, while the logarithmic quantization method is chosen as the non-uniform quantization method. A comparison of the two compression algorithms is made in Section 4.
3.1. Logarithmic Compression Algorithm and Model
The logarithmic compression algorithm (LCA) is a lossy compression method employing non-uniform quantization. It uses amplitude non-uniform quantization to compress the original data; this is similar to the block adaptive quantization algorithm. In comparison to the BAQ algorithm, it has no block, no average mean, and no quantization code table [14]. The LCA can be implemented on a single FPGA, uses few resources, and has good real-time performance.
The maximum echo signal of the RoSPR low-frequency channel is about 2 dBm, and its noise floor is −85 dB. Therefore, the dynamic range of the low-frequency channel is about 87 dB. Considering the margin, 90 dB is taken. RoSPR pulse compression is achieved in the FPGA, which is carried out by FFT multiplication in the frequency domain. The FFT operation result should be at least about 15 bits (90 dB/6 dB/bit). Considering the design margin and accumulation requirements, the FFT result is represented by a 20-bit signed number that covers the 90 dB dynamic range.
A 20-bit signed data becomes a 5-bit signed data after 4:1 compression. The data maximum before compression is (2^20 = 1,048,576), and the data maximum after compression is (2^5 = 32). The base of the logarithmic is 10, and the compression formula is given as follows:
The symbol indicates that the data are rounded down. ini_data represents the 20-bit signed data after radar pulse compression, and compress_data1 represents the compressed data.
Similarly, the data become 8-bit signed data after 2.5:1 compression. The maximum number of data before compression is (2^20 = 1,048,576), and the maximum number of data after compression is (2^7 = 128). The compression formula is as follows:
compress_data2 represents the compressed data after 2.5:1 compression.
3.2. Algorithm Flow
The LOG quantizer is used to encode the input data. The establishment of the LOG quantizer depends on the width of the input data and the compression ratio. Its block diagram is shown in Figure 3.
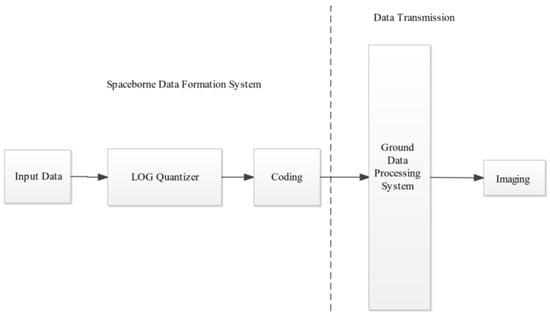
Figure 3.
Block diagram of logarithmic compression algorithm.
The specific LCA process is as follows:
- (1)
- According to the width of the input data and the compression ratio, the operation coefficient of logarithmic compression is determined.
- (2)
- According to the width of the input data and the operation coefficient of compression, the LOG quantizer is established.
- (3)
- The input data are passed through the LOG quantizer, and the compressed coded value is output.
- (4)
- The compressed value is transmitted to the ground.
- (5)
- The compressed operating coefficient is reused on the ground to decompress the coded value.
4. BAQ and Logarithmic Compression Algorithm Test Comparison
4.1. BAQ Algorithm
The BAQ quantizers with different bit rates are used to improve the overall compression performance of the TerraSAR-X system [15,16,17]. In view of the approximate Gaussian distribution statistical characteristics for microwave imaging radar data [16], the dynamic range of the signal in a short time interval is much smaller than that of the entire echo data set. After the data are divided into blocks, the dynamic range of most compressed data blocks is reduced [18]. The BAQ algorithm block diagram is shown in Figure 4.
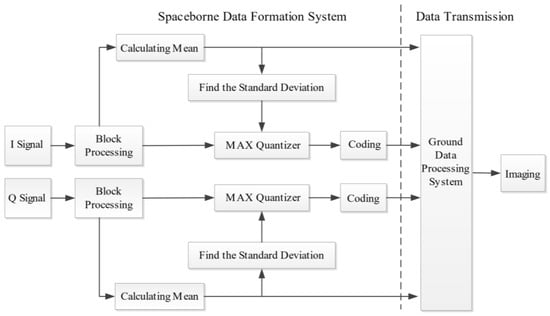
Figure 4.
Block diagram of BAQ algorithm.
The specific BAQ algorithm process is as follows:
- (1)
- The data are divided into blocks, the average amplitude of the samples in the blocks is calculated, and the standard deviation is obtained from a look-up table with the obtained mean value.
- (2)
- The optimal quantization level threshold is determined from the standard deviation, and the code is obtained by comparing the data samples in the blocks with the threshold, which contains 1 sign bit.
- (3)
- The code and the corresponding block amplitude mean are transmitted down to the ground.
- (4)
- On the ground, the codes and the mean amplitudes of the corresponding data blocks are used to decompress the data according to the decoding value table.
4.2. Test Comparison of the Two Methods
The two compression algorithms were compared with the measured data in the laboratory. A loopback test was carried out to obtain data after pulse compression based on a flight model. The chirp signal transmitted by the transmitter was attenuated by 20 dB by a fixed attenuator, and loopback to the receiver was carried out through a Radio Frequency (RF) cable. The data were directly output after pulse compression was carried out in the FPGA.
We used the logarithmic compression algorithm and the BAQ compression algorithm to complete 4:1 data compression, respectively, and we compared the data compression and decompression results, as shown in Figure 5, where INI represents the initial data.
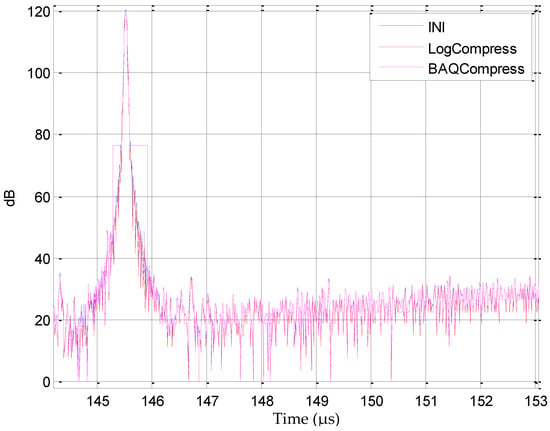
Figure 5.
Comparison before and after compression by two algorithms.
When the input data have no targets (148 μs~153 μs), the noise follows a Gaussian distribution, and BAQ compression performs better than logarithmic compression. However, for targeted data (144 μs~148 μs), due to their high dynamics, the sidelobe compression effect of logarithmic compression is significantly better than that of BAQ. In the later analysis of the RoSPR data, the loss of the echo signal needs to be concerned. The sidelobe loss of BAQ compression has a significant impact on the later data analysis, while the noise loss before and after compression has little impact.
To analyze the errors of the data compression algorithms, it is necessary to separately calculate the average error and peak error of the data before and after compression.
- (1)
- Average error
The peak signal-to-noise ratio (PSNR) parameter is adopted to evaluate the average error before and after compression. The peak signal-to-noise ratio (PSNR) is expressed as follows:
x represents the signal before compression, and MSE is the mean square error of the data before and after compression:
y represents the recovery signal after decompression.
According to the PSNR requirements for image and sound compression, it should be between 30 dB and 50 dB, so the radar data compression algorithm specifies that the PSNR should be no less than 30 dB.
- (2)
- Peak error
The peak error before and after compression is evaluated using the peak-signal-to-peak-noise ratio (PSPNR) parameter:
r represents the compression error:
The PSPNR should be greater than 50; that is, the maximum compression error should be less than 2% of the signal peak.
The performance of the two compression algorithms is evaluated by comparing the decompressed data The PSNR and PSPNR are employed for evaluation [19]. The results show that the compression error of the logarithmic compression algorithm is smaller than that of the BAQ algorithm. And the BAQ algorithm does not meet the strict index requirements, but the logarithmic compression does, as shown in Table 1.

Table 1.
Comparison of the root mean square errors of the compression algorithms.
Through a comprehensive comparison, it is found that the compression error of the logarithmic compression algorithm is smaller than that of the BAQ algorithm and meets the index requirements. Therefore, the logarithmic lossy compression algorithm is more effective in RoSPR data compression.
5. Realization of Logarithmic Data Compression in FPGA
The principle of FPGA implementation for this algorithm is to complete logarithmic operations. The conventional method used to implement the logarithm operation in the FPGA is the look-up table method [20]. However, when conventional method is used to perform the logarithmic operation for a large volume of data and large-width data, a very large proportion of storage resources is required.
In this design, we adopted the principle of successive approximation to realize logarithmic operations. The implementation process is described in detail below. Assuming that the input data are N and that y = log10(N) is what we want to compute, the successive approximation implementation of the logarithm operation includes the following:
Variable x and coefficient sequence k are introduced. The value of sequence k is given, assuming k = {k1, k2, k3, …, kn}, and the approximate value of y_close = log10(N/()) = log10(N/x) − log10(ki).
The initial value of x is N divided by the maximum k value kmax in the sequence and then by x = N/kmax at the beginning.
Compensate the value of x for k; that is, let . ki is the maximum of k such that x is not greater than 1. Update the approximation value of y_close synchronously; i.e., subtract the compensated log10(ki) [21].
Repeat step (3) until the minimum k value of x compensation is still greater than 1; then, the compensation is abandoned, and the approximate value of y_close is output.
Taking the 4:1 logarithmic compression algorithm as an example, the logarithmic computation is completed by successive approximation. The logarithmic compression coefficient of 4:1 successive approximation based on the FPGA is shown in Table 2.

Table 2.
The 4:1 successive approximation parameter value.
In the initialization process of data compression, the initial value is input_data/2^20, where input_data is the input data before compression. The approximation operation requires 25 steps in total, that is, the serial numbers 2~26 in Table 2. The convergence condition of the approximation operation is to judge whether the products of the approximation parameter k and x are greater than 2^20 before each step of operation: if the result is not greater than 2^20, the approximation operation of the k value is completed; otherwise, this approximation operation is abandoned, the result of the last operation is assigned to this result, and then the next attempt to perform the approximation operation of the k value is made. If x is still greater than 2^20 after the minimum k value is compensated, the compensation is abandoned, and the compressed data are output. When the data is zero, it is not compressed and is stored directly after its width is converted. A flowchart of the FPGA implementation for the data compression algorithm is shown in Figure 6.
Figure 6.
FPGA processing flow block diagram.
When the algorithm is implemented on the FPGA in ISE13.2, the proportion of resources is evaluated as shown in Figure 7. The registers are only 1% utilized, and the LUTs are only 2% utilized. The proportion of resources used by logarithmic compression in the FPGA is very small, almost negligible [22]. Therefore, it is feasible to implement the logarithmic operation in the FPGA using the method of successive approximation.
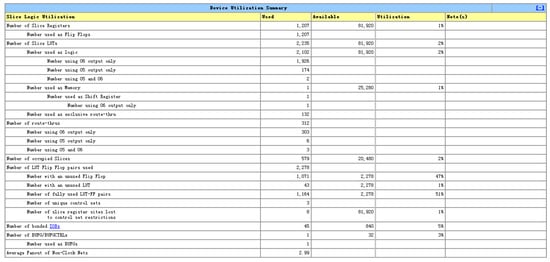
Figure 7.
FPGA resources using for LCA.
6. Experimental Verification
In September 2020, a field validation test was carried out at No. 29 Laohugou Glacier in Qilian Mountain, Gansu Province. Subsequently, in October 2020, an outfield validation test was carried out in Ulanhada Volcanic Geological Park, Chahar Right Rear Banner, Ulanqab City, Inner Mongolia Province, as shown in Figure 8a,b.

Figure 8.
Site map of the RoSPR detection test. (a) Field exploration of glaciers; (b) Field exploration of craters.
This paper selects the test data of the above two scenarios for a data compression analysis. In order to more intuitively compare the errors of the data before and after compression, one trace data is intercepted and compared before and after compression. A comparison of the two compression ratios of 2.5:1 and 4:1 is shown in Figure 9a,b.
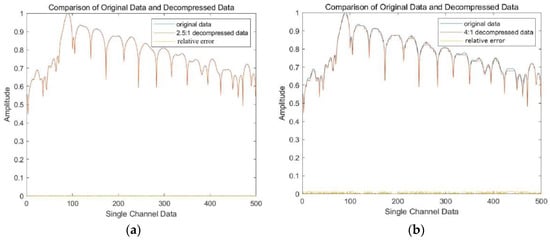
Figure 9.
Comparison of the errors between the original glacier data and the decompressed data. (a) Original data and 2.5:1 decompressed data; (b) Original data and 4:1 decompressed data.
The decompressed data with a compression ratio of 2.5:1 have a high degree of curve coincidence with the original data, and the error curve is close to the horizontal axis after normalization. The maximum relative error of the single-channel data before and after compression is 0.37%, which can be ignored. The decompressed data with a compression ratio of 4:1 are slightly different from the original data, with a maximum relative error of less than 0.6%. Compared with the huge storage space occupied by the uncompressed data, the error is acceptable.
When the crater high-frequency channel data are input, the processing result is similar to that of the of the glacier data, as shown in Figure 10a,b. Compared with the 2.5:1 compression ratio, a higher 4:1 compression ratio will also result in higher compression errors. The maximum relative error before and after single-channel data compression is 1.38%; the compression error is still acceptable compared to the size of the original data.
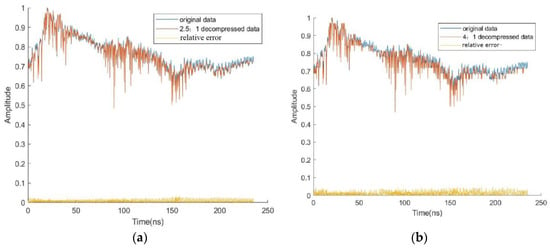
Figure 10.
Comparison of the errors between the original crater data and the decompressed data. (a) Original data and 2.5:1 decompressed data; (b) Original data and 4:1 decompressed data.
7. Conclusions
This paper proposes a logarithmic lossy compression algorithm for the Tianwen-1 Mars rover subsurface-penetrating radar. The algorithm is implemented based on the FPGA platform, a suitable logarithmic compression model is given according to the compression ratios of 4:1 and 2.5:1, and data compression with a high compression ratio is realized. The logarithm operation of the FPGA is realized by the successive approximation method. The register utilization rate of this method is only 1%, and the look-up table utilization rate is only 2%, so it uses a small proportion of resources. The FPGA only elapses 300 ns to compress a 20-bit signed data. The LCA is a very efficient compression algorithm. The relative error of a single trace data point before and after the compression of glacier and crater data is less than 2%. This can provide a reference for subsurface-penetrating radar data compression.
Author Contributions
Theory analysis, S.S. and X.H.; Data acquisition, S.S. and B.Z.; Project administration, B.Z.; Software, S.S. and X.H.; Validation, S.S.; Writing of manuscript, S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was designed based on the research of the RoSPR’s payload from 2016 to 2021.
Data Availability Statement
All data underlying the results are available as part of the article, and no additional source data are required.
Acknowledgments
The authors would like to thank DanPing Lu for the handling and processing of data; De Zhi Li, Qing Liu, ChuanJun Tang, Yu Xi Li, and ShiDong Li of the Aerospace Information Research Institute, Chinese Academy of Sciences, for their contribution to equipment development; and the anonymous reviewers for their helpful edits and comments.
Conflicts of Interest
Author Xiaolei Hua was employed by the company China Mobile Communications Group Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wan, W.X.; Wang, C.; Li, C.L.; Wei, Y.; Liu, J.J. The payloads of planetary physics research onboard China’s First Mars Mission(Tianwen-1). J. Earth Planet. Phys. 2020, 4, 331–332. [Google Scholar] [CrossRef]
- Huang, B. Satellite Data Compression; Springer, Science + Business Media, LLC: Madison, WI, USA, 2011; pp. 29–45. [Google Scholar]
- Xu, B. Research on the Development of Abroad Satellite Data Compression Algorithms. Space Int. 2014, 35, 41–47. (In Chinese) [Google Scholar]
- Xu, B. New Development of Data Compression Algorithms on Abroad Radar Satellites. Space Int. 2015, 36, 46–52. (In Chinese) [Google Scholar]
- Huneycutt, B.L. Spaceborne imaging radar-C instrument. J. IEEE Trans Geosci. Remote Sens. 1987, 27, 164–169. [Google Scholar] [CrossRef][Green Version]
- Kwok, R.; Johnson, W.T.K. Block adaptive quantization of Magellan SAR data. J. IEEE Trans Geosci. Remote Sens. 1989, 27, 375–383. [Google Scholar] [CrossRef]
- Mcleod, I.; Cumming, I. ENVISAT ASAR data reduction: Impact on SAR interferometry. J. IEEE Trans Geosci. Remote Sens. 1998, 36, 589–602. [Google Scholar] [CrossRef]
- Tian, Y.; Chen, Z.; Hui, F.; Cheng, X.; Ou Yang, L. ESA Sentinel-2A/B satellite: Characteristics and applications. Chin. J. J. Beijing Norm. Univ. (Nat. Sci.) 2019, 55, 57. [Google Scholar] [CrossRef]
- Moureaux, J.M.; Gauthier, P.; Barlaud, M.; Bellemain, P. Vector quantization of raw SAR data. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Adelaide, Australia, 19–22 April 1994; Volume 5, pp. 189–192. [Google Scholar]
- Yang, C.; Gao, H.; Zhang, L.-Y.; Hu, X.; Yu, Z.-Y.; Li, D.-S. A lossy compression method for aot sequence data based on tensor decomposition. Chin. J. J. Geo-Inf. Sci. 2021, 23, 134–142. [Google Scholar]
- Yu, Y. SAR Image Compression Based on Block Adaptive Residual Vector Quantization. J. Syst. Simulaton 2014, 26, 1799–1806. [Google Scholar]
- Li, P.; Liu, X.-J.; Fang, G.-Y. Study on quantization and encoding algorithm for subsurface sounding radar data in Chinese. J. Electron. Meas. Technol. 2018, 41, 94–99. [Google Scholar]
- Zhou, B.; Shen, S.X.; Lu, W.; Liu, Q.; Tang, C.J.; Li, S.D.; Fang, G.Y. The Mars rover subsurface penetrating radar onboard China’s Mars 2020 mission. Earth Planet. Phys. 2020, 4, 345–354. [Google Scholar] [CrossRef]
- Benz, U.; Strodl, K.; Moreira, A. A comparison of several algorithms for SAR raw data compression. J. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1266–1276. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. J. IEEE Trans Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Martone, M.; Brautigam, B.; Krieger, G. Azimuth-switched quantization for SAR systems and performance analysis on TanDEM-X data. J. IEEE Trans Geosci. Remote Sens. 2014, 11, 181–185. [Google Scholar] [CrossRef][Green Version]
- Martone, M.; Brautigam, B.; Krieger, G. Quantization effects in TanDEM-X Data. J. IEEE Trans Geosci. Remote Sens. 2015, 53, 583–597. [Google Scholar] [CrossRef]
- Li, C.X.; Jiang, Q.L.; Lu, F.; Liu, D. Segmental adaptive threshold wavelet based data compression method for subway sliding doors. Chin. J. J. Harbin Inst. Technol. 2020, 52, 101–106. [Google Scholar]
- An, W.; Cui, Y.; Zhang, W.; Yang, J. Data compression for multilook polarimetric sar data. J. IEEE Geosci. Remote Sens. Lett. 2009, 6, 476–480. [Google Scholar]
- Seidner, D. Efficient implementation of log10 lookup table in FPGA. In Proceedings of the 2008 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems, Tel-Aviv, Israel, 13–14 May 2008; pp. 1–9. [Google Scholar]
- Yu, Q.; Yu, W.; Yang, P.; Zheng, J.; Zheng, X.; He, Y. An efficient adaptive binary arithmetic coder based on logarithmic domain. J. IEEE Trans. Image Process. 2015, 24, 4225–4239. [Google Scholar] [CrossRef] [PubMed]
- Li, K.H.; Yang, J.F.; Song, K.Z. Data Compression and FPGA Implementation in Seismic Data Acquisition System. Chin. J. J. Data Acquis. Process. 2020, 35, 753–761. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).