Control Performance Requirements for Automated Driving Systems
Abstract
1. Introduction
- The control system requirements should apply to all types of controllers (i.e., fuzzy logic, robust, model predictive control, nonlinear, etc.).
- Requirements should be independent of the vehicle, operational design domain, and dynamic driving task. Therefore, a methodology that has this characteristic can be used to determine which operational design domains the ADS can safely operate in and which it cannot.
- Requirements should account for uncertainty (i.e., specify the maximum allowable error or a desired distribution of errors). The methodology proposed in this paper accounts for the uncertainty in the operational design domain and dynamic driving task by providing requirements in the form of characteristics of a stochastic distribution. This also aids in their ability to be verified with experimental data, which is demonstrated in Section 3.1.
- The control requirements should be specific enough to provide binary determinations of the controller’s safety. For instance, it should provide a maximum standard deviation of the lateral error so that if the tested controller’s distribution does not meet this requirement, it is easy to argue that the controller provides insufficient performance.
- A new set of definitions is proposed for each module’s performance metrics. These definitions balance specificity and generality so that quantifiable requirements can be derived from each module’s performance while also being applicable to a wide range of module implementations. A consequence of these definitions is that their performances are interdependent. Therefore, this contribution makes the argument that performance requirements should be allocated to the planner, pose, and control modules simultaneously rather than being treated independently, as is done in [19].
- A new method is presented that directly links the desired safety of the VDS to the performance metrics of the planner, pose, and control modules.
- This work addresses a deficient assumption in [19]’s definitions underlying their risk allocation, which has the effect of making the method less overly conservative and therefore more practical.
2. Materials and Methods
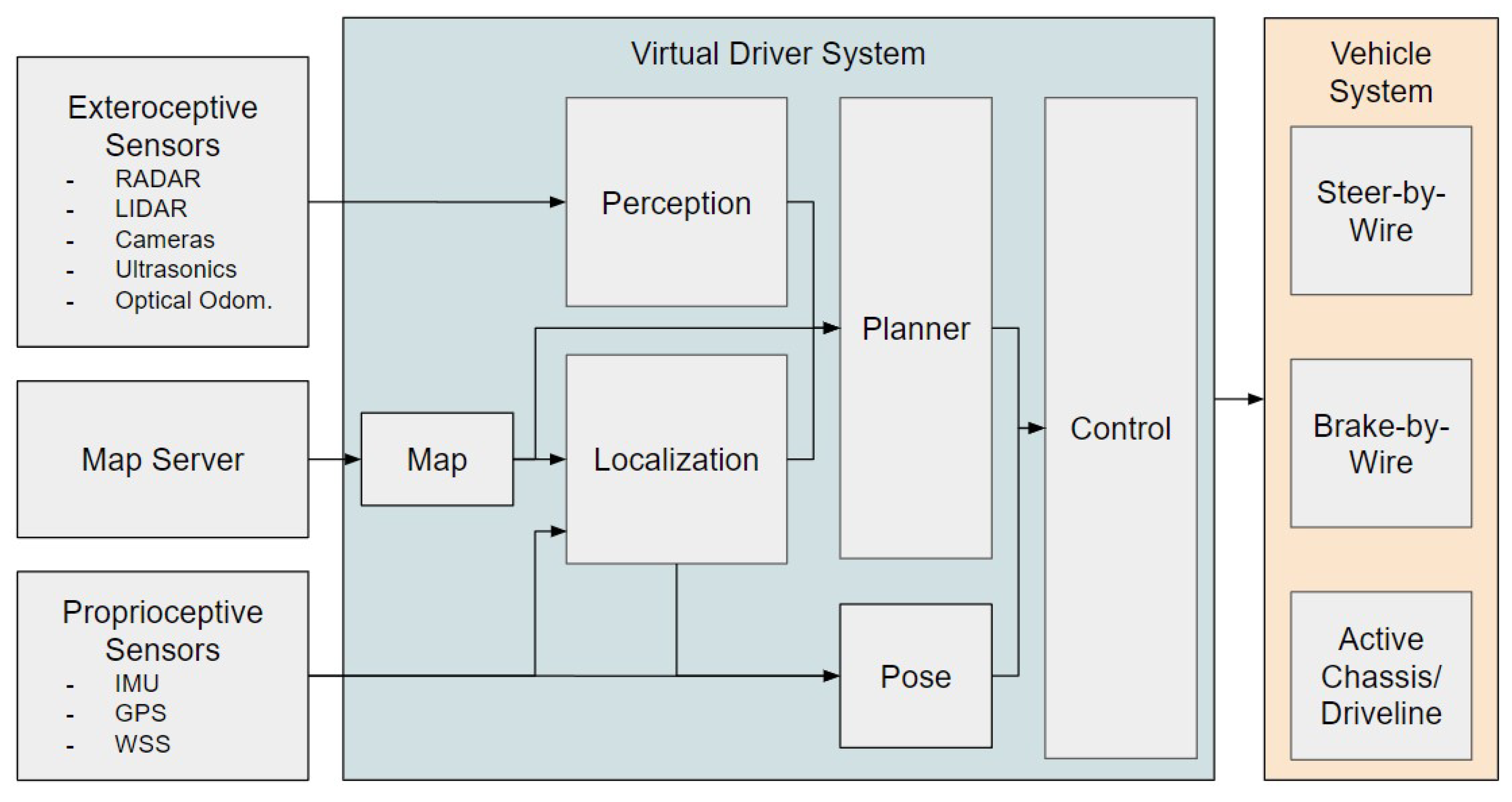
2.1. Terminology
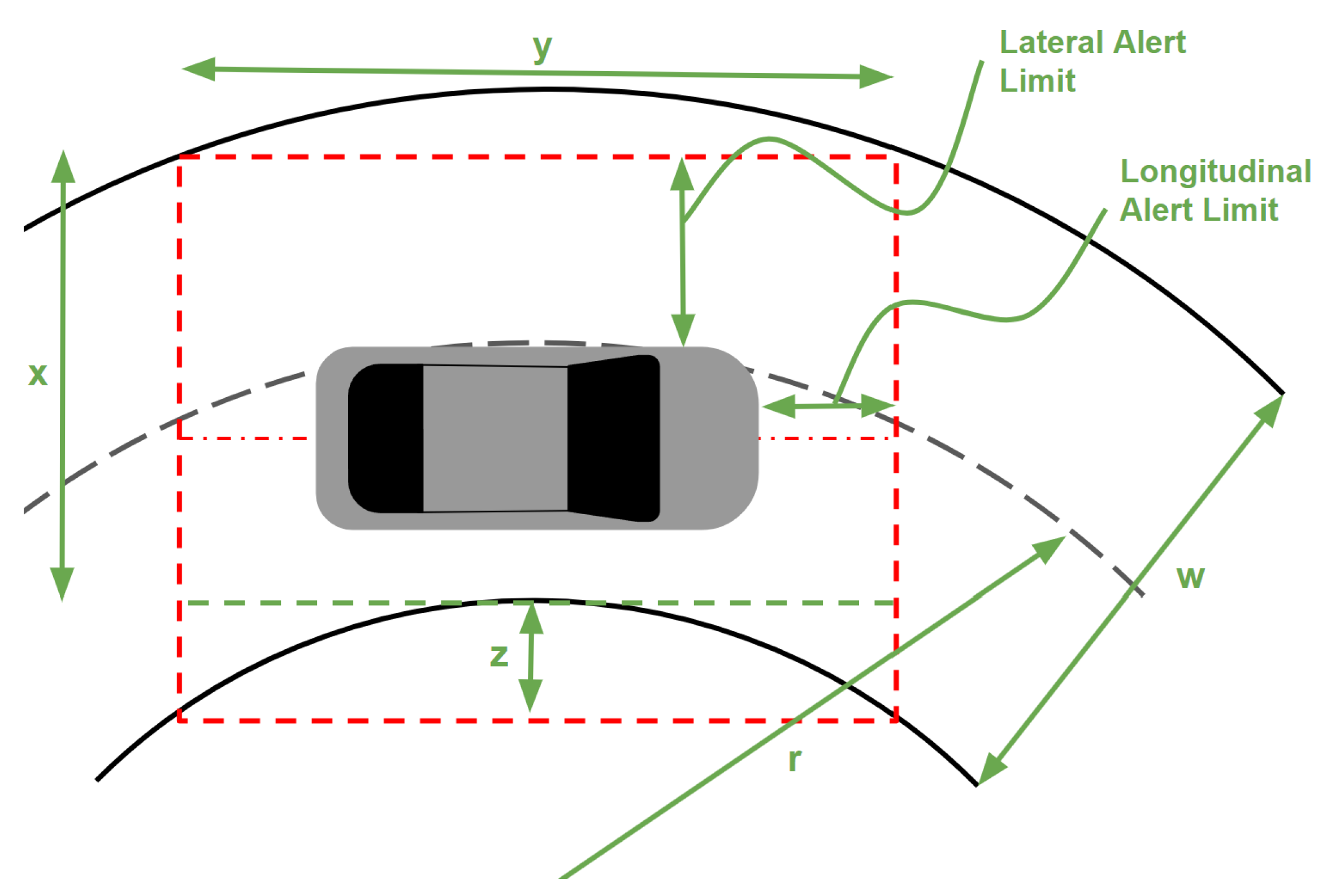
2.2. Risk Allocation
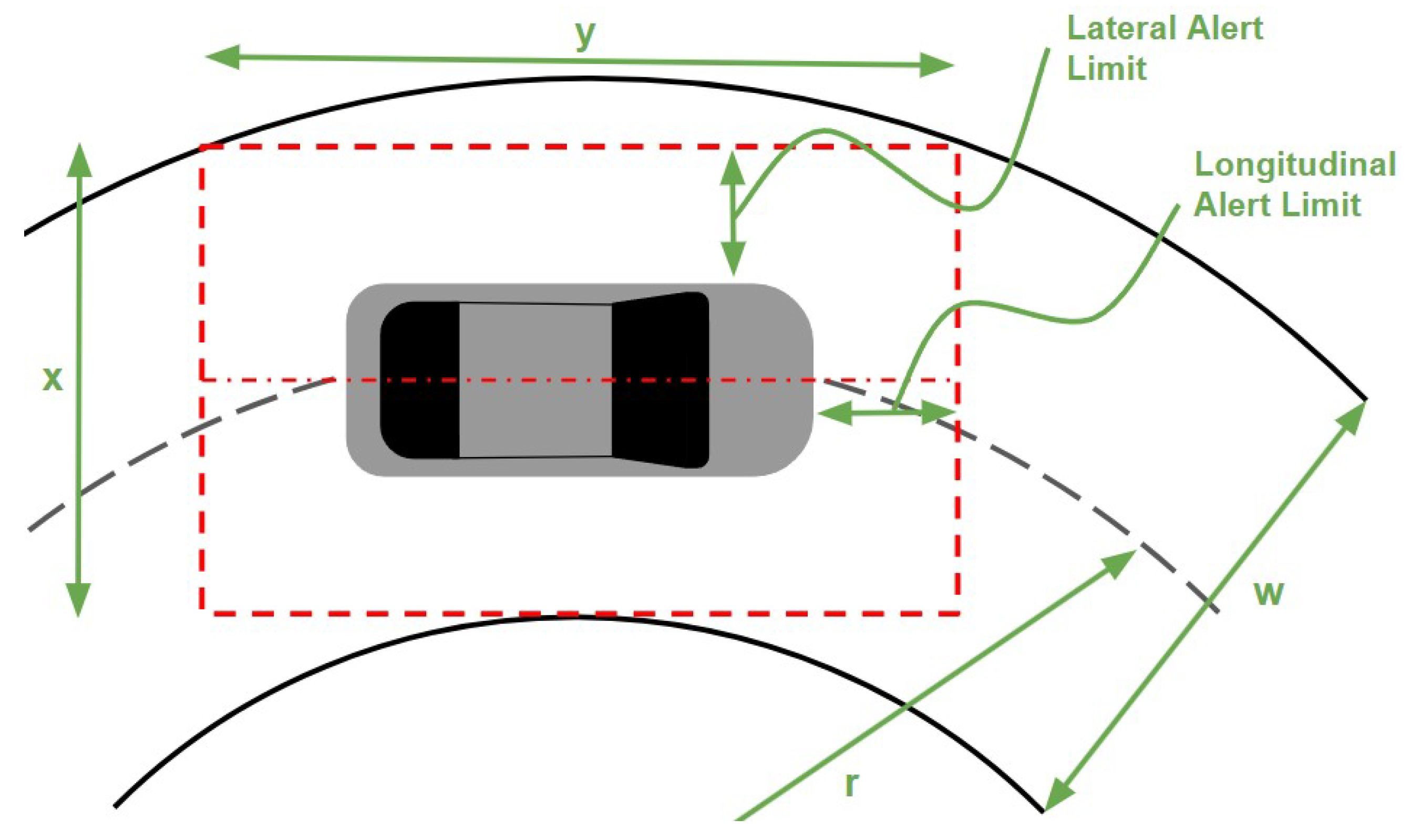
- An ideal trajectory is a trajectory that traverses the virtual corridor, thereby guaranteeing that the current driving task is accomplished collision-free.
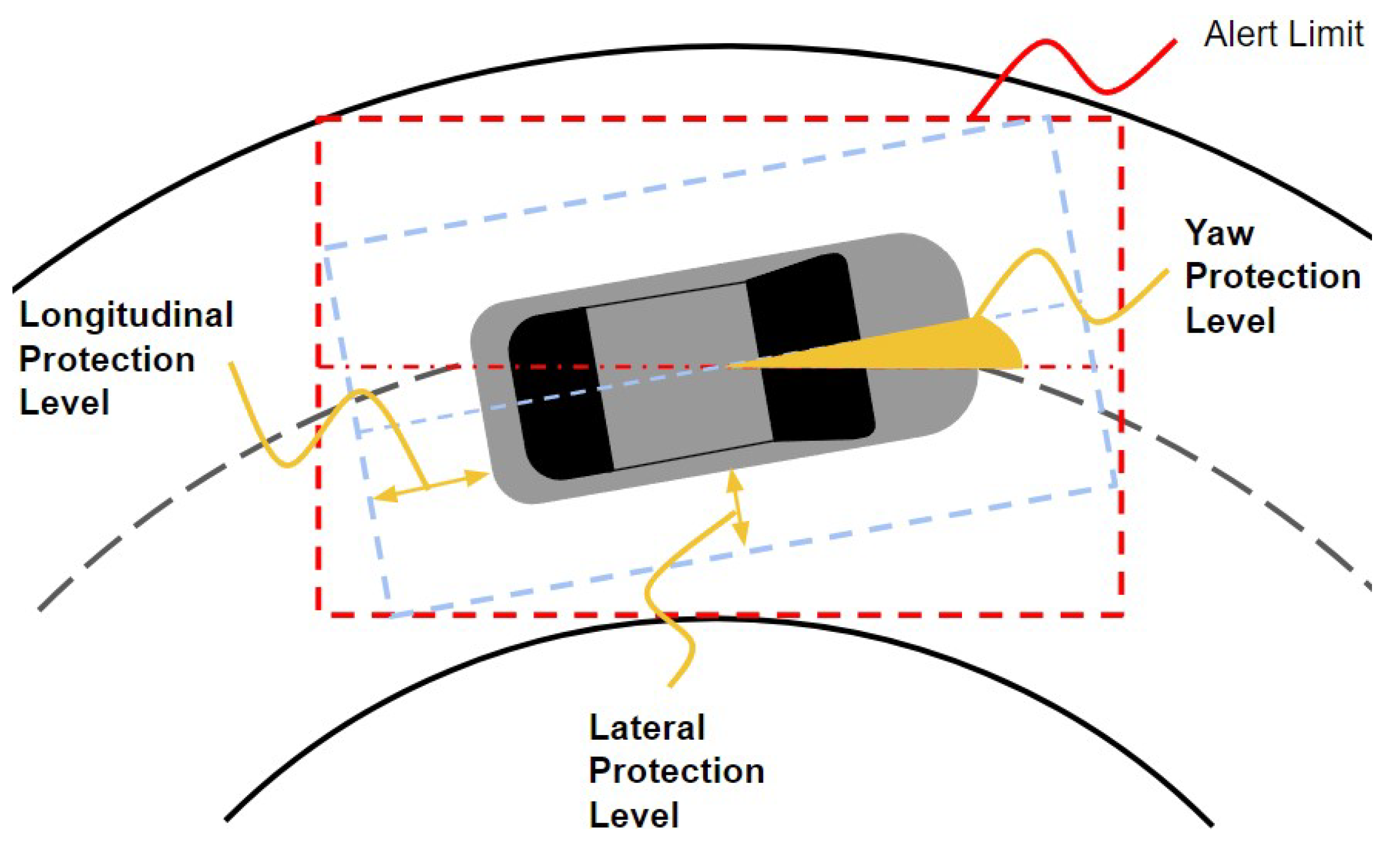
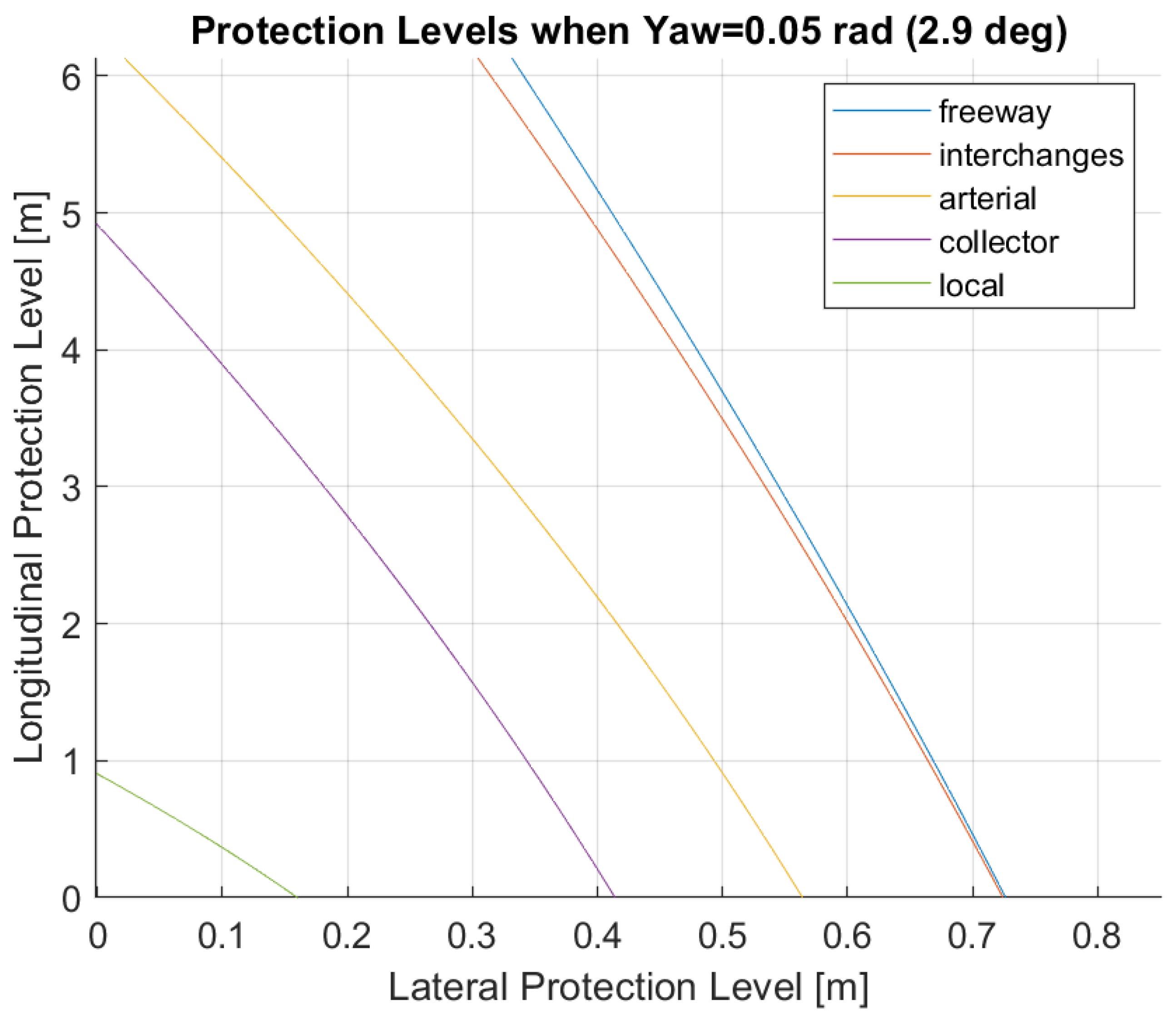
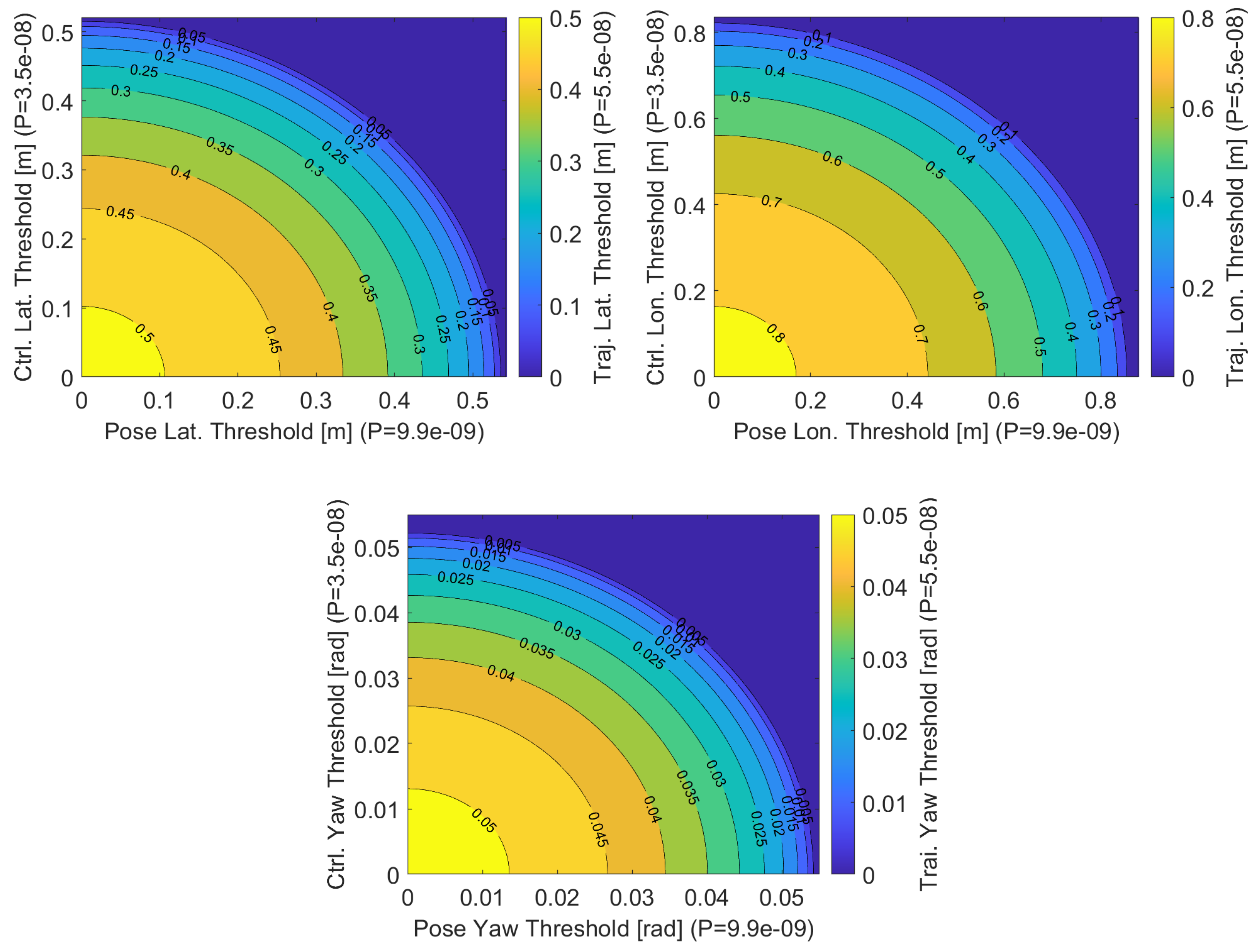
- A planner failure is when any of the lateral, longitudinal, or yaw trajectory errors, , (where ∗ is used to represent , , and ) exceed their corresponding thresholds: . The trajectory error is the difference between the generated trajectory and the ideal trajectory. Under a zero mean, the Gaussian assumption is the following: 2).
- A pose failure is when any of the pose errors, , exceed their corresponding thresholds: . The pose error is the difference between where the VDS believes the ego vehicle is and where the ego vehicle truly is in the world. Under a zero mean, the Gaussian assumption is the following: 2).
- A control failure is when any of the control errors, , exceed their corresponding thresholds . The control error is the difference between the generated trajectory and where the VDS believes the ego vehicle is in the world. Under a Gaussian assumption, it is the following: 2).
3. Results
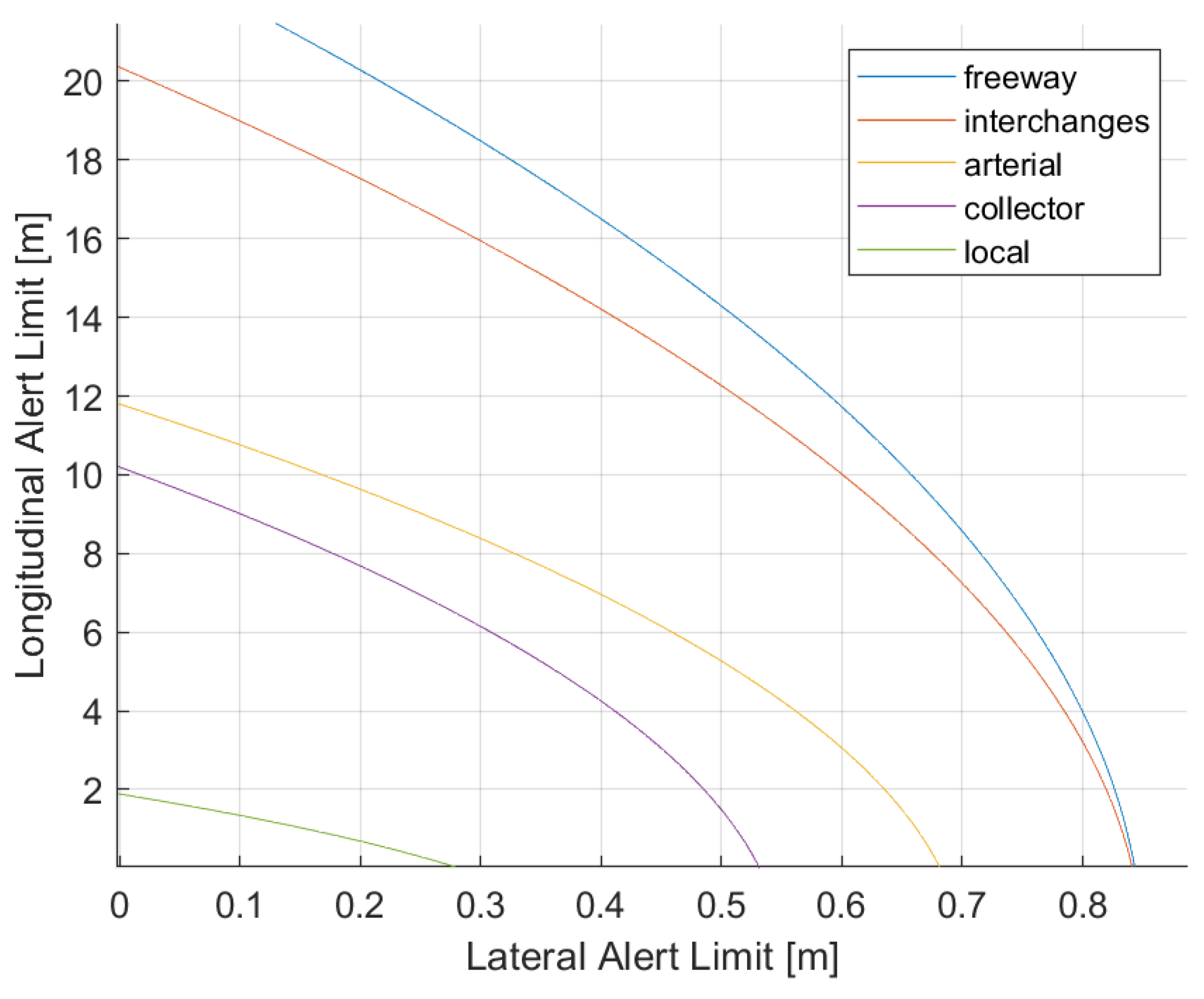
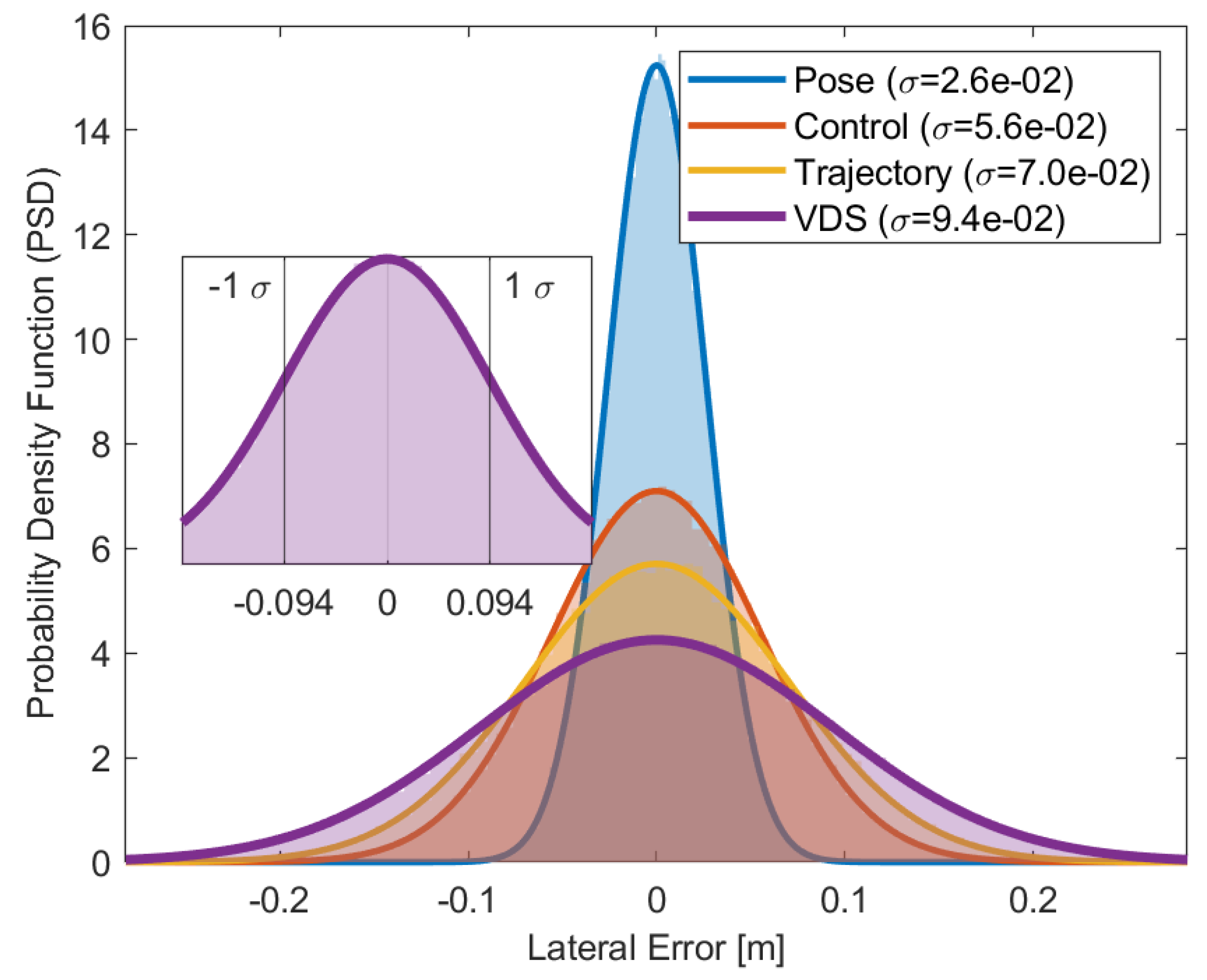
3.1. A Case Study Showing Feasibility
3.2. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- On-Road Automated Driving (ORAD) Committee. Taxonomy and Definitions for Terms Related to Driving Automation Systems for On-Road Motor Vehicles; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Vidano, T.; Assadian, F.; Gulati, N. Artificially Intelligent Active Safety Systems. In AI-Enabled Technologies for Autonomous and Connected Vehicles; Murphey, Y.L., Kolmanovsky, I., Watta, P., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 213–254. [Google Scholar] [CrossRef]
- Favaro, F.; Fraade-Blanar, L.; Schnelle, S.; Victor, T.; Peña, M.; Engstrom, J.; Scanlon, J.; Kusano, K.; Smith, D. Building a Credible Case for Safety: Waymo’s Approach for the Determination of Absence of Unreasonable Risk. arXiv 2023, arXiv:2306.01917. [Google Scholar]
- Cruise. Cruise Safety Report; Technical Report; Cruise: San Francisco, CA, USA, 2022. [Google Scholar]
- Hirshorn, S.R.; Voss, L.D.; Bromley, L.K. Nasa Systems Engineering Handbook; Technical Report; NASA: Washington, DC, USA, 2017. [Google Scholar]
- Giusto, P.; Ramesh, S.; Sudhakaran, M. Modeling and analysis of automotive systems: Current approaches and future trends. In Proceedings of the 2016 4th International Conference on Model-Driven Engineering and Software Development (MODELSWARD), Rome, Italy, 19–21 February 2016; pp. 704–710. [Google Scholar]
- Ioannou, P.A. (Ed.) Automated Highway Systems; Springer: New York, NY, USA, 1997. [Google Scholar]
- ISO/DIS 21448; Road Vehicles—Safety of the Intended Functionality. International Organization for Standardization: Geneva, Switzerland, 2019.
- ISO 26262; Road vehicles—Functional safety. International Organization for Standardization: Geneva, Switzerland, 2018.
- de Gelder, E.; Elrofai, H.; Saberi, A.K.; Paardekooper, J.P.; Op den Camp, O.; de Schutter, B. Risk Quantification for Automated Driving Systems in Real-World Driving Scenarios. IEEE Access 2021, 9, 168953–168970. [Google Scholar] [CrossRef]
- Khastgir, S.; Brewerton, S.; Thomas, J.; Jennings, P. Systems Approach to Creating Test Scenarios for Automated Driving Systems. Reliab. Eng. Syst. Saf. 2021, 215, 107610. [Google Scholar] [CrossRef]
- Martin, H.; Tschabuschnig, K.; Bridal, O.; Watzenig, D. Functional Safety of Automated Driving Systems: Does ISO 26262 Meet the Challenges? In Automated Driving: Safer and More Efficient Future Driving; Springer International Publishing: Cham, Switzerland, 2017; pp. 387–416. [Google Scholar] [CrossRef]
- Guldner, J.; Tan, H.S.; Patwardhan, S. Study of design directions for lateral vehicle control. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; Volume 5, pp. 4732–4737. [Google Scholar] [CrossRef]
- Tan, H.S.; Huang, J. Design of a High-Performance Automatic Steering Controller for Bus Revenue Service Based on How Drivers Steer. IEEE Trans. Robot. 2014, 30, 1137–1147. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; Technical Report; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous Automobile Trajectory Tracking for Off-Road Driving: Controller Design, Experimental Validation and Racing. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 2296–2301. [Google Scholar] [CrossRef]
- Spielberg, N.A.; Brown, M.; Kapania, N.R.; Kegelman, J.C.; Gerdes, J.C. Neural network vehicle models for high-performance automated driving. Sci. Robot. 2019, 4, eaaw1975. [Google Scholar] [CrossRef] [PubMed]
- Reid, T.G.; Houts, S.E.; Cammarata, R.; Mills, G.; Agarwal, S.; Vora, A.; Pandey, G. Localization Requirements for Autonomous Vehicles. SAE Int. J. Connect. Autom. Veh. 2019, 2, 173–190. [Google Scholar] [CrossRef]
- Development of Satellite Navigation for Aviation Technical Description of Project and Results; Technical Report; Stanford University: Stanford, CA, USA, 2009.
- Feng, Y.; Wang, C.; Karl, C. Determination of Required Positioning Integrity Parameters for Design of Vehicle Safety Applications. In Proceedings of the 2018 International Technical Meeting of The Institute of Navigation, Reston, VA, USA, 1–29 January 2018; pp. 129–141. [Google Scholar]
- Kigotho, O.N.; Rife, J.H. Comparison of Rectangular and Elliptical Alert Limits for Lane-Keeping Applications. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; pp. 93–104. [Google Scholar]
- Cicchino, J.B. Effects of lane departure warning on police-reported crash rates. J. Saf. Res. 2018, 66, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Schafer, H.; Santana, E.; Haden, A.; Biasini, R. A Commute in Data: The comma2k19 Dataset. arXiv 2018, arXiv:1812.05752. [Google Scholar]
- Kapania, N.R.; Gerdes, J.C. Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P. Protection level calculation using measurement residuals: Theory and results. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2288–2296. [Google Scholar]
- Wood, M.; Earnhart, N.; Kennett, K. Airbag deployment thresholds from analysis of the NASS EDR database. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2014, 7, 230–245. [Google Scholar] [CrossRef]
- Huang, J.; Tan, H.S. Control System Design of an Automated Bus in Revenue Service. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2868–2878. [Google Scholar] [CrossRef]
- Huang, J.; Tan, H.S. Development and Validation of an Automated Steering Control System for Bus Revenue Service. IEEE Trans. Autom. Sci. Eng. 2016, 13, 227–237. [Google Scholar] [CrossRef]
- Chan, C.Y.; Tan, H.S. Evaluation of Magnetic Markers as a Position Reference System for Ground Vehicle Guidance and Control; Technical Report; California Path Program, Institute of Transportation Studies: Berkeley, CA, USA, 2003. [Google Scholar]
- Chan, C.Y.; Bougler, B.; Nelson, D.; Kretz, P.; Tan, H.S.; Zhang, W.B. Characterization of magnetic tape and magnetic markers as a position sensing system for vehicle guidance and control. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No.00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 1, pp. 95–99. [Google Scholar] [CrossRef]
- Thole, C.; Cain, A.; Flynn, J. The EmX Franklin Corridor BRT Project Evaluation; Technical Report; National Bus Rapid Transit Institute: Los Angeles, CA, USA, 2009. [Google Scholar]
- EmX Map and Schedule. Available online: https://www.ltd.org/system-map/route_103/ (accessed on 17 August 2023).
- All Motor Vehicle Crashes 2007–2021. Available online: https://www.lcog.org/thempo/page/advanced-user-data (accessed on 17 August 2023).
| Vehicle Class | Vehicle Name | Width [m] | Length [m] |
|---|---|---|---|
| A | 2019 Fiat 500 | 1.63 | 3.55 |
| B | 2019 Ford Fiesta Hatchback | 1.72 | 4.06 |
| C | 2024 Mercedes Benz A-Class | 1.80 | 4.55 |
| J | 2019 Jeep Cherokee | 1.9 | 4.6 |
| Vehicle | [m] | [m] | [rad] | [m] | [m] |
|---|---|---|---|---|---|
| 2019 Fiat 500 | 0.68 | 0.8 | 0.05 | 0.81 | 0.87 |
| 2019 Ford Fiesta Hatchback | 0.62 | 0.8 | 0.05 | 0.76 | 0.87 |
| 2024 Mercedes Benz A-Class | 0.56 | 0.8 | 0.05 | 0.71 | 0.87 |
| 2019 Jeep Cherokee | 0.50 | 0.8 | 0.05 | 0.66 | 0.87 |
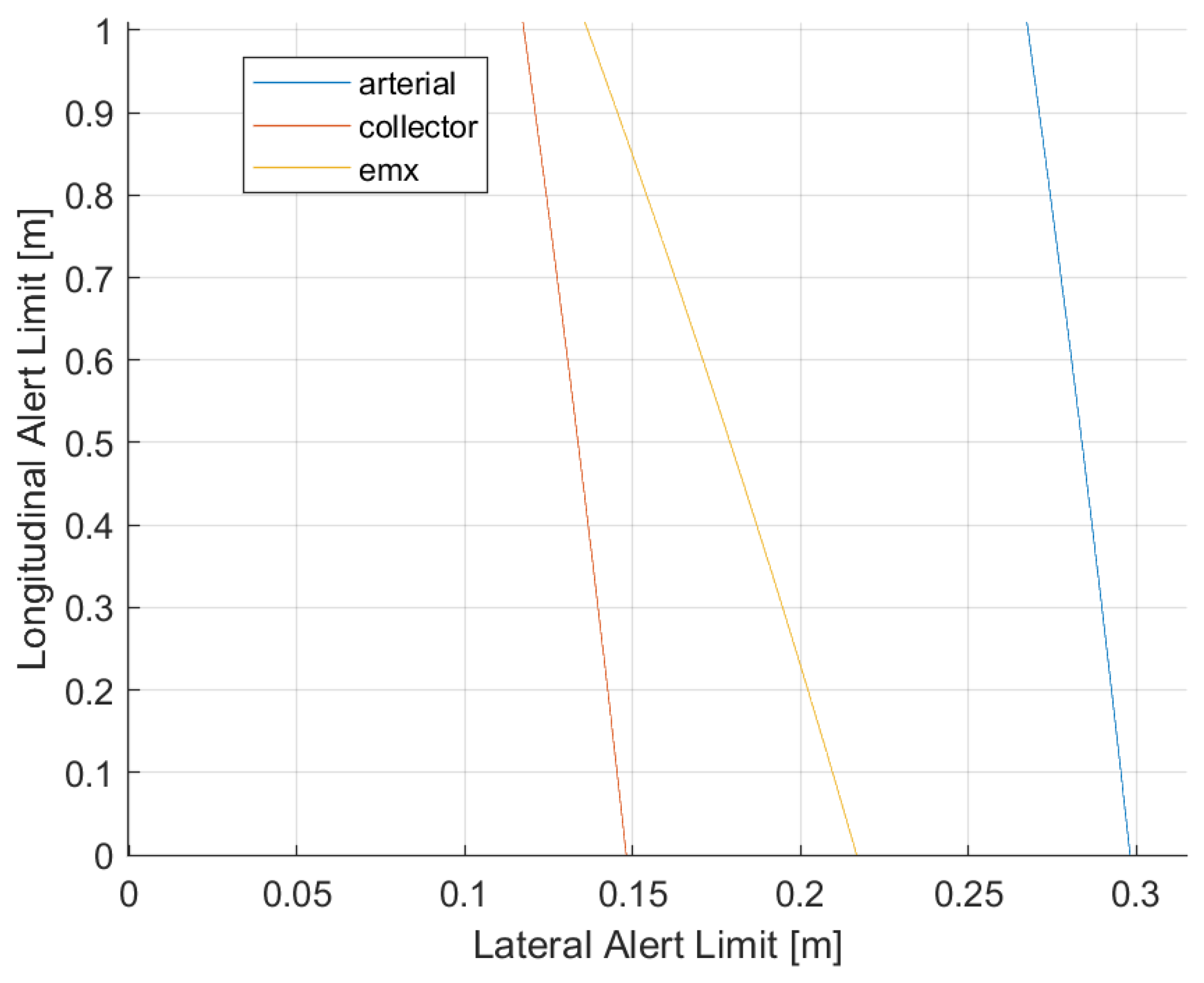
| Road | [m] | [m] | [rad] (deg) | [m] | [m] |
|---|---|---|---|---|---|
| Arterial | 0.180 | 0.300 | 0.03 (1.5) | 0.29 | 0.34 |
| Collector | 0.110 | 0.126 | 0.009 (0.5) | 0.14 | 0.14 |
| EmX | 0.163 | 0.322 | 0.007 (0.4) | 0.19 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidano, T.; Assadian, F. Control Performance Requirements for Automated Driving Systems. Electronics 2024, 13, 902. https://doi.org/10.3390/electronics13050902
Vidano T, Assadian F. Control Performance Requirements for Automated Driving Systems. Electronics. 2024; 13(5):902. https://doi.org/10.3390/electronics13050902
Chicago/Turabian StyleVidano, Trevor, and Francis Assadian. 2024. "Control Performance Requirements for Automated Driving Systems" Electronics 13, no. 5: 902. https://doi.org/10.3390/electronics13050902
APA StyleVidano, T., & Assadian, F. (2024). Control Performance Requirements for Automated Driving Systems. Electronics, 13(5), 902. https://doi.org/10.3390/electronics13050902







