1. Introduction
Drones are small unmanned aerial vehicles (UAVs) that have become popular, among other things, due to their adaptation for recreational use, environmental monitoring, surveillance, security, commercial use, etc. Although their use can have undoubted advantages, there has also been an increase in the use of drones for illegal activities. Some examples of these illicit acts are detailed in [
1], including their use in airports and rescue operations, where they could disrupt operations and cause possible collisions between planes, helicopters, and drones. There have also been reports of drones being used for smuggling in prisons as penetration nodes in cyber-attacks to access WiFi networks in offices and in residences and patrols, where they are used as spy cameras. The development of technologies to detect drones as a means to control these illegal practices or to manage the movement of drones in cases of legal use is necessary.
Several techniques for drone detection can be found in the literature. Technologies based on optical sensors, radio frequency, radar, and acoustic sensors are compared in [
2], detailing their advantages and disadvantages. A comprehensive description of these techniques is also given in [
3]. It is pointed out that visual inspection techniques with cameras require a clear line of sight, which is not possible in rainy, foggy scenarios or in the presence of occlusions. The cameras used can work in the visible spectrum or the infrared spectrum, but in the latter case, the cost is higher. Nevertheless, detection based on images obtained with cameras can exploit powerful image processing and classification algorithms, such as YOLO (You Only Look Once) [
4].
Detection of the radio frequency signal emitted in the drone’s communication with the controller offers good performance but is not possible with autonomous UAVs [
5]. Radar sensors are effective but expensive and have limitations for detecting static or low-speed drones due to the application of digital signal processing techniques for clutter cancellation. A comprehensive review of the state of the art in the above techniques is beyond the scope of this paper, which focuses on acoustic detection as an alternative.
Acoustic detection offers unique advantages that overcome certain limitations of visual, radio frequency, and radar-based methods. Unlike optical and radar systems, acoustic detection does not rely on the line of sight, making it highly effective in environments with physical obstructions or where drones operate at low altitudes, often below radar coverage. This characteristic is particularly advantageous in urban or forested landscapes where line-of-sight obstructions are common. In addition, acoustic systems excel in scenarios where visual clarity is compromised, such as in foggy, dusty, or nighttime conditions.
Moreover, unlike radio frequency detection, acoustic methods remain effective against autonomous UAVs that do not rely on active communication signals, extending the range of detectable drone activity. Furthermore, preliminary studies, such as the one presented in [
6], suggest that acoustic detection of UAVs is cost-effective and presents itself as an efficient and economical alternative, thus providing a scalable solution for wide-area surveillance.
Although it is generally assumed that the effective range of acoustic detection may be limited, mainly due to factors such as sound attenuation over distance, sensor sensitivity, and the presence of ambient noise, this method still holds significant advantages. Detection is favored because the rotation of a drone’s blades generates a characteristic acoustic footprint, which makes it possible to distinguish the sound generated by the drone from other sound sources, even if the signal-to-noise ratio is low. Advanced signal processing and machine learning techniques have further enhanced the capability of acoustic detection systems to accurately identify and classify drone sounds, as demonstrated by the growing body of research in this field.
Furthermore, acoustic detection can complement other drone detection systems, offering a multi-layered security approach. By integrating acoustic data with information from radio frequency, electro-optical, or infrared systems, a more comprehensive and robust drone detection framework can be achieved, improving overall situational awareness and response capabilities. With these considerations in mind, our research focuses on the acoustic detection of UAVs and explores its potential as a stand-alone solution.
There are numerous works in the literature about the acoustic detection of UAVs. For example, in [
7], a real-time system using a single microphone for drone detection and monitoring is presented based solely on the spectral analysis of the input signal. In [
8], the authors present a method that calculates the spectrogram of the received signal to find robust points in the time-frequency domain and thus use the fingerprinting technique for feature extraction.
However, currently, most work on UAV acoustic detection employs some form of machine learning method, with a clear trend towards research in deep learning models.
In the field of machine learning, innovative approaches have been proposed for UAV detection. In [
9], a drone detection system using multiple acoustic nodes and machine learning models is presented. This system uses an empirically optimized configuration of nodes, enabling them to detect drones in protected areas. Another example of the use of machine learning algorithms is illustrated in [
10], which explores various short-term parameterizations in the time-frequency domain of ambient audio data. The extracted parameters are used to feed an unmanned aerial vehicle warning system, which employs support vector machines (SVMs) to recognize the sound fingerprint of drones, leading to effective preliminary results.
The efficacy of deep learning algorithms with metrics such as accuracy, F1 score, precision, and recall has been assessed in [
11]. In [
12], a CNN is proposed to which features extracted by STFT preprocessing of the drone acoustic signal are applied. Acoustic signals from motorcycles and scooters are also employed in the experiments, as they have similar harmonic characteristics to the drone signal. The performance of the model is evaluated as a function of the number of training epochs. This approach achieved a detection rate of 98.97% with a false alarm rate of 1.28% for a 100-epoch model. Furthermore, an approach to drone detection using deep learning, which combines Mel-frequency cepstral coefficients (MFCCs) and Log-Mel spectrogram features extracted from the sound signal, is proposed in [
13]. Additionally, ref. [
14] investigates the use of Recurrent Neural Networks (RNN) in real-time UAV sound recognition systems, specifically employing Mel-spectrograms with Kapre layers. Another interesting paper recently available is [
15], where authors combine time and frequency domain features to improve the accuracy of drone detection systems based on deep learning, obtaining an accuracy of 0.98 in the best case.
The main difficulty for the development of drone or UAV detection systems with deep learning techniques lies in the availability of useful data for training. Strategies to overcome this problem include the use of data augmentation or transfer learning. In [
16], pre-trained CNN fitting is explored using a custom acoustic dataset to classify sounds and detect drone-specific features. The obtained results show an average accuracy of 0.88. On the other hand, in [
17], a performance comparison between a CNN network, RNN networks, and Convolutional Recurrent Neural Networks (CRNNs) is carried out. The results reveal superior performance for the convolutional network in accurately detecting drones from acoustic signals. These studies highlight the potential of transfer learning in improving audio-based drone detection systems.
Finally, it is worth mentioning the comprehensive review presented in [
18] on detection and classification methods up to the time of publication, covering various modalities, including detection by acoustic signals, which remains an emerging research area. The study highlights the difficulty of benchmarking due to variations in drones, ranges, characteristics, classification methods, and performance metrics used by different authors. However, it highlights the lack of in-depth research on the impact of range on detection effectiveness. A more recent review paper on UAV detection techniques is [
19], which reviews the knowledge about drone detection, studying the threats and challenges faced due to drones’ dynamic behavior, size and speed diversity, battery life, etc. Novel processing techniques to improve the accuracy and efficiency of UAV detection and identification are also studied.
However, a significant gap persists in the literature, where no studies of the impact of sound source distance on the effectiveness of drone detection systems can be found. The most recent studies focus on the ability to distinguish UAVs from other similar sound sources, neglecting attenuation and the presence of noise and interference. In addition, to our knowledge, the suitability of training detectors using signals emitted at different distances has not been explored. Previous studies have not thoroughly investigated this crucial factor, which motivates the present investigation. This work aims to fill this research gap by focusing on the performance of machine learning algorithms (including deep learning) for detecting drones at different distance ranges using acoustic signals. The main objective is to determine the maximum distance at which reliable detection can be achieved. In addition, the performance of different complexity learning machines is compared, and the possibility of implementing a real-time detector is considered.
The development of systems that can increase the distance at which the drone can be accurately detected would allow early detection in security systems, increasing the ability to implement countermeasures to minimize the effects of this threat (drones are being used in military applications, for espionage, as vectors for cyber-attacks, etc.). In addition, to be a competitive system with other types of sensors, such as radar sensors and vision systems, it is necessary to increase the detection range. Today, with radar systems, it is possible to detect small drones at distances of a few kilometers, so the objective of the research is focused on that direction, trying to develop systems with ranges that compete with those of radar systems.
To systematically present the innovations, we organize them into the following sections:
Comparison of detection methods: A detailed comparison between different detection methods is performed. This includes an evaluation of simple machine learning algorithms and sophisticated methods based on deep learning with transfer learning, representing the most prevalent approaches in the literature. The machine learning methods evaluated include linear discriminant analysis, multilayer perceptron, support vector machine, random forest, and YAMNet, which serves as an example of a deep learning system using transfer learning.
Distance-dependent performance: The study rigorously explores the feasibility of detecting drones at different distances. It seeks to identify the maximum distance at which reliable detection is achievable with each detector, providing valuable insights into the distance-dependent performance of the implemented algorithms.
Detection capability against comparable sound sources: Beyond distance assessment, the study extends its scope to evaluate the detection capability against other sound sources with comparable spectral characteristics. This comprehensive analysis increases the applicability and robustness of the proposed drone detection systems.
Exploration of training strategies: The study introduces a novel aspect by exploring two different training strategies. In the first approach, the learning machines are trained using unattenuated signals, preserving the inherent information of sound sources. Subsequently, testing is conducted in attenuated conditions at various distances. The second strategy involves training and testing with attenuated signals as a function of distance. Each approach has effective detection ranges that differ from the other, opening avenues for specialized detectors tailored to specific distance ranges, therefore improving the practical application of effective drone detection systems.
The paper is organized as follows. After this introductory section,
Section 2 presents the main characteristics of the signals emitted by the drones, which will be taken into account in the design of the sound detection system.
Section 3 describes the machine learning-based detectors tested in this work.
Section 4 includes the description of the sound database used in the training and testing of the detection systems, the features calculated from the signal, and some training and testing details. The results obtained are presented and discussed in
Section 5, and the main conclusions drawn from this study are presented in
Section 6.
2. Signal Characterization
The sound of a drone is mainly generated by the motors and blades that propel it. The signal is typically non-stationary since the rotation of these components generates a stationary harmonic sound only if the speed is constant. However, during flight in different directions, the blades must rotate at varying speeds, and in the case of drones with multiple rotors, each one may rotate at a different speed, generating sounds with unrelated fundamental frequencies and creating a non-periodic signal.
The variations in the energy distribution of the received signal can be best studied in the frequency domain, where different patterns are observed that can be useful for UAV detection. On the one hand, energy is concentrated in characteristic frequency bands associated with average rotational speeds for lift and motion. In addition, most of the energy resides in low-frequency bands. On the other hand, the envelope of the spectrum has peaks and valleys resulting from the combined signals of the engines and blades.
These peaks and valleys refer to regions of increasing or decreasing signal energy observed in the spectrogram. The spectrogram is an image representing the magnitude of the short-term Fourier transform (STFT), which, briefly, is a set of Fourier transforms of windowed signal frames. The peaks appear at frequencies related to the rotational speed of the rotors, which is the source of the sound produced by the drone. The periodic motion of the rotors produces harmonic signals, and the STFT shows the harmonically related frequencies where the energy is concentrated. When the sound is the composition of signals produced by different rotors, there are frequencies with constructive interference and others with destructive interference, and the resulting STFT presents characteristics similar to those of periodic signals.
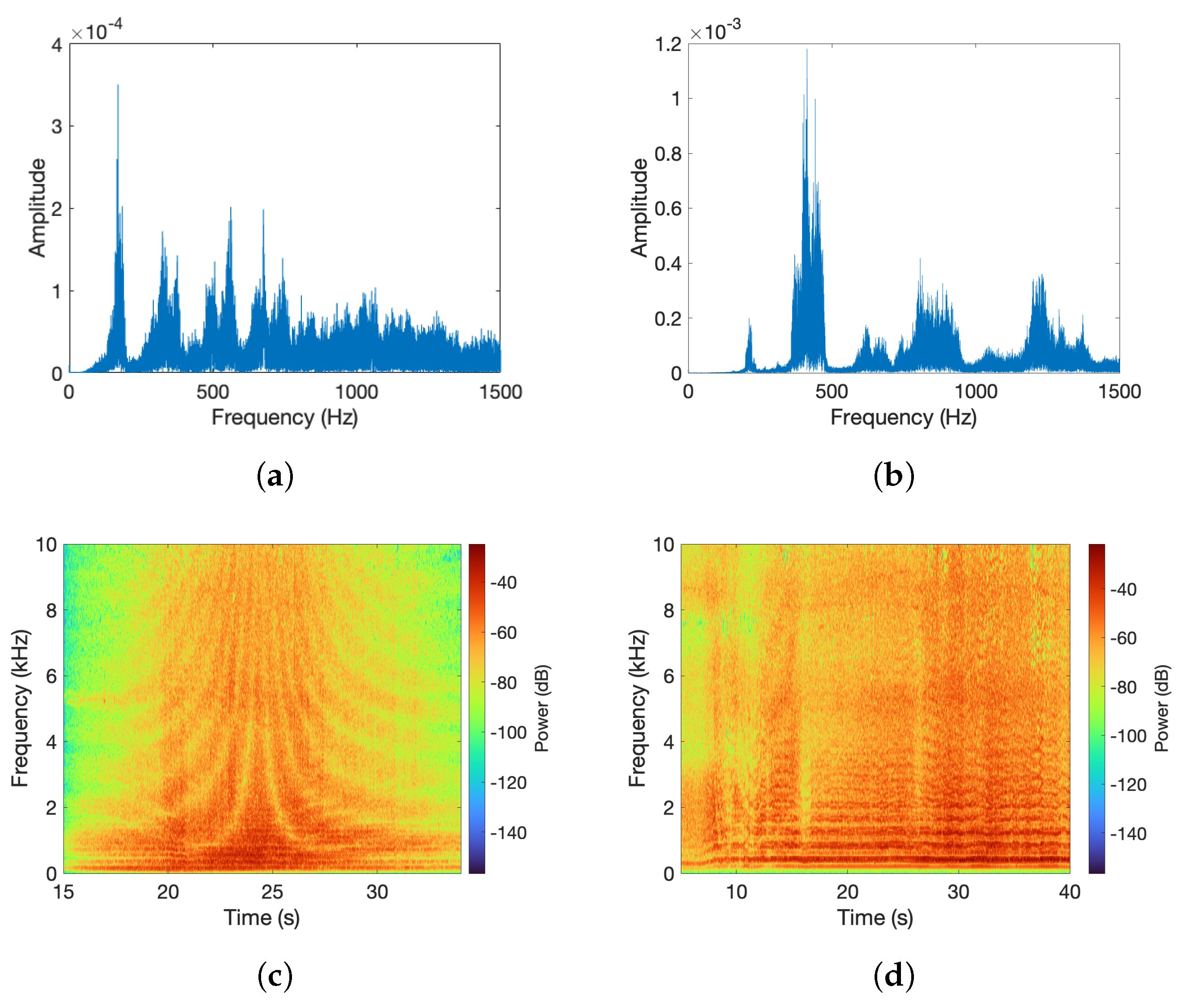
These peaks and valleys are approximately equidistant and vary slowly in practice. It is important to note that different drone types may exhibit variations in these frequency patterns due to distinctions in design, size, and propulsion systems. The frequencies and the shape of the spectrum envelope are related to the type of UAV, providing valuable information for detection, classification, and identification purposes. To illustrate this diversity, we provide in
Figure 1a the magnitude spectra of two distinct drones, highlighting how their unique designs result in variations in the acoustic signatures. Despite these differences, our study recognizes the common trends that enable the generalization of findings across various drone types.
In particular, there is a low-frequency band where most of the energy of the spectrum is concentrated, giving rise to quasi-horizontal lines known as HElicopter Rotor Modulation (HERM). These lines appear when a time-frequency analysis is performed with the short-term Fourier transform, using a window length large enough to cover several rotation cycles of the drone’s propellers. Examples of these lines can be observed in the spectrogram in
Figure 1b. This low-frequency information could be crucial for distinguishing drones from other devices, especially since low-frequency sounds are less attenuated than high-frequency sounds when they propagate through the air, making detection at long distances easier.
The distinctive acoustic signature of drone signals in the frequency domain provides the basis for understanding the rationale behind the extracted features, which will be explained in
Section 4. This understanding provides the context for explaining why features extracted in the frequency domain are fundamental inputs to the machine learning methods discussed in
Section 3. The aim is to provide a sound basis for a coherent explanation of the machine learning methods and the formation of the database of distinctive features extracted in the frequency domain.
3. Detection System Based on Machine Learning
This paper studies machine learning-based drone detection capabilities as a function of distance. As a novel aspect in comparison with other papers where the performance of the detector is measured with parameters such as Accuracy, Precision, Recall, or F1, detection is studied from the point of view of the Neyman–Pearson criterion [
20]. This detector maximizes the probability of detection (
) for a given probability of false alarm (
) and is particularly useful in binary hypothesis testing when assigning costs and determining a priori probabilities is challenging.
The possibility of approximating the Neyman–Pearson detector with learning machines has been previously demonstrated, when the mean squared error [
21] or the cross-entropy error [
22] are used as the error function for training. The Neyman–Pearson detector can also be approximated with appropriately trained SVMs [
23]. In this paper, machine learning-based detectors that approximate the Neyman–Pearson detector are trained and then tested by comparing their output to a threshold. Threshold variation allows for varying the values of the
, and for each estimated value, the corresponding
is determined. The representation of
versus
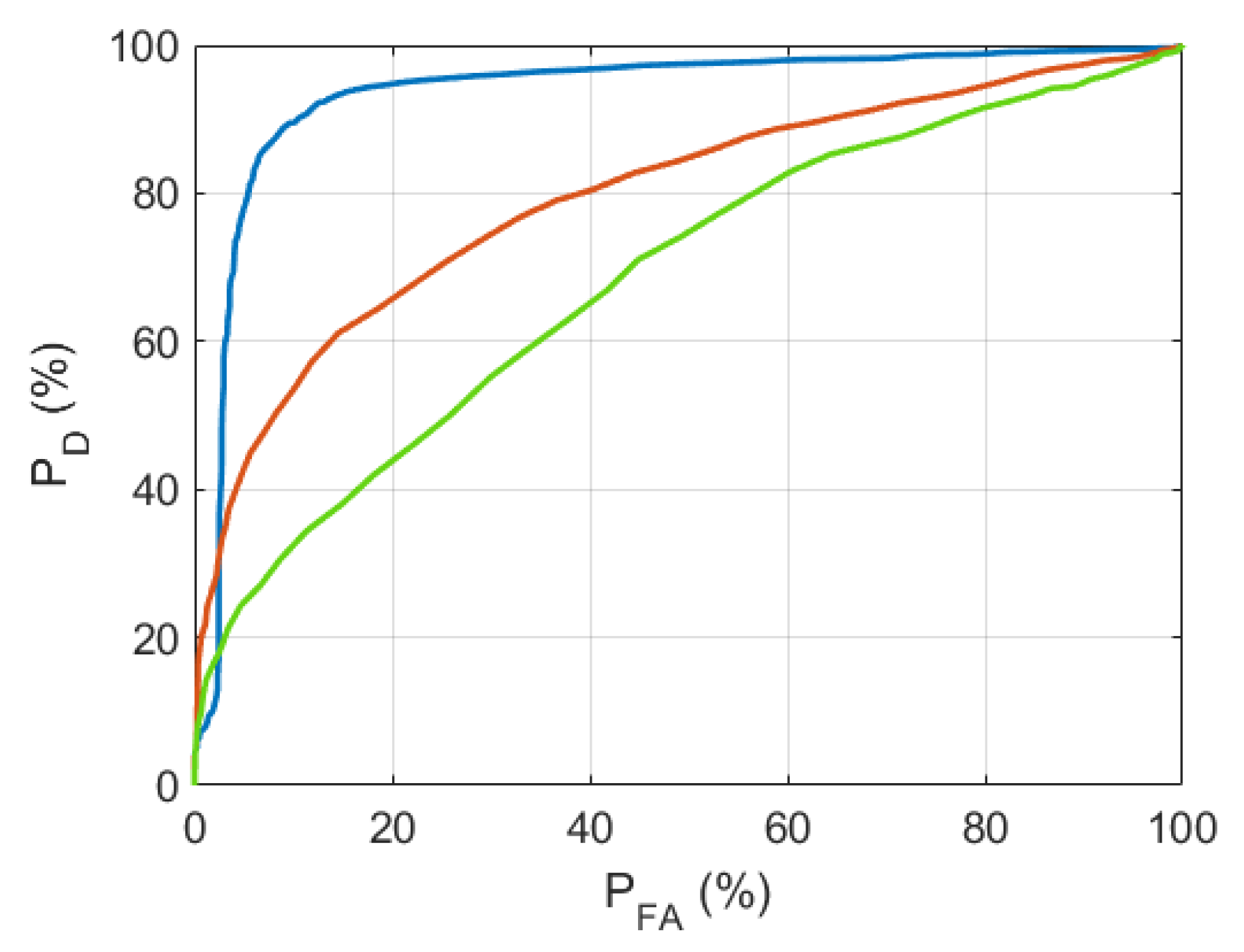
is the ROC (Receiver Operating Characteristic) curve, which allows the evaluation of the quality of the detector. These curves, as can be seen in
Figure 2, serve as a graphical representation of the relationship between the true positive rate or probability of detection (
) and the false positive rate or probability of false alarm (
). Each point on the ROC curve is determined by comparing the detector outputs with a specific threshold. The higher the
for a given
, the better the detector for that value. In general, the larger the area under the ROC curve (AUC), the better the detector performance.
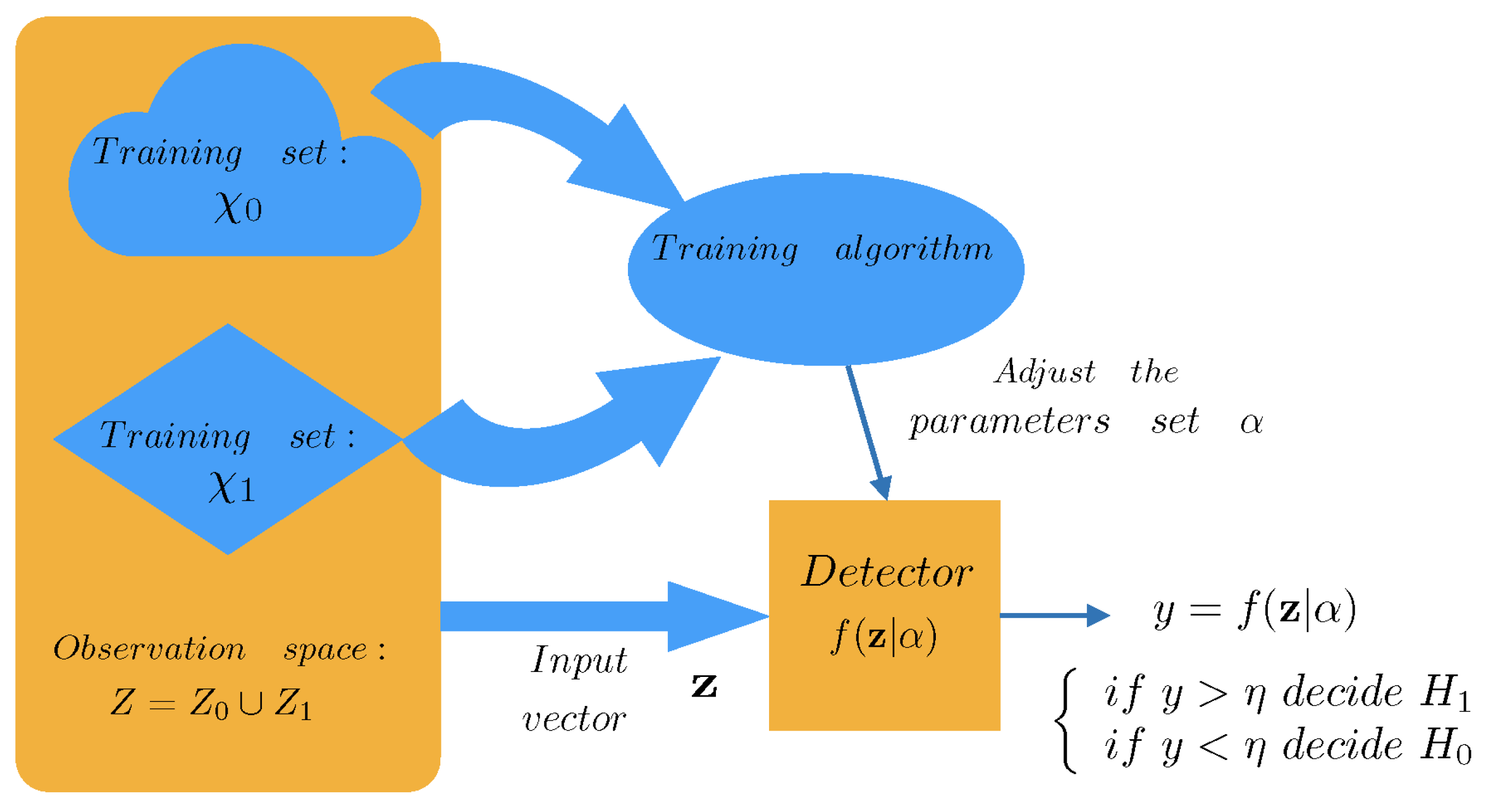
A learning machine is considered with only one output to classify input vectors
into two hypotheses or classes,
and
, representing the absence of drones and the presence of drones, respectively. The set of all possible input vectors generated under hypothesis
is
, with probability density function
, and the ensemble of all possible input vectors is
. A training set
, with
elements of each class (
is available. This training set is labeled, with desired or target outputs
. The vector
contains the desired outputs of the patterns applied to the classifier. The output of the learning machine is
for the input vector
, representing
the set of parameters fitted during training. The learning-machine-based structure is depicted in
Figure 3.
To evaluate the detection of sounds at different distances, the original dataset has been used to generate attenuated versions, taking into account the distance between the sound source and the acoustic sensor. The original dataset is composed of sounds recorded at 1 m from the source. The distances considered in the extended dataset are 50 m, 100 m, 200 m, 300 m, and 500 m. All signals are stored in a uniform format for easy manipulation. During the machine learning process, all these signals are loaded simultaneously. A distinctive aspect is the implementation of an indexing system in the dataset, which allows the selection of equivalent sound samples at different distances for training. This strategy ensures that repetition of samples in the test and training sets is avoided, thus avoiding the problem of overfitting and improving the robustness and accuracy in detecting sounds at different distances. The fact that each signal in the dataset, corresponding to a specific distance, is properly labeled is exploited during testing. This allows the data to be differentiated according to their source distance, allowing ROC curves to be presented and analyzed for each distance separately. This approach significantly improves the understanding and evaluation of the performance of the detection system in each specific distance range.
To evaluate the variation of the drone detection probability as a function of the distance between the drone and the system, machine-learning-based detectors have been implemented to approximate the optimal Neyman–Pearson detector. These have been tested with audio signals that are attenuated according to a function dependent on frequency and distance. The learning machines used to develop these detectors are the following.
3.1. Least-Squares Lineal Classifier
Linear discriminant (LD) is a supervised classification method that involves computing a linear combination of various features to differentiate between two specific classes. In the process, the least-squares classifier projects the data into a lower-dimensional space, pursuing the objective of maximizing the separation between classes and facilitating the classification task. The vector of linear discriminant outputs for the feature vectors in the test set is calculated using the following expression:
where
is a
vector with the weights of the linear discriminant (including the bias),
t is a
vector containing the target values (+1 and −1) of the P design patterns and
is a
matrix containing a row of ones for the bias and the L features of the P design patterns. The weights vector is calculated after least-squares minimization, with expression (
2), where
is a vector with the desired outputs for the training data, and
is a matrix containing the training patterns:
3.2. Multilayer Perceptron (MLP)
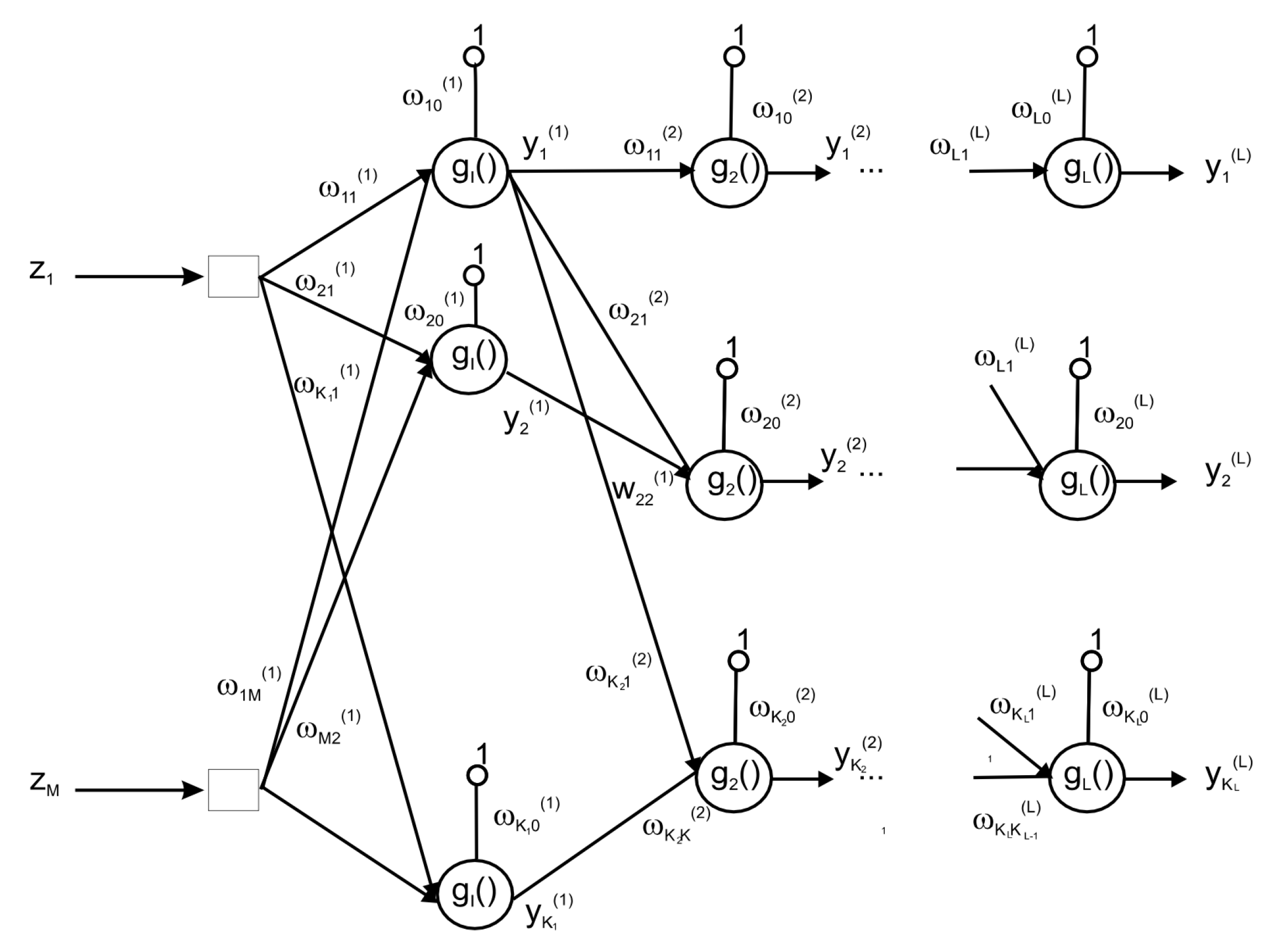
The MLP is an artificial neural network that can identify complex patterns in data by adjusting the connection weights between neurons during the training process. The operation of MLP involves applying a processing step to an input vector
, during which it is multiplied by weight vectors to obtain the input to the activation function of neurons in the hidden layers,
. The outputs of these hidden neurons are similarly processed, ultimately yielding the desired output. The architecture of the MLP with multiple outputs is depicted in
Figure 4.
In this paper, we opt for a perceptron featuring a single hidden layer, as it possesses the capability to approximate any discriminant function given a sufficient number of neurons in the hidden layer. These neurons are connected to the output layer, and the resulting output is compared with a predefined threshold for decision-making in the detection and classification process. Our approach involves the utilization of the Quasi-Newton-based backpropagation training algorithm, wherein connection weights undergo adjustment during each iteration or epoch in batch mode, i.e., utilizing subsets of training data instead of the entire set. This not only alleviates the computational burden but also significantly expedites the training process.
To implement our MLP model, we use a neural network configured with a single layer of 10 neurons and the Levenberg-Marquardt training method. The neural network was initialized, and the transfer function of the hidden layer was set as a hyperbolic tangent sigmoid. During the training process, 80% of the data were used for training and 20% for validation, excluding test data. The efficiency of the model was evaluated by calculating the Mean Squared Error (MSE) between the predictions and the actual labels, repeating this process several times, and selecting the final model according to the lowest MSE obtained. This approach provides an optimized MLP configuration that balances accuracy and generalization, adapting to the characteristics of our data.
3.3. Support Vector Machine (SVM)
The SVM method operates by transforming the input vectors into a higher-dimensional space, where they can be clearly separated using a hyperplane that divides the two classes [
24]. This method can be understood as a two-layer neural network: the first layer uses a kernel function, typically a radial basis function (RBF), while the second layer employs a linear basis. This combination results in a model capable of handling complex, high-dimensional data, even those that do not follow linear patterns.
Therefore, the function implemented by the SVM is a linear function of the results of mapping the input pattern
into a higher-dimensional space
with the kernel functions
, being
M the dimension of the new space. The parameters of the SVM are the weights vector
, the bias constant, and the parameters on which the functions
depend. The output of the SVM is obtained as follows, where
is a vector with the outputs of the kernel functions:
Before processing the data with this method, normalization has been applied to ensure that all data have the same scale. This technique is essential as it ensures an accurate fit of the model to the data and prevents certain characteristics from having a disproportionate weight in the decision-making process.
To implement the approximation to the Neyman–Pearson detector, the 2C-SVM must be used [
23]. Its training consists of solving the following optimization problem with constraints:
subject to:
This optimization is equivalent to minimizing the following objective function [
23]:
where parameters
and
C are used to control the costs associated with the errors in classifying patterns of each hypothesis,
is the desired output for pattern
, and
is the Heaviside step function. After training, the weights vector and the parameters of the kernel functions are obtained.
In our study, we use an SVM model for regression, opting for a radial basis function (RBF) kernel due to its capacity to handle complex patterns in the data. We automatically optimized the main hyperparameters using MATLAB, focusing on four essential aspects. The C parameter, which controls the error penalty, was set in the range . The Epsilon value, which sets the tolerable error margin, was explored in a range based on the interquartile range (IQR) of the data. The KernelScale, which is crucial for the RBF kernel, was explored between , and we also considered whether to standardize the features. The optimization process utilized a Bayesian optimization function with a maximum of 30 evaluation iterations to search the hyperparameter space efficiently. This hyperparameter configuration provides a balance between accuracy and generalization, automatically adapting to the specific characteristics of our data.
3.4. Random Forest
Random Forest is an algorithm that relies on the creation of multiple decision trees during the training process. What distinguishes it from a conventional decision tree is that instead of relying on a single tree structure, Random Forest builds multiple trees using random subsets of data and training features. The purpose is to reduce overfitting and increase the model’s ability to generalize to a variety of situations. In this way, the use of multiple trees gives Random Forest the advantage of dealing with complex and non-linear data, thus improving the accuracy of predictions. In addition, to make final decisions, the algorithm employs a voting method. Each tree in the forest produces an output, and these outputs are averaged at the end to obtain the final prediction. The structure of this classifier is represented in
Figure 5.
In the specific context of this paper, 100 trees have been implemented, and each tree has been trained with a random set of data and features, which contributes to the diversity and robustness of the final model.
In the specific context of this paper, we use a regression ensemble using the least-squares boosting method with 100 standard regression trees. Each tree has been trained with a random set of data and features, which contributes to the diversity and robustness of the final model. The hyperparameter configuration was automatically optimized. During this optimization process, different combinations for the number of ensemble learning cycles were explored, with a logarithmic search in the range . Additionally, the learning rate was tuned by exploring positive real values logarithmically within the range . These parameters provide a configuration tailored to the specific characteristics of the input data.
3.5. YAMNet Deep Neural Network
To study the variation of detection performance with distance with deep learning networks, we have used the deep neural network YAMNet, which is a pre-trained CNN that specializes in the task of audio classification. In this way, using transfer learning techniques, the training and binary classification of our problem is performed.
After being trained on the AudioSet-Youtube corpus using the depth-wise-separable convolution architecture Movilenet_v1 [
25], YAMNet can predict 521 classes of audio events. This deep neural network is composed of 86 layers, including 27 layers for convolutional operations, 27 layers for batch normalization and ReLU activation, 1 average pooling layer, 1 fully connected layer, 1 SoftMax layer, and a final classification layer. The final structure of YAMNet is depicted in
Figure 6.
The choice and organization of these layers are not random; they are the result of a careful design. The convolutional layers play a key role in extracting meaningful features from the input audio waveforms. Each of these layers is complemented by a batch normalization layer to ensure that the data are properly normalized, avoiding training challenges and improving learning speed. In addition, a ReLU activation function is incorporated after normalization, thus controlling the computational complexity of the network. During the classification phase, a fully connected layer is employed to consolidate information from each neuron between adjacent layers. This approach enables a comprehensive analysis of all input information, facilitating informed and accurate decision-making [
26].
Subsequently, if the problem is categorized as a classification issue, similar to the case of the original YAMNet network, a SoftMax layer is employed that applies a SoftMax loss function to the input. This allows the actual values to be compared with the predictions and the classification task to be performed. In addition, a final classification layer is used to compute the cross-entropy loss, considering classification tasks and weighted classification with mutually exclusive classes. In contrast, if the problem is considered to be a regression problem, the SoftMax and classification layers are replaced by a final regression layer, which calculates the mean squared error loss by splitting the regression tasks.
4. Materials and Methods
4.1. Database
The database utilized for design and testing aligns with the dataset employed in previous studies, specifically [
27,
28]. This dataset includes audio recordings from several drones, including models such as DJI Phantom 3, Cheerson CX 10, Parrot AR, Machine Racer, and Hobbyking FPV250, among others. In addition, the dataset includes sounds that could cause false alarms in practical situations. These sounds are selected because they have similarities to drone sounds, with their origin also in rotary engines or propellers found in airplanes, motorcycles, helicopters, and other less common sources, such as lawnmowers, or because they also have pseudo-periodic characteristics although their origin is different, such as fire sirens and rolling processes. These sounds have, for example, fundamental frequencies like that of sounds produced by drones and could confuse detectors, producing false detections (false alarms in detection theory).
It is worth mentioning that our database has been meticulously curated and updated for this study, compared to the datasets utilized in our previous works mentioned earlier. Sounds that, while sharing similar spectral characteristics, would not be realistic in genuine environments (e.g., the hum of a hairdryer) have been excluded from the current dataset to enhance the contextual relevance of our study.
This study focuses on analyzing the degradation of detection as a function of distance. The results obtained when the sensors are close to the source, at a distance of 1 m, are presented as a reference to know the limits in the detection capability of each detector. Since this is a detection problem equivalent to binary classification, the database has been split into 2 classes: “drones” and “non-drones”, with a total of 3532.27 s of audio files. Of these, 1919.34 s correspond to drone acoustic signals, representing 54.33% of the total, so the database is balanced between the 2 considered classes. The description of this dataset is presented in
Table 1, with information about signals length, the drone model, and the kind of interfering signals considered in the study. Unfortunately, the model of all the drones used is unknown, and they are only known to be different. Drones whose model is unknown are listed in the table as drone-n, where n is an integer.
The audio signals were originally sampled at 24 kHz and 44.1 kHz, but all of them have been resampled to 16 kHz, as there is no relevant information for frequencies above 8 kHz in the signal spectrum.
On the other hand, it is worth mentioning that the detection task (binary classification) would be performed when a sound source has been localized in the environment, using array processing techniques. The use of microphone arrays for the localization task allows the application of spatial filtering techniques for quality enhancement and noise and interference reduction. For this reason, and to make the analysis as realistic as possible, in the database, signals coming from the ground have been attenuated by 20 dB compared to signals captured at another elevation. If the sensor array detects a sound from a drone flying at a certain height, it is not attenuated by the application of spatial filtering techniques. However, sounds from sources at 0-degree elevations, such as those generated by motorcycles, construction sites, lawnmowers, bulldozers, the Litchfield fire siren, and wheel cuts, are attenuated by 20 dB, as they would have been picked up by a secondary lobe of the microphone array beam pattern.
The amplitudes of the signals produced by the UAVs are scaled so that the sound pressure level (SPL) is 80 dB for all of them, except for those coming from an elevation angle of 0 degrees, to which an additional 20 dB attenuation is applied, taking into account the application of spatial filtering, as mentioned above. The same procedure is applied to the background noise signals, adjusting them to a sound pressure level of 40 dB. This choice is based on the assumption that the used sensor array scans the space continuously with a beam narrow enough to achieve good directivity in the measurements. Because of this directivity, it is possible to attenuate noise and interfering signals in other directions, thus confirming that the input noise values are appropriate for the problem in question.
Table 2 provides an overview of the dataset parameters mentioned above. Our dataset, which includes a variety of drone models, provides the variability necessary for robust model training. In particular, the intentional inclusion of sounds that mimic possible false alarms in a real-world scenario enriches the realism of the dataset. Compared to our previous work, this dataset has undergone meticulous selection, excluding unrealistic sounds, such as the hum of a hairdryer, which increases its contextual relevance. In our refined database, spatial filtering is also considered, applying a 20 dB attenuation to sounds coming from the ground (at 0 degrees elevation). This attenuation is applied considering that the microphone array captures sound from the ground through a secondary lobe in the radiation pattern. This precaution is made for the worst-case scenario; in situations where the array collects sound through a different lobe or a null in the radiation pattern, the attenuation would be even more significant. This deliberate design not only provides quantitative information but also highlights the characteristics of the dataset, which is critical for evaluating drone detection systems in complex real-world environments.
To analyze performance concerning distance, we use a model to estimate frequency-dependent attenuation at specific distances from the source. The model used is defined in the ISO 9613-1 [
29] and 9613-2 [
30] standards and provides the attenuation suffered by a sound source at a distance as a function of frequency and under normal temperature and pressure conditions. In
Figure 7, the attenuation is depicted as a function of distance and frequency under normal temperature and pressure conditions. During training and testing, this attenuation is only applied to the signal of interest, as the interfering sound sources are considered to be at a fixed distance from the sensor, without any movement.
4.2. Preprocessing for Feature Extraction
The signals are preprocessed to extract useful features, which are applied as input vectors to the detectors. Previously, the signal is divided into frames of 512 samples, with an overlap of 50%. Each frame is subjected to an edge enhancement process, and the following spectral features are calculated for each one of them (a more detailed explanation of most of them can be found in [
31,
32]):
Mel-Frequency Cepstral Coefficients (MFCC). These coefficients are based on the human peripheral auditory system, so they represent frequency information on a scale that resembles human auditory perception. They are calculated with the following steps [
33]:
- −
Divide the signal in short time frames.
- −
Apply the Discrete Fourier Transform to each frame and obtain the power spectrum.
- −
Apply a filter bank corresponding to the Mel Scale to the power spectrum obtained in the previous step and add the energies in each sub-band.
- −
Take the logarithm of all the energies obtained in the previous step.
- −
Apply the discrete cosine transform to the logarithm of the power vector.
The relationship between frequency and the Mel frequency
is expressed in (
5):
-MFCC. These coefficients allow capturing changes in MFCC coefficients as they evolve, providing valuable information on how the acoustic properties of sound signals vary at different times. This technique uses the least squares to calculate the rate of change of these MFCC features, allowing a more detailed understanding of the temporal variations in the analyzed sound.
--MFCC. They represent the acceleration of changes in MFCC coefficients as they evolve. This involves providing information on the rate of change in the -MFCC coefficients, which adds a level of detail to the temporal variations in the acoustic signals. In addition, the ability to analyze the rate of change in the -MFCC coefficients allows them to be combined with other features, improving the accuracy and utility of audio and speech processing applications.
Pitch. It refers to the human perception of the fundamental frequency of a sound if it exhibits periodicity properties. In the context of our analysis, pitch and fundamental frequency are practically identical, which means that the characteristic we perceive as pitch coincides closely with the fundamental frequency of the sound signal.
Harmonic ratio. It is a measure that represents the ratio between the energy of the harmonics of a sound and the total energy of the signal. It provides information about the harmonic structure of the sound signal.
Spectral roll-off point. A metric that describes the shape of the power spectrum of a signal. It indicates the frequency below which a specific proportion of the total power of the spectrum is found. In other words, this parameter reveals what portion of the signal spectrum is concentrated at frequencies below a given value, thus providing information about the acoustic signal power distribution at different frequencies.
Spectral centroid. It is an indicator that characterizes the center of mass of a signal’s frequency spectrum, i.e., it represents the energy-weighted average frequency of the signal, providing information about its spectral distribution.
Spectral flux. It is a measure that indicates the rate of change in the spectral content of a signal as time elapses to capture abrupt transitions in the acoustic signal spectrum.
The mean and standard deviation (std) of the parameters calculated in the different time frames of the signals are obtained. The final set of features is presented in
Table 3, resulting in a total number of 160 features at the end of the process.
4.3. YAMNet Fine-Tuning
In this paper, we use a YAMNet network with regression rather than classification because it is more appropriate. This involves predicting continuous values rather than assigning features to predefined classes. This decision is based on the variable and continuous nature of the sounds and noises in our scenario, which requires assessing the similarity of the sound to that of a drone and capturing the continuous variability in the data.
Moreover, following the guidelines of the YAMNet documentation in Matlab, the audio signal is segmented into 0.98-second frames, and the selected sampling frequency is 16 kHz. Also, an initial learning rate value of is selected to ensure convergence of the model during training. Through experimentation, it is determined that 20 epochs are enough to effectively address our problem.
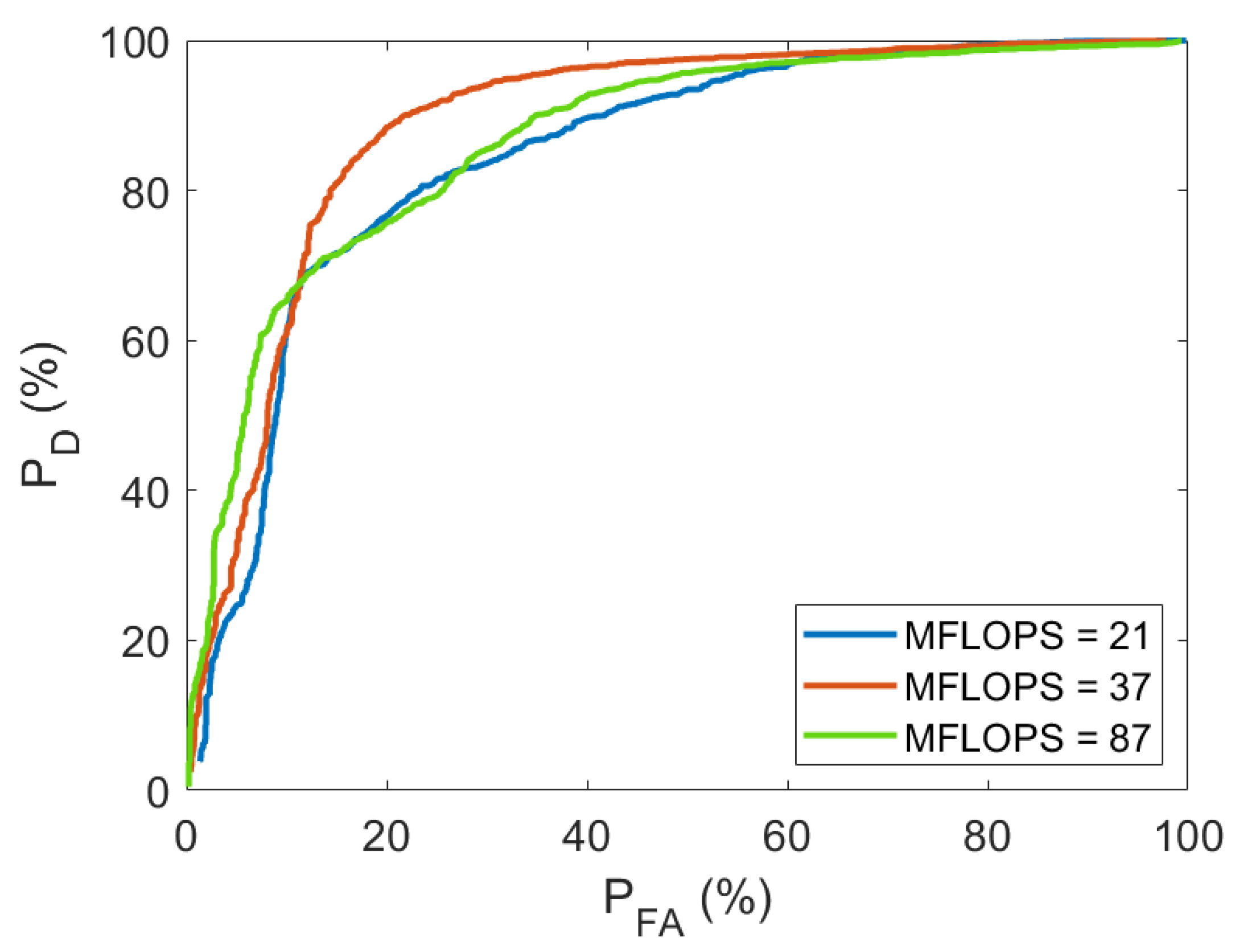
Additionally, we experimented with different numbers of layers in the network to infer the minimum network size, which produces good results to avoid wasting computational resources. YAMNet allows us to choose the number of layers, which is related to the computational complexity, measured in Million Floating Point Operations Per Second (MFLOPS) to process 1 s of audio. When only the first 20 layers are used, the computational complexity is 21 MFLOPs. When the first 40 layers are utilized, the computational complexity is 37 MFLOPS. When the complete structure is used, the computational complexity is 87 MFLOPS.
In addition to these considerations, in all scenarios, two final layers are incorporated: a 2D global average pooling layer to reduce the dimensionality of the feature maps before the output layer and a fully connected layer to predict continuous values in regression. In addition, to adapt the problem to our specific binary classification needs, a final layer is included to compute the mean square error of the obtained outputs.
The determination of how many layers to use in our problem is carried out through experimentation.
Figure 8 shows the ROC curve obtained by analyzing the detection problem at a distance of 1 m between the sound source and the array, i.e., without applying any attenuation. It is observed that the best solution is obtained when the computational complexity is 37 MFLOPS, corresponding to 40 layers of the original YAMNet structure. This number of layers is chosen in the experiments carried out from this point.
4.4. Performance Evaluation Using k-Fold Cross-Validation
Finally, to improve the performance evaluation of machine learning and transfer learning models, the k-fold technique (k = 10) has been implemented. K-fold cross-validation is a technique for evaluating predictive models [
34]. The dataset is divided into k subsets or folds. The model is trained and evaluated k times, using a different fold as the validation set each time. Performance metrics from each fold are averaged to estimate the model’s generalization performance. This process ensures a more accurate and reliable assessment of performance. Using the complete dataset for training and validation, a robust and accurate performance assessment of the different compared systems is obtained.
5. Results and Discussion
This paper evaluates the effectiveness of drone detection with several methods based on machine learning, from simple methods such as linear discriminants to sophisticated deep networks taking advantage of transfer learning (TL). The experiments performed and the results obtained are presented in this section.
Starting with a detailed overview of the hardware infrastructure, the experiments were run on a server with ample computing resources, including 128 GB of RAM and an Intel Xeon CPU running at 3.00 GHz with 12 primary processors and 24 logical processors. The server was further enhanced with an NVIDIA RTX A4000 GPU, which was used specifically for the tasks using the YAMNet method.
Initially, the learning machines are trained using the database without attenuation, i.e., with data collected at a distance of 1 m. Nevertheless, the detectors are tested with signals emitted at different distance ranges to evaluate the capacity of detecting drones at distances different from the distance between the drones and the sensor in the signals used for training. ROC curves are used to evaluate detector performance.
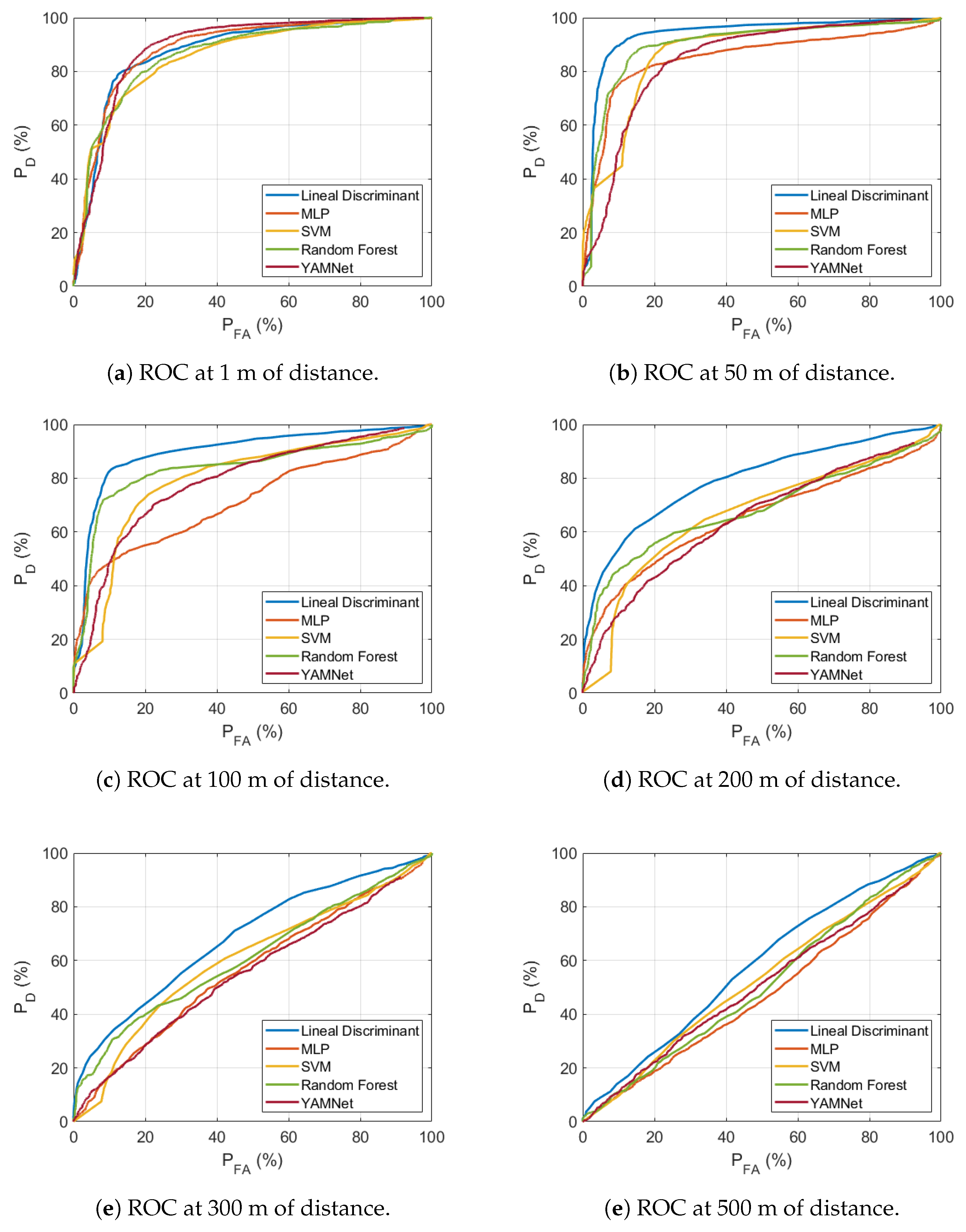
Figure 9 represents the ROC curves obtained by training the linear discriminant, MLP, SVM, Random Forest, and YAMNet with transfer learning, using non-attenuated data. At a distance of 50 m between the sound source and the microphone array, both the linear discriminant and Random Forest methods exhibit notable performance, achieving an AUC of approximately 90% (specifically, 93.66% for linear discriminant and 89.83% for Random Forest). Conversely, the values of the AUC for the MLP-based detector are 85.22%, and 86.94% for SVM. The worst result is obtained with the YAMNet-based detector, whose AUC is just 76.49%.
By doubling the distance to 100 m, the AUC values of all detectors, except MLP, decrease by 4–7%. In particular, the AUC of the MLP-based detector undergoes a substantial decrease, reaching a value of 71.58%, reflecting a decrease of 14% with respect to the previous value. This decrease in performance may be because it overfits short-distance data and, therefore, does not generalize well to longer distances, as the model does not account for attenuated and distorted signals. Further doubling the distance to 200 m, the detection results are still acceptable for the linear discriminant, exhibiting values greater than 60% for values below 10%, and an AUC of 79.59%. In contrast, the other methods yield AUC values around 65%. Therefore, the detector that best generalizes to data obtained at distances different from the distance used to obtain the training data is the simplest detector based on the linear discriminant.
The ROC curves depicted in
Figure 9e for a distance of 300 m have an AUC just above 50% for most methods (68.5% for the best detector, the linear discriminant). The least effective method is the YAMNet-based approach. This trend becomes even more pronounced in
Figure 9f, which represents the ROC curves at 500 m. Here, the values of AUC fall below 50% for all methods except for the linear discriminant, with an AUC of 57.76%, suggesting that detection becomes practically unfeasible at these distances. There seems to be a relationship between the complexity of the detector and the ability to generalize to signals coming from distances other than the one used in the training. Thus, the system that generalizes best is the linear discriminant, and the system that generalizes worst is the YAMNet deep network. This result may be surprising since a priori, one might expect a better performance of the more complex and powerful system. Therefore, with this approach for training, we conclude that acoustic detection is not feasible at distances greater than 200 m.
After obtaining these results, the model is trained with data attenuated by the effect of distance to simulate real detection conditions. The attenuation is applied in the frequency domain, as it depends on frequency. With this approach, the learning machines are intended to perform well over a larger range of distances, thanks to the fact that data obtained over a wide range of distances between the source and the sensor have been applied during training.
Specifically, we have expanded the dataset to cover a wider range of distances. The original dataset, which included mainly unattenuated audio segments, has been expanded to incorporate segments with varying degrees of attenuation, corresponding to distances of 50 m, 100 m, 200 m, 300 m, and 500 m, increasing the size of our dataset by a factor of six. This expanded dataset offers a wide range of audio samples at different distances and under different signal attenuation conditions. This diverse and expanded dataset, when used to train our detection models, allows them to adapt and perform more effectively in a wider range of distance scenarios.
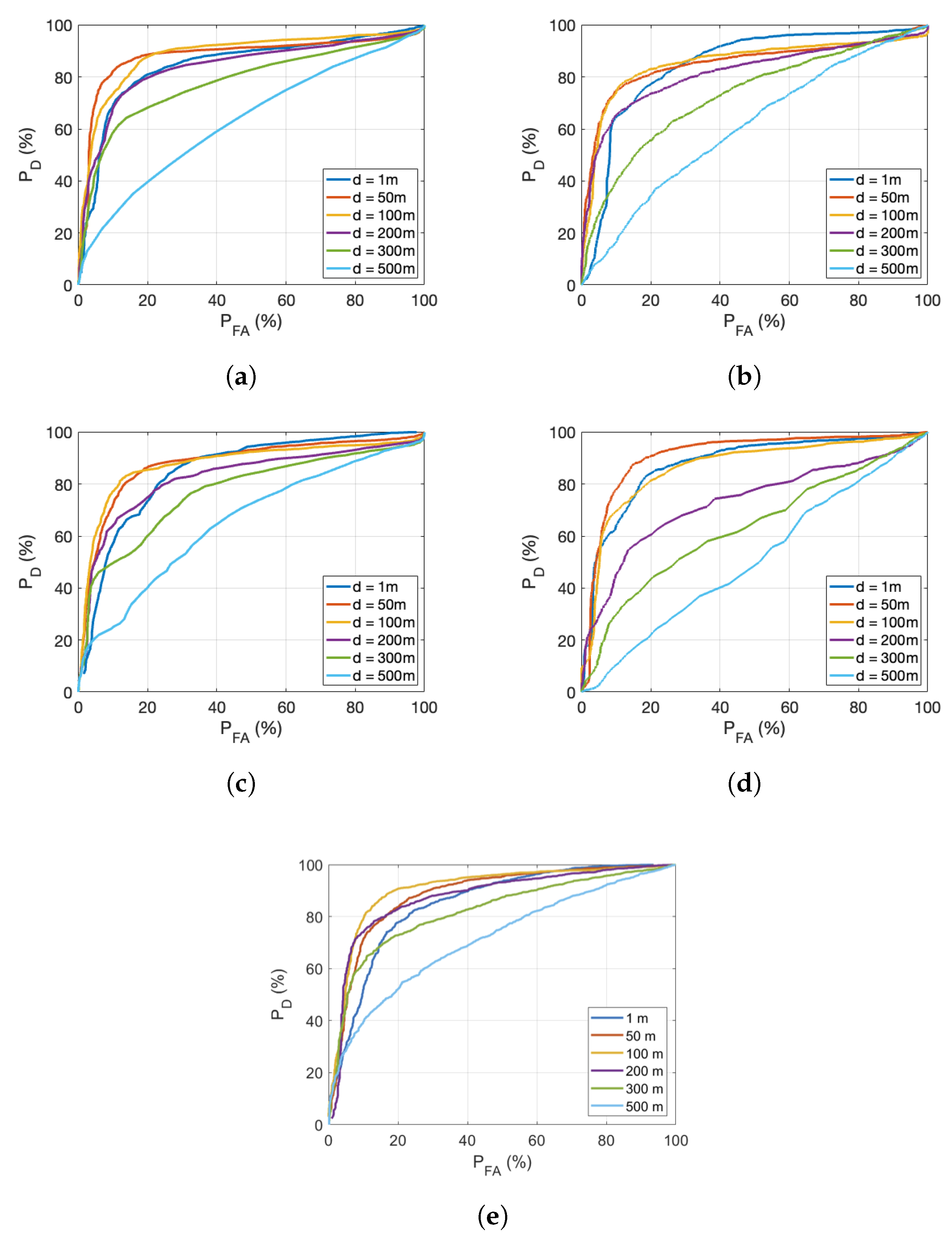
Table 4 shows the values of the area under the ROC curves.
Figure 10a–e presents the ROC curves obtained for all the distance ranges evaluated and for all the detectors considered (note that, in this case, each curve plot corresponds to a different detector). At a distance of 100 m from the source, the AUC is approximately 90% for all detectors. The linear discriminant, SVM, and YAMNet show similar performance, with values of AUC above 80% at 200 m, decreasing by 5% at 300 m. However, the MLP and Random Forest-based detectors are more sensitive to distance, and the AUC values decrease by approximately 10% as the distance is extended from 200 to 300 m. These detectors demonstrate the ability to make acceptable detections up to 200 m but face limitations at greater distances.
Finally, when increasing the distance to 500 m, only the YAMNet-based detector with transfer learning achieves a of 40% for a false alarm probability of less than 10%, which corresponds to an AUC of about 71%. The ability of the YAMNet neural network-based detector to detect at longer distances can be attributed to its ability to learn with large training sets that consider all possible variants. YAMNet, with its ability to robustly learn patterns at different distances, outperforms other detectors in long-distance detection scenarios. However, its limitation lies in its dependence on the quality and diversity of the training data. If the data used for training does not cover the wide variety of scenarios affected by distance, the model’s ability to generalize to new long-distance environments may be compromised.
The results obtained with a training set that includes audio collected at different distances (therefore, with different attenuation) are, in general, better than those obtained when training with data collected at a short distance from the source. On the one hand, the detectors perform well at greater distances from the sound source, but on the other hand, the results are worse at short distances. For instance, with a non-attenuated training set, when the drone is merely 1 m from the microphone array, AUC values around 90% are observed for all methods. In contrast, with the attenuated training set, AUC values are around 80%). This shows that the detectors perform better overall but do not reach the detection probabilities that were obtained when training and testing with signals collected in the same distance range.
Therefore, a crucial element in achieving acceptable detection at long distances from the source is to train with a database that includes sounds and interferences also collected at long distances from the source. With this approach, reliable detections are obtained at distances up to 200 m for all the detectors studied, up to 300 m for the simplest detector (linear discriminant), and up to 500 m for the YAMNet-based detector, which exploits transfer learning. However, when addressing the acoustic detection of drones at distances exceeding 500 m, we encounter notable challenges, primarily due to a significant reduction in the signal-to-noise ratio (SNR). At these distances, the task of distinguishing the drone’s signal from background noise becomes considerably more complex. In addition, the situation can be further complicated by environmental factors such as wind or rain, which result in higher attenuations, which can alter or even mask the drone’s acoustic signature, posing an additional obstacle to accurate detection at long distances.
In urban environments, where the required detection ranges are not very high, typically not exceeding 300 m, the methods used show reliable results and can be used, for example, for security applications. In these areas, any of the methods could be used if the training set includes signals collected over a wide range of distances. In rural areas, where detection distances may be greater, our results suggest that methods such as the YAMNet-based detector, which is effective up to 500 m, could be advantageous. In addition, combining our detection techniques with other technologies, such as radar, could mitigate the limitations of long-range detection and improve the overall effectiveness of the system. Finally, for short-range security scenarios with coverages of 100 m or less, the linear discriminant method is particularly effective. This approach, especially when trained on datasets without attenuation, provides optimal results for close-range drone detection. Continuous adaptation and improvement of detection algorithms, informed by ongoing research and data, is essential to maintain the relevance and effectiveness of these systems in practical applications.
Another interesting result obtained when training with the dataset, including sounds at all distances considered, is that the performance at short distances is worse than the performance at medium distances for all the detectors studied. In some cases, such as YAMNet or the detector based on linear discriminants, the detection performance at 200 m exceeds that obtained without applying attenuation at 1 m. The best performance of detectors trained with this dataset occurs when the sound source is at a medium distance from the sensor.
The approach of including sounds collected at different distances from the sensor in the training dataset is adequate to extend the detection range when only one detector is used, but the results could be better when training and testing with data collected at the same distance, which suggest the usage of ensembles of detectors specialized at different distances to obtain full coverage. The application of one or another detector would depend on the result obtained in the localization of the sound source by means of array processing techniques.
Using the hardware resources described above, the times required for training and detection have been analyzed for the different systems evaluated. Using k-fold (k = 10) cross-validation for training and employing 1-s audio segments as inputs to the learning machines, the time required for training is variable, ranging from 0.010520 s with the linear discriminant to more than 4 min with Random Forest. Regarding testing, each fold of audio segments used for validation with k-fold cross-validation is processed in 0.2 ms with the linear discriminant and in 1.23 s with YAMNet, the most complex system. This means that the time required to process a 1-second-long frame is 4 ms with the most complex system, indicating that real-time implementation is feasible.
These results are promising and stimulate research into array processing techniques to solve the problem of localizing sound sources and maximizing interference attenuation. These advances are essential to achieve a final solution that allows detection over wide ranges of distances with a high AUC. In addition, the possibility of developing specialized detectors for each distance range, which would be selected based on the information provided by a localization system based on microphone arrays, has been proposed and will be explored in future work. Taken together, these results suggest that acoustic detection can be considered a competitive and complementary method to detections obtained with other types of sensors.
6. Conclusions
A comprehensive evaluation of drone acoustic detection performance at different distances has been carried out in this paper, providing valuable insights for future research and practical applications. The evaluation was performed by extracting relevant features in the frequency domain and applying machine learning methods, including, among them, a deep neural network, YAMNet, with the transfer learning technique. For the application of these methods, a carefully designed database including drone sounds and interferences has been used, simulating realistic conditions by specific attenuation of the interferences.
The results obtained reveal the significant impact of distance variation on detection results attributed to frequency-dependent sound propagation attenuation. In addition, the detector performance was found to be dependent on the training dataset. When a training set is used in which the data are not attenuated, good detection results are achieved at distances up to 200 m. Specifically, when the distance between the drone and microphone array is low, the AUC values range between 80% and 90%, depending on the method used. At 200 m, the detection results are still acceptable for the linear discriminant, with values of AUC around 80%, but this drops to approximately 65% for other methods. At greater distances, however, the AUC values fall below 70% for all methods. In contrast, if the training set includes sounds at different distances, detection results improve significantly at medium and long distances. This approach results in more consistent detection performance, with good results over a wider range of distances. For example, at 1 m, all methods show AUC values between 81% and 88%. The results are better at medium-range distances (50 m and 100 m), with AUC values always higher than 87%. At 200 m, the results are similar to those obtained without attenuation for most methods, and in particular, YAMNet still produces an AUC value higher than 87%, showing a 10% increase over the result obtained at 1 m. At 500 m, the AUC values fall below 70% for all methods except YAMNet, which remains slightly above this value. These results demonstrate how incorporating a distance-diverse training set can enhance detection capabilities, particularly for advanced methods like YAMNet, allowing detection at distances up to 500 m with the best type of detector.
These results highlight the critical role of incorporating distance diversity into training sets and provide clarity on the optimal choice of machine learning methods based on specific scenarios. For scenarios where simplicity is paramount, the linear discriminant is an effective choice, especially when trained on unattenuated data and at low distances. Conversely, for scenarios requiring increased accuracy at medium and long ranges, the deep learning approach with YAMNet emerges as the preferred option, demonstrating its potential for drone detection at long distances.
As a future research line, it is essential to investigate advanced array processing techniques to improve interference reduction through spatial filtering and to achieve precise localization of sound sources. This information can be used as input to a system to select the best detector based on the distance from the sound source.
In addition, it is necessary to develop machine learning and transfer learning models capable of handling distance variations with high precision. Moreover, it is considered crucial to expand the constructed database to avoid possible biases and improve generalization to new data. More thorough preprocessing of the input data is also emerging as a fundamental improvement to minimize noise as much as possible.
Furthermore, the fact that the best results are obtained with a deep network like YAMNet suggests research with networks of this type. To train these networks, it is necessary to have enormous amounts of data, which cannot be easily achieved in real environments. For this reason, research into techniques for increasing data volume is also considered. Strategies to address this challenge include data augmentation, where existing data are manipulated or transformed to create new variations. Additionally, synthetic data generation, which involves the creation of artificial data that mimics real-world phenomena, can be a viable approach. The use of publicly available databases is also a practical solution to supplement limited datasets. These methods help mitigate the limitations imposed by the lack of large-scale, diverse datasets, allowing more effective training of deep neural networks such as YAMNet.
Finally, another possible avenue for future research is to delve into advanced feature extraction techniques and investigate data preprocessing strategies. The goal is to improve the accuracy and robustness of our detection methods while minimizing the effect of noise on the sound signals.
The development of acoustic systems that detect a drone accurately at large distances would allow early detection in security systems, increasing the ability to implement countermeasures to minimize the effects of this threat (drones are being used in military applications, for espionage, as vectors for cyber-attacks, etc.). In addition, to be a competitive system with other types of sensors, such as radar sensors and vision systems, it is necessary to increase the detection range. Today, with radar systems, it is possible to detect small drones at distances of a few kilometers, so the research objective is focused on that direction, trying to develop systems with ranges that compete with those of radar systems. This need encourages research to achieve detectors with better performance and robustness, capable of providing accurate detections over wide ranges of distances. This study not only expands our understanding of drone acoustic detection but also suggests that this technology has the potential to be a valuable tool in real-world applications. By complementing other detection methods, it can provide comprehensive and reliable solutions in diverse environments, marking a significant advancement in the field of acoustic drone detection.
The final proposed detection architecture could consist of a set of detectors, each one specialized in specific distance ranges, controlled by a central unit that decides which results are predominant or that is in charge of fusing the information from the different detectors, considering the estimated distance with a localization system, probably based on array processing methods. This acoustic localization system must collaborate in real scenarios with other sensors, such as radar and image sensors, to overcome the specific drawbacks of each one, providing a sensing system applicable in a wide range of distances, with different visibilities and interfering signals. For example, cameras and radars cannot work with obstacles that avoid illuminating the target, but acoustic sensors are sensible to acoustic interferences and only work well at low and medium ranges.