An Efficient Dual Application of the Adaptive Cross Approximation for Scattering and Radiation Problems
Abstract
1. Introduction
2. Description of the Proposed Approach
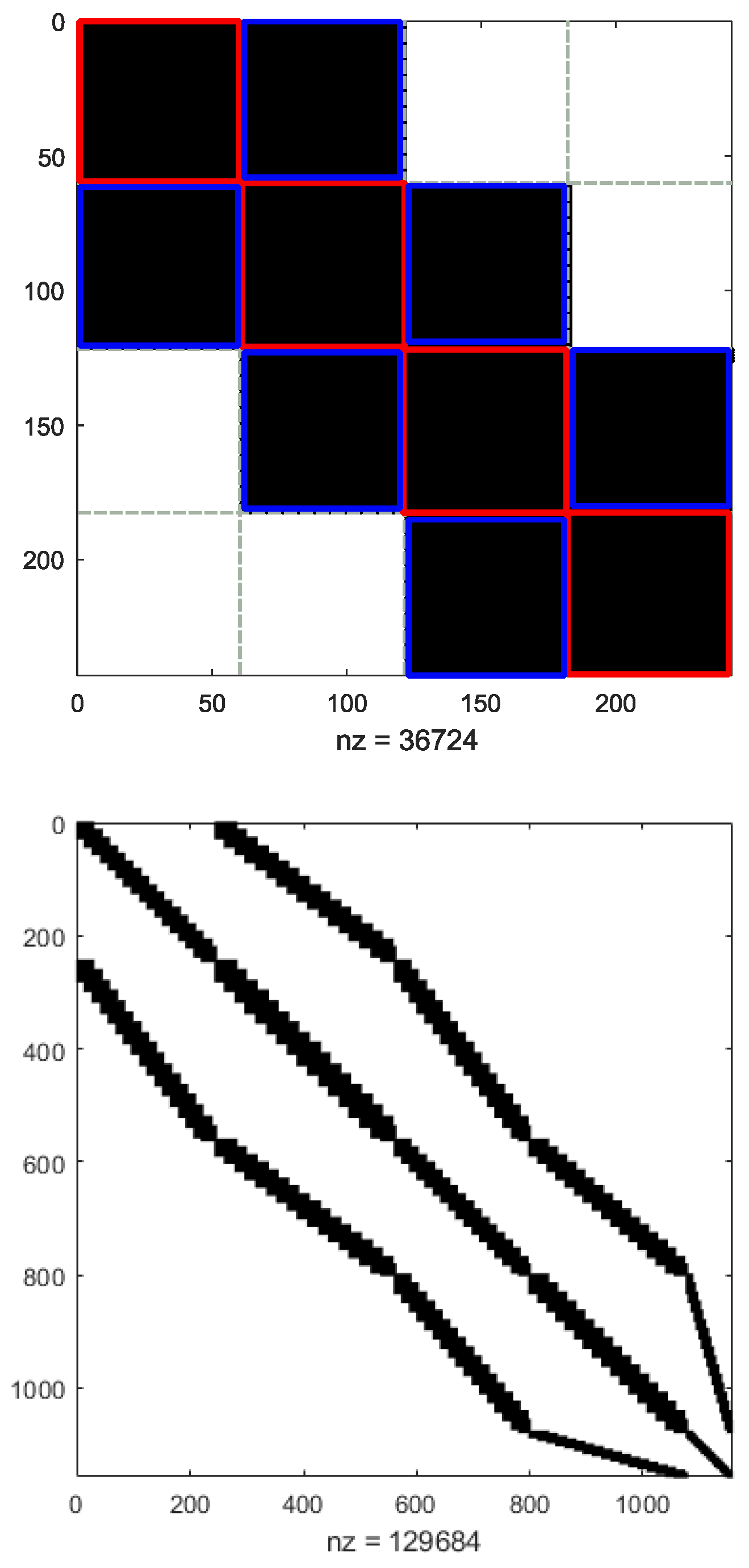
2.1. Application of the ACA to the Reduced Matrix Computation with the CBFM
2.2. Dual Use of the ACA in the Calculation of the Reduced Matrix with ACA-CBFM
2.3. Combination of ACA and MLFMM with the CBFM
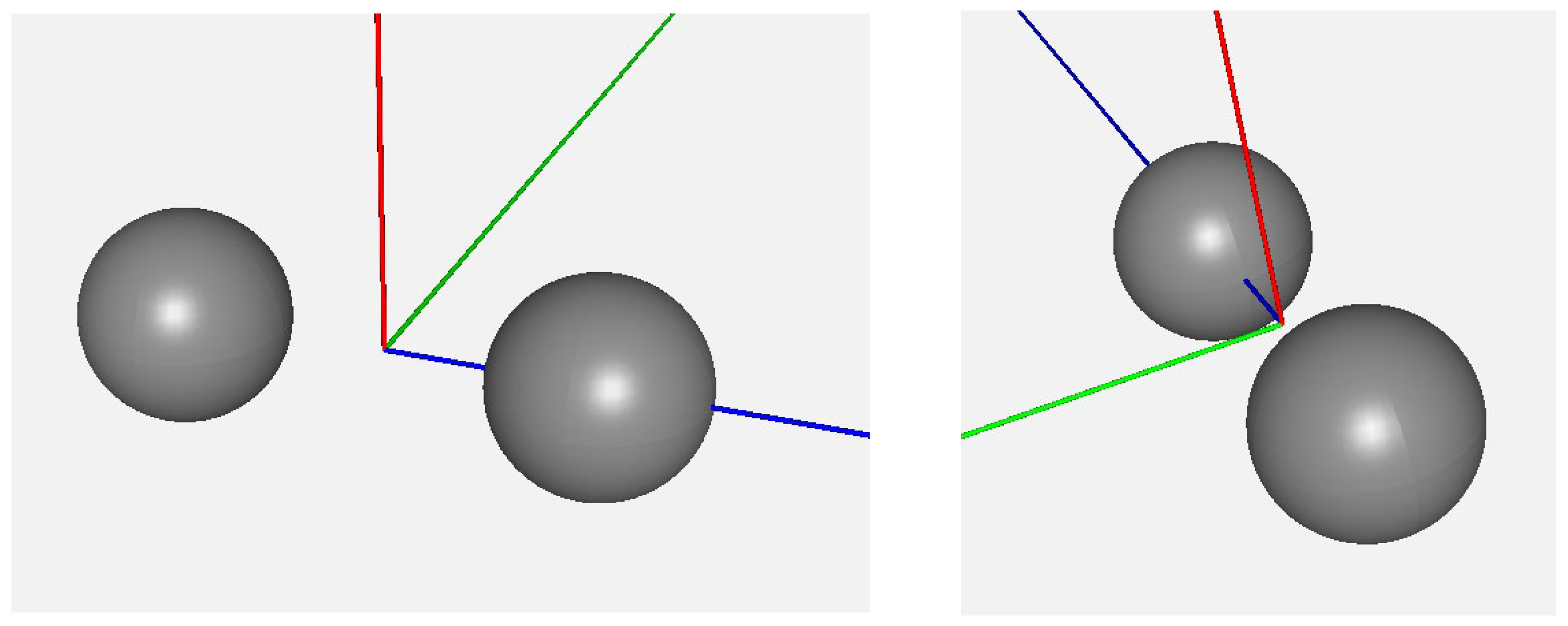
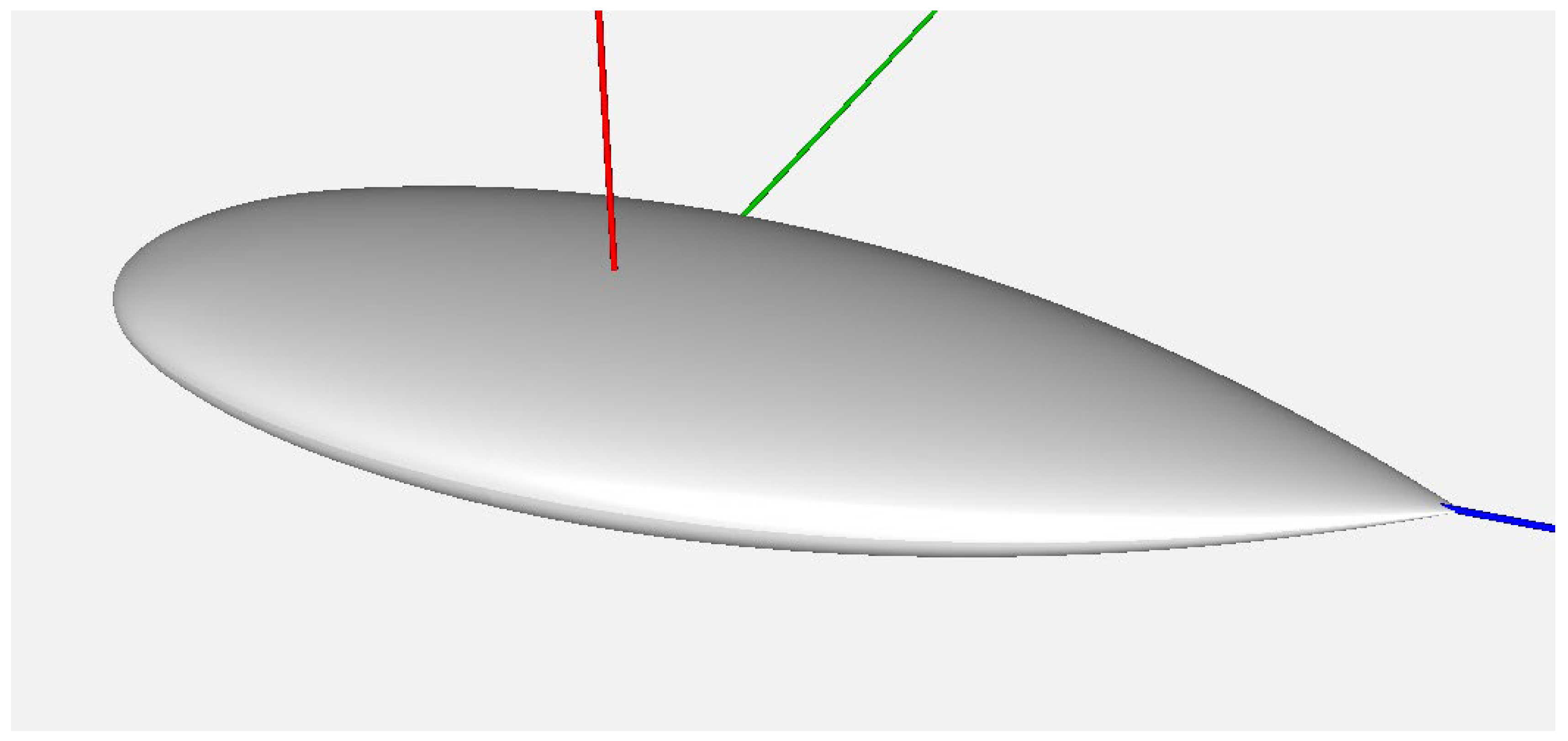
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harrington, R.F. Field Computation by Moment Methods; McMillan: New York, NY, USA, 1968. [Google Scholar]
- Chew, W.C.; Jin, J.; Michielssen, E.; Song, J. (Eds.) Fast and Efficient Algorithms in Computational Electromagnetics; Artech House Inc.: Norwood, MA, USA, 2001. [Google Scholar]
- Gurel, L.; Ergul, O. Hierarchical parallelization of the multilevel fast multipole algorithm (MLFMM). Proc. IEEE 2013, 101, 332–341. [Google Scholar] [CrossRef]
- Delgado, C.; Cátedra, M.F. Combination of ray-tracing and the method of moments for electromagnetic radiation analysis using reduced meshes. J. Comput. Phys. 2018, 361, 412–423. [Google Scholar] [CrossRef]
- Eibert, T.F. A diagonalized multilevel fast multipole method with spherical harmonics expansion of the k-space Integrals. IEEE Trans. Antennas Propag. 2005, 53, 814–817. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Catedra, F. Efficient Interpolation Technique for the Analysis of RCS Problems. IEEE Trans. Antennas Propag. 2024, 72, 6831–6836. [Google Scholar] [CrossRef]
- Boag, A.; Mittra, R. Complex multipole beam approach to electromagnetic scattering problems. IEEE Trans. Antennas Propagat. 1994, 42, 366–372. [Google Scholar] [CrossRef]
- Bleszynski, E.; Bleszynski, M.; Jaroszewicz, T. AIM: Adaptative Integral Method for Solving Large Scale Electromagnetic Scattering and Radiation Problems. Radio Sci. 1996, 31, 1225–1251. [Google Scholar] [CrossRef]
- Canning, F.X. The Impedance Matrix Localization (IML) Method for Moment-Method Calculations. IEEE Antennas Propag. Mag. 1990, 32, 18–30. [Google Scholar] [CrossRef]
- Prakash, V.V.S.; Mittra, R. Characteristic Basis Function Method: A New Technique for Efficient Solution of Method of Moments Matrix Equation. Microw. Opt. Technol. Lett. 2003, 36, 95–100. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. Efficient Iterative Analysis Technique of Complex Radome Antennas Based on the Characteristic Basis Function Method. IEEE Trans. Antennas Propag. 2021, 69, 5881–5891. [Google Scholar] [CrossRef]
- Matekovits, L.; Laza, V.A.; Vecchi, G. Analysis of Large Complex Structures with the Synthetic-Functions Approach. IEEE Trans. Antennas Propagat. 2007, 55, 2509–2521. [Google Scholar] [CrossRef]
- Maaskant, R.; Mittra, R.; Tijhuis, A. Fast Analysis of Large Antenna Arrays Using the Characteristic Basis Function Method and the Adaptive Cross Approximation Algorithm. IEEE Trans. Antennas Propag. 2008, 56, 3440–3451. [Google Scholar] [CrossRef]
- Lucente, E.; Monorchio, A.; Mittra, R. An iteration-free MoM approach based on excitation independent characteristic basis functions for solving large multiscale electromagnetic scattering problems. IEEE Trans. Antennas Propag. 2008, 56, 999–1007. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. A Computationally Efficient Technique Using Characteristic Basis Functions and Large Block Sizes. IEEE Antennas Wirel. Propag. Lett. 2024, 23, 1341–1345. [Google Scholar] [CrossRef]
- Iupikov, O.A.; Craeye, C.; Maaskant, R.; Ivashina, M.V. Domain-Decomposition Approach to Krylov Subspace Iteration. IEEE Antennas Wireless Propag. Lett. 2016, 15, 1414–1417. [Google Scholar] [CrossRef]
- Ozdemir, N.A.; González-Ovejero, D.; Craeye, C. On the Relationship Between Multiple-Scattering Macro Basis Functions and Krylov Subspace Iterative Methods. IEEE Trans. Antennas Propag. 2013, 61, 2088–2098. [Google Scholar] [CrossRef]
- Delgado, C.; Cátedra, M.F. Efficient Generation of Macro Basis Functions for Radiation Problems Using Ray-Tracing Derived Dynamic Thresholds. IEEE Trans. Antennas Propag. 2018, 66, 3231–3236. [Google Scholar] [CrossRef]
- Wang, Z.G.; Nie, W.Y.; Lin, H. Characteristic basis functions enhanced compressive sensing for solving the bistatic scattering problems of three-dimensional targets. Microw. Opt. Technol. Lett. 2020, 62, 3132–3138. [Google Scholar] [CrossRef]
- Li, M.; Ding, D.; Heldring, A.; Hu, J.; Chen, R.; Vecchi, G. Low-Rank Matrix Factorization Method for Multiscale Simulations: A Review. IEEE Open J. Antennas Propag. 2021, 2, 286–301. [Google Scholar] [CrossRef]
- Zhao, K.; Vouvakis, M.N.; Lee, J.F. The adaptive cross approximation algorithm for accelerated method of moments computations of EMC problems. IEEE Trans. Electromagn. Compat. 2005, 47, 763–773. [Google Scholar] [CrossRef]
- Lü, Z.-Q.; An, X. Fast monostatic radar cross-section computation for perfectly electric conducting targets using low-rank compression and adaptive integral method. IET Microw. Antennas Propag. 2014, 8, 46–51. [Google Scholar] [CrossRef]
- Burkholder, R.J.; Lee, J.F. Fast Dual-MGS Block-Factorization Algorithm for Dense MoM Matrices. IEEE Trans. Antennas Propag. 2004, 52, 1693–1699. [Google Scholar] [CrossRef]
- Huang, F.; Sun, Y.F. Efficient solution of electromagnetic scattering from dielectric objects via charac-teristic basis function method based on large-size blocks with multilevel subdivision. IEEE Access 2019, 7, 71741–71748. [Google Scholar] [CrossRef]
- Fang, X.X.; Cao, Q.S.; Wang, Y. Accelerated direct solver with multiscale compressed block decom-position and multilevel characteristic basis function method. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 2226–2229. [Google Scholar] [CrossRef]
- Blackburn, J.N.; Young, J.C.; Adams, R.J. A Weighted Average Adaptive Cross Approximation. IEEE Trans. Antennas Propag. 2023, 71, 8121–8129. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, D. Fast O(N log N) Algorithm for Generating Rank-Minimized H2-Representation of Electrically Large Volume Integral Equations. IEEE Trans. Antennas Propag. 2022, 70, 6944–6956. [Google Scholar] [CrossRef]
- García, E.; Delgado, C.; Cátedra, F. Use of the Adaptive Cross Approximation for the Efficient Computation of the Reduced Matrix with the Characteristic Basis Function Method. Mathematics 2024, 12, 1565. [Google Scholar] [CrossRef]
- Chen, X.; Gu, C.; Ding, J.; Li, Z.; Niu, Z. Multilevel Fast Adaptive Cross-Approximation Algorithm With Characteristic Basis Functions. IEEE Trans. Antennas Propag. 2015, 63, 3994–4002. [Google Scholar] [CrossRef]
- Sleijpen, G.L.G.; Fokkema, D.R. Bi-CGSTAB(l) for linear equations involving unsymmetric matrices with complex spectrum. Electron. Trans. Numer. Anal. 1993, 1, 11–32. [Google Scholar]
- Delgado, C.; Cátedra, M.F. Sparse Approximate Inverse Preconditioner with Parametric Sparsity Pattern Applied to the Macrobasis Function Methods. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 849–852. [Google Scholar] [CrossRef]
- EM JINA 2006. 9 November 2006, Nice, France. Available online: www.em-jina2006.org (accessed on 30 November 2024).




| MLFMM-MoM | MLFMM-CBFM | ACA-CBFM | |
|---|---|---|---|
| Pre-processing CPU time | 13 s | 72 s | 59 s |
| Solution CPU time | 180 s | 20 s | 18 s |
| Total CPU time | 193 s | 92 s | 77 s |
| Memory requirements | 584 Mb | 123 Mb | 109 Mb |
| MLFMM-MoM | MLFMM-CBFM | ACA-CBFM | |
|---|---|---|---|
| Number of unknowns | 80,961 | 18,634 | 18,634 |
| Pre-processing CPU time | 89 s | 257 s | 197 s |
| Solution CPU time | 562 s | 245 s | 211 s |
| Total CPU time | 651 s | 502 s | 408 s |
| Memory requirements | 1196 MB | 935 MB | 654 MB |
| MLFMM-MoM | MLFMM-CBFM | ACA-CBFM | |
|---|---|---|---|
| Pre-processing CPU time | 6139 s | 10,359 s | 8632 s |
| Solution CPU time | 19,802 s | 7184 s | 5043 s |
| Total CPU time | 25,939 s | 17,543 s | 13,675 |
| Memory requirements | 18.874 GB | 13.604 GB | 8.731 GB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, E.; Delgado, C.; Cátedra, F. An Efficient Dual Application of the Adaptive Cross Approximation for Scattering and Radiation Problems. Electronics 2024, 13, 4890. https://doi.org/10.3390/electronics13244890
García E, Delgado C, Cátedra F. An Efficient Dual Application of the Adaptive Cross Approximation for Scattering and Radiation Problems. Electronics. 2024; 13(24):4890. https://doi.org/10.3390/electronics13244890
Chicago/Turabian StyleGarcía, Eliseo, Carlos Delgado, and Felipe Cátedra. 2024. "An Efficient Dual Application of the Adaptive Cross Approximation for Scattering and Radiation Problems" Electronics 13, no. 24: 4890. https://doi.org/10.3390/electronics13244890
APA StyleGarcía, E., Delgado, C., & Cátedra, F. (2024). An Efficient Dual Application of the Adaptive Cross Approximation for Scattering and Radiation Problems. Electronics, 13(24), 4890. https://doi.org/10.3390/electronics13244890







