CoCENet: Collaborative Channel Estimation Network for Rapidly Time-Varying UAV Systems

Abstract

Wireless communication capability is vital for remote transmission between unmanned aerial vehicle (UAV) coordination systems, but the communication link between highly dynamic UAV systems is unstable and severely disturbed due to its rapidly time-varying channel. Current channel estimation methods suffer from insufficient inter-symbol interference (ISI) and inter-carrier interference (ICI) suppression and inadequate noise filtering. Therefore, a collaborative channel estimation network (CoCENet) is proposed in this paper, and it can restrain the channel interference by capturing the amplitude–phase and time–frequency correlation at the same time. Moreover, CoCENet applies a multi-scale fusion strategy to optimize the purity of the estimated outcome. Our experiment results demonstrate that CoCENet has preferable performance in terms of the suppression of channel interference and noise in rapidly time-varying UAV systems in a complex environment without stationarity assumption. At a signal-to-noise ratio (SNR) of −10 dB, the mean square error (MSE) of CoCENet is improved by 1.7–2.3 dB compared to existing methods, and at a SNR of 20 dB, the MSE is improved by 1.1–2.2 dB.

1. Introduction

Unmanned aerial vehicle (UAV) systems play an important role in fields requiring lightweight, flexible, and intelligent features, such as logistics transportation [1,2], remote detection [3,4], communication relay [5,6], and military strikes [7]. Figure 1 shows a typical UAV application scenario. Currently, the typically used high-mobility UAV networking modes include ground–air command and air–air ad-hoc [8,9]. In UAV systems, various nodes can be flexibly linked together through terminals, significantly enhancing the operational efficiency of each sector. However, the long-distance communication and high-speed mobile connection between terminals pose challenges to the performance of the communication system. For UAV collaboration systems in complex environments, whether behavior control or image transmission, efficient and reliable information exchange between terminals is a crucial foundation for achieving synchronization. Ensuring the normal operation of the wireless communication system is vital to maintaining the functionality of UAV systems.

However, frequent relative movements and powerful noise interference are present in highly dynamic UAV networks [10], resulting in a fast-fading channel and high-disturbance link, which severely distort receiving signals [11] significantly effect communication performance. It is a challenge to determine how to effectively suppress the negative impacts on channel in rapidly time-varying UAV systems, thereby ensuring the coordination between terminals and UAV networking capability.

Channel estimation enhances anti-fading abilities by obtaining channel state information (CSI) from pilots [12] and is therefore widely used in UAV systems [13]. However, in traditional channel estimation algorithms, the least squares (LS) method is sensitive to noise and has significant error at a low signal-to-noise ratio (SNR) [14]. The minimum mean square error (MMSE) method is complex and time-consuming for calculating auto-correlation matrices [15]. The linear minimum mean square error (LMMSE) requires prior knowledge which is difficult to capture [16,17], thus having notable influence on the system effectiveness. Further, traditional algorithms’ assumption of a channel stationarity cannot be applied to rapidly time-varying channels.

In recent studies, the non-linear fitting ability of deep learning (DL) has shown promising application prospects in data prediction and estimation [18,19,20]. DL-based channel estimation methods construct cascaded mapping layers to fit the fast-fading channels, achieving end-to-end estimation [21,22,23,24]. These methods mainly include three domains. The first domain involves equalizing signal distortion. Mehran Soltani et al. pointed out that the filling data estimated from pilots contains deviation caused by algorithm limitations [25]; therefore, an equalizer can improve channel estimation performance. Rugui Yao et al. used a channel parameter-based (CPB) algorithm to transfer Doppler characteristics into a basis vector and proposed FC-DNN for basis matrix estimation [26], which can weaken the specific effects of relative movements and reduce the influence of ICI in results. Yi Sun et al. proposed ICInet to evade the limitations of stationarity by establishing a pre-extract module directly focusing on the Doppler mapping matrix [27], and this significantly intensified the equalization. Lyu Siting et al. proposed HNN to capture the inherent characteristics of the received data and the channel [28]. Sanggeun Lee et al. proposed a DL-based channel estimation method to refine the CSI of spatially correlated channels [29]. The second domain involves suppressing noise interference. Liu et al. believed that irregular and high-frequency amplitude changes have a negative impact on channel estimation accuracy [30]. Inspired by DnCnn, Li et al. proposed a cascaded model named ReEsNet with transpose convolution to denoise pilots [31], and ReEsNet can ensure that the pilots are precise enough to provide guidance on up-sampling. Yong Liao et al. focused on the temporal continuity of channel fading amplitude and used conditional recurrent unit (CRU) to capture data correlation [32], improving the utilization of vital features and avoiding high-frequency noise in communication links. Qi Peng et al. designed CRCENet to combat the influence of noise on the attention mechanism [33]. Muhammad Umer Zia et al. proposed a DL-based TDD, FDD, and a parametric channel model to avoid pilot contamination [34]. The third domain involves optimizing the learning strategy. Kai Mei et al., regarding the diversity in different scenarios, adopt online training to fine-tune the weight parameters during the estimation process [35], so their model can achieve better fitting in practical applications. Mao et al. pointed out that effective label-determined samples are few, so they proposed meta-learning-based RoemNet [36], further enhancing the model adapting capability in the actual communication environment.

However, signal distortion equalization typically analyzes the Doppler shift specifically, without considering that high-mobility UAV systems are also affected by dynamic multi-path, neglecting the interference caused by adjacent symbols. Additionally, the model used for noise suppression has a relatively fixed receptive field which does not perform collaborative features on multiple modals and lacks the ability to capture noise influence at different L2 distances. Learning strategy optimization requires high computational load, and the hardware resources occupied for fine-tuning are not conducive to the miniaturization of the UAVs.

Motivated by these examples, we proposed a collaborative channel estimate network (CoCENet) for rapidly time-varying UAV systems, which consists of a complex-valued reconstructor (CVR) to restrain the channel interference simultaneously and a multi-scale filter (MSF) to further purify the estimation results. Our main contributions are summarized as follows:

• We proposed CVR in CoCENet which captures collaborative features between time, frequency, amplitude, and phase with 2D complex-valued convolution to enhance the utilization of relevant features in initial estimation and match the characteristics of rapidly time-varying UAV systems.
• We proposed MSF in CoCENet to restrain the noise influence by providing multiple receptive fields with a learnable fusion strategy. By effectively restraining the noise effect in CSI, the estimation results can be better fit to the actual channels.

The rest of this paper is organized as follows: Section 2 elaborates the background of our system model and explains the existing problems. Section 3 describes the structure and process of CoCENet as well as the modules included. In Section 4, we present and analyze the comparison experiment results. Finally, Section 5 concludes our work in this paper.

2. System Model and Problem Statement

Communication between UAVs requires the ability to receive and transmit information in complex environments, so OFDM has become a widely used technical in UAV coordination systems due to its high spectral efficiency, strong anti-fading capability, and simple hardware implementation [37]. Therefore, in this article, we describe our system model with OFDM. The digital communication process of an OFDM frame with N subcarriers and T symbols in discrete form can be represented by Formula (1)

$$Y_{\left(n,t\right)}=H_{\left(n,t\right)}{X}_{\left(n,t\right)}+W_{\left(n,t\right)}$$

(1)

where $\left(n,t\right)$ is the index of current data in the OFDM frame, in other words, the t-th symbol at the n-th subcarrier, $n\in \left[0,N-1\right]$, $t\in \left[0,T-1\right]$. X represents the transmitted signal after the pilot inserted, Y represents the received signal, W represents the Gaussian white noise obeying $N\left(0,{\sigma }^2\right)$, and $H_{\left(n,t\right)}$ represents the frequency amplitude response of $X_{\left(n,t\right)}$ in the current data frame.

The overall process of channel estimation can be broken down into two stages—interval reconstruction and filtering optimization—as shown in Figure 2. $P_t$ and $P_{t+1}$ represent the pilot at t and $t+1$ time slot. The interval reconstruction obtains a complete approximation matrix based on the pilots, with the goal of expanding data size to construct an identity mapping for feature analysis [38]. Then the filtering optimization filters a noisy CSI to obtain a pure estimated CSI. The effect of rapidly time-varying UAV systems is mainly manifested in the channel changing over time [39], so, in this paper, we choose a comb pattern as the pilot insert strategy. After obtaining the record of pilot positions, it is necessary to calculate a complete CSI through rough estimation, which is generally represented in the form of a channel frequency response (CFR) matrix. The UAV should be adopted with a rough estimation method that does not require prior knowledge. The LS is simple enough to implement and fast to operate [40], so it is proper to use the LS for interpolation estimation. The process of LS calculating the CFR is shown in Formula (2)

$${\widehat{H}}_p^{LS}=Y_p{X}_p^{-1}$$

(2)

where p represents the data on pilot locations, and ${\widehat{H}}_p^{LS}$ represents the fading amplitude obtained by LS from received pilots. In fact, the SNR is often low in typical UAV scenarios. If $MS{E}_p$ represents the mean square error between the true CFR $H_p$ and the LS estimation result ${\widehat{H}}_p^{LS}$, then there is a relationship as shown in Formula (3)

$${MSE}_p=E\left[{∥{\widehat{H}}_p^{LS}-H_p∥}^2\right]={\displaystyle \frac{{\sigma }_W^2}{{\sigma }_X^2}}$$

(3)

where ${\sigma }_W^2$ represents the variance of noise, and ${\sigma }_X^2$ represents the signal’s variation. It can be seen that there is an inverse relationship with the SNR; that is, the greater the noise, the more significant the deviation of LS results. Therefore, LS is fragile and sensitive, so to obtain more accurate CFR, it is necessary to further deal with LS results.

Formula (1) shows the process through which the signal is affected by the channel during transmission, when the UAV moves relatively frequently and the electromagnetic environment is complex. Therefore, in non-stationary and rapidly time-varying UAV systems, the coherent bandwidth is occasionally less than the critical threshold. In addition, the low signal rate may cause UAV-facing follower jamming. Those above will produce dynamic multi-path effects on OFDM systems, so, except for adjacent subcarriers, the symbols nearby will have a certain degree of information correlation with each other. In short, part of the amplitude attenuation of the signal comes from both the adjacent time slot and the frequency point. Considering the influence of ISI and ICI, the received signal can be shown in Formula (4):

$$H_{\left(n,t\right)}{X}_{\left(n,t\right)}=\sum _{I_n=0}^{N-1}\sum _{I_t=0}^{T-1}{H}_{\left(n,t\right)}^{\left(I_n,I_t\right)}{X}_{\left(I_n,I_t\right)}$$

(4)

where $H_{\left(n,t\right)}$ represents the combined effect of the signals from various locations on the current location, where $I_n$ and $I_t$ represent the subcarriers and symbol indices that are generating interference and $H_{\left(n,t\right)}^{\left(I_n,I_t\right)}$ is the frequency-amplitude response of $X_{\left(I_n,I_t\right)}$ at $\left(n,t\right)$. Moreover, when the signals undergo the influence from multi-paths and Doppler, its time-domain form can be shown in Formula (5):

$$h\left(\tau ,t\right)=\sum _{n=0}^{N\left(t\right)}{\alpha }_n\left(t\right)e^{-j{\varphi }_n\left(t\right)}\delta \left(\tau -{\tau }_n\left(t\right)\right)$$

(5)

where N represents the number of multi-paths, ${\alpha }_n$ denotes the fading of each path, ${\varphi }_n$ stands for phase deviation, and ${\tau }_n$ indicates the multi-path delay. Formula (5) demonstrates the impact of Doppler shift and multi-path superposition reflected in amplitude and phase. Current DL-based channel estimation methods solely consider the subcarrier direction and separately process the real and imaginary parts of signal while neglecting the collaborative information between time and frequency and between amplitude and phase. Therefore, during the interval reconstruction process, besides considering adjacent subcarriers, simultaneously taking adjacent symbols along the time direction into account can positively advance accurate prediction. Retaining the capability of signal processing from both the real and imaginary parts enables effective extraction of their collaborative information, which plays a crucial role in enhancing feature utilization and improving estimation performance.

Filtering optimization is a stage of noise suppression for reconstruction results. The prior knowledge that traditional algorithms need, such as the auto-correlation matrix, is difficult to obtain. The existing DL-based channel estimation methods present the problem of a fixed and limited receptive field. However, the channel parameter momentum in UAV systems is not a step but a continuous change. For data with strong correlation, the larger receptive field can capture the overall dynamic trend, focusing on the analysis of background information, while the smaller field can obtain the local details of noise and signal, focusing on the analysis of foreground information. The combination of the fields can achieve feature extraction from coarse to fine, further improving the filtering optimization performance.

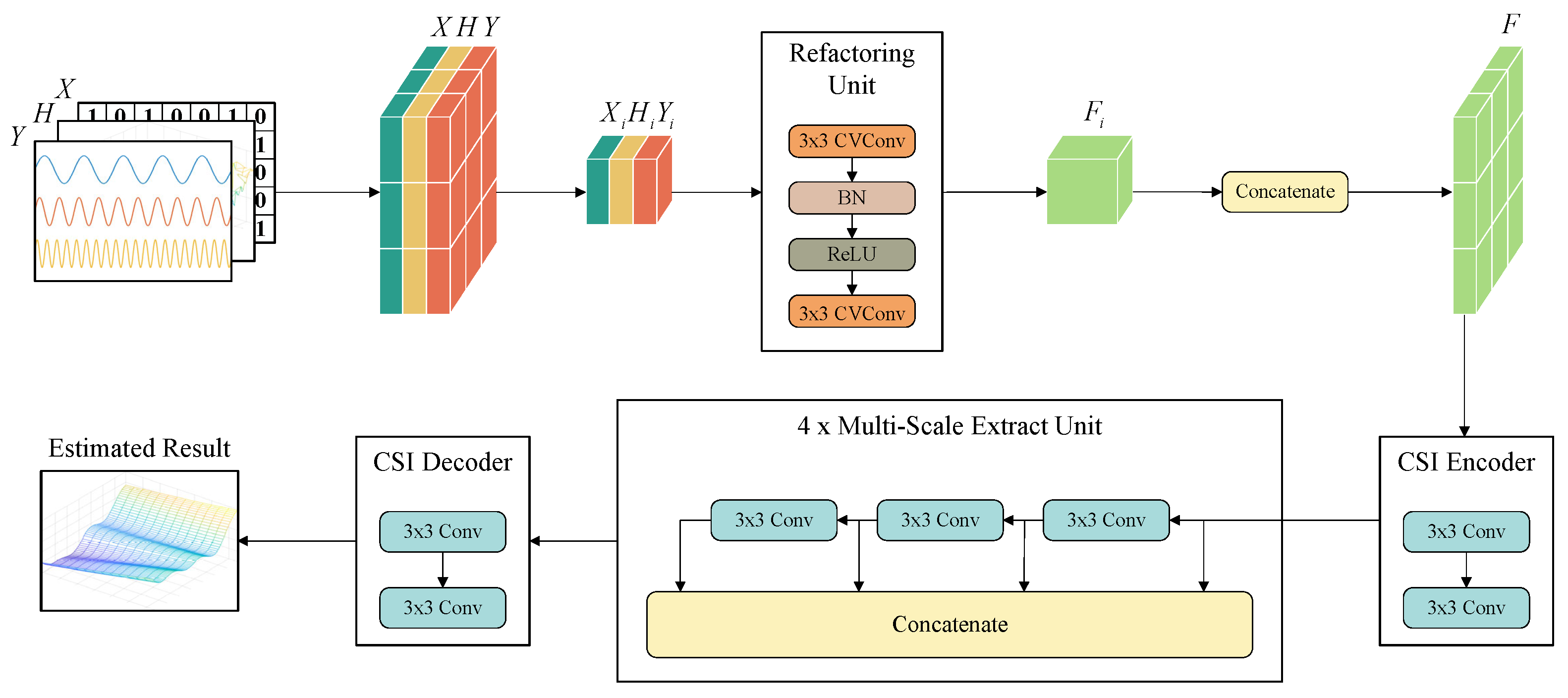
3. Structure of Collaborative Channel Estimation Network

In view of the limitations discussed in Section 2, in this paper, we propose CoCENet to collaboratively analyze a variety of related features. The CVR and MSF are constructed according to the interval reconstruction and filter optimization stage. The overall network structure is shown in Figure 3. Y, H, and X are the multi-modal input, F is the feature extracted, and i stands for the index of each element. The output of the CoCENet is the estimated result, with warm colors representing high gain parts and cool colors representing low gain parts. In this section, we will specifically explain the preprocessing and structure of CVR and MSF in CoCENet, respectively.

3.1. Preprocessing Stage

Signals with different modulation modes show different fading forms after passing through the channel. The achievements in blind estimation have proven that the signal characteristics can guide the fading trend, so the collected signals have effective information for channel estimation. The distortion at the receiving end is continuous and prone to estimation errors. However, the discrete characteristics of the decoded symbols at terminals help to correct and converge. Therefore, in the preprocessing stage, multi-modal data are concatenated as the input of CoCENet. In Figure 3, Y, H, and X represent the received signal, the complete CFR matrix obtained by LS, and the estimated transmission symbol sequence calculated by them, respectively.

It should be noted that there are no further adjacent elements in the edge, and unreasonable padding strategies like zero padding will break the continuity of the data. CoCENet’s sensitivity in terms of feature correlation may lead to sudden errors in the results. Therefore, we adopt a cyclic padding strategy, using the same principle as cyclic prefix (CP) and cyclic suffix (CS), for each OFDM frame, copying the data with a length of $N_t$ from the head of each dimension to the tail and the same length from the tail to the head. This padding strategy preserves the convolutional cyclicity of the signal, reduces the generation of edge effects in forward process, and avoids error propagation.

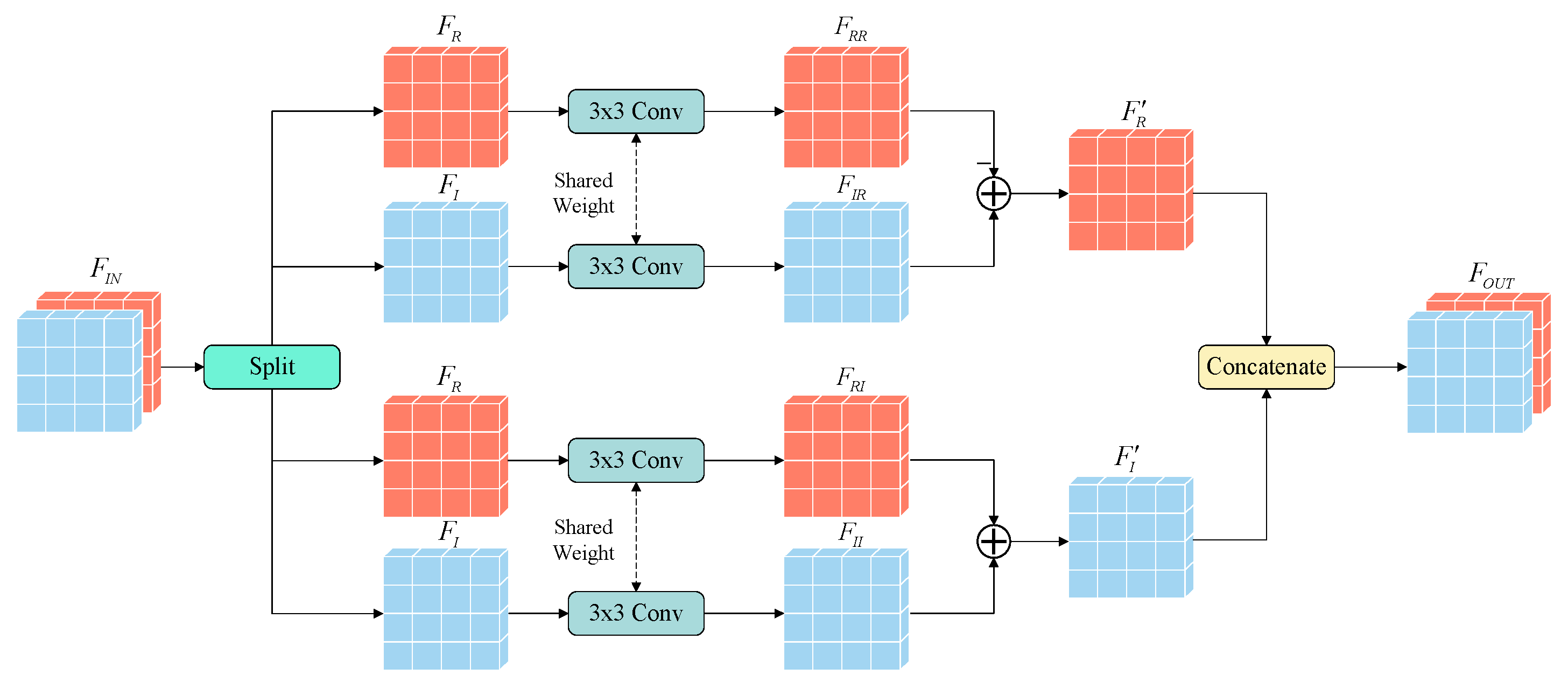
3.2. Complex-Valued Reconstructor

The key to solving the problems of insufficient ISI analysis capability and incomplete interval reconstruction is to improve the utilization of collaborative information carried by signals. Compared to ICI, the impact of ISI is mainly reflected in the time vector. When CFR is regarded as a 2D matrix and the input of the neural network, time–frequency correlation is also equivalent to spatial correlation. Inspired by Huang et al. [41], this article takes all elements of each feature as the center one by one and establishes a total of $N\times T$ hyper-estimation blocks $B\in {\mathbb{C}}^{\left(2\times N_I+1\right)\times \left(2\times N_I+1\right)}$ along each direction by including its nearby $N_I$ elements. Each hyper-estimation block is sent to a refactoring unit (RU). Using hyper-estimation blocks as the basic unit can expand the learning ability of local features, improve feature utilization, and reduce convergence difficulty under low parameter growth. Each RU consists of two complex-valued convolutional layers. The complex-valued structure is shown in Figure 4.

$F_{IN}$ and $F_{OUT}$ represent the input and output features of complex-valued convolution, respectively. $F_R$ and $F_I$ represent the real and imaginary portions of input data. The real portion $F_R$ of the input feature $F_{IN}$ undergoes a normal $3\times 3$ convolution to obtain $F_{RR}$, which means real portion to real portion as the intermediate feature, while the imaginary portion $F_I$ also undergoes a normal $3\times 3$ convolution to obtain $F_{IR}$, which means imaginary portion to real portion. These two convolutional layers share weights in order to achieve a common mapping. Subtracting $F_{RR}$ from $F_{IR}$ yields the real portion ${F^{\prime }}_R$ of the output feature $F_{OUT}$. Similarly, $F_{RI}$ and $F_{II}$ are obtained from $F_R$ and $F_I$ with same method, and the two convolution layers also share weights. The difference is that, as part of the imaginary multiplication, $F_{RI}$ and $F_{II}$ perform addition to obtain the imaginary portion ${F^{\prime }}_I$ of the output. ${F^{\prime }}_R$ and ${F^{\prime }}_I$ are concatenated along the channel dimension to jointly form the output of the complex-valued convolution. The complex-valued convolutions enable the information extracted from the amplitude and phase portions to mixing sufficiently, which can be represented by Formula (6):

$$Comp\left(f\right)=\left[{conv}_r\left(f_r\right)-{conv}_i\left(f_i\right)\right]+i\left[{conv}_r\left(f_i\right)+{conv}_i\left(f_r\right)\right]$$

(6)

$Comp\left(·\right)$ represents complex convolution; ${conv}_r\left(·\right)$ and ${conv}_i\left(·\right)$ represent two independent ordinary convolutions, where f represents the feature matrix to be processed; and $f_r$ and $f_i$ are the real and imaginary parts extracted from it, respectively. Unlike real-valued convolution, complex-valued convolution exchanges collaborative information between the real and imaginary portions of the data, establishing a connection between the amplitude and phase offsets of the signal, preserving the characteristics of the signal itself, and helping to improve the ability to suppress interference from a new perspective.

The process of each RU can be represented by Formula (7):

$$F_{(n,t)}=\sum {Comp}_2\left(\partial \left({Comp}_1\left(B_{\left(n,t\right)}\right)\right)\right)$$

(7)

Two $Comp\left(·\right)$ represent two complex-valued convolutional layers, $\sum \left(·\right)$ represents the sum of all elements in the matrix, and $\partial \left(·\right)$ is the activation function and BN layer.

The overall process of CVR is described in Algorithm 1. The input hyper-estimation blocks are sent into RU one by one. After the complex-valued process, the output can be regarded as a correction factor. By performing the Hadamard product on input features, LS results $H_{\left(i,j\right)}$ with the $F_{\left(i,j\right)}$, and the deviation caused by LS can be adjusted. For all $N\times T$ hyper-estimation blocks contained in the input, the result will also generate $N\times T$ fading amplitude data. All of them will be reorganized into a complete CFR matrix based on their source indices, which will be used as the input of the MSF for further optimization.  

Algorithm 1: The process of the complex-valued reconstructor

Input:  B: the hyper-estimate blocks set; H: the LS estimation result; $N_s$: the number of symbols; $N_c$: the number of sub-carriers; f: the first complex-valued convolution layer; g: the second complex-valued convolution layer; $\sigma$: the activation function ReLU and batch normalization;  Output:  F: reconstructed channel;    1: Random initialize f and g;    2: for i in $\left[1,\dots ,N_s\right]$ do    3:     for j in $\left[1,\dots ,N_c\right]$ do    4:         Convert $B_{\left(i,j\right)}$ into real part $F_R$ and imaginary part $F_I$;    5:         $F_{OUT}\leftarrow \sigma \left(f_j\left(F_R,F_I\right)\right)$;    6:         Convert $F_{OUT}$ into real part $F_R$ and imaginary part $F_I$;    7:         $F_{OUT}\leftarrow g_j\left(F_R,F_I\right)$;    8:         $F_{\left(i,j\right)}\leftarrow \sum F_{OUT}$;    9:         $F_{\left(i,j\right)}\leftarrow H_{\left(i,j\right)}\odot F_{\left(i,j\right)}$;   10:     end for   11: end for   12: Concatenate $\left\{F_{\left(1,1\right)},\dots ,F_{\left(N_c,N_s\right)}\right\}$ into $F\in {\mathbb{C}}^{N_c\times N_s}$;   13: Return F;

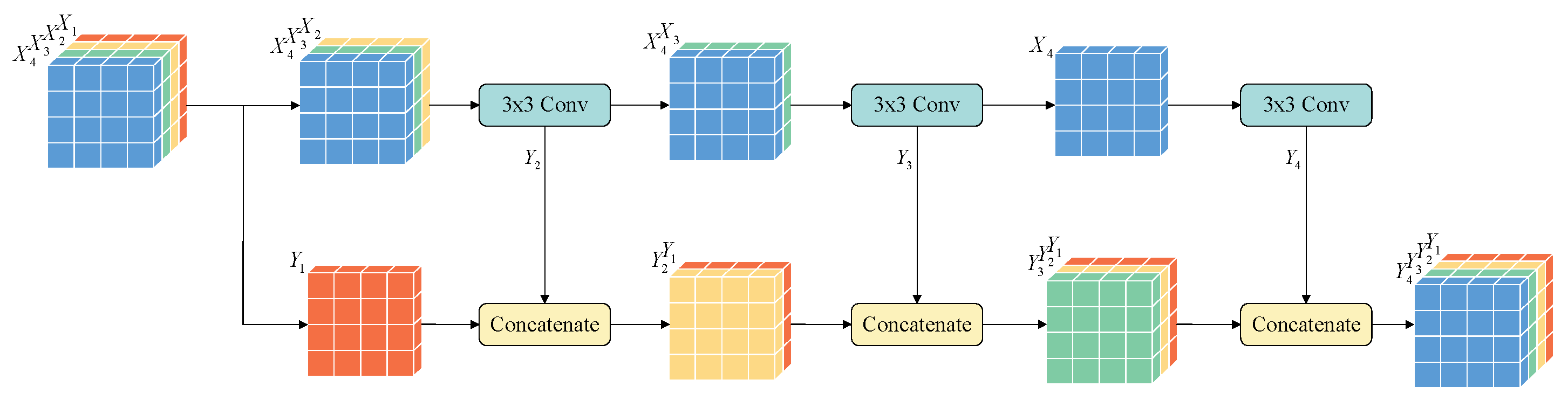
3.3. Multi-Scale Filter

In addition to suppressed ISI and ICI, the communication environment of UAVs also includes intense interference of complex types, so the reconstructed CFR from CVR requires further filtering. Our use of a residual structure as the backbone network in MSF in the filtering optimization stage in CoCENet is mainly due to the following two advantages: First, by establishing an identity mapping from the noisy matrix to the noiseless one, the model can ignore the similar information contained in both and focus on eliminating high-frequency interference terms, thereby improving learning efficiency. Second, the residual structure can solve the problem of gradient vanishing and reduce the difficulty of convergence.

In Section 2, we mentioned the idea of feature fusion by combining multiple receptive fields. Considering that the incidence levels with different L2 distances are unequal, the weight of various features obtained from different receptive fields should also be judged. Therefore, we use the learnable multi-scale feature fusion strategy proposed by Gao et al. [42] to establish MSF. The outputs from different branches are non-linearly fused, and the generated filter matrix will be used to suppress the noise of the estimated CFR. MSF attains multiple receptive field branches by combining convolutions of different layers, and the high-frequency noise components and low-frequency data components can both be extracted from coarse to fine. The MSF contains four cascaded multi-scale extract units (MSEU). The structure of each MSEU is shown in Figure 5. $X_1$, $X_2$, $X_3$, and $X_4$ represent the four groups split from input features, and $Y_1$, $Y_2$, $Y_3$, and $Y_4$ represent the outcome of each group.

The overall process of MSF is shown in Algorithm 2. The input will be split into a real part and an imaginary part and will then be encoded by the CSI encoder before being sent into the MSEU. After multi-scale processing, both global and local information can be captured, and the collaborative information from different receptive fields can be forcibly fused during the segmentation and concatenation. The output of MSEU is regarded as a filter matrix, and the noise will be effectively suppressed by adding it to the fulfilled CFR. Finally, the output feature will be considered the final estimation result.  

Algorithm 2: The multi-scale filter process

Input:  F: the reconstructed channel; f: the CSI encoder; g: the MSEU; h: the CSI decoder; $N_l$: the number of MSEU; $N_b$: the number of patches in MSEU;  Output:  $\tilde{H}$: estimated channel;    1: Random initialize f, g and h;    2: $X\leftarrow f\left(F\right)$;    3: fori in $\left[1,\dots ,N_l\right]$ do    4:     Split X into $N_b$ non-overlap batches $\left\{X_1,\dots ,X_{N_b}\right\}$    5:     $Y_1\leftarrow X_1$;    6:     for j in $\left[2,\dots N_b\right]$ do    7:         $Y_{N_b}\leftarrow g_{N_b-1}\left(Y_{N_b-1}+X_{N_b}\right)$;    8:     end for    9:     Concatenate $\left\{Y_1,\dots ,Y_{Nb}\right\}$ as X;   10: end for   11: $\tilde{H}\leftarrow h\left(X\right)+F$;   12: Return $\tilde{H}$;

4. Experiments Results

In this article, we simulated a rapidly time-varying UAV system communication environment based on SISO-OFDM with a Rayleigh and Rician channel to better match the real situation in dynamic scenes. Based on that, a channel dataset with a total of 40,000 samples was created, which was divided into a training set, testing set, and validation set in a ratio of 7:2:1. The initial learning rate of the model was set to 0.001 and was reduced by 0.1 times each time the epochs of training reached 20 for a total of 200 epochs. The basic parameters of the dataset are given in

Table 1. Dataset channel parameters.

Attribute	Parameters
Channel model	Rayleigh, Rician
Number of subcarriers	128
FFT points	128
Modulation mode	QPSK
Length of CP	32
Noise model	Gaussian
Carrier frequency	2.1 GHz
Maximum paths	3, 7, 12
Maximum relative speed	30, 70, 120 km/h
Maximum bandwidth	1.6 MHz
Number of symbols	14

below:

In subsequent experiments, we will use MSE, BER, and PSNR as our metrics for evaluating the channel estimation capability of each model. MSE represents the difference between the estimated channel and the actual channel. BER indicates the state of error decoding after channel estimation in an actual UAV communication system. PSNR reflects the extent to which irrelevant variables, such as noise, are suppressed in the channel estimation results.

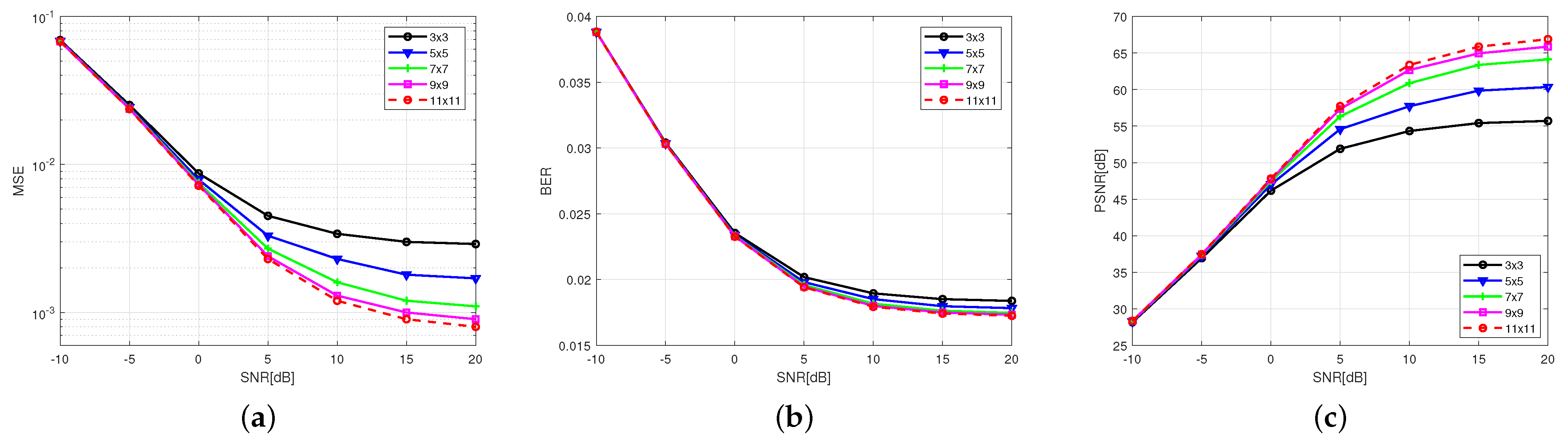
4.1. Hyper-Estimation Block Evaluation

To verify the viewpoint that the simultaneous suppression of ISI and ICI has a positive effect on channel estimate performance and select a reasonable size of the hyper-estimated block, we conducted a size comparison experiment. Too large of a hyper-estimation block will increase the convergence difficulty of the model, and one that is too small will lead to incomplete feature acquisition. Therefore, we adopted different sizes of hyper-estimation block $N_S\in \left[3\times 3,5\times 5,7\times 7,9\times 9,11\times 11\right]$, under the same experimental configuration. The experimental results are shown in Figure 6.

Our experimental results show that as the size of the hyper-estimation block increases, the MSE and BER of channel estimation decrease, and the PSNR increases accordingly. Specifically, when the hyper-estimation block is smaller than $7\times 7$, MSE and BER significantly decrease, and PSNR increases with increasing the hyper-estimation block size. This indicates that there is a correlation between adjacent subcarriers and symbols and the central element and that the more collaborative information included in the calculation within an appropriate range, the better and more significant the performance improvement of the model. This proves that the collaborative strategy adopted in CoCENet in this article is effective, and the application of CVR in order to endow the model with a two-dimensional feature utilization capability has a positive effect on reducing ISI and ICI and improving channel estimation performance.

However, when the size of the hyper-estimation block is greater than $7\times 7$, the performance improvement weakens, and the computational complexity increases exponentially. The floating-point operations per second (FLOPs) of each parameter are shown in

Table 2. FLOPs with different sizes of hyper-estimation blocks.

Size of Hyper-Estimation Block	FLOPs
$3\times 3$	332.90 M
$5\times 5$	345.55 M
$7\times 7$	359.51 M
$9\times 9$	380.80 M
$11\times 11$	407.41 M

. To balance model performance and computational load, all subsequent experiments conducted in this paper adopt a hyper-estimate size of $7\times 7$.

4.2. Performance Evaluation

To demonstrate the ability of CoCENet to improve feature utilization and channel estimation performance by extracting collaborative features, this paper conducted comparative experiments on model performance under different signal-to-noise ratios using the same dataset. An LS algorithm was selected in the traditional algorithm field, and the ChannelNet, ReEsNet, InvoNet, and CVR + ReEsNet methods were selected in the deep learning field. The result are shown in Figure 7:

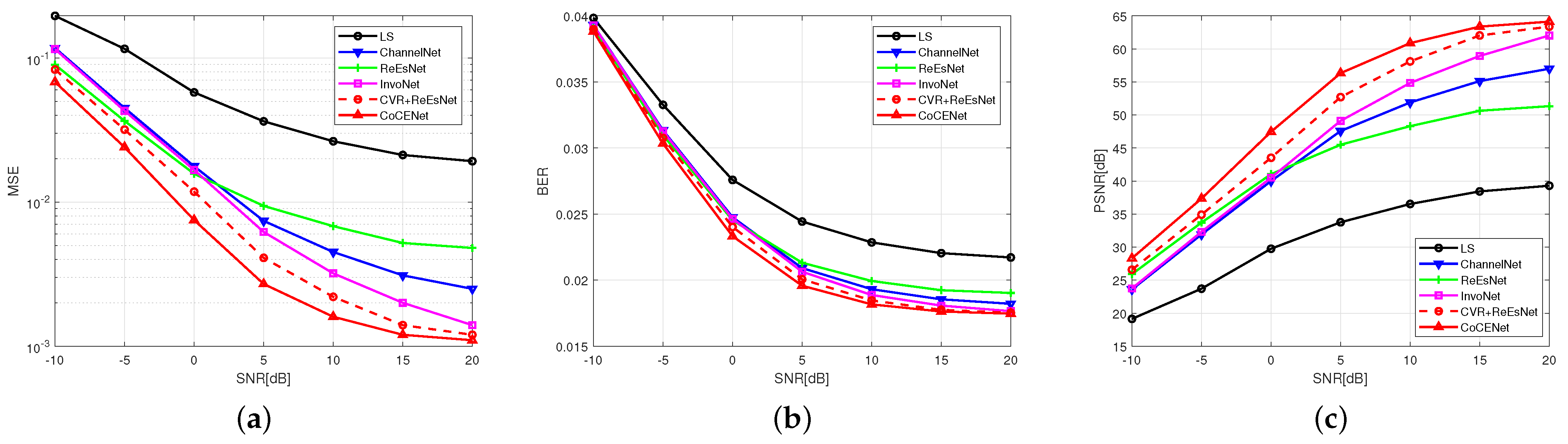
Our experimental results demonstrate that DL-based channel estimation methods exhibit superior performance compared to traditional algorithms in rapidly time-varying channels. Particularly when the SNR is over 0 dB, CoCENet has better convergence bounds. Specifically, CoCENet achieves an MSE improvement of 4.6 dB compared to the LS algorithm at an SNR of −10 dB and of 12.4 dB at an SNR of 20 dB when the number of multi-paths is 3 and the relative speed is 30 km/h. These experimental results confirm that CoCENet’s nonlinear fitting characteristics are able to eliminate the need for the assumption of stationarity and are more applicable to UAV communication systems compared to traditional algorithms.

Compared with other models without a multi-scale fusion strategy, such as InvoNet, our experiment results show that the MSF in CoCENet has a more accurate estimation performance at a low SNR condition of −10–0 dB and also lower convergence bounds when SNR is over 0 dB. This proves that the flexible receptive field and learnable fusion strategy in the filtering optimization stage help to filter out the influence of high-frequency independent parameters. The idea that simultaneously maintaining the global and local information perception capability of CoCENet can optimize the filtering at low SNR has been verified. CoCENet can provide a guarantee for UAV coordination systems in environments with severe electromagnetic interference.

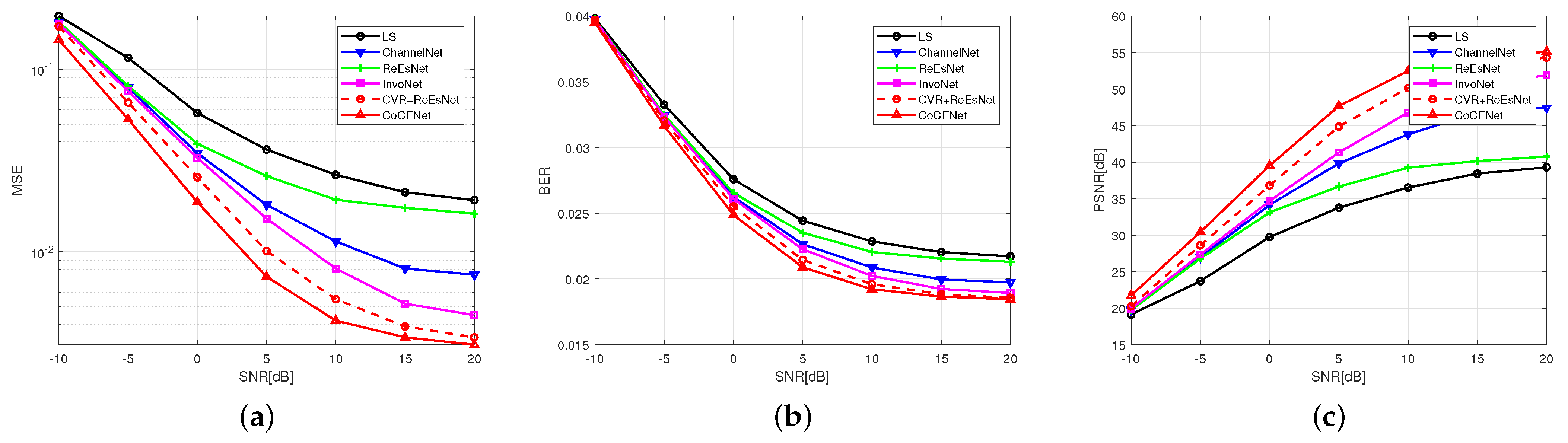
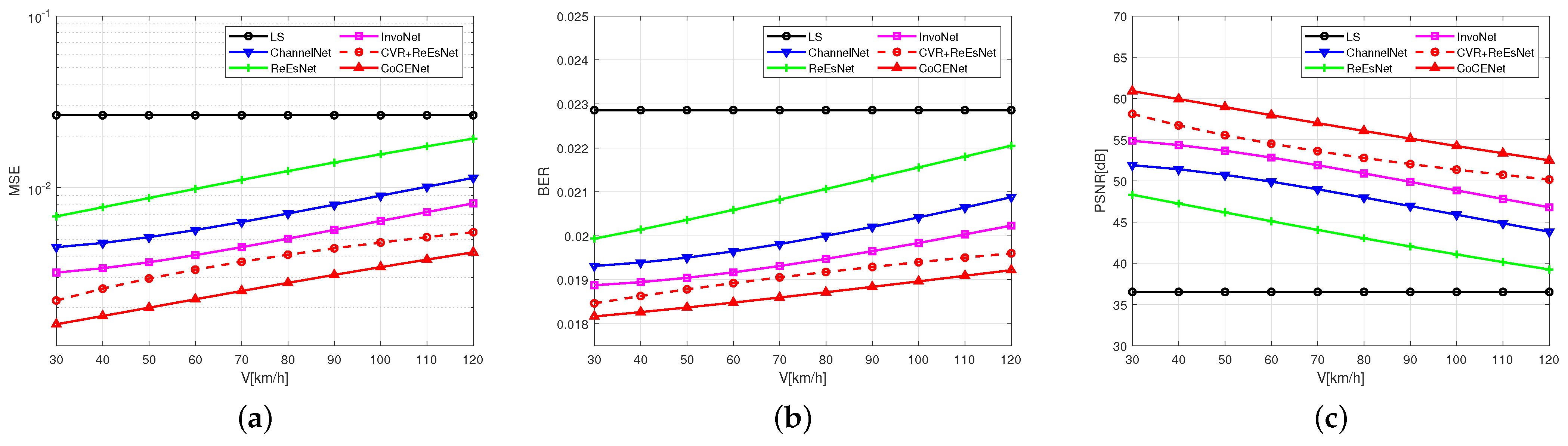
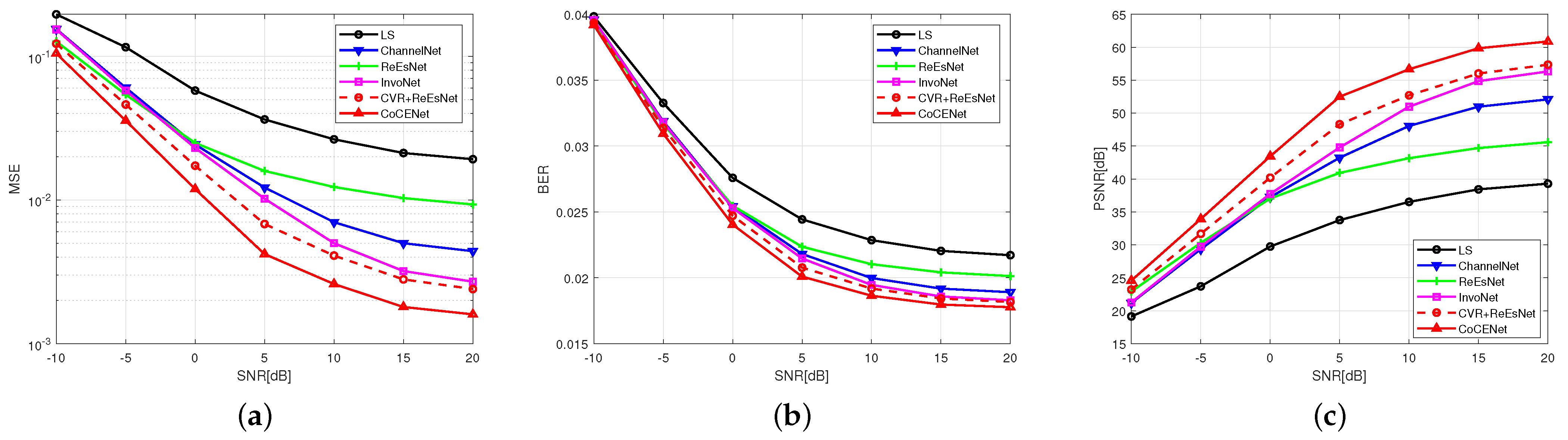
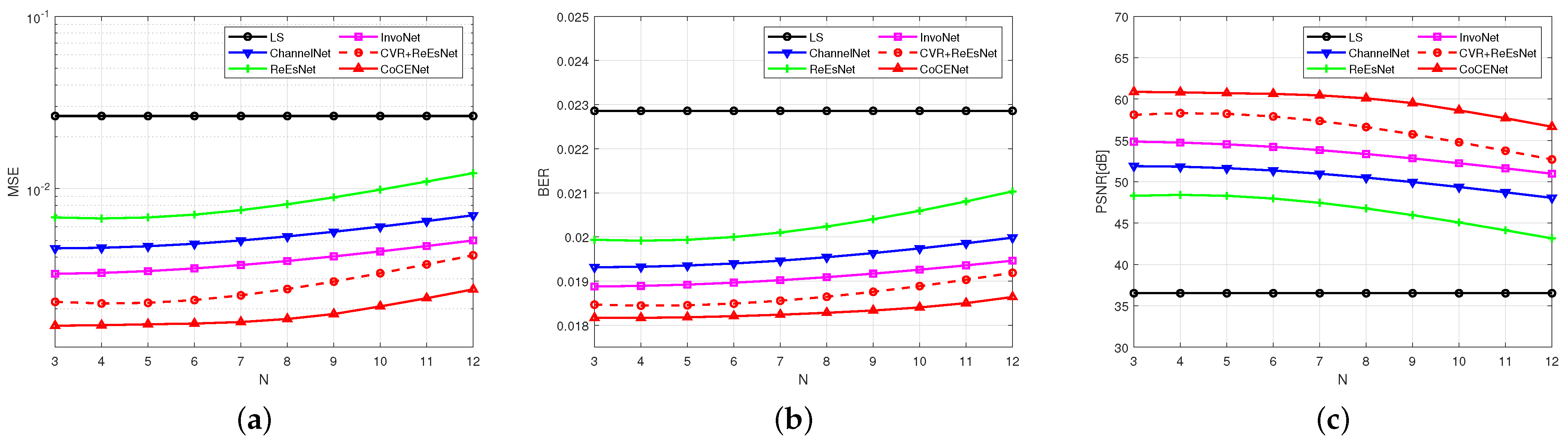
In fact, the rapidly time-varying UAV system is not only reflected in the distortion caused by noise interference but also in the interference caused by the change of channel parameters. To verify the application significance of CoCENet in actual scenarios, Figure 8 and Figure 9 show the performance of CoCENet and comparison models at other maximum relative speeds, represented by V. Figure 10 and Figure 11 show them at other maximum numbers of multi-paths, represented by N.

The above experiments analyzed the comparison of different maximum relative movement speeds. CVR + ReEsNet and ReEsNet have different functions in the interval reconstruction stage, so they have different abilities to suppress ICI. The experimental results show that especially at a high SNR condition of 0–20 dB, CVR + ReEsNet has better performance than ReEsNet, demonstrating that CVR is helpful in fitting channel response. This proves that the 2D complex-valued convolution and the hyper-estimation block method have positive effects in capturing channel characteristics. With the increase of relative speed and number of multi-paths, CoCENet incurs a significant improvement compared to ReEsNet. This indicates that the collaborative features between time–frequency and between amplitude–phase have a positive effect on the suppression of ICI. It also proves that the CVR in CoCENet contributes to correcting the deviation of the internal reconstruction stage, which is helpful for improving the performance of channel estimation and resolving the interference distortion caused by UAV communication channels.

The above experiments analyze the comparison of different maximum multi-path numbers. With an increase in number of multi-paths, the ISI effect in UAV is more severe, which may be shown as the MSE ascending. CoCENet has better MSE, BER, and PSNR when facing complex channels, and the loss does not significantly increase with an increase in number of multi-paths, which proves that CoCENet can more effectively suppress ISI by analyzing amplitude–phase correlation in the time–frequency dimension. The collaborative features in time–frequency and amplitude–phase captured by CVR and MSF are conducive to countering the ISI in rapidly time-varying channels in UAV communication systems.

Our experiments demonstrate that CoCENet possesses the capability to enhance channel estimation by utilizing the hidden information between collaborative features. Through the extraction of time–frequency- and amplitude–phase-related features in CVR and the multi-scale-related features in MSF, the characteristics of the channel can be well fitted. CoCENet not only eliminates the need for prior knowledge and channel stationarity assumptions, but also exhibits strong capabilities in suppressing ISI, ICI, and noise under complex channel parameters and low SNRs. CoCENet can play a significant role in improving the accuracy of channel estimation in rapidly time-varying UAV systems.

5. Conclusions

In this paper, we proposed a DL-based channel estimation method—CoCENet—for rapidly time-varying UAV systems. By constructing the CVR with time–frequency and amplitude–phase analysis abilities and the MFS with a multi-scale fusion strategy, this model has preferable interval reconstruction and filtering optimization stages and achieves highly accurate channel estimation without negative impacts on the effectiveness of the UAV communication systems. Our experimental results indicate that, when the maximum relative speed is 30 km/h and the number of multi-paths is 5, compared to traditional algorithms, CoCENet achieves an MSE improvement of 4.6 dB at a SNR of −10 dB and of and 12.4 dB at a SNR of 20 dB. Furthermore, when the maximum relative speed increases to 120 km/h and the number of multi-paths increases to 12 at a SNR of 10 dB, the MSE of CoCENet improves by 7.9 dB and 10.8 dB, respectively. This demonstrates that CoCENet can achieve high-accuracy channel estimation without relying on the assumption of stationarity. Additional experiments reveal that, under time-varying channel parameter conditions, CoCENet outperforms existing algorithms by 1.7–2.2 dB in MSE at an SNR of −10 dB and by 1.1–2.3 dB at an SNR of 20 dB compared to other methods. It has been proven that CoCENet possesses the ability to correct channel interference, suppress noise impact, and enhance the performance of channel estimation in the model.

However, in the dataset used for model training, the presence of a certain number of pilots is necessary. During missions with a significant pilot shortage or blind estimation, performance loss is inevitable. Meanwhile, to ensure good model performance, the training cost is relatively high. Further exploration can be conducted in the future to balance the large training costs with the accuracy of the model.