An Innovative Nonlinear Bounded Component Analysis Algorithm Based on Multivariate Nonlinear Chirp Mode Decomposition
Abstract
1. Introduction
2. Materials and Methods
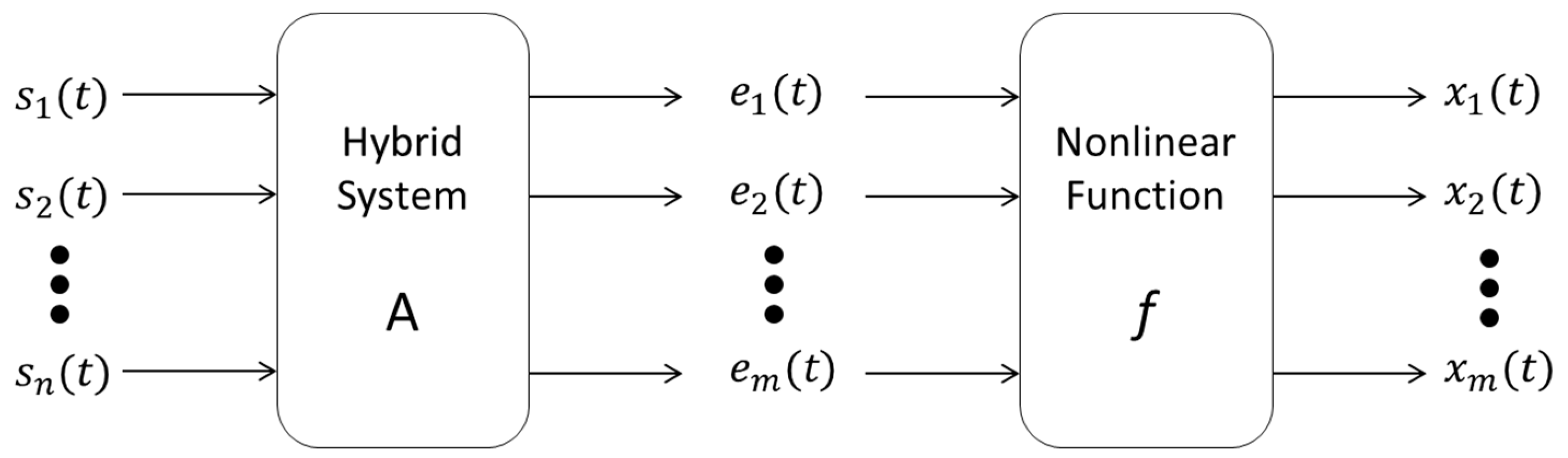
2.1. Underdetermined Nonlinear Mixed Model
2.2. Nonlinear Bounded Component Analysis (NLBCA)
| Algorithm 1 NLBCA |
Inputs: maximum number of iterations M, line progress length , initial matrix , iterations k = 0
|
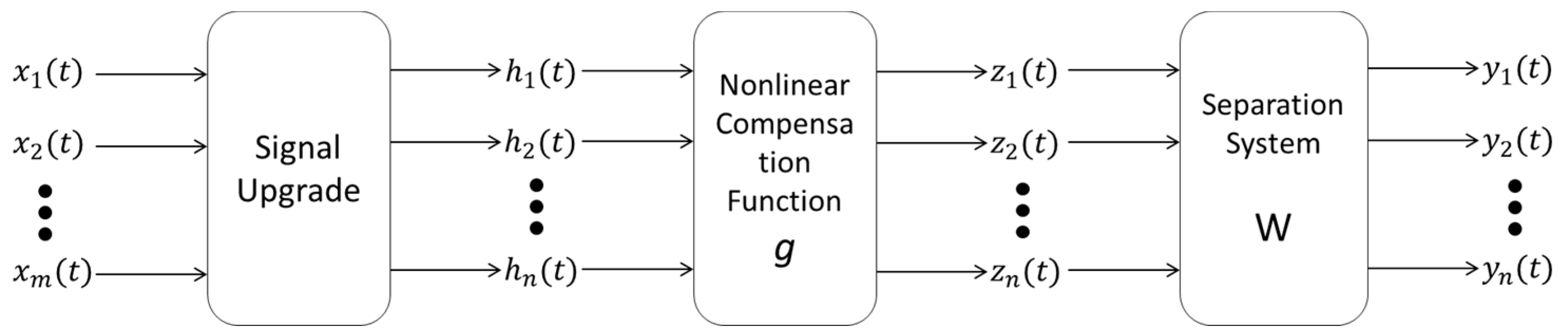
2.3. Nonlinear Bounded Component Analysis Based on Multivariate Nonlinear Chirp Mode Decomposition (MNCMD-NLBCA)
- (1)
- Pre-process the received mixed signal , including de-averaging and pre-whitening.
- (2)
- Perform MNCMD processing on the pre-processed observation signal to obtain k NCM components, .
- (3)
- Perform one-dimensional reconstruction on these k NCM components by assigning different random weights between (0, 1) and adding them together to obtain a new signal . Then, make to obtain a new observation signal.
- (4)
- Carry out nonlinear transformation of the new observation signals.
- (5)
- Select the normalized boundary objective function and use the subgradient descent algorithm to solve the mixed matrix W.
- (6)
- Complete signal separation.
3. Experiment and Results
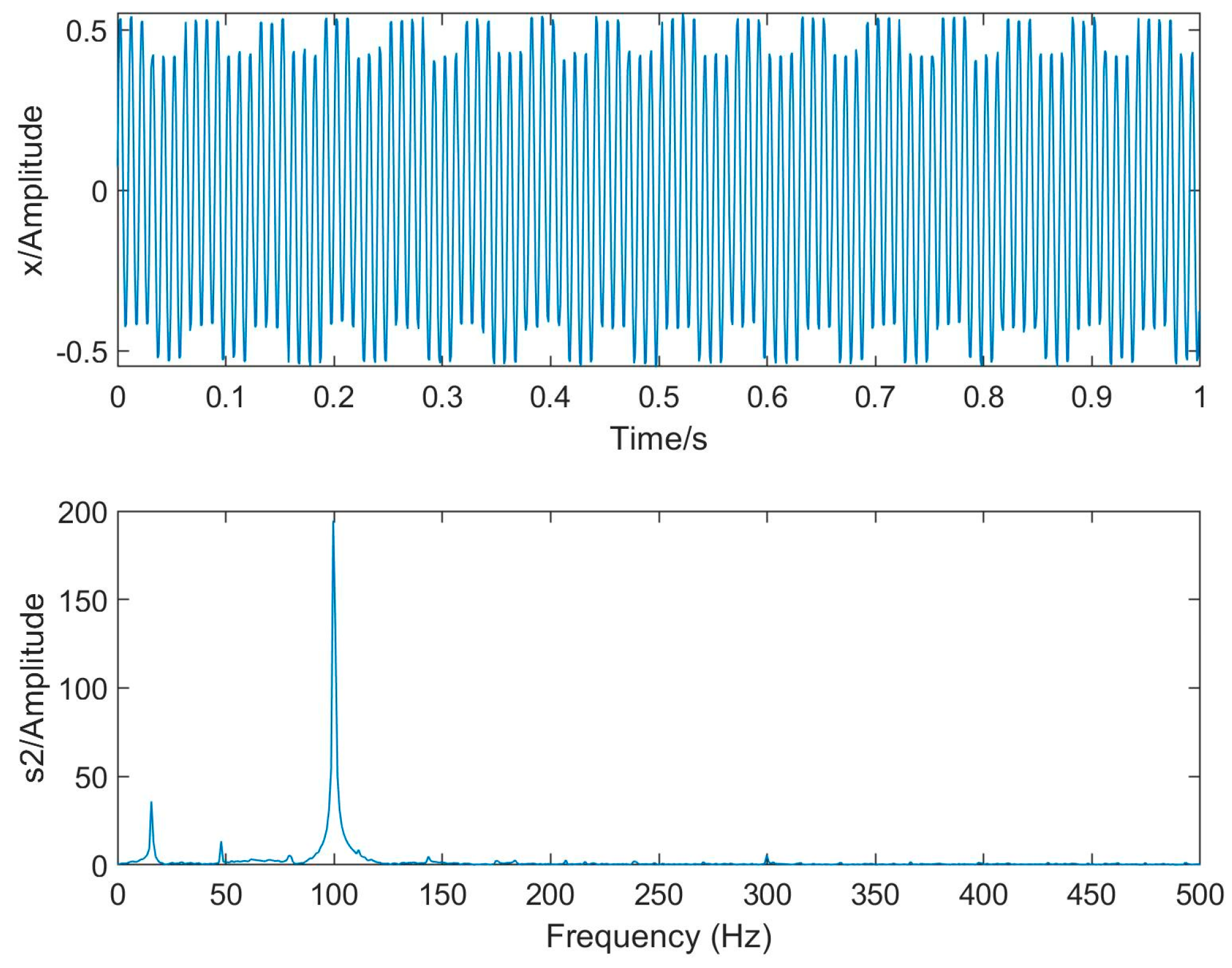
3.1. Simulation Dataset
3.2. ADFECGD Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khan, J.B.; Jan, T.; Khalil, R.A.; Saeed, N.; Almutiry, M. An Efficient Multistage Approach for Blind Source Separation of Noisy Convolutive Speech Mixture. Appl. Sci. 2021, 11, 5968. [Google Scholar] [CrossRef]
- Kan, X.; Kanyang, J.; Qiyu, Y. Multi-channel underdetermined blind source separation for recorded audio mixture signals using an unmanned aerial vehicle. IET Commun. 2021, 15, 1412–1422. [Google Scholar]
- Cardoso, J.-F. Super-Symmetric Decomposition of the Fourth-Order Cumulant Tensor-Blind Identification of More Sources than Sensors. In Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing, Toronto, ON, Canada, 14–17 April 1991; Volume 5, pp. 3109–3112. [Google Scholar]
- Gorodnitsky, I.F.; Rao, B.D.; George, J. Source localization in magnetoencephalography using an iterative weighted minimum norm algorithm. In Proceedings of the 26th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–28 October 1992; Volume 1, pp. 167–171. [Google Scholar]
- Lewicki, M.; Sejnowski, T.J. Learning nonlinear overcomplete representations for efficient coding. Adv. Neural Inf. Process. Syst. 1992, 10, 815–821. [Google Scholar]
- Shaobo, W.; Ying, G.; Sui, P.; Hongguang, L.; Yang, X. Underdetermined mixed matrix estimation algorithm based on parallel factor analysis. J. Detect. Control 2019, 41, 101–106. [Google Scholar]
- Niu, M. Underdetermined blind source separation algorithm based on deep learning. unpublished.
- Jize; Mu, W.; Geng, R. Under fixed blind source separation algorithm based on A-DBSCAN. Syst. Eng. Electron. Technol. 2020, 42, 2676–2683. [Google Scholar]
- Deville, Y.; Duarte, L.T.; Hosseini, S. Nonlinear Blind Source Separation and Blind Mixture Identification; Springer: Cham, Germany, 2021. [Google Scholar]
- Rongjie, W.; Yiju, Z.; Haifeng, Z. Post nonlinear blind source separation method based on NPCA. J. Instrum. 2015, 36, 2666–2673. [Google Scholar]
- Burel, G. Blind separation of sources: A nonlinear neural algorithm. Neural Netw. 1992, 5, 937–947. [Google Scholar] [CrossRef]
- Lappalainen, H.; Honkela, A. Bayesian Nonlinear Independent Component Analysis by Multi-layer Perceptions. In Advance in Independent Component Analysis; Springer: London, UK, 2000; pp. 93–121. [Google Scholar]
- Tan, Y.; Wang, J.; Zurada, J.M. Nonlinear blind source separation using a radial basis function network. IEEE Trans. Neural Netw. 2001, 12, 124–134. [Google Scholar]
- Almeida, L.B. MISEP-Linear and Nonlinear IC Based on Mutual Information. J. Mach. Learn. Res. 2003, 4, 1297–1318. [Google Scholar]
- Mingyang, T.; Yafeng, W. A Blind Source Separation Method Based on Bounded Component Analysis Optimized by the Improved Beetle Antennae Search. Sensors 2023, 23, 8325. [Google Scholar] [CrossRef]
- Cruces, S. Bounded component analysis of linear mixtures: Acriterion of minimum convex perimeter. IEEE Trans. Signal Process 2010, 58, 2141–2154. [Google Scholar] [CrossRef]
- Erdogan, A.T. A class of bounded component analysis algorithms for the separation of both independent and dependent sources. IEEE Trans. Signal Process 2013, 61, 5730–5743. [Google Scholar] [CrossRef]
- Gong, T.; Zhang, Z.; Luo, X.; Li, Y. Quantitative identification of independent and dependent sources based on bounded component analysis. Meas. Sci. Technol. 2021, 32, 035009. [Google Scholar] [CrossRef]
- Behar, J.; Andreotti, F.; Zaunseder, S.; Oster, J.; Clifford, G.D. A practical guide to non-invasive fetal electrocardiogram extraction and analysis. Physiol. Meas. 2016, 37, R1–R5. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Huang, K.; Qiu, Y.; Shen, H.; Ming, Z. Morphology extraction of fetal electrocardiogram by slow-fast LSTM network. Biomed. Signal Process. Control 2021, 68, 102664. [Google Scholar] [CrossRef]
- Ye, F.; Chen, J.; Gao, L.; Nie, W.; Sun, Q. A Mixing Matrix Estimation Algorithm for the Time-Delayed Mixing Model of the Underdetermined Blind Source Separation Problem. Circuits Syst. Signal Process. 2019, 38, 1889–1906. [Google Scholar] [CrossRef]
- Xi, C. Research on blind source separation based on post nonlinear mixed model. unpublished.
- Martinez, D.; Bray, A. Nonlinear blind source separation using kernels. IEEE Trans. Neural Netw. 2003, 14, 228–235. [Google Scholar] [CrossRef]
- Erdogan, A.T. A family of Bounded Component Analysis algorithms. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 1881–1884. [Google Scholar]
- Inan, H.A.; Erdogan, A.T. An extended family of bounded component analysis algorithms. In Proceedings of the 48th Asilomar Conf. on Signals, Systems and Computers, Pacific Grove, CA, USA, 2–5 November 2014; pp. 442–445. [Google Scholar]
- Chen, Q.; Xie, L.; Su, H. Multivariate nonlinear chirp mode decomposition. Signal Process. 2020, 176, 107667. [Google Scholar] [CrossRef]
- Chen, S.; Dong, X.; Peng, Z.; Zhang, W.; Meng, G. Nonlinear chirp mode decomposition: A variational method. IEEE Trans. Signal Process. 2017, 65, 6024–6037. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational modedecomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. Analysis of modulated multivariate oscillations. IEEE Trans. Signal Process. 2011, 60, 600–612. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F.; Huang, J.; Wang, W.; Yuan, C. A nonconvex penalty function with integral convolution approximation for compressed sensing. Signal Process. 2019, 158, 116–128. [Google Scholar] [CrossRef]
- Weihua, W. Blind Source Separation Algorithm and Application Research. Ph.D. Thesis, Harbin Engineering University, Heilongjiang, China, 2009. [Google Scholar]
- Ali, M.N.; Falavigna, D.; Brutti, A. Time-Domain Joint Training Strategies of Speech Enhancement and Intent Classification Neural Models. Sensors 2022, 22, 374. [Google Scholar] [CrossRef] [PubMed]
- Kotas, M.; Jezewski, J.; Horoba, K.; Matonia, A. Application of spatio-temporal filtering to fetal electrocardiogram enhancement. Comput. Methods Programs Biomed. 2011, 104, 1–9. [Google Scholar] [CrossRef]
- Jezewski, J.; Matonia, A.; Kupka, T.; Roj, D.; Czabanski, R. Determination of the fetal heart rate from abdominal signals: Evaluation of beat-to-beat accuracy in relation to the direct fetal electrocardiogram. Biomed. Eng.-Biomed. Tech. 2012, 57, 383–394. [Google Scholar] [CrossRef]


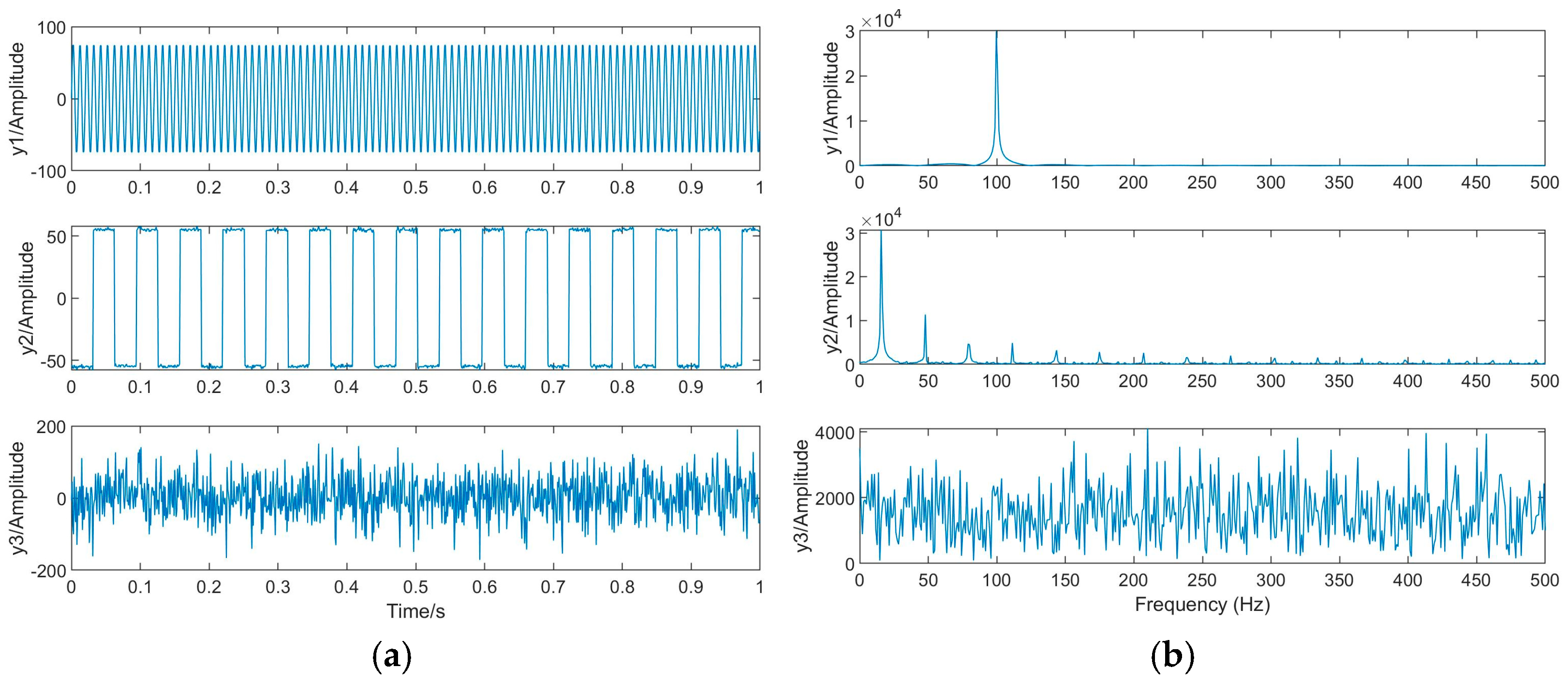
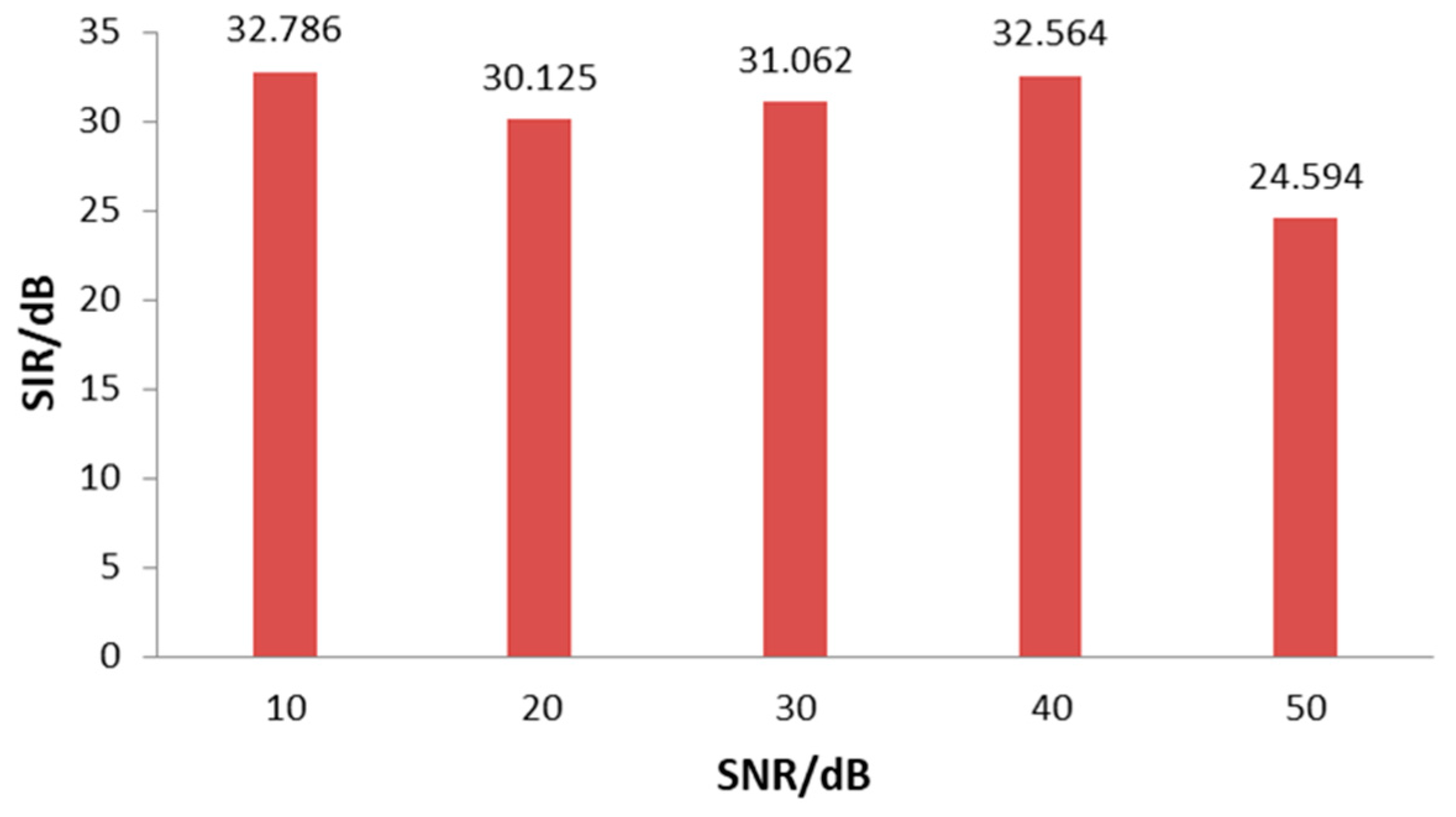

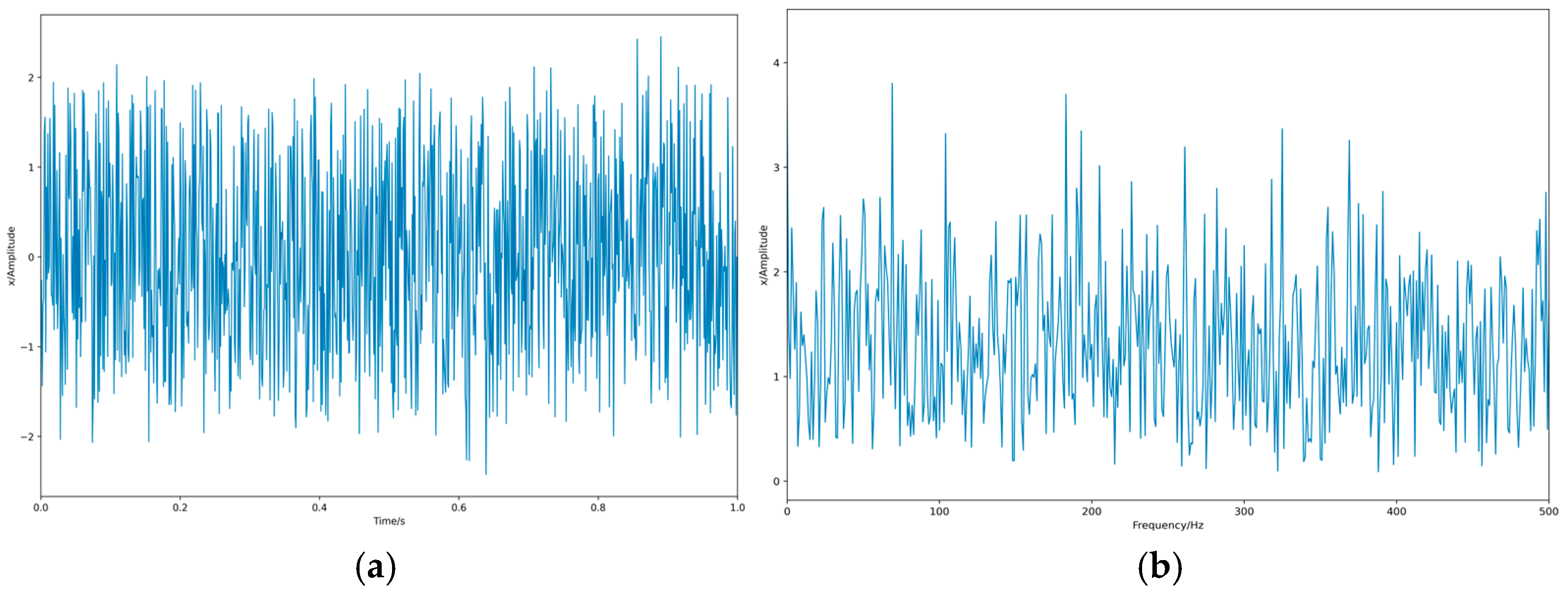

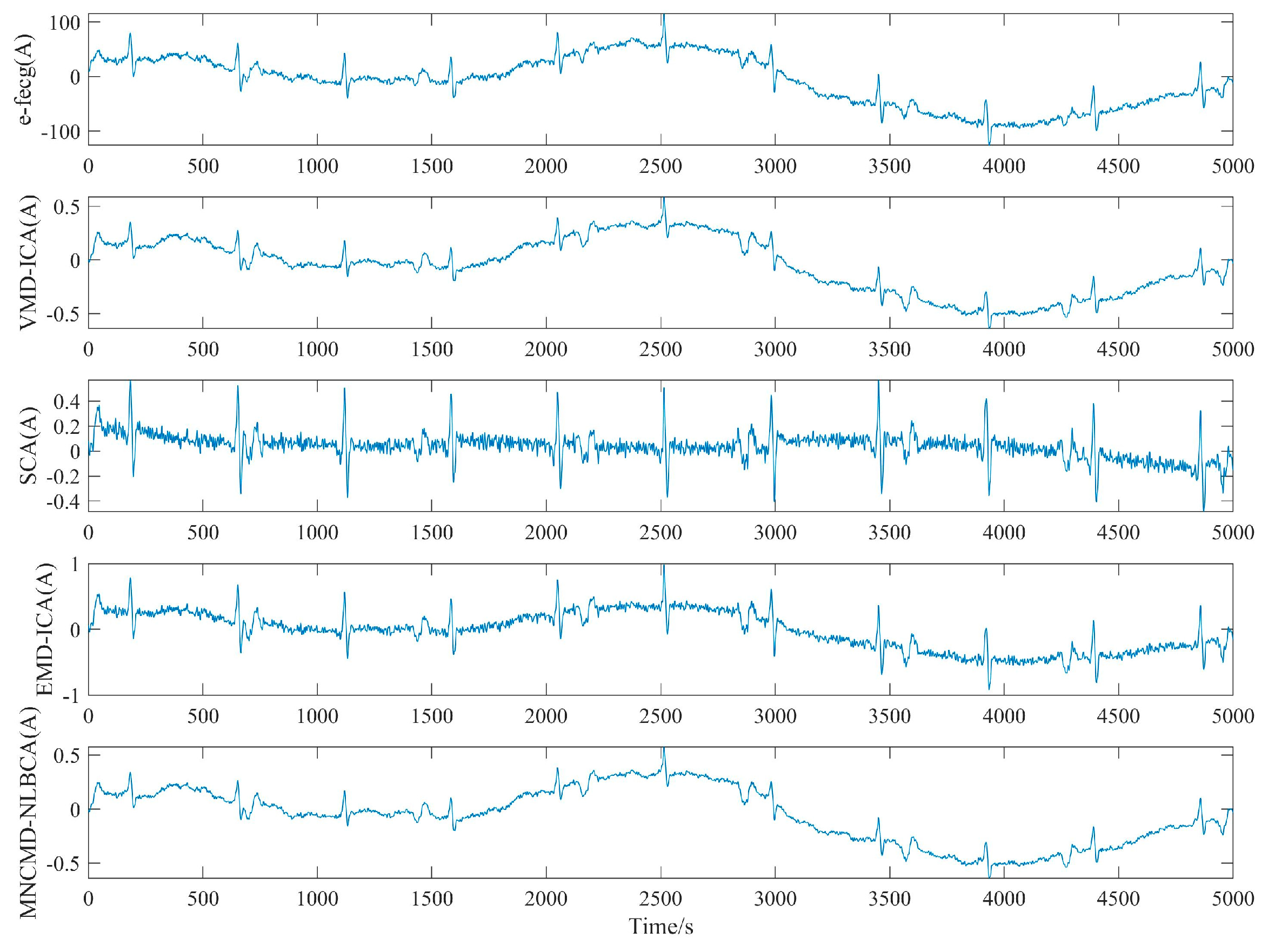
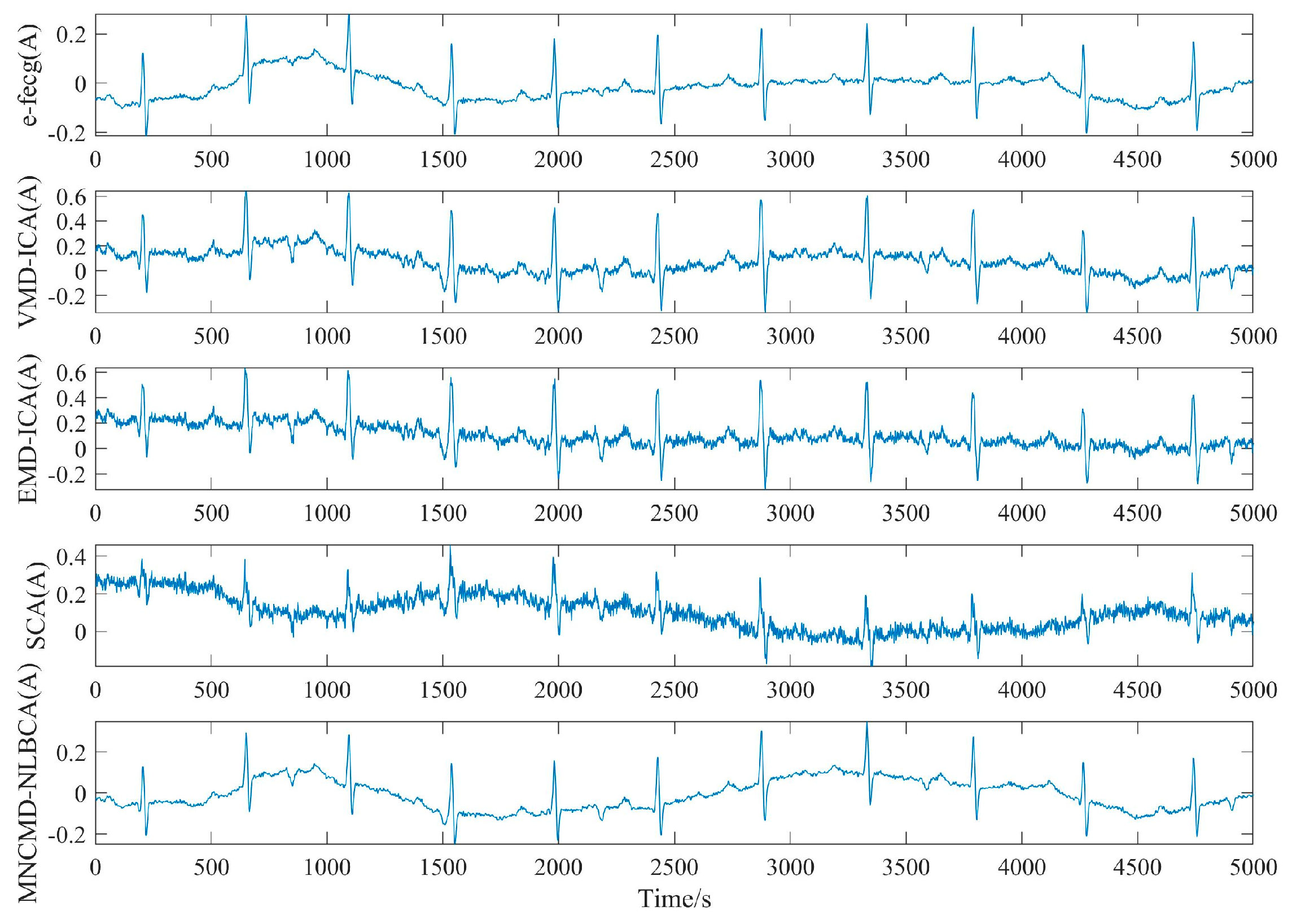
| y1 | y2 | y3 | |
|---|---|---|---|
| s1 | 0.99782904 | 0.01841561 | 0.00165612 |
| s2 | 0.00404252 | 0.98984297 | 0.04701977 |
| s3 | 0.00741474 | 0.04752748 | 0.99377657 |
| y1 | y2 | y3 | |
|---|---|---|---|
| s1 | 0.97778428 | 0.52447726 | 0.21264333 |
| s2 | 0.55792012 | 0.98634734 | 0.60709731 |
| s3 | 0.2556597 | 0.54286605 | 0.96087454 |
| VMD-ICA | EMD-ICA | SCA | MNCMD-NLBCA | |
|---|---|---|---|---|
| Similarity Coefficient | 0.785 | 0.732 | 0.611 | 0.964 |
| MSE | 2.0204 | 3.1207 | 3.0299 | 0.0452 |
| SIR | 12.39 | 10.29 | 9.23 | 21.26 |
| Response time | 16.32 | 17.28 | 22.54 | 20.16 |
| Methods | Record “r01” | Record “r08” | ||||
|---|---|---|---|---|---|---|
| Similarity Coefficient | MSE | SIR | Similarity Coefficient | MSE | SIR | |
| VMD-ICA | 0.947 | 0.0312 | 11.23 | 0.914 | 0.0204 | 9.95 |
| EMD-ICA | 0.894 | 0.0391 | 6.02 | 0.901 | 0.0237 | 4.56 |
| SCA | 0.462 | 0.0263 | 8.01 | 0.611 | 0.0299 | 7.92 |
| MNCMD-NLBCA | 0.981 | 0.0306 | 14.36 | 0.964 | 0.0154 | 11.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, M.; Wu, Y. An Innovative Nonlinear Bounded Component Analysis Algorithm Based on Multivariate Nonlinear Chirp Mode Decomposition. Electronics 2024, 13, 4555. https://doi.org/10.3390/electronics13224555
Tang M, Wu Y. An Innovative Nonlinear Bounded Component Analysis Algorithm Based on Multivariate Nonlinear Chirp Mode Decomposition. Electronics. 2024; 13(22):4555. https://doi.org/10.3390/electronics13224555
Chicago/Turabian StyleTang, Mingyang, and Yafeng Wu. 2024. "An Innovative Nonlinear Bounded Component Analysis Algorithm Based on Multivariate Nonlinear Chirp Mode Decomposition" Electronics 13, no. 22: 4555. https://doi.org/10.3390/electronics13224555
APA StyleTang, M., & Wu, Y. (2024). An Innovative Nonlinear Bounded Component Analysis Algorithm Based on Multivariate Nonlinear Chirp Mode Decomposition. Electronics, 13(22), 4555. https://doi.org/10.3390/electronics13224555






