Guaranteed Cost Control of Singular Fuzzy Time-Delay Systems Based on Proportional Plus Derivative Feedback

Abstract

This paper explores the guaranteed cost control issue for singular Takagi-Sugeno (T-S) fuzzy systems with time delay. An augmented Lyapunov-Krasovskii functional (LKF) is adopted to analyze the system’s stabilization, and sufficient conditions are established based on Lyapunov stability theory. The method of free weight matrices is employed to provide a systematic approach for determining the controller parameters. Additionally, two compelling examples are presented to demonstrate the viability of the proposed methods.

1. Introduction

Singular systems are a unique class of dynamical systems characterized by the presence of algebraic equations alongside differential equations in their formulation [1]. At present, significant research advancements have been accomplished within the domain of singular systems, including filter design [2], finite-time $H_{\infty }$ control [3], optimal control [4], input-to-state stability [5], etc. Nonlinear systems are prevalent across many domains, including biology, physics, and economics, where interactions often lead to complex, unpredictable behaviors that cannot be understood through simple linear models [6,7]. T-S fuzzy systems are a highly efficient method that encapsulates nonlinear behaviors through a set of fuzzy rules, allowing complex systems to be expressed in a manageable form [8]. Incorporating T-S fuzzy models into nonlinear singular systems to create singular fuzzy systems is instrumental to the evolution of control strategies applied to complex systems [9]. In [10], the authors investigated an asynchronous irregular-event sliding manifold control strategy for T-S fuzzy singular systems, utilizing an abstract unified representation for an effective triggering function that guarantees practical sliding modes and a positive lower bound for inter-execution times. Lu et al. [11] proposed a robust observer-oriented controller for T-S fuzzy systems utilizing a sliding mode methodology, featuring a practical state observer and new criteria that consider the impact of the difference matrix in the design. In [12], the authors focused on examining the finite-time stability and the process of estimating faults in T-S fuzzy singular systems, considering the challenges posed by time delays and potential faults.

Time delay is frequently observed in practical dynamic systems, posing significant challenges for system control. Moreover, it can result in a decline in performance and potentially lead to instability within control systems [13,14,15,16]. Consequently, considering the impact of time delay in singular fuzzy systems is highly significant. In light of this, several important research contributions regarding singular fuzzy time-delay systems are outlined below. In [17], the behavior of the positive T-S fuzzy singular system with time-varying delays was investigated via the creation of a modified system to derive and verify the necessary conditions for positivity and establish conditions for asymptotic stability. The delay-dependent control design and exponential stability analysis were carried out for T-S fuzzy singular uncertain systems by using a T-S fuzzy framework to establish stability and performance conditions and converting design problems into linear matrix inequalities (LMIs) to improve flexibility and minimize computational complexity [18]. In [19], the evaluation of admissibility for T-S fuzzy descriptor time-delay systems was conducted using a novel piecewise LKF, which is structured around delay intervals, along with a zero-equation approach to derive admissibility criteria by incorporating the Bessel–Legendre-type integral inequality. Additional relevant findings regarding singular fuzzy time-delay systems are available in [20,21,22], and the references therein.

In modern control theory, exploring proportional plus derivative state feedback (PDSF) in singular systems is vital for improving stability and response quality when conventional strategies may falter. PDSF control effectively adjusts system dynamics through proportional and derivative controls, offering a refined method for managing the complexities of singular systems [23]. The issues of simultaneous robust normalization and $H_{\infty }$ stabilization for uncertain T-S fuzzy singular time-delay systems were tackled through the implementation of a novel fuzzy PDSF controller, resulting in new criteria expressed as strict LMIs to ensure robust normal and stable (NS) conditions for all admissible uncertainties without model transformations in [24]. For the same class of singular fuzzy time-delay systems, ref. [25] employed PD feedback control to investigate the state feedback and output feedback problems, and presented the algorithms that used an iterative method to solve for the controller, ultimately ensuring that the closed-loop system was NS. The authors in [26] addressed the stability assessment and controller design for nonlinear singular systems through a T-S fuzzy model, designing a parallel distributed compensation (PDC) fuzzy controller and a novel fuzzy observer to facilitate the estimation of states and ensure system stability. Liu et al. [27] explored feedback regulation for a type of uncertain continuous-time singular system with polytopic structures, subject to input discretization and actuator malfunctions, achieving asymptotic stabilization and prescribed induced $L_{\infty }$ performance through the design of a reliable PDSF controller and dynamic quantizer.

Guaranteed cost control is rooted in the capability to develop control strategies that adapt to dynamic variations, thus guaranteeing the effectiveness and stability of performance in complex and changing environments. Research on guaranteed cost control has been implemented in numerous systems, for example, networked control systems [28], polynomial fuzzy systems [29], switched linear systems [30], uncertain stochastic systems [31], fractional-order systems [32], singular fuzzy time-delay systems [33,34,35], and so on. In [33], the study of optimal guaranteed cost control for T-S fuzzy descriptor systems with time-varying delay was conducted, demonstrating that the designed controller ensured asymptotic stability and provided an improved upper limit of the guaranteed cost. Additionally, based on the findings presented in [33], scenarios where uncertainties are present in the system matrices were explored in [34]. Ref. [35] further designed a state controller with variable feedback gain based on the PDC algorithm while considering system uncertainties and provided sufficient conditions for guaranteeing system admissibility in the form of LMIs.

By synthesizing the aforementioned literature, it is easy to conclude that references [24,26] investigated the PDSF management challenge for singular fuzzy systems; however, the controller design methods presented in these papers are not applicable to the parameter solutions of the controller discussed in this article. The authors in [25] presented a controller solving method based on iterative algorithms, which was completely different to the approach taken for controller solving. References [33,34,35] focused on the performance-preserving control issue for singular fuzzy systems with time delays, but they only designed state feedback controllers, which differ from the controller form studied in the current study. The analysis of stability for singular fuzzy systems with time delays using PD feedback under an augmented LKF framework currently lacks a unified approach for solving the controller. Additionally, research regarding memory-based PD feedback controllers remains sparse. When it comes to analyzing the guaranteed cost control properties of the system, few studies employ the augmented LKF. These insights form the core motivation of this study, highlighting that employing the augmented LKF to analyze system stability and solve for controller parameters presents significant challenges. These challenges greatly motivate the research undertaken in this work. We explores the guaranteed cost control problem for singular T-S fuzzy systems subject to time delays. An augmented LKF is used to evaluate the system’s stabilization, and sufficient criteria are derived through the principles of Lyapunov stability theory. The approach of free-weight matrices is employed to offer a structured method for determining the parameters of the controller.

The key insights derived from our research are highlighted below:

(1)

A memorial PDSF controller is designed, and a solution for determining the controller gains is provided based on the free-weight matrix method.

(2)

By designing an augmented Lyapunov functional that includes multiple integral terms and applying the technique of integral inequality scaling, results that ensure the system is NS can be obtained.

Notations: The symbols in our paper are described according to established standards. ${\mathbb{R}}^n$ denotes the n-dimensional Euclidean space. ${\mathbb{R}}^{n\times m}$ represents the collection of all real matrices with dimensions $n\times m$. $\mathrm{sym}\left(Z\right)$ refers to $Z+Z^T$. I and 0 denote the identity matrix and the zero matrix, respectively. The symbols ‘*’, ‘T’ and ‘$-1$’ are used to represent the symmetric part of a symmetric matrix, the transpose operation on a matrix, and the matrix inverse, respectively. $U>0$ represents that U is symmetric and positive definite. We presume the matrix has proper dimensions unless indicated otherwise.

2. Problem Formulation and Preliminaries

Consider the following nonlinear singular time-delay system:

Plant Rule i: If ${\epsilon }_1\left(t\right)$ is ${\psi }_{i1}$ and ⋯ and ${\epsilon }_p\left(t\right)$ is ${\psi }_{ip}$, then

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E\dot{\chi }\left(t\right)=A_i\chi \left(t\right)+A_{di}\chi (t-h)+A_{Di}{\int }_{t-h}^t\chi \left(s\right)ds+B_{i}u\left(t\right)\hfill \\ \chi \left(t\right)=\phi \left(t\right), t\in [-h,0]\hfill \end{array}\right.\end{array}$$

(1)

where ${\epsilon }_q\left(t\right)$ denotes the premise variable and ${\psi }_{iq}$ signifies the corresponding fuzzy set. $q\in \{1,2,\dots ,p\}$ and $i\in \{1,2,\dots ,\mathcal{l}\}$, where p is the count of premise variables and ℓ is the total number of fuzzy rules. $\chi \left(t\right)\in {\mathbb{R}}^n$ and $u\left(t\right)\in {\mathbb{R}}^m$ represent the state vector and the control input, respectively, while $\phi \left(t\right)$ denotes the system’s initial state. The matrix E is singular and has $\mathrm{rank}\left(E\right)=l<n$. The matrices $A_i$, $A_{di}$, $A_{Di}$, and $B_i$ are constant and have suitable dimensions.

By utilizing fuzzy interpolation methods, such as single-point fuzzification, product-based inference, and mean-weighted defuzzification, the complete representation of the system (1) is characterized as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E\dot{\chi }\left(t\right)={\displaystyle \sum _{i=1}^{\mathcal{l}}}{\mu }_i\left(\epsilon \left(t\right)\right)(A_i\chi \left(t\right)+A_{di}\chi (t-h)+A_{Di}{\int }_{t-h}^t\chi \left(s\right)ds+B_{i}u\left(t\right))\hfill \\ \chi \left(t\right)=\phi \left(t\right), t\in [-h,0]\hfill \end{array}\right.\end{array}$$

(2)

where

$$\begin{array}{c}\hfill {\beta }_i\left(\epsilon \left(t\right)\right)={\displaystyle \prod _{q=1}^p}{\psi }_{iq}\left({\epsilon }_q\left(t\right)\right), {\mu }_i\left(\epsilon \left(t\right)\right)={\displaystyle \frac{{\beta }_i\left(\epsilon \left(t\right)\right)}{{\sum }_{i=1}^{\mathcal{l}}{\beta }_i\left(\epsilon \left(t\right)\right)}}\end{array}$$

and ${\psi }_{iq}\left({\epsilon }_q\left(t\right)\right)$ represents the membership grade of ${\epsilon }_q\left(t\right)$ in ${\psi }_{iq}$, and ${\beta }_i\left(\epsilon \left(t\right)\right)$ meets the condition stated below:

$$\begin{array}{c}\hfill {\beta }_i\left(\epsilon \left(t\right)\right)\ge 0, {\displaystyle \sum _{i=1}^{\mathcal{l}}}{\beta }_i\left(\epsilon \left(t\right)\right)>0\end{array}$$

Therefore, it follows that

$$\begin{array}{c}\hfill {\mu }_i\left(\epsilon \left(t\right)\right)\ge 0, {\displaystyle \sum _{i=1}^{\mathcal{l}}}{\mu }_i\left(\epsilon \left(t\right)\right)=1.\end{array}$$

Utilizing the PDC approach, the memorial PDSF controller is developed in the manner described below:

Controller Rule j: If ${\epsilon }_1\left(t\right)$ is ${\psi }_{j1}$ and ⋯ and ${\epsilon }_p\left(t\right)$ is ${\psi }_{jp}$, then

$$\begin{array}{c}\hfill u\left(t\right)=K_{pj}\chi \left(t\right)+K_{pdj}\chi (t-h)-K_{dj}\dot{\chi }\left(t\right)\end{array}$$

(3)

where $K_{pj}$ and $K_{pdj}$ denote the state feedback gains and $K_{dj}$ represents the derivative state feedback gain, respectively, and $j\in \{1,2,\cdots ,\mathcal{l}\}$. The overall control input is expressed as follows:

$$\begin{array}{c}\hfill u\left(t\right)={\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_j\left(\epsilon \left(t\right)\right)(K_{pj}\chi \left(t\right)+K_{pdj}\chi (t-h)-K_{dj}\dot{\chi }\left(t\right))\end{array}$$

(4)

For brevity, ${\mu }_i$ will represent ${\mu }_i\left(\epsilon \left(t\right)\right)$ in the subsequent text. By integrating (2) and (4), we derive the closed-loop system as below:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\begin{array}{cc}\hfill {\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}(E+B_i{K}_{dj})\dot{\chi }\left(t\right)=& {\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j[(A_i+B_i{K}_{pj})\chi \left(t\right)+(A_{di}+B_i{K}_{pdj})\chi (t-h)\hfill \\ & +A_{Di}{\int }_{t-h}^t\chi \left(s\right)ds]\hfill \end{array}\hfill \\ \chi \left(t\right)=\phi \left(t\right), t\in [-h,0]\hfill \end{array}\right.\end{array}$$

(5)

Considering the positive definite matrices $Q_1$, $Q_2$, and $Q_3$, the cost function takes the form of [36].

$$\begin{array}{c}\hfill J={\int }_0^{\infty }[{\chi }^T\left(t\right)Q_1\chi \left(t\right)+{\dot{\chi }}^T\left(t\right)Q_2\dot{\chi }\left(t\right)+u^T\left(t\right)Q_{3}u\left(t\right)]dt.\end{array}$$

(6)

Remark 1.

Guaranteed cost control focuses on optimizing various performance metrics, such as response speed, accuracy, and robustness, while ensuring system stability. This control strategy aims to enhance overall system performance and efficiency while maintaining basic stability requirements.

To derive the key findings of our paper, introducing the subsequent definition and lemma is indispensable.

Definition 1

([37]). A linear singular time-delay system $E\dot{\chi }\left(t\right)=A\chi \left(t\right)+A_d\chi (t-h)+Bu\left(t\right)$ is considered NS if a PDSF controller $u\left(t\right)=K_p\chi \left(t\right)-K_d\dot{\chi }\left(t\right)$ can be found such that the closed-loop system $(E+B{K}_d)\dot{\chi }\left(t\right)=(A_i+B{K}_p)\chi \left(t\right)+A_{di}\chi (t-h)$ meets the following criteria:

(1) 

The matrix $E+B{K}_d$ is nonsingular.

(2) 

The closed-loop system is stable.

Lemma 1

([38]). Assume $R>0$, and let ς be a differentiable function in $[\sigma ,\upsilon ]\to$ ${\mathbb{R}}^n$; the inequality given below is valid:

$$\begin{array}{c}\hfill {\int }_{\sigma }^{\upsilon }{\dot{\varsigma }}^T\left(s\right)R\dot{\varsigma }\left(s\right)ds\ge {\displaystyle \frac{1}{\upsilon -\sigma }}{\Pi }_1^{T}R{\Pi }_1+{\displaystyle \frac{3}{\upsilon -\sigma }}{\Pi }_2^{T}R{\Pi }_2+{\displaystyle \frac{5}{\upsilon -\sigma }}{\Pi }_3^{T}R{\Pi }_3\end{array}$$

where

$$\begin{array}{cc}\hfill & {\Pi }_1=\varsigma \left(\upsilon \right)-\varsigma \left(\sigma \right)\hfill \\ \hfill & {\Pi }_2=\varsigma \left(\upsilon \right)+\varsigma \left(\sigma \right)-{\displaystyle \frac{2}{\upsilon -\sigma }}{\int }_{\sigma }^{\upsilon }\varsigma \left(s\right)ds\hfill \\ \hfill & {\Pi }_3=\varsigma \left(\upsilon \right)-\varsigma \left(\sigma \right)+{\displaystyle \frac{6}{\upsilon -\sigma }}{\int }_{\sigma }^{\upsilon }\varsigma \left(s\right)ds-{\displaystyle \frac{12}{{(\upsilon -\sigma )}^2}}{\int }_{\sigma }^{\upsilon }{\int }_u^{\upsilon }\varsigma \left(s\right)dsdu.\hfill \end{array}$$

3. Main Results

This section provides sufficient conditions for ensuring that the singular fuzzy time-delay system is NS when using the memorial PDSF controller, and the approach to solving the controller is given with the help of LMIs.

Theorem 1.

Consider the system described in (2) along with the cost function given in (6). For given scalar h, matrices $Q_1\in {\mathbb{R}}^{n\times n}>0, Q_2\in {\mathbb{R}}^{n\times n}>0, Q_3\in {\mathbb{R}}^{m\times m}>0$; if there exist matrices $P\in {\mathbb{R}}^{3n\times 3n}>0$, $Q\in {\mathbb{R}}^{n\times n}>0$, $R\in {\mathbb{R}}^{n\times n}>0$ and any invertible matrices $G_1, G_2, G_3, G_4\in {\mathbb{R}}^{n\times n}$, which satisfy the following inequalities for all $i,j\in \{1,2,\dots ,\mathcal{l}\}$:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Xi }_{ii}<0\hfill \\ {\Xi }_{ij}+{\Xi }_{ji}<0, i<j\hfill \end{array}\right.\end{array}$$

(7)

then the closed-loop system in (5) is NS, while the cost function in (6) meets

$$\begin{array}{c}\hfill \begin{array}{c}J\le {\left[\begin{array}{c}\phi \left(0\right)\\ {\int }_{-h}^0\chi \left(s\right)ds\\ {\int }_{-h}^0{\int }_{\theta }^0\chi \left(s\right)dsd\theta \end{array}\right]}^{T}P\left[\begin{array}{c}\phi \left(0\right)\\ {\int }_{-h}^0\chi \left(s\right)ds\\ {\int }_{-h}^0{\int }_{\theta }^0\chi \left(s\right)dsd\theta \end{array}\right]+{\int }_{-h}^0{\chi }^T\left(s\right)Q\chi \left(s\right)ds\hfill \\ +h{\int }_{-h}^0{\int }_{\theta }^0{\dot{\chi }}^T\left(s\right)R\dot{\chi }\left(s\right)dsd\theta \hfill \end{array}\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill & {\Xi }_{ij}=\mathrm{sym}\left\{{\Xi }_1^{T}P{\Xi }_2\right\}+e_2^{T}Q{e}_2-e_3^{T}Q{e}_3+h^2{e}_1^{T}R{e}_1-{\Pi }_1^{T}R{\Pi }_1-3{\Pi }_2^{T}R{\Pi }_2-5{\Pi }_3^{T}R{\Pi }_3\hfill \\ \hfill & +e_2^T{Q}_1{e}_2+e_1^T{Q}_2{e}_1+{(K_{pj}{e}_2+K_{pdj}{e}_3-K_{dj}{e}_1)}^T{Q}_3(K_{pj}{e}_2+K_{pdj}{e}_3-K_{dj}{e}_1)\hfill \\ \hfill & +\mathrm{sym}\{(e_1^T{G}_1^T+e_2^T{G}_2^T+e_3^T{G}_3^T+h{e}_4^T{G}_4^T)[-(E+B_i{K}_{dj})e_1+(A_i+B_i{K}_{pj})e_2\hfill \\ \hfill & +(A_{di}+B_i{K}_{pdj})e_3+h{A}_{Di}{e}_4\left]\right\}\hfill \\ \hfill & {\Xi }_1={\left[\begin{array}{ccc}{e}_2^T& h{e}_4^T& 0.5h^2{e}_5^T\end{array}\right]}^T, {\Xi }_2={\left[\begin{array}{ccc}{e}_1^T& {(e_2-e_3)}^T& h{e}_2^T-h{e}_4^T\end{array}\right]}^T\hfill \\ \hfill & e_i=\left[\begin{array}{ccc}{0}_{n\times (i-1)n}& I_n& 0_{n\times (5-i)n}\end{array}\right], i=1,2,3,4,5\hfill \\ \hfill & {\Pi }_1=e_2-e_3,{\Pi }_2=e_2+e_3-2e_4, {\Pi }_3=e_2-e_3+6e_4-6e_5.\hfill \end{array}$$

Proof of Theorem 1. 

For the purpose of analyzing the system’s stabilization, we adopt the given augmented LKF:

$$\begin{array}{c}\hfill V\left({\chi }_t\right)=V_1\left({\chi }_t\right)+V_2\left({\chi }_t\right)+V_3\left({\chi }_t\right)\end{array}$$

(9)

where

$$\begin{array}{cc}\hfill & V_1\left({\chi }_t\right)={\epsilon }^T\left(t\right)P\epsilon \left(t\right)\hfill \\ \hfill & V_2\left({\chi }_t\right)={\int }_{t-h}^t{\chi }^T\left(s\right)Q\chi \left(s\right)ds\hfill \\ \hfill & V_3\left({\chi }_t\right)=h{\int }_{-h}^0{\int }_{t+\theta }^t{\dot{\chi }}^T\left(s\right)R\dot{\chi }\left(s\right)dsd\theta \hfill \\ \hfill & \epsilon \left(t\right)={\left[\begin{array}{ccc}{\chi }^T\left(t\right)& {\int }_{t-h}^t{\chi }^T\left(s\right)ds& {\int }_{-h}^0{\int }_{t+\theta }^t{\chi }^T\left(s\right)dsd\theta \end{array}\right]}^T.\hfill \end{array}$$

To enhance the clarity of the derivation process, we introduce a new variable as follows:

$$\begin{array}{c}\hfill \eta \left(t\right)={\left[\begin{array}{ccccc}{\dot{\chi }}^T\left(t\right)\hfill & {\chi }^T\left(t\right)& {\chi }^T(t-h)& {\displaystyle \frac{1}{h}}{\int }_{t-h}^t{\chi }^T\left(s\right)ds& {\displaystyle \frac{2}{h^2}}{\int }_{-h}^0{\int }_{t+\theta }^t{\chi }^T\left(s\right)dsd\theta \end{array}\right]}^T.\end{array}$$

By differentiating $V\left({\chi }_t\right)$, we arrive at the subsequent results:

$$\begin{array}{c}\hfill {\dot{V}}_1\left({\chi }_t\right)={\eta }^T\left(t\right)\mathrm{sym}\left\{{\Xi }_1^{T}P{\Xi }_2\right\}\eta \left(t\right)\end{array}$$

(10)

$$\begin{array}{c}\hfill {\dot{V}}_2\left({\chi }_t\right)={\eta }^T\left(t\right)(e_2^{T}Q{e}_2-e_3^{T}Q{e}_3)\eta \left(t\right)\end{array}$$

(11)

$$\begin{array}{c}\hfill {\dot{V}}_3\left({\chi }_t\right)=h^2{\eta }^T\left(t\right)e_1^{T}R{e}_1\eta \left(t\right)-h{\int }_{t-h}^t{\dot{\chi }}^T\left(s\right)R\dot{\chi }\left(s\right)ds.\end{array}$$

(12)

By applying Lemma 1, from (11), one can derive the following:

$$\begin{array}{c}\hfill -h{\int }_{t-h}^t{\dot{\chi }}^T\left(s\right)R\dot{\chi }\left(s\right)ds\le -{\eta }^T\left(t\right)({\Pi }_1^{T}R{\Pi }_1+3{\Pi }_2^{T}R{\Pi }_2+5{\Pi }_3^{T}R{\Pi }_3)\eta \left(t\right).\end{array}$$

(13)

Introducing the reversible free weighting matrices $G_1$, $G_2$, $G_3$, and $G_4$ allows us to derive the following equality.

$$\begin{array}{c}\hfill \begin{array}{c}2[{\dot{\chi }}^T\left(t\right)G_1^T+{\chi }^T\left(t\right)G_2^T+{\chi }^T(t-h)G_3^T+{\int }_{t-h}^t{\chi }^T\left(s\right)ds{G}_3^T]\hfill \\ \times [-{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(E+B_i{K}_{dj})\dot{\chi }\left(t\right)+{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(A_i+B_i{K}_{pj})\chi \left(t\right)\hfill \\ +{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(A_{di}+B_i{K}_{pdj})\chi (t-h)+{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\mu }_i{A}_{Di}{\int }_{t-h}^t\chi \left(s\right)ds]=0.\hfill \end{array}\end{array}$$

(14)

With the variable $\eta \left(t\right)$ defined, (14) can be reformulated as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{\eta }^T\left(t\right)\mathrm{sym}\{e_1^T{G}_1^T+e_2^T{G}_2^T+e_3^T{G}_3^T+h{e}_4^T{G}_4^T]\hfill \\ \times [-{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(E+B_i{K}_{dj})e_1+{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(A_i+B_i{K}_{pj})e_2\hfill \\ +{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j(A_{di}+B_i{K}_{pdj})e_3+{\displaystyle \sum _{i=1}^{\mathcal{l}}}{\mu }_{i}h{A}_{Di}{e}_4]\eta \left(t\right)=0.\hfill \end{array}\end{array}$$

(15)

Using the formulas given in (4) and (9)–(15), we can determine

$$\begin{array}{c}\hfill \dot{V}\left({\chi }_t\right)+{\chi }^T\left(t\right)Q_1\chi \left(t\right)+{\dot{\chi }}^T\left(t\right)Q_2\dot{\chi }\left(t\right)+u^T\left(t\right)Q_{3}u\left(t\right)\le {\displaystyle \sum _{i=1}^{\mathcal{l}}}{\displaystyle \sum _{j=1}^{\mathcal{l}}}{\mu }_i{\mu }_j{\eta }^T\left(t\right){\Xi }_{ij}\eta \left(t\right).\end{array}$$

(16)

With regard to the properties of fuzzy membership functions, satisfying the inequalities (7) leads to the conclusion that ${\Xi }_{ij}<0$. Meanwhile, due to $Q_1>0$, $Q_2>0$, and $Q_3>0$, it follows that $\dot{V}\left({\chi }_t\right)<0$, which ensures the stability of the closed-loop system in (5).

By integrating both sides of (16) over the interval $[0,\infty ]$, one can obtain

$$\begin{array}{c}\hfill \begin{array}{c}J={\int }_0^{\infty }[{\chi }^T\left(t\right)Q_1\chi \left(t\right)+{\dot{\chi }}^T\left(t\right)Q_2\dot{\chi }\left(t\right)+u^T\left(t\right)Q_{3}u\left(t\right)]dt\hfill \\ \le -{\int }_0^{\infty }\dot{V}\left({\chi }_t\right)dt=V\left({\chi }_0\right)-V\left({\chi }_{\infty }\right)=V\left({\chi }_0\right).\hfill \end{array}\end{array}$$

(17)

From (17), it can be deduced that the cost function is bounded above by $V\left({\chi }_0\right)$, which is shown in (8).

Given that ${\Xi }_{ij}<0$, we can deduce

$$\begin{array}{c}\hfill -G_1^T(E+B_i{K}_{dj})-{(E+B_i{K}_{dj})}^T{G}_1+Q_2+h^{2}R+K_{dj}^T{Q}_3{K}_{dj}<0.\end{array}$$

(18)

Considering $R>0$, $Q_2>0$ and $Q_3>0$, we can obtain

$$\begin{array}{c}\hfill -G_1^T(E+B_i{K}_{dj})-{(E+B_i{K}_{dj})}^T{G}_1<0\end{array}$$

(19)

Therefore, we have $-{\sum }_{i=1}^{\mathcal{l}}{\sum }_{i=1}^{\mathcal{l}}[G_1^T(E+B_i{K}_{dj})+{(E+B_i{K}_{dj})}^T{G}_1]<0$, which shows that the matrix ${\sum }_{i=1}^{\mathcal{l}}{\sum }_{i=1}^{\mathcal{l}}(E+B_i{K}_{dj})$ is nonsingular, thus completing the proof. □

Remark 2.

In control theory, incorporating invertible free weight matrices, such as, $G_1$, $G_2$, $G_3$, and $G_4$, is essential for determining controller parameters. These matrices add flexibility to the design process, facilitating the transformation of system dynamics into more tractable formats. Utilizing invertible free weight matrices ensures that the resulting conditions are feasible and also improves the robustness and efficiency of the system’s behavior.

Since Theorem 1 does not take the form of LMIs, we are unable to utilize it directly to solve for the controller parameters. To address this, we need to perform some transformations on the formulas in Theorem 1. Therefore, we present Theorem 2 as follows:

Theorem 2.

Consider the system described in (2) along with the cost function given in (6). For given scalars h, ${\epsilon }_1$, ${\epsilon }_2$ and ${\epsilon }_3$, matrices $Q_1\in {\mathbb{R}}^{n\times n}>0, Q_2\in {\mathbb{R}}^{n\times n}>0, Q_3\in {\mathbb{R}}^{m\times m}>0$; if there exist matrices $\overline{P}\in {\mathbb{R}}^{3n\times 3n}>0$, $\overline{Q}\in {\mathbb{R}}^{n\times n}>0$, $\overline{R}\in {\mathbb{R}}^{n\times n}>0$, any invertible matrix $X\in {\mathbb{R}}^{n\times n}$ and matrices $Y_{di}\in {\mathbb{R}}^{m\times n}$, $Y_{pi}\in {\mathbb{R}}^{m\times n}$, $Y_{pdi}\in {\mathbb{R}}^{m\times n}$, which satisfy the following inequalities for all $i,j\in \{1,2,\dots ,\mathcal{l}\}$:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\Sigma }_{ii}<0\hfill \\ {\Sigma }_{ij}+{\Sigma }_{ji}<0, i<j\hfill \end{array}\right.\end{array}$$

(20)

then the closed-loop system in (5) is NS, and the controller gains are provided below:

$$\begin{array}{c}\hfill K_{dj}=Y_{dj}{X}^{-1}, K_{pj}=Y_{pj}{X}^{-1}, K_{pdj}=Y_{pdj}{X}^{-1}\end{array}$$

(21)

and the cost function (6) meets

$$\begin{array}{c}\hfill \begin{array}{c}J\le {\left[\begin{array}{c}\phi \left(0\right)\\ {\int }_{-h}^0\chi \left(s\right)ds\\ {\int }_{-h}^0{\int }_{\theta }^0\chi \left(s\right)dsd\theta \end{array}\right]}^T\mathrm{diag}\{X^{-T},X^{-T},X^{-T}\}\overline{P}\mathrm{diag}\{X^{-1},X^{-1},X^{-1}\}\hfill \\ \times \left[\begin{array}{c}\phi \left(0\right)\\ {\int }_{-h}^0\chi \left(s\right)ds\\ {\int }_{-h}^0{\int }_{\theta }^0\chi \left(s\right)dsd\theta \end{array}\right]+{\int }_{-h}^0{\chi }^T\left(s\right)X^{-T}\overline{Q}{X}^{-1}\chi \left(s\right)ds\hfill \\ +h{\int }_{-h}^0{\int }_{\theta }^0{\dot{\chi }}^T\left(s\right)X^{-T}\overline{R}{X}^{-1}\dot{\chi }\left(s\right)dsd\theta \hfill \end{array}\end{array}$$

(22)

where

$$\begin{array}{c}\hfill \begin{array}{c}{\Sigma }_{ij}=\left[\begin{array}{cccc}{\overline{\Xi }}_{ij}& e_2^T{X}^T& e_1^T{X}^T& {(Y_{pj}{e}_2+Y_{pdj}{e}_3-Y_{dj}{e}_1)}^T\\ \ast & -Q_1^{-1}& 0& 0\\ \ast & \ast & -Q_2^{-1}& 0\\ \ast & \ast & \ast & -Q_3^{-1}\end{array}\right]\hfill \\ {\overline{\Xi }}_{ij}=\mathrm{sym}\left\{{\Xi }_1^T\overline{P}{\Xi }_2\right\}+e_2^T\overline{Q}{e}_2-e_3^T\overline{Q}{e}_3+h^2{e}_1^T\overline{R}{e}_1-{\Pi }_1^T\overline{R}{\Pi }_1-3{\Pi }_2^T\overline{R}{\Pi }_2-5{\Pi }_3^T\overline{R}{\Pi }_3\hfill \\ +\mathrm{sym}\{(e_1^T+{\epsilon }_1{e}_2^T+{\epsilon }_2{e}_3^T+h{\epsilon }_3{e}_4^T)[-(EX+B_i{Y}_{dj})e_1+(A_{i}X+B_i{Y}_{pj})e_2\hfill \\ +(A_{di}X+B_i{Y}_{pdj})e_3+h{A}_{Di}X{e}_4\left]\right\}.\hfill \end{array}\end{array}$$

Proof of Theorem 2. 

For the purpose of calculating the controller gains, we let $G_1=G,$ $G_2={\epsilon }_{1}G, G_3={\epsilon }_{2}G, G_4={\epsilon }_{3}G, X=G^{-1}$.

Applying pre- and post-multiplication to the inequality ${\Xi }_{ij}<0$ with $\mathrm{diag}\{X^T,X^T,X^T,$ $X^T,X^T\}$ and its transpose, we can identify the following transformations:

$$\begin{array}{c}\hfill \begin{array}{c}\overline{P}=\mathrm{diag}\{X^T,X^T,X^T\}P\mathrm{diag}\{X,X,X\}, \overline{Q}=X^{T}QX\hfill \\ \overline{R}=X^{T}RX, Y_{dj}=K_{dj}X, Y_{pj}=K_{pj}X, Y_{pdj}=K_{pdj}X\hfill \end{array}\end{array}$$

Then, we can obtain

$$\begin{array}{c}\hfill \begin{array}{c}{\overline{\Xi }}_{ij}+e_2^T{X}^T{Q}_{1}X{e}_2+e_1^T{X}^T{Q}_{2}X{e}_1+(Y_{pj}{e}_2+Y_{pdj}{e}_3\hfill \\ -Y_{dj}{e}_1{)}^T{Q}_3(Y_{pj}{e}_2+Y_{pdj}{e}_3-Y_{dj}{e}_1)<0\hfill \end{array}\end{array}$$

(23)

According to the Schur complement, it follows that inequality ${\Sigma }_{ij}<0$ ensures the validity of the inequality (23). Additionally, utilizing the properties of fuzzy membership functions, the inequalities (20) guarantee that ${\Sigma }_{ij}<0$ holds true. This completes the proof. □

When guaranteed cost control is not considered, purely from the perspective of controller design, the following corollary can be derived from Theorem 2:

Corollary 1.

Consider the system described in (2). For given scalars h, ${\epsilon }_1$, ${\epsilon }_2$ and ${\epsilon }_3$, matrices $Q_1\in {\mathbb{R}}^{n\times n}>0, Q_2\in {\mathbb{R}}^{n\times n}>0, Q_3\in {\mathbb{R}}^{m\times m}>0$; if there exist matrices $\overline{P}\in {\mathbb{R}}^{3n\times 3n}>0$, $\overline{Q}\in {\mathbb{R}}^{n\times n}>0$, $\overline{R}\in {\mathbb{R}}^{n\times n}>0$, any invertible matrix $X\in {\mathbb{R}}^{n\times n}$ and matrices $Y_{di}\in {\mathbb{R}}^{m\times n}$, $Y_{pi}\in {\mathbb{R}}^{m\times n}$, $Y_{pdi}\in {\mathbb{R}}^{m\times n}$, which satisfy the following inequalities for all $i,j\in \{1,2,\dots ,\mathcal{l}\}$:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{\Xi }}_{ii}<0\hfill \\ {\overline{\Xi }}_{ij}+{\overline{\Xi }}_{ji}<0, i<j\hfill \end{array}\right.\end{array}$$

(24)

then the closed-loop system in (5) is NS, and the controller gains are provided below:

$$\begin{array}{c}\hfill K_{dj}=Y_{dj}{X}^{-1}, K_{pj}=Y_{pj}{X}^{-1}, K_{pdj}=Y_{pdj}{X}^{-1}.\end{array}$$

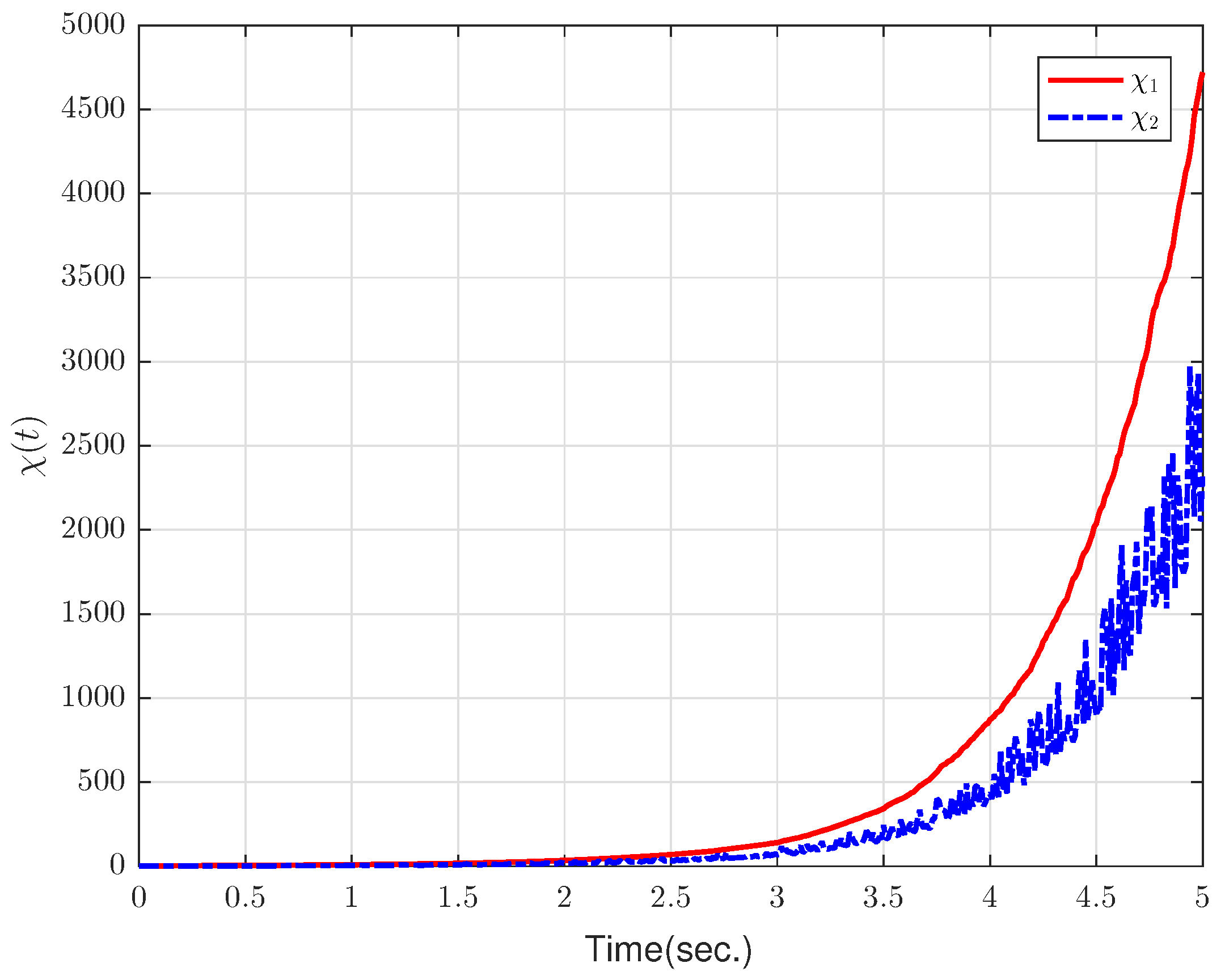
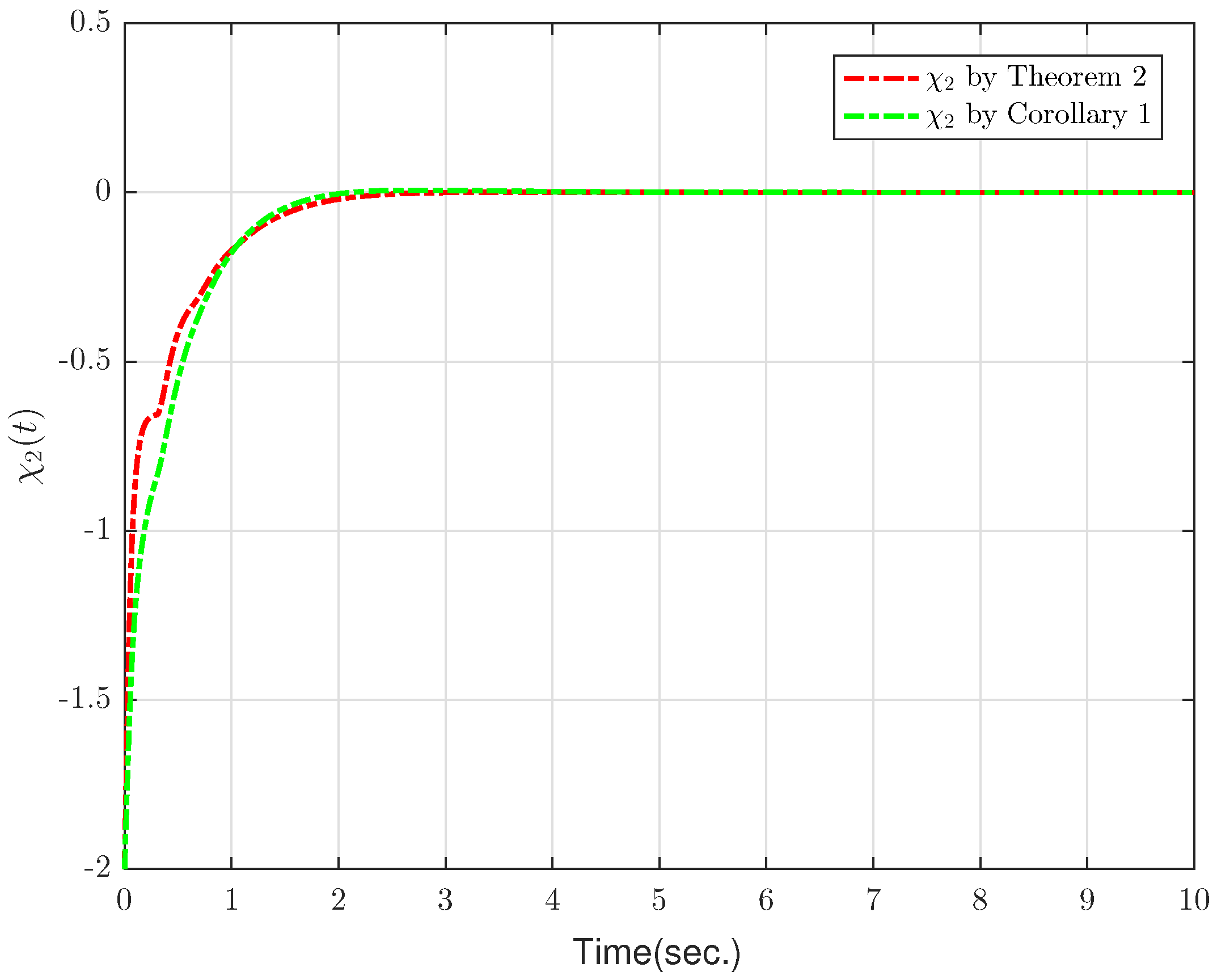
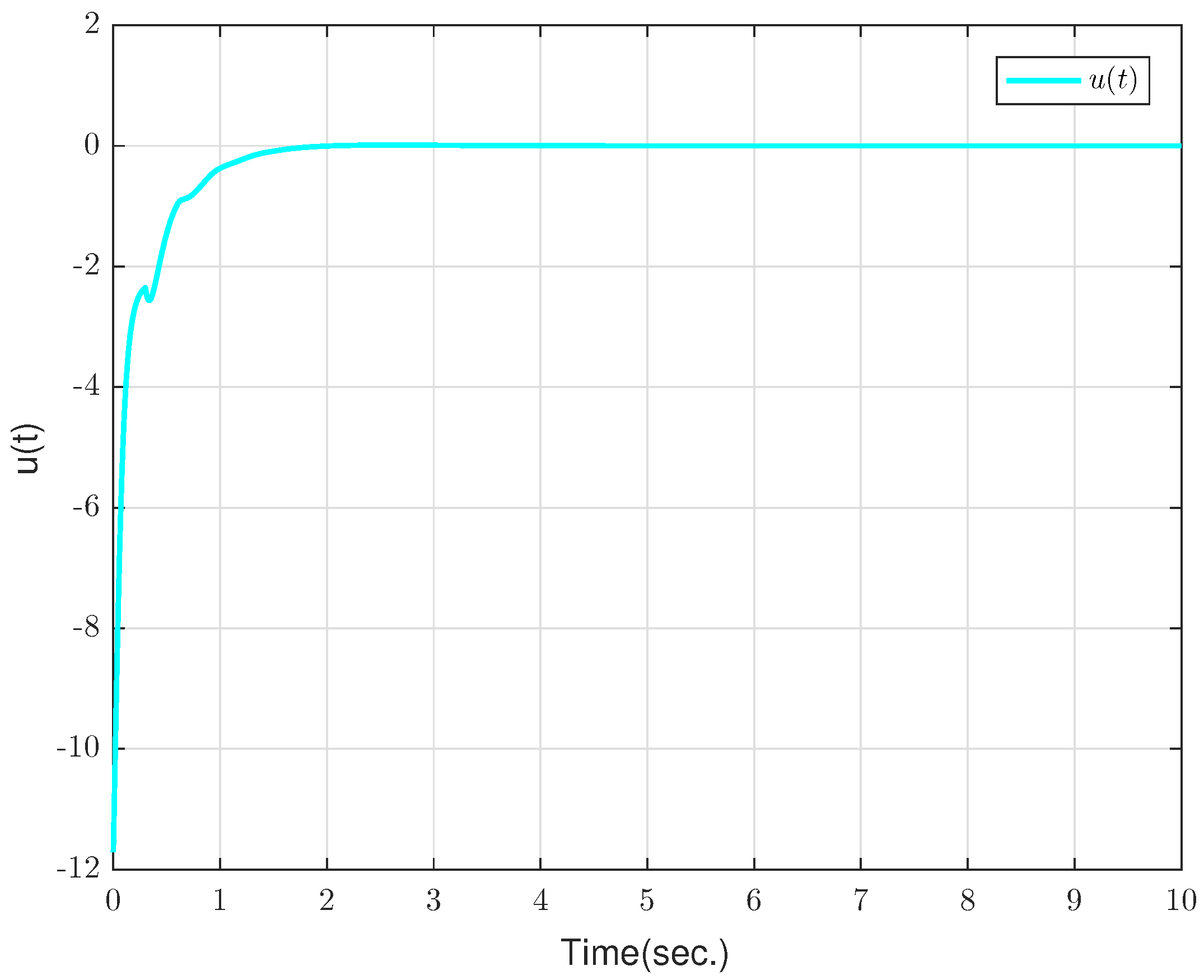
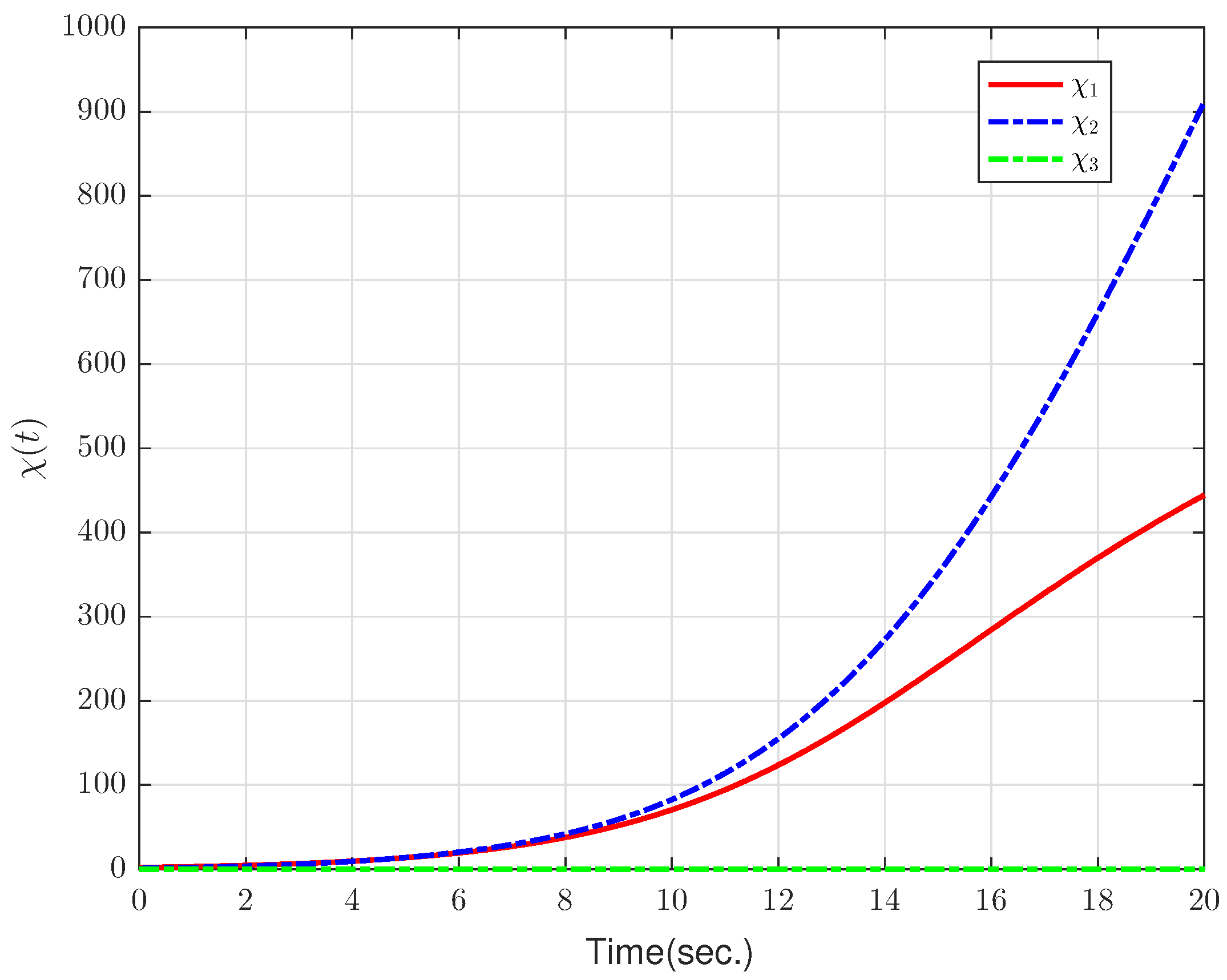
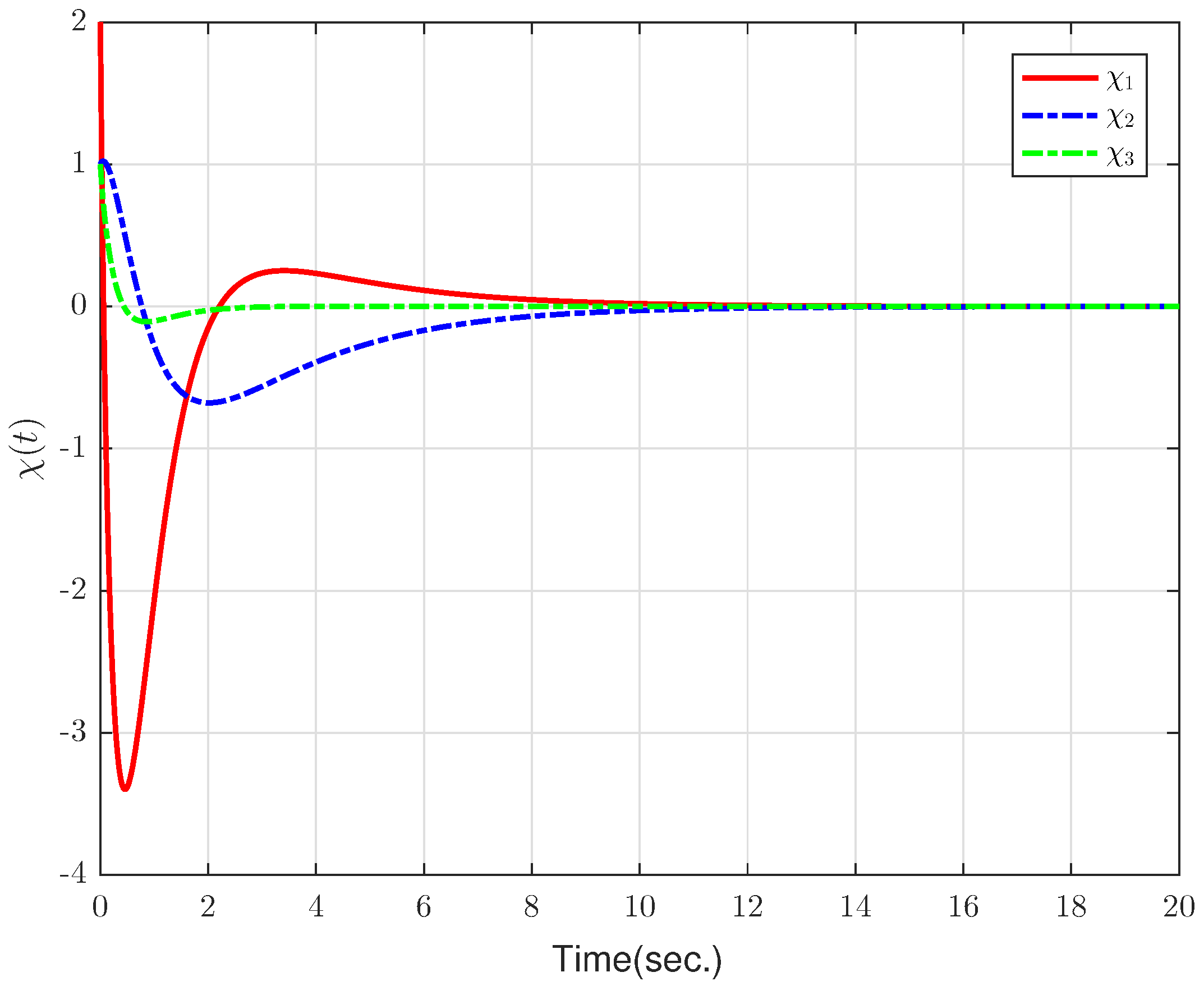
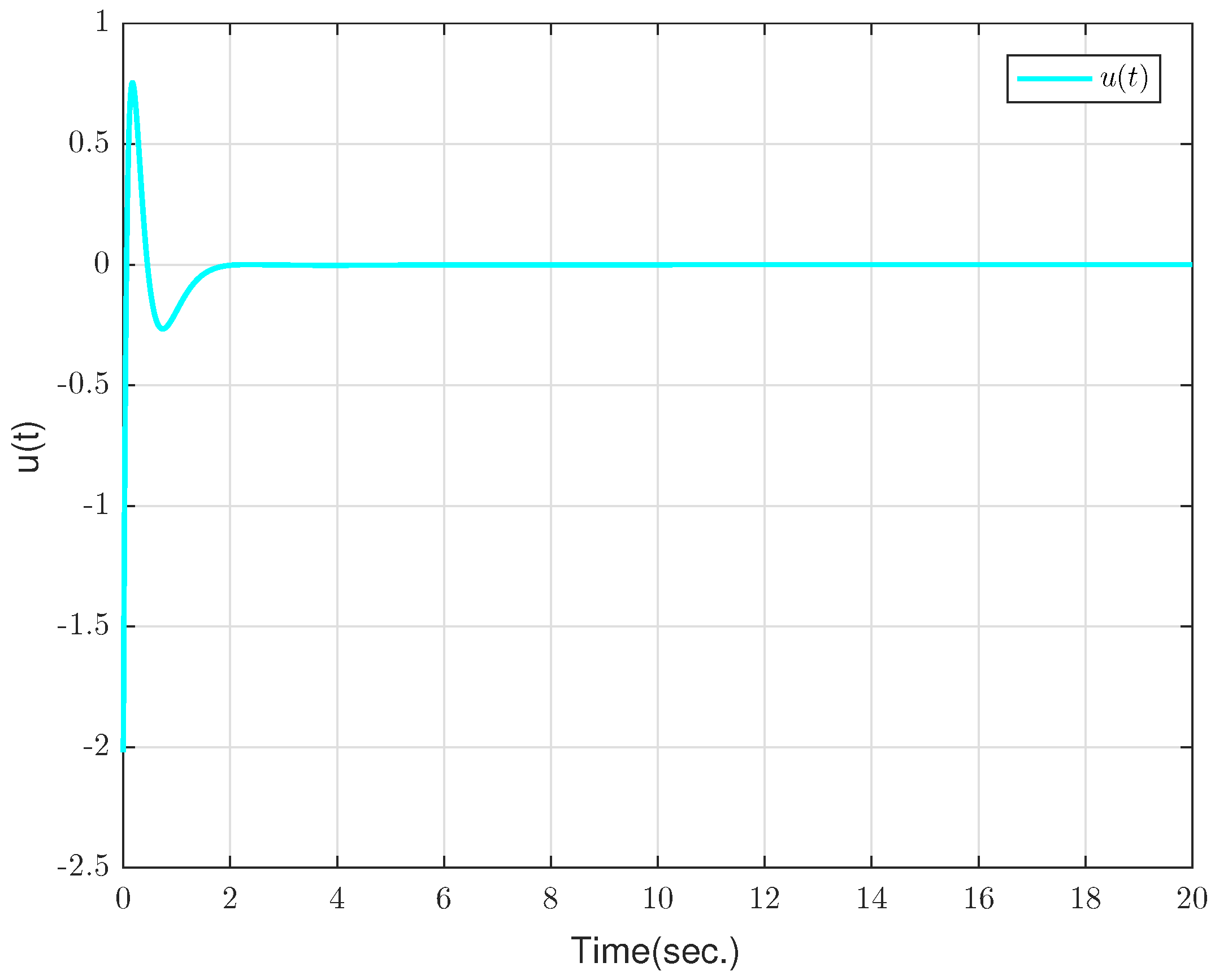
4. Numerical Examples

This section will elaborate on illustrating the effectiveness of the proposed method by presenting two persuasive examples that clearly underscore its benefits.

Example 1.

A singular fuzzy time-delay system, characterized by a set of two fuzzy rules, is given by

$$\begin{array}{cc}\hfill & A_1=\left[\begin{array}{cc}1.7& 1.3\\ -1.3& 2.3\end{array}\right], A_2=\left[\begin{array}{cc}2.6& -6.2\\ -2.3& 4.6\end{array}\right], E=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\hfill \\ \hfill & A_{d1}=\left[\begin{array}{cc}1.2& 0\\ 0& -1.1\end{array}\right], A_{d2}=\left[\begin{array}{cc}1.1& 0\\ 0& 0.8\end{array}\right], A_{D1}=\left[\begin{array}{cc}0.2& 0\\ 0& 0\end{array}\right]\hfill \\ \hfill & A_{D2}=\left[\begin{array}{cc}0.2& 0\\ 0& 0\end{array}\right], B_1=\left[\begin{array}{c}1.1\\ -0.5\end{array}\right], B_2=\left[\begin{array}{c}3.5\\ -1.3\end{array}\right].\hfill \end{array}$$

The positive definite matrices for the cost function are selected as below:

$$\begin{array}{c}\hfill Q_1=\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right], Q_2=\left[\begin{array}{cc}0.2& 0\\ 0& 0.2\end{array}\right], Q_3=0.6.\end{array}$$

In this simulation setup, we have chosen the values $h=0.3$, ${\epsilon }_1=1.1$, ${\epsilon }_2=0.2$, and ${\epsilon }_3=0.3$. By applying the findings of Theorem 2, we are able to derive the controller gain matrices along with other relevant parameter matrices, which are presented in the following results:

$$\begin{array}{cc}\hfill & K_{p1}=\left[\begin{array}{cc}7.5839& 8.5038\end{array}\right], K_{p2}=\left[\begin{array}{cc}8.8156& 10.2386\end{array}\right]\hfill \\ \hfill & K_{d1}=\left[\begin{array}{cc}-7.0030& -6.7099\end{array}\right], K_{d2}=\left[\begin{array}{cc}-8.0098& -7.9620\end{array}\right]\hfill \\ \hfill & K_{pd1}=\left[\begin{array}{cc}1.7319& 1.5185\end{array}\right], K_{pd2}=\left[\begin{array}{cc}1.8448& 2.0901\end{array}\right]\hfill \\ \hfill & \overline{P}=\left[\begin{array}{cccccc}4.9242& -1.6407& -5.5407& 0.7701& -6.1022& 0.3289\\ -1.6407& 2.8272& 1.7399& -1.4596& 0.2189& -2.6799\\ -5.5407& 1.7399& 9.5923& -1.4762& 5.6317& -3.3730\\ 0.7701& -1.4596& -1.4762& 3.8128& -6.4015& -4.7032\\ -6.1022& 0.2189& 5.6317& -4.7032& 173.0275& -12.6862\\ 0.3289& -2.6799& -3.3730& -4.7032& -12.6862& 134.9671\end{array}\right]\hfill \\ \hfill & \overline{Q}=\left[\begin{array}{cc}4.4731& -2.0235\\ -2.0235& 3.7925\end{array}\right], \overline{R}=\left[\begin{array}{cc}0.2835& 0.0200\\ 0.0200& 0.3134\end{array}\right], X=\left[\begin{array}{cc}-0.2119& 0.5839\\ -0.0401& -0.4793\end{array}\right].\hfill \end{array}$$

Using the same simulation parameters, by solving Corollary 1, the controller parameters are as follows:

$$\begin{array}{cc}\hfill & K_{p1}=\left[\begin{array}{cc}0.1415& 3.8751\end{array}\right], K_{p2}=\left[\begin{array}{cc}-0.2096& 3.5223\end{array}\right]\hfill \\ \hfill & K_{d1}=\left[\begin{array}{cc}-1.3283& -1.5699\end{array}\right], K_{d2}=\left[\begin{array}{cc}-0.5651& -0.7330\end{array}\right]\hfill \\ \hfill & K_{pd1}=\left[\begin{array}{cc}-0.9389& -0.7816\end{array}\right], K_{pd2}=\left[\begin{array}{cc}-0.3362& -0.0689\end{array}\right].\hfill \end{array}$$

The following fuzzy membership functions are considered:

$$\begin{array}{c}\hfill {\mu }_1\left(\chi \left(t\right)\right)={cos}^2\left({\chi }_1\left(t\right)\right), {\mu }_2\left(\chi \left(t\right)\right)=1-{\mu }_1\left(\chi \left(t\right)\right).\end{array}$$

The initial condition for the system is set to ${\chi }_0={\left[\begin{array}{cc}2& -2\end{array}\right]}^T$. Figure 1 reveals that the open-loop system fails to achieve stability. Figure 2 and Figure 3 show the trajectories of the state curves. From the analysis of the figures, one can observe that the controller parameters obtained using Theorem 2 enable the system to reach a stable state more quickly and without overshoot. Figure 4 displays the evolution of the control input. According to the final analysis results, the controller design presented in this paper proves to be effective.

Example 2.

We now present the following single-species bio-economic system for consideration [39]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\dot{\chi }}_1\left(t\right)=(-{\displaystyle \frac{\alpha \beta }{r_2}}-{\displaystyle \frac{\eta c}{p}}){\chi }_1\left(t\right)+\alpha {\chi }_2\left(t\right)-{\displaystyle \frac{c}{p}}{\chi }_3\left(t\right)-\eta {\chi }_1^2\left(t\right)-{\chi }_1\left(t\right){\chi }_3\left(t\right)+\tau {\chi }_1(t-h)\hfill \\ {\dot{\chi }}_2\left(t\right)=\beta {\chi }_1\left(t\right)-r_2{\chi }_2\left(t\right)\hfill \\ 0=p({\displaystyle \frac{\alpha \beta }{r_2}}-r_1-\beta -{\displaystyle \frac{\eta c}{p}}){\chi }_1\left(t\right)+p{\chi }_1\left(t\right){\chi }_3\left(t\right)+u\left(t\right)\hfill \end{array}\right.\end{array}$$

where ${\chi }_1\left(t\right)\in [-l,l], (l>0), \alpha =0.15, \beta =0.5, \eta =0.001, r_1=0.2, r_2=0.1, p=1, c=40,$ $l=10, \tau =1$.

Using the approach of fuzzy integration, fuzzy models for the nonlinear dynamics of a single-species bio-economic system can be constructed in the following manner:

$$\begin{array}{c}\hfill E\dot{\chi }\left(t\right)=A_i\chi \left(t\right)+A_{di}\chi (t-h)+A_{Di}{\int }_{t-h}^t\chi \left(s\right)ds+B_{i}u\left(t\right)\end{array}$$

where

$$\begin{array}{cc}\hfill & E=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array}\right], A_1=\left[\begin{array}{ccc}-{\displaystyle \frac{\alpha \beta }{r_2}}-{\displaystyle \frac{\eta c}{p}}+\eta l& \alpha & -{\displaystyle \frac{c}{p}}+l\\ \beta & -r_2& 0\\ p({\displaystyle \frac{\alpha \beta }{r_2}}-r_1-\beta -{\displaystyle \frac{\eta c}{p}})& 0& -pl\end{array}\right]\hfill \\ \hfill & A_2=\left[\begin{array}{ccc}-{\displaystyle \frac{\alpha \beta }{r_2}}-{\displaystyle \frac{\eta c}{p}}-\eta l& \alpha & -{\displaystyle \frac{c}{p}}-l\\ \beta & -r_2& 0\\ p({\displaystyle \frac{\alpha \beta }{r_2}}-r_1-\beta -{\displaystyle \frac{\eta c}{p}})& 0& pl\end{array}\right], B_1=B_2=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\hfill \\ \hfill & A_{d1}=A_{d2}=\left[\begin{array}{ccc}\tau & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right], A_{D1}=A_{D2}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right].\hfill \end{array}$$

The remaining matrices and parameters are provided below:

$$\begin{array}{cc}\hfill & Q_1=\left[\begin{array}{ccc}0.5& 0& 0\\ 0& 0.5& 0\\ 0& 0& 0.5\end{array}\right], Q_2=\left[\begin{array}{ccc}0.2& 0& 0\\ 0& 0.2& 0\\ 0& 0& 0.2\end{array}\right], Q_3=0.6\hfill \\ \hfill & h=0.1, {\epsilon }_1=1.1, {\epsilon }_2=0.2, {\epsilon }_3=0.3.\hfill \end{array}$$

By applying Theorem 2, the fuzzy controller gains and other related parameter matrices can be determined as follows:

$$\begin{array}{cc}\hfill & K_{p1}=\left[\begin{array}{ccc}23.4392& 14.5695& -191.4713\end{array}\right], K_{p2}=\left[\begin{array}{ccc}23.2206& 14.4436& -193.2114\end{array}\right]\hfill \\ \hfill & K_{d1}=\left[\begin{array}{ccc}-23.3268& -14.5173& 192.1653\end{array}\right], K_{d2}=\left[\begin{array}{ccc}-23.2066& -14.4227& 191.1313\end{array}\right]\hfill \\ \hfill & K_{pd1}=\left[\begin{array}{ccc}7.9993& 4.9701& -65.6735\end{array}\right], K_{pd2}=\left[\begin{array}{ccc}7.8927& 4.9079& -65.0063\end{array}\right]\hfill \\ \hfill & \overline{P}=\left[\begin{array}{cc}{\overline{P}}_{11}& {\overline{P}}_{12}\\ {\overline{P}}_{12}^T& {\overline{P}}_{22}\end{array}\right], {\overline{P}}_{11}=\left[\begin{array}{cccc}14.0838& -0.9246& 0.5142& -4.3903\\ -0.9246& 3.0800& 0.0330& 0.3768\\ 0.5142& 0.0330& 2.7480& 0.0088\\ -4.3903& 0.3768& 0.0088& 11.4824\end{array}\right]\hfill \\ \hfill & {\overline{P}}_{12}=\left[\begin{array}{ccccc}-0.4395& -0.2004& 1.2650& -1.3657& 0.3586\\ -5.1600& -0.0382& 0.0845& -2.3250& -0.0049\\ -0.0501& -4.6033& 0.1813& -0.0389& -0.5688\\ 0.0355& 0.1325& 4.6078& 0.2083& 0.0534\end{array}\right]\hfill \\ \hfill & {\overline{P}}_{22}=\left[\begin{array}{ccccc}13.5580& -0.0018& -0.1881& 6.2067& -0.0890\\ -0.0018& 13.2153& -0.0495& -0.0428& 3.5691\\ -0.1881& -0.0495& 29.4069& -0.3785& 0.2638\\ 6.2067& -0.0428& -0.3785& 25.2706& -0.0609\\ -0.0890& 3.5691& 0.2638& -0.0609& 24.6559\end{array}\right]\hfill \\ \hfill & \overline{Q}=\left[\begin{array}{ccc}13.1149& -0.8719& 0.4717\\ -0.8719& 3.9198& 0.0579\\ 0.4717& 0.0579& 4.4716\end{array}\right], \overline{R}=\left[\begin{array}{ccc}0.1044& 0.0003& -0.0009\\ 0.0003& 0.1135& -0.0001\\ -0.0009& -0.0001& 0.1127\end{array}\right]\hfill \\ \hfill & X=\left[\begin{array}{ccc}2.3081& -0.9148& -0.0781\\ -0.1397& 1.3363& 0.0169\\ 0.2699& -0.0102& 0.0001\end{array}\right].\hfill \end{array}$$

By using the same parameters to determine the controller gains through Corollary 1, it is found that Corollary 1 cannot calculate the controller gains, thereby demonstrating the significance of studying guaranteed cost control.

Consider the following fuzzy membership functions:

$$\begin{array}{c}\hfill {\mu }_1\left(\chi \left(t\right)\right)={\displaystyle \frac{1}{2}}(1-{\chi }_1\left(t\right)/l), {\mu }_2\left(\chi \left(t\right)\right)=1-{\mu }_1\left(\chi \left(t\right)\right).\end{array}$$

In the experiment, the initial state is defined as ${\chi }_0={\left[\begin{array}{ccc}2& 1& 1\end{array}\right]}^T$. Figure 5 illustrates the unstable behavior of the open-loop system. Meanwhile, Figure 6 emphasizes the stability attained by the feedback-controlled system with the implemented controller. Figure 7 presents the state trajectories for the control input. The final analysis results indicate that the controller design discussed in this paper is effective.

5. Conclusions

This paper explores the problem of guaranteed cost control for singular T-S fuzzy systems with time delay. To analyze the stabilization of the system, an augmented LKF is utilized, leading to the establishment of sufficient conditions grounded in Lyapunov stability theory. A systematic approach for determining the controller parameters is achieved through the method of free weight matrices. Furthermore, two convincing examples are included to illustrate the efficacy of the given methods. Future work may focus on incorporating system uncertainties and time-varying delays.